Research on Energy Efficiency Optimization of Visible Light Communication Based on Non-Orthogonal Multiple Access
Abstract
:1. Introduction
- We formulate such a joint problem as a complex nonlinear EE optimization problem, which considers the non-negative constraint of an LED signal, per-LED optical power constraint, and minimum data rate constraint. The optimization problem can be solved in two steps, i.e., power allocation with known LED association and joint LA–PA;
- With the analysis of channel capacity, the EE optimization problem is converted into convex form, and then an iterative algorithm is designed to obtain the optimal power allocation with known LED association under the non-negative constraint, per-LED optical power constraint, and data rate requirement;
- Taking into account the non-negative constraint of a signal, per-LED optical power constraint, the power constraint required for SIC, and channel gain between the transceiver signals, the feasibility condition of the LED association is derived. The feasible LEDs that can achieve the maximum EE jointly with the former power allocation algorithm can be associated;
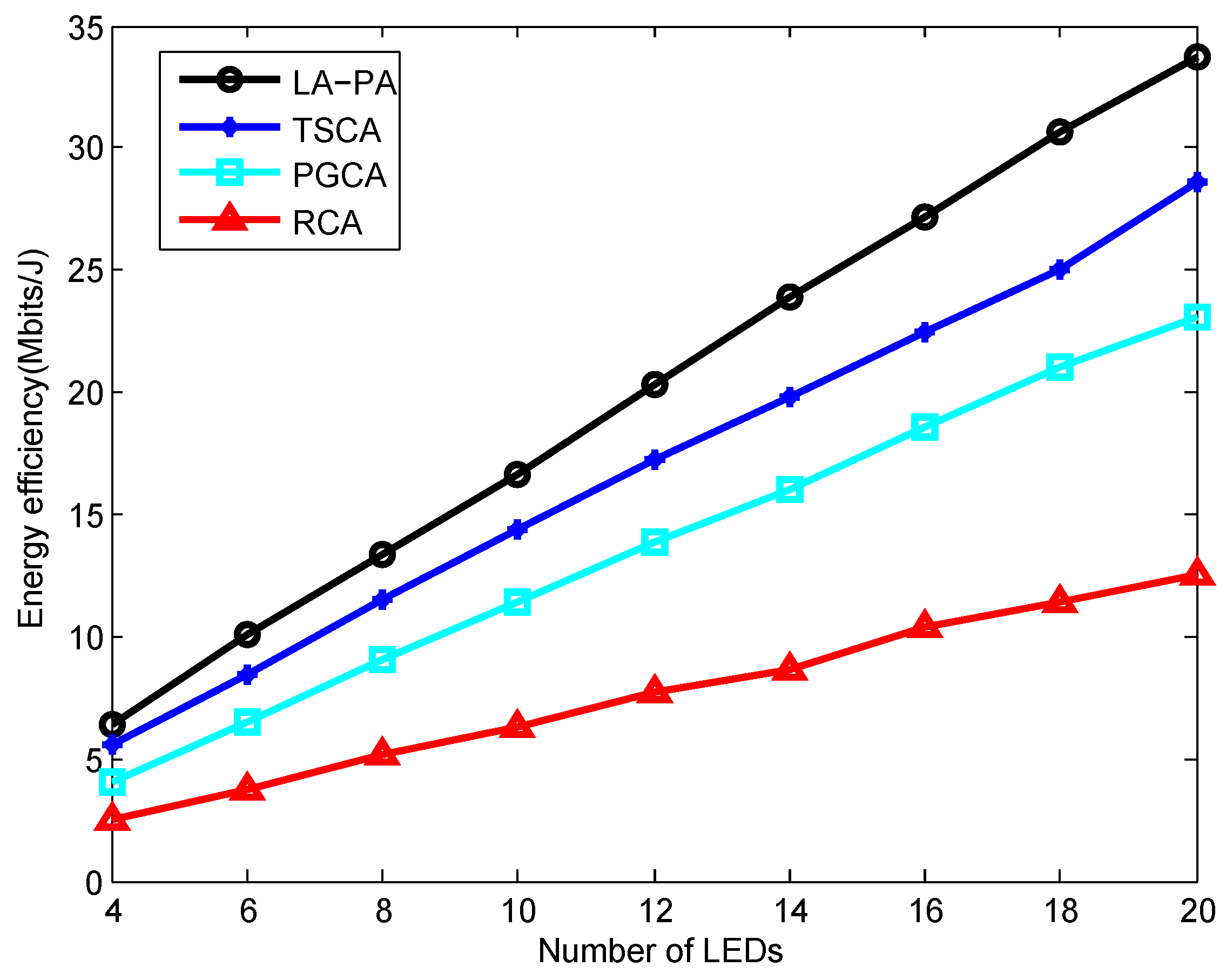
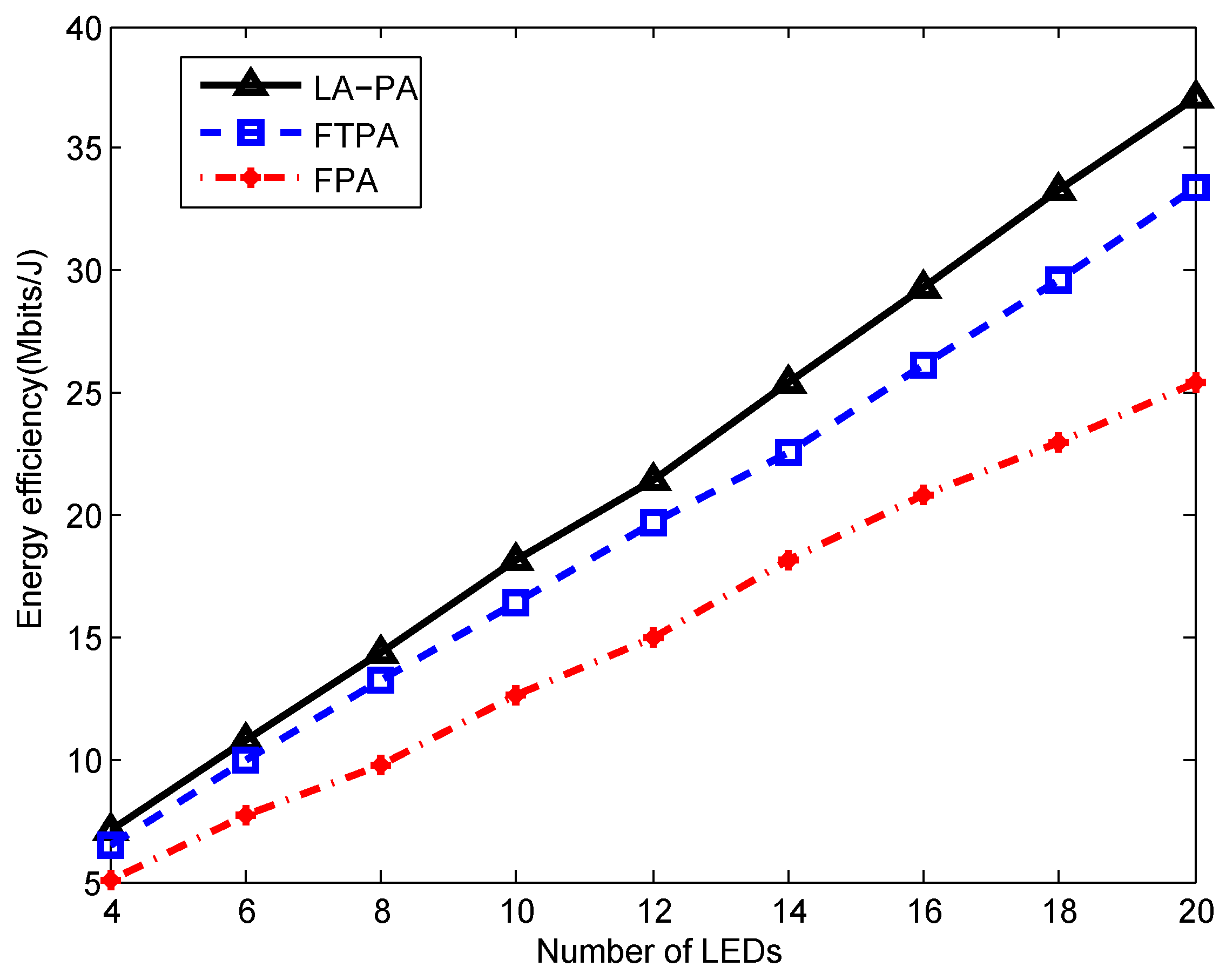
- Simulation results and performance comparisons illustrate the improved performance of the proposed scheme. Compared to the existing random clustering algorithm (RCA), traversal search clustering algorithm (TSCA), and pre-grouping clustering algorithm (PGCA) [26], the proposed LED association scheme achieves a significantly high EE gain. Compared to the existing fixed power allocation (FPA) [27] and fractional transmit power allocation (FTPA) [28], the simulation results show that the design of an efficient power allocation algorithm effectively improves the EE of NOMA-based VLC systems.
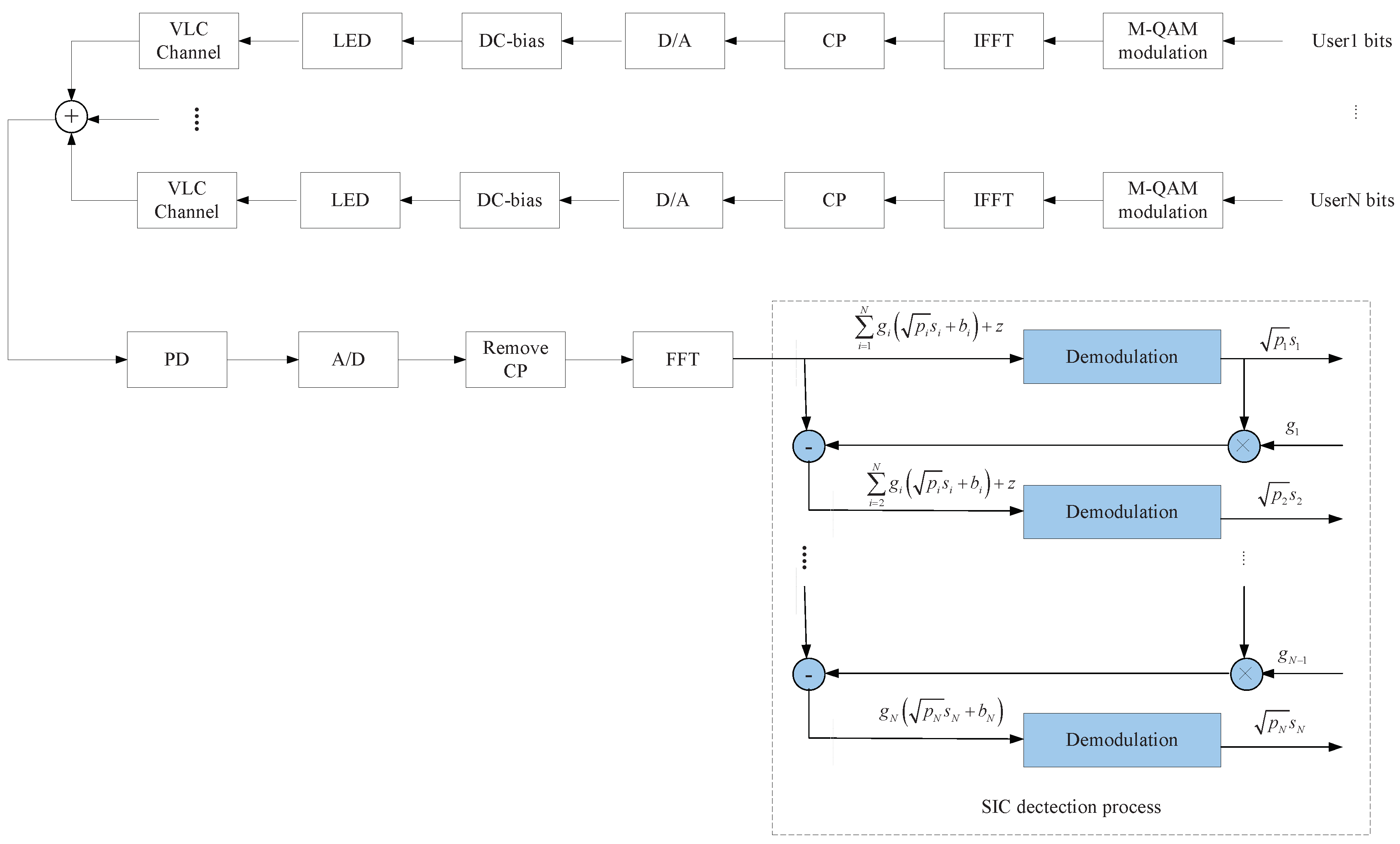
2. System Model
2.1. Channel Model
2.2. Signal Model
2.3. Channel Capacity Analysis
3. EE Optimization Problem Description and Solution
3.1. Problem Description
3.2. Problem Transformation
3.3. Problem Solution
| Algorithm 1 Proposed EE maximization power allocation algorithm |
|
1: Initialize , the iteration number . 2: while do 3: Define convex approximation of as 4: . 5: Solve the convex problem 6: 7: 8: end while |
4. Joint LED Association and Power Allocation
- (a)
- The order of SIC in NOMA is usually based on the descending order of the channel gain, , where M is the number of LEDs in the system.
- (b)
- The light-emitting device can be associated together if the transmitted power belong to the condition of , which satisfies the maximum transmission power constraints, the power constraint required for SIC, and the power constraint of the DC bias condition. From , we can obtain
| Algorithm 2 Proposed joint LED association and power allocation algorithm |
| 1: Initialize , , , , M, , . 2: while do 3: . . . . . 4: 5: while do 6: for to J do 7: if then 8: , . . . 9: ; 10: else 11: . 12: end if 13: end for 14: end while 15: 16: Calculate the EE using Algorithm 1. 17: while do 18: . . . . Go to . 19: if EE increases then 20: Reserve the set of and . 21: end if 22: . 23: end while 24: end while |
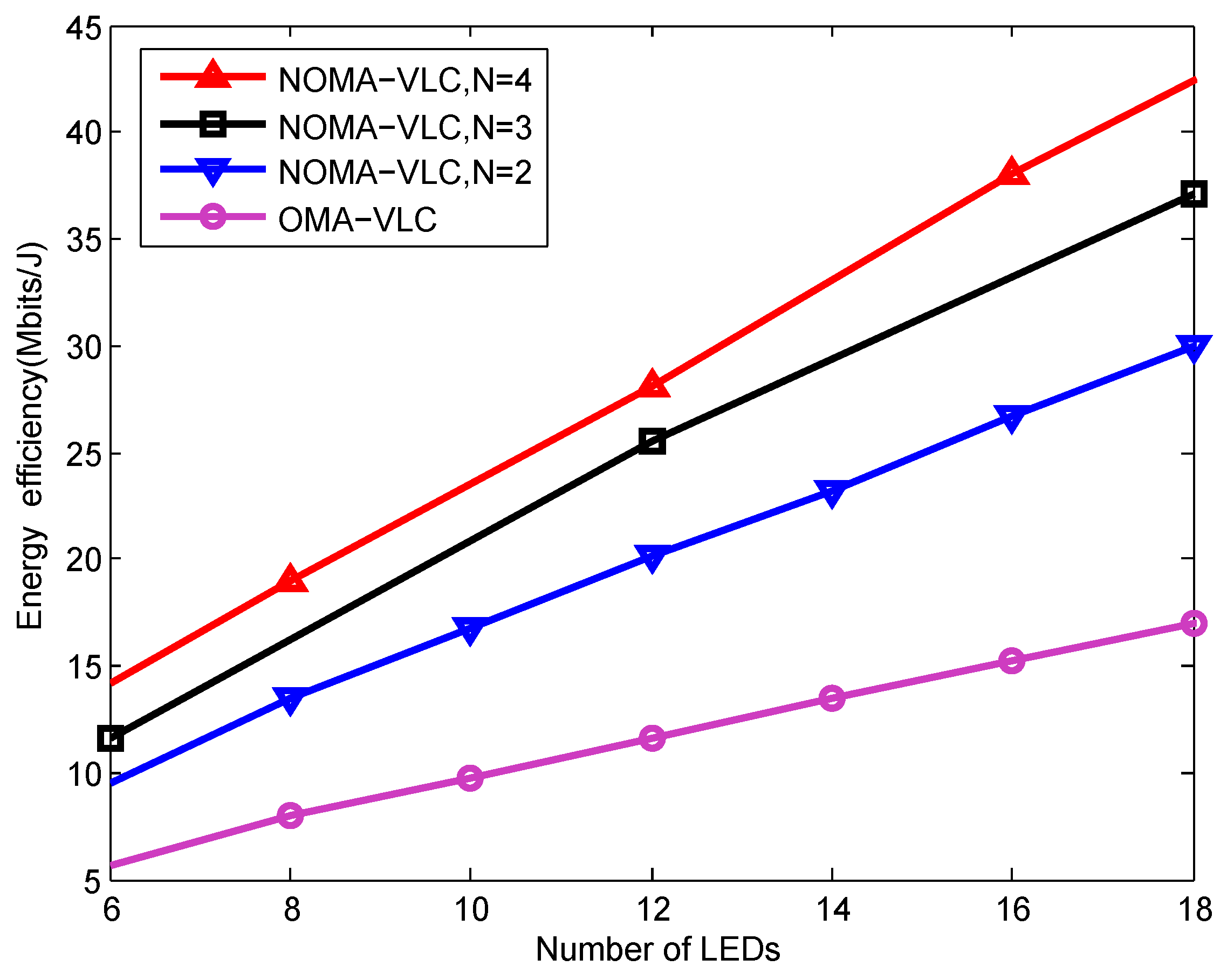
5. Results
6. Challenges and Future Directions for NOMA-Based VLC Networks
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Zhou, Y.; Liu, L.; Wang, L.; Hui, N.; Cui, X.; Wu, J.; Peng, Y.; Qi, Y.; Xing, C. Service-aware 6G: An intelligent and open network based on the convergence of communication, computing, and caching. Digit. Commun. Netw. 2020, 6, 253–260. [Google Scholar] [CrossRef]
- Matheus, L.E.M.; Vieira, A.B.; Vieira, L.F.M.; Vieira, M.A.M.; Gnawali, O. Visible Light Communication: Concepts, Applications and Challenges. IEEE Commun. Surv. Tutor. 2019, 21, 3204–3237. [Google Scholar] [CrossRef]
- Hassan, R.; Flayyih, M.S.; Mahdi, A.; Inn, A.; Sadeq, A.S.; Murad, D.F. Visibile Light Communication Technology For Data Transmission Using Li-Fi. In Proceedings of the 2020 2nd International Conference on Computer and Information Sciences (ICCIS), Sakaka, Saudi Arabia, 13–15 October 2020. [Google Scholar]
- Meucci, M.; Seminara, M.; Nawaz, T.; Caputo, S.; Mucchi, L.; Catani, J. Bidirectional Vehicle-to-Vehicle Communication System Based on VLC: Outdoor Tests and Performance Analysis. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11465–11475. [Google Scholar] [CrossRef]
- Ata, Y.; Abumarshoud, H.; Bariah, L.; Muhaidat, S.; Imran, M.A. Intelligent Reflecting Surfaces for Underwater Visible Light Communications. IEEE Photonics J. 2023, 15, 7300609. [Google Scholar] [CrossRef]
- Kolade, O.; Cheng, L. Memory Channel Models of a Hybrid PLC-VLC Link for a Smart Underground Mine. IEEE Internet Things J. 2022, 9, 11893–11903. [Google Scholar] [CrossRef]
- Xu, B.; Hussain, B.; Liu, X.; Min, T.; Cheng, H.C.; Yue, C.P. Smart-Home Control System Using VLC-Enabled High-Power LED Lightbulb. In Proceedings of the 2021 IEEE 10th Global Conference on Consumer Electronics (GCCE), Kyoto, Japan, 12–15 October 2021. [Google Scholar]
- Sivasakthi, T.; Palani, U.; Vasanthi, D.; Subhashree, S.; Roshini, S.; Saundariya, K. Underwater Communication Through Li-Fi for Data Transmission. In Proceedings of the 2021 International Conference on System, Computation, Automation and Networking (ICSCAN), Puducherry, India, 30–31 July 2021. [Google Scholar]
- Costanzo, A.; Loscri, V.; Biagi, M. Adaptive Modulation Control for Visible Light Communication Systems. J. Light. Technol. 2021, 39, 2780–2789. [Google Scholar] [CrossRef]
- Kisacik, R.; Yagan, M.Y.; Uysal, M.; Pusane, A.E.; Yalcinkaya, A.D. A New LED Response Model and its Application to Pre-Equalization in VLC Systems. IEEE Photonics Technol. Lett. 2021, 33, 955–958. [Google Scholar] [CrossRef]
- Wang, C.; Yang, Y.; Yang, Z.; Feng, C.; Cheng, J.; Guo, C. Joint SIC-Based Precoding and Sub-Connected Architecture Design for MIMO VLC Systems. IEEE Trans. Commun. 2023, 71, 1044–1058. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Sadiq, M.; Li, Y.; Shvetsov, A.V.; Shvetsova, S.V.; Shafiq, M. NOMA-Based VLC Systems: A Comprehensive Review. Sensors 2023, 23, 2960. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Ding, Z.; Wang, Z.; Chen, S.; Hanzo, L. A Survey of Non-Orthogonal Multiple Access for 5G. IEEE Commun. Surv. Tutor. 2018, 20, 2294–2323. [Google Scholar] [CrossRef]
- Yang, F.; Ji, X.; Liu, X.; Peng, M. Power Allocation Optimization for NOMA based Visible Light Communications. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021. [Google Scholar]
- Yin, L.; Popoola, W.O.; Wu, X.; Haas, H. Performance Evaluation of Non-orthogonal Multiple Access in Visible Light Communication. IEEE Trans. Commun. 2016, 64, 5162–5175. [Google Scholar] [CrossRef]
- Li, G.; Wang, P.; Yang, T.; Che, H. Secrecy Sum-Rate Enhancement for NOMA-VLC System With Pseudo User. IEEE Commun. Lett. 2023, 27, 243–247. [Google Scholar] [CrossRef]
- Chen, C.; Zhong, W.-D.; Yang, H.; Du, P. On the performance of MIMO-NOMA-based visible light communication systems. IEEE Photonics Technol. Lett. 2017, 30, 307–310. [Google Scholar] [CrossRef]
- Raj, R.; Jindal, K.; Dixit, A. Fairness Enhancement of Non-Orthogonal Multiple Access in VLC-Based IoT Networks for Intravehicular Applications. IEEE Trans. Veh. Technol. 2022, 71, 7414–7427. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, F.; Sun, S.; Song, J.; Han, Z. Sum Rate Maximization for NOMA-Based VLC With Optical Intelligent Reflecting Surface. IEEE Wirel. Commun. Lett. 2023, 12, 848–852. [Google Scholar] [CrossRef]
- Palitharathna, K.W.S.; Suraweera, H.A.; Godaliyadda, R.I.; Herath, R.I.; Ding, Z. Neural-Network-Based Blockage Prediction and Optimization in Lightwave Power-Transfer-Enabled Hybrid VLC/RF Systems. IEEE Internet Things J. 2024, 11, 5237–5248. [Google Scholar] [CrossRef]
- Obeed, M.; Dahrouj, H.; Salhab, A.M.; Chaaban, A.; Zummo, S.A.; Alouini, M.-S. Power Allocation and Link Selection for Multicell Cooperative NOMA Hybrid VLC/RF Systems. IEEE Commun. Lett. 2021, 25, 560–564. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, F.; Song, J.; Han, J. Multiple Access for Downlink Multi-User VLC System: NOMA or OMA User Pairing? IEEE Wirel. Commun. Lett. 2023, 12, 1916–1920. [Google Scholar] [CrossRef]
- Raj, R.; Dixit, A. An Energy-Efficient Power Allocation Scheme for NOMA-Based IoT Sensor Networks in 6G. IEEE Sens. J. 2022, 22, 7371–7384. [Google Scholar] [CrossRef]
- Rallis, K.G.; Papanikolaou, V.K.; Diamantoulakis, P.D.; Tegos, S.A.; Dowhuszko, A.A.; Khalighi, M.-A.; Karagiannidis, G.K. Energy Efficient Cooperative Communications in Aggregated VLC/RF Networks With NOMA. IEEE Trans. Commun. 2023, 71, 5408–5419. [Google Scholar] [CrossRef]
- Fang, F.; Zhang, L.; Wu, Z.; Jiang, J. Energy Consumption Minimization for Multi-carrier NOMA Visible Light Communication Downlinks. In Proceedings of the 2021 IEEE/CIC International Conference on Communications in China (ICCC), Xiamen, China, 28–30 July 2021. [Google Scholar]
- Mahady, I.A.; Bedeer, E.; Ikki, S.; Yanikomeroglu, H. Sum-Rate Maximization of NOMA Systems under Imperfect Successive Interference Cancellation. IEEE Commun. Lett. 2019, 23, 474–477. [Google Scholar] [CrossRef]
- Lin, B.; Ye, W.; Tang, X.; Ghassemlooy, Z. Experimental demonstration of bidirectional NOMA-OFDMA visible light communications. Opt. Exp. 2017, 25, 4348–4355. [Google Scholar] [CrossRef] [PubMed]
- Marshoud, H.; Kapinas, V.M.; Karagiannidis, G.K.; Muhaidat, S. Non-orthogonal multiple access for visible light communications. IEEE Photonics Technol. Lett. 2016, 28, 51–54. [Google Scholar] [CrossRef]
- Feng, L.; Yang, H.; Hu, R.Q.; Wang, J. MmWave and VLC-based indoor channel models in 5G wireless networks. IEEE Wirel. Commun. 2018, 25, 70–77. [Google Scholar] [CrossRef]
- Marshoud, H.; Sofotasios, P.C.; Muhaidat, S.; Karagiannidis, G.K.; Sharif, B.S. On the performance of visible light communication systems with non-orthogonal multiple access. IEEE Trans. Wirel. Commun. 2017, 16, 6350–6364. [Google Scholar] [CrossRef]
- Zeng, L.; OBrien, D.C.; Minh, H.L.; Faulkner, G.E.; Lee, K.; Jung, D.; Oh, Y.; Won, E.T. High data rate multiple input multiple output (MIMO) optical wireless communications using white LED lighting. IEEE J. Sel. Areas Commun. 2009, 27, 1654–1662. [Google Scholar] [CrossRef]
- Ma, S.; He, Y.; Li, H.; Lu, S.; Zhang, F.; Li, S. Optimal Power Allocation for Mobile Users in Non-Orthogonal Multiple Access Visible Light Communication Networks. IEEE Trans. Commun. 2019, 67, 2233–2244. [Google Scholar] [CrossRef]
- Kha, H.H.; Tuan, H.D.; Nguyen, H.H. Fast Global Optimal Power Allocation in Wireless Networks by Local D.C. Programming. IEEE Trans. Wirel. Commun. 2012, 11, 510–515. [Google Scholar] [CrossRef]
- Tao, S.; Yu, H.; Li, Q.; Tang, Y. Strategy-Based Gain Ratio Power Allocation in Non-Orthogonal Multiple Access for Indoor Visible Light Communication Networks. IEEE Access 2019, 7, 15250–15261. [Google Scholar] [CrossRef]
- Kha, H.H.; Tuan, H.D.; Nguyen, H.H. Demonstration of Performance Improvement in Multi-User NOMA VLC System Using Joint Transceiver Optimization. Photonics 2022, 9, 168. [Google Scholar] [CrossRef]



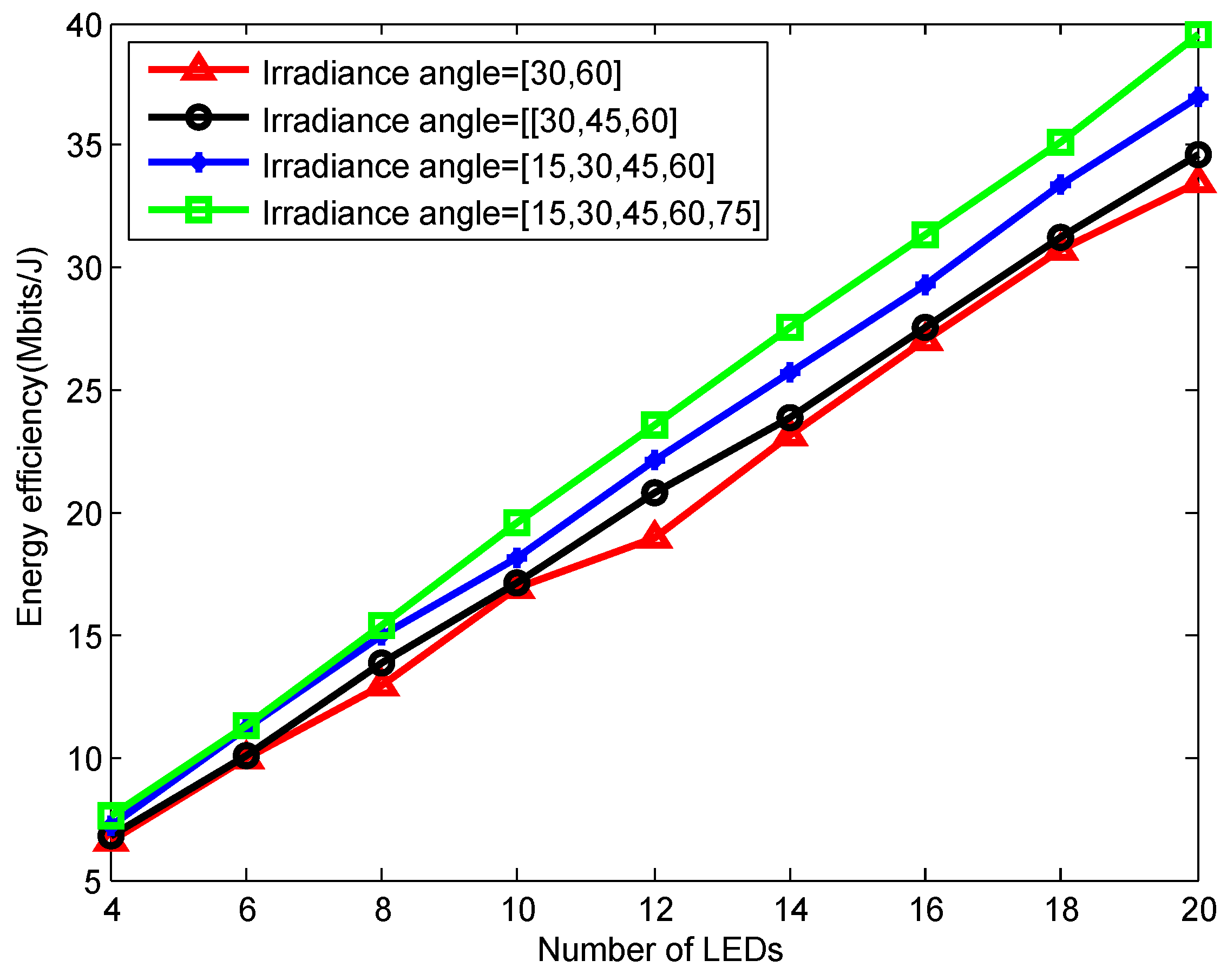

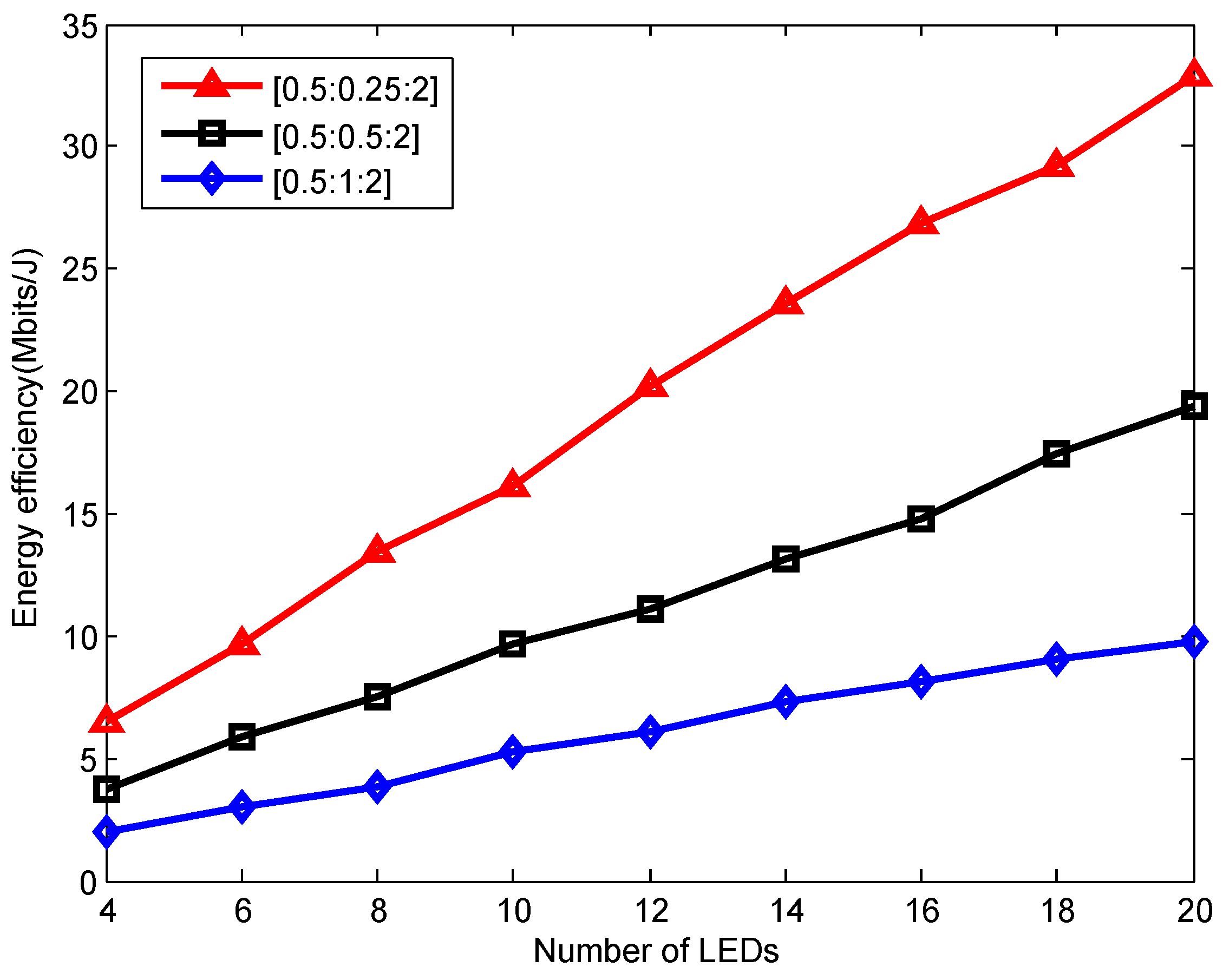
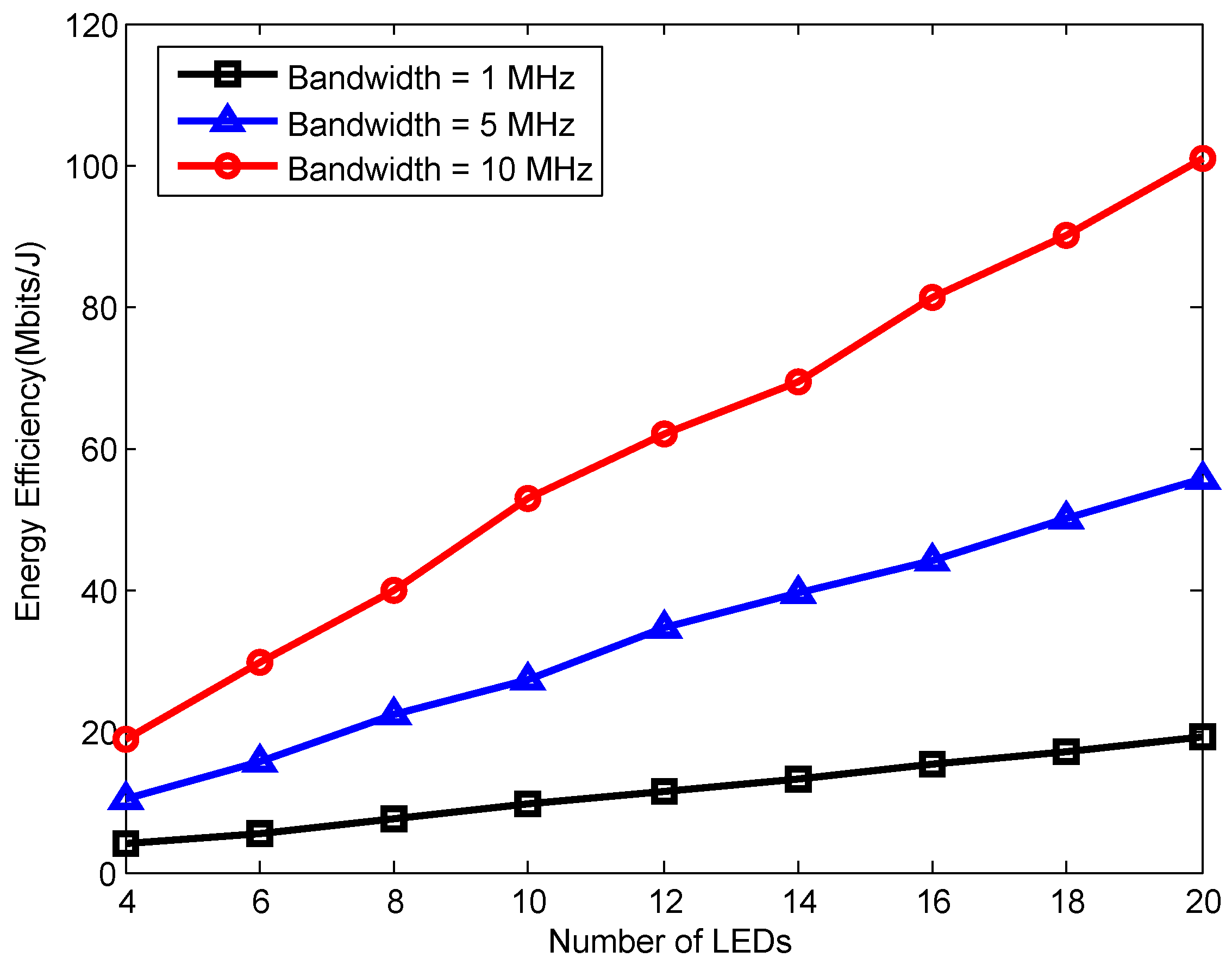
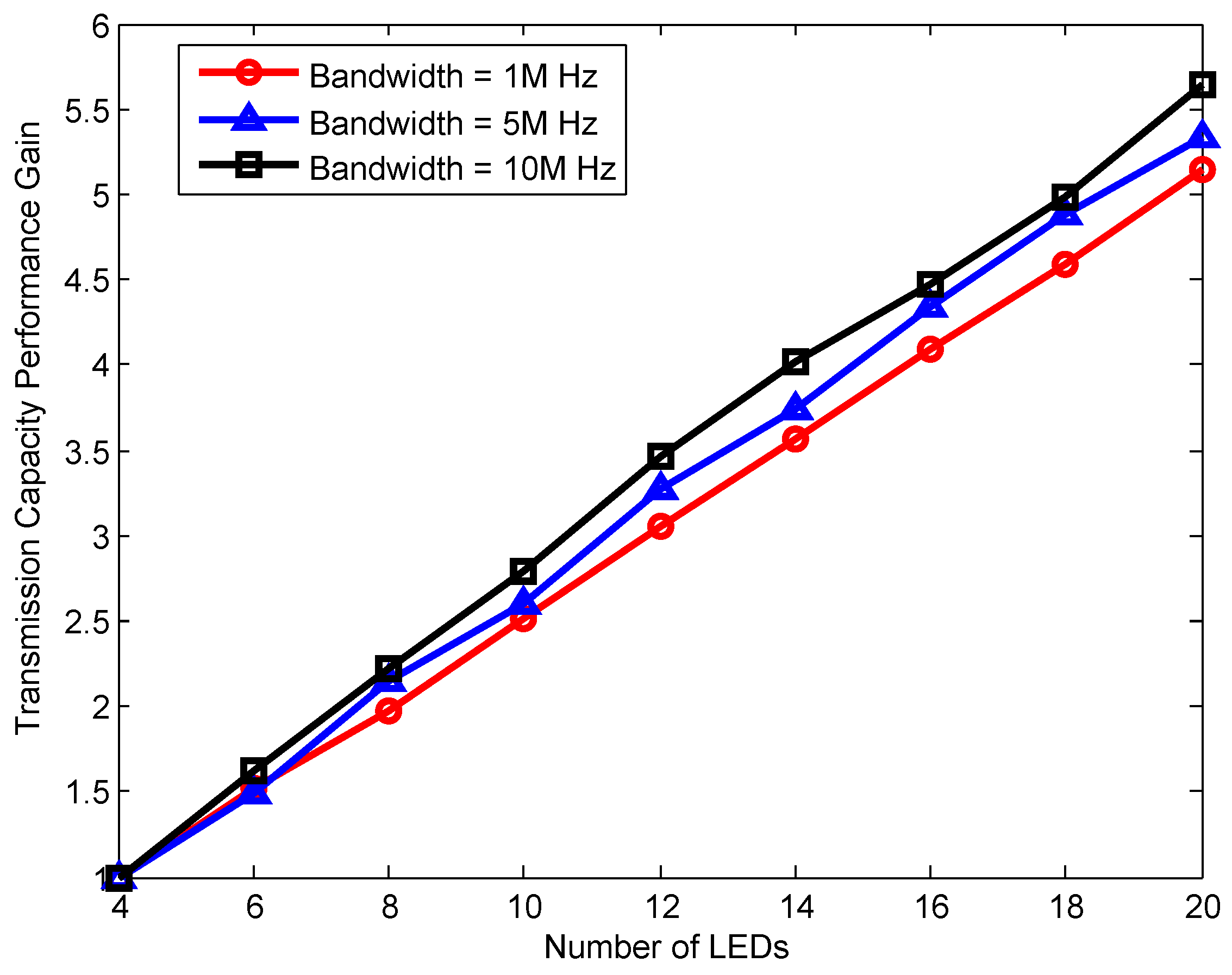
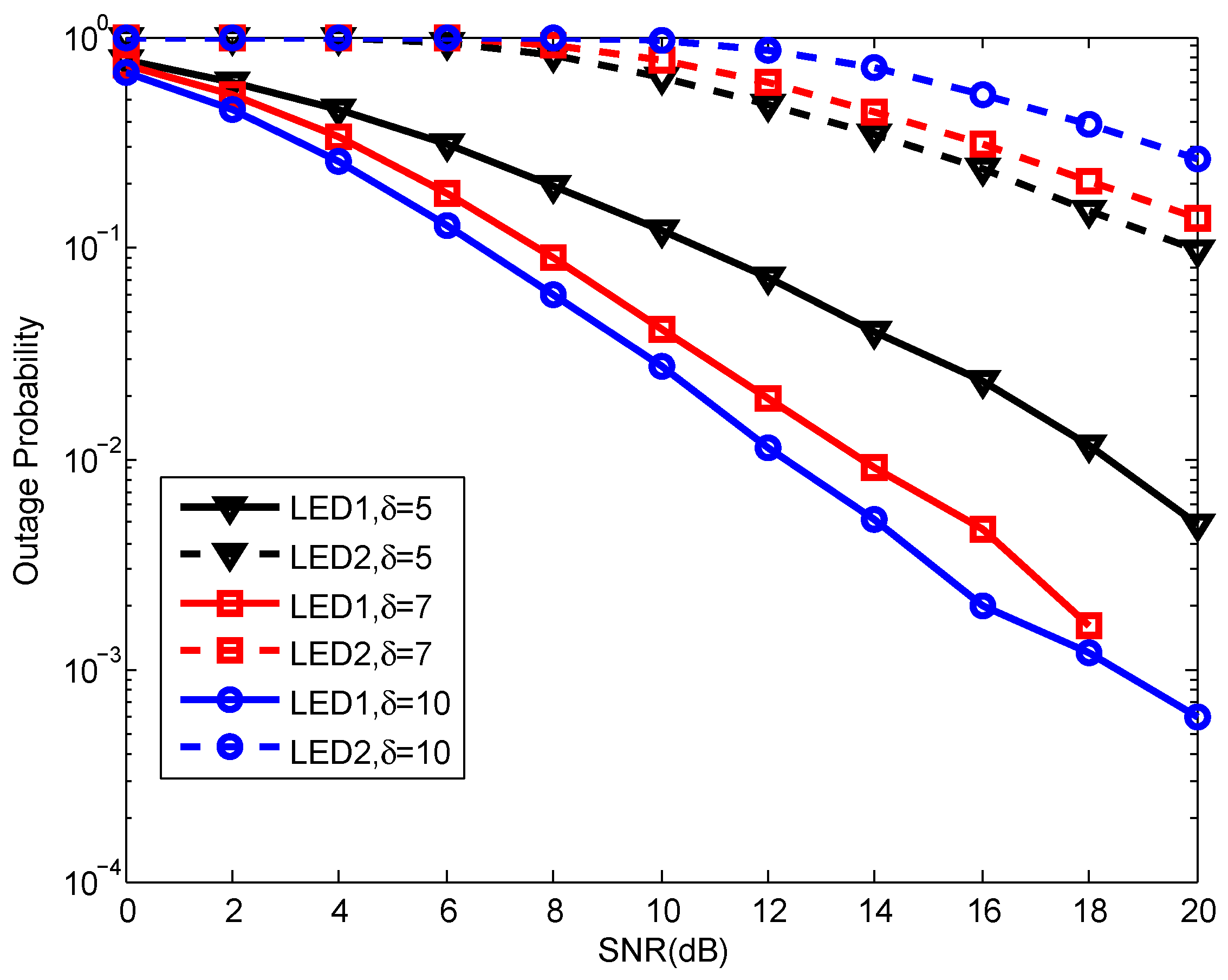
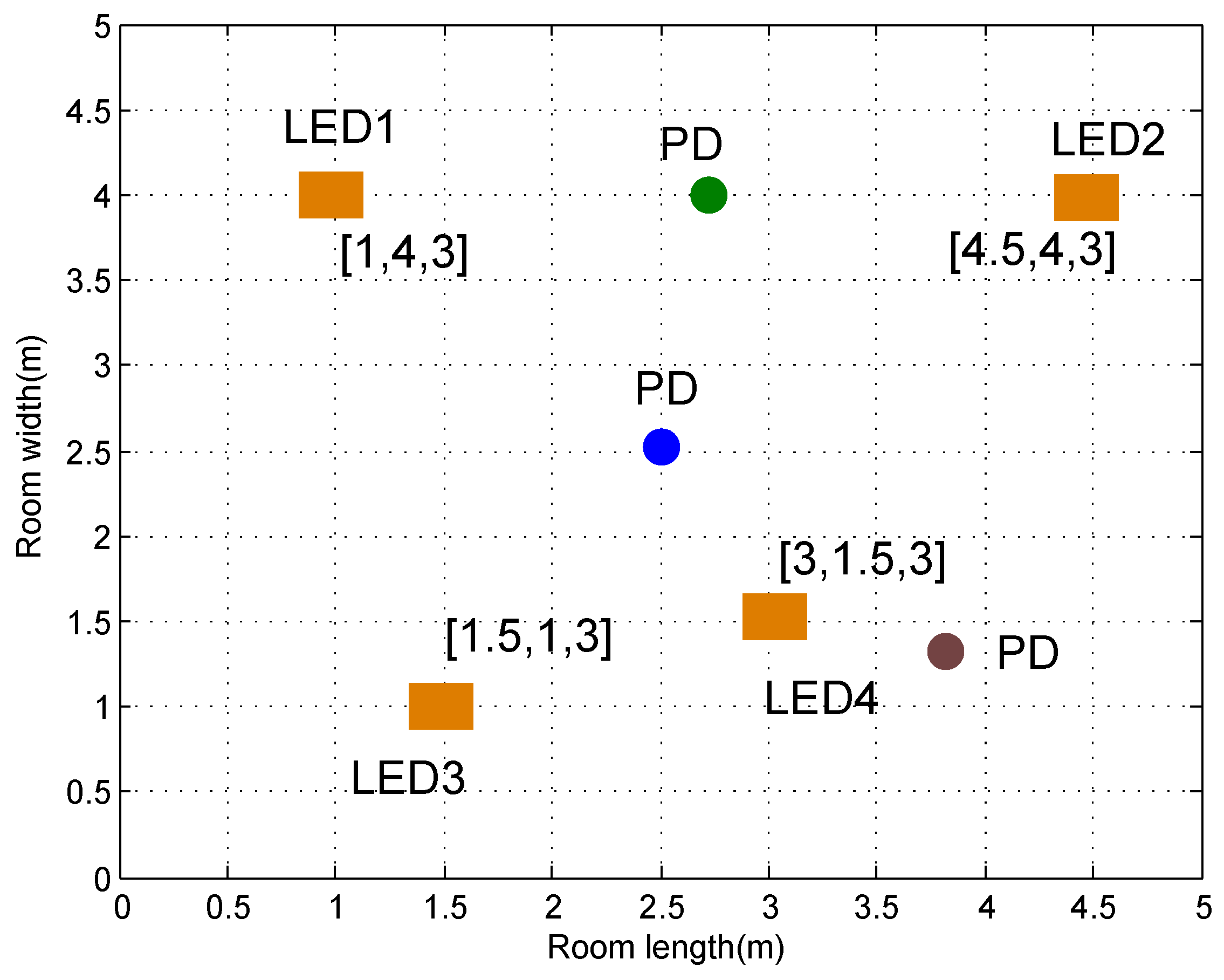

| Symbol | Parameter | Value |
|---|---|---|
| /(°) | Emission semi-angle of LED | 30 |
| /W | Transmitted power of LED | 8 |
| /(°) | Irradiance angle of LED | [30,60] |
| /Mbps | Data rate requirement | |
| /(°) | Receiver FOV | 30 |
| /m | Linear distance interval of the LEDs and PD | [0.5:0.25:2] |
| / | Effective receiving area of PD | 1 |
| n | Reflective index | 1.5 |
| Gain of optical filter | 1.0 | |
| N | Power multiplexing factor | 2 |
| /dBm | Detection threshold at SIC receiver | 10 |
| Aspects | TSCA | RCA | PGCA [25] |
|---|---|---|---|
| Principle | Exhaustive search | Random selection | Based on the channel gain difference |
| Advantage | Good performance | Implement simply | Compromise between performance and simplicity |
| Disadvantage | High complexity | Poor effect without considering the channel condition | Harder to choose an appropriate channel threshold interval |
| Aspects | FPA [26] | FTPA [27] | FSPA |
|---|---|---|---|
| Principle | Set a fixed power distribution factor | Dynamic power allocation based on channel gain | Exhaustive search |
| Advantage | Implement simply | Compromise between performance and simplicity | Good performance |
| Disadvantage | Unguaranteed system performance | Harder to set the power allocation factor | High complexity, not applicable to actual scenarios |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Sun, L.; Liu, X.; Lin, X. Research on Energy Efficiency Optimization of Visible Light Communication Based on Non-Orthogonal Multiple Access. Electronics 2024, 13, 1562. https://doi.org/10.3390/electronics13081562
Wu Y, Sun L, Liu X, Lin X. Research on Energy Efficiency Optimization of Visible Light Communication Based on Non-Orthogonal Multiple Access. Electronics. 2024; 13(8):1562. https://doi.org/10.3390/electronics13081562
Chicago/Turabian StyleWu, Yali, Lei Sun, Xiaoshuang Liu, and Xiaoran Lin. 2024. "Research on Energy Efficiency Optimization of Visible Light Communication Based on Non-Orthogonal Multiple Access" Electronics 13, no. 8: 1562. https://doi.org/10.3390/electronics13081562
APA StyleWu, Y., Sun, L., Liu, X., & Lin, X. (2024). Research on Energy Efficiency Optimization of Visible Light Communication Based on Non-Orthogonal Multiple Access. Electronics, 13(8), 1562. https://doi.org/10.3390/electronics13081562






