Beampattern Synthesis and Optimization Method Based on Circular Frequency Diverse Array Engineering Model
Abstract
:1. Introduction
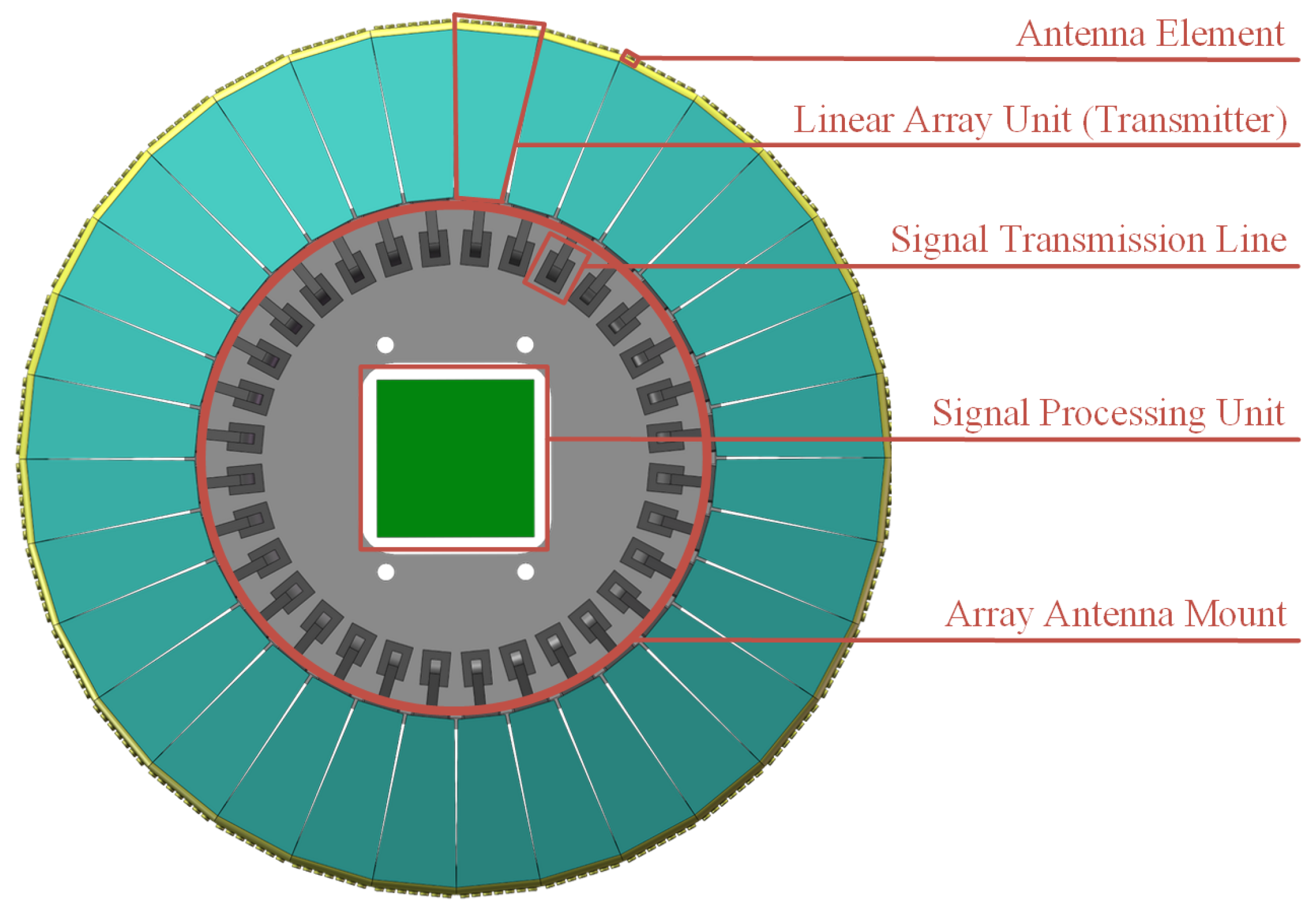
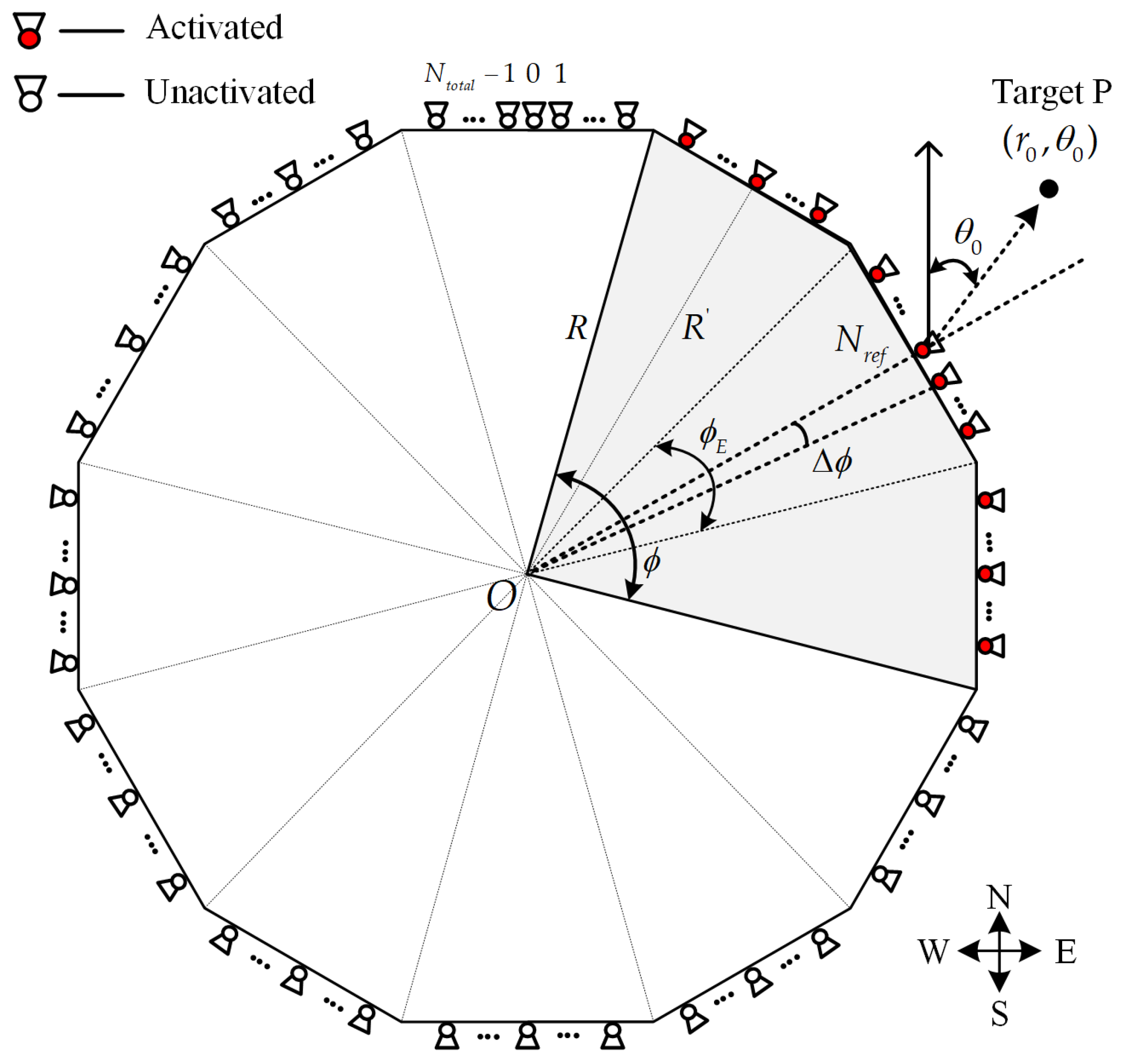
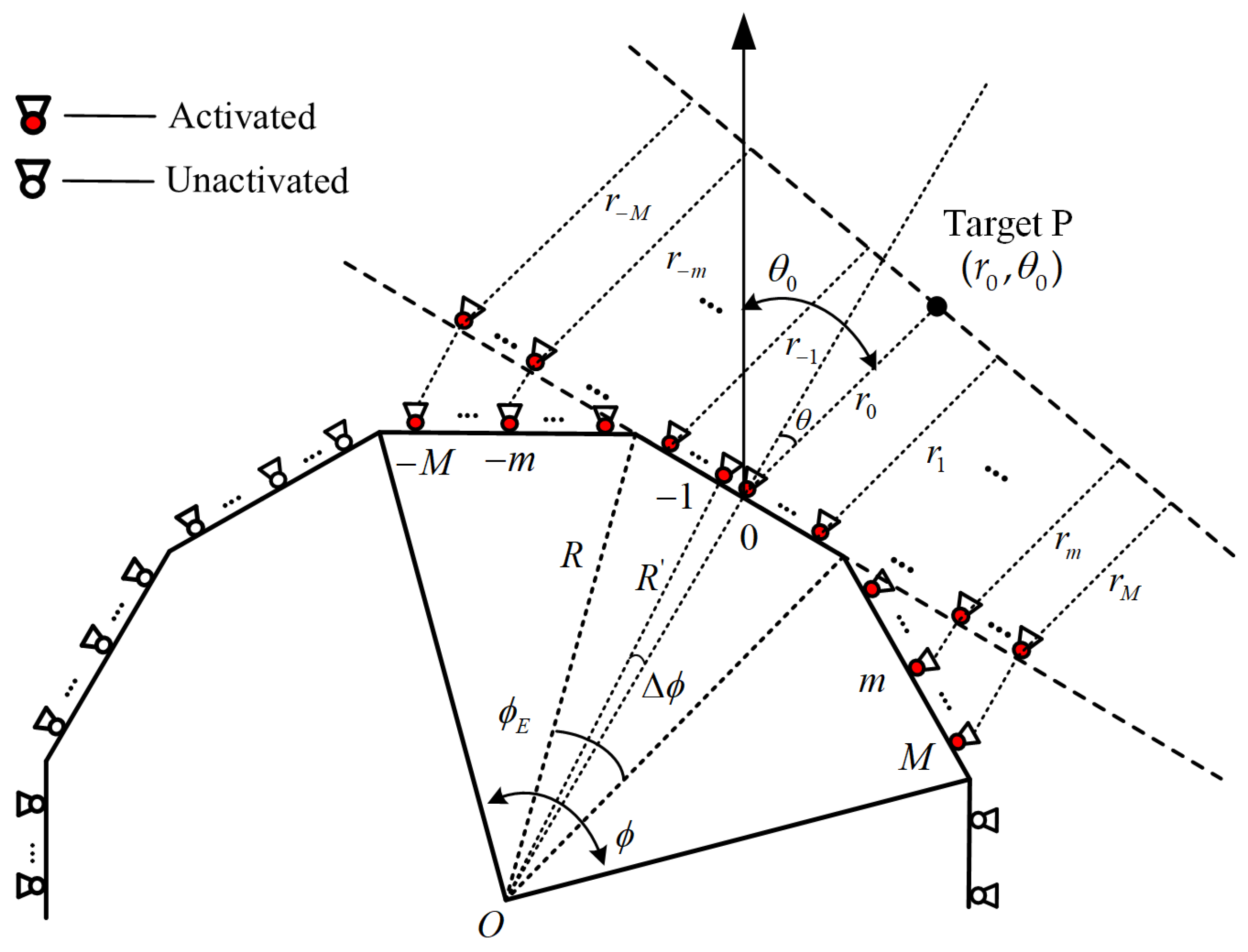
2. Proposed Structure Model
3. Beampattern Synthesis
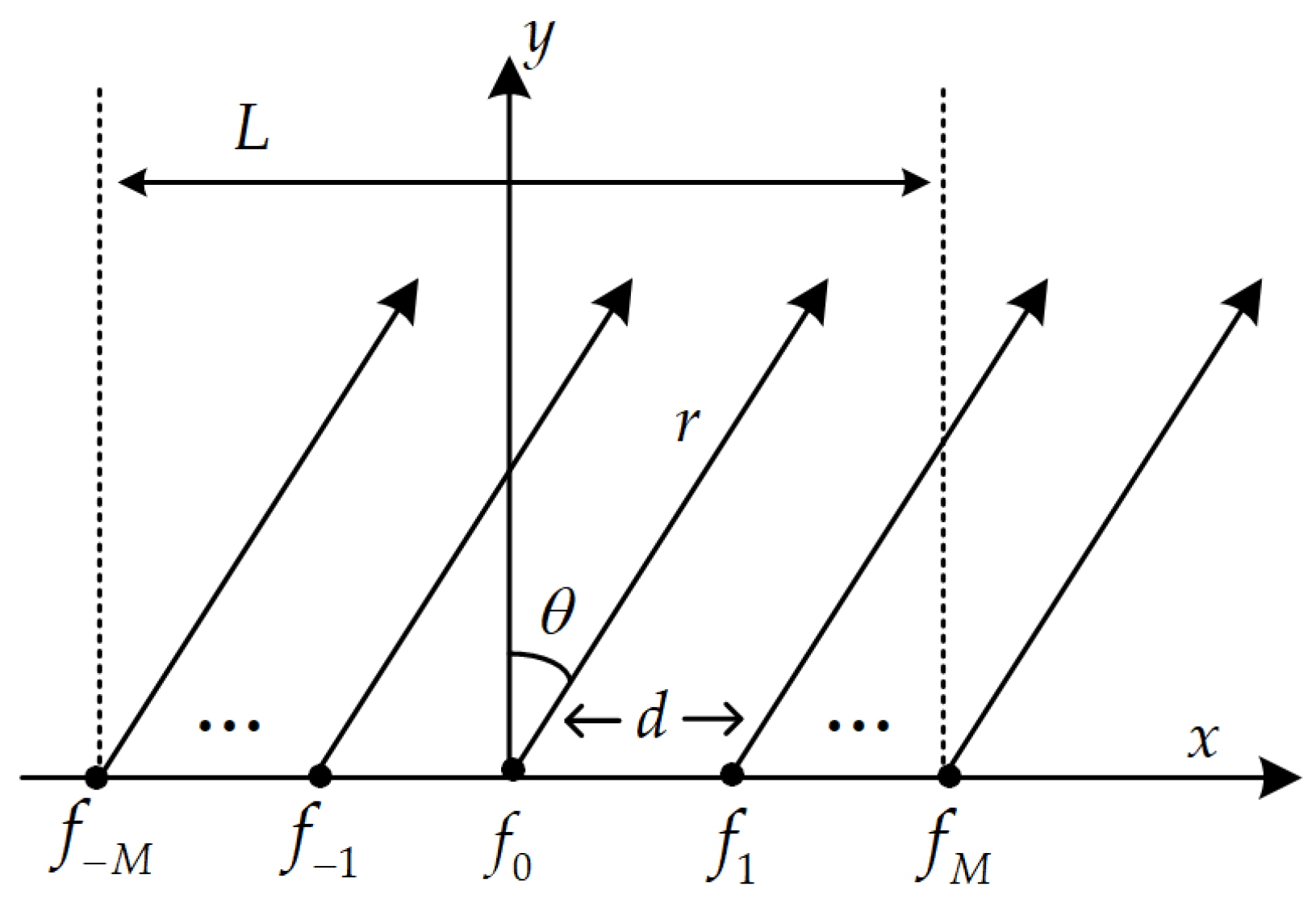
3.1. Conventional Linear FDA Radar
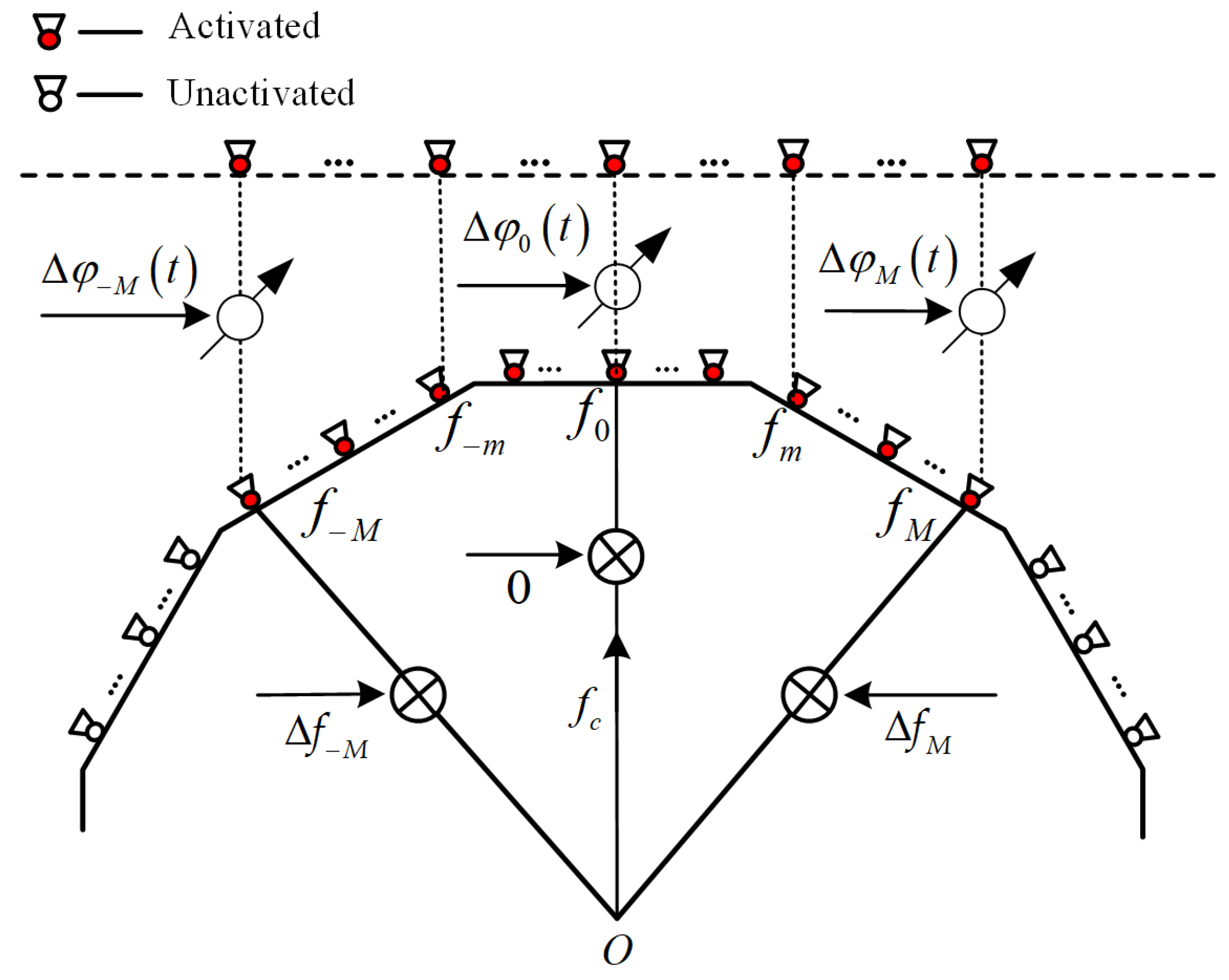
3.2. Proposed CFDA Radar
3.2.1. Phase Compensation
3.2.2. Beampattern Synthesis
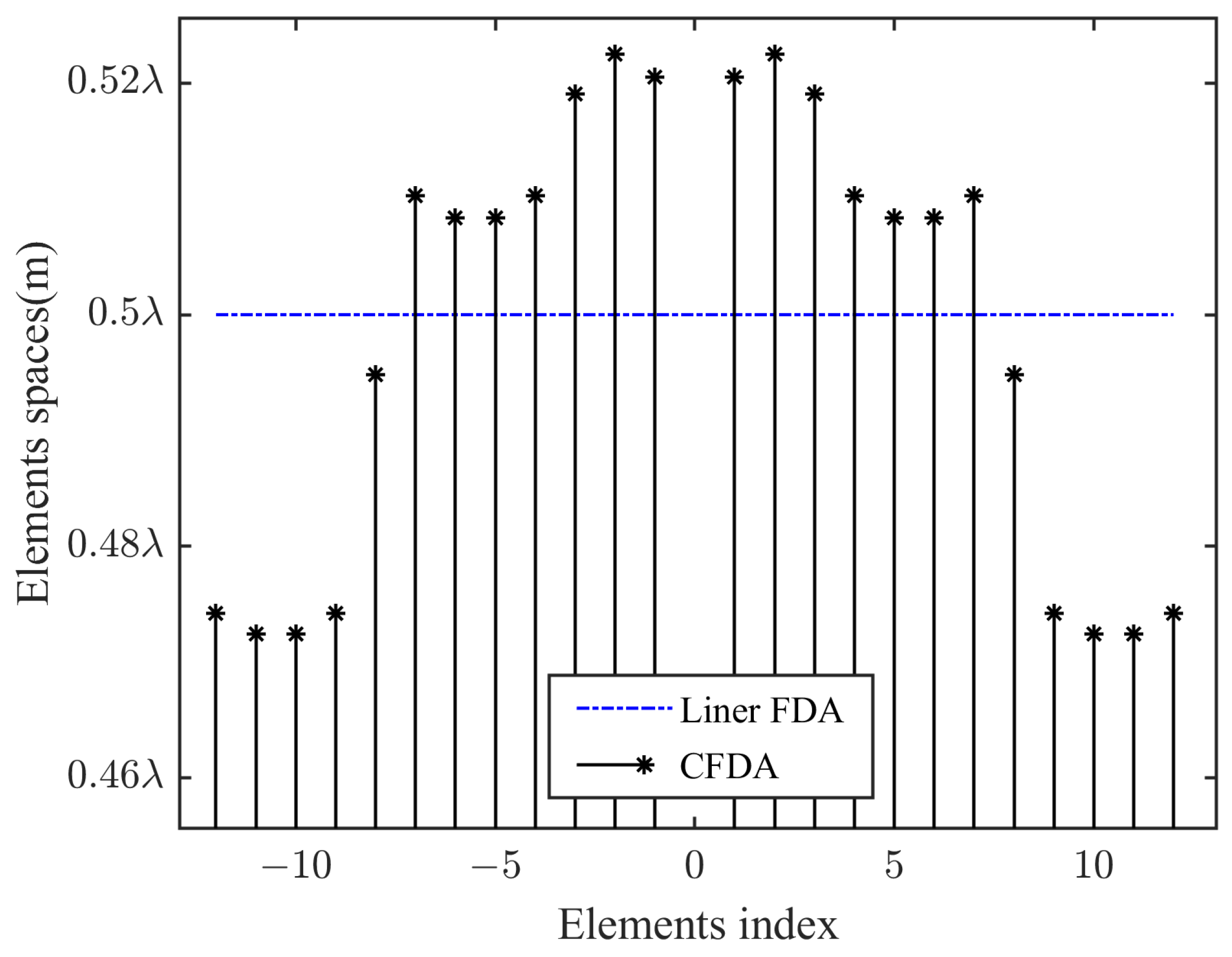
3.3. Beampatterns Optimization
3.3.1. Frequency Offset Optimization
3.3.2. Sidelobe Suppression
4. Comparative Analysis of Simulation Results
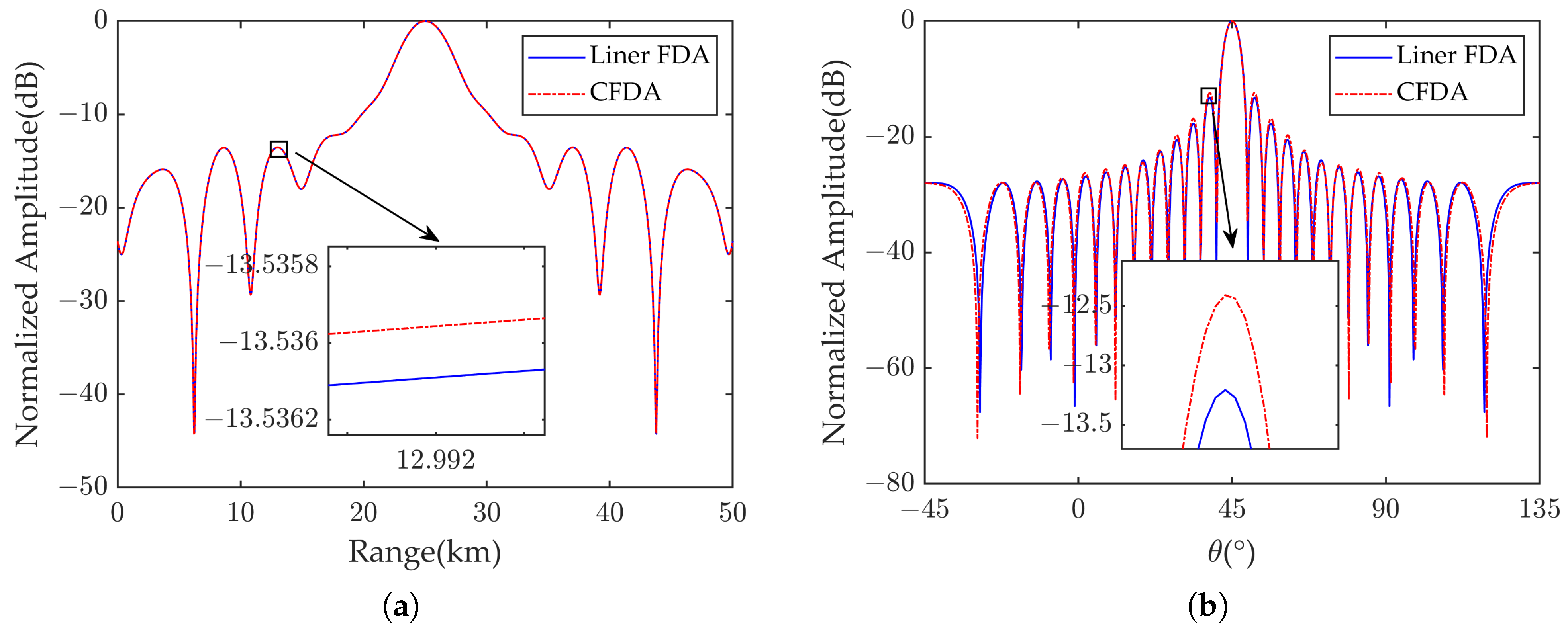
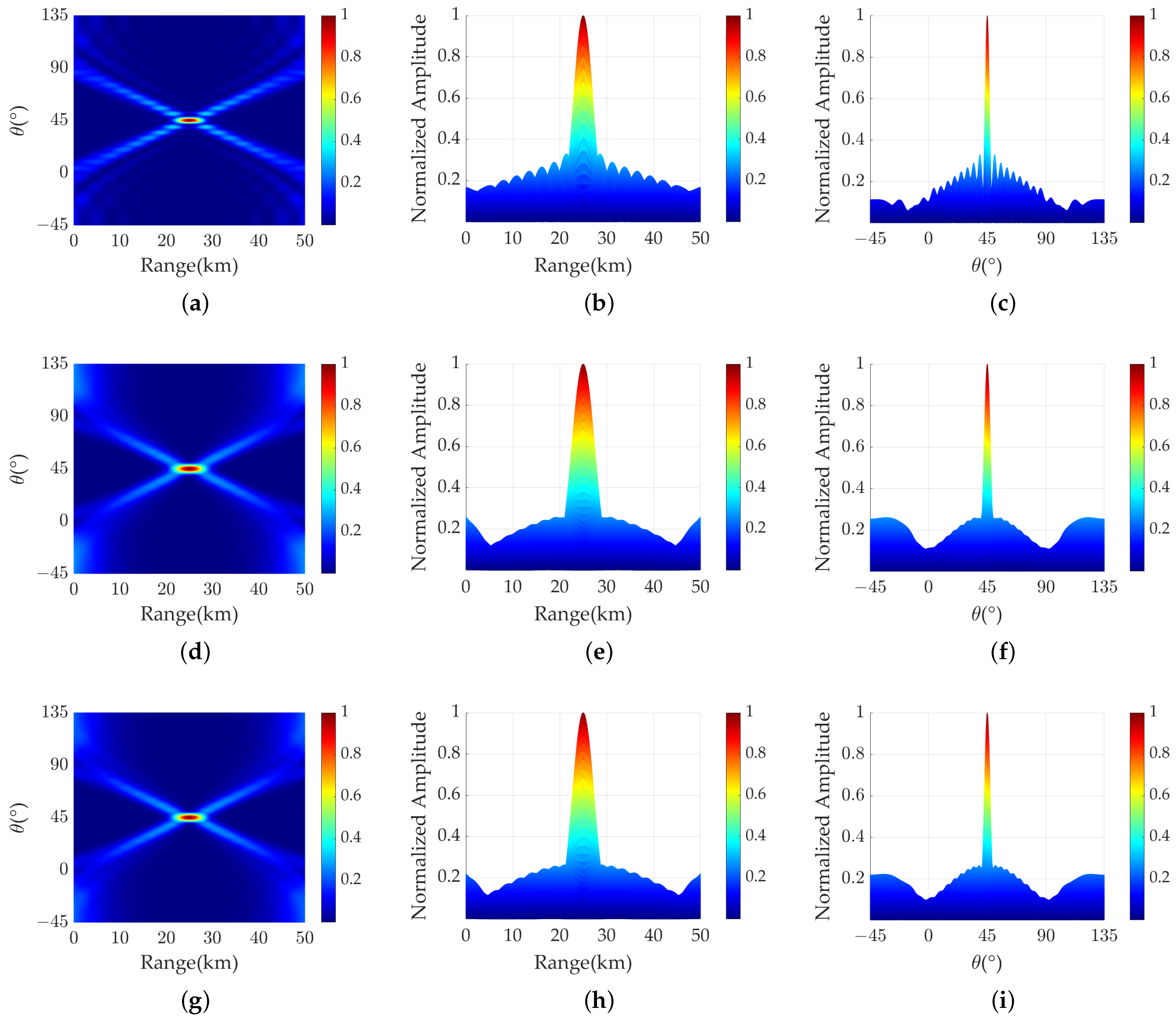
4.1. Analysis of Simulation Results before Optimization
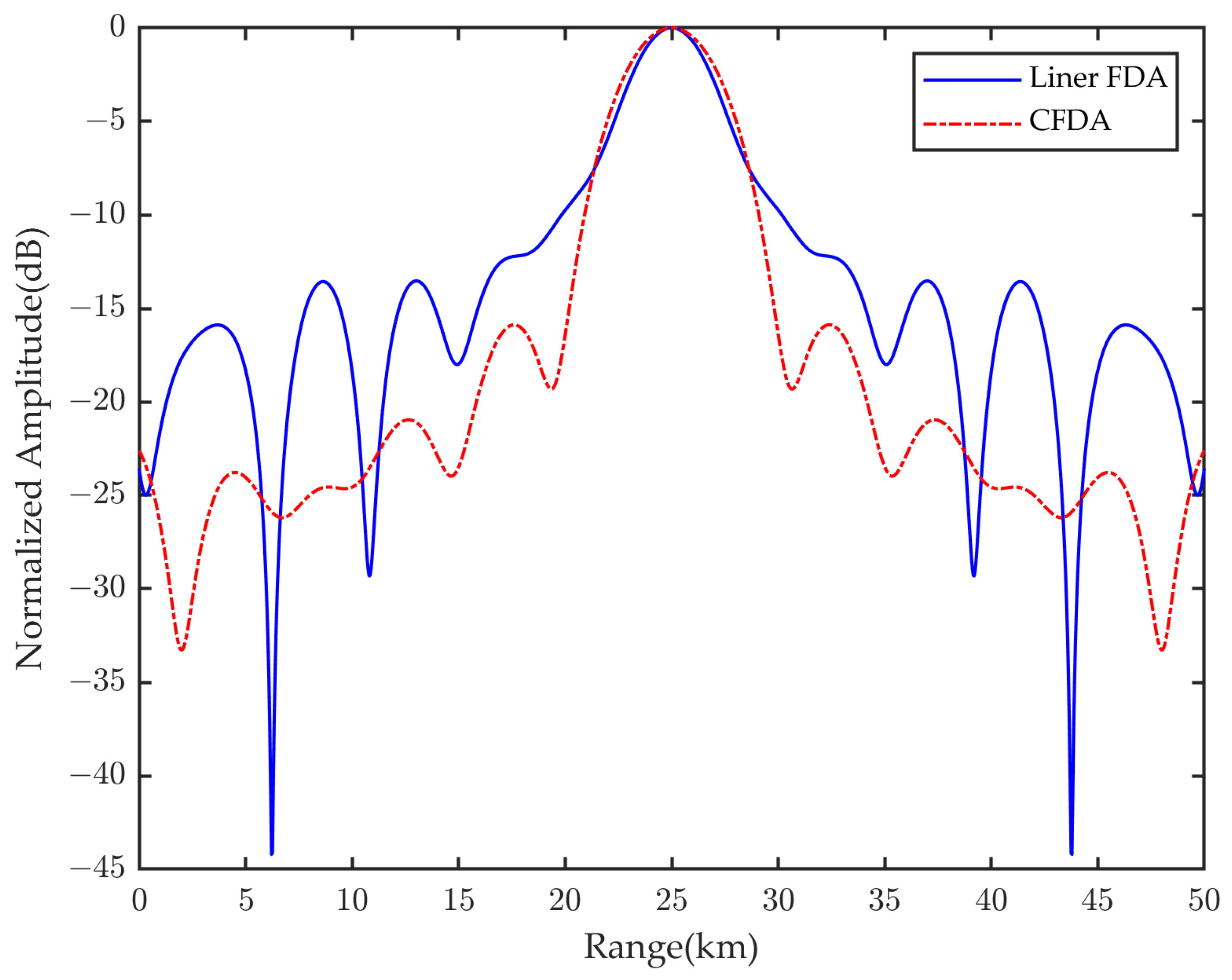
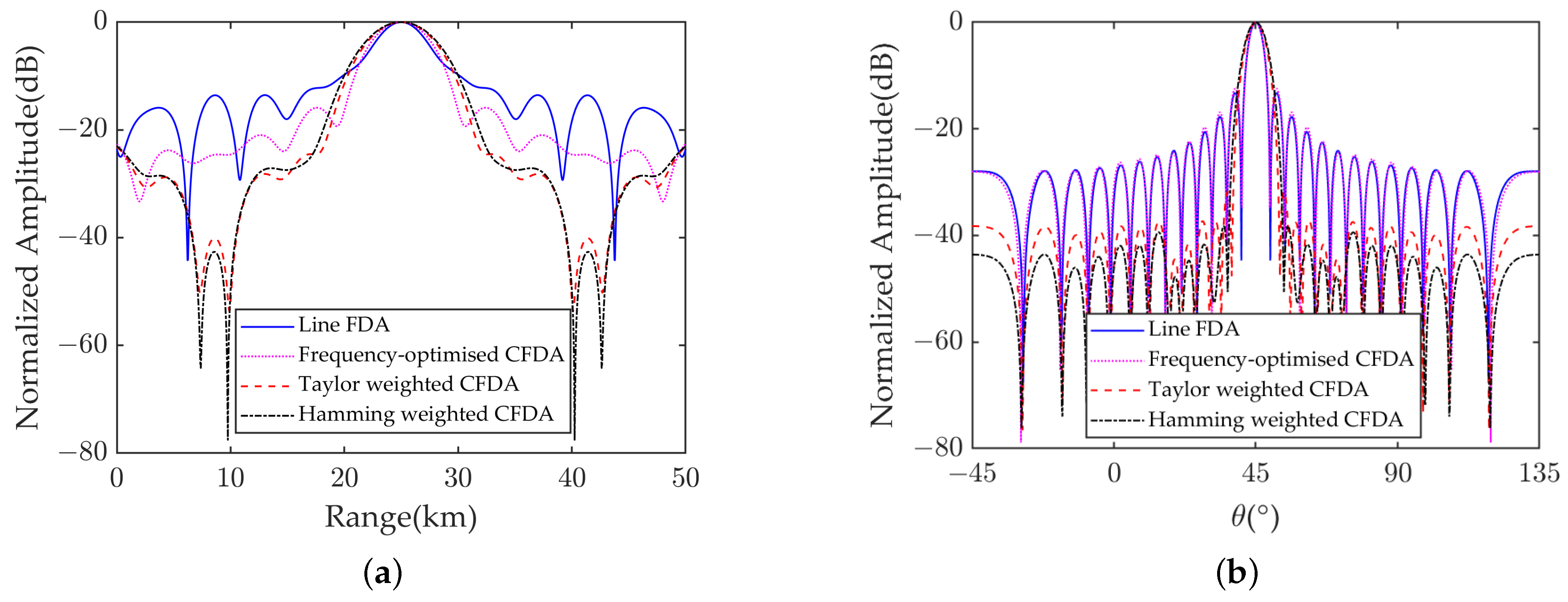
4.2. Analysis of Simulation Results after Optimization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Antonik, P.; Wicks, M.C.; Griffiths, H.D.; Baker, C.J. Frequency diverse array radars. In Proceedings of the 2006 IEEE Conference on Radar, Verona, NY, USA, 24–27 April 2006; pp. 215–217. [Google Scholar] [CrossRef]
- Xu, J.W.; Zhu, S.Q.; Liao, G.H.; Zhang, Y.H. An overview of Frequency Diverse Array radar technology. J. Radars 2018, 7, 167–182. [Google Scholar] [CrossRef]
- Wang, W.Q. Overview of frequency diverse array in radar and navigation applications. IET Radar Sonar Navig. 2016, 10, 1001–1012. [Google Scholar] [CrossRef]
- Wang, W.Q.; Chen, H.; Zheng, Z.; Zhang, S.S. Advances on frequency diverse array radar and its applications. J. Radars 2018, 7, 153–166. [Google Scholar] [CrossRef]
- Wang, W.Q.; Shao, H.Z.; Chen, H. Frequency diverse array radar: Concept, principle and application. J. Electron. Inf. Technol. 2016, 38, 1000–1011. [Google Scholar] [CrossRef]
- Khan, W.; Qureshi, I.M.; Saeed, S. Frequency diverse array radar with logarithmically increasing frequency offset. IEEE Antennas Wirel. Propag. Lett. 2014, 14, 499–502. [Google Scholar] [CrossRef]
- Liu, Y.M.; Ruan, H.; Wang, L.; Nehorai, A. The random frequency diverse array: A new antenna structure for uncoupled direction-range indication in active sensing. IEEE J. Sel. Top. Signal Process. 2016, 11, 295–308. [Google Scholar] [CrossRef]
- Wang, W.Q. Subarray-based frequency diverse array radar for target range-angle estimation. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3057–3067. [Google Scholar] [CrossRef]
- Shao, H.Z.; Dai, J.; Xiong, J.; Chen, H.; Wang, W.Q. Dot-shaped range-angle beampattern synthesis for frequency diverse array. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1703–1706. [Google Scholar] [CrossRef]
- Liao, Y.; Tang, H.; Chen, X.L.; Wang, W.Q. Frequency diverse array beampattern synthesis with Taylor windowed frequency offsets. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1901–1905. [Google Scholar] [CrossRef]
- Zubair, M.; Ahmed, S.; Alouini, M.S. Frequency diverse array radar: New results and discrete Fourier transform based beampattern. IEEE Trans. Signal Process. 2020, 68, 2670–2681. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, W.Q.; Shao, H.Z.; Chen, H. Frequency diverse array transmit beampattern optimization with genetic algorithm. IEEE Antennas Wirel. Propag. Lett. 2016, 16, 469–472. [Google Scholar] [CrossRef]
- Lan, L.; Liao, G.S.; Xu, J.W.; Wen, J. Range-angle pencil-beamforming for non-uniformly distributed array radar. Multidimens. Syst. Signal Process. 2018, 29, 867–886. [Google Scholar] [CrossRef]
- Wang, W.Q.; Dai, M.M.; Zheng, Z. FDA radar ambiguity function characteristics analysis and optimization. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 1368–1380. [Google Scholar] [CrossRef]
- Chen, K.; Yang, S.W.; Chen, Y.k.; Qu, S.W. Accurate Models of Time-Invariant Beampatterns for Frequency Diverse Arrays. IEEE Trans. Antennas Propag. 2019, 67, 3022–3029. [Google Scholar] [CrossRef]
- Xu, Y.H.; Shi, X.W.; Xu, J.W.; Li, P. Range-angle-dependent beamforming of pulsed frequency diverse array. IEEE Trans. Antennas Propag. 2015, 63, 3262–3267. [Google Scholar] [CrossRef]
- Khan, W.; Qureshi, I.M. Frequency Diverse Array Radar With Time-Dependent Frequency Offset. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 758–761. [Google Scholar] [CrossRef]
- Yao, A.M.; Wu, W.; Fang, D.G. Frequency Diverse Array Antenna Using Time-Modulated Optimized Frequency Offset to Obtain Time-Invariant Spatial Fine Focusing Beampattern. IEEE Trans. Antennas Propag. 2016, 64, 4434–4446. [Google Scholar] [CrossRef]
- Liao, Y.; Zeng, G.H.; Luo, Z.B.; Liu, Q.H. Time-Variance Analysis for Frequency-Diverse Array Beampatterns. IEEE Trans. Antennas Propag. 2023, 71, 6558–6567. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W. A method of mainlobe deception jamming countermeasure in FDA-MIMO radar. Radar Sci. Technol. 2017, 15, 671–676. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Xie, J.W.; Li, X.; Sheng, C.; Hu, Q.Y. Discrimination method of range deception jamming based on FDA-MIMO. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 738–746. [Google Scholar] [CrossRef]
- Li, Z.H.; Zhang, Y.S.; Ge, Q.C.; Xue, B. A robust deceptive jamming suppression method based on covariance matrix reconstruction with frequency diverse array MIMO radar. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Lan, L.; Liao, G.; Xu, J.; Xu, Y.; So, H.C. Beampattern Synthesis Based on Novel Receive Delay Array for Mainlobe Interference Mitigation. IEEE Trans. Antennas Propag. 2023, 71, 4470–4485. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Liao, G.S.; Xu, J.W.; Zhang, X.P.; Lan, L. A Method to Suppress Interferences Based on Secondary Compensation with QPC-FDA-MIMO Radar. Remote Sens. 2023, 15, 4711. [Google Scholar] [CrossRef]
- Wang, W.Q. Cognitive frequency diverse array radar with situational awareness. IET Radar Sonar Navig. 2016, 10, 359–369. [Google Scholar] [CrossRef]
- Lan, L.; Liao, G.S.; Xu, J.W.; Zhang, Y.H.; Fioranelli, F. Suppression approach to main-beam deceptive jamming in FDA-MIMO radar using nonhomogeneous sample detection. IEEE Access 2018, 6, 34582–34597. [Google Scholar] [CrossRef]
- Fusco, V.F.; Chepala, A.; Abbasi, M.A.B. Target location using dual-beam directional modulated circular array. IEEE Trans. Antennas Propag. 2018, 66, 7525–7529. [Google Scholar] [CrossRef]
- Longhi, M.; Vellucci, S.; Barbuto, M.; Monti, A.; Zarghani, H. Array Synthesis of Circular Huygens Metasurfaces for Antenna Beam-Shaping. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 2649–2653. [Google Scholar] [CrossRef]
- Khalaj-Amirhosseini, M.; Farhoudi, L. Synthesis of circular arrays with sidelobes of individually arbitrary levels. Int. J. Microw.-Comput.-Aided Eng. 2019, 29, e21752. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, X. Three-dimensional parameter estimation of uniform circular frequency diverse array radar with two-stage estimator. IEEE Sens. J. 2021, 21, 17775–17784. [Google Scholar] [CrossRef]
- Ma, J.; Cai, J.; Zheng, Z.; Gao, X.; Huang, S. Spatiotemporal Evolution of Orbital Angular Momentum (OAM) Beams Based on a Uniform Circular Frequency Diverse Array (UC-FDA). IEEE Trans. Antennas Propag. 2023, 71, 4183–4193. [Google Scholar] [CrossRef]
- Xu, W.; Deng, Z.; Huang, P.; Tan, W.; Gao, Z. Beampattern synthesis and optimization for frequency diverse arc array based on the virtual element. Electronics 2023, 12, 2231. [Google Scholar] [CrossRef]


| Parameters | Symbol | Value |
|---|---|---|
| Carrier frequency | 10 Ghz | |
| Frequency offset | 10 Khz | |
| Number of linear array units | 29 | |
| Number of linear array elements | 5 | |
| Activated element number | 25 | |
| Aperture angle | ||
| Array radius | R | 0.36 m |
| Desired target range | 25 Km | |
| Desired target angle |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Pei, C.; Huang, P.; Tan, W.; Gao, Z. Beampattern Synthesis and Optimization Method Based on Circular Frequency Diverse Array Engineering Model. Electronics 2024, 13, 1618. https://doi.org/10.3390/electronics13091618
Xu W, Pei C, Huang P, Tan W, Gao Z. Beampattern Synthesis and Optimization Method Based on Circular Frequency Diverse Array Engineering Model. Electronics. 2024; 13(9):1618. https://doi.org/10.3390/electronics13091618
Chicago/Turabian StyleXu, Wei, Changyu Pei, Pingping Huang, Weixian Tan, and Zhiqi Gao. 2024. "Beampattern Synthesis and Optimization Method Based on Circular Frequency Diverse Array Engineering Model" Electronics 13, no. 9: 1618. https://doi.org/10.3390/electronics13091618
APA StyleXu, W., Pei, C., Huang, P., Tan, W., & Gao, Z. (2024). Beampattern Synthesis and Optimization Method Based on Circular Frequency Diverse Array Engineering Model. Electronics, 13(9), 1618. https://doi.org/10.3390/electronics13091618






