Multi-Objective Optimization in 3D Floorplanning
Abstract
:1. Introduction
- Three-dimensional floorplanning is set as a multi-objective optimization problem and applies a MOSA method to optimize area, wirelength, and via count. By generating neighboring solutions through random perturbations and exploring the solution space, heuristic decision criteria are formulated based on the dominance relationship of solutions.
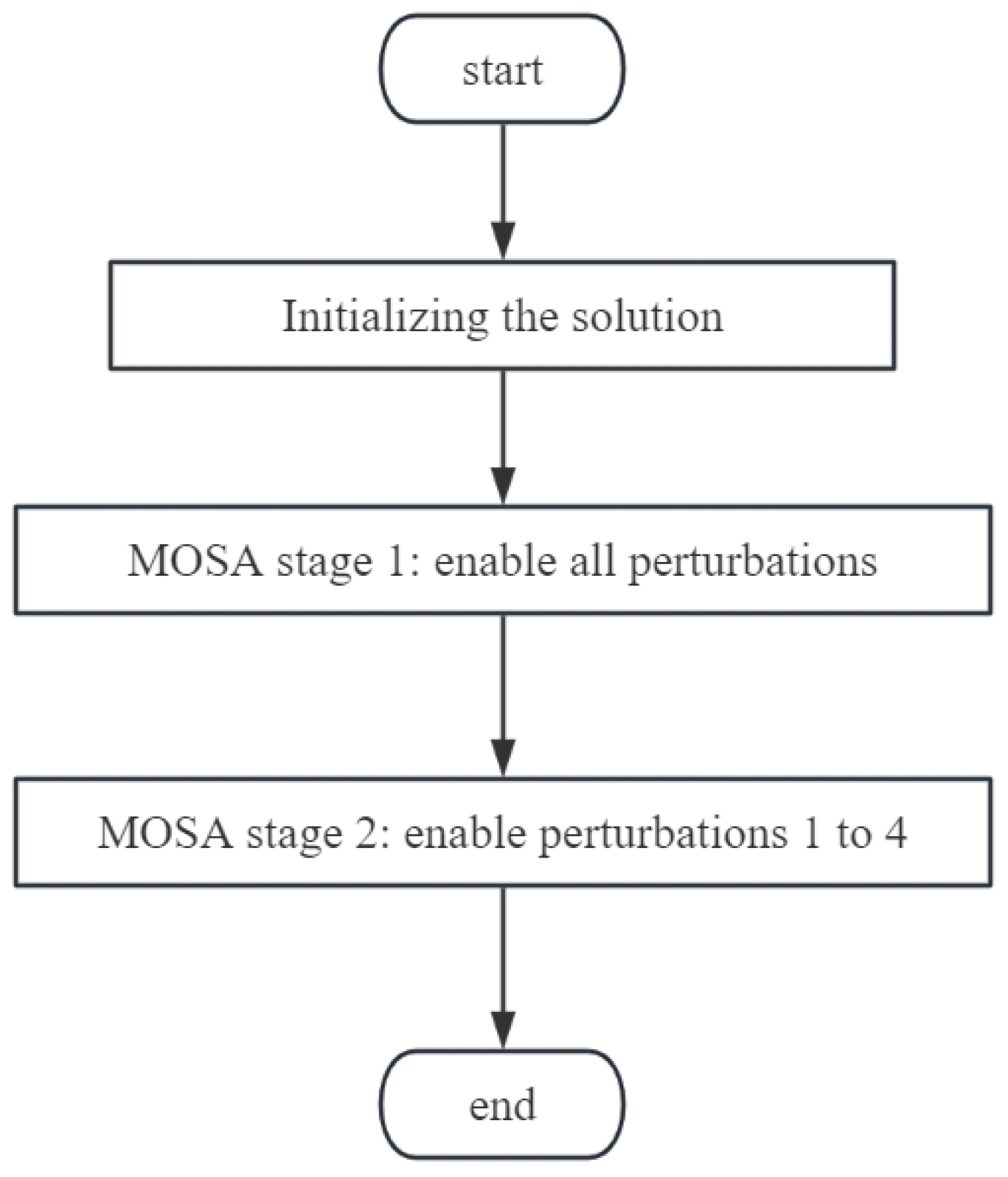
- The heuristic search process is divided into two stages. In the first stage, all objectives including area, wirelength, and via count are optimized synchronously. Both inter-layer and intra-layer perturbations are performed simultaneously. Inter-layer perturbations encourage the algorithm to spontaneously explore layer assignment schemes, enabling them to better adapt to area and wirelength optimization. In the second stage, only intra-layer perturbations are retained, without adjusting the layer assignment scheme, focusing solely on optimizing area and wirelength.
- The test results on the GSRC [26] benchmark indicate that compared to other similar studies, the method proposed in this paper achieves more favorable outcomes in terms of area and wirelength.
2. Background
2.1. Three-Dimensional Floorplanning
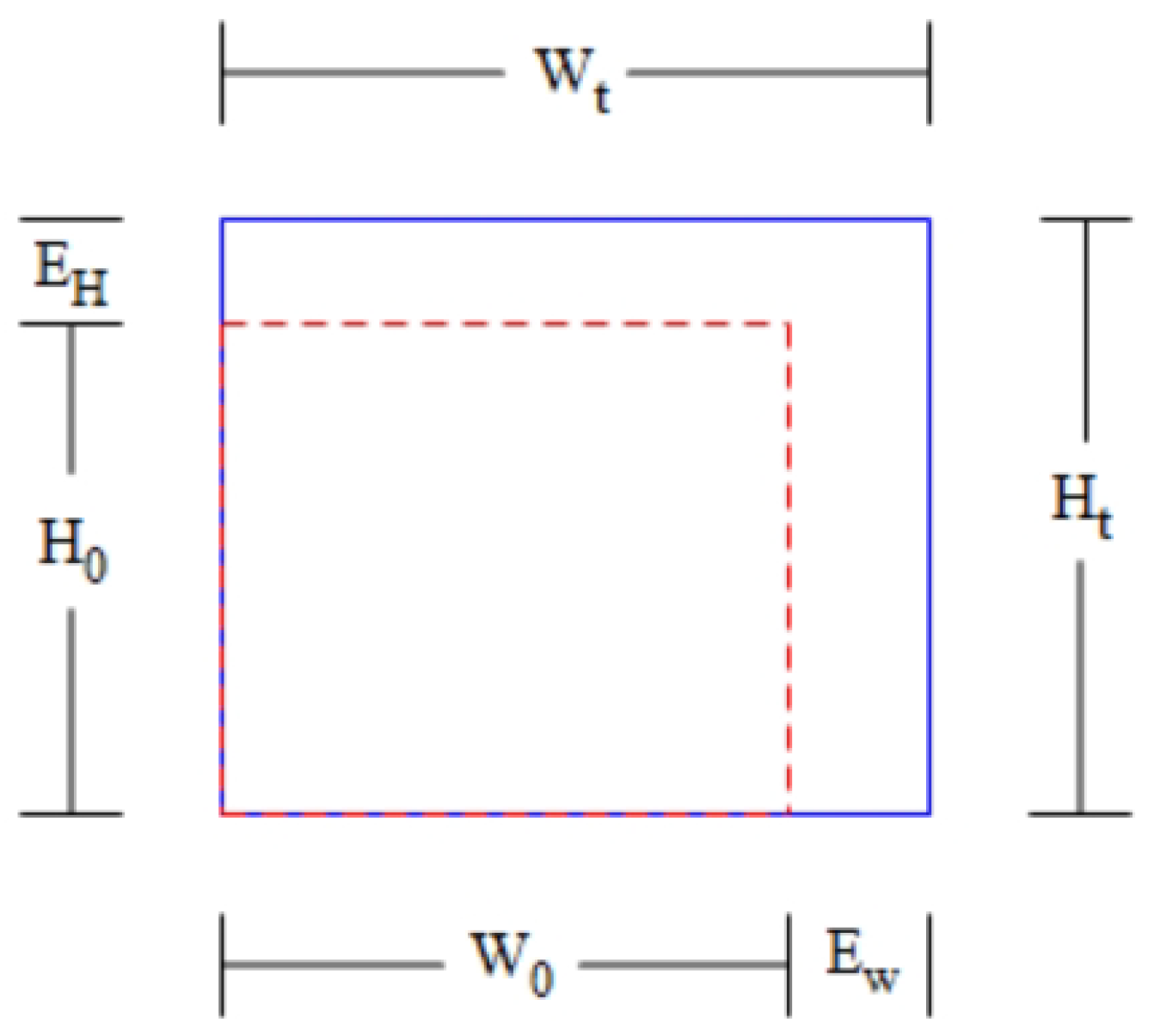
- Minimize via count. In 3D IC with F2F stacking, the number of layers is 2 (). If a net spans both two layers, it requires an ITV.
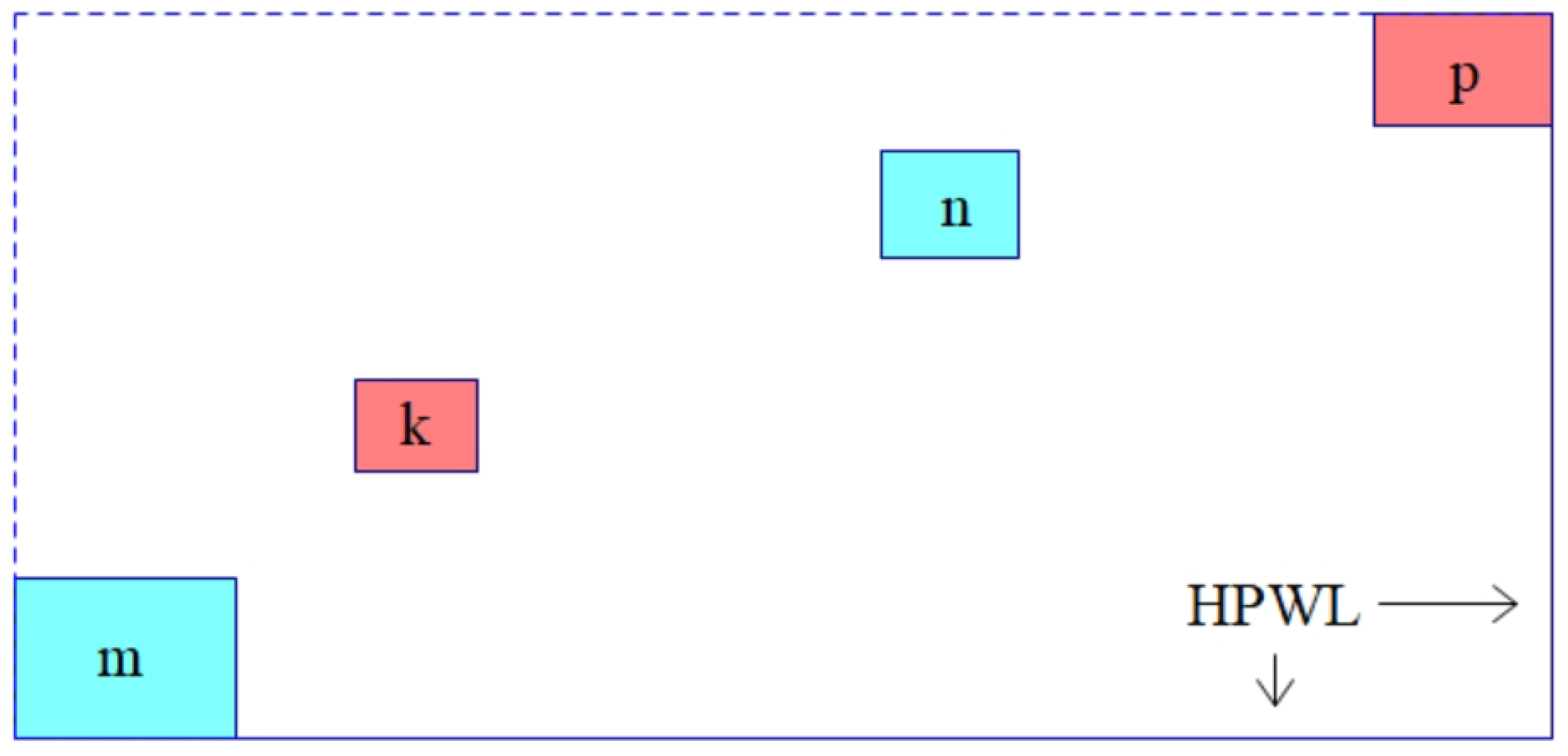
- Minimize Half-Perimeter Wirelength (HPWL). HPWL model [11] is the most commonly used approximation for evaluating circuit wirelength. Its expression is as follows:where denotes the maximum x-coordinates of all the pins involved in a net, and similar meanings apply to , , and .
2.2. Multi-Objective Optimization
- Pareto Dominance. Given two solutions and , if is at least as good as in all objectives and strictly better in at least one objective, then dominates , denoted as . The dominance relation is defined as
- Pareto Front. The Pareto Front (PF) is the set of solutions in the decision variable space that are not dominated by any other solution. This represents a collection of different balanced solutions where no solution is superior in all objectives. It is formally expressed as
- Diversity and Balance. MOO aims to find a set of solutions that form a balance in the objective space. Let denote the vector of objectives for solution x. The objective is to find a set of non-dominated solutions that are widely distributed in the objective space, representing the Pareto Front.
- Hypervolume Indicator. For a given set of points P on the Pareto front, the hypervolume indicator HI is the Lebesgue measure of the hypervolume covered by all boxes with points from P as upper corners and the reference point r as the lower corner.
3. Methods
3.1. Objective Function
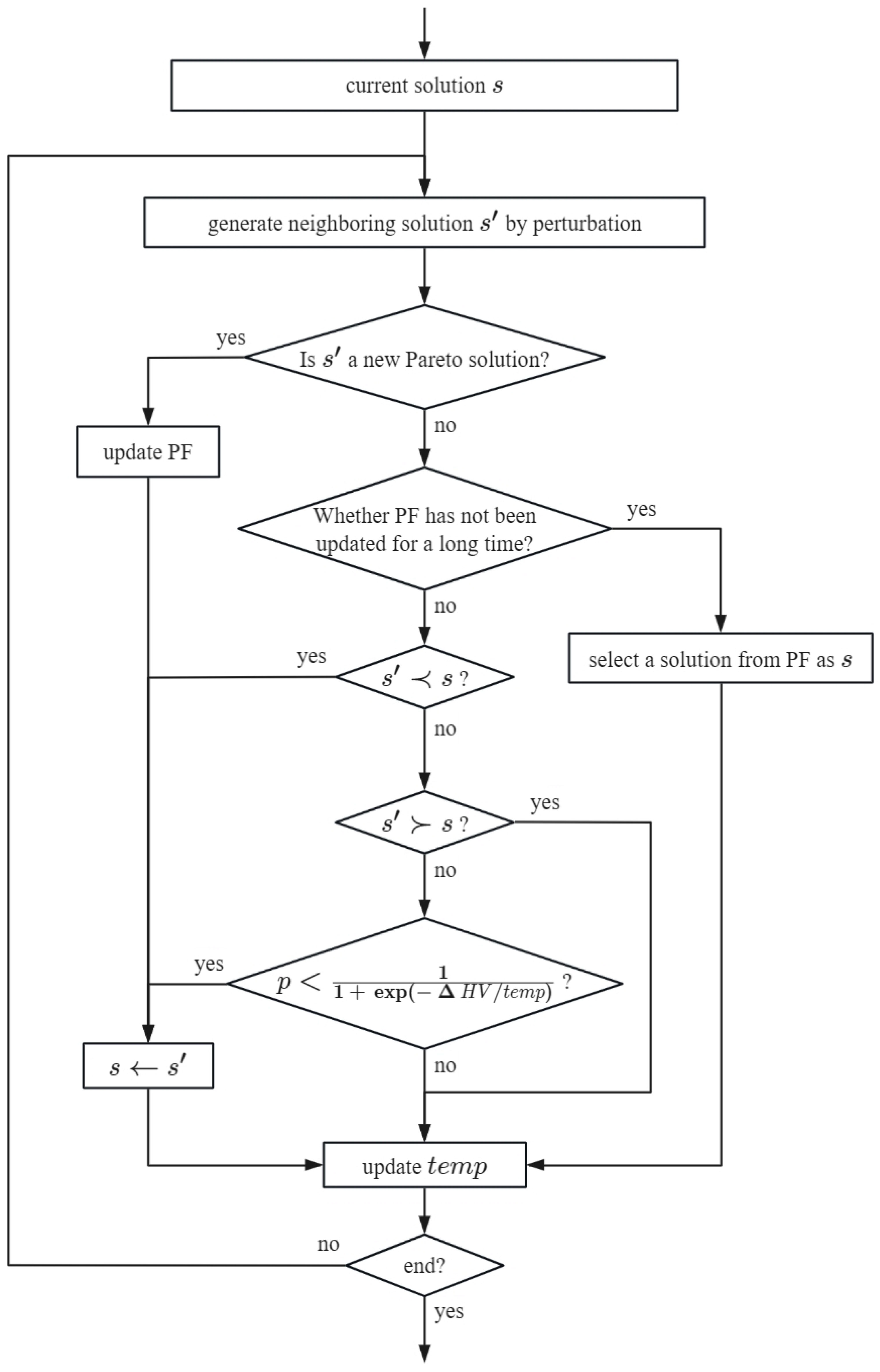
3.2. Overall Flow
- In any layer t, randomly swap a pair of blocks in either sequence or .
- In any layer t, randomly swap the same pair of blocks in both sequences and .
- In any layer t, randomly select a block and place it in a new position in both sequences and .
- In any layer t, randomly select a block and rotate its orientation by 90 degrees.
- Select a block in any layer t and place it in a new random position on another layer.This is the only type of inter-layer perturbation. To avoid excessively large jumps in a single perturbation, we restrict the selection of blocks within a defined range. We ensure that the increase in ITV count in a single perturbation does not exceed , and it does not result in being less than .
3.3. Multi-Objective Simulated Annealing
- The neighboring solution dominates the current solution. In this case, the neighboring solution is accepted.
- The neighboring solution and the current solution are mutually non-dominated. In this case, the neighboring solution is accepted with a probability:where represents the hypervolume improvement of the neighboring solution relative to the current solution, and represents the annealing temperature, which decreases gradually as the search process progresses. It is similar to a sigma function, where the acceptance probability is 1/2 when equals 0, and as increases, the acceptance probability also increases. When the temperature is low enough, for greater than 0, the acceptance probability approaches 1, and for less than 0, the acceptance probability approaches 0.
- The neighboring solution is dominated by the current solution. In this case, the neighboring solution is refused.
4. Results
5. Discussion and Conclusions
- Due to the 3D stacking technology, 3D approaches have achieved significant advancements in both area and wirelength optimization compared to the 2D method [25].
- Compared to 3D-SOO [16], 3D-MOOFP leads across all objectives overall, benefiting from the advantages of multi-objective optimization. It only falls behind in optimizing via count for n300, which might be attributed to sacrifices made for area and wirelength optimization.
- Compared to 3D-MOOHL, 3D-MOOFP excels across all objectives in wirelength optimization. It benefits from the synergistic optimization of all objectives in the first MOSA stage. When employing the hMETIS [40] tool for layer partitioning, it is restricted to optimizing via count solely under the condition of relatively balanced area, without taking into account the potential impact of this partitioning scheme on area and wirelength. In contrast, our approach enables the consideration of all optimization objectives simultaneously. This allows us to identify layer partitioning schemes that are more conducive to wirelength optimization.
- In terms of via count optimization, the performance difference between the 3D-MOOFP and 3D-MOOHL methods is quite noticeable. It may be attributed to fundamental differences in the partitioning approach. In 3D-MOOHL, a professional partitioning tool is for layer assignment, which may be more proficient in via count optimization. In 3D-MOOFP, layer assignment is explored step by step through a heuristic approach, hence it performs well only on datasets with simpler structures. For the entire floorplanning approach, we provide an effective approach.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IC | Integrated Circuit |
| VLSI | Very Large Scale Integration |
| EDA | Electronic Design Automation |
| NP | Non-deterministic Polynomial-time |
| GA | Genetic Algorithm |
| BSG | Bounded Slice-line Grid |
| CBL | Corner Block List |
| PF | Pareto Front |
| FOFP | Fixed-Outline Floorplanning |
| M3D | Monolithic 3D Integration |
| F2F | Face-to-Face |
| TSV | Through Silicon Via |
| ITV | Inter-Tier Via |
| MIV | Monolithic Integrated Vias |
| HPWL | Half Perimeter Wirelength |
| SP | Sequence Pairs |
| P-SP | Partitioned Sequence Pairs |
| SA | Simulated Annealing |
| MOO | Multi-Objective Optimization |
| MOSA | Multi-Objective Simulated Annealing |
| MHEC | Modified Hyperedge Coarsening |
| SOO | Single-Objective Optimization |
| MOOHL | Multi-Objective Optimization hMETIS Layering |
| MOOFP | Multi-Objective Optimization Floorplanning |
References
- Souri, S.J.; Banerjee, K.; Mehrotra, A.; Saraswat, K.C. Multiple Si layer ICs: Motivation, performance analysis, and design implications. In Proceedings of the 37th Annual Design Automation Conference, Los Angeles, CA, USA, 5–9 June 2000; pp. 213–220. [Google Scholar]
- Joyner, J.W.; Zarkesh-Ha, P.; Meindl, J.D. A global interconnect design window for a three-dimensional system-on-a-chip. In Proceedings of the IEEE 2001 International Interconnect Technology Conference (Cat. No. 01EX461), Burlingame, CA, USA, 6 June 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 154–156. [Google Scholar]
- Vanna-Iampikul, P.; Shao, C.; Lu, Y.C.; Pentapati, S.; Lim, S.K. Snap-3D: A constrained placement-driven physical design methodology for face-to-face-bonded 3D ICs. In Proceedings of the 2021 International Symposium on Physical Design, Virtual, 22–24 March 2021; pp. 39–46. [Google Scholar]
- Lim, S.K. 3D-MAPS: 3D massively parallel processor with stacked memory. In Design for High Performance, Low Power, and Reliable 3D Integrated Circuits; Springer: New York, NY, USA, 2013; pp. 537–560. [Google Scholar]
- Gomes, W.; Khushu, S.; Ingerly, D.B.; Stover, P.N.; Chowdhury, N.I.; O’Mahony, F.; Balankutty, A.; Dolev, N.; Dixon, M.G.; Jiang, L.; et al. 8.1 Lakefield and Mobility Compute: A 3D Stacked 10 nm and 22FFL Hybrid Processor System in 12× 12 mm 2, 1 mm Package-on-Package. In Proceedings of the 2020 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 16–20 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 144–146. [Google Scholar]
- Hu, K.S.; Chi, H.Y.; Lin, I.J.; Wu, Y.H.; Chen, W.H.; Hsieh, Y.T. 2023 ICCAD CAD Contest Problem B: 3D Placement with Macros. In Proceedings of the 2023 IEEE/ACM International Conference on Computer Aided Design (ICCAD), San Francisco, CA, USA, 29 October–2 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Otten, R.H. What is a floorplan? In Proceedings of the 2000 International Symposium on Physical Design, San Diego, CA, USA, 9–12 April 2000; pp. 201–206. [Google Scholar]
- Chen, T.C.; Chang, Y.W. Modern floorplanning based on B/sup*/-tree and fast simulated annealing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2006, 25, 637–650. [Google Scholar] [CrossRef]
- Kahng, A.B. Classical floorplanning harmful? In Proceedings of the 2000 International Symposium on Physical Design, San Diego, CA, USA, 9–12 April 2000; pp. 207–213. [Google Scholar]
- Adya, S.N.; Markov, I.L. Fixed-outline floorplanning: Enabling hierarchical design. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2003, 11, 1120–1135. [Google Scholar] [CrossRef]
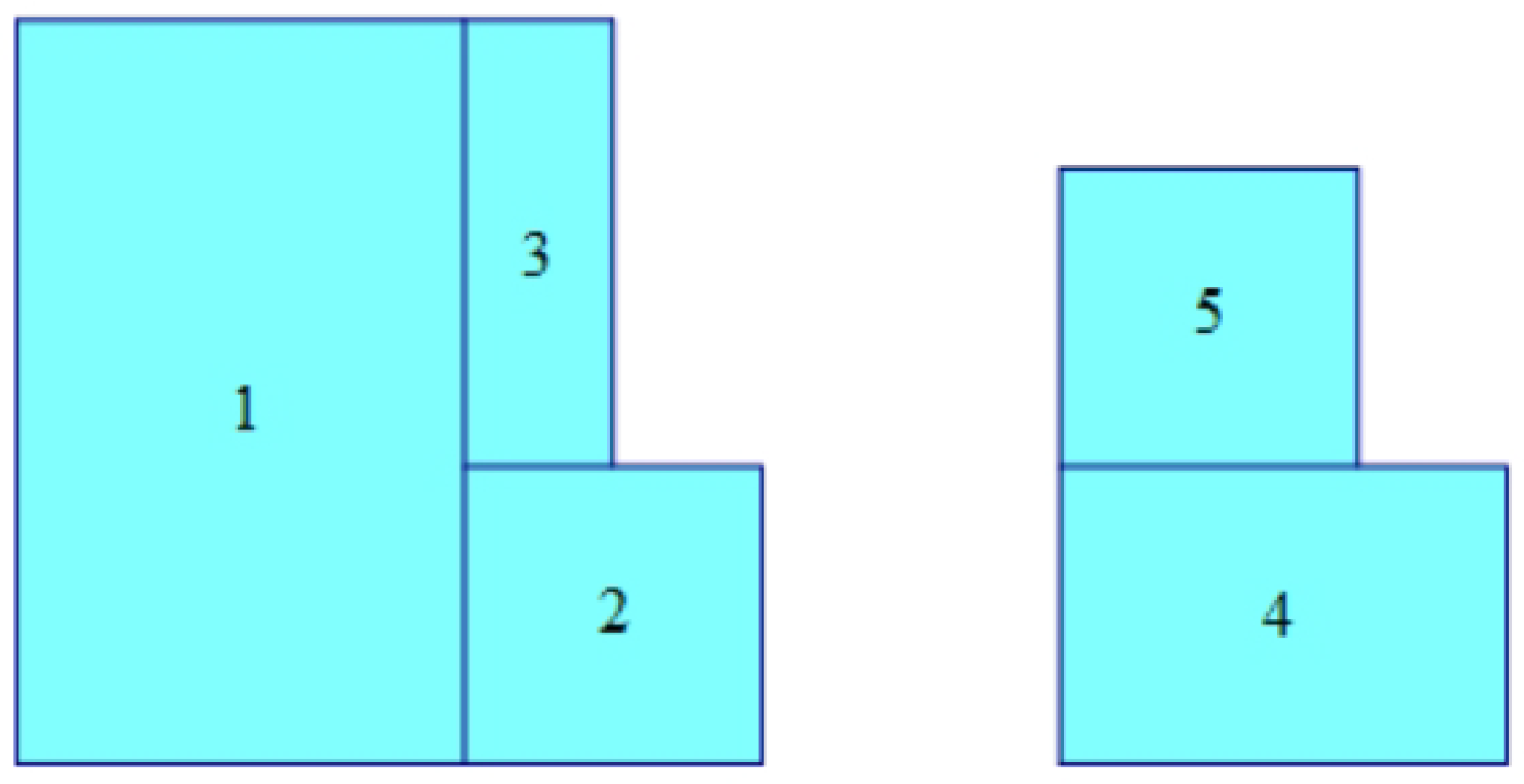
- Murata, H.; Fujiyoshi, K.; Nakatake, S.; Kajitani, Y. VLSI module placement based on rectangle-packing by the sequence-pair. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1996, 15, 1518–1524. [Google Scholar] [CrossRef]
- Frantz, F.; Labrak, L.; O’Connor, I. 3D-IC floorplanning: Applying meta-optimization to improve performance. In Proceedings of the 2011 IEEE/IFIP 19th International Conference on VLSI and System-on-Chip, Kowloon, Hong Kong, 3–5 October 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 404–409. [Google Scholar]
- Chen, S.; Yoshimura, T. Multi-layer floorplanning for stacked ICs: Configuration number and fixed-outline constraints. Integration 2010, 43, 378–388. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, S.; Li, B. Combining the ant system algorithm and simulated annealing for 3D/2D fixed-outline floorplanning. Appl. Soft Comput. 2016, 40, 150–160. [Google Scholar] [CrossRef]
- Guler, A.; Jha, N.K. Hybrid monolithic 3-D IC floorplanner. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2018, 26, 1868–1880. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Zhang, M.S.; He, Y.F.; Huang, Y.H. Floorplanning for 3D-IC with Through-Silicon via co-design using simulated annealing. In Proceedings of the 2018 IEEE International Symposium on Electromagnetic Compatibility and 2018 IEEE Asia-Pacific Symposium on Electromagnetic Compatibility (EMC/APEMC), Singapore, 14–18 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 550–553. [Google Scholar]
- Shanthi, J.; Rani, D.G.N.; Rajaram, S. Thermal Aware Floorplanner for Multi-Layer ICs with Fixed-Outline Constraints. In Proceedings of the 2021 2nd International Conference on Communication, Computing and Industry 4.0 (C2I4), Bangalore, India, 16–17 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Lin, J.M.; Chang, W.Y.; Hsieh, H.Y.; Shyu, Y.T.; Chang, Y.J.; Lu, J.M. Thermal-aware floorplanning and TSV-planning for mixed-type modules in a fixed-outline 3-D IC. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, 29, 1652–1664. [Google Scholar] [CrossRef]
- Kadambarajan, J.P.; Pothiraj, S.; Kadarkarai, P. GPU Implementation of Thermal Aware 3D IC Floorplanning. Int. J. Comput. Inf. Syst. Ind. Manag. Appl. 2021, 13, 8. [Google Scholar]
- Meitei, N.Y.; Baishnab, K.L.; Trivedi, G. Fast power density aware three-dimensional integrated circuit floorplanning for hard macroblocks using best operator combination genetic algorithm. Int. J. Circuit Theory Appl. 2023, 51, 4879–4896. [Google Scholar] [CrossRef]
- Guan, W.; Tang, X.; Lu, H.; Zhang, Y.; Zhang, Y. A novel thermal-aware floorplanning and tsv assignment with game theory for fixed-outline 3-D ICs. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2023, 31, 1639–1652. [Google Scholar] [CrossRef]
- He, Z.; Ma, Y.; Zhang, L.; Liao, P.; Wong, N.; Yu, B.; Wong, M.D. Learn to floorplan through acquisition of effective local search heuristics. In Proceedings of the 2020 IEEE 38th International Conference on Computer Design (ICCD), Hartford, CT, USA, 18–21 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 324–331. [Google Scholar]
- Xu, Q.; Geng, H.; Chen, S.; Yuan, B.; Zhuo, C.; Kang, Y.; Wen, X. GoodFloorplan: Graph Convolutional Network and Reinforcement Learning-Based Floorplanning. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 41, 3492–3502. [Google Scholar] [CrossRef]
- Amini, M.; Zhang, Z.; Penmetsa, S.; Zhang, Y.; Hao, J.; Liu, W. Generalizable Floorplanner through Corner Block List Representation and Hypergraph Embedding. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 2692–2702. [Google Scholar]
- Jiang, Z.; Li, Z.; Yao, Z. Multi-Objective Optimization in Fixed-Outline Floorplanning through Reinforcement Learning. Comput. Electr. Eng. 2024. submitted to publication. [Google Scholar]
- GSRC Benchmark. Available online: http://vlsicad.eecs.umich.edu/BK/GSRCbench (accessed on 9 October 2023).
- Deng, Y.; Maly, W.P. Interconnect characteristics of 2.5-D system integration scheme. In Proceedings of the 2001 International Symposium on Physical Design, Sonoma County, CA, USA, 1–4 April 2001; pp. 171–175. [Google Scholar]
- Shiu, P.H.; Ravichandran, R.; Easwar, S.; Lim, S.K. Multi-layer floorplanning for reliable system-on-package. In Proceedings of the 2004 IEEE International Symposium on Circuits and Systems (ISCAS), Vancouver, BC, Canada, 23–26 May 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 5, pp. 69–72. [Google Scholar]
- Yamazaki, H.; Sakanushi, K.; Nakatake, S.; Kajitani, Y. The 3D-packing by meta data structure and packing heuristics. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2000, 83, 639–645. [Google Scholar]
- Cheng, L.; Deng, L.; Wong, M.D. Floorplanning for 3-D VLSI design. In Proceedings of the 2005 Asia and South Pacific Design Automation Conference, Shanghai, China, 18–21 January 2005; pp. 405–411. [Google Scholar]
- Ma, Y.; Hong, X.; Dong, S.; Cheng, C. 3D CBL: An efficient algorithm for general 3D packing problems. In Proceedings of the 48th Midwest Symposium on Circuits and Systems, Cincinnati, OH, USA, 7–10 August 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 1079–1082. [Google Scholar]
- Tang, X.; Tian, R.; Wong, D. Fast evaluation of sequence pair in block placement by longest common subsequence computation. In Proceedings of the Conference on Design, Automation and Test in Europe, Paris, France, 27–30 March 2000; pp. 106–111. [Google Scholar]
- Collette, Y.; Siarry, P. Multiobjective Optimization: Principles and Case Studies; Springer Science & Business Media: Berlin, Germany, 2004. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Ulungu, L.; Teghem, J.; Ost, C. Interactive simulated annealing in a multiobjective framework: Application to an industrial problem. J. Oper. Res. Soc. 1998, 49, 1044–1050. [Google Scholar] [CrossRef]
- Suppapitnarm, A.; Seffen, K.A.; Parks, G.T.; Clarkson, P. A simulated annealing algorithm for multiobjective optimization. Eng. Optim. 2000, 33, 59–85. [Google Scholar] [CrossRef]
- Suman, B. Study of simulated annealing based algorithms for multiobjective optimization of a constrained problem. Comput. Chem. Eng. 2004, 28, 1849–1871. [Google Scholar] [CrossRef]
- Chen, S.; Yoshimura, T. Fixed-outline floorplanning: Block-position enumeration and a new method for calculating area costs. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2008, 27, 858–871. [Google Scholar] [CrossRef]
- Karypis, G.; Aggarwal, R.; Kumar, V.; Shekhar, S. Multilevel hypergraph partitioning: Application in VLSI domain. In Proceedings of the 34th Annual Design Automation Conference, Anaheim, CA, USA, 9–13 June 1997; pp. 526–529. [Google Scholar]
- Karypis, G.; Kumar, V. Multilevel k-way hypergraph partitioning. In Proceedings of the 36th Annual ACM/IEEE Design Automation Conference, New Orleans, LA, USA, 21–25 June 1999; pp. 343–348. [Google Scholar]



| Circuit | # Blocks | # Terminals | # Nets |
|---|---|---|---|
| n100 | 100 | 334 | 885 |
| n200 | 200 | 564 | 1585 |
| n300 | 300 | 569 | 1893 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Li, Z.; Yao, Z. Multi-Objective Optimization in 3D Floorplanning. Electronics 2024, 13, 1696. https://doi.org/10.3390/electronics13091696
Jiang Z, Li Z, Yao Z. Multi-Objective Optimization in 3D Floorplanning. Electronics. 2024; 13(9):1696. https://doi.org/10.3390/electronics13091696
Chicago/Turabian StyleJiang, Zhongjie, Zhiqiang Li, and Zhenjie Yao. 2024. "Multi-Objective Optimization in 3D Floorplanning" Electronics 13, no. 9: 1696. https://doi.org/10.3390/electronics13091696
APA StyleJiang, Z., Li, Z., & Yao, Z. (2024). Multi-Objective Optimization in 3D Floorplanning. Electronics, 13(9), 1696. https://doi.org/10.3390/electronics13091696






