A W-Band Chebyshev Waveguide Bandpass Filter with Wide Stopband Performance
Abstract
:1. Introduction
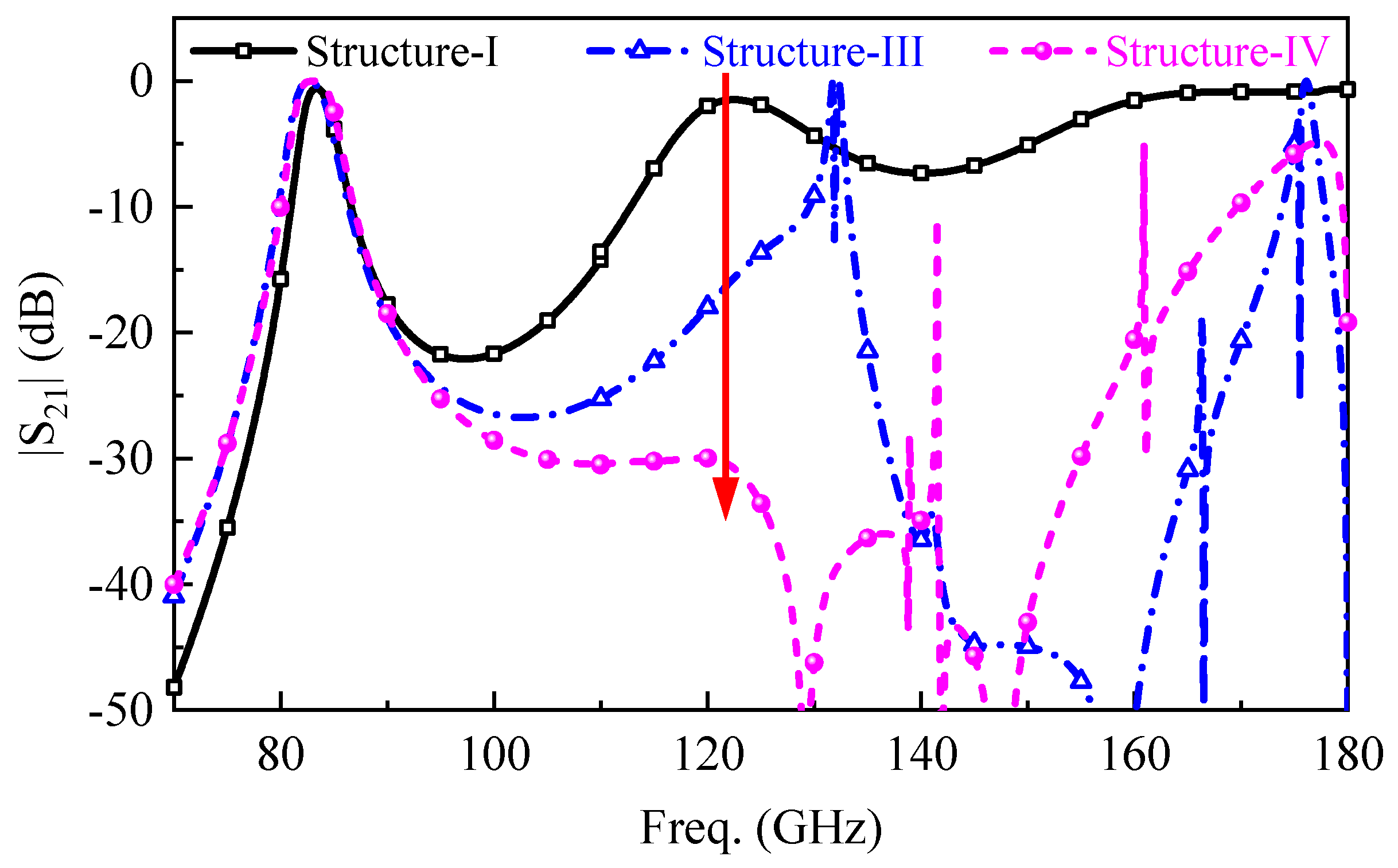
2. Spurious Suppression Methods
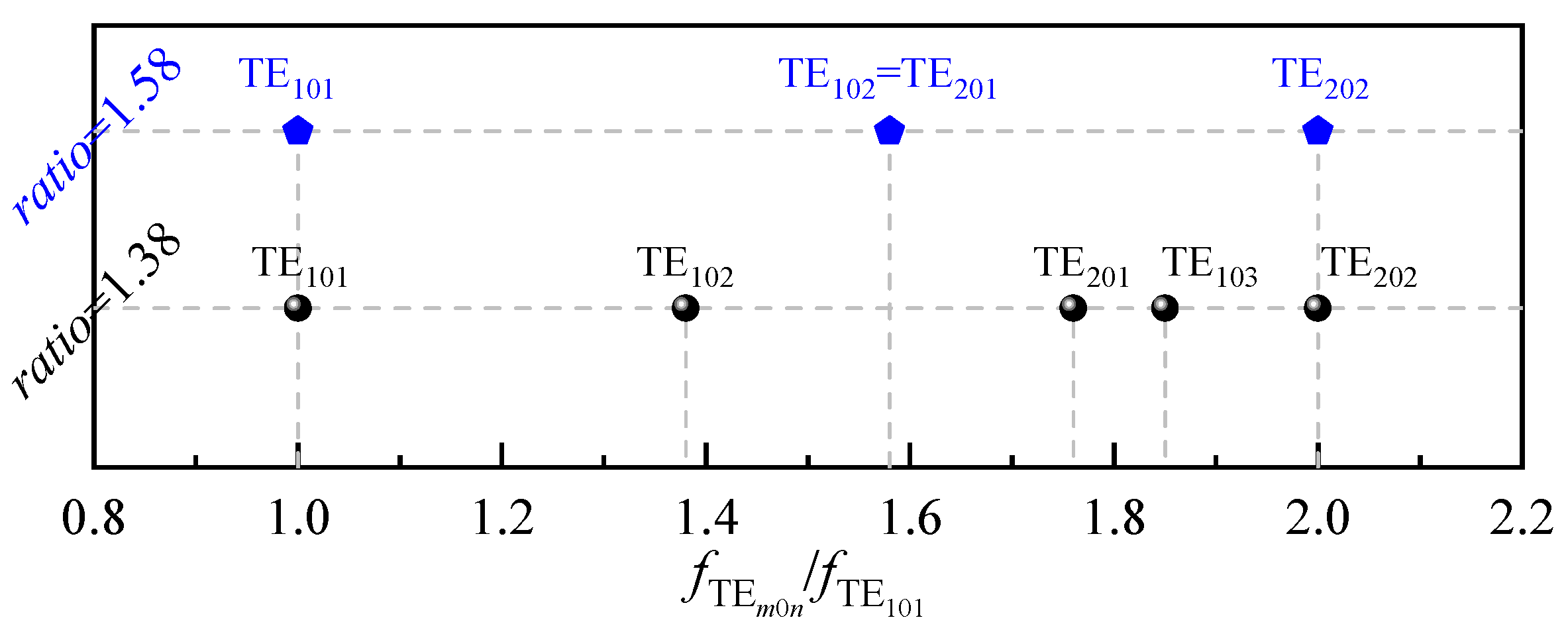
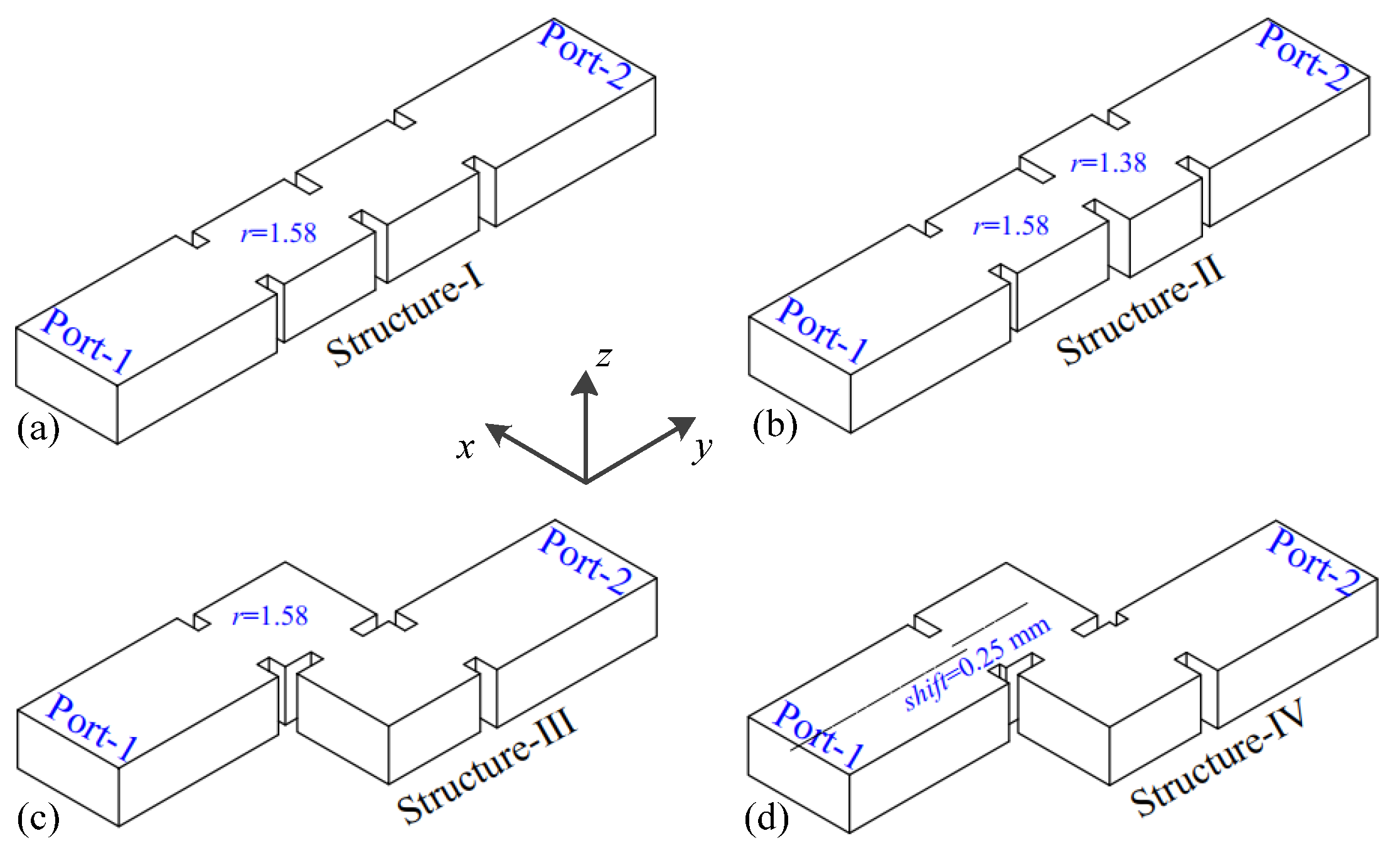
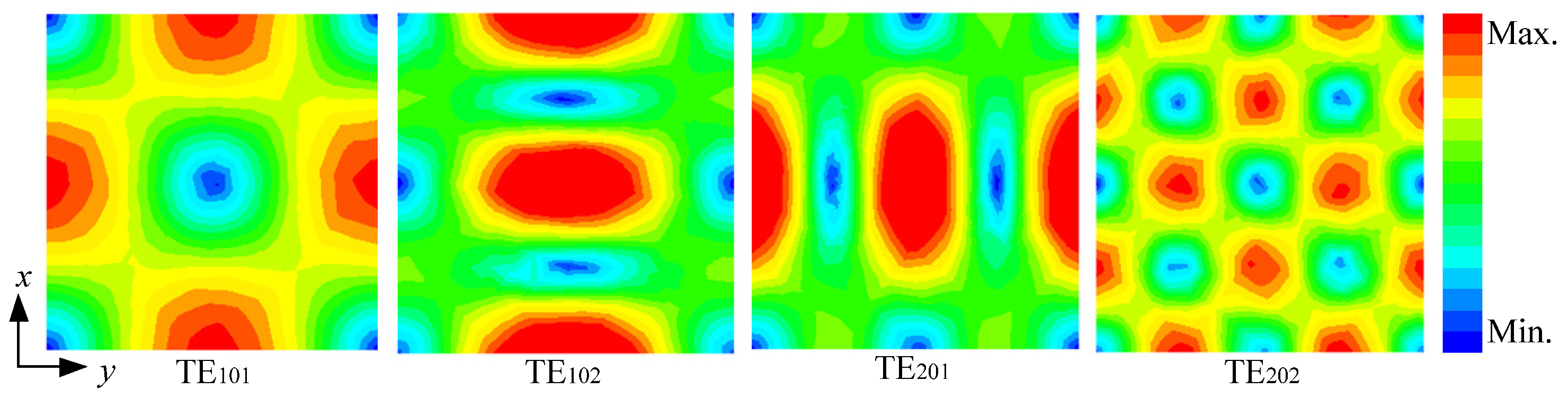
2.1. Harmonic-Staggered Method
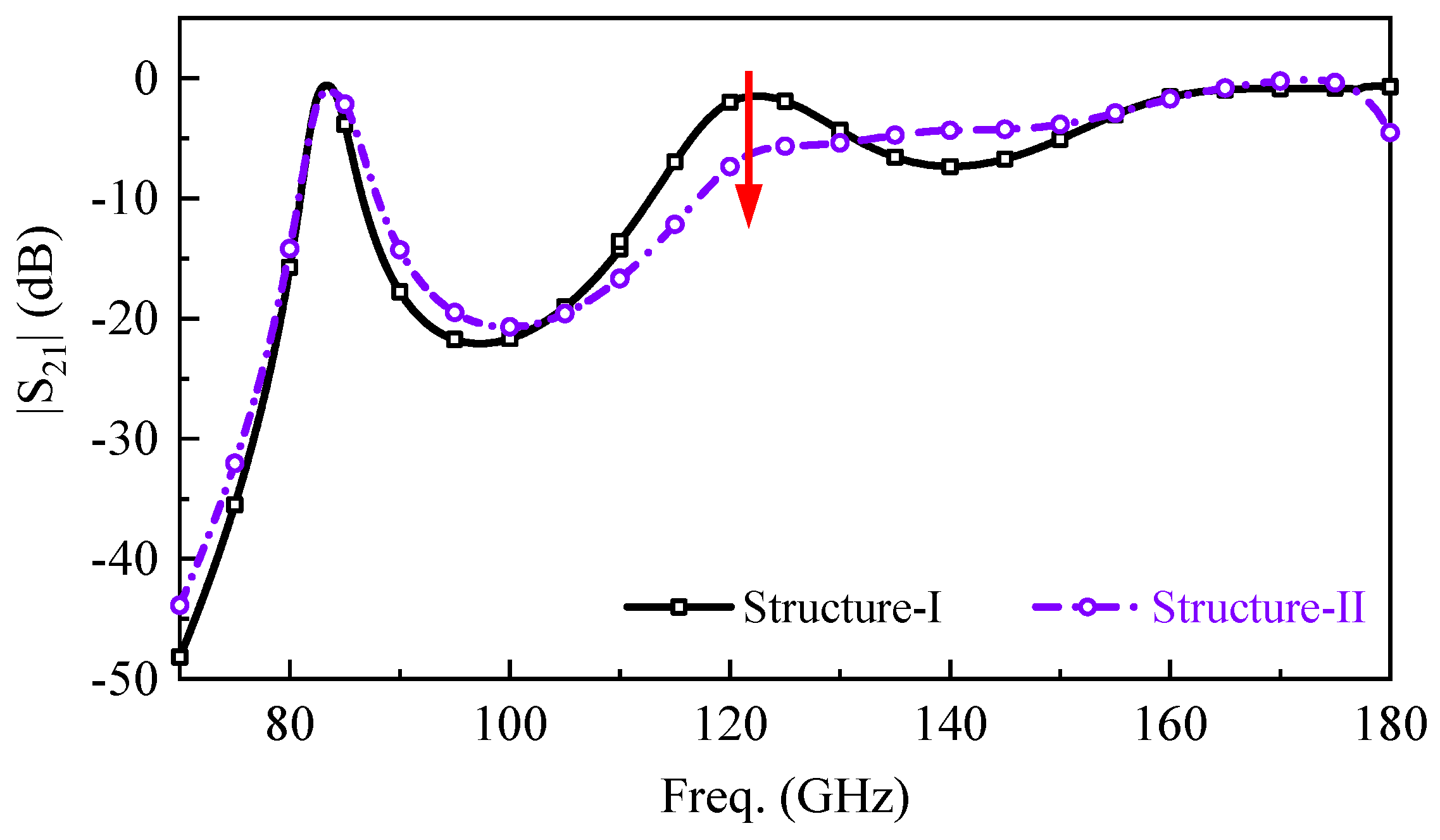
2.2. Harmonic-Coupling Control Scheme
3. Filter Design
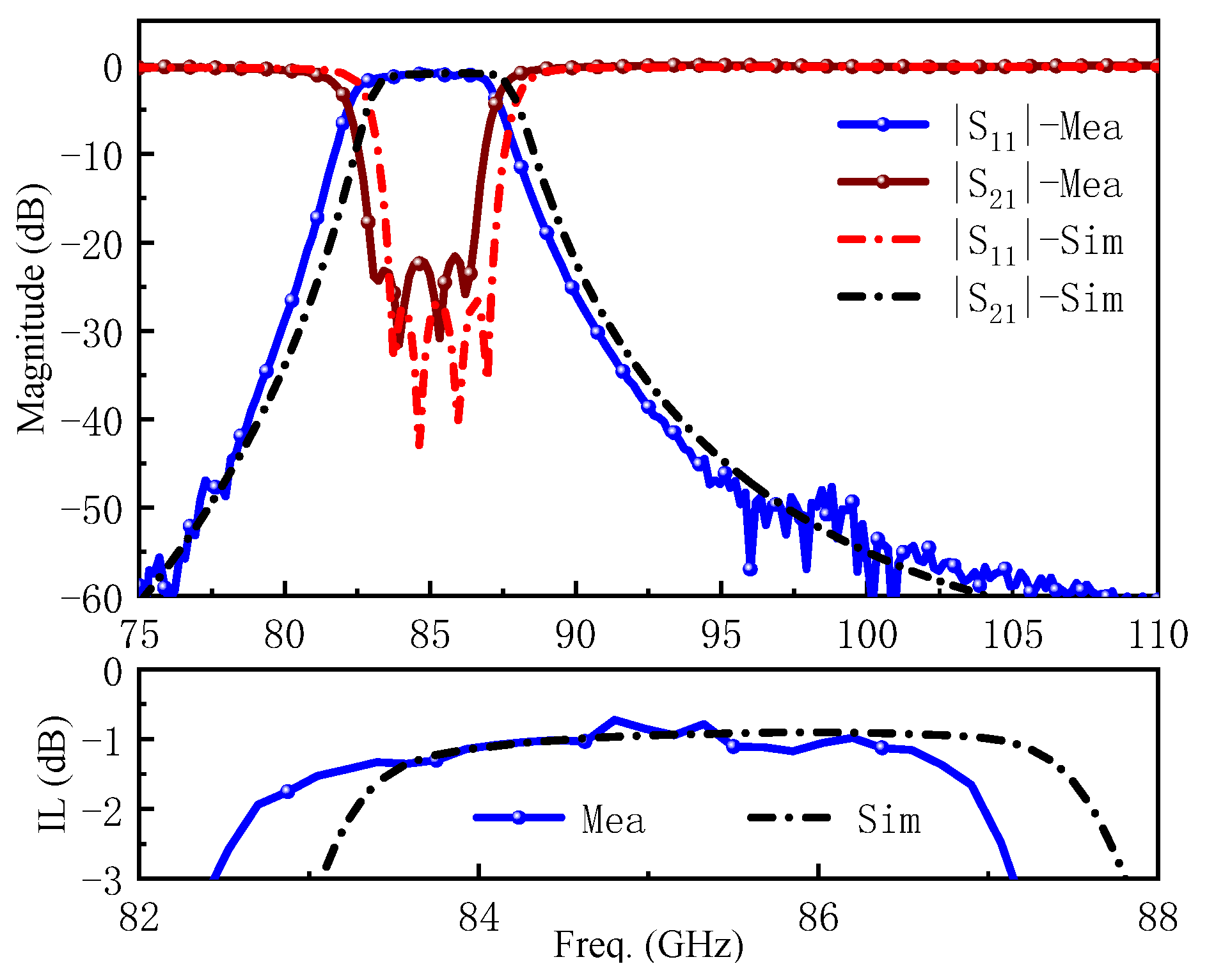
4. Simulation and Measurement Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Giordani, M.; Polese, M.; Mezzavilla, M.; Rangan, S.; Zorzi, M. Toward 6G networks: Use cases and technologies. IEEE Commun. Mag. 2020, 58, 55–61. [Google Scholar] [CrossRef]
- Cooper, K.B.; Chattopadhyay, G. Submillimeter-wave radar: Solid-state system design and applications. IEEE Microw. Mag. 2014, 15, 51–67. [Google Scholar] [CrossRef]
- Kulesa, C. Terahertz spectroscopy for astronomy: From comets to cosmology. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 232–240. [Google Scholar] [CrossRef]
- Li, S.; Yao, Q.; Liu, D.; Duan, W.; Zhang, K.; Jin, J.; Lin, Z.; Wu, F.; Yang, J.; Miao, W.; et al. Terahertz superconducting radiometric spectrometer in Tibet for atmospheric science. J. Infrared Millim. Terahertz Waves 2019, 40, 166–177. [Google Scholar] [CrossRef]
- IAkyildiz, F.; Kak, A.; Nie, S. 6G and beyond: The future of wireless communications systems. IEEE Access 2020, 8, 133995–134030. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Sun, J.; Song, Z.; Ye, H.; Zhang, Y.; Zhang, L. Experimental study on a high-power subterahertz source generated by an overmoded surface wave oscillator with fast startup. IEEE Trans. Electron. Devices 2013, 60, 2931–2935. [Google Scholar] [CrossRef]
- Mehdi, I.; Siles, J.; Lee, C.; Schlecht, E. THz diode technology: Status, prospects, and applications. Proc. IEEE 2017, 105, 990–1007. [Google Scholar] [CrossRef]
- Peter Westig, M.; Justen, M.; Jacobs, K.; Stutzki, J.; Schultz, M.; Schomacker, F.; Honingh, N. A 490 GHz planar circuit balanced Nb-Al2O3-Nb quasiparticle mixer for radio astronomy: Application to quantitative local oscillator noise determination. J. Appl. Phys. 2012, 112, 093919. [Google Scholar] [CrossRef]
- Westig, P.; Klapwijk, M. Josephson parametric reflection amplifier with integrated directionality. Phys. Rev. Appl. 2018, 9, 064010. [Google Scholar] [CrossRef]
- Zhu, Z.; Hu, W.; Qin, T.; Li, S.; Li, X.; Zeng, J.; Lin, X.; Ligthart, L.P. A high-precision terahertz retrodirective antenna array with navigation signal at a different frequency. Front. Inform. Technol. Electron. Eng. 2020, 21, 377–383. [Google Scholar] [CrossRef]
- Ding, J.-Q.; Shi, S.-C.; Zhou, K.; Zhao, Y.; Liu, D.; Wu, W. WR-3 band quasi-elliptical waveguide filters using higher order mode resonances. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 302–309. [Google Scholar] [CrossRef]
- Hong, J.-S.; Lancaster, M.J. Microstrip Filters for RF/Microwave Applications; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Wang, Y.; Yang, B.; Tian, Y.; Donnan, R.S.; Lancaster, M.J. Micromachined thick mesh filters for millimeter-wave and terahertz applications. IEEE Trans. Terahertz Sci. Technol. 2014, 4, 247–253. [Google Scholar] [CrossRef]
- Hao, Z.-C.; Ding, W.-Q.; Hong, W. Developing low-cost W-band SIW bandpass filters using the commercially available printed-circuitboard technology. IEEE Trans. Microw. Theory Tech. 2016, 64, 1775–1786. [Google Scholar] [CrossRef]
- Xiao, Y.; Shan, P.; Zhao, Y.; Sun, H.; Yang, F. Design of a W-band GaAs-based SIW chip filter using higher order mode resonances. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 104–106. [Google Scholar] [CrossRef]
- Barry, P.S.; Shirokoff, E.; Kovács, A.; Reck, T.J.; Hailey-Dunsheath, S.; McKenney, C.M.; Swenson, L.J.; Hollister, M.I.; Leduc, H.G.; Doyle, S.; et al. Electromagnetic design for SuperSpec, a lithographically-patterned millimeter-wave spectro-graph. Proc. SPIE 2012, 8452, 738–747. [Google Scholar]
- Eblabla, A.M.; Li, X.; Wallis, D.J.; Guiney, I.; Elgaid, K. GaN on low-resistivity silicon THz high-Q passive device technology. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 93–97. [Google Scholar] [CrossRef]
- Song, S.; Yoo, C.S.; Seo, K.S. W-band bandpass filter using micromachined air-waveguide resonator with current probes. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 205–207. [Google Scholar] [CrossRef]
- Song, S.; Seo, K.-S. A -band air-cavity filter integrated on a thin-film substrate. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 200–202. [Google Scholar] [CrossRef]
- Shang, X.; Penchev, P.; Guo, C.; Lancaster, M.J.; Dimov, S.; Dong, Y.; Favre, M.; Billod, M.; de Rijk, E. W-band waveguide filters fabricated by laser micromachining and 3-D printing. IEEE Trans. Microw. Theory Tech. 2016, 64, 2572–2580. [Google Scholar] [CrossRef]
- Leal-Sevillano, C.A.; Pisano, G.; Montejo-Garai, J.R.; Maffei, B.; Ruiz-Cruz, J.A.; Ng, M.W.; Rebollar, J.M. Development of low loss waveguide filters for radio-astronomy applications. Infrared Phys. Technol. 2013, 61, 224–229. [Google Scholar] [CrossRef]
- Leal-Sevillano, C.A.; Montejo-Garai, J.R.; Ke, M.; Lancaster, M.J.; Ruiz-Cruz, J.A.; Rebollar, J.M. A pseudo-elliptical response filter at W-band fabricated with thick SU-8 photo-resist technology. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 105–107. [Google Scholar] [CrossRef]
- Chattopadhyay, G.; Reck, T.; Lee, C.; Jung-Kubiak, C. Micromachined packaging for terahertz systems. Proc. IEEE 2017, 105, 1139–1150. [Google Scholar] [CrossRef]
- Xu, J.; Ding, J.-Q.; Zhao, Y.; Ge, J.-X. W-band broadband waveguide filter based on H-plane offset coupling. J. Infrared Milli. Terahertz Waves 2019, 40, 412–418. [Google Scholar] [CrossRef]
- Shang, X.; Lancaster, M.; Dong, Y.-L. W-band waveguide filter based on large TM120 resonators to ease CNC milling. IET Electron. Lett. 2017, 53, 488–490. [Google Scholar] [CrossRef]
- Ding, J.; Liu, D.; Shi, S.C.; Wu, W. W-band quasi-elliptical waveguide filter with cross-coupling and source-load coupling. Electron. Lett. 2016, 52, 1960–1961. [Google Scholar] [CrossRef]
- Leal-Sevillano, C.A.; Montejo-Garai, J.R.; Ruiz-Cruz, J.A.; Rebollar, J.M. Low-loss elliptical response filter at 100 GHz. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 459–461. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, K.-D.; Li, J.; Guo, Y.-J.; Zhang, A.; Chen, Q. Millimeter-wave E-plane waveguide bandpass filters based on spoof surface plasmon polaritons. IEEE Trans. Microw. Theory Tech. 2022, 70, 4399–4409. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, Z.-Y.; Liu, B.-Y.; Zhang, X.-F.; Wang, C.; Wu, W.-W.; Yuan, N.-C. W-band E-plane waveguide filter using compact beeline resonator. IEEE Microw. Wirel. Compon. Lett. 2022, 32, 289–292. [Google Scholar] [CrossRef]
- Bartlett, C.; Bornemann, J.; Höft, M. Improved TM dual-mode filters with reduced fabrication complexity. IEEE J. Microw. 2023, 3, 60–69. [Google Scholar] [CrossRef]
- Xu, K.-D.; Xia, S.; Guo, Y.; Cui, J.; Zhang, A.; Chen, Q. W-Band E-plane waveguide bandpass filter based on meander ring resonator. IEEE Microw. Wirel. Compon. Lett. 2021, 31, 1267–1270. [Google Scholar] [CrossRef]
- Cameron, R.J.; Yu, M.; Wang, Y. Direct-coupled microwave filters with single and dual stopbands. IEEE Trans. Microw. Theory Tech. 2005, 53, 3288–3297. [Google Scholar] [CrossRef]
- Budimir, D. Optimized E-plane bandpass filters with improved stopband performance. IEEE Trans. Microw. Theory Tech. 1997, 45, 212–220. [Google Scholar] [CrossRef]
- Morelli, M.; Hunter, I.; Parry, R.; Postoyalko, V. Stopband performance improvement of rectangular waveguide filters using stepped impedance resonators. IEEE Trans. Microw. Theory Tech. 2002, 50, 1657–1664. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, C.-X.; Wu, W. Resonance characteristics of substrate-integrated rectangular cavity and their applications to dualband and wide-stopband bandpass filters design. IEEE Trans. Microw. Theory Tech. 2017, 65, 1511–1524. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, F.; Yang, Y.; Shi, X. An effective approach to suppressing the spurious mode in rectangular waveguide filters. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 703–705. [Google Scholar] [CrossRef]
- Chu, P.; Guo, L.; Zhang, L.; Xu, F.; Hong, W.; Wu, K. Wide stopband substrate integrated waveguide filter implemented by orthogonal ports’ offset. IEEE Trans. Microw. Theory Tech. 2020, 68, 964–970. [Google Scholar] [CrossRef]
- Cameron, R.J. Advanced coupling matrix synthesis techniques for microwave filters. IEEE Trans. Microw. Theory Tech. 2003, 51, 1–10. [Google Scholar] [CrossRef]
- Soto, P.; Tarín, E.; Boria, V.E.; Vicente, C.; Gil, J.; Gimeno, B. Accurate Synthesis and Design of Wideband and Inhomogeneous Inductive Waveguide Filters. IEEE Trans. Microw. Theory Tech. 2010, 58, 2220–2230. [Google Scholar] [CrossRef]
- Groiss, S. Numerical Analysis of Lossy Cavity Resonators. Ph.D. Thesis, Technical University of Graz, Graz, Austria, June 1996. [Google Scholar]

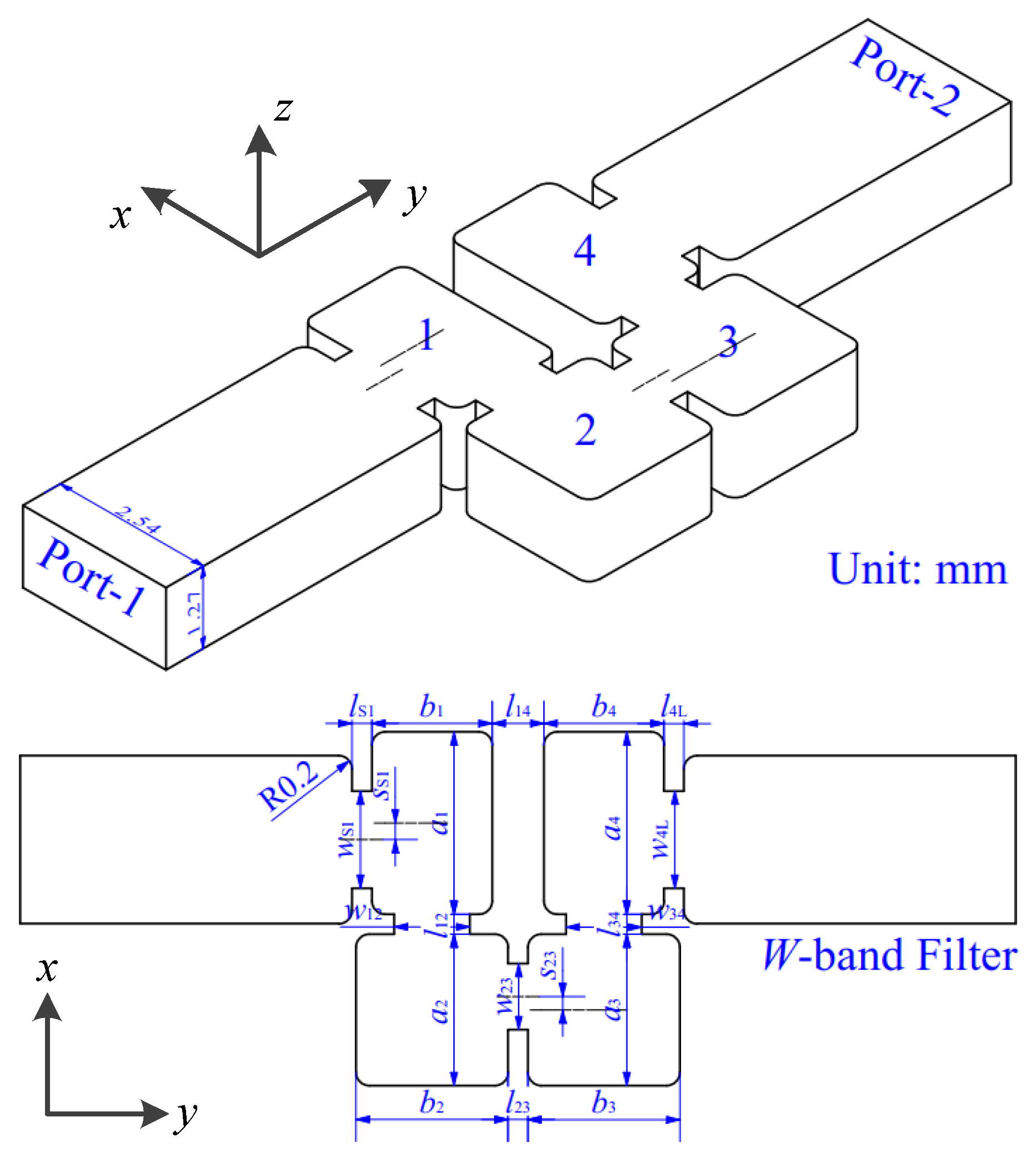


| MS1 | M12 | M23 | M34 | M4L | |
|---|---|---|---|---|---|
| Coupling coefficient | 0.0674 | 0.061 | 0.045 | 0.061 | 0.0674 |
| Para. | Value | Para. | Value | Para. | Value | Para. | Value |
|---|---|---|---|---|---|---|---|
| a | 2.54 | a3 | a1 | w12 | 1.14 | L14 | 0.78 |
| b | 1.27 | l3 | l1 | l12 | 0.3 | w4L | wS1 |
| a1 | 2.76 | a4 | a2 | w23 | 1.0 | l4L | lS1 |
| l1 | 1.81 | l4 | l2 | l23 | 0.3 | sS1 | 0.25 |
| a2 | 2.29 | wS1 | 1.47 | w34 | w12 | s23 | 0.2 |
| l2 | a2 | lS1 | 0.3 | l34 | l12 | R | 0.2 |
| Ref. | Center Frequency | Filter Order | No. of TZs | 3 dB FBW | IL/dB (Average) | RL/dB | Stopband Suppression | Technology |
|---|---|---|---|---|---|---|---|---|
| [14] | 80 GHz | 4 | 1 | 2.5% | 3.9 | 10 | No | PCB-based SIW |
| [15] | 93 GHz | 4 | 2 | 3.4% | 4.3 | 13.5 | No | GaAs-based SIW |
| [18] | 93.7 GHz | 4 | — | 4.9% | 1.3 | 16 | No | DRIE |
| [19] | 94 GHz | 2 | — | 1.3% | 1.75 | 15 | No | Wet-etching |
| [20] | 100 GHz | 4 | — | 4% | 0.8 | 15 | No | Laser Micromachining |
| [20] | 87.5 GHz | 4 | — | 11.5% | 0.5 | 18 | No | 3D-printing |
| [21] | 90 GHz | 10 | — | 20% | 0.4 | 15 | 10th-order, 1st spurious@1.5f0 | Electroforming |
| [22] | 100 GHz | 4 | 2 | 5% | 1.2 | 10 | No | SU-8 Photoresist |
| [24] | 91.3 GHz | 5 | — | 20% | 0.6 | 15 | No | Offset-coupling, CNC |
| [25] | 100 GHz | 4 | — | 6% | 0.5 | 13 | No | TM120-mode, CNC |
| [26] | 92.6 GHz | 4 | 4 | 5.5% | 1.2 | 15 | No | Cross-coupling, CNC |
| [27] | 100 GHz | 4 | 1 | 10% | 0.6 | 18 | No | Extracted pole, CNC |
| [29] | 88.55 GHz | 2 | 3 | 3.6% | 1.15 | 18 | No | PCB, CNC |
| [30] | 90 GHz | 4 | 2 | 7.3% | 0.63 | 20 | No | TM-mode, CNC |
| Proposed Filter | 85 GHz | 4 | — | 5.5% | 0.9 | 20 | Yes, better than −25 dB, 1st spurious@2f0 | CNC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Hu, W.; Xu, K.; Bai, Y.; Li, S. A W-Band Chebyshev Waveguide Bandpass Filter with Wide Stopband Performance. Electronics 2024, 13, 1793. https://doi.org/10.3390/electronics13091793
Zhu Z, Hu W, Xu K, Bai Y, Li S. A W-Band Chebyshev Waveguide Bandpass Filter with Wide Stopband Performance. Electronics. 2024; 13(9):1793. https://doi.org/10.3390/electronics13091793
Chicago/Turabian StyleZhu, Zhongbo, Weidong Hu, Kaida Xu, Yuming Bai, and Sheng Li. 2024. "A W-Band Chebyshev Waveguide Bandpass Filter with Wide Stopband Performance" Electronics 13, no. 9: 1793. https://doi.org/10.3390/electronics13091793
APA StyleZhu, Z., Hu, W., Xu, K., Bai, Y., & Li, S. (2024). A W-Band Chebyshev Waveguide Bandpass Filter with Wide Stopband Performance. Electronics, 13(9), 1793. https://doi.org/10.3390/electronics13091793











