Enhancing Fault Ride-Through and Power Quality in Wind Energy Systems Using Dynamic Voltage Restorer and Battery Energy Storage System
Abstract
1. Introduction
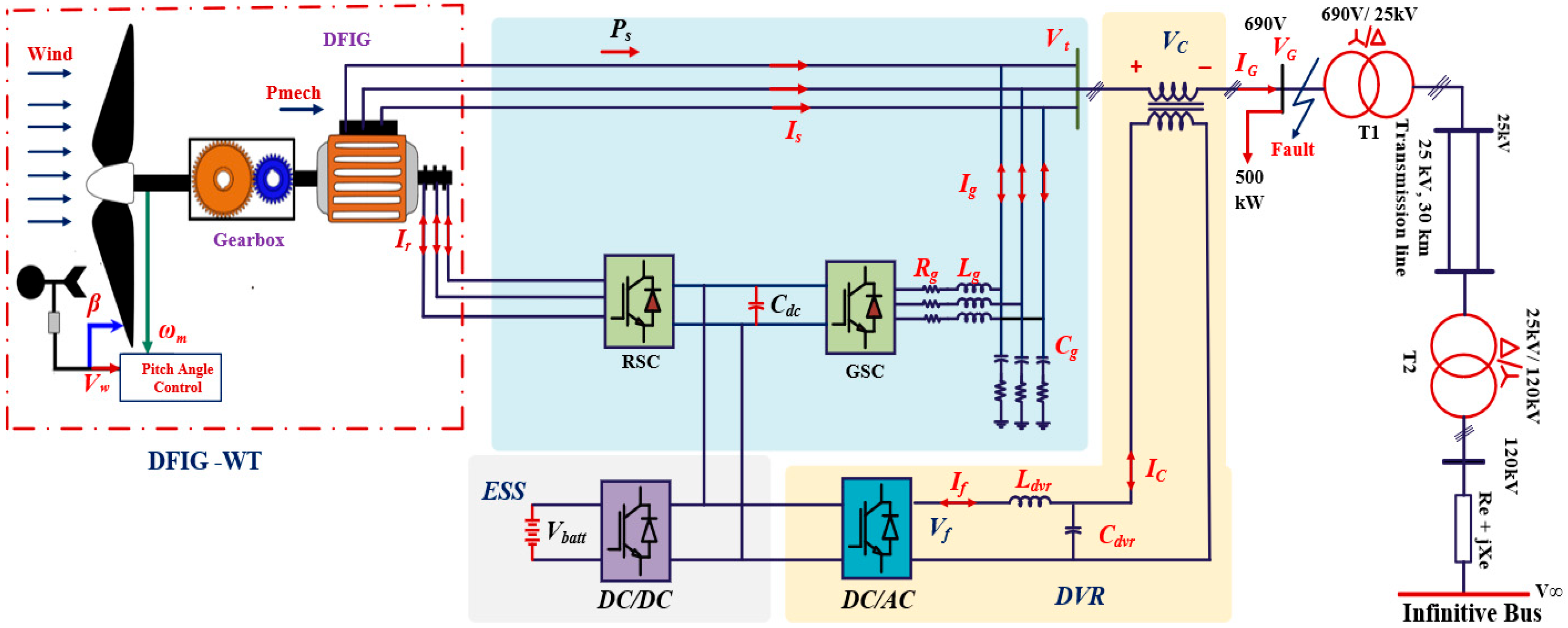
- DVR-Based System Design: This study introduces an innovative DVR configuration, integrated at the WES terminal. It replaces the conventional DC source of the DVR with the DC link of a DFIG and a BESS. This ensures protection against grid disturbances and effectively mitigates system instabilities during grid faults.
- Comprehensive Disturbance Evaluation: The proposed system is rigorously analyzed under various grid voltage disturbances, including voltage sags, swells, flickers, and harmonics, to validate its robustness and effectiveness.
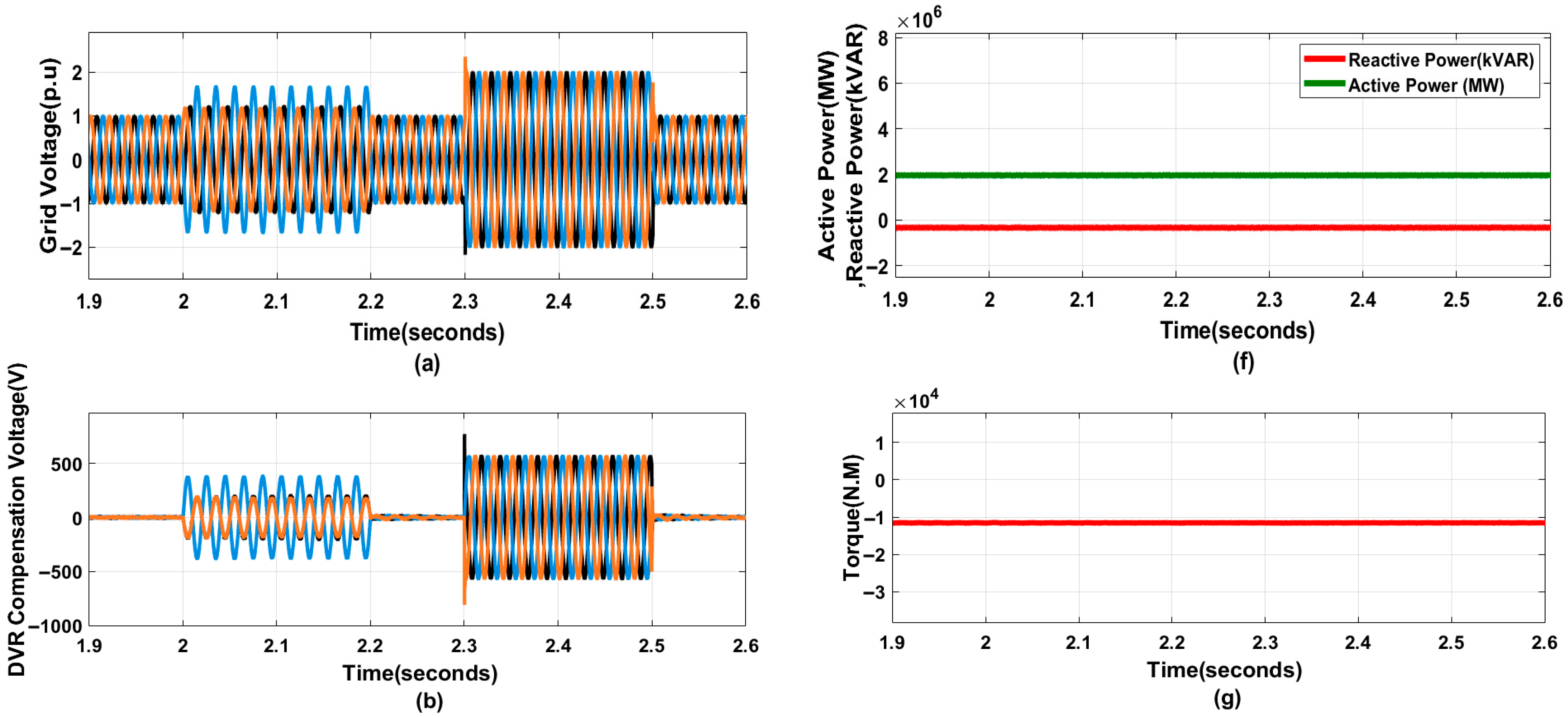
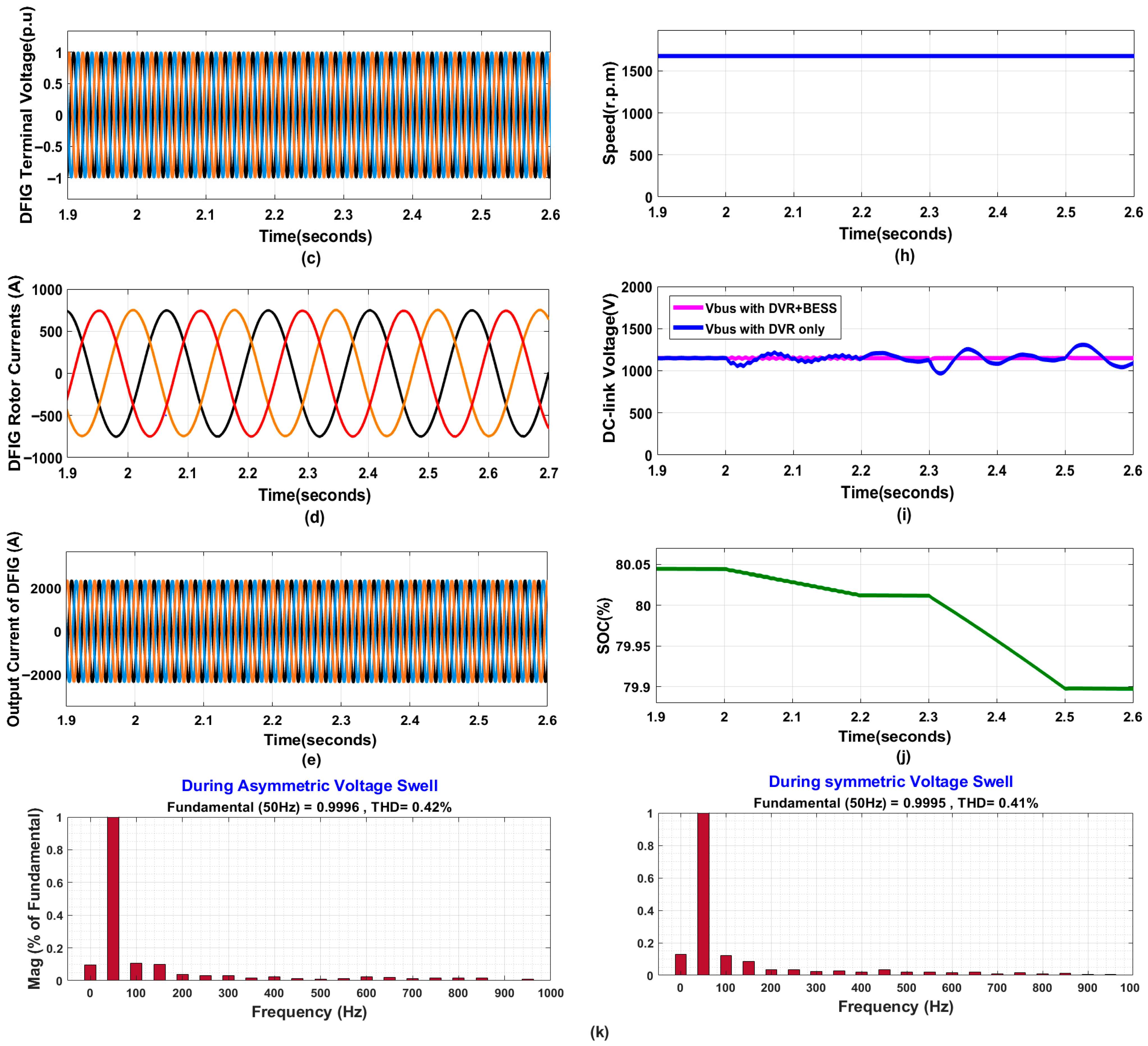
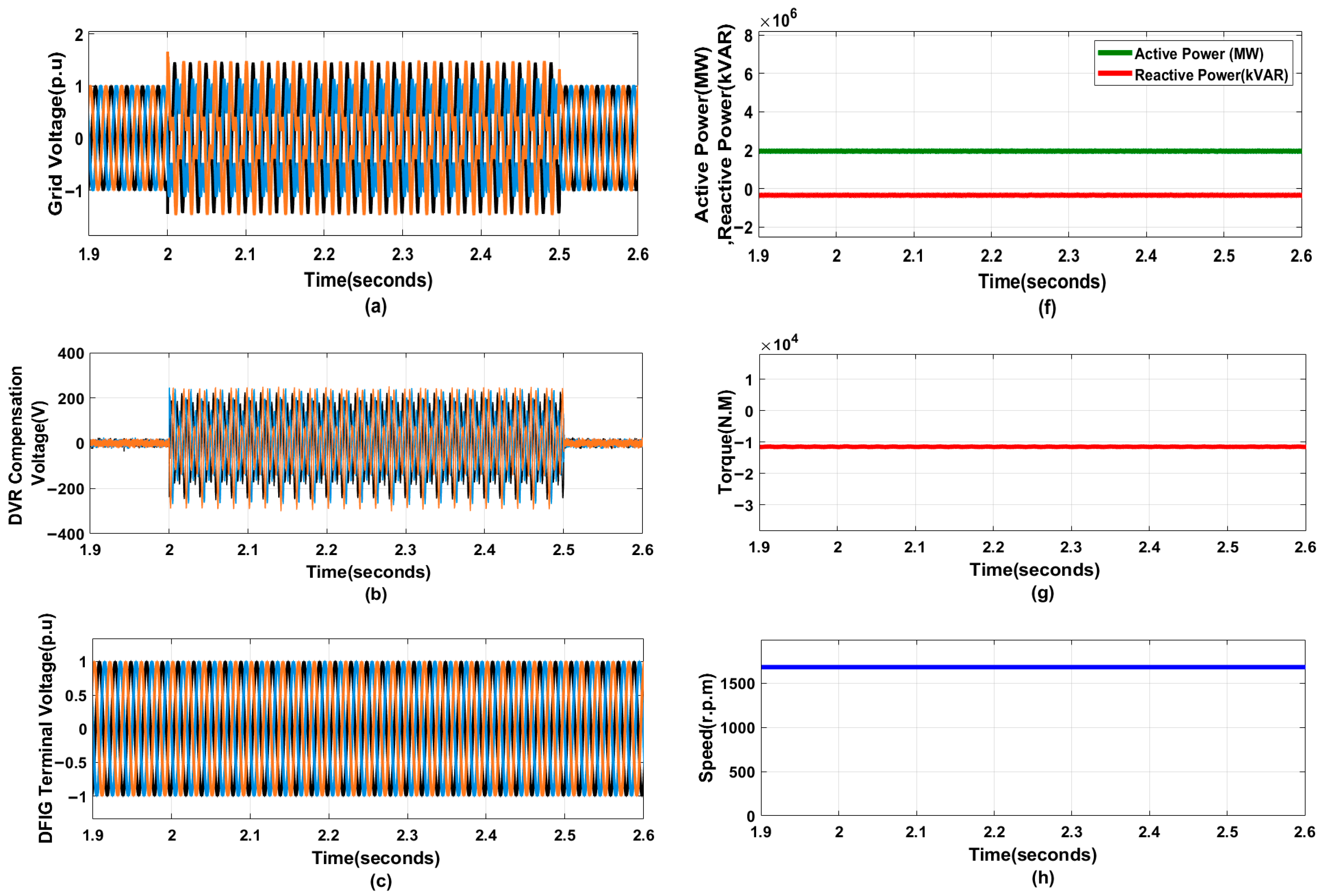
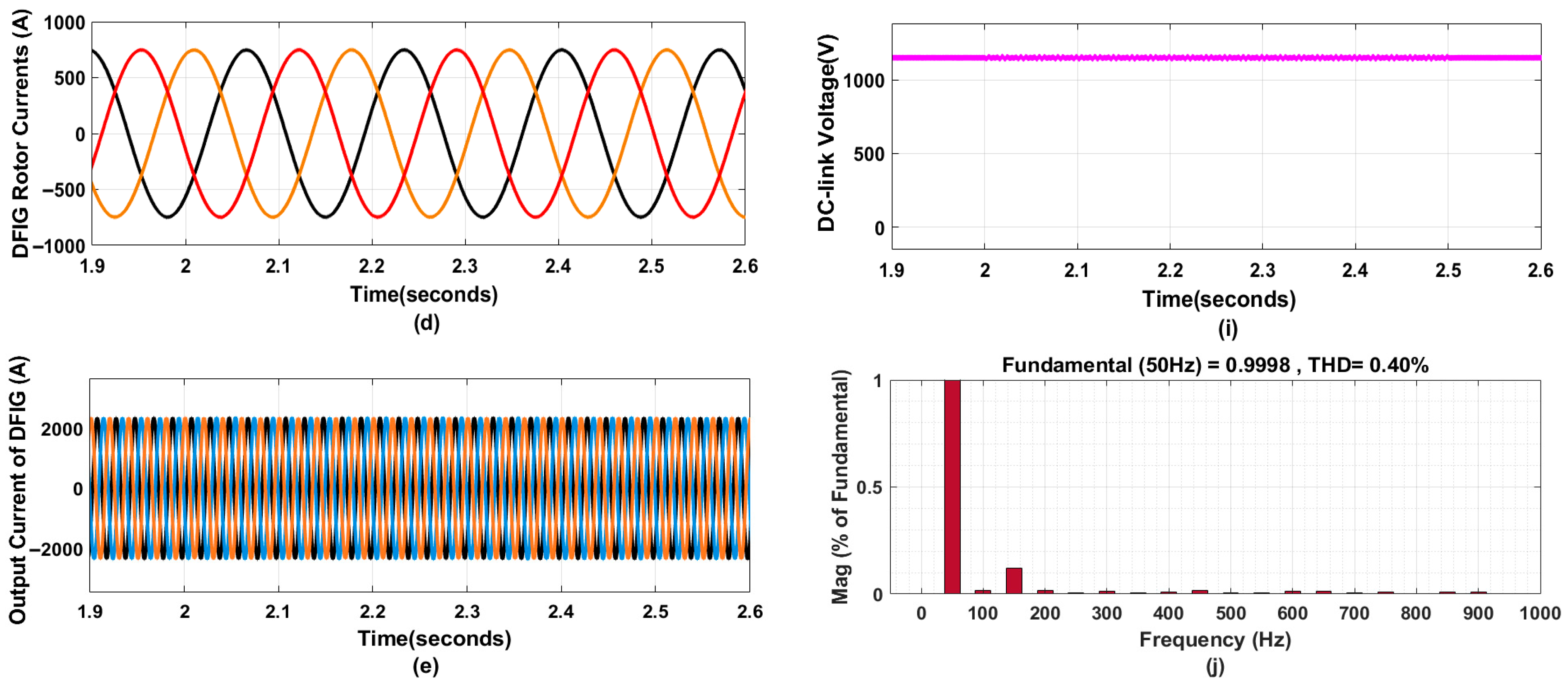
- Enhanced Stability and FRT: The simulation results show that the proposed approach augments the stability and FRT capability of the DFIG-based WES by keeping key parameters, including rotor and output currents, active and reactive power, and DC voltage, within acceptable limits during faults.
- Harmonic Reduction: The system achieves excellent harmonic rejection, maintaining Total Harmonic Distortion (THD) levels below 5%, thereby adhering to IEEE standards and improving overall PQ.
2. Configuration, Operation, and Modeling of the Proposed System
2.1. Modeling Equations of the DFIG-WES
2.1.1. DFIG During Normal Operation
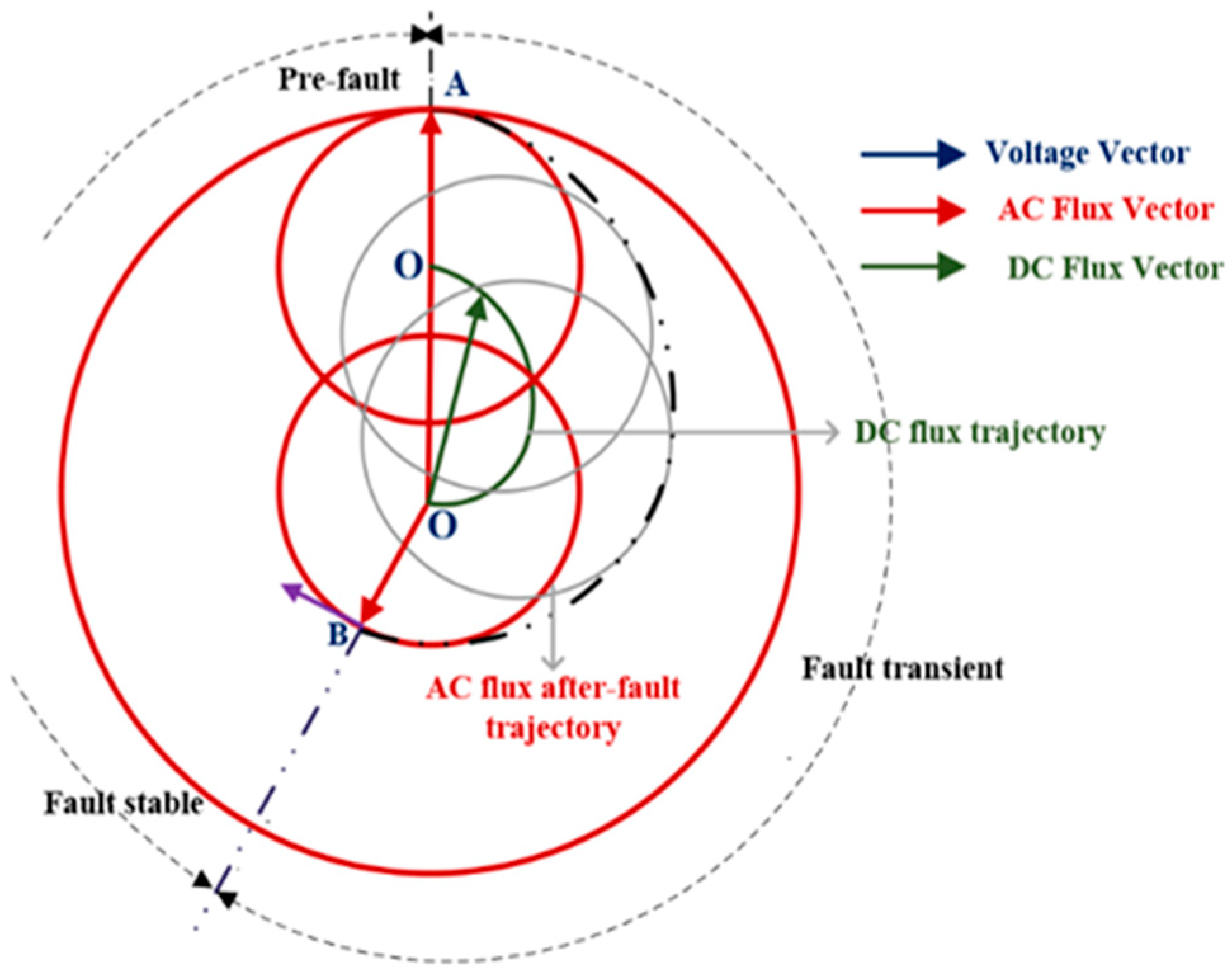
2.1.2. DFIG During Grid Faults
2.2. Grid Code Requirements
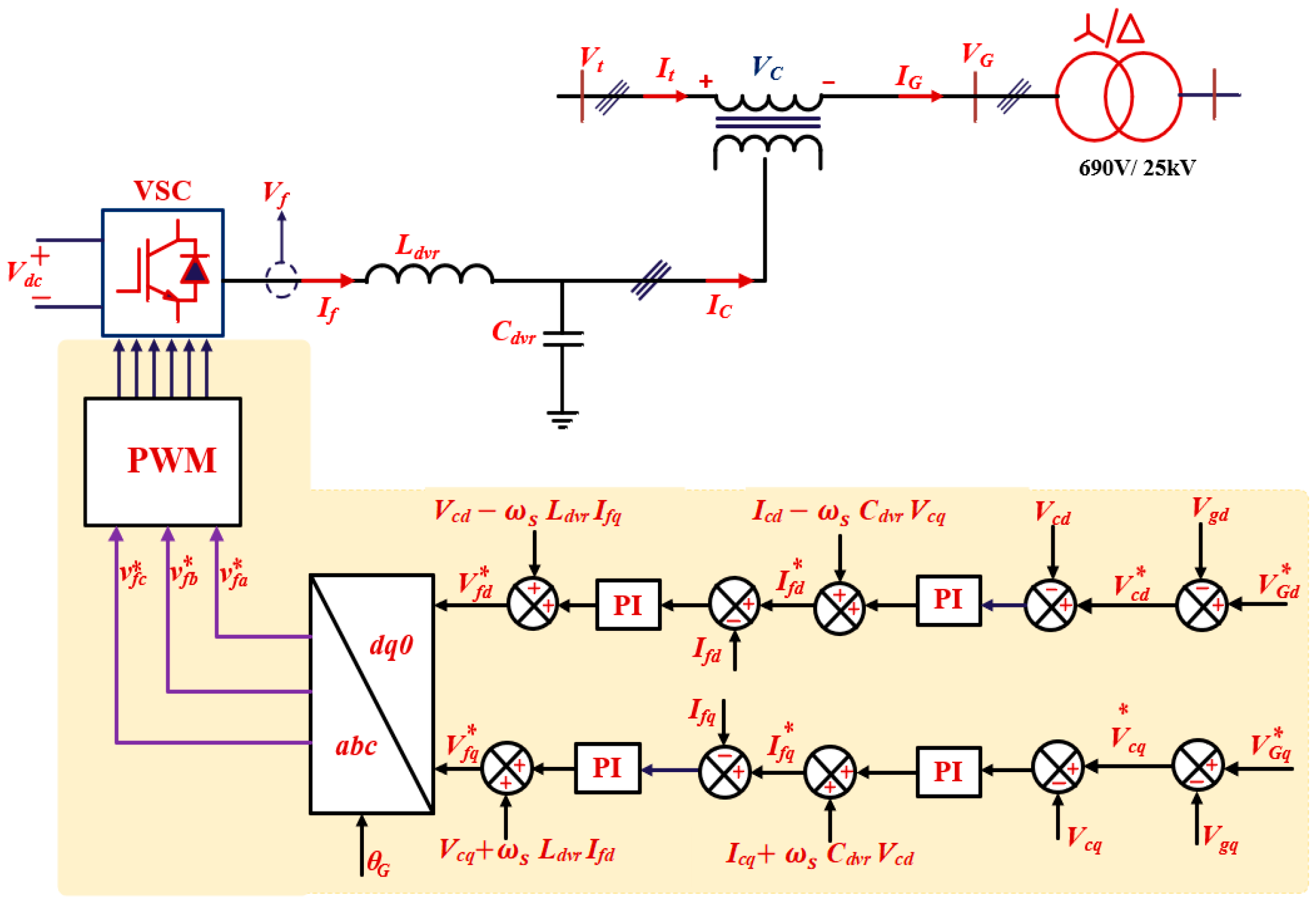
2.3. DVR Model and Design
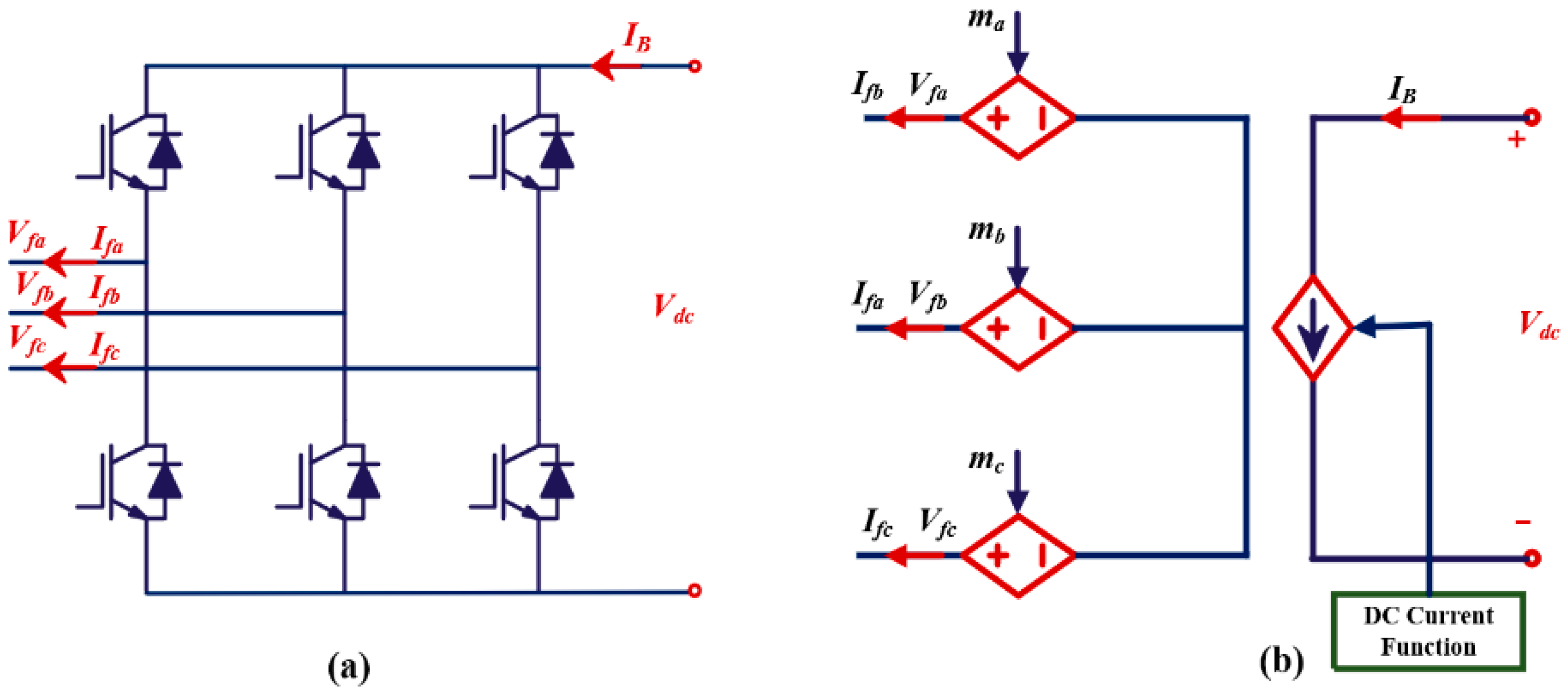
2.3.1. DVR Model
2.3.2. DVR Parameters Design
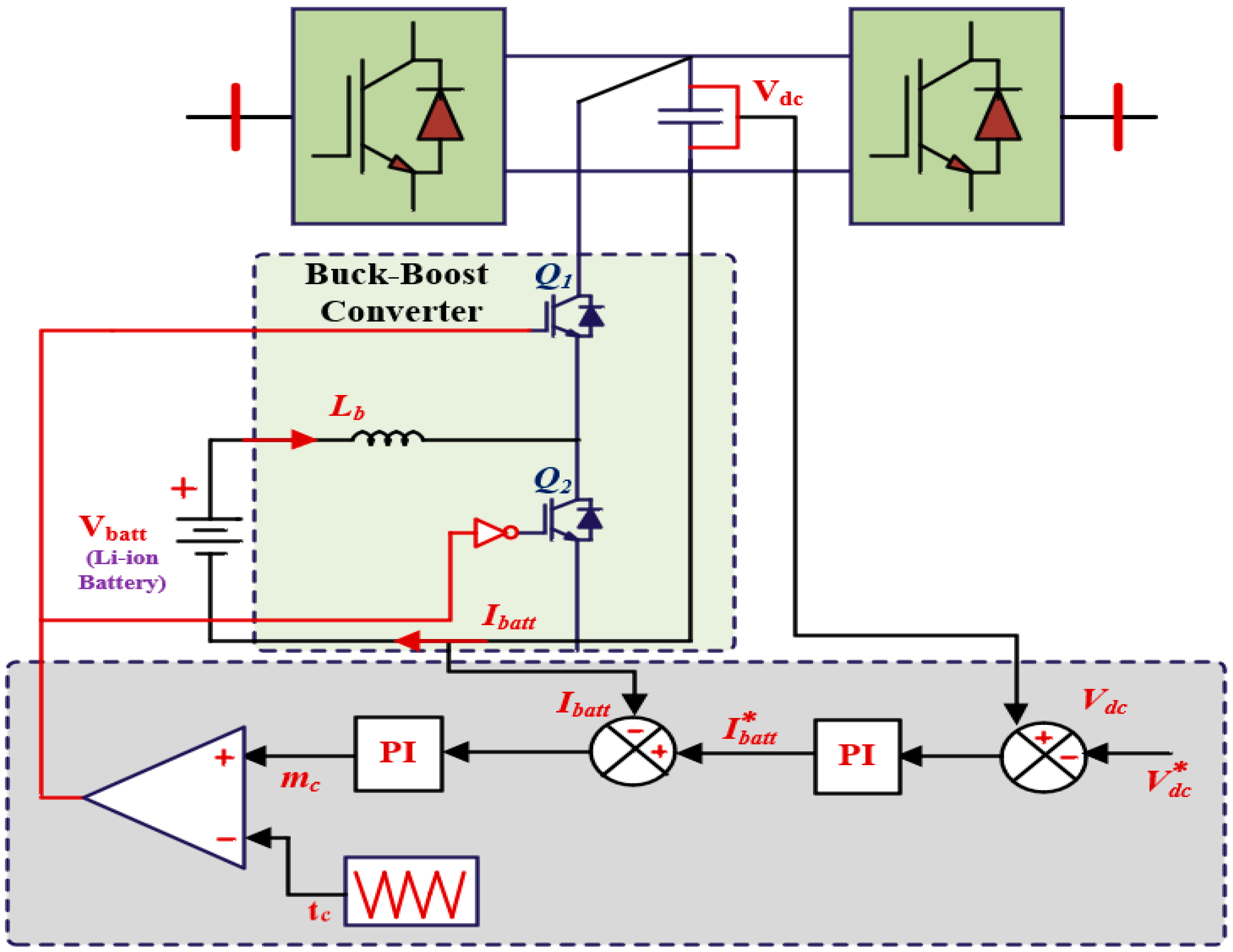
2.4. Battery Energy Storage System Model
2.4.1. Battery Modeling
2.4.2. DC/DC Converter Modeling
2.4.3. Parameter Design of BESS and DC/DC Converter
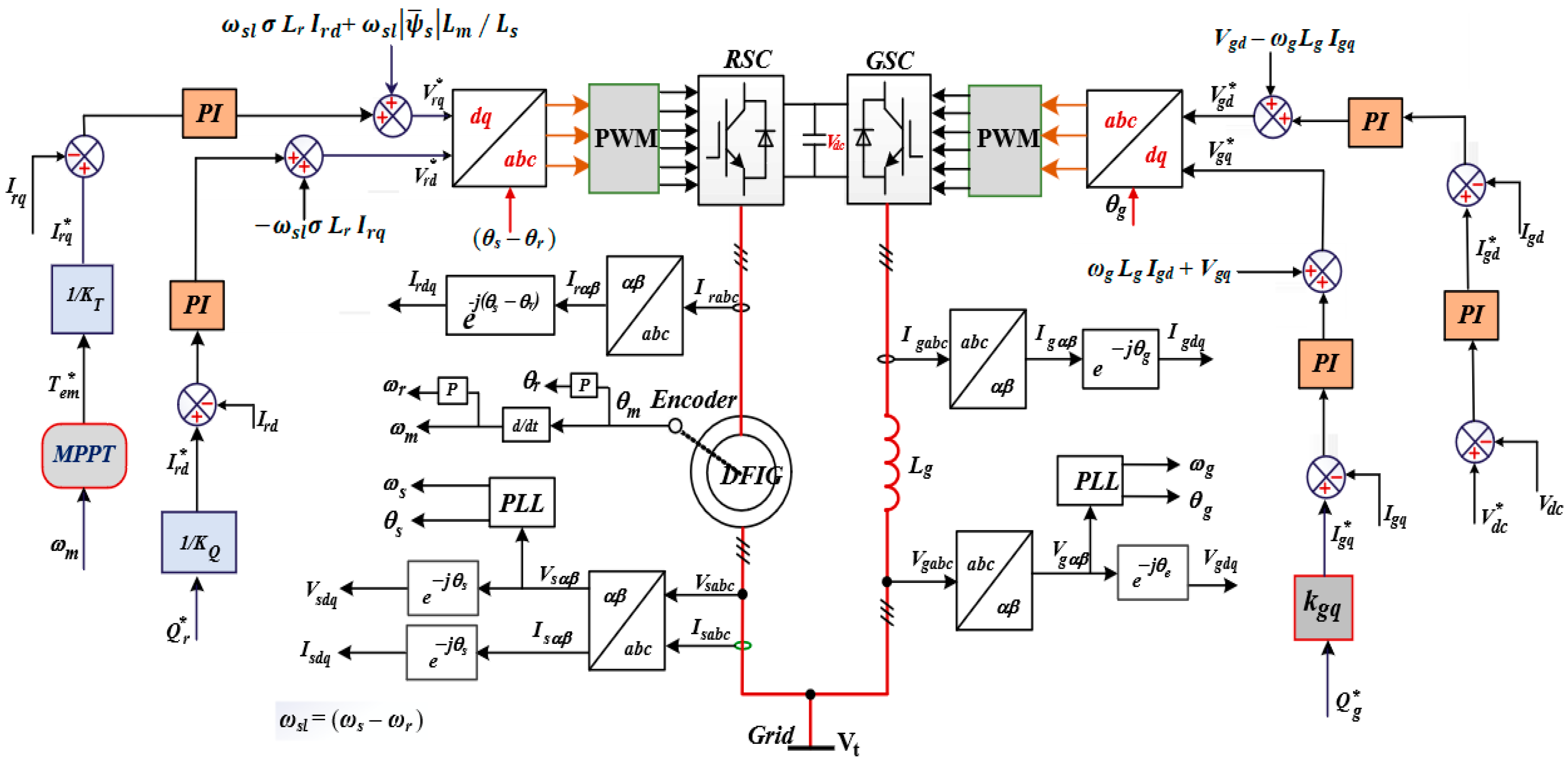
3. Control Schemes for Studied System
3.1. Control of Back-to-Back Converters
3.2. Control of DVR
3.3. Control of DC/DC Converter
4. Simulation Results and Discussion
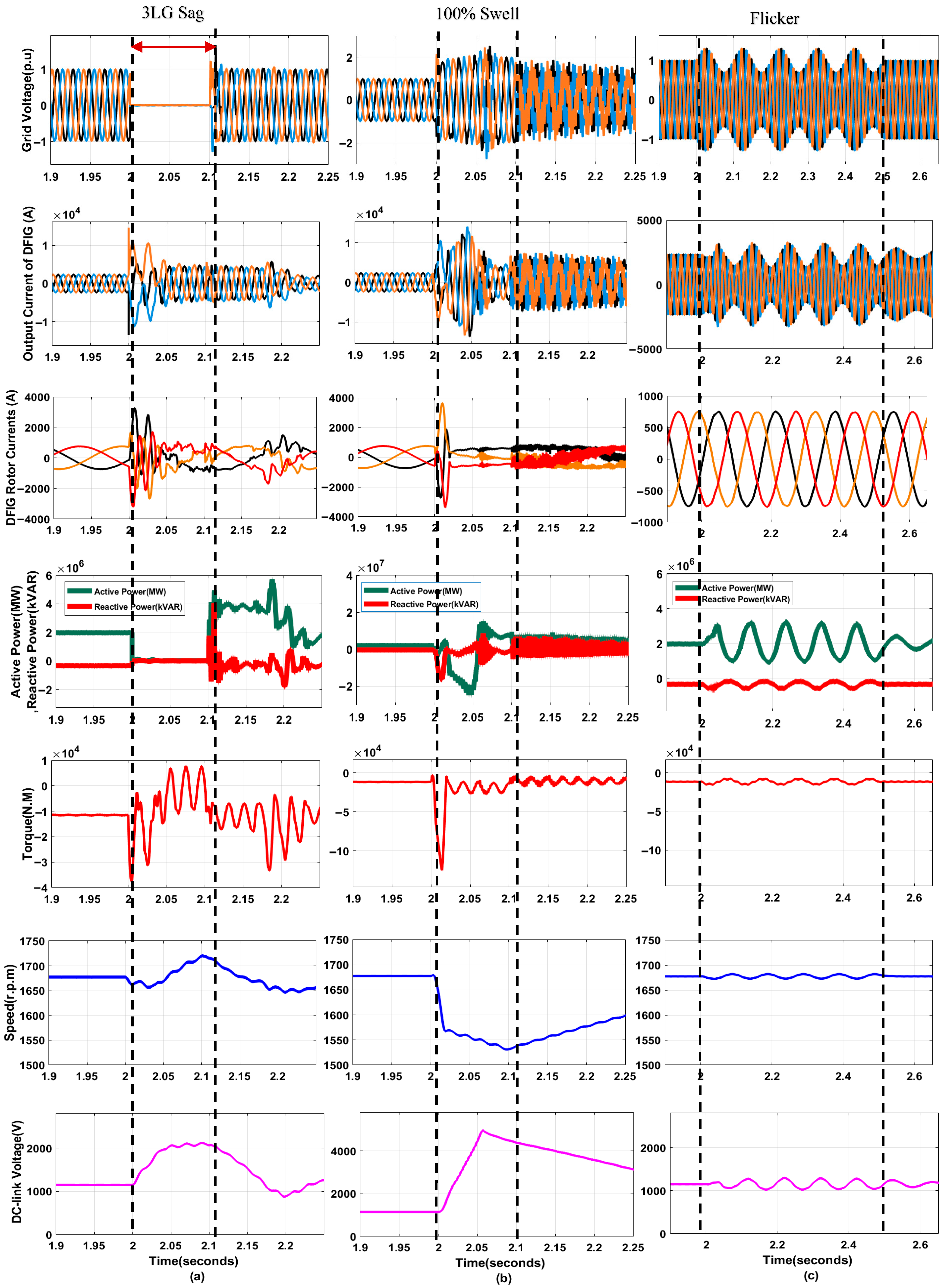
4.1. DFIG Behaviors Without Protection
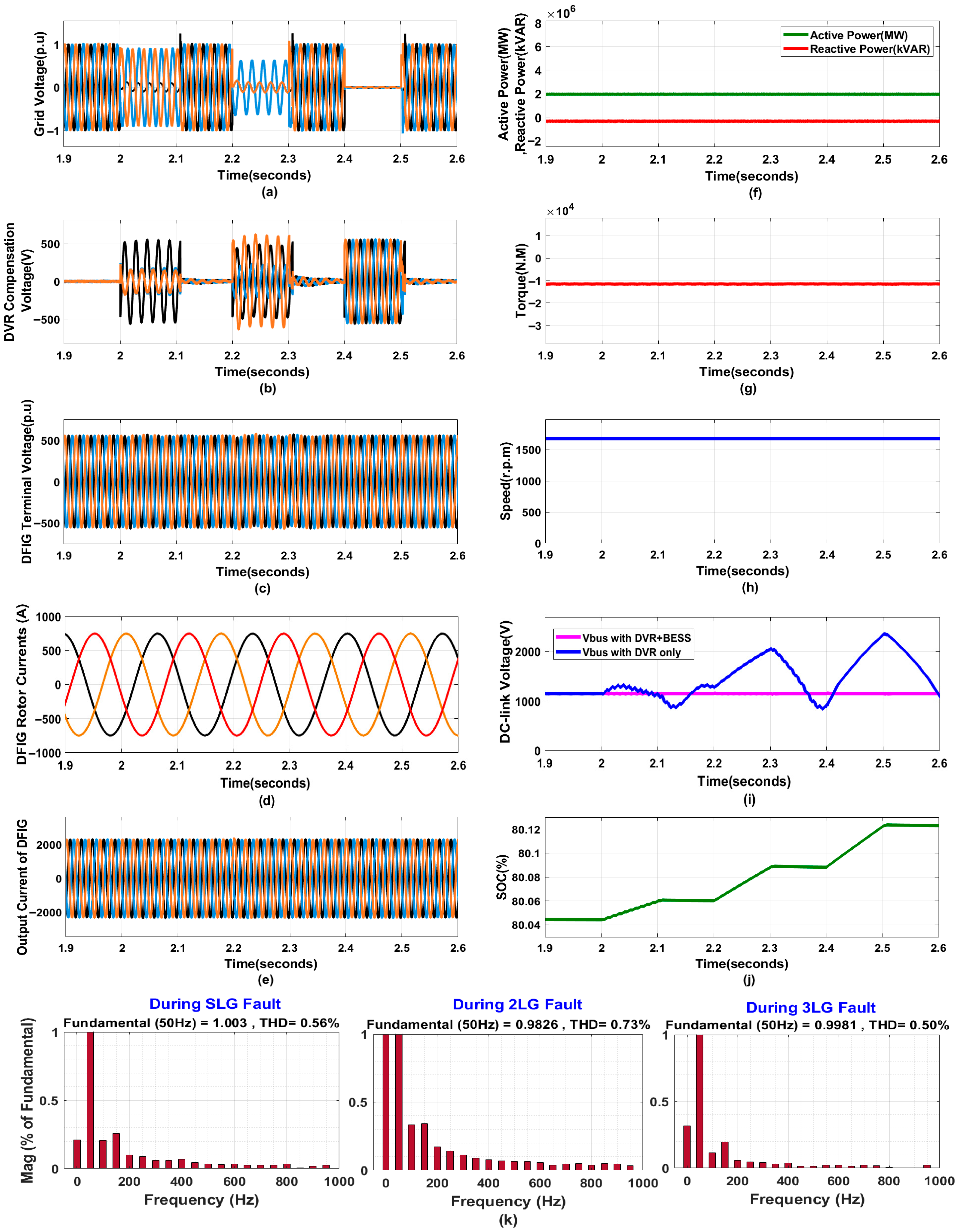
4.2. DFIG Behaviors with Protection
4.2.1. Multiple Voltage Sags
4.2.2. Multiple Voltage Swells
4.2.3. Voltage Flicker
4.2.4. Voltage Harmonics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hadi, H.A.; Kassem, A.; Amoud, H.; Nadweh, S.; Ghazaly, N.M.; Moubayed, N. Using Active Filter Controlled by Imperialist Competitive Algorithm ICA for Harmonic Mitigation in Grid-Connected PV Systems. Int. J. Robot. Control Syst. 2024, 4, 581–605. [Google Scholar]
- Abdulabbas, A.K.; Alawan, M.A.; Shary, D.K. Limits of reactive power compensation of a doubly fed induction generator-based wind turbine system. Bull. Electr. Eng. Inform. 2023, 12, 2521–2534. [Google Scholar]
- Hassan, Q.; Algburi, S.; Sameen, A.Z.; Salman, H.M.; Jaszczur, M. A review of hybrid renewable energy systems: Solar and wind-powered solutions: Challenges, opportunities, and policy implications. Results Eng. 2023, 20, 101621. [Google Scholar]
- Ravi, T.; Kumar, K.S.; Dhanamjayulu, C.; Khan, B.; Rajalakshmi, K. Analysis and mitigation of PQ disturbances in grid connected system using fuzzy logic based IUPQC. Sci. Rep. 2023, 13, 22425. [Google Scholar]
- Amalorpavaraj, R.A.J.; Palanisamy, K.; Umashankar, S.; Thirumoorthy, A.D. Power quality improvement of grid connected wind farms through voltage restoration using dynamic voltage restorer. Int. J. Renew. Energy Res. 2016, 6, 53–60. [Google Scholar]
- Qasim, A.Y.; Tahir, F.R.; Alsammak, A.N.B. Voltage Sag, Voltage Swell and Harmonics Reduction Using Unified Power Quality Conditioner (UPQC) Under Nonlinear Loads. Iraqi J. Electr. Electron. Eng. 2021, 17, 140–150. [Google Scholar]
- Yuan, L.; Meng, K.; Huang, J.; Dong, Z.Y.; Zhang, W.; Xie, X. Development of HVRT and LVRT control strategy for PMSG-based wind turbine generators. Energies 2020, 13, 5442. [Google Scholar] [CrossRef]
- Adware, R.; Chandrakar, V. Power quality enhancement in a wind farm connected grid with a fuzzy-based STATCOM. Eng. Technol. Appl. Sci. Res. 2023, 13, 10021–10026. [Google Scholar]
- Delavari, H.; Sharifi, A. Adaptive fractional order control of doubly fed induction generator based wind energy conversion system under uncertainty. J. Renew. Sustain. Energy 2021, 13, 033311. [Google Scholar]
- Soomro, M.; Memon, Z.A.; Baloch, M.H.; Mirjat, N.H.; Kumar, L.; Tran, Q.T.; Zizzo, G. Performance improvement of grid-integrated doubly fed induction generator under asymmetrical and symmetrical faults. Energies 2023, 16, 3350. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Yarmohammadi, H.; Esmaili, M. Enhancing FRT performance and smoothing output power of DFIG wind farm equipped by SFCL and SMES in a fuzzy framework. Eng. Sci. Technol. Int. J. 2019, 22, 801–810. [Google Scholar]
- Raghavendran, C.R.; Roselyn, J.P.; Devaraj, D. Development and performance analysis of intelligent fault ride through control scheme in the dynamic behaviour of grid connected DFIG based wind systems. Energy Rep. 2020, 6, 2560–2576. [Google Scholar]
- Döşoğlu, M.K. Crowbar hardware design enhancement for fault ride through capability in doubly fed induction generator-based wind turbines. ISA Trans. 2020, 104, 321–328. [Google Scholar]
- Yadav, M.; Pal, N.; Saini, D.K. Low voltage ride through capability for resilient electrical distribution system integrated with renewable energy resources. Energy Rep. 2023, 9, 833–858. [Google Scholar]
- Hossain, M.E. Performance analysis of diode-bridge-type non-superconducting fault current limiter in improving transient stability of DFIG based variable speed wind generator. Electr. Power Syst. Res. 2017, 143, 782–793. [Google Scholar]
- Rafiee, Z.; Najafi, S.S.; Rafiee, M.; Aghamohammadi, M.R.; Pourgholi, M. Optimized control of Coordinated Series Resistive Limiter and SMES for improving LVRT using TVC in DFIG-base wind farm. Phys. C Supercond. Its Appl. 2020, 570, 1353607. [Google Scholar]
- Mukherjee, P.; Rao, V.V. Effective location of SMES for power fluctuation mitigation of grid connected doubly fed induction generator. J. Energy Storage 2020, 29, 101369. [Google Scholar]
- Elshiekh, M.; Elwakeel, A.; Venuturumilli, S.; Alafnan, H.; Pei, X.; Zhang, M.; Yuan, W. Utilising SMES-FCL to improve the transient behaviour of a doubly fed induction generator DC wind system. Int. J. Electr. Power Energy Syst. 2021, 131, 107099. [Google Scholar]
- Falehi, A.D.; Rafiee, M. Maximum efficiency of wind energy using novel Dynamic Voltage Restorer for DFIG based Wind Turbine. Energy Rep. 2018, 4, 308–322. [Google Scholar]
- Muisyo, I.N.; Muriithi, C.M.; Kamau, S.I. STATCOM Controller Tuning to Enhance LVRT Capability of Grid-Connected Wind Power Generating Plants. J. Electr. Comput. Eng. 2022, 2022, 2873053. [Google Scholar]
- Falehi, A.D.; Rafiee, M. LVRT/HVRT capability enhancement of DFIG wind turbine using optimal design and control of novel PIλDμ-AMLI based DVR. Sustain. Energy Grids Netw. 2018, 16, 111–125. [Google Scholar]
- Jerin, A.; Ann, R.; Kaliannan, P.; Subramaniam, U. Improved fault ride through capability of DFIG based wind turbines using synchronous reference frame control based dynamic voltage restorer. ISA Trans. 2017, 70, 465–474. [Google Scholar]
- Chung, P.D. Voltage Enhancement on DFIG Based Wind Farm Terminal During Grid Faults. Eng. Technol. Appl. Sci. Res. 2019, 9, 4783–4788. [Google Scholar]
- Bouaziz, F.; Masmoudi, A.; Abdelkafi, A.; Krichen, L. Coordinated control of SMES and DVR for improving fault ride-through capability of DFIG-based wind turbine. Int. J. Renew. Energy Res. 2022, 12, 359–371. [Google Scholar]
- Moghassemi, A.; Padmanaban, S. Dynamic voltage restorer (DVR): A comprehensive review of topologies, power converters, control methods, and modified configurations. Energies 2020, 13, 4152. [Google Scholar] [CrossRef]
- Bouaziz, F.; Abdelkafi, A.; Masmoudi, A.; Krichen, L. Improved LVRT/HVRT Capability of DFIG Wind Turbine Using DVR. In Proceedings of the 2022 5th International Conference on Advanced Systems and Emergent Technologies (IC_ASET), Hammamet, Tunisia, 22–25 March 2022; pp. 555–559. [Google Scholar]
- Huang, P.-H.; El Moursi, M.S.; Xiao, W.; Kirtley, J.L., Jr. Novel fault ride-through configuration and transient management scheme for doubly fed induction generator. IEEE Trans. Energy Convers. 2012, 28, 86–94. [Google Scholar]
- Du, K.-J.; Zheng, Z.-X.; Xiao, X.-Y.; Huang, C.-J.; Ren, J.; Chen, X.-Y. Suppressing output power fluctuation and improving FRT Capability of DFIG-based wind energy conversion system with SMES and dual-mode protection scheme. IET Gener. Transm. Distrib. 2021, 15, 1820–1829. [Google Scholar]
- Chen, X.; Yan, L.; Zhou, X.; Sun, H. A novel DVR-ESS-embedded wind-energy conversion system. IEEE Trans. Sustain. Energy 2017, 9, 1265–1274. [Google Scholar]
- Falehi, A.D.; Torkaman, H. Promoted supercapacitor control scheme based on robust fractional-order super-twisting sliding mode control for dynamic voltage restorer to enhance FRT and PQ capabilities of DFIG-based wind turbine. J. Energy Storage 2021, 42, 102983. [Google Scholar]
- Li, L.; Liang, Y.; Niu, J.; He, J.; Liu, H.; Li, B.; Li, C.; Cao, Y. The Fault ride-through characteristics of a double-fed induction generator using a dynamic voltage restorer with superconducting magnetic energy storage. Appl. Sci. 2023, 13, 8180. [Google Scholar]
- Falehi, A.D. Novel chattering free binomial hyperbolic sliding mode controller for asymmetric cascaded E-type bonded T-type multilevel inverter-based dynamic voltage restorer to meliorate FRT capability of DFIG-based wind turbine. Results Eng. 2024, 23, 102370. [Google Scholar]
- Wang, T.; Nian, H.; Zhu, Z. Hybrid virtual impedance-based control strategy for DFIG in hybrid wind farm to disperse negative sequence current during network unbalance. IET Renew. Power Gener. 2020, 14, 2268–2277. [Google Scholar]
- Yan, Q.; Yuan, C.; Gu, W.; Liu, Y.; Tang, Y. Coordinated Rotor-Side Control Strategy for Doubly-Fed Wind Turbine under Symmetrical and Asymmetrical Grid Faults. Energy Eng. 2022, 120, 49–68. [Google Scholar]
- Jin, J.X.; Yang, R.H.; Zhang, R.T.; Fan, Y.J.; Xie, Q.; Chen, X.Y. Combined low voltage ride through and power smoothing control for DFIG/PMSG hybrid wind energy conversion system employing a SMES-based AC-DC unified power quality conditioner. Int. J. Electr. Power Energy Syst. 2021, 128, 106733. [Google Scholar]
- Shuaibu, M.; Abubakar, A.S. An improved dynamic voltage restorer model for ensuring fault ride-through capability of dfig-based wind turbine systems. ELEKTRIKA-J. Electr. Eng. 2020, 19, 9–16. [Google Scholar]
- Islam, M.R.; Hasan, J.; Shipon, M.R.R.; Sadi, M.A.H.; Abuhussein, A.; Roy, T.K. Neuro fuzzy logic controlled parallel resonance type fault current limiter to improve the fault ride through capability of DFIG based wind farm. IEEE Access 2020, 8, 115314–115334. [Google Scholar]
- Shuaibu, M.; Abubakar, A.S.; Shehu, A.F. Techniques for ensuring fault ride-through capability of grid connected dfig-based wind turbine systems: A review. Niger. J. Technol. Dev. 2021, 18, 39–46. [Google Scholar]
- Elyaalaoui, K.; Ouassaid, M.; Cherkaoui, M. Dispatching and control of active and reactive power for a wind farm considering fault ride-through with a proposed PI reactive power control. Renew. Energy Focus 2019, 28, 56–65. [Google Scholar]
- Behabtu, H.A.; Vafaeipour, M.; Kebede, A.A.; Berecibar, M.; Van Mierlo, J.; Fante, K.A.; Messagie, M.; Coosemans, T. Smoothing intermittent output power in grid-connected doubly fed induction generator wind turbines with li-ion batteries. Energies 2023, 16, 7637. [Google Scholar]
- Baala, Y.; Mouslime, S.; Oubella, M.; Kourchi, M.; Rachdy, A. Enhanced LVRT capability of wind turbine based on DFIG using dynamic voltage restorer controlled by ADRC-based feedback control. In Proceedings of the E3S Web of Conferences; EDP Sciences, Morocco, Agadir, 22–24 December 2021; Volume 229, p. 01016. [Google Scholar]
- Hu, H.; Cheng, X.; Wang, J.; Zou, X. Control and simulation of bi-directional DC/DC converter for 5KW distributed wind/solar hybrid system. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 7039–7044. [Google Scholar]
- Bharath, K.R.; Choutapalli, H.; Kanakasabapathy, P. Control of bidirectional DC-DC converter in renewable based DC microgrid with improved voltage stability. Int. J. Renew. Energy Res. 2018, 8, 871–877. [Google Scholar]
- Li, B.Y.; Xu, C.; Lib, C.; Guan, Z. Working principle analysis and control algorithm for bidirectional DC/DC converter. J. Power Technol. 2017, 97, 327–335. [Google Scholar]
- Gambhir, J.; Thakur, T.; Verma, H. Wind Energy Integration with Grid Using an Energy Storage. In Proceedings of the World Congress on Engineering, London, UK, 29 June–1 July 2016; Volume 1. [Google Scholar]
- Oti, S.E.; Benneth, N.D.; Uche, O.; Stella, N.; Stephen, A. Simulation of wind energy system employing doubly fed induction generator. Appl. Model. Simul. 2020, 4, 47–56. [Google Scholar]
- Wu, L.; Liu, H.; Zhang, J.; Liu, C.; Sun, Y.; Li, Z.; Li, J. Identification of control parameters for converters of doubly fed wind turbines based on hybrid genetic algorithm. Processes 2022, 10, 567. [Google Scholar] [CrossRef]
- IEEE Std 519-2014; IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: New York, NY, USA, 2014.





| Parameters | Value |
| System frequency | 50 Hz |
| Nominal voltage | 0.69 kV |
| Nominal output power | 2 MW |
| Rated wind speed | 12 m/s |
| Stator resistance | 2.6 × 10−3 Ω |
| Rotor resistance | 2.9 × 10−3 Ω |
| Stator leakage inductance | 87 × 10−6 H |
| Magnetizing inductance | 2.5 × 10−3 H |
| Winding turns ratio | 0.34 |
| DC bus voltage | 1.15 kV |
| Transformer (690 V/25 kV) | Value |
| Apparent power rating | 3 MVA |
| Leakage resistance | 0.025/30 pu |
| Leakage inductance | 0.025 pu |
| Rated frequency | 50 Hz |
| Voltage transformation ratio | 0.69/25 kV |
| Transformer (25 kV/120 kV) | Value |
| Power capacity | 47 MVA |
| Leakage resistance | 0.0026667 pu |
| Leakage inductance | 0.08 pu |
| Operating frequency | 50 Hz |
| DVR | Value |
| Rated power | 3 MVA |
| Filter inductance | 0.3 mH |
| Filter capacitance | 10 μF |
| Switching frequency | 10 kHz |
| DC-link voltage of DVR | 1150 V |
| Series transformer ratio | 1:1 |
| Energy storage battery bank | Value |
| Nominal voltage | 600V |
| Capacity | 200 Ah |
| Initial state of charge | 80% |
| Battery response time | 1 s |
| DC-DC buck/boost converter | Value |
| Inductance | 70 μH |
| Switching frequency | 20 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nori, A.M.; Abdulabbs, A.K.; Al-Shammaa, A.A.; Farh, H.M.H. Enhancing Fault Ride-Through and Power Quality in Wind Energy Systems Using Dynamic Voltage Restorer and Battery Energy Storage System. Electronics 2025, 14, 2760. https://doi.org/10.3390/electronics14142760
Nori AM, Abdulabbs AK, Al-Shammaa AA, Farh HMH. Enhancing Fault Ride-Through and Power Quality in Wind Energy Systems Using Dynamic Voltage Restorer and Battery Energy Storage System. Electronics. 2025; 14(14):2760. https://doi.org/10.3390/electronics14142760
Chicago/Turabian StyleNori, Ahmed Muthanna, Ali Kadhim Abdulabbs, Abdullrahman A. Al-Shammaa, and Hassan M. Hussein Farh. 2025. "Enhancing Fault Ride-Through and Power Quality in Wind Energy Systems Using Dynamic Voltage Restorer and Battery Energy Storage System" Electronics 14, no. 14: 2760. https://doi.org/10.3390/electronics14142760
APA StyleNori, A. M., Abdulabbs, A. K., Al-Shammaa, A. A., & Farh, H. M. H. (2025). Enhancing Fault Ride-Through and Power Quality in Wind Energy Systems Using Dynamic Voltage Restorer and Battery Energy Storage System. Electronics, 14(14), 2760. https://doi.org/10.3390/electronics14142760








