Permanent Fault Identification Scheme for Transmission Lines Based on Amplitude Difference for LCC Injection Signal
Abstract
1. Introduction
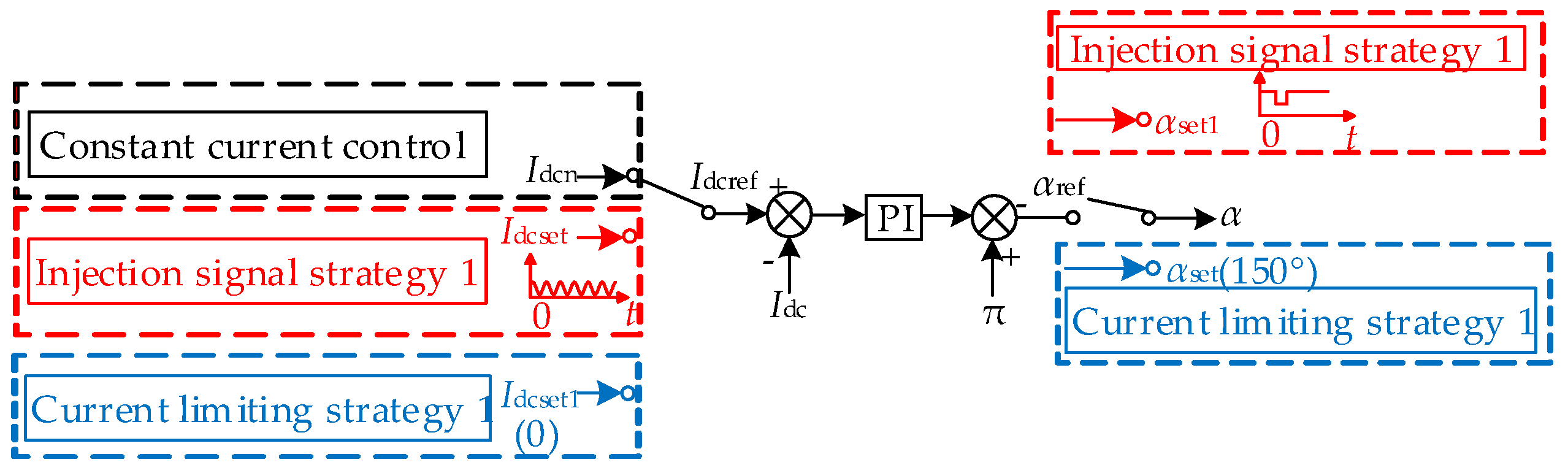
- The proposed scheme uses LCC to inject a voltage signal without PI regulation and has faster response speed.
- The proposed scheme uses the amplitude difference of LCC injection signal to identify permanent faults and only uses single end data, which is not affected by the data channel.
- The proposed scheme fully considers the influence of fault resistance, noise, sampling rates, sampling interval, and DC boundary.
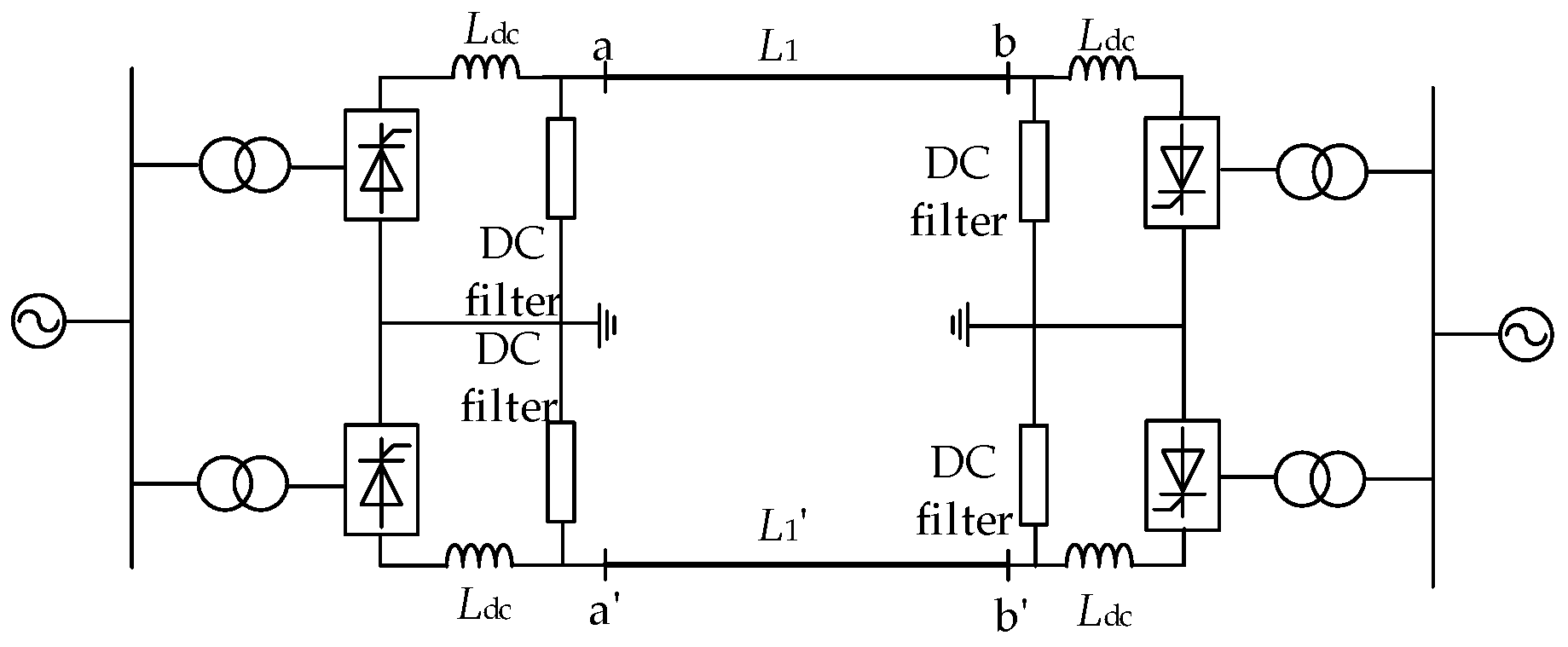
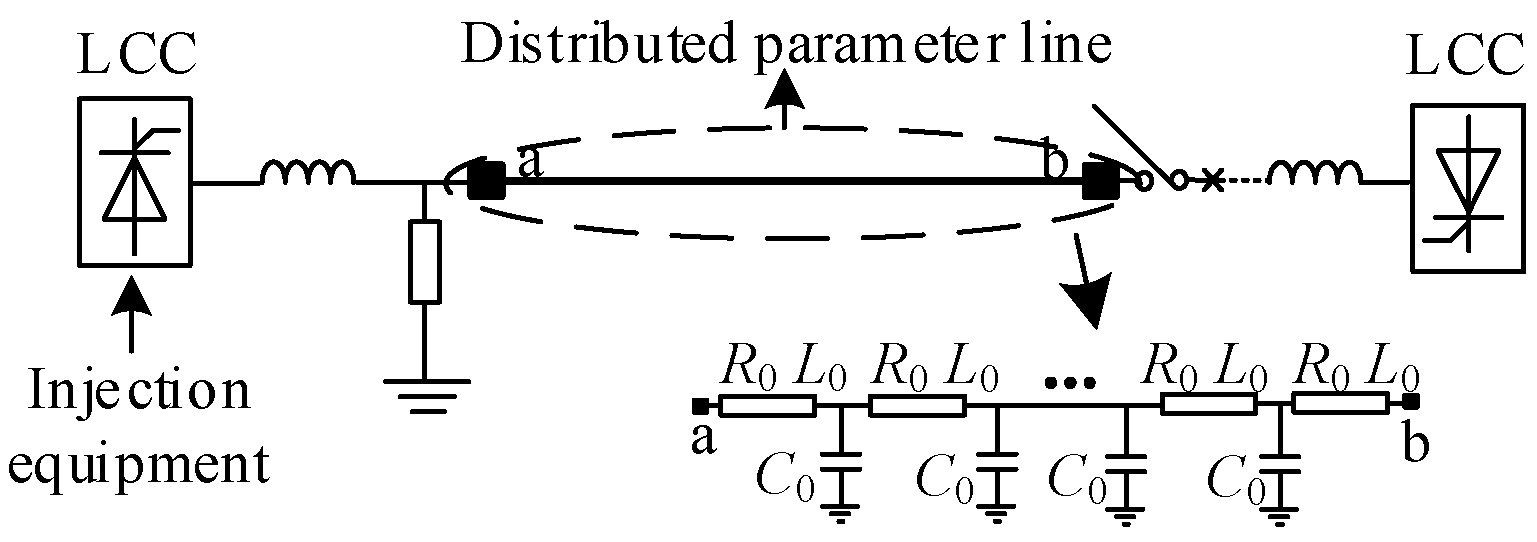
2. Basic Realization Ideas
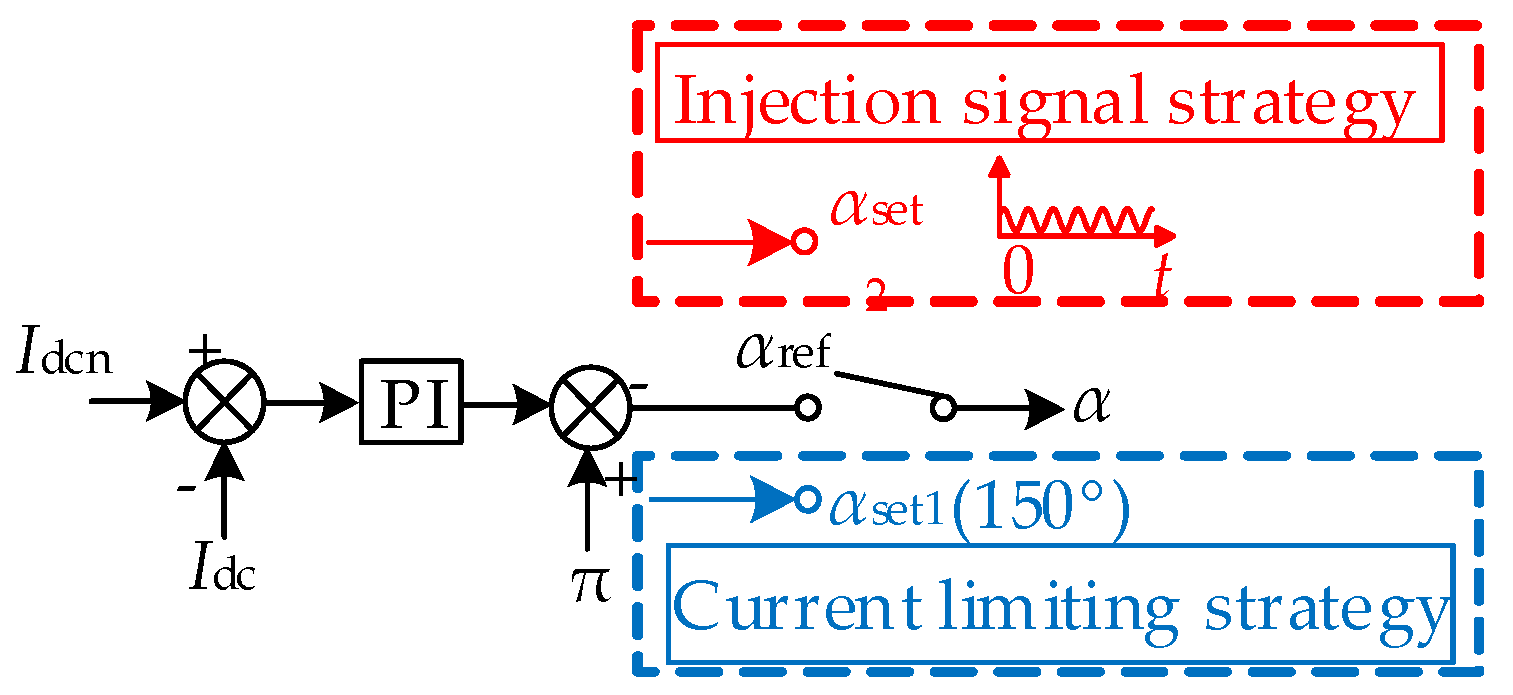
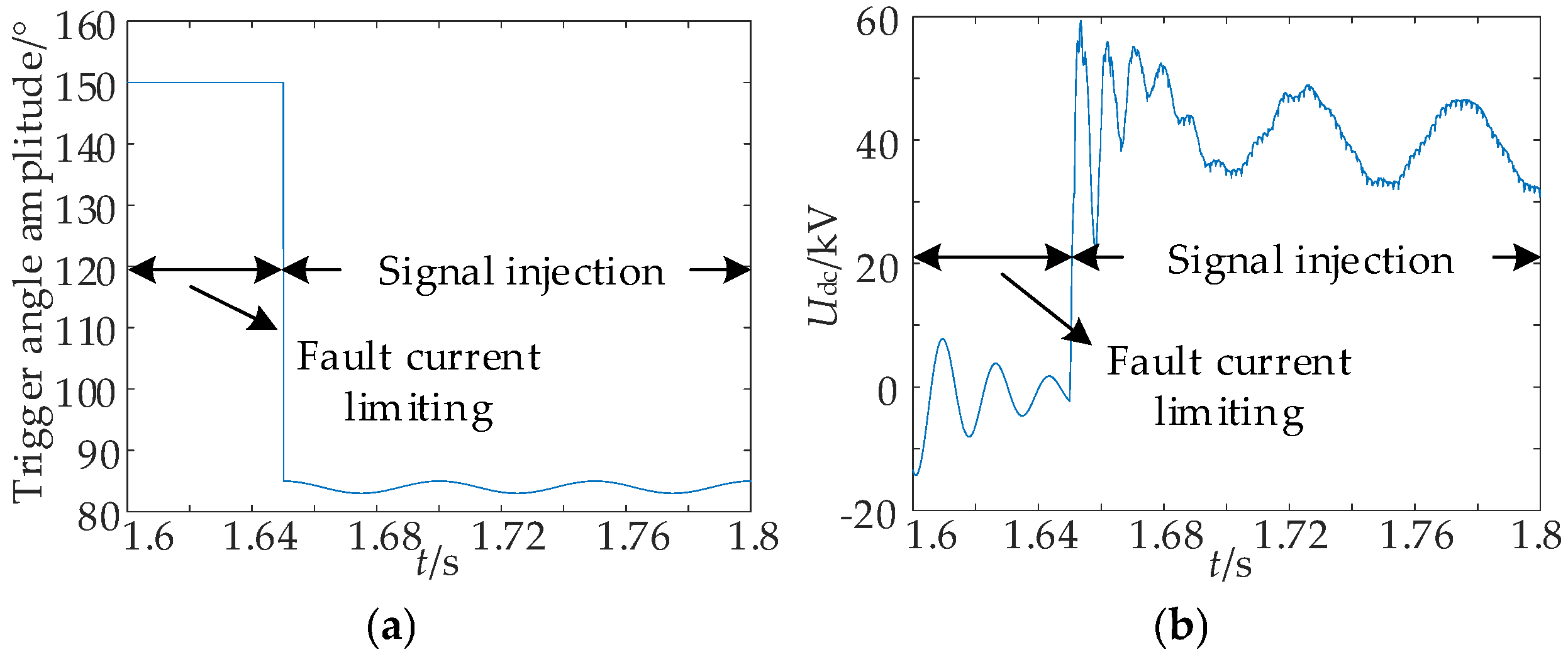
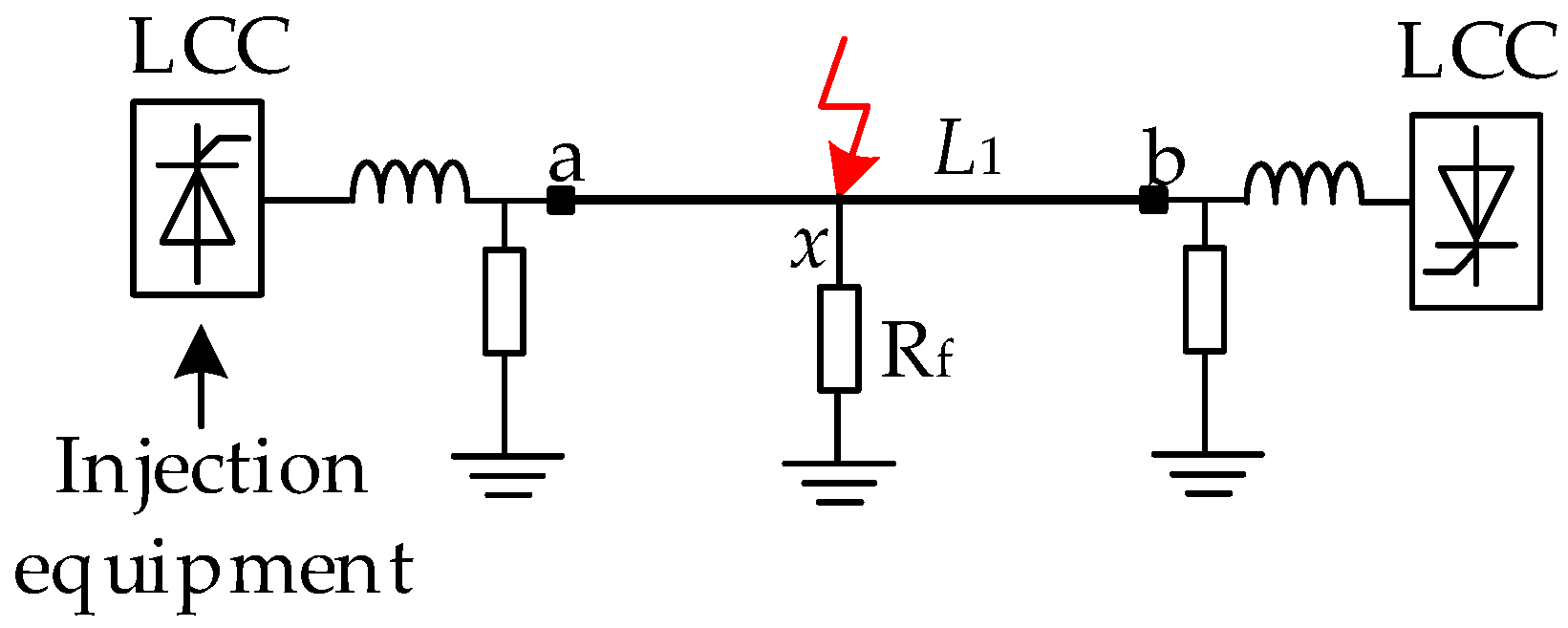
3. Injection Signal Strategy
4. Injection Signal Selection
4.1. Length of Injection Signal
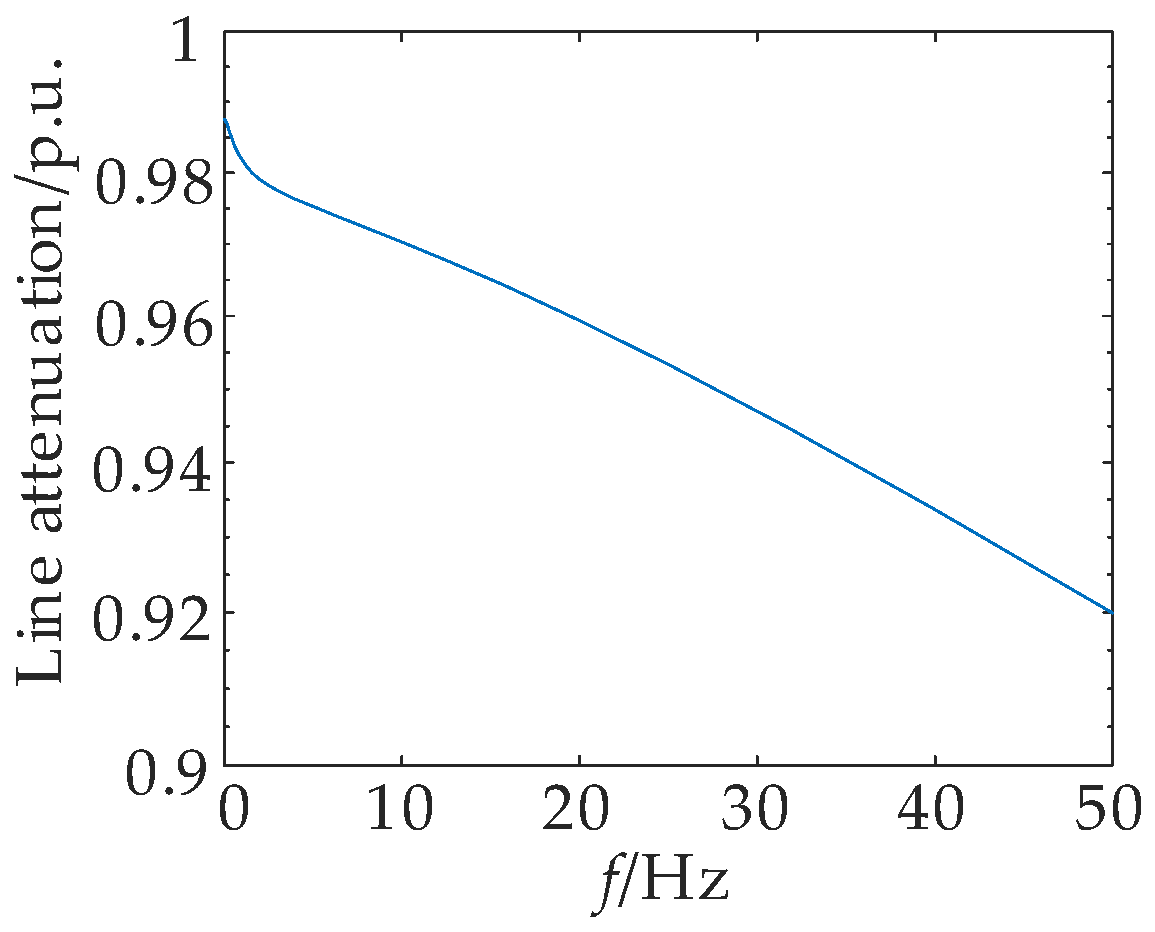
4.2. Frequency of Injection Signal
4.3. Amplitude of Injection Signal
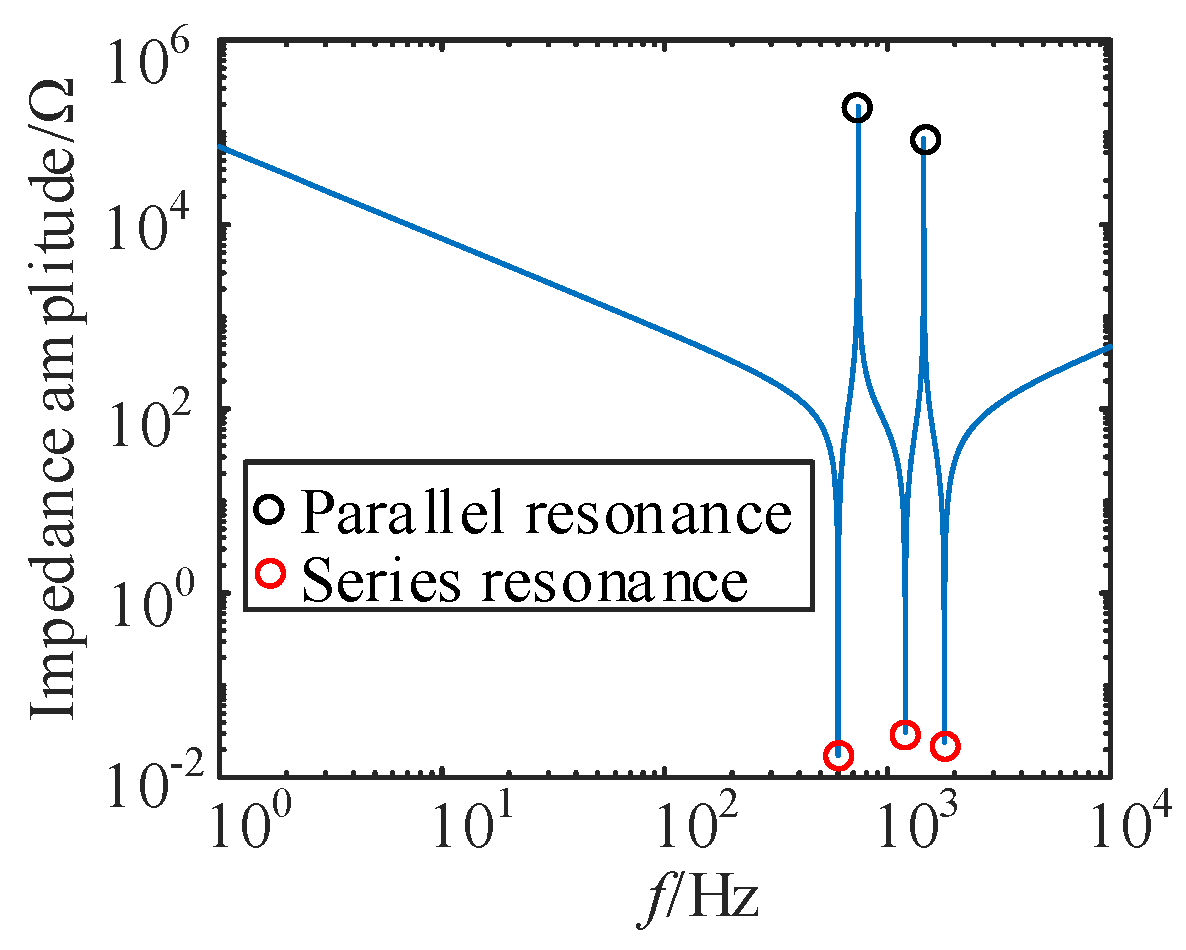
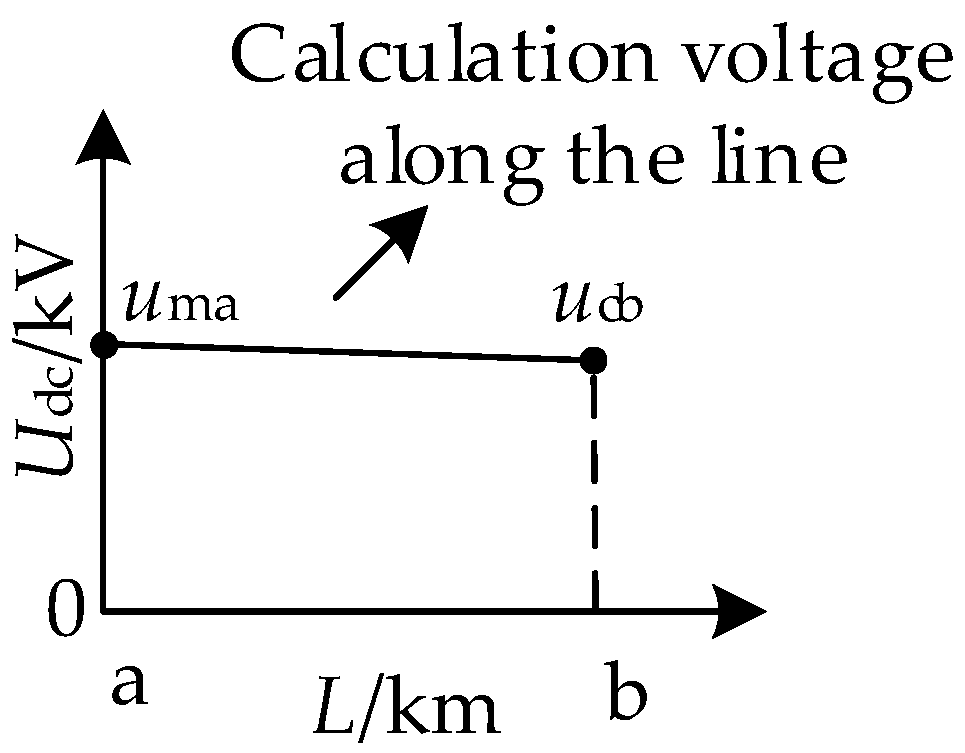
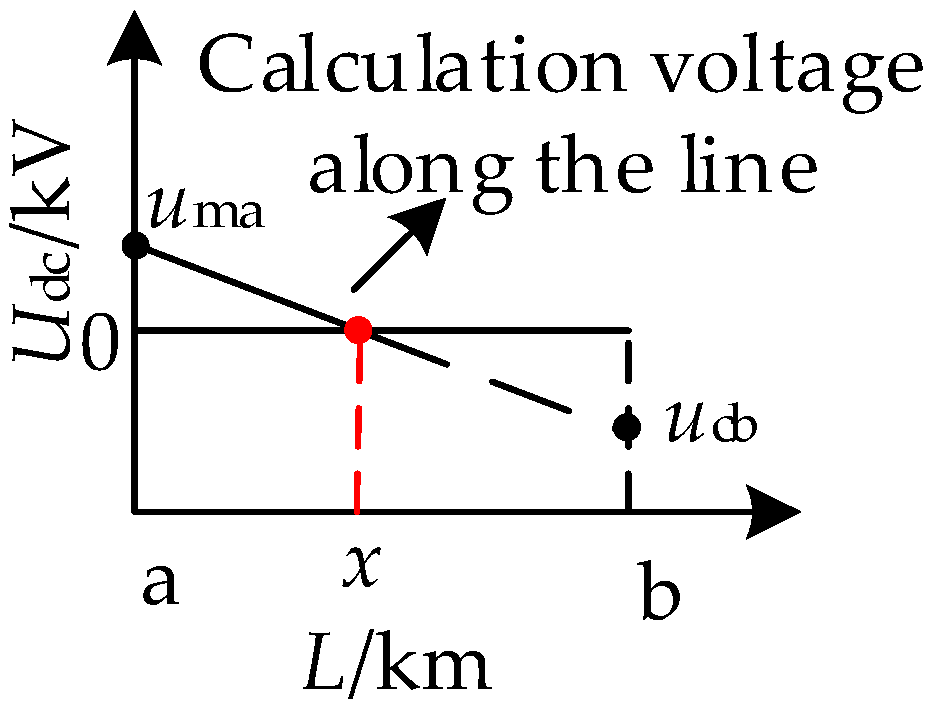
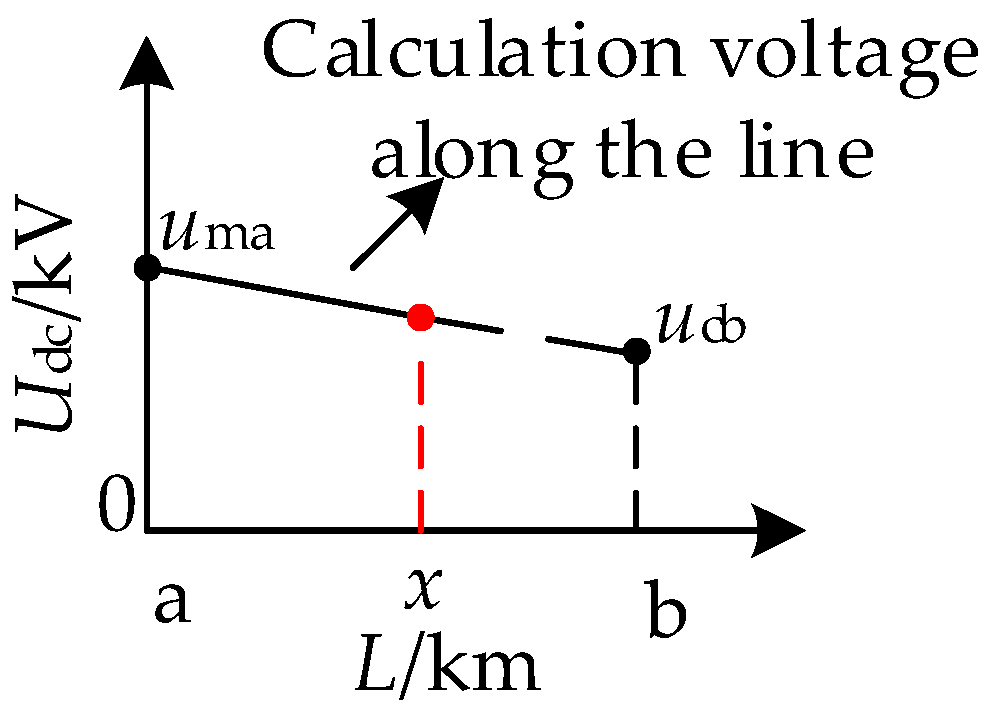
5. Analysis of the Difference Characteristics of Injection Signals Under the Distributed Parameter Model
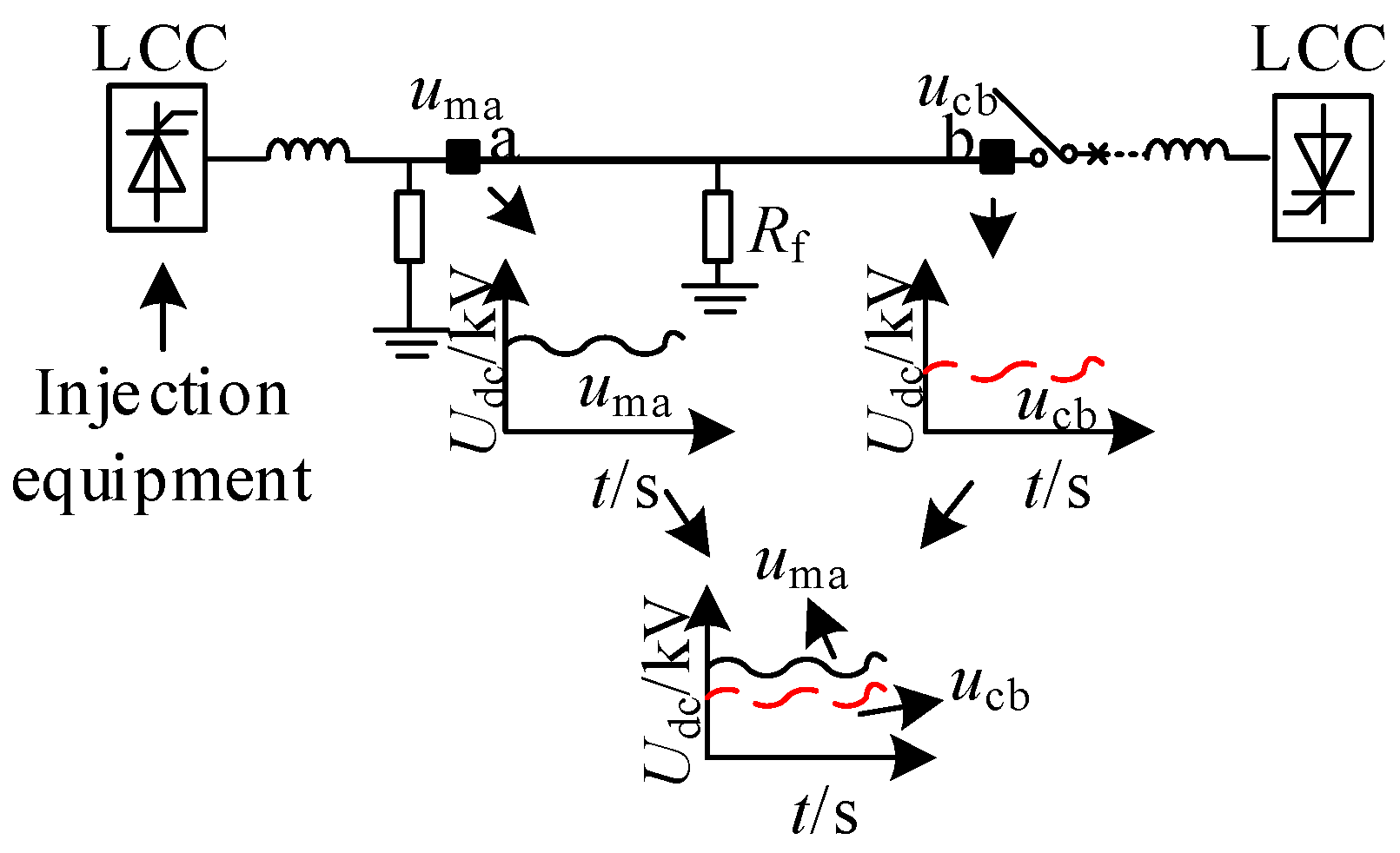
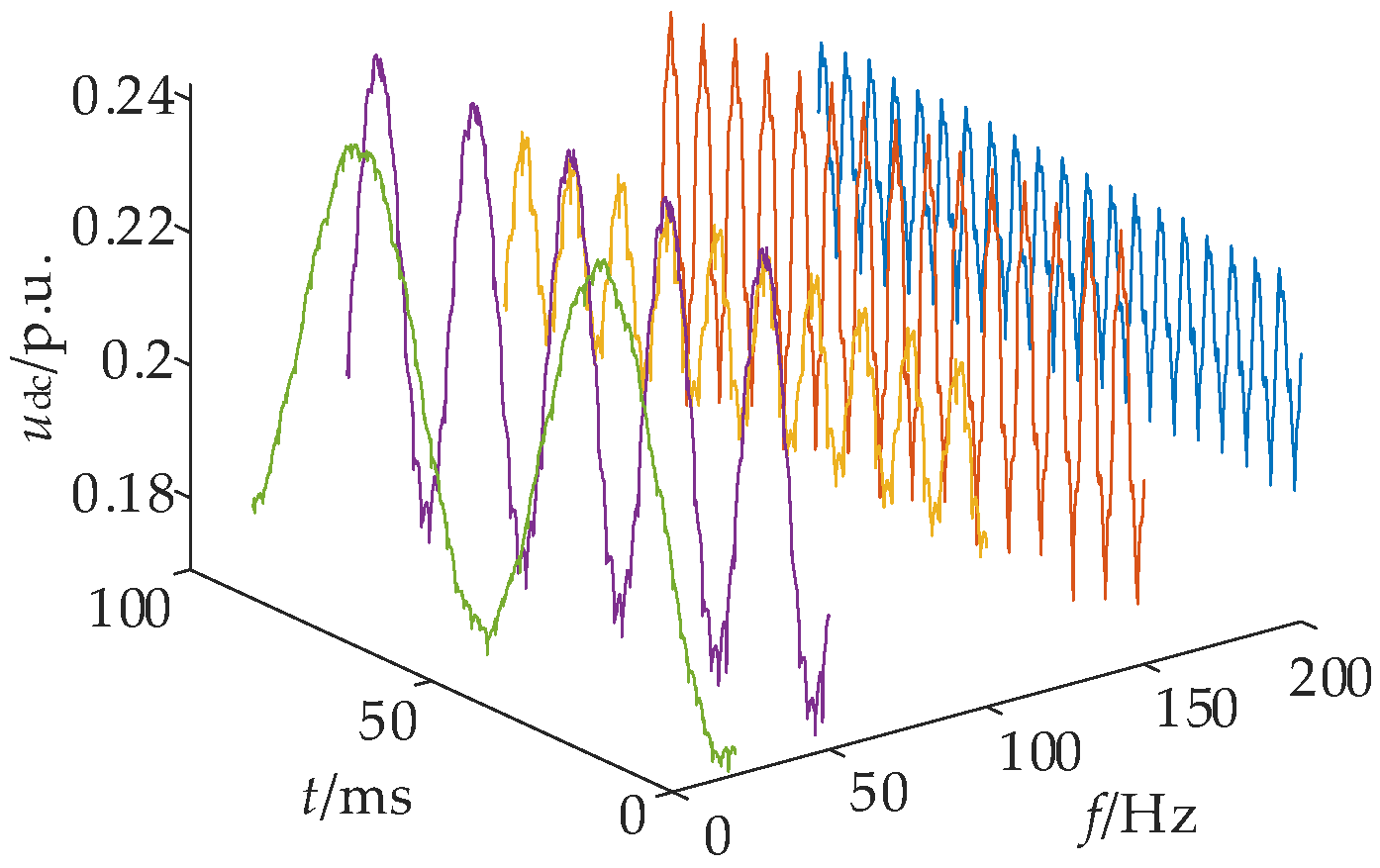
5.1. Temporary Fault
5.2. Permanent Fault
6. Permanent Fault Identification Scheme
6.1. Fault Identification Scheme
6.2. Flow Chart of Fault Identification Scheme
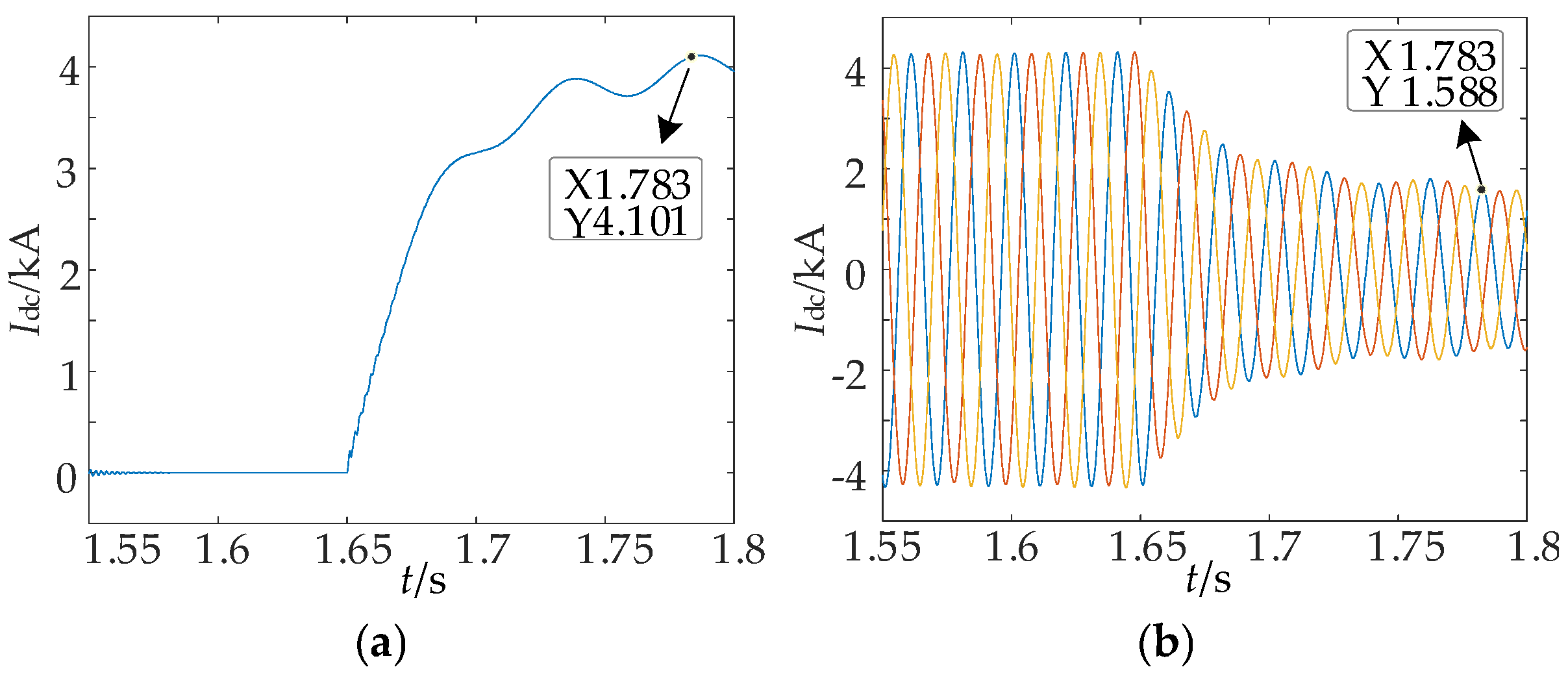
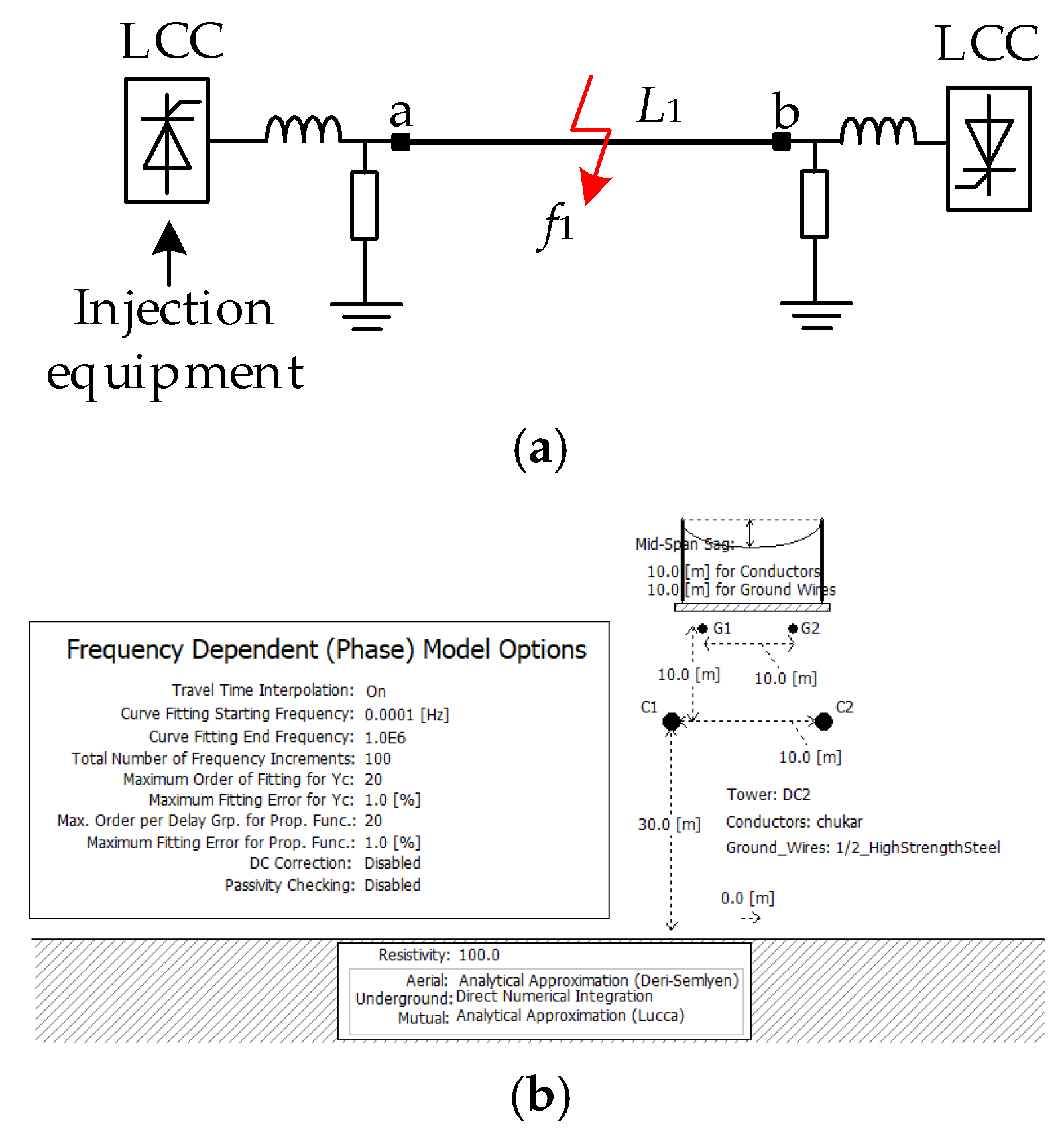
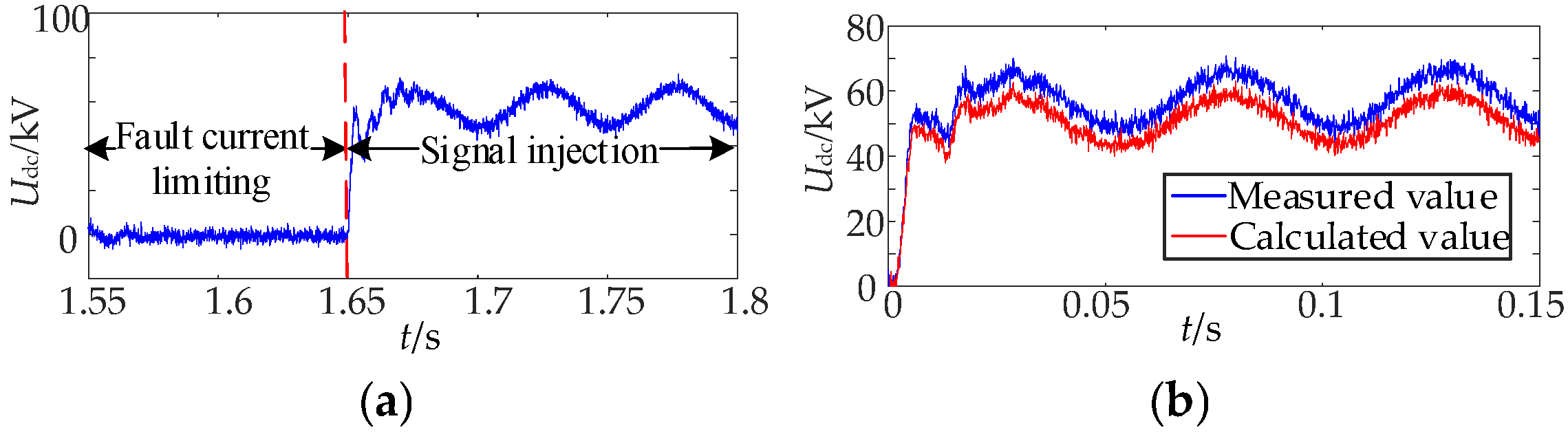
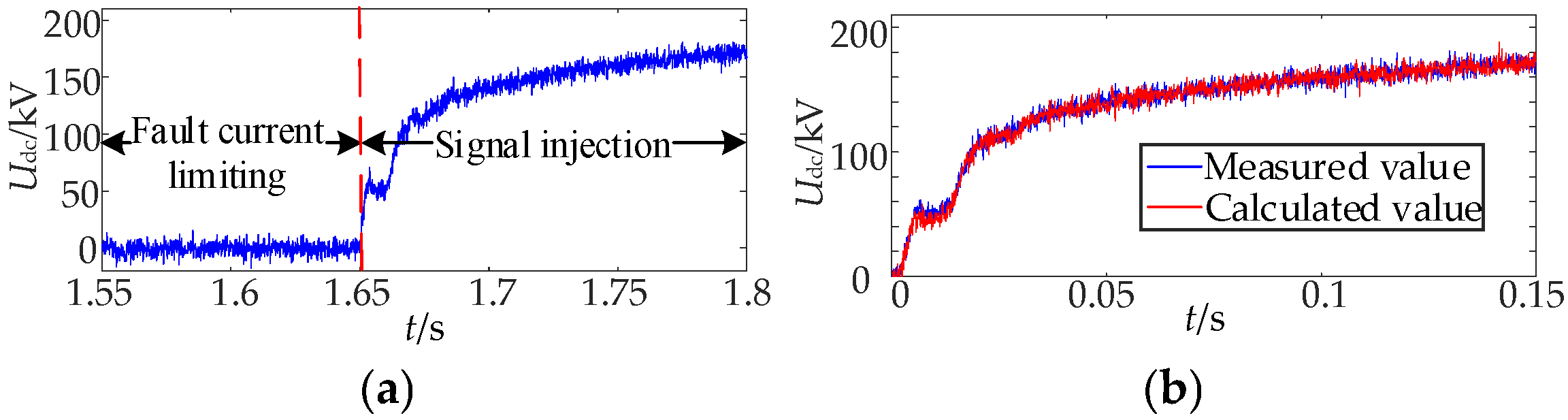
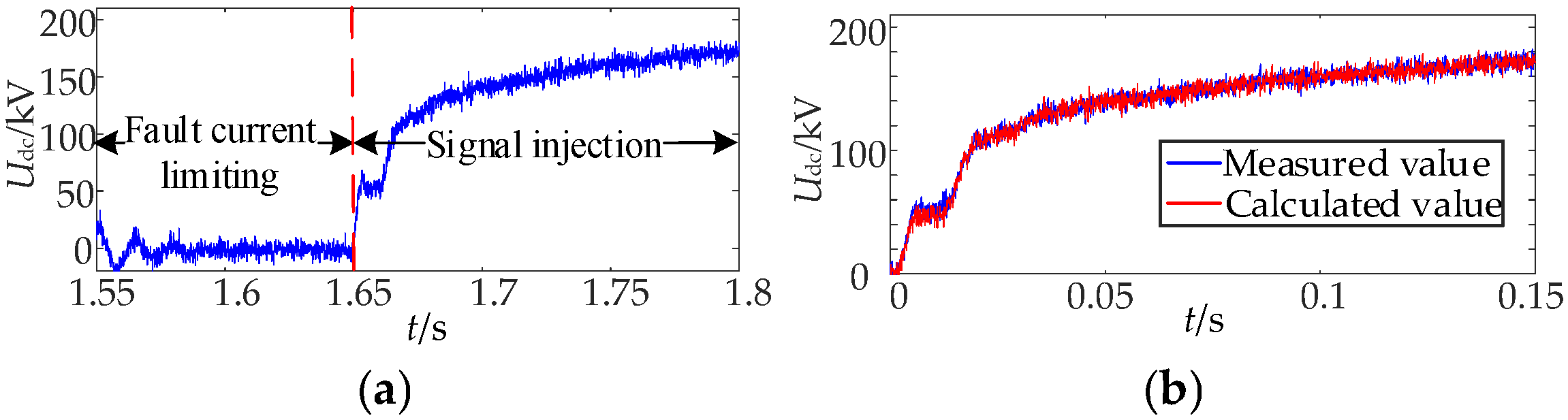
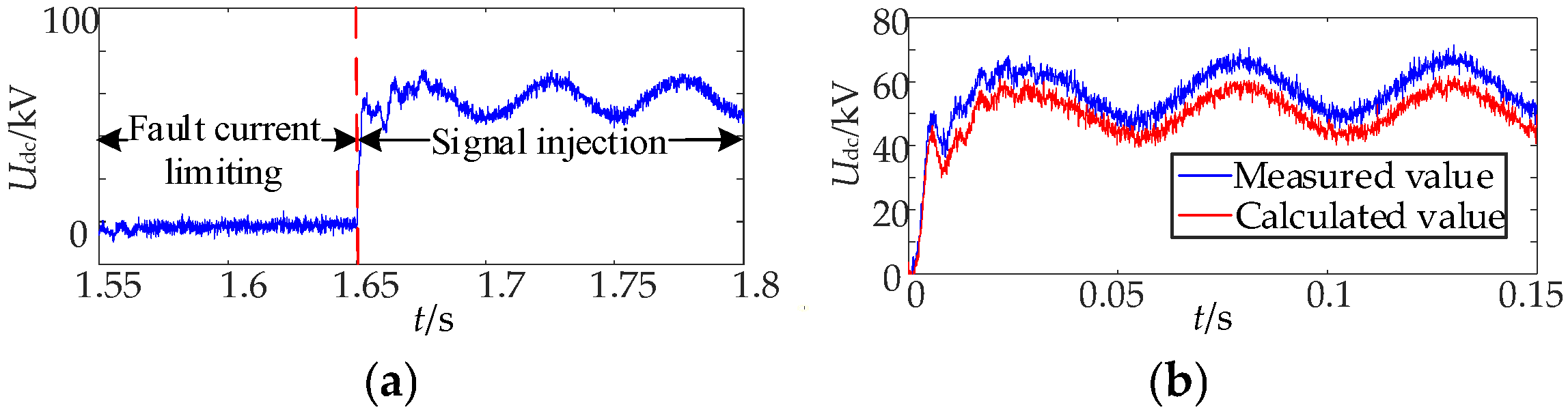
7. Simulation Verification
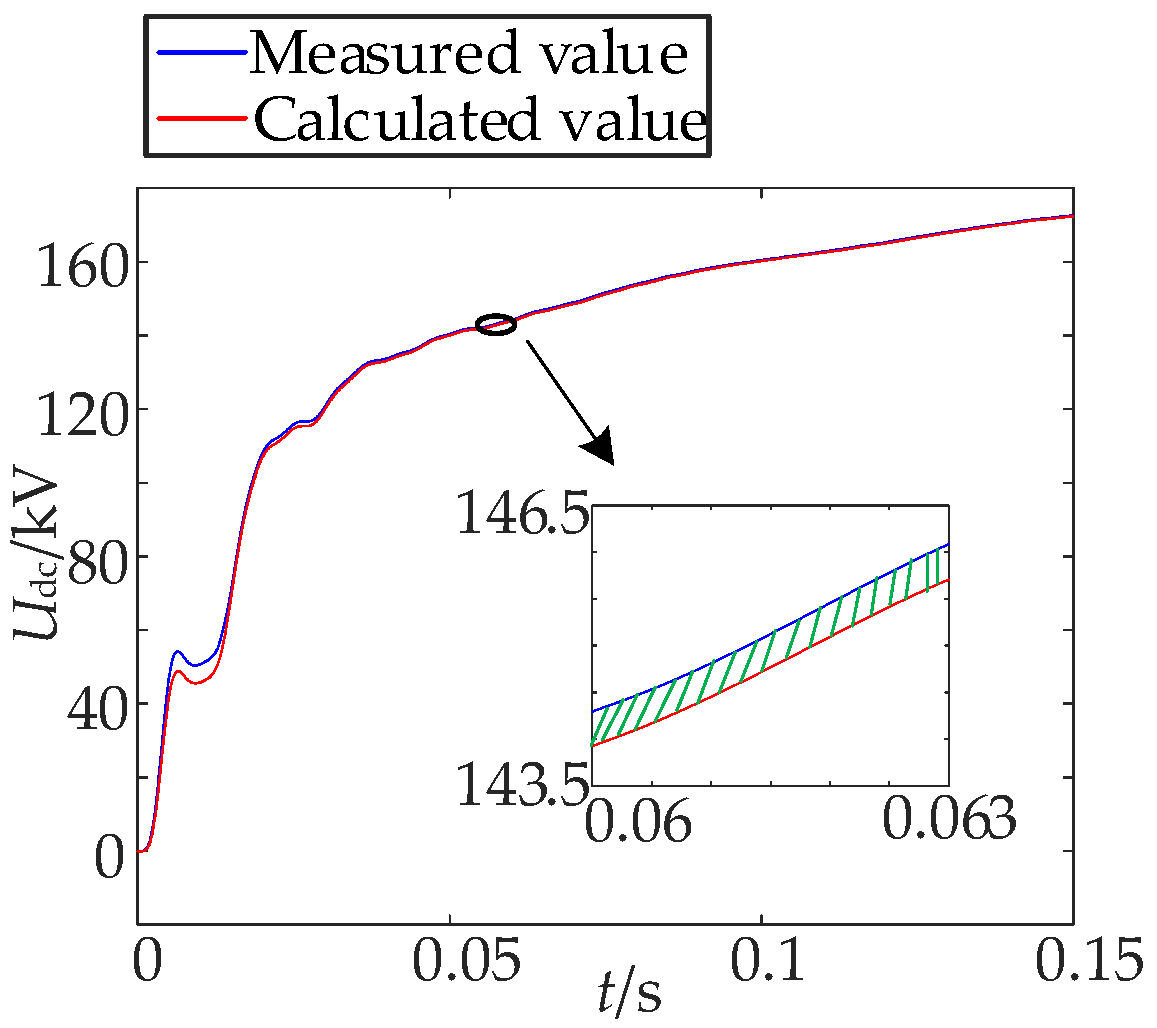
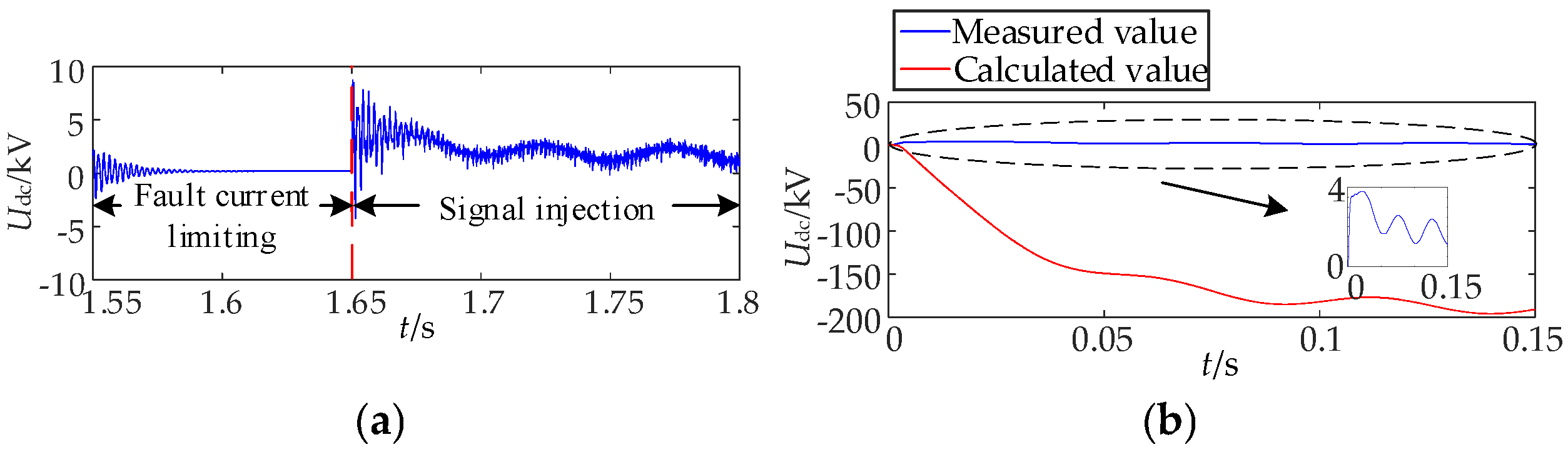
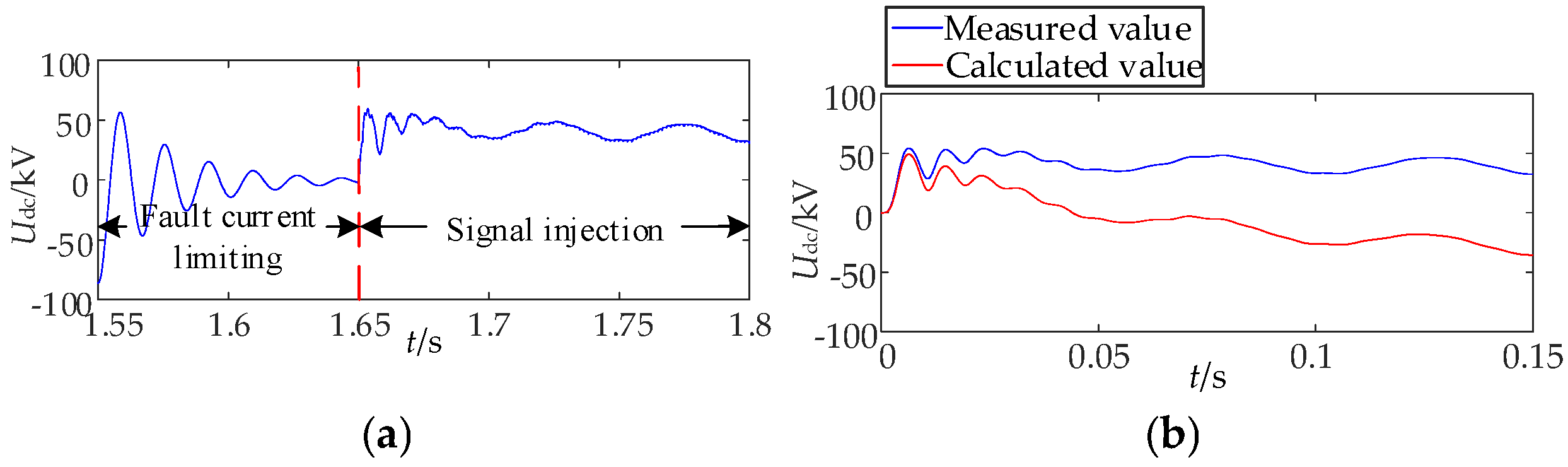
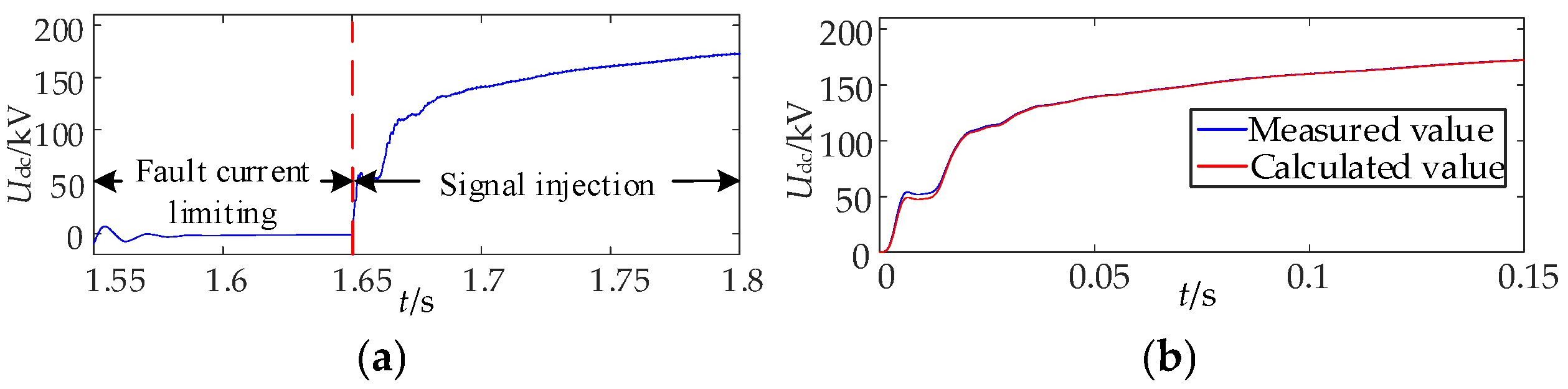
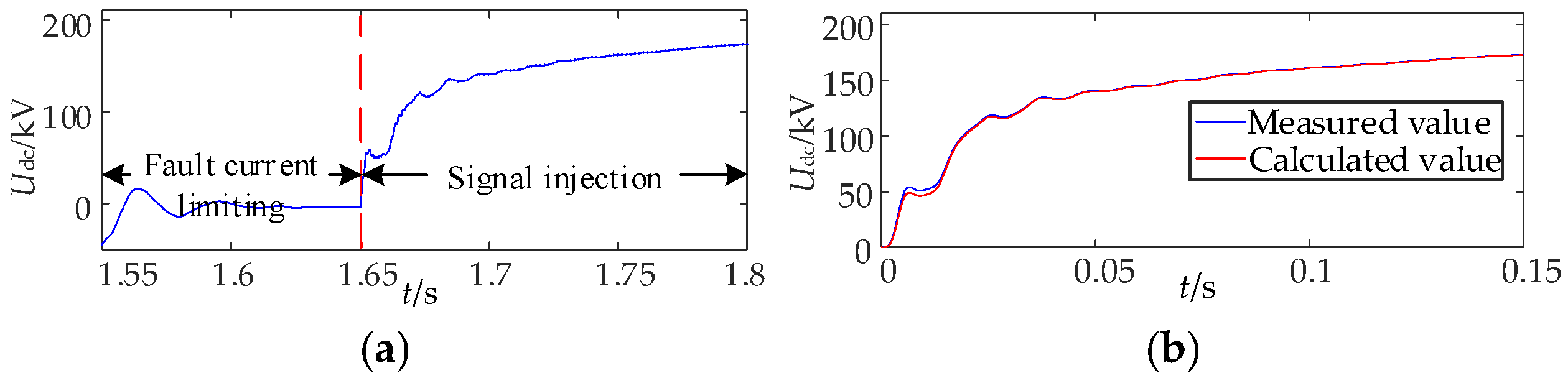
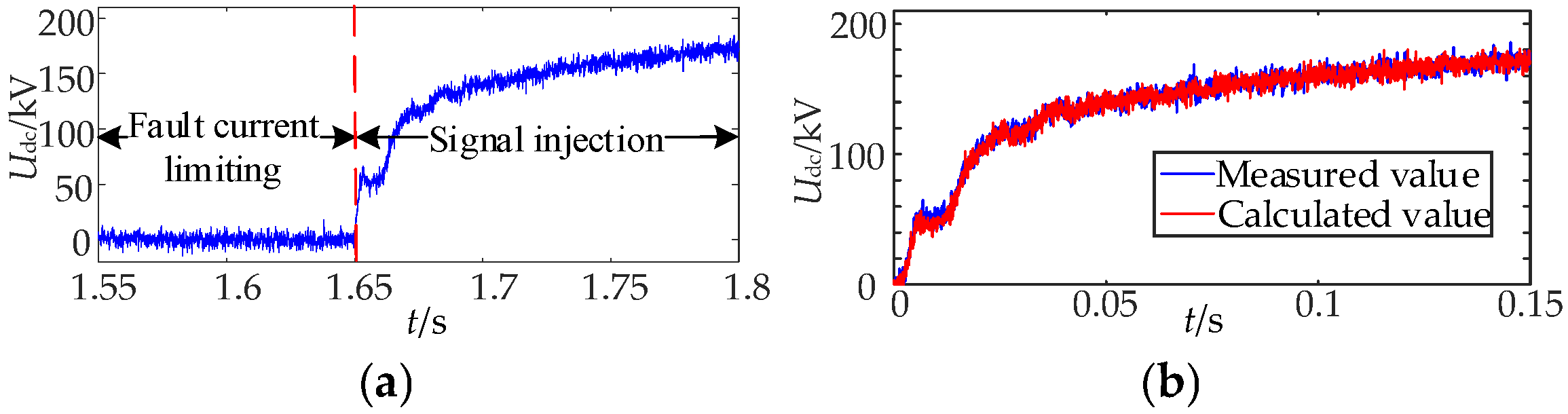
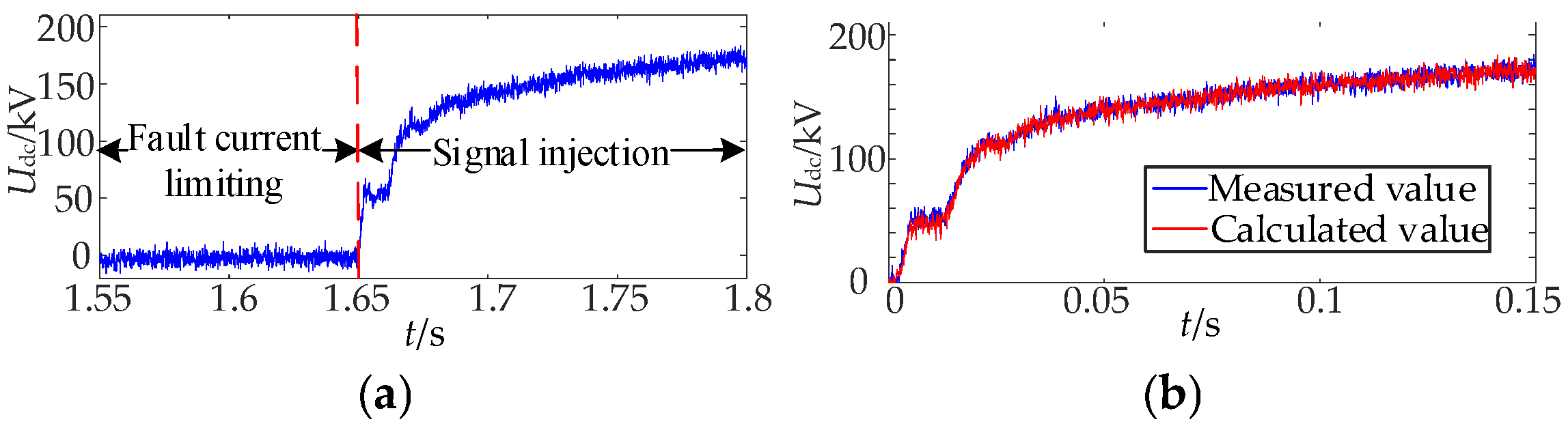
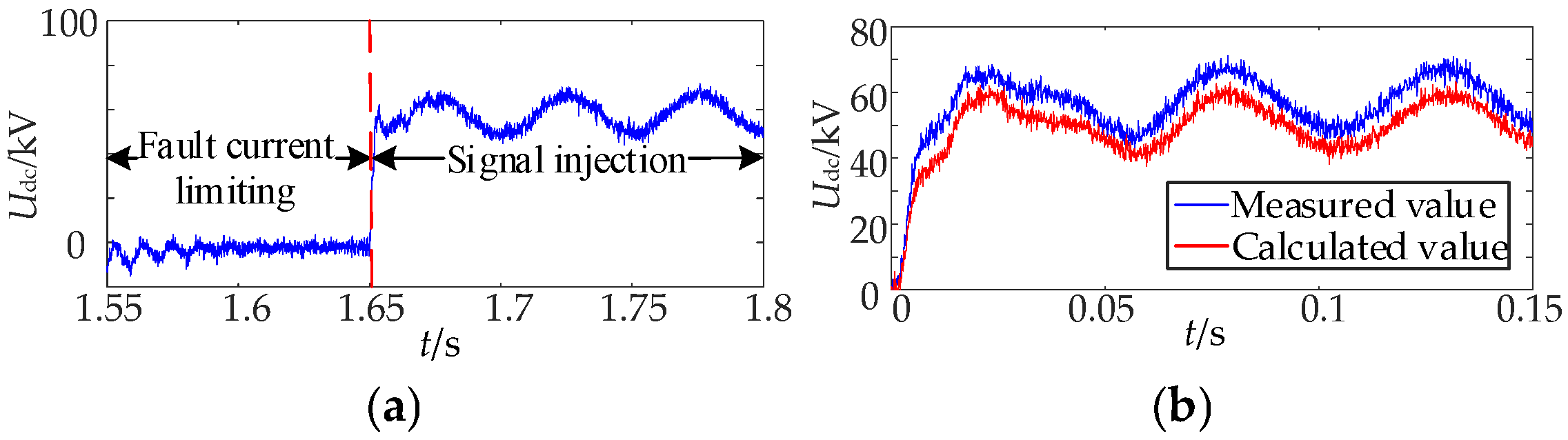
7.1. Analysis of Simulation Results of Permanent Fault Identification
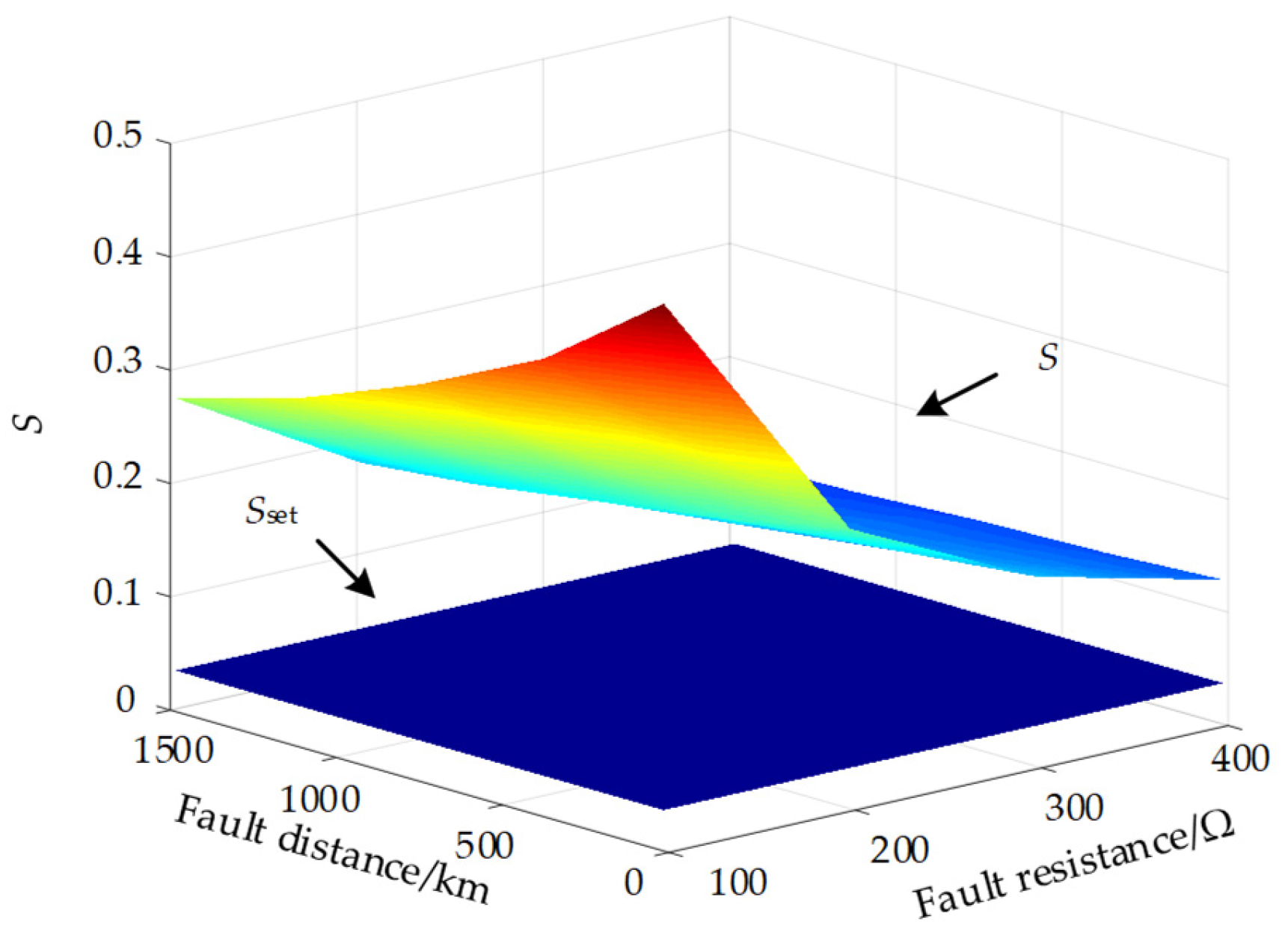
7.2. Influence Analysis of the Proposed Scheme Under the PTG Fault with Fault Resistance
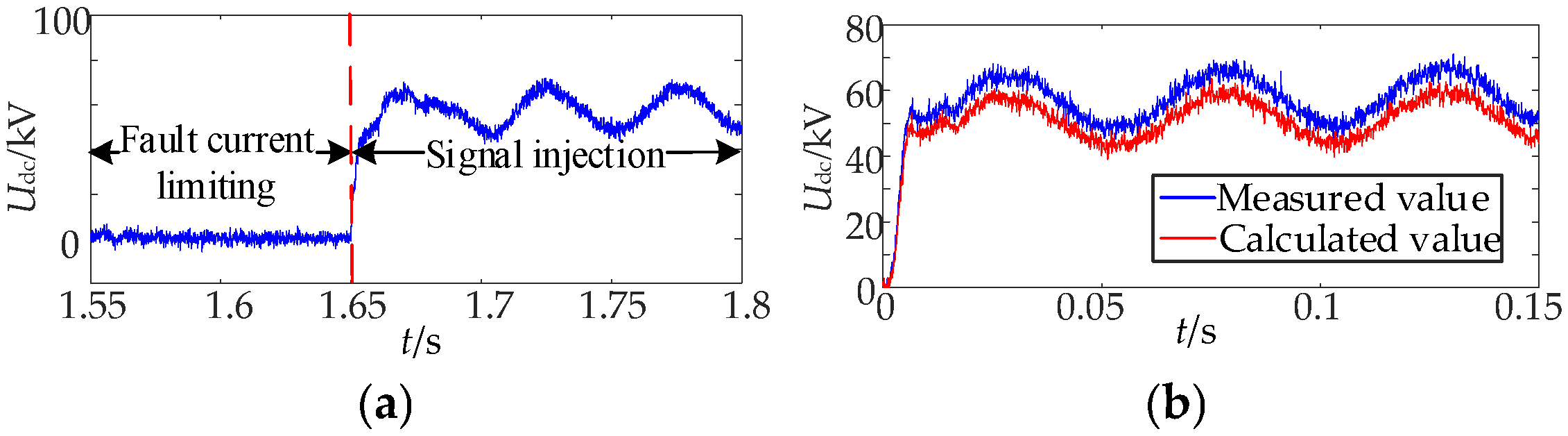
7.3. Influence Analysis of the Proposed Scheme Under the PTG Fault with Noise Interference
7.4. Influence Analysis of the Proposed Scheme Under the PTG Fault with Different Sampling Rates
7.5. Influence Analysis of the Proposed Scheme Under the PTG Fault with Different DC Boundary
7.6. Performance of Time-Varying Resistance
7.7. Compared with Existing Methods
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, N.; Zha, K.P.; Qu, H.T.; Li, F.L.; Xue, Y.; Zhang, X.P. Economy Analysis of Flexible LCC-HVDC Systems with Controllable Capacitors. CSEE J. Power Energy Syst. 2022, 8, 1708–1719. [Google Scholar] [CrossRef]
- Niu, S.; Jia, Q.; Hu, Y.; Yang, C.; Jian, L. Safety Management Technologies for Wireless Electric Vehicle Charging Systems: A Review. Electronics 2025, 14, 2380. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, L.; Egea-Alvarez, A.; Marshall, B. Accurate and General Small-Signal Impedance Model of LCC-HVDC in Sequence Frame. IEEE Trans. Power Deliv. 2023, 38, 4226–4241. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Huang, H.Z.; Wu, J.; Wang, Y.H. Zero-faulty sample machinery fault detection via relation network with out-of-distribution data augmentation. Eng. Appl. Artif. Intell. 2025, 141, 109753. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Huang, H.Z.; Deng, Z.W.; Wu, J. Shrinkage mamba relation network with out-of-distribution data augmentation for rotating machinery fault detection and localization under zero-faulty data. Mech. Syst. Signal Process. 2025, 224, 112145. [Google Scholar] [CrossRef]
- Shu, H.C.; Cao, Y.R.; Dai, Y.; An, N. An Adaptive Reclosing Scheme for Flexible DC Ring Grid Based on Residual Voltage Waveform Offset Detection. IEEE Trans. Ind. Electron. 2024, 71, 7829–7838. [Google Scholar] [CrossRef]
- Zhang, D.H.; Liang, C.G.; Li, M.; Luo, Y.P.; Chen, K.; Mirsaeidi, S.; He, J.H. Voltage frequency-based adaptive reclosing strategy for flexible DC power grids. Int. J. Electr. Power Energy Syst. 2021, 131, 10. [Google Scholar] [CrossRef]
- Yu, J.Q.; Zhang, Z.R.; Xu, Z. Adaptive sequential reclosing strategy for hybrid HVDC circuit breakers in MMC-based DC grids. High Volt. 2022, 7, 890–902. [Google Scholar] [CrossRef]
- Wang, T.; Song, G.B.; Hussain, K.S.T. Adaptive Single-Pole Auto-Reclosing Scheme for Hybrid MMC-HVDC Systems. IEEE Trans. Power Deliv. 2019, 34, 2194–2203. [Google Scholar] [CrossRef]
- Hou, J.J.; Song, G.B.; Sun, Y.; Fan, Y.F.; Wu, X.F.; Chang, P.; Chang, N.N. Permanent fault identification and location scheme for MTDC grid based on equivalent impedance phase characteristics and distributed parameter line. Int. J. Electr. Power Energy Syst. 2023, 153, 16. [Google Scholar] [CrossRef]
- Cai, P.C.; Xiang, W.; Zhou, M.; Ni, B.Y.; Wen, J.Y. Research on Adaptive Reclosing of DC Fault Based on Active Signal Injected by Hybrid MMC. Proc. CSEE 2020, 40, 3867–3878. [Google Scholar]
- Li, Z.; Zheng, Y.C.; Lin, X.N.; Tong, N.; Wei, F.R.; Xiao, S.Y. Adaptive Reclosing Scheme for VSC-MTDC Line Based on the Transient Current Waveform Similarity Matching. High Volt. Eng. 2023, 49, 1326–1339. [Google Scholar]
- Yang, S.Z.; Xiang, W.; Yang, R.Z.; He, Y.J.; Wen, J.Y. Research on Adaptive Reclosing Technology for the Half-bridge MMC and Hybrid DC Circuit Breaker Based on HVDC Systems. Proc. CSEE 2020, 40, 4440–4451+4724. [Google Scholar]
- Mei, J.; Ge, R.; Zhu, P.F.; Fan, G.Y.; Wang, B.B.; Yan, L.X. An Adaptive Reclosing Scheme for MMC-HVDC Systems Based on Pulse Injection From Parallel Energy Absorption Module. IEEE Trans. Power Deliv. 2021, 36, 1809–1818. [Google Scholar] [CrossRef]
- Han, P.; Zhao, X.C.; Wu, Y.N.; Zhou, Z.Y.; Qi, Q. Adaptive Reclosing Scheme Based on Traveling Wave Injection For Multi-Terminal dc Grids. Energy Eng. 2023, 120, 1271–1285. [Google Scholar] [CrossRef]
- Zhang, S.; Zou, G.B.; Xu, C.H.; Sun, W.J. A Reclosing Scheme of Hybrid DC Circuit Breaker for MMC-HVdc Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 7126–7137. [Google Scholar] [CrossRef]
- Zhang, D.H.; Yang, Y.C.; Liang, C.G.; Li, M.; Liu, Y.M.; He, J.H. Adaptive Reclosing Scheme for Flexible DC Power Grid Based on Improved DC Circuit Breaker Injecting Signal. Autom. Electr. Power Syst. 2022, 46, 123–132. [Google Scholar]
- Xu, R.D.; Song, G.B.; Hou, J.J.; Chang, Z.X. Adaptive restarting method for LCC-HVDC based on principle of fault location by current injection. Glob. Energy Interconnect. 2021, 4, 554–563. [Google Scholar] [CrossRef]
- Hou, J.J.; Song, G.B.; Fan, Y.F. Fault properties identification scheme for hybrid MTDC system based on LCC signal injection and distributed parameter line model. IET Gener. Transm. Distrib. 2023, 17, 3718–3738. [Google Scholar] [CrossRef]
- Liang, C.G.; Zhang, D.H.; Li, M.; Nie, M.; Mirsaeidi, S.; Xu, Y.; He, J.H. Waveform Difference Based Adaptive Restart Strategy for LCC-MMC Hybrid DC System. IEEE Trans. Power Deliv. 2022, 37, 4237–4247. [Google Scholar] [CrossRef]
- Wang, L.; Sun, X.F.; Wang, B.C.; Zhao, W.; Li, X. Research on Protection Scheme of DC Line Fault in LCC-MMC Hybrid HVDC System. Proc. CSEE 2021, 41, 7339–7352. [Google Scholar]
- Hou, J.J.; Song, G.B.; Fan, Y.F. Fault identification scheme for protection and adaptive reclosing in a hybrid multi-terminal HVDC system. Prot. Control Mod. Power Syst. 2023, 8, 17. [Google Scholar] [CrossRef]
- Zhu, M.M.; Wang, D.; Liao, Y.H.; Cao, P.L.; Shu, H.C.; Yang, B.; Duan, R.M. Field test and analysis of delay characteristics of a DC electronic voltage transformer. Power Syst. Prot. Control 2023, 51, 126–132. [Google Scholar]
- Zhao, W.J.; Xie, G.E.; Zeng, N.C. High Voltage Direct Current Transmission Engineering Technology, 2nd ed.; China Electric Power Press: Beijing, China, 2011; pp. 60–77. [Google Scholar]
- Song, G.B.; Rao, J.; Gao, S.P.; Cai, X.L.; Suo, N.J.L. Monopole Protection for HVDC Transmission Lines Based on Compensating Voltage. Autom. Electr. Power Syst. 2013, 37, 102–106+113. [Google Scholar]
- Zheng, J.C.; Wen, M.H.; Chen, Y.; Shao, X.N. A novel differential protection scheme for HVDC transmission lines. Int. J. Electr. Power Energy Syst. 2018, 94, 171–178. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, G.X.; Li, L.Z.; Zhu, X.M.; Luo, C.M. Error analysis of electronic instrument transformers. J. Tsinghua Univ. (Sci. Technol.) 2007, 47, 1105–1108. [Google Scholar]








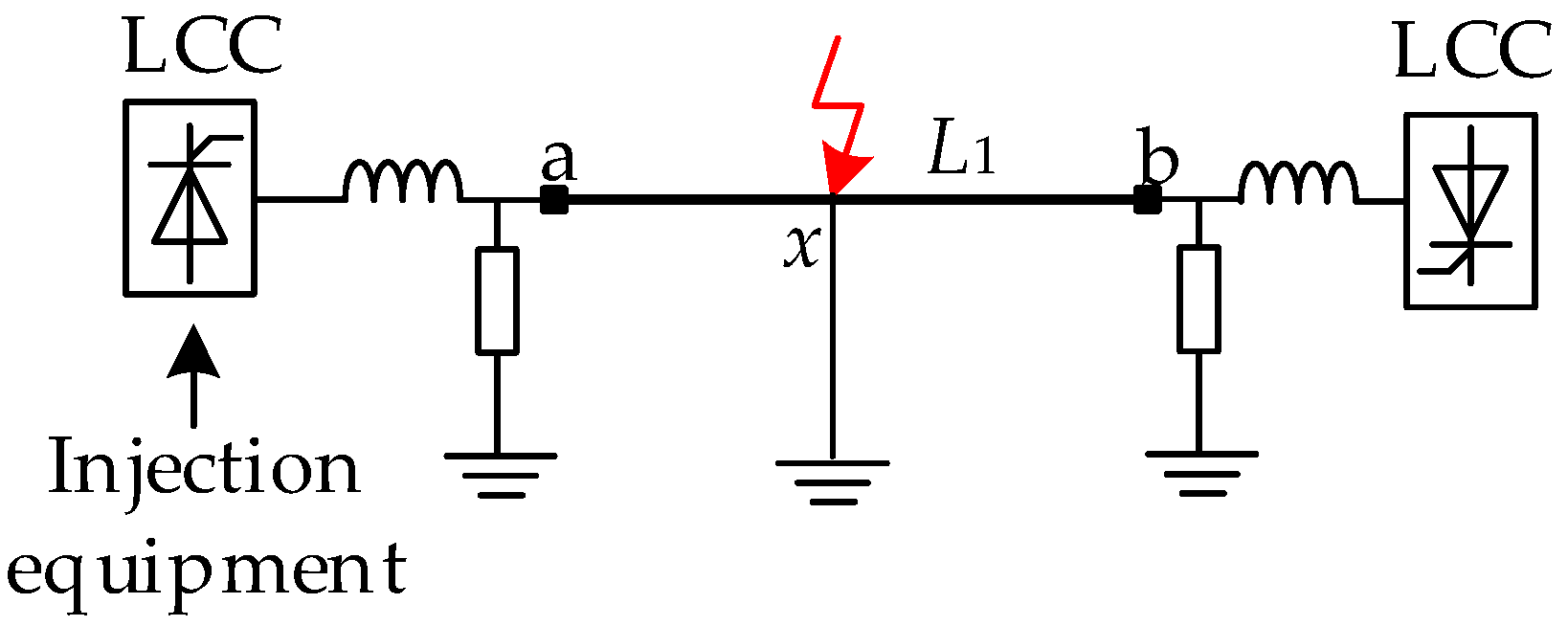











| Parameter Name | Parameter Value |
|---|---|
| AC system voltage | 530 kV |
| DC system voltage | ±500 kV |
| System rating capacity | 1500 MVA |
| Smoothing Reactor | 150 mH |
| Length of transmission line | 1500 km |
| Solution time step | 50 μs |
| Sampling frequency | 10 kHz |
| Fault Location | Fault Properties | Normalized Area Difference | Fault Identification Results |
|---|---|---|---|
| f15 | P | 78.6965 | P |
| T | 0.0109 | T | |
| f375 | P | 2.3665 | P |
| T | 0.0136 | T | |
| f750 | P | 1.1497 | P |
| T | 0.1168 | T | |
| f1125 | P | 0.7577 | P |
| T | 0.0088 | T | |
| f1485 | P | 0.5722 | P |
| T | 0.0329 | T |
| Fault Location | Fault Properties | Normalized Area Difference | Fault Identification Results |
|---|---|---|---|
| f15 | P | 0.1091 | P |
| T | 0.0100 | T | |
| f375 | P | 0.1288 | P |
| T | 0.0139 | T | |
| f750 | P | 0.0736 | P |
| T | 0.0225 | T | |
| f1125 | P | 0.1275 | P |
| T | 0.0133 | T | |
| f1485 | P | 0.0587 | P |
| T | 0.0173 | T |
| Sampling Rate | Fault Location | Fault Properties | Normalized Area Difference | Fault Identification Results |
|---|---|---|---|---|
| 5 kHz | f15 | P | 0.1313 | P |
| T | 0.0163 | T | ||
| f375 | P | 0.1227 | P | |
| T | 0.0162 | T | ||
| f750 | P | 0.1176 | P | |
| T | 0.0155 | T | ||
| f1125 | P | 0.1149 | P | |
| T | 0.0158 | T | ||
| f1485 | P | 0.0947 | P | |
| T | 0.0171 | T | ||
| 20 kHz | f15 | P | 0.1261 | P |
| T | 0.0199 | T | ||
| f375 | P | 0.1213 | P | |
| T | 0.0115 | T | ||
| f750 | P | 0.1159 | P | |
| T | 0.0115 | T | ||
| f1125 | P | 0.1118 | P | |
| T | 0.0135 | T | ||
| f1485 | P | 0.1054 | P | |
| T | 0.0122 | T |
| Smoothing Reactor | Fault Location | Fault Properties | Normalized Area Difference | Fault Identification Results |
|---|---|---|---|---|
| 50 mH | f15 | P | 0.1271 | P |
| T | 0.0131 | T | ||
| f375 | P | 0.1215 | P | |
| T | 0.0134 | T | ||
| f750 | P | 0.1169 | P | |
| T | 0.014 | T | ||
| f1125 | P | 0.1099 | P | |
| T | 0.0153 | T | ||
| f1485 | P | 0.1083 | P | |
| T | 0.0131 | T | ||
| 300 mH | f15 | P | 0.1287 | P |
| T | 0.0140 | T | ||
| f375 | P | 0.1220 | P | |
| T | 0.0109 | T | ||
| f750 | P | 0.1158 | P | |
| T | 0.0283 | T | ||
| f1125 | P | 0.1294 | P | |
| T | 0.0119 | T | ||
| f1485 | P | 0.1087 | P | |
| T | 0.0177 | T |
| Fault Location | Fault Properties | Normalized Area Difference | Fault Identification Results |
|---|---|---|---|
| f15 | P | 80.3757 | P |
| T | 0.0109 | T | |
| f375 | P | 2.3678 | P |
| T | 0.0136 | T | |
| f750 | P | 1.1499 | P |
| T | 0.0194 | T | |
| f1125 | P | 0.7578 | P |
| T | 0.0088 | T | |
| f1485 | P | 0.5722 | P |
| T | 0.0250 | T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Chen, J.; Zhou, J.; Zhang, S.; Tan, J.; Zhang, L. Permanent Fault Identification Scheme for Transmission Lines Based on Amplitude Difference for LCC Injection Signal. Electronics 2025, 14, 3526. https://doi.org/10.3390/electronics14173526
Zhao Q, Chen J, Zhou J, Zhang S, Tan J, Zhang L. Permanent Fault Identification Scheme for Transmission Lines Based on Amplitude Difference for LCC Injection Signal. Electronics. 2025; 14(17):3526. https://doi.org/10.3390/electronics14173526
Chicago/Turabian StyleZhao, Qi, Jun Chen, Jie Zhou, Shuobo Zhang, Jinlong Tan, and Lu Zhang. 2025. "Permanent Fault Identification Scheme for Transmission Lines Based on Amplitude Difference for LCC Injection Signal" Electronics 14, no. 17: 3526. https://doi.org/10.3390/electronics14173526
APA StyleZhao, Q., Chen, J., Zhou, J., Zhang, S., Tan, J., & Zhang, L. (2025). Permanent Fault Identification Scheme for Transmission Lines Based on Amplitude Difference for LCC Injection Signal. Electronics, 14(17), 3526. https://doi.org/10.3390/electronics14173526





