An Attention-Driven Multi-Scale Framework for Rotating-Machinery Fault Diagnosis Under Noisy Conditions
Abstract
1. Introduction
2. Relevant Studies and Methodological Strategy
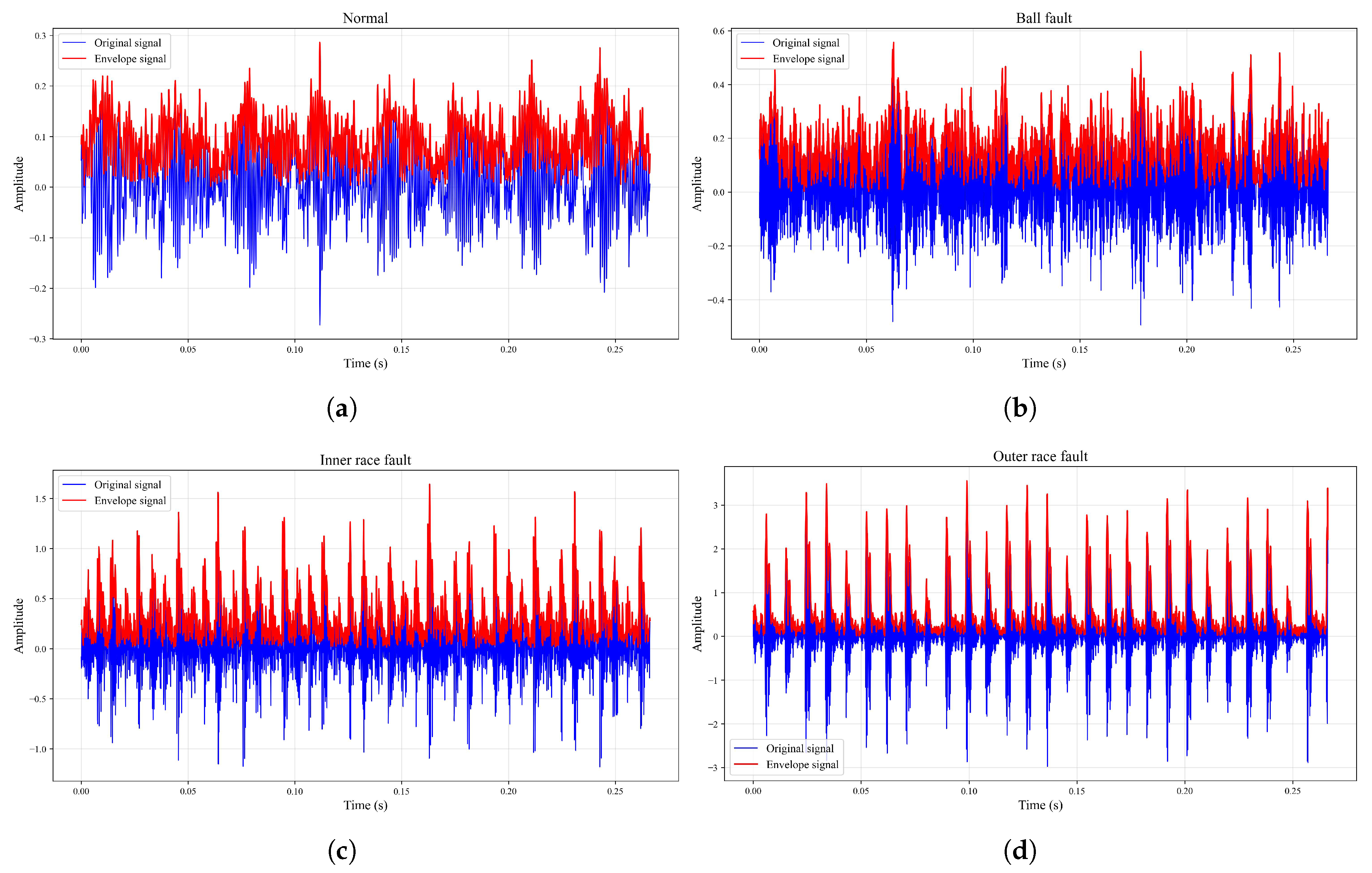
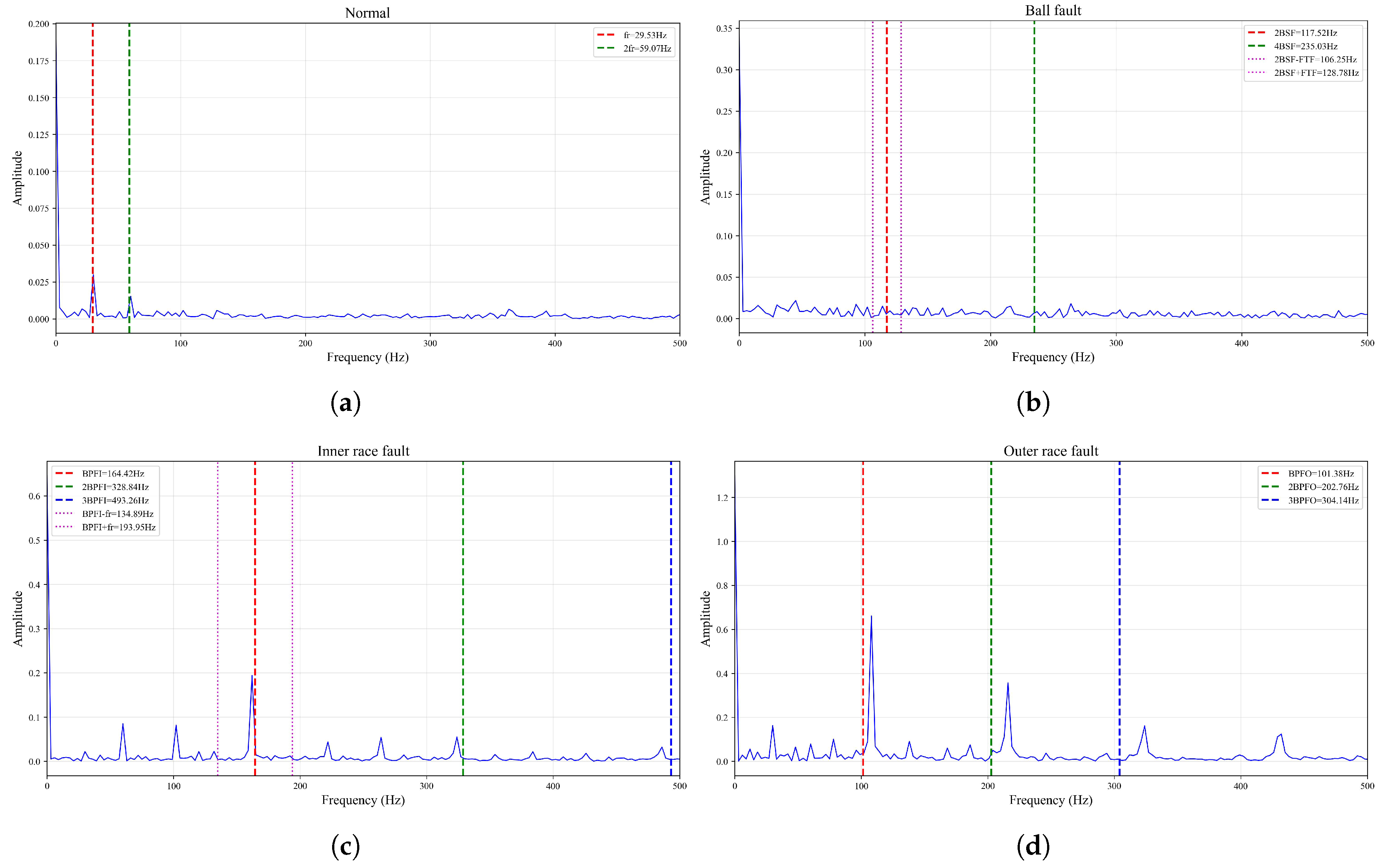
2.1. Spectrum Characteristic Analysis
2.2. Feature-Extraction Methods for Mechanical Fault Diagnosis
2.3. Comparative Analysis and Research Gaps
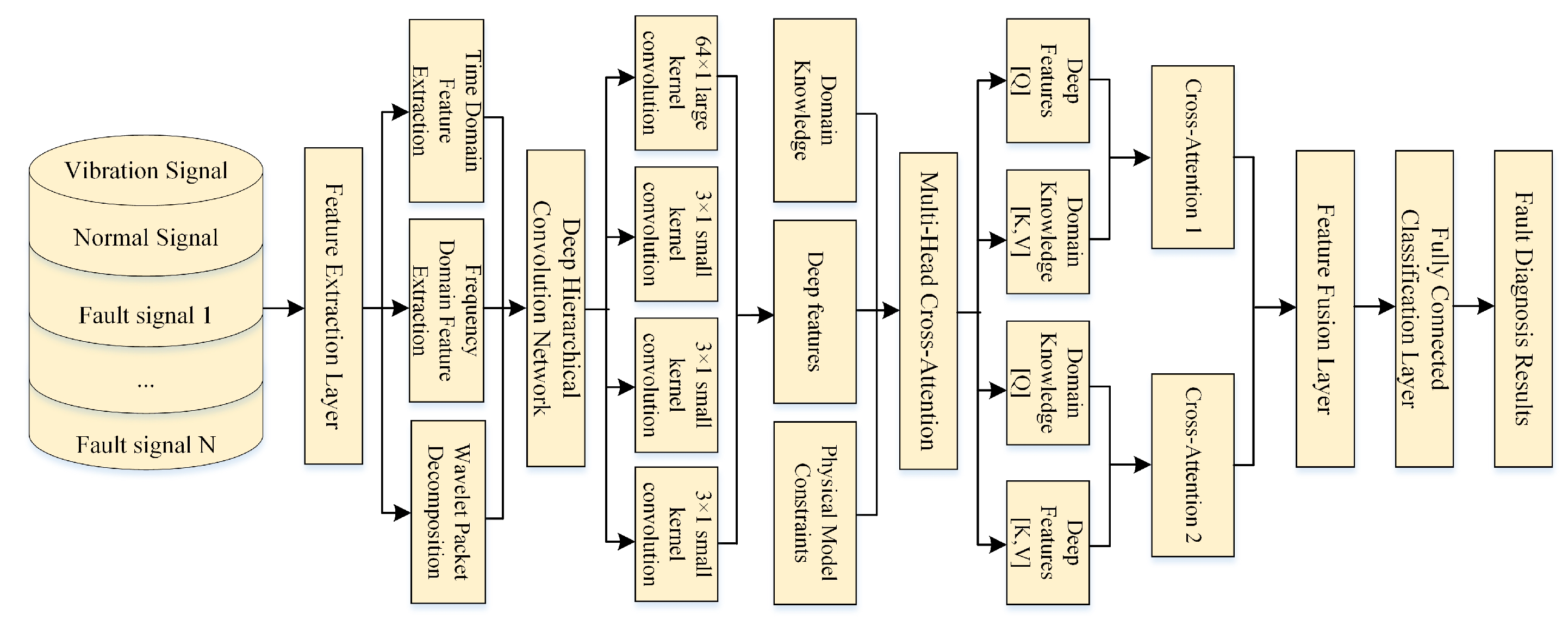
3. Proposed Algorithm
3.1. Domain Knowledge-Driven Adaptive Feature Extraction
3.2. Deep Hierarchical Convolutional Feature Learning
3.3. Enhanced Hybrid Attention Fusion and Classification
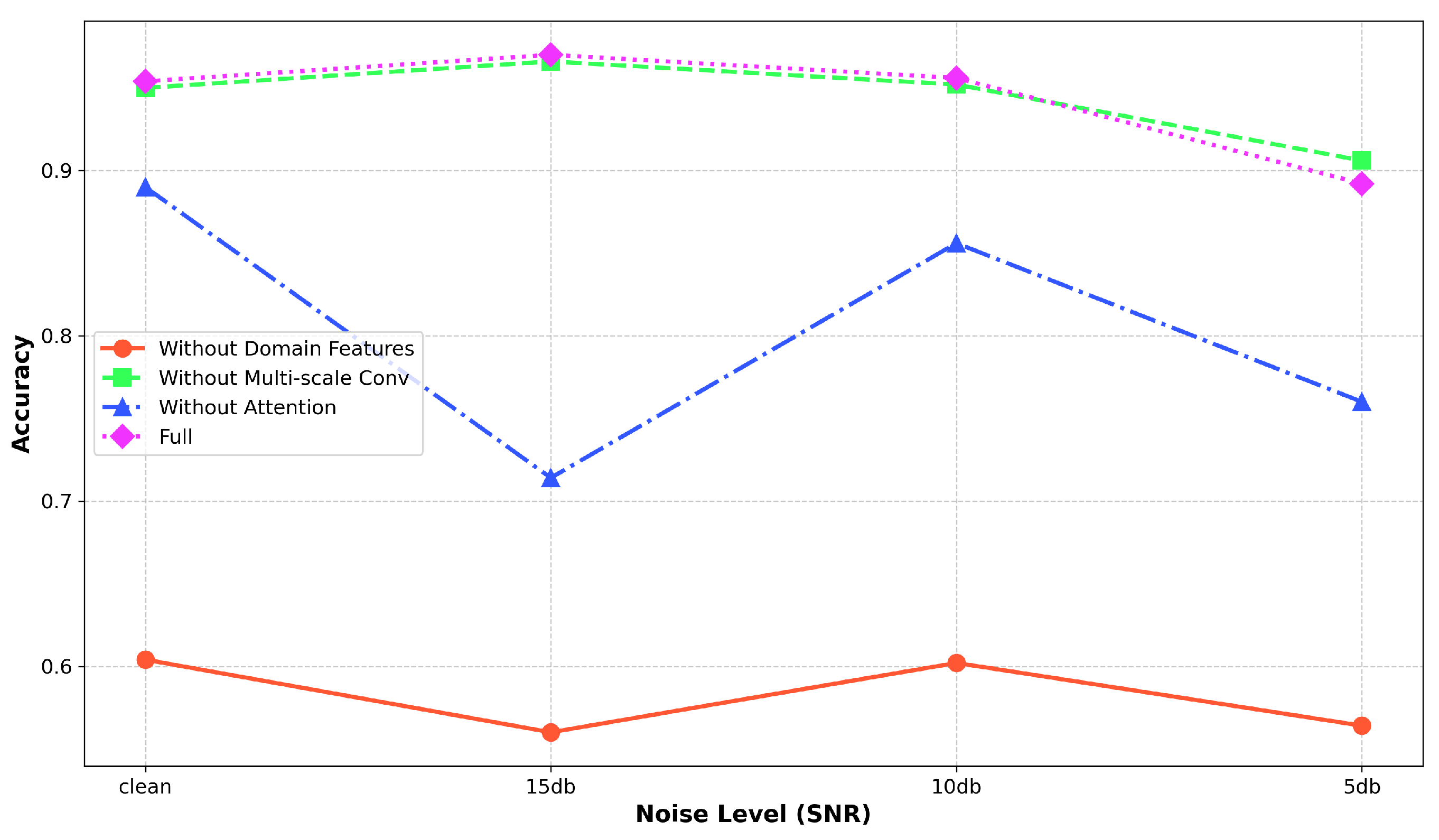
4. Experimental Results
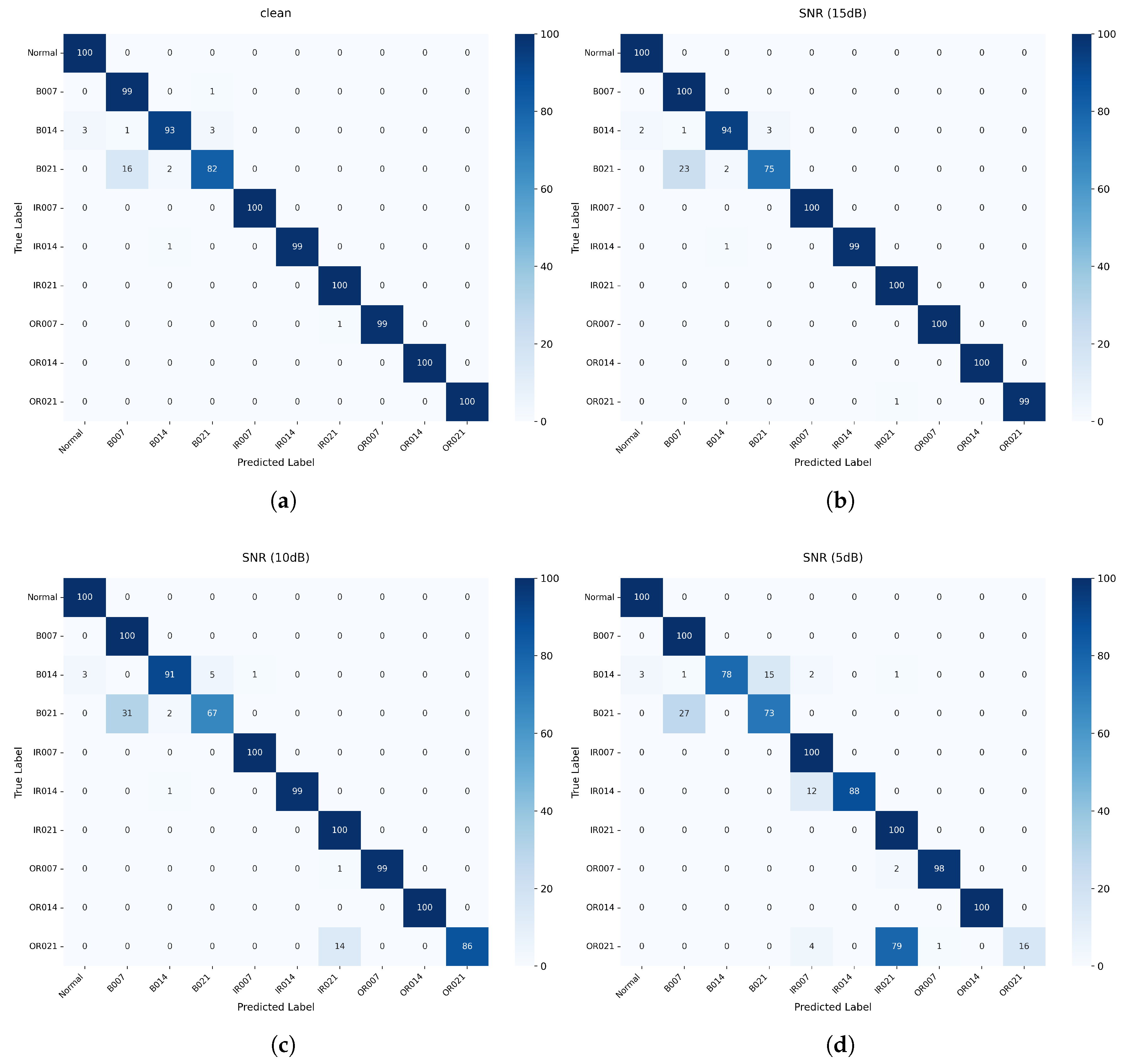
4.1. Case I: Rotating-Machinery Fault Classification Results Using CWRU Dataset
4.1.1. Data Preparation
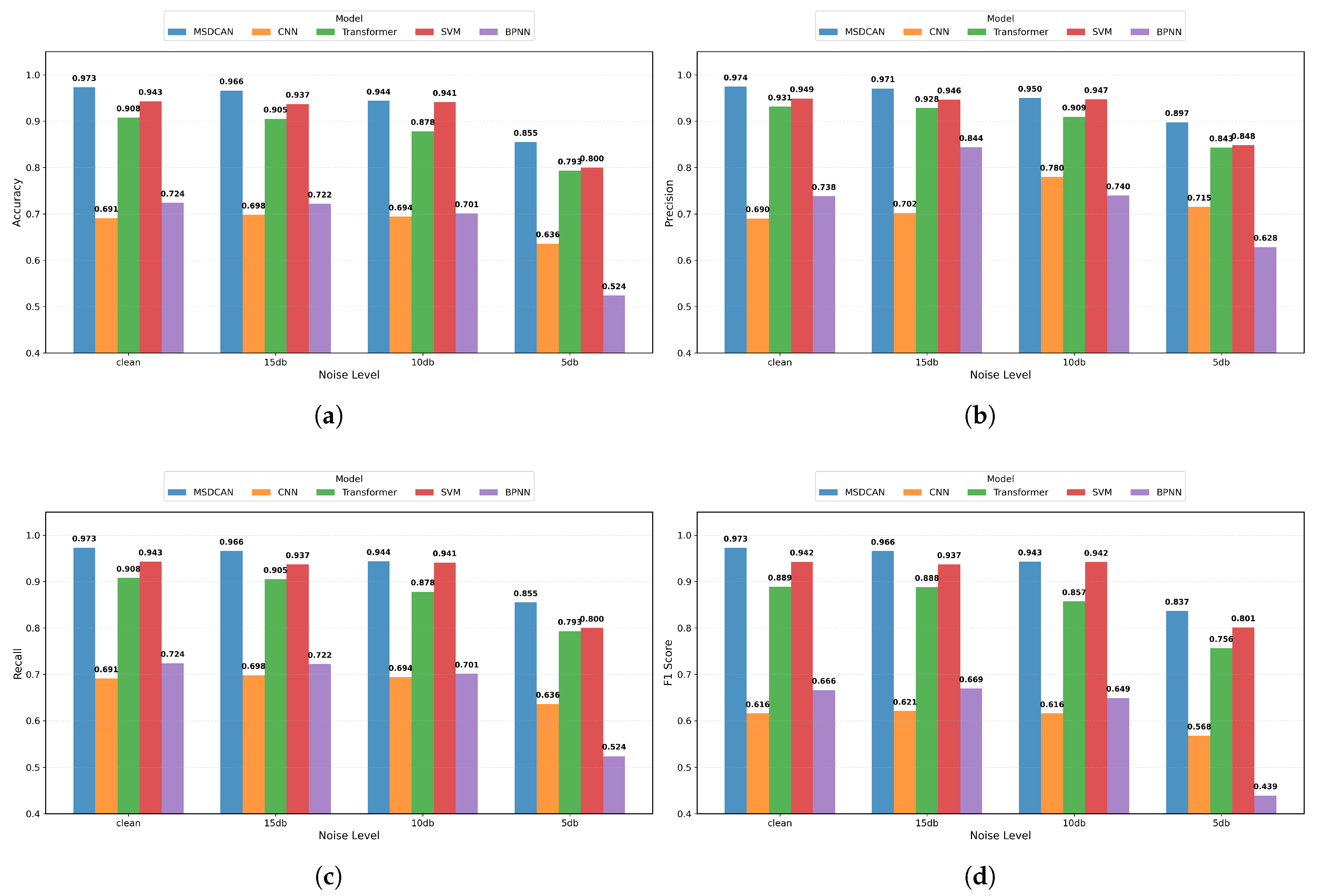
4.1.2. Rotating-Machinery Fault Diagnosis Results
4.2. Case II: Gear Fault Classification Results Using XJTU Dataset
4.2.1. Data Preparation
4.2.2. Gear Fault Diagnosis Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Artigao, E.; Martín-Martínez, S.; Honrubia-Escribano, A.; Gómez-Lázaro, E. Wind Turbine Reliability: A Comprehensive Review towards Effective Condition Monitoring Development. Appl. Energy 2018, 228, 1569–1583. [Google Scholar] [CrossRef]
- Du, Y.; Geng, X.; Zhou, Q.; Cheng, S. A Fault Diagnosis Method for Offshore Wind Turbine Bearing Based on Adaptive Deep Echo State Network and Bidirectional Long Short Term Memory Network in Noisy Environment. Ocean Eng. 2024, 312, 119101. [Google Scholar] [CrossRef]
- Zhong, J.-H.; Liang, J.; Yang, Z.-X.; Wong, P.K.; Wang, X.-B. An Effective Fault Feature Extraction Method for Gas Turbine Generator System Diagnosis. Shock Vib. 2016, 2016, 9359426. [Google Scholar] [CrossRef]
- Jalayer, M.; Kaboli, A.; Orsenigo, C.; Vercellis, C. Fault Detection and Diagnosis with Imbalanced and Noisy Data: A Hybrid Framework for Rotating Machinery. Machines 2022, 10, 237. [Google Scholar] [CrossRef]
- Jing, Q.; Yan, J.; Wang, Y.; Huang, J.; Xiao, H.; Ding, R.; Wang, J.; Geng, Y. A Novel Small-Sample Diagnosis Method for GIS Partial Discharge by Transfer Robust Support Matrix Machine. Measurement 2025, 255, 118054. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, T.; Liu, L. A Fault Segment Location Method for Distribution Networks Based on Spiking Neural P Systems and Bayesian Estimation. Prot. Control Mod. Power Syst. 2023, 8, 47. [Google Scholar] [CrossRef]
- Chen, R.; Li, X.; Chen, Y. Optimal Layout Model of Feeder Automation Equipment Oriented to the Type of Fault Detection and Local Action. Prot. Control Mod. Power Syst. 2023, 8, 2. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Li, H.; Qi, D.; Yan, Y.; Chen, Z.; Huang, X. Bird Pecking Damage Risk Assessment of UHV Transmission Line Composite Insulators Based on Deep Learning. IET Gener. Trans. Dist. 2023, 17, 2788–2798. [Google Scholar] [CrossRef]
- Lan, L.; Liu, G.; Zhu, S.; Hou, M.; Liu, X. Fault Recovery Strategy for Urban Distribution Networks Using Soft Open Points. Energy Convers. Econom. 2024, 5, 42–53. [Google Scholar] [CrossRef]
- Li, D.; Lu, J.; Zhang, T.; Ding, J. Feature Hybrid Fusion-Based Fault Diagnosis of Multi-Scale and Multi-Stage Industrial Processes. J. Process Control 2025, 152, 103460. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, X.; Peng, Z.; Hui, Y.; Xu, R.; Chen, P. An Interpretable Frequency-Enhanced Domain Adaptive Network for Cross-Domain Fault Diagnosis of Rotating Machinery. Appl. Acoust. 2025, 240, 110934. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, H.; Tao, Z.; Wang, Y. Intelligent Fault Diagnosis of Rolling Bearing Based on Time–Frequency Processing and DLKA-YOLO. Franklin Open 2025, 10, 100228. [Google Scholar] [CrossRef]
- Wei, J.; Chen, H.; Yuan, Y.; Huang, H.; Wen, L.; Jiao, W. Novel Imbalanced Multi-Class Fault Diagnosis Method Using Transfer Learning and Oversampling Strategies-Based Multi-Layer Support Vector Machines (ML-SVMs). Appl. Soft Comput. 2024, 167, 112324. [Google Scholar] [CrossRef]
- Qin, H.; Yang, R.; Guo, C.; Wang, W. Fault Diagnosis of Electric Rudder System Using PSOFOA-BP Neural Network. Measurement 2021, 186, 110058. [Google Scholar] [CrossRef]
- Yang, T.; Jiang, L.; Guo, Y.; Han, Q.; Li, X. LTFM-Net Framework: Advanced Intelligent Diagnostics and Interpretability of Insulated Bearing Faults in Offshore Wind Turbines under Complex Operational Conditions. Ocean Eng. 2024, 309, 118533. [Google Scholar] [CrossRef]
- Tang, S.; Ma, J.; Yan, Z.; Zhu, Y.; Khoo, B.C. Deep Transfer Learning Strategy in Intelligent Fault Diagnosis of Rotating Machinery. Eng. Appl. Artif. Intell. 2024, 134, 108678. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Yang, Y. Fault Diagnosis of Rolling Bearings Using an Improved Multi-Scale Convolutional Neural Network with Feature Attention Mechanism. ISA Trans. 2021, 110, 379–393. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of Machine Learning to Machine Fault Diagnosis: A Review and Roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Chen, H.; Li, J.; Wang, X.-B.; Yu, L.-Q.; Yang, Z.-X. Review of Intelligent Fault Diagnosis for Rotating Machinery under Imperfect Data Conditions. Expert Syst. Appl. 2025, 285, 127726. [Google Scholar] [CrossRef]
- Yang, D.; Karimi, H.R.; Pawelczyk, M. A New Intelligent Fault Diagnosis Framework for Rotating Machinery Based on Deep Transfer Reinforcement Learning. Control Eng. Pract. 2023, 134, 105475. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep Learning and Its Applications to Machine Health Monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Arabian-Hoseynabadi, H.; Oraee, H.; Tavner, P.J. Failure Modes and Effects Analysis (FMEA) for Wind Turbines. Int. J. Electr. Power Energy Syst. 2010, 32, 817–824. [Google Scholar] [CrossRef]
- Xin, G.; Zhong, Q.; Jin, Y.; Li, Z.; Chen, Y.; Li, Y.-F.; Antoni, J. Autonomous Bearing Fault Diagnosis Based on Fault-Induced Envelope Spectrum and Moving Peaks-Over-Threshold Approach. IEEE Trans. Instrum. Meas. 2024, 73, 1–12. [Google Scholar] [CrossRef]
- Djemili, I.; Medoued, A.; Soufi, Y. A Wind Turbine Bearing Fault Detection Method Based on Improved CEEMDAN and AR-MEDA. J. Vib. Eng. Technol. 2024, 12, 4225–4246. [Google Scholar] [CrossRef]
- Nayana, B.R.; Geethanjali, P. Analysis of Statistical Time-Domain Features Effectiveness in Identification of Bearing Faults from Vibration Signal. IEEE Sens. J. 2017, 17, 5618–5625. [Google Scholar] [CrossRef]
- Zhou, Q.; Tang, J. An Interpretable Parallel Spatial CNN-LSTM Architecture for Fault Diagnosis in Rotating Machinery. IEEE Internet Things J. 2024, 11, 31730–31744. [Google Scholar] [CrossRef]
- Missaoui, I.; Lachiri, Z. Stationary Wavelet Filtering Cepstral Coefficients (SWFCC) for Robust Speaker Identification. Appl. Acoust. 2025, 231, 110435. [Google Scholar] [CrossRef]
- Lu, Z.; Liang, L.; Zhu, J.; Zou, W.; Mao, L. Rotating Machinery Fault Diagnosis Under Multiple Working Conditions via a Time-Series Transformer Enhanced by Convolutional Neural Network. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Wang, C.; Deng, X.; Sun, Y.; Yan, L. Research on Image Classification Based on Residual Group Multi-Scale Enhanced Attention Network. Comput. Electr. Eng. 2024, 118, 109351. [Google Scholar] [CrossRef]
- Li, H.; Yu, H.; Liu, Z.; Li, F.; Wu, X.; Cao, B.; Zhang, C.; Liu, D. Long-term Scenario Generation of Renewable Energy Generation Using Attention-based Conditional Generative Adversarial Networks. Energy Convers. Econ. 2024, 5, 15–27. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Gu, Y.; Yan, Y.; Li, Q.; Gao, M.; Dong, Z. A Lightweight Vehicle Mounted Multi-Scale Traffic Sign Detector Using Attention Fusion Pyramid. J. Supercomput. 2024, 80, 3360–3381. [Google Scholar] [CrossRef]
- Yin, H.; Chen, Q.; Chen, L.; Shen, C. Cross-Attention Transformer-Based Domain Adaptation: A Novel Method for Fault Diagnosis of Rotating Machinery with High Generalizability and Alignment Capability. IEEE Sens. J. 2024, 24, 40049–40058. [Google Scholar] [CrossRef]
- Wang, X.; Chen, H.; Zhao, J.; Song, C.; Zhang, Y.; Yang, Z.-X.; Wong, P.K. Wind Turbine Fault Diagnosis for Class-Imbalance and Small-Size Data Based on Stacked Capsule Autoencoder. IEEE Trans. Ind. Inf. 2024, 20, 12694–12704. [Google Scholar] [CrossRef]



| Framework | Noise Handling Strategies | Description | Reference |
|---|---|---|---|
| CPAEBL | Improved CEEMDAN with correlation–skewness IMF selection plus phase-space reconstruction suppresses noise while preserving nonlinear dynamics. | Integrates noise-robust IMF selection and phase-space reconstruction with adaptive deep reservoir and BiLSTM for high-noise bearing diagnosis. | [2] |
| GAN-CLSTM-ELM | FFT/CWT multi-domain feature extraction and WGAN-GP augmentation mitigate random noise and imbalance. | Uses spectral–time–frequency fusion plus GAN augmentation and weighted ELM to address noise and class imbalance. | [4] |
| C-Trans | Multi-scale convolutions and attention highlight salient fault patterns under noisy multi-condition signals. | Combines multi-scale CNN feature extraction with transformer attention to relate fault patterns to classes. | [28] |
| Parallel CNN–LSTM | Parallel raw and wavelet branches exploit time–frequency localization to attenuate background noise. | Dual branches fuse raw temporal features and wavelet coefficients to enhance discriminative representation with minimal manual features. | [26] |
| Symbol | Value | Parameter |
|---|---|---|
| B | 32 | Batch Size |
| 0.0001 | Learning Rate | |
| 1 × | Weight Decay | |
| E | 40 | Number of Epochs |
| 0.3 | Dropout Rate | |
| 1.0 | Gradient Clipping | |
| P | 5 | Scheduler Patience |
| 0.5 | Scheduler Factor |
| Model | Clean | SNR (15 dB) | SNR (10 dB) | SNR (5 dB) |
|---|---|---|---|---|
| CNN | 0.691 | 0.698 | 0.694 | 0.636 |
| Transformer | 0.908 | 0.905 | 0.878 | 0.793 |
| SVM | 0.943 | 0.937 | 0.941 | 0.800 |
| BPNN | 0.724 | 0.722 | 0.701 | 0.524 |
| MSDCAN | 0.973 | 0.966 | 0.944 | 0.855 |
| Model | Clean | SNR (15 dB) | SNR (10 dB) | SNR (5 dB) |
|---|---|---|---|---|
| CNN | 0.628 | 0.650 | 0.634 | 0.568 |
| Transformer | 0.816 | 0.838 | 0.850 | 0.788 |
| SVM | 0.876 | 0.694 | 0.552 | 0.310 |
| BPNN | 0.582 | 0.410 | 0.404 | 0.384 |
| MSDCAN | 0.948 | 0.950 | 0.836 | 0.638 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.-M.; Wong, P.K.; Gao, Z.-J.; Yang, Z.-X.; Zhao, J.; Wang, X.-B. An Attention-Driven Multi-Scale Framework for Rotating-Machinery Fault Diagnosis Under Noisy Conditions. Electronics 2025, 14, 3805. https://doi.org/10.3390/electronics14193805
Xu L-M, Wong PK, Gao Z-J, Yang Z-X, Zhao J, Wang X-B. An Attention-Driven Multi-Scale Framework for Rotating-Machinery Fault Diagnosis Under Noisy Conditions. Electronics. 2025; 14(19):3805. https://doi.org/10.3390/electronics14193805
Chicago/Turabian StyleXu, Le-Min, Pak Kin Wong, Zhi-Jiang Gao, Zhi-Xin Yang, Jing Zhao, and Xian-Bo Wang. 2025. "An Attention-Driven Multi-Scale Framework for Rotating-Machinery Fault Diagnosis Under Noisy Conditions" Electronics 14, no. 19: 3805. https://doi.org/10.3390/electronics14193805
APA StyleXu, L.-M., Wong, P. K., Gao, Z.-J., Yang, Z.-X., Zhao, J., & Wang, X.-B. (2025). An Attention-Driven Multi-Scale Framework for Rotating-Machinery Fault Diagnosis Under Noisy Conditions. Electronics, 14(19), 3805. https://doi.org/10.3390/electronics14193805











