Optimized Design and Experimental Study of an Axis-Encircling Beam with Gently Varying Cusp Magnetic Field
Abstract
:1. Introduction
2. The Relativistic Theory of an Axis-Encircling Beam
3. Optimization Design and Numerical Simulation
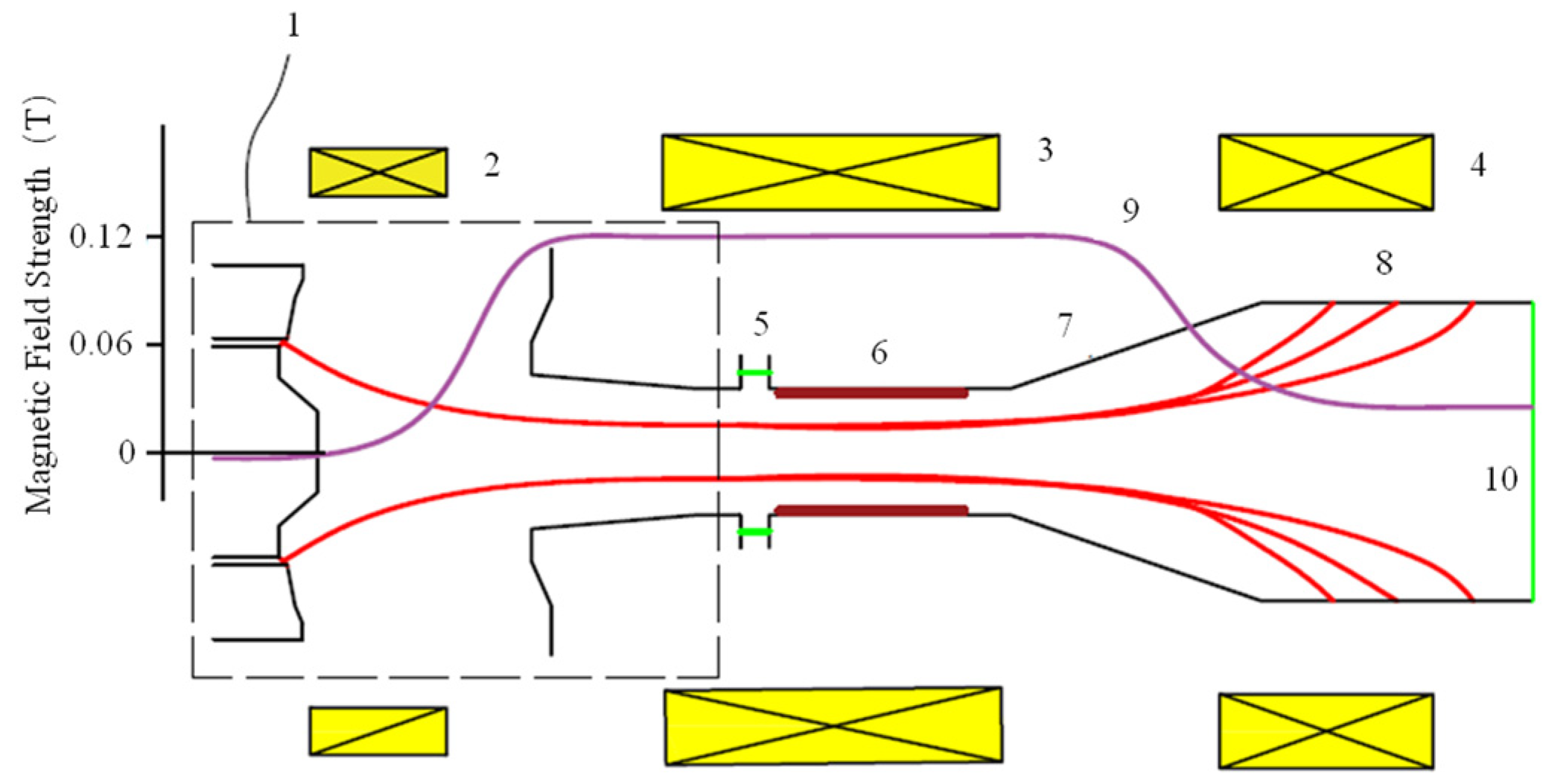
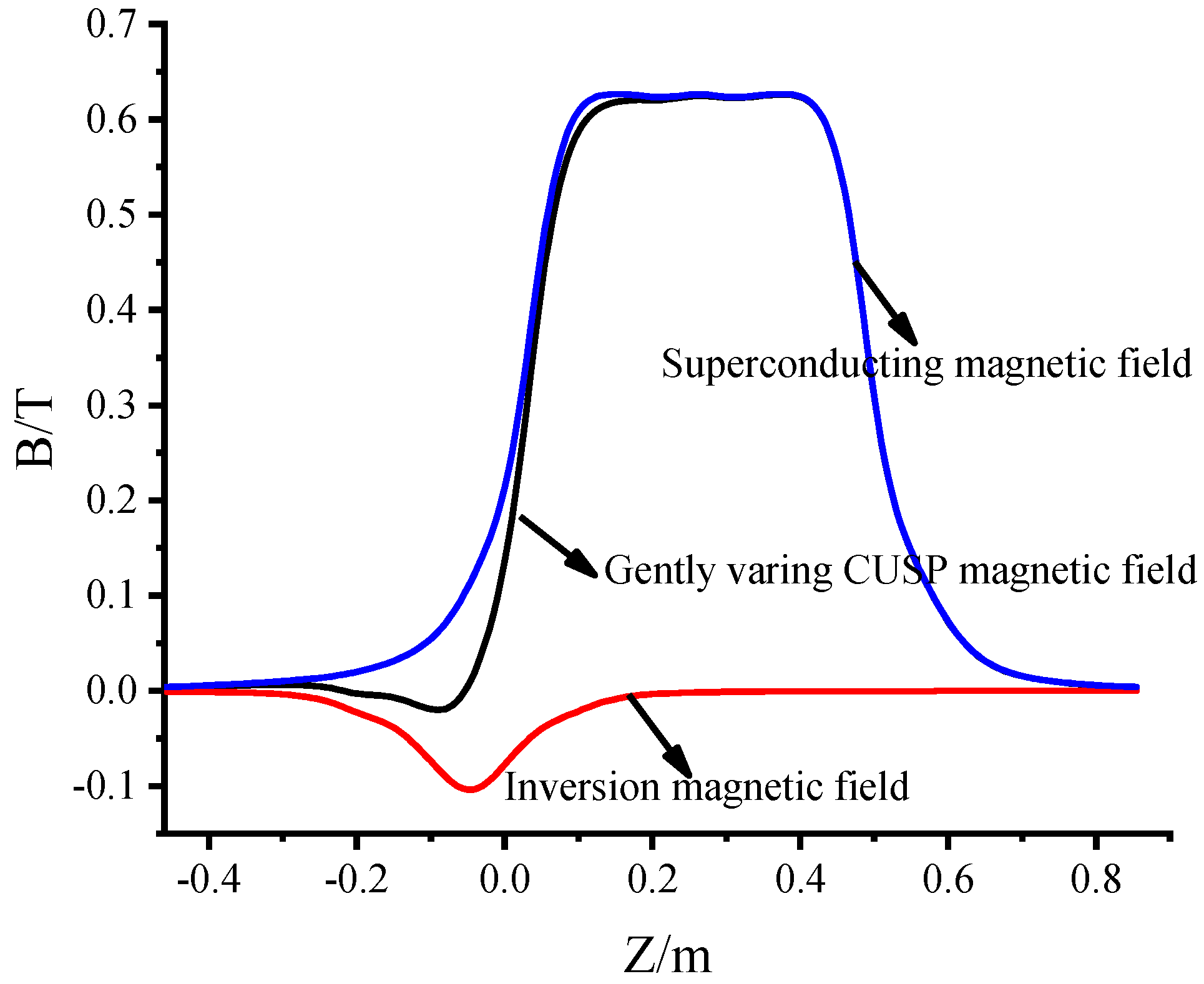
3.1. Configuration of the Magnetic Field
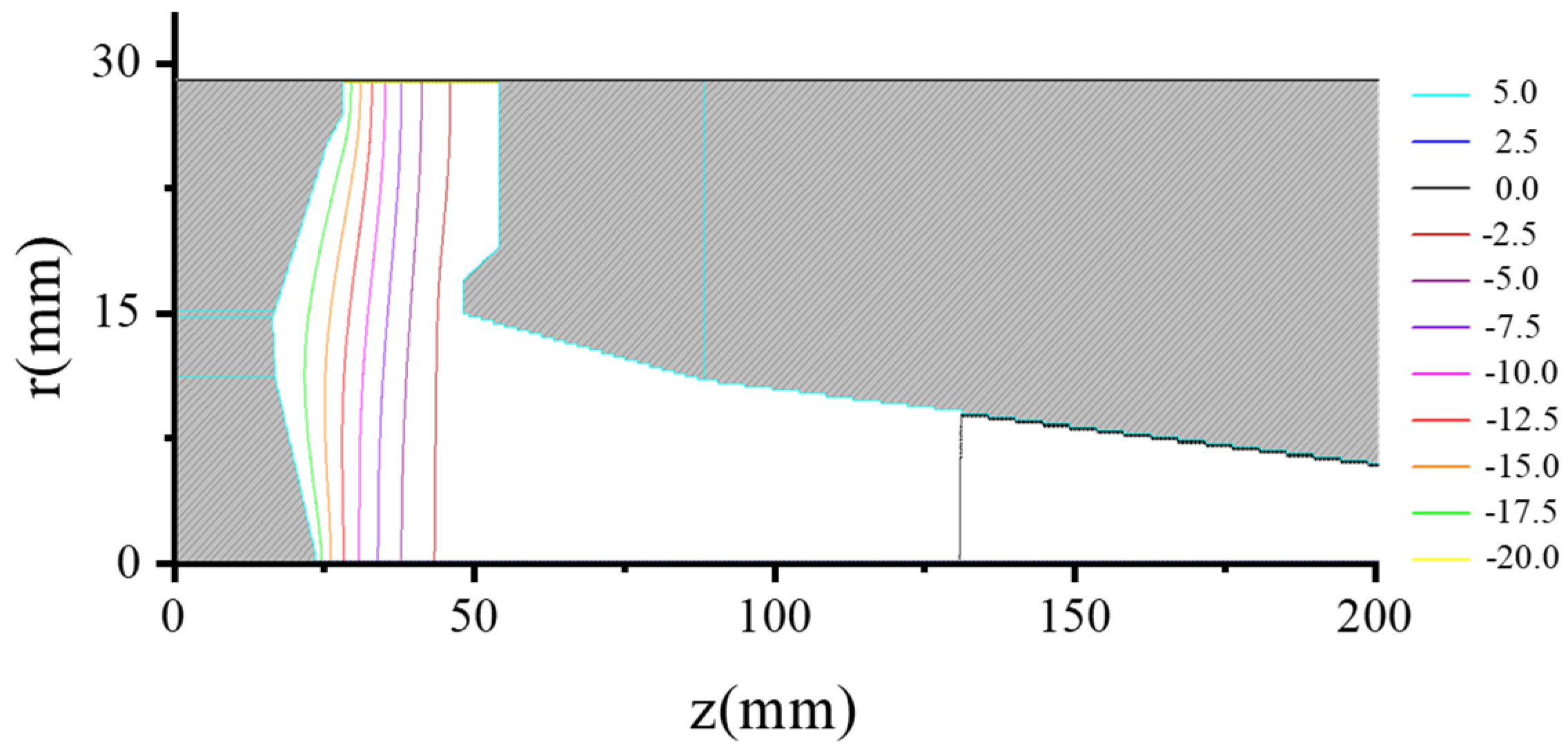
3.2. Optimized Design of the Electron Optical System with an Axis-Encircling Beam
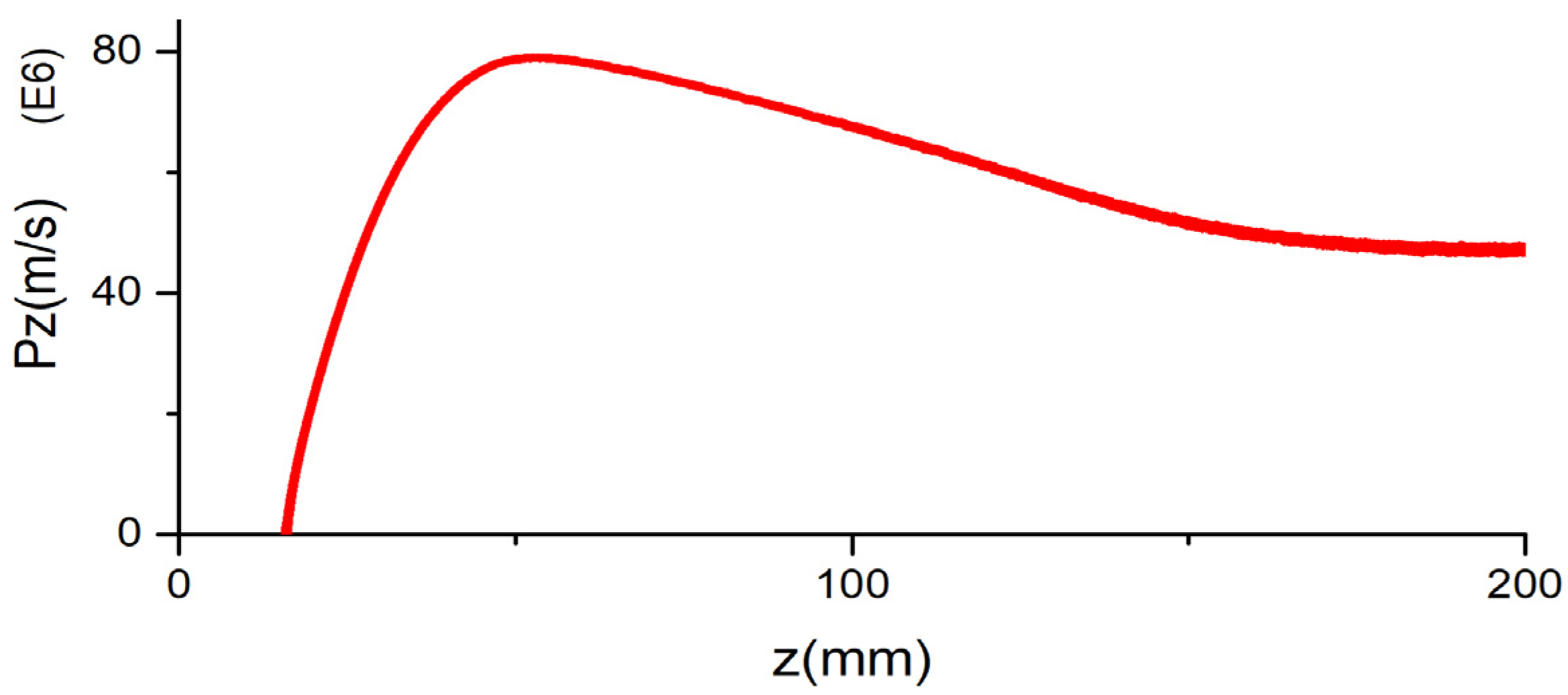
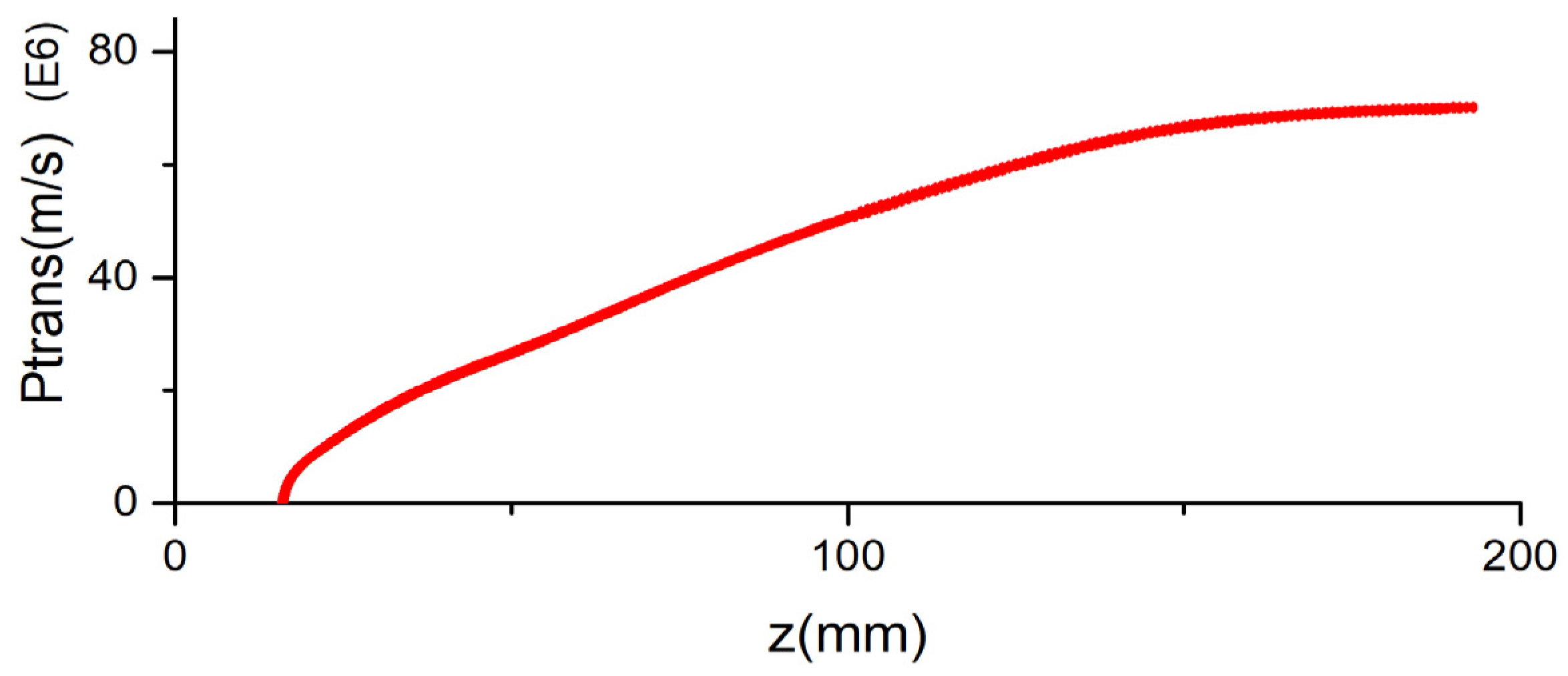
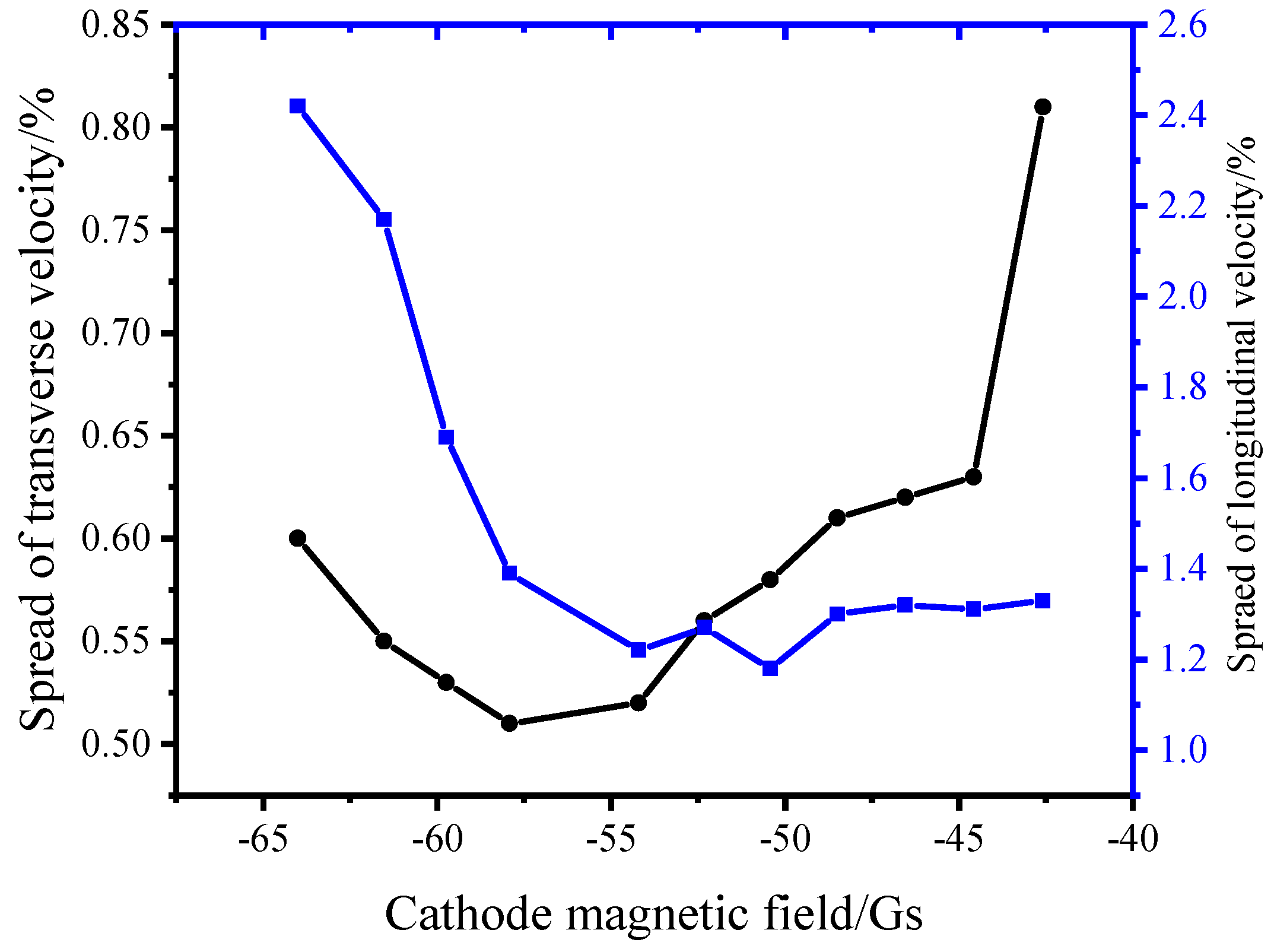
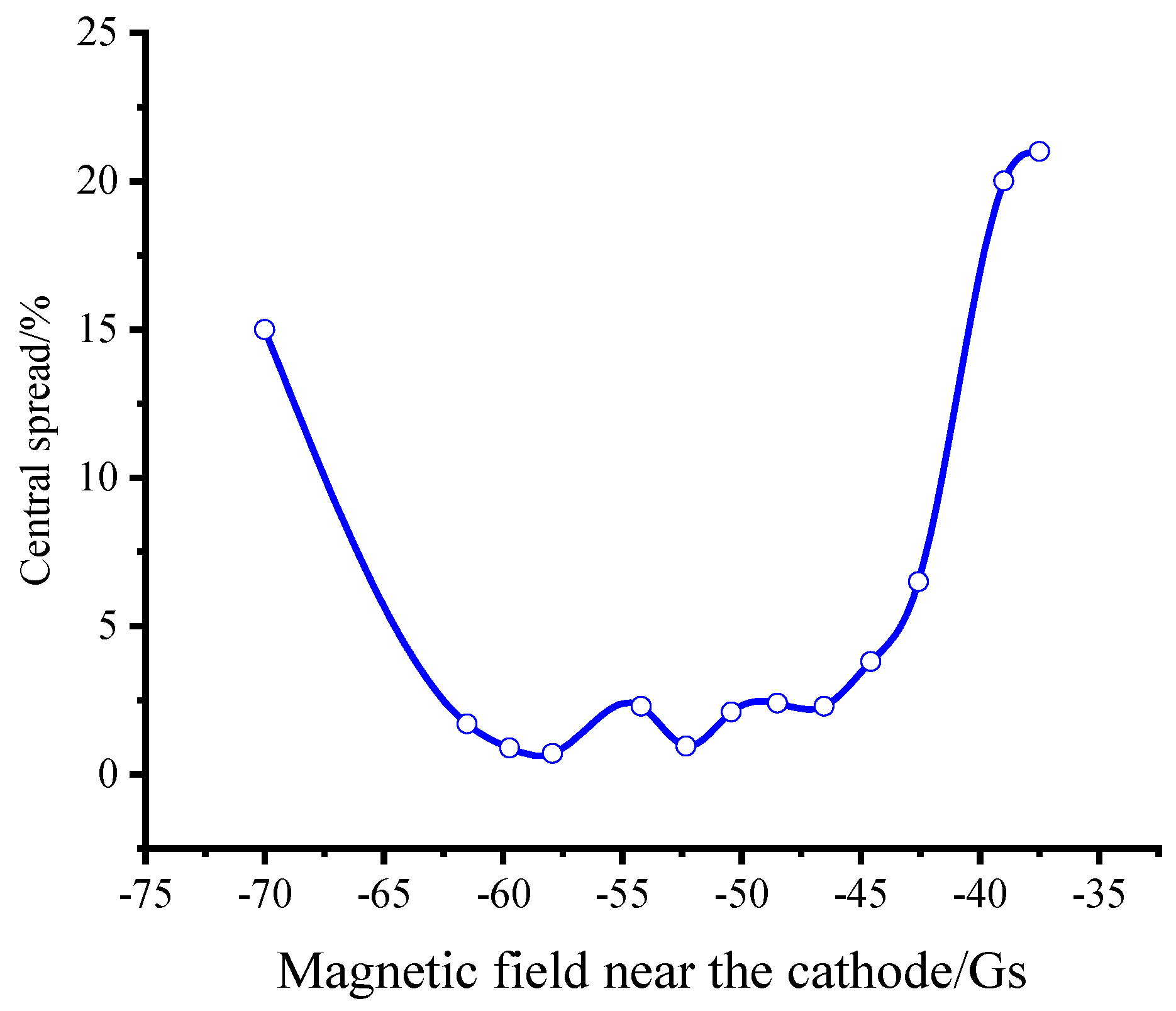
3.3. The Character of the Beam
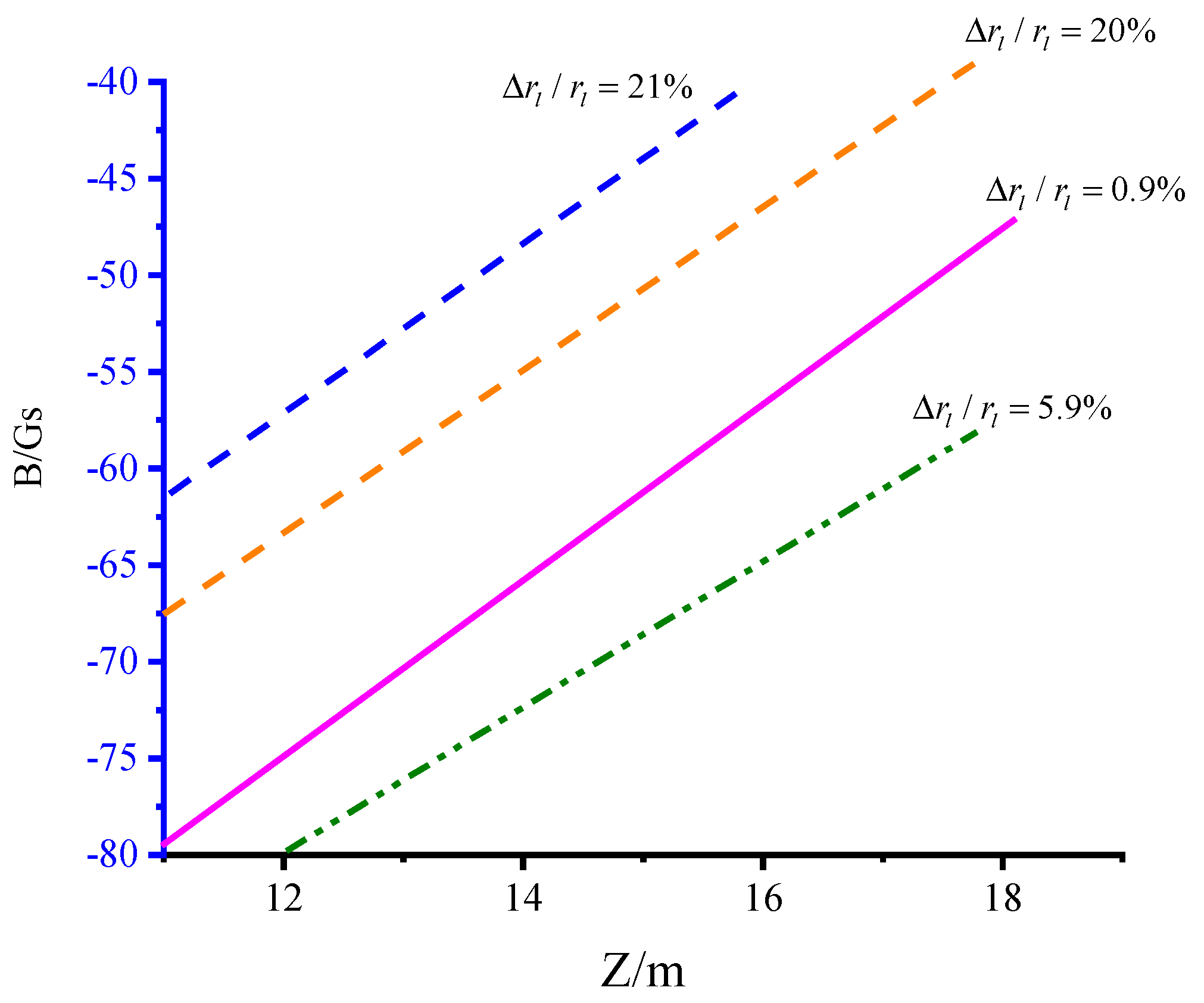
4. Experimental Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thumm, M. State-of-the-Art of High-Power Gyro-Devices and Free Electron Masers. J. Infrared Millim. Terahertz Waves 2020, 41, 1–120. [Google Scholar]
- Zhao, Q.; Ma, M.; Li, X.; Wang, Z.; Yu, S. The Multi-modes, Multi-harmonics Behavior of a THz Large-orbit Gyrotron. J. Infrared Millim. Waves 2022, 41, 457–1453. [Google Scholar]
- Sinitsyn, O.V.; Nusinovich, G.S.; Antonsen, T.M. Stability of Gyrotron Operation in very High-order Modes. Phys. Plasmas 2012, 19, 063114. [Google Scholar] [CrossRef]
- Thumm, M.K. Recent Advances in the Worldwide Fusion Gyrotron Development. IEEE Trans. Plasma Sci. 2014, 42, 590–1599. [Google Scholar] [CrossRef]
- Jelonnek, J.; Albajar, F.; Alberti, S.; Avramidis, K.; Benin, P.; Bonicelli, T.; Cismondi, F.; Erckmann, V.; Gantenbein, G.; Hesch, K.; et al. From Series Production of Gyrotrons for W7-X Toward EU-1 MW Gyrotrons for ITER. IEEE Trans. Plasma Sci. 2014, 42, 1135–11143. [Google Scholar] [CrossRef]
- Singh, U.; Kumar, N.; Sinha, A.K. Magnetron Injection Gun for a Short Pulse, 0.67 THz Gyrotron for Remote Detection of Radioactive Materials. IEEE Trans. Terahertz Sci. Technol. 2014, 4, 509–1514. [Google Scholar] [CrossRef]
- Ruess, S.; Gantenbein, G.; Illy, S.; Kobarg, T.; Pagonakis, I.G.; Rzesnicki, T.; Thumm, M.; Weggen, J.; Jelonnek, J. Tolerance Studies on an Inverse Magnetron Injection Gun for a 2-MW 170-GHz Coaxial-cavity Gyrotron. IEEE Trans. Electron Devices 2017, 64, 3870–13876. [Google Scholar] [CrossRef]
- Thumm, M. Gyro-devices and Their applications. In Proceedings of the 2011 IEEE International Vacuum Electronics Conference (IVEC), Bangalore, India, 21–24 February 2011; pp. 521–524. [Google Scholar]
- Samsonov, S.V.; Levitan, B.A.; Murzin, V.N.; Gachev, I.G.; Denisov, G.G.; Bogdashov, A.A.; Mishakin, S.V.; Fiks, A.S.; Soluyanova, E.A.; Tai, E.M.; et al. Ka-band Gyrotron Traveling-wave Tubes with the Highest Continuous-wave and Average Power. IEEE Trans. Electron Devices 2014, 61, 4264–14267. [Google Scholar] [CrossRef]
- Naidu, V.B.; Kesari, V.; Karmakar, S.; Seshadri, R. Particle-In-Cell Simulation of a Tapered Cavity for a Millimeter Wave Gyrotron. IEEE Trans. Plasma Sci. 2018, 46, 2460–12464. [Google Scholar] [CrossRef]
- Louksha, O.I.; Malkin, A.G.; Trofimov, P.A. First Experiments on Multistage Energy Recovery in a 4-mm Wavelength Gyrotron. IEEE Electron Device Lett. 2024, 45, 1638–11641. [Google Scholar] [CrossRef]
- Gao, J.; Li, B.; Yu, W.; Chen, Y.; Yin, H.; Xu, B.; He, W. Study of a Broadband and High-power Terahertz Gyrotron Traveling-wave Amplifier. IEEE Electron Device Lett. 2023, 44, 1744–11747. [Google Scholar] [CrossRef]
- Kao, S.H.; Chiu, C.C.; Pao, K.F.; Chu, K.R. Competition between Harmonic Cyclotron Maser Interactions in the Terahertz Regime. Phys. Rev. Lett. 2011, 107, 105101. [Google Scholar] [CrossRef] [PubMed]
- Notake, T.; Saito, T.; Tatematsu, Y.; Fujii, A.; Ogasawara, S.; Agusu, L.; Ogawa, I.; Idehara, T.; Manuilov, V.N. Development of a Novel High Power Sub-THz Second Harmonic Gyrotron. Phys. Rev. Lett. 2009, 103, 225002. [Google Scholar] [CrossRef]
- He, W.; Donaldson, C.R.; Zhang, L.; Ronald, K.; Phelps, A.D.R.; Cross, A.W. Broadband Amplification of Low-Terahertz Signals Using Axis-Encircling Electrons in a Helically Corrugated Interaction Region. Phys. Rev. Lett. 2017, 119, 184801.1–1184801.5. [Google Scholar] [CrossRef] [PubMed]
- Kiya, T.; Yamane, H.; Yamakawa, K.; Honda, N.; Ouchi, K. Recording Performance of Perpendicular Magnetic Recording Media Measured With Contact-Type Cusp-Field Write Head. IEEE Trans. Magn. 2006, 42, 2378–12380. [Google Scholar] [CrossRef]
- Wang, J.; Luo, Y.; Luhmann, N.C. The Simulation of a High-Power Low-Velocity-Spread Space-Charge-Limited (SCL) Cusp Gun. IEEE Trans. Plasma Sci. 2010, 38, 3356–13362. [Google Scholar] [CrossRef]
- Donaldson, C.R.; He, W.; Cross, A.W.; Li, F.; Phelps, A.D.R.; Zhang, L.; Ronald, K.; Robertson, C.W.; Whyte, C.G.; Young, A.R. A CUSP Electron Gun for Millimeter Wave Gyrodevices. Appl. Phys. Lett. 2010, 96, 141501. [Google Scholar] [CrossRef]
- Jeon, S.G.; Baik, C.W.; Kim, D.H.; Park, G.S.; Sato, N.; Yokoo, K. Study on velocity spread for axis-encircling electron beams generated by single magnetic cusp. Appl. Phys. Lett. 2002, 80, 3703–13705. [Google Scholar] [CrossRef]
- Du, C.H.; Chang, T.H.; Liu, P.K.; Yuan, C.P.; Yu, S.J.; Liu, G.F.; Bratman, V.L.; Glyavin, M.Y.; Kalynov, Y.K. Development of a Magnetic Cusp Gun for Terahertz Harmonic Gyrodevices. IEEE Trans. Electron Devices 2012, 59, 3635–13640. [Google Scholar] [CrossRef]
- Du, C.-H.; Qi, X.-B.; Hao, B.-L.; Chang, T.-H.; Liu, P.-K. Conformal Cross-Flow Axis-Encircling Electron Beam for Driving THz Harmonic Gyrotron. IEEE Electron Device Lett. 2015, 36, 960–1962. [Google Scholar] [CrossRef]
- Schmidt, G. Nonadiabatic Particle Motion in Axial symmetric Fields. Phys. Fluids 1962, 5, 994–11002. [Google Scholar] [CrossRef]
- Jaynes, R.; Gilgenbach, R.; Hochman, J.; Eidietis, N.; Rintamaki, J.; Cohen, W.; Peters, C.; Lau, Y.; Spencer, T. Velocity Ratio Measurement Diagnostics and Simulations of a Relativistic Electron Beam in an Axis Encircling Gyrotron. IEEE Trans. Plasma Sci. 1999, 27, 136–1137. [Google Scholar] [CrossRef]
- Scheitrum, G.P.; Symons, R.S.; True, R.B. Low velocity spread axis encircling electron beam forming system. In Proceedings of the International Technical Digest on Electron Devices Meeting, Washington, DC, USA, 3–6 December 1989; pp. 743–1746. [Google Scholar]
- Wu, X. Study of the Forming Technology and Application of Larage-Orbit Electron Beam. Ph.D. Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2013; pp. 20–30. [Google Scholar]
- MJRhee, W.W. Destler. Relativistic electron dynamics in a cusped magnetic field. Phys. Fluids 1974, 17, 1574–1581. [Google Scholar]
- Zhou, J.; Liu, D.; Liao, C.; Li, Z. CHIPIC: An Efficient Code for Electromagnetic PIC Modeling and Simulation. IEEE Trans. Plasma Sci. 2009, 37, 2002–2011. [Google Scholar] [CrossRef]




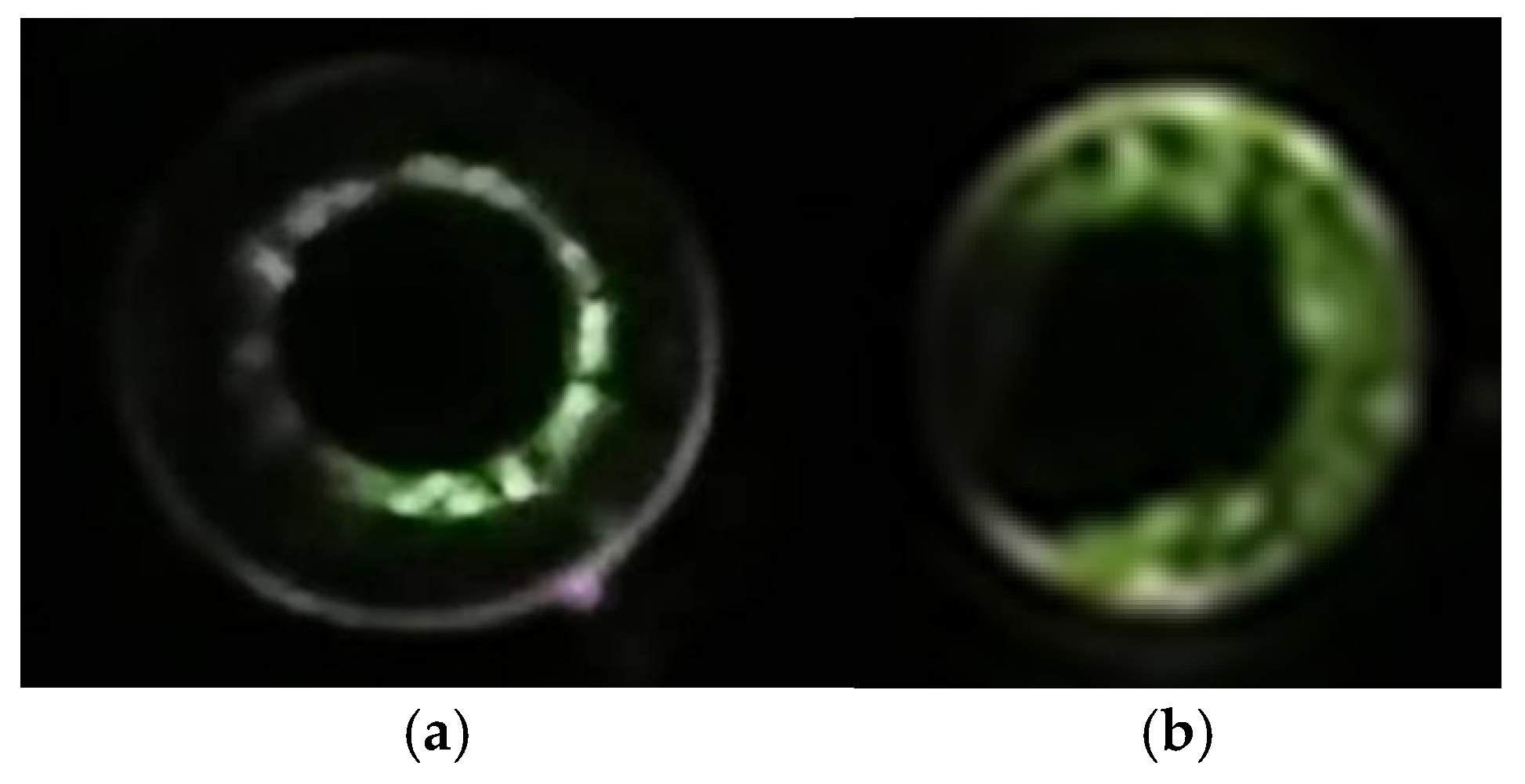
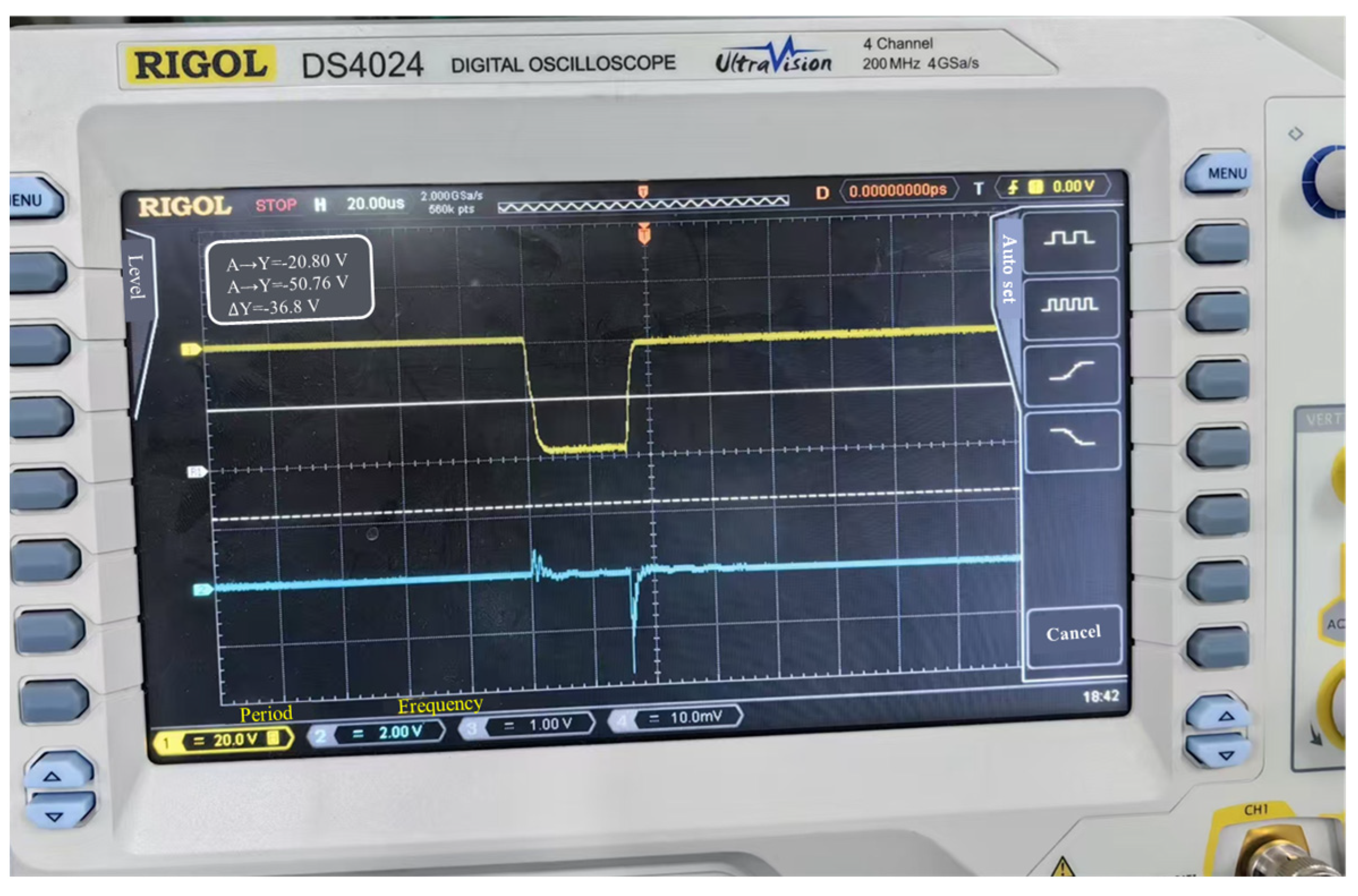
| The Name of Parameters | Value |
|---|---|
| Beam voltage | 20 kV |
| Beam current | 0.5 A |
| Magnetic field | 0.122 T |
| Cathode radius | 15 mm |
| Pitch factor | 1.5 |
| Current density | 0.94 A/cm2 |
| Larmor radius | 3.3 mm |
| Transverse velocity spread | = 0.6% |
| Longitudinal velocity spread | = 1.2% |
| Guiding center spread | = 0.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, C.; Wang, E.; Zhao, Q.; Shi, S.; Gao, D.; Li, S.; Zhang, Y.; Feng, J. Optimized Design and Experimental Study of an Axis-Encircling Beam with Gently Varying Cusp Magnetic Field. Electronics 2025, 14, 390. https://doi.org/10.3390/electronics14020390
Lei C, Wang E, Zhao Q, Shi S, Gao D, Li S, Zhang Y, Feng J. Optimized Design and Experimental Study of an Axis-Encircling Beam with Gently Varying Cusp Magnetic Field. Electronics. 2025; 14(2):390. https://doi.org/10.3390/electronics14020390
Chicago/Turabian StyleLei, Chaojun, E’Feng Wang, Qixiang Zhao, Shaoliang Shi, Dongshuo Gao, Shufeng Li, Yichi Zhang, and Jinjun Feng. 2025. "Optimized Design and Experimental Study of an Axis-Encircling Beam with Gently Varying Cusp Magnetic Field" Electronics 14, no. 2: 390. https://doi.org/10.3390/electronics14020390
APA StyleLei, C., Wang, E., Zhao, Q., Shi, S., Gao, D., Li, S., Zhang, Y., & Feng, J. (2025). Optimized Design and Experimental Study of an Axis-Encircling Beam with Gently Varying Cusp Magnetic Field. Electronics, 14(2), 390. https://doi.org/10.3390/electronics14020390







