Task Offloading Strategy for UAV-Assisted Mobile Edge Computing with Covert Transmission
Abstract
1. Introduction
- We establish a system that employs a UAV-BS and a UAV-Jammer to assist UEs with demanding computational tasks while remaining undetected by a warden. In this system, both the UEs and the UAV-BS can perform calculations while simultaneously transmitting and receiving information. After developing transmission and computation models for the UEs and UAV-BS, as well as formulating binary hypothesis testing to assess the surveillance mechanisms of the warden, we frame the overall task offloading strategy of the system as an optimization problem.
- The optimization problem is reformulated as a Markov decision process (MDP), and we employ a Deep Deterministic Policy Gradient (DDPG) algorithm to obtain the best policy. To improve the efficiency of experience replay in DDPG and accelerate the learning process, we integrate a prioritized experience replay (PER) mechanism into the DDPG framework and propose a novel PER-DDPG algorithm, which means we switch from the previous uniform sampling method to priority sampling. By adopting this approach, we accelerate the algorithm’s convergence and significantly enhance its performance.
- To evaluate the performance of our proposed method, extensive simulations are performed. Initially, we verify the impact of various parameters on the convergence of the proposed algorithm. Subsequently, ablation experiments are carried out to confirm the effectiveness of the proposed algorithm. Ultimately, simulation results from our comparisons demonstrate that our proposed solution outperforms existing methods regarding reductions in both system delay and the detection accuracy of the warden.
2. System Model
2.1. Communications Model
2.2. Computational Model
2.3. Binary Hypothesis Testing at Warden
2.4. Problem Formulation
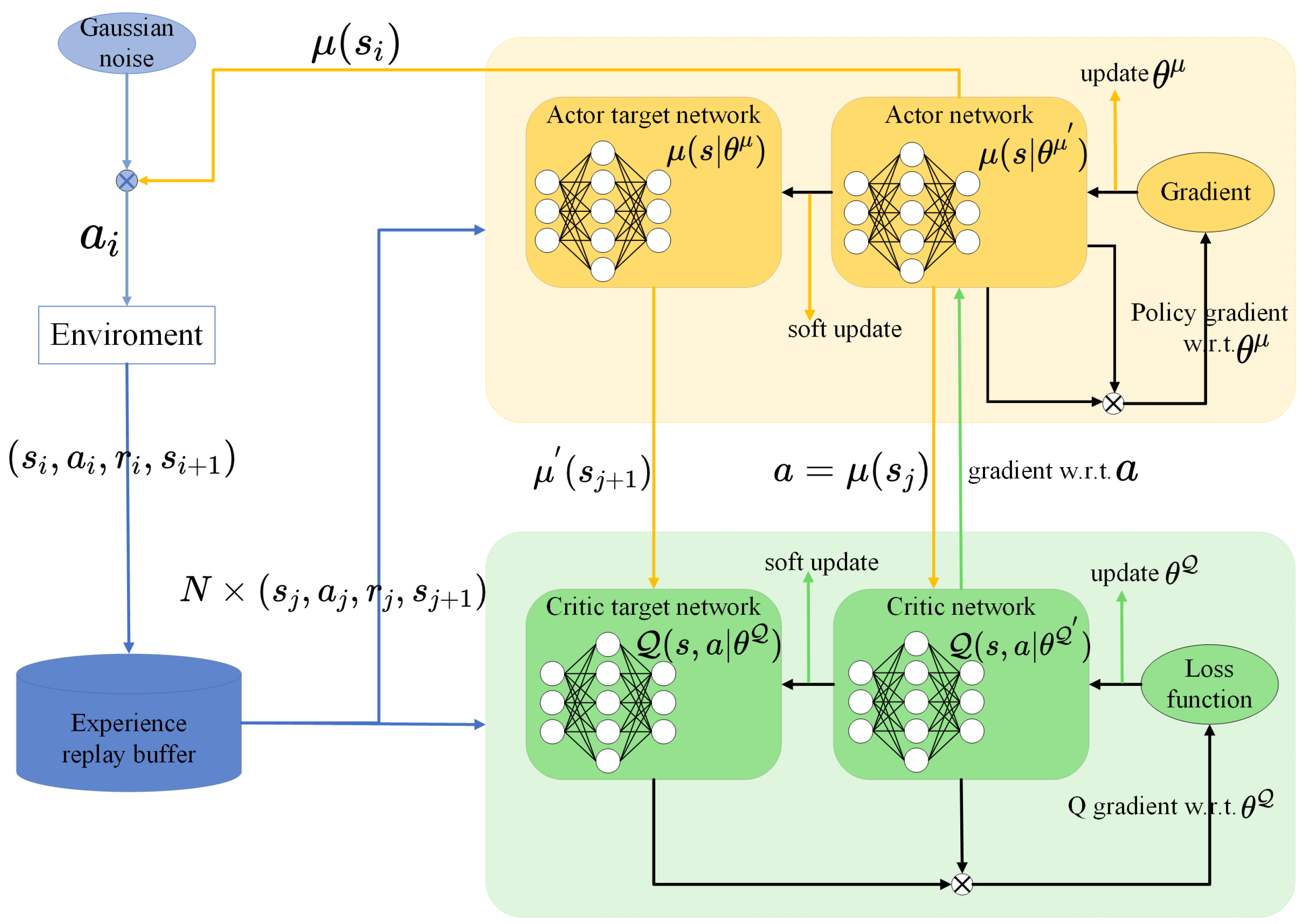
3. PER-DDPG-Based Task Offloading Optimization
3.1. Construction of MDP
3.1.1. State Space
3.1.2. Action Space
3.1.3. Reward Function
3.2. PER-DDPG-Based Solution
| Algorithm 1 PER-DDPG-based task offloading algorithm. |
|
4. Simulation Results
4.1. Parameters Setting
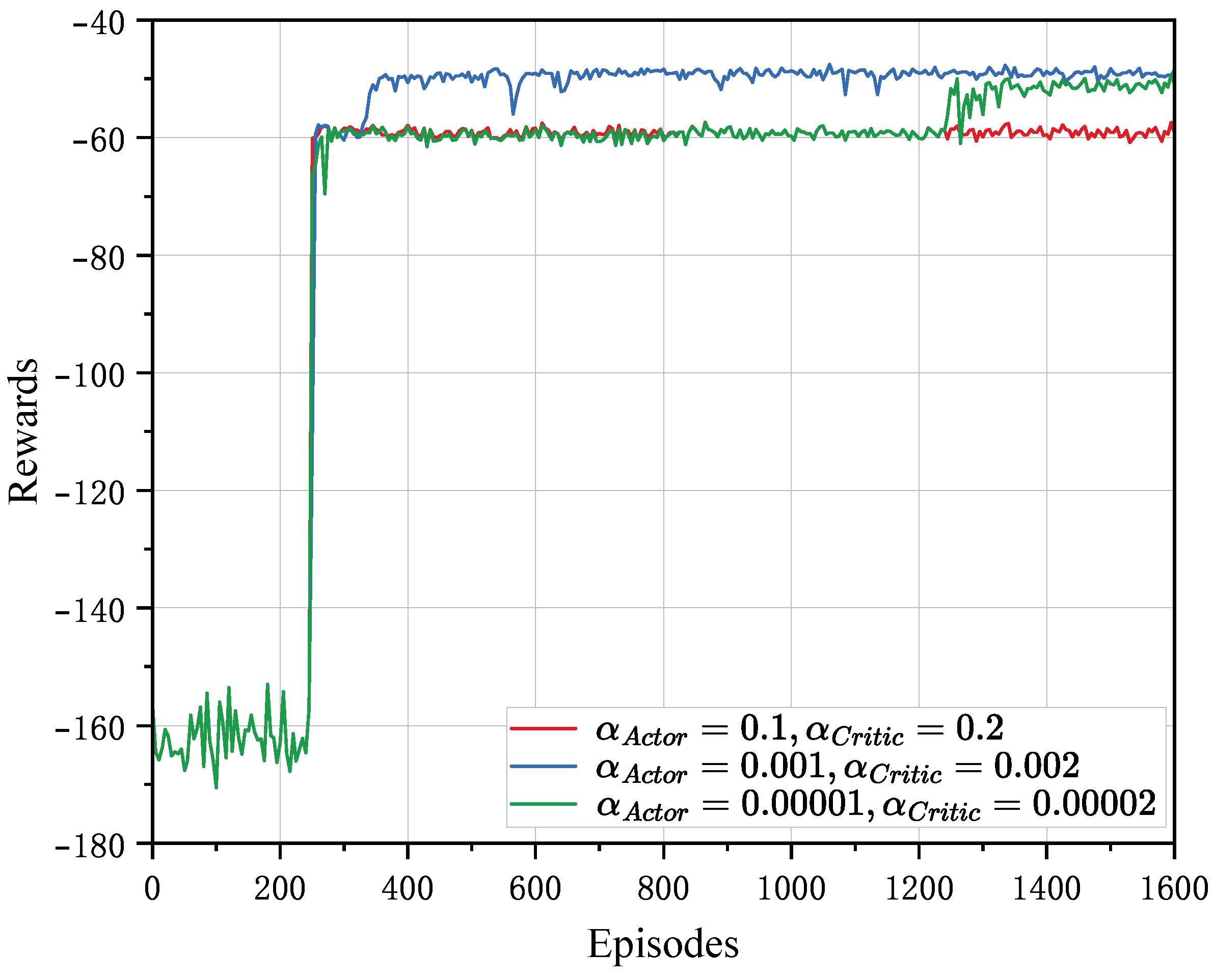
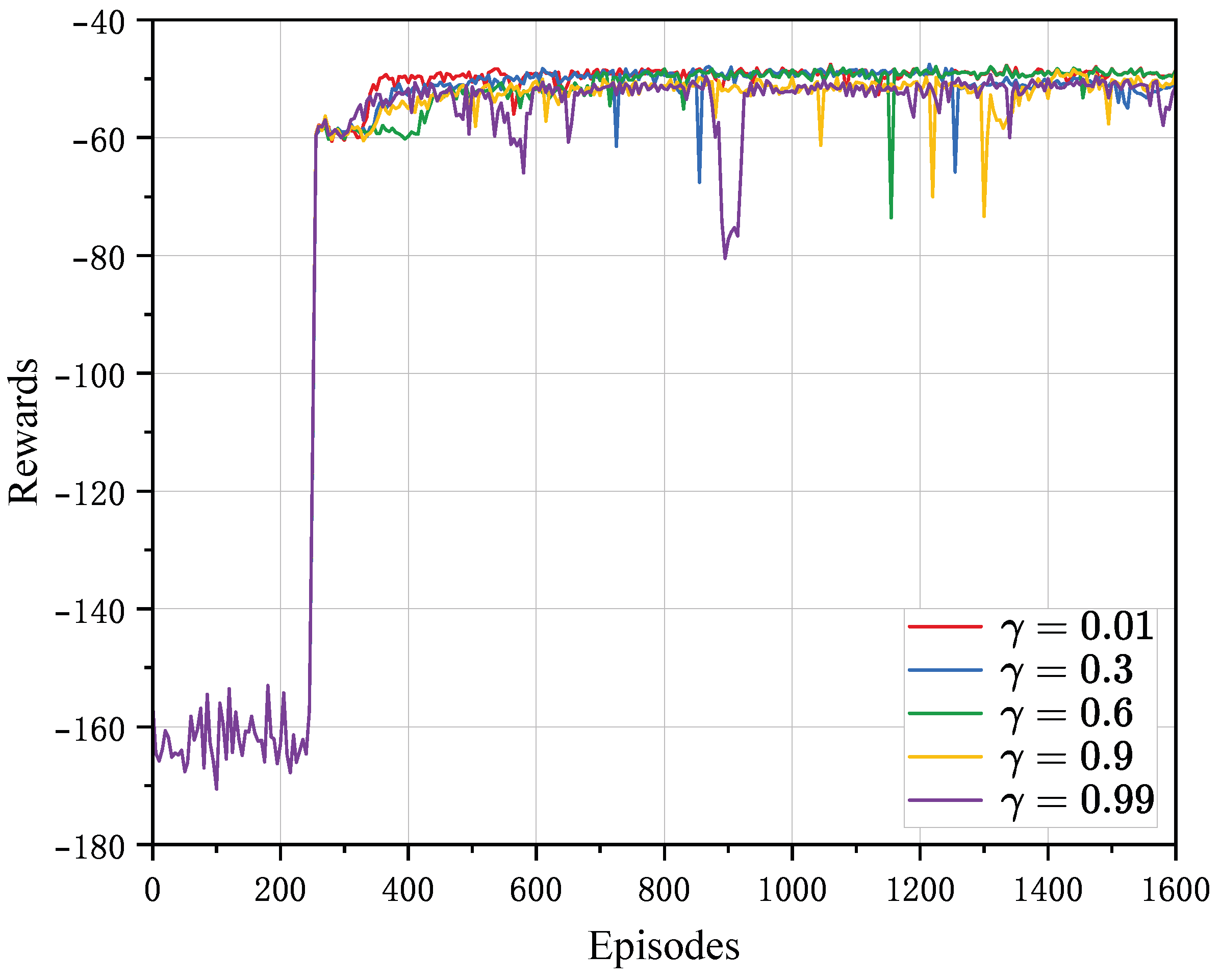
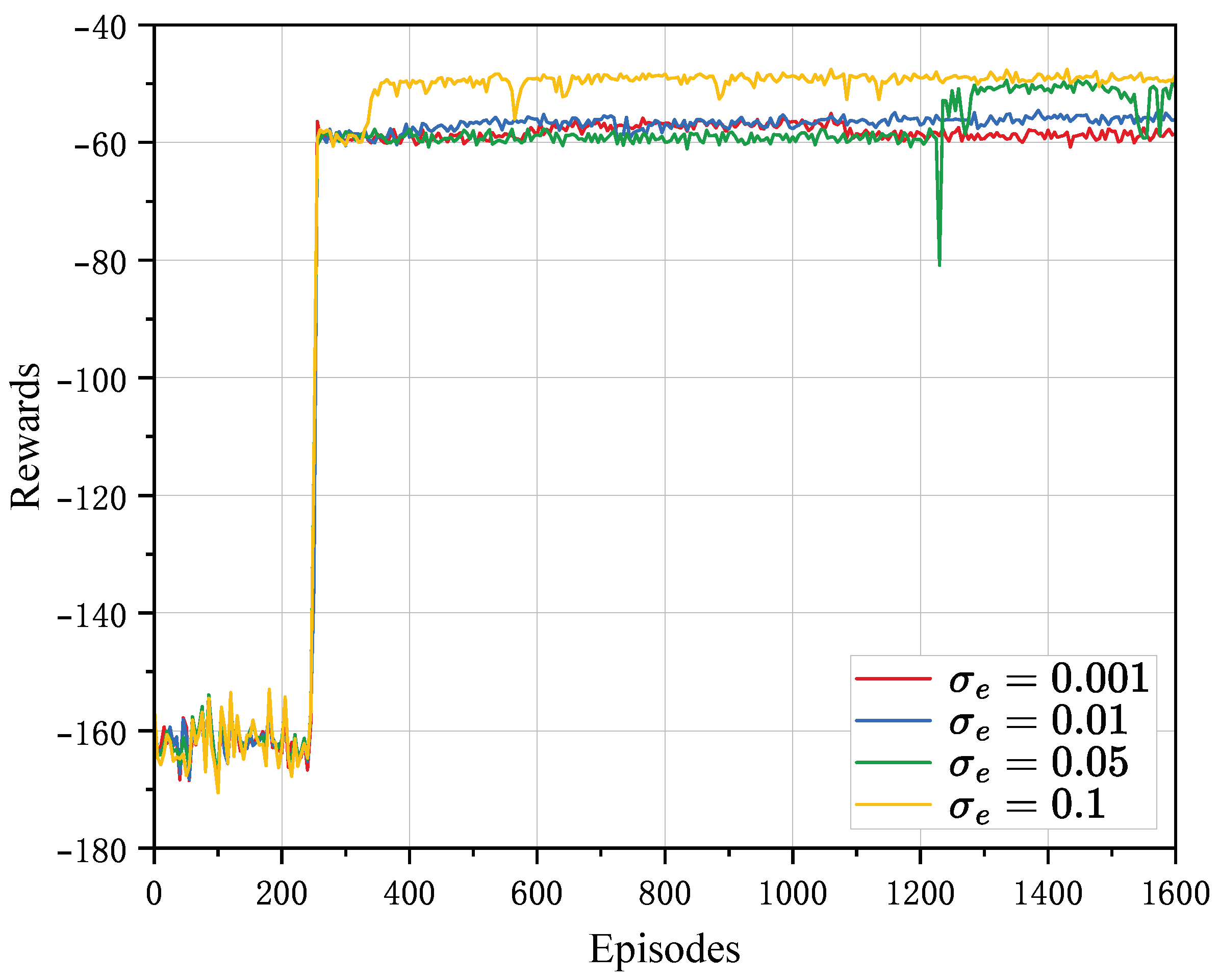
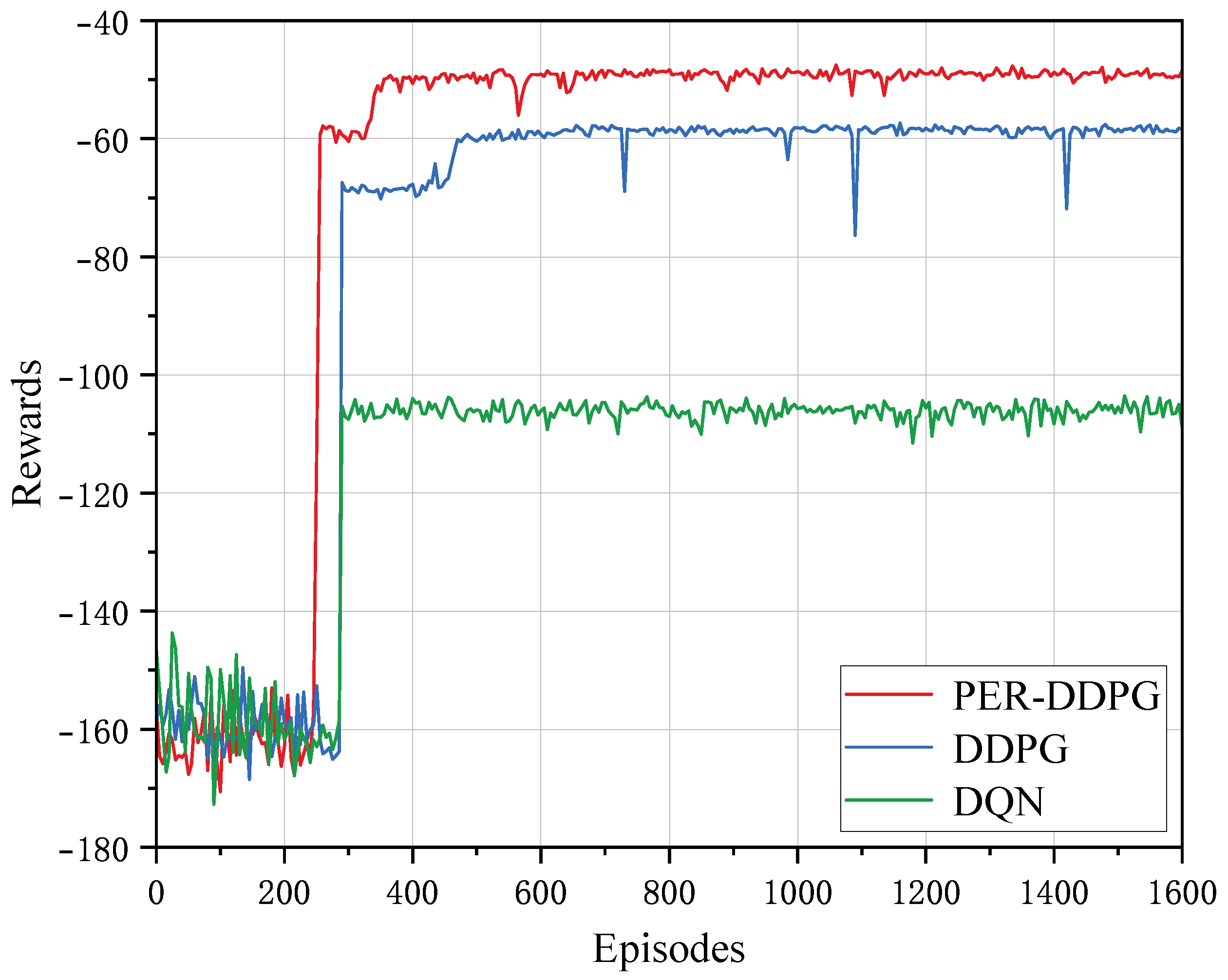
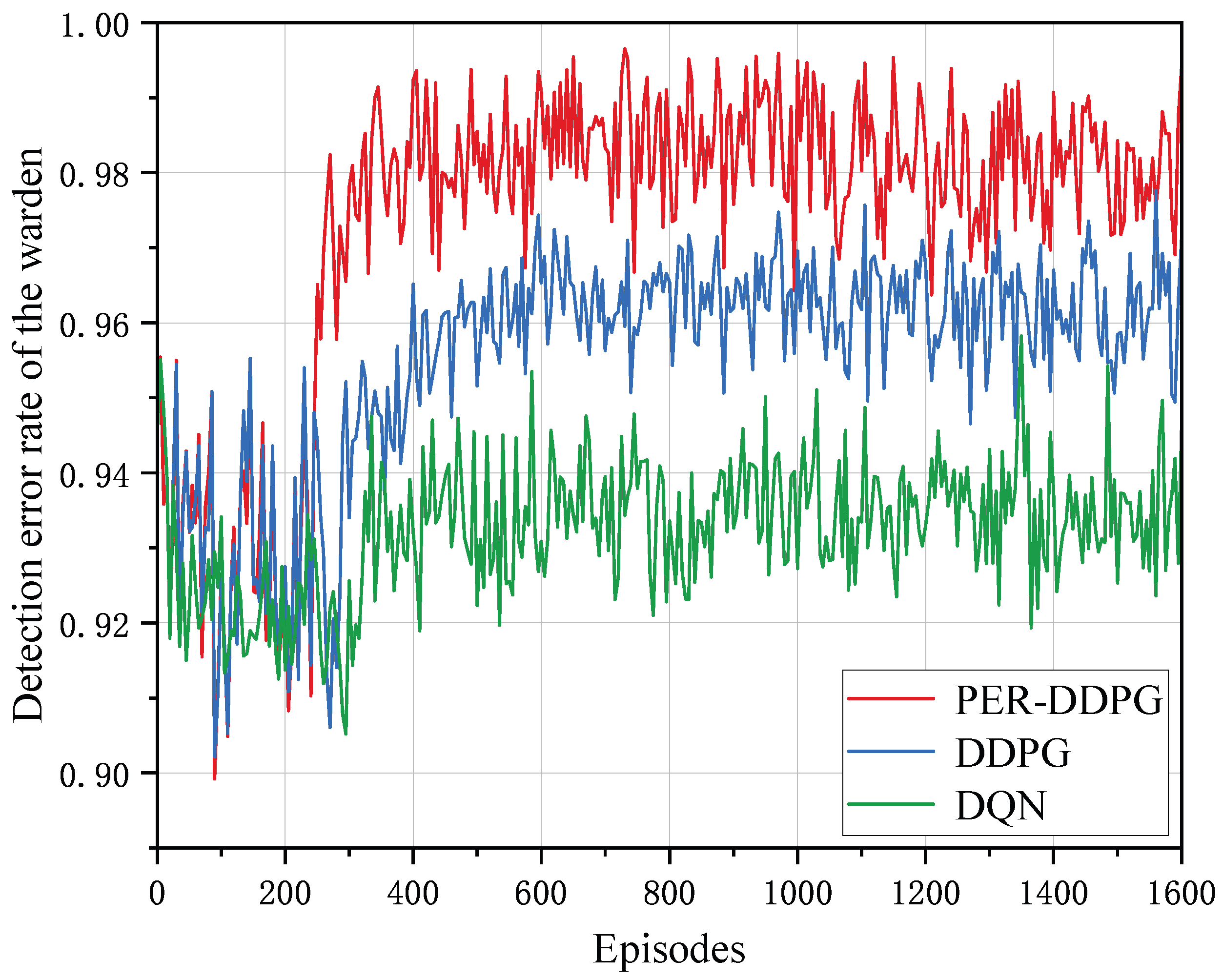
4.2. Convergence Analysis
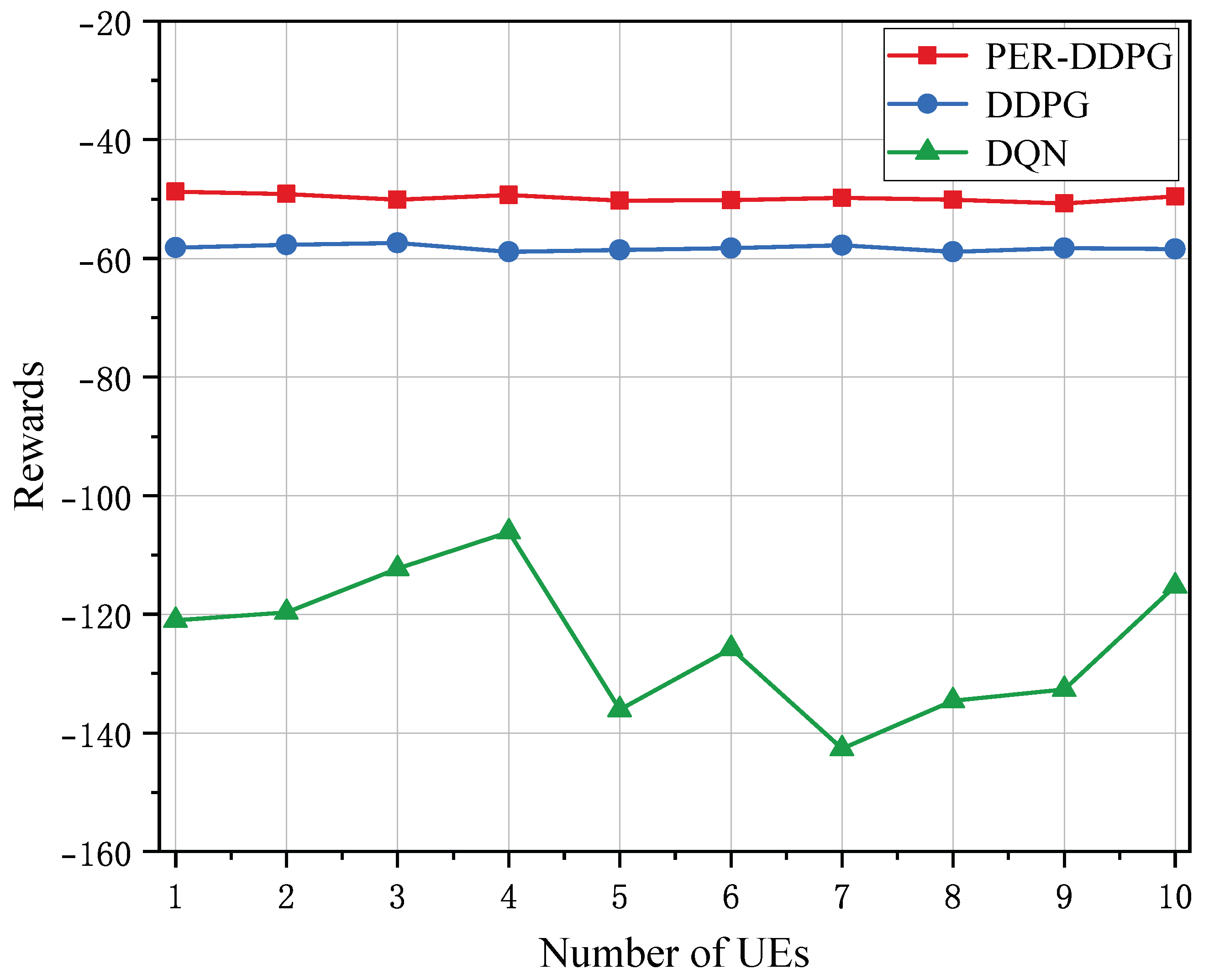
4.3. Performance Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Angel, N.A.; Ravindran, D.; Vincent, P.M.D.R.; Srinivasan, K.; Hu, Y.C. Recent Advances in Evolving Computing Paradigms: Cloud, Edge, and Fog Technologies. Sensors 2022, 22, 196. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Han, P.; Zhang, X.; Yang, B.; Liu, Y.; Guo, L. Computation Offloading in Mobile Edge Computing Networks: A Survey. J. Netw. Comput. Appl. 2022, 202, 103366. [Google Scholar] [CrossRef]
- Huda, S.A.; Moh, S. Survey on Computation Offloading in UAV-Enabled Mobile Edge Computing. J. Netw. Comput. Appl. 2022, 201, 103341. [Google Scholar] [CrossRef]
- Li, M.; Cheng, N.; Gao, J.; Wang, Y.; Zhao, L.; Shen, X. Energy-Efficient UAV-Assisted Mobile Edge Computing: Resource Allocation and Trajectory Optimization. IEEE Trans. Veh. Technol. 2020, 69, 3424–3438. [Google Scholar] [CrossRef]
- Diao, X.; Zheng, J.; Cai, Y.; Wu, Y.; Anpalagan, A. Fair Data Allocation and Trajectory Optimization for UAV-Assisted Mobile Edge Computing. IEEE Commun. Lett. 2019, 23, 2357–2361. [Google Scholar] [CrossRef]
- Lin, N.; Tang, H.; Zhao, L.; Wan, S.; Hawbani, A.; Guizani, M. A PDDQNLP Algorithm for Energy Efficient Computation Offloading in UAV-Assisted MEC. IEEE Trans. Wirel. Commun. 2023, 22, 8876–8890. [Google Scholar] [CrossRef]
- Selim, M.M.; Rihan, M.; Yang, Y.; Ma, J. Optimal Task Partitioning, Bit Allocation and Trajectory for D2D-assisted UAV-MEC Systems. Peer-Peer Netw. Appl. 2021, 14, 215–224. [Google Scholar] [CrossRef]
- Ouyang, J.; Pan, Y.; Xu, B.; Lin, M.; Zhu, W.P. Achieving Secrecy Energy Efficiency Fairness in UAV-Enabled Multi-User Communication Systems. IEEE Wirel. Commun. Lett. 2022, 11, 918–922. [Google Scholar] [CrossRef]
- Tsao, K.Y.; Girdler, T.; Vassilakis, V.G. A Survey of Cyber Security Threats and Solutions for UAV Communications and Flying Ad-Hoc Networks. Hoc Netw. 2022, 133, 102894. [Google Scholar] [CrossRef]
- Yoon, K.; Park, D.; Yim, Y.; Kim, K.; Yang, S.K.; Robinson, M. Security Authentication System Using Encrypted Channel on UAV Network. In Proceedings of the 2017 First IEEE International Conference on Robotic Computing (IRC), Taichung, Taiwan, 10–12 April 2017; pp. 393–398. [Google Scholar] [CrossRef]
- Wang, H.M.; Zhang, X.; Jiang, J.C. UAV-Involved Wireless Physical-Layer Secure Communications: Overview and Research Directions. IEEE Wirel. Commun. 2019, 26, 32–39. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Q.; Cui, M.; Zhang, R. Securing UAV Communications via Joint Trajectory and Power Control. IEEE Trans. Wirel. Commun. 2019, 18, 1376–1389. [Google Scholar] [CrossRef]
- Hua, M.; Wang, Y.; Wu, Q.; Dai, H.; Huang, Y.; Yang, L. Energy-Efficient Cooperative Secure Transmission in Multi-UAV-Enabled Wireless Networks. IEEE Trans. Veh. Technol. 2019, 68, 7761–7775. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, X.; Tang, J.; Zhao, N.; Zhang, X.Y.; Niyato, D.; Wong, K.K. Covert Communication in UAV-Assisted Air-Ground Networks. IEEE Wirel. Commun. 2021, 28, 190–197. [Google Scholar] [CrossRef]
- Chen, X.; An, J.; Xiong, Z.; Xing, C.; Zhao, N.; Yu, F.R.; Nallanathan, A. Covert Communications: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2023, 25, 1173–1198. [Google Scholar] [CrossRef]
- Yan, S.; Cong, Y.; Hanly, S.V.; Zhou, X. Gaussian Signalling for Covert Communications. IEEE Trans. Wirel. Commun. 2019, 18, 3542–3553. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, Q.; Zhang, R. Accessing From the Sky: A Tutorial on UAV Communications for 5G and Beyond. Proc. IEEE 2019, 107, 2327–2375. [Google Scholar] [CrossRef]
- Yan, S.; Hanly, S.V.; Collings, I.B. Optimal Transmit Power and Flying Location for UAV Covert Wireless Communications. IEEE J. Sel. Areas Commun. 2021, 39, 3321–3333. [Google Scholar] [CrossRef]
- Chen, Z.; Yan, S.; Zhou, X.; Shu, F.; Ng, D.W.K. Intelligent Reflecting Surface-Assisted Passive Covert Wireless Detection. IEEE Trans. Veh. Technol. 2024, 73, 2954–2959. [Google Scholar] [CrossRef]
- Mao, H.; Liu, Y.; Xiao, Z.; Han, Z.; Xia, X.G. Energy Efficient Defense Against Cooperative Hostile Detection and Eavesdropping Attacks for UAV-Aided Short-Packet Transmissions. IEEE Trans. Veh. Technol. 2024, 1–14. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, Z.; Zhao, N.; Chen, Y.; Ding, Z.; Wang, X. Resource Allocation and Trajectory Optimization for UAV-Enabled Multi-User Covert Communications. IEEE Trans. Veh. Technol. 2021, 70, 1989–1994. [Google Scholar] [CrossRef]
- Zhou, X.; Yan, S.; Hu, J.; Sun, J.; Li, J.; Shu, F. Joint Optimization of a UAV’s Trajectory and Transmit Power for Covert Communications. IEEE Trans. Signal Process. 2019, 67, 4276–4290. [Google Scholar] [CrossRef]
- Arzykulov, S.; Celik, A.; Nauryzbayev, G.; Eltawil, A.M. Artificial Noise and RIS-Aided Physical Layer Security: Optimal RIS Partitioning and Power Control. IEEE Wirel. Commun. Lett. 2023, 12, 992–996. [Google Scholar] [CrossRef]
- Zhou, X.; Yan, S.; Shu, F.; Chen, R.; Li, J. UAV-Enabled Covert Wireless Data Collection. IEEE J. Sel. Areas Commun. 2021, 39, 3348–3362. [Google Scholar] [CrossRef]
- Du, H.; Niyato, D.; Xie, Y.A.; Cheng, Y.; Kang, J.; Kim, D.I. Performance Analysis and Optimization for Jammer-Aided Multiantenna UAV Covert Communication. IEEE J. Sel. Areas Commun. 2022, 40, 2962–2979. [Google Scholar] [CrossRef]
- Wang, M.; Yao, Y.; Xia, B.; Chen, Z.; Wang, J. Covert and Reliable Short-Packet Communications Over Fading Channels Against a Proactive Warder: Analysis and Optimization. IEEE Trans. Wirel. Commun. 2024, 23, 3932–3945. [Google Scholar] [CrossRef]
- Ji, X.; Zhu, R.; Zhang, Q.; Li, C.; Cao, D. Enhancing Covert Communication in OOK Schemes by Phase Deflection. IEEE Trans. Inf. Forensics Secur. 2024, 19, 9775–9788. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Gong, Y.; Wu, Y.C. RIS-Aided Cooperative Mobile Edge Computing: Computation Efficiency Maximization via Joint Uplink and Downlink Resource Allocation. IEEE Trans. Wirel. Commun. 2024, 23, 11535–11550. [Google Scholar] [CrossRef]
- Lillicrap, T. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic Policy Gradient Algorithms. In Proceedings of the 31st International Conference on Machine Learning, Bejing, China, 22–24 June 2014; Xing, E.P., Jebara, T., Eds.; Volume 32, Proceedings of Machine Learning Research. pp. 387–395. [Google Scholar]
- Zhu, M.; Tian, K.; Wen, Y.Q.; Cao, J.N.; Huang, L. Improved PER-DDPG based nonparametric modeling of ship dynamics with uncertainty. Ocean. Eng. 2023, 286, 115513. [Google Scholar] [CrossRef]
- Tang, X.; Zhou, H.; Wang, F.; Wang, W.; Lin, X. Longevity-Conscious Energy Management Strategy of Fuel Cell Hybrid Electric Vehicle Based on Deep Reinforcement Learning. Energy 2022, 238, 121593. [Google Scholar] [CrossRef]
- Kong, X.; Lu, W.; Wu, J.; Wang, C.; Zhao, X.; Hu, W.; Shen, Y. Real-Time Pricing Method for VPP Demand Response Based on PER-DDPG Algorithm. Energy 2023, 271, 127036. [Google Scholar] [CrossRef]




| Parameter | Descriptions | Value |
|---|---|---|
| K | Number of UEs | 4 |
| T | Entire time period | 320 s |
| I | Time slots | 40 |
| UAV-BS flight height | 100 m | |
| Jammer flight height | 110 m | |
| UAV weight | 9.65 kg | |
| Maximum flight speed | 50 m/s | |
| Flight time | 1 s | |
| Carrier frequency | 2GHz | |
| Path loss factor for LoS links | 3 dB | |
| Path loss factor for NLoS links | 23 dB | |
| B | Communications bandwidth | 1 MHz |
| Variance of AWGN | −100 dBm | |
| Allowed correct detection rate | 0.05 | |
| UE transmit power | 0.1 W | |
| UAV-BS battery | 500 kJ | |
| s | Required CPU cycles per bit | 1000 cycles/bit |
| UE computing capability | 0.2 GHz | |
| UAV-BS computing capability | 1.2 GHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Zhou, D.; Shen, C.; Wang, T.; Liu, L. Task Offloading Strategy for UAV-Assisted Mobile Edge Computing with Covert Transmission. Electronics 2025, 14, 446. https://doi.org/10.3390/electronics14030446
Hu Z, Zhou D, Shen C, Wang T, Liu L. Task Offloading Strategy for UAV-Assisted Mobile Edge Computing with Covert Transmission. Electronics. 2025; 14(3):446. https://doi.org/10.3390/electronics14030446
Chicago/Turabian StyleHu, Zhijuan, Dongsheng Zhou, Chao Shen, Tingting Wang, and Liqiang Liu. 2025. "Task Offloading Strategy for UAV-Assisted Mobile Edge Computing with Covert Transmission" Electronics 14, no. 3: 446. https://doi.org/10.3390/electronics14030446
APA StyleHu, Z., Zhou, D., Shen, C., Wang, T., & Liu, L. (2025). Task Offloading Strategy for UAV-Assisted Mobile Edge Computing with Covert Transmission. Electronics, 14(3), 446. https://doi.org/10.3390/electronics14030446






