A Personalized Federated Learning Algorithm Based on Dynamic Weight Allocation
Abstract
:1. Introduction
- We propose a model aggregation algorithm based on dynamic weight assignment, which assigns aggregation weights based on the cosine similarity of model updates between clients, ensuring collaboration between similar clients and attenuating interference between dissimilar clients. On this basis, additional personalized models are trained for each client, which attenuates the influence of data heterogeneity among clients.
- We propose a personalized federated learning algorithm. In the local update phase, additional personalization models are trained for each client to further attenuate the impact of data heterogeneity.
- A performance evaluation on five image datasets, CIFAR-10, CIFAR-100, Tiny-Imag-eNet, MNIST, and Fashion-MNIST, shows that the proposed algorithm has higher accuracy compared with seven comparison baseline algorithms.
2. Related Work
2.1. Federated Learning for Data Heterogeneous Scenarios
2.2. Clustered Federated Learning
3. Problem Formulation
3.1. Federated Learning Objective
3.2. FedDWA Objective
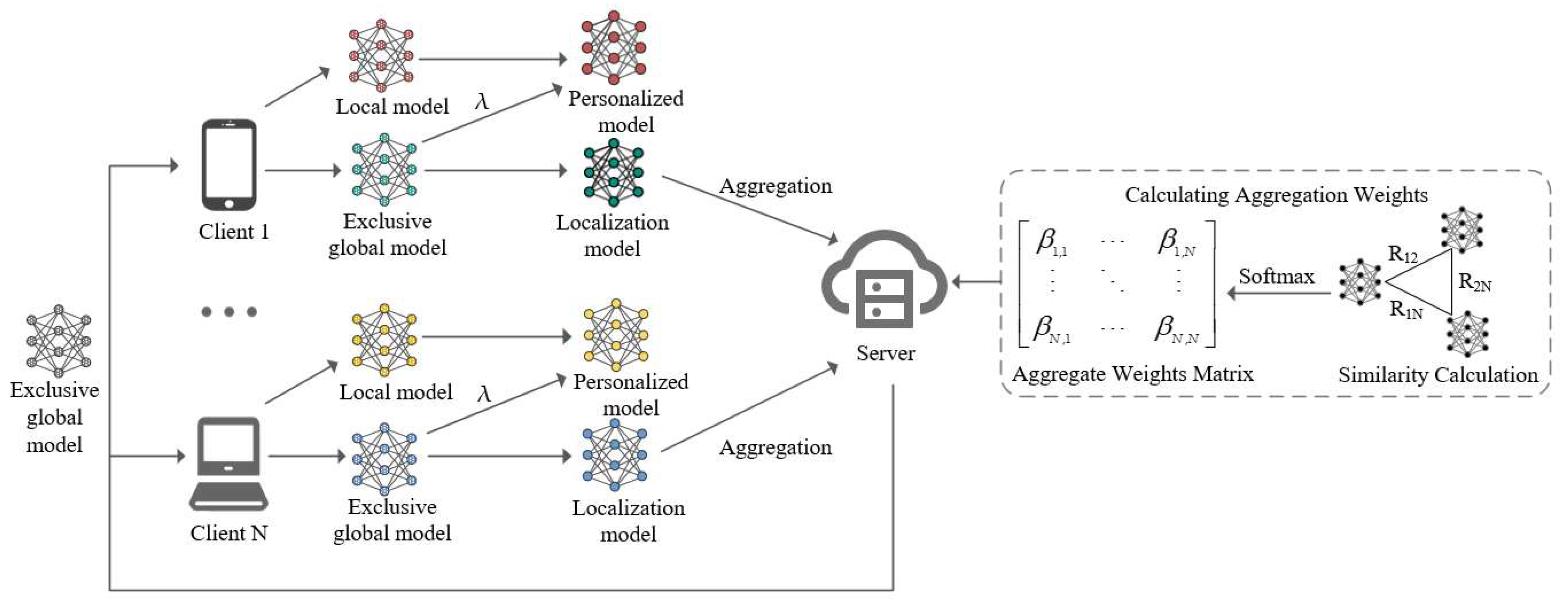
4. Overview and Implementation
4.1. Overview
4.2. Implementation and Algorithm Description
| Algorithm 1. FedDWA Client Algorithm. |
| Input: Exclusive global model Output: //exclusive global model after training |
| 1: Client receives its corresponding exclusive global model |
| 2: for each local epoch do |
| do |
| 6: end for |
| 7: end for |
| 8: return |
| Algorithm 2. FedDWA Server Algorithm. |
| Input: client set , where , total communication rounds T, learning rate , local epochs , Client participation rate . Output: personalized models Initialize: exclusive global model , personalized models |
| clients |
| do |
| 3: for each client i in parallel do |
| to client . |
| ) |
| do |
| . |
| //Normalize to get the aggregation weight. |
| 9: end for |
| 11: end for |
| 12: end for |
4.3. Computational Complexity Analysis
- 1.
- Model Training:
- 2.
- Exclusive global model aggregation:
- 1.
- Clients:
- 2.
- Server:
5. Experiments and Analysis
5.1. Datasets
5.2. Model Settings
5.3. Baselines
5.4. Parameter Settings
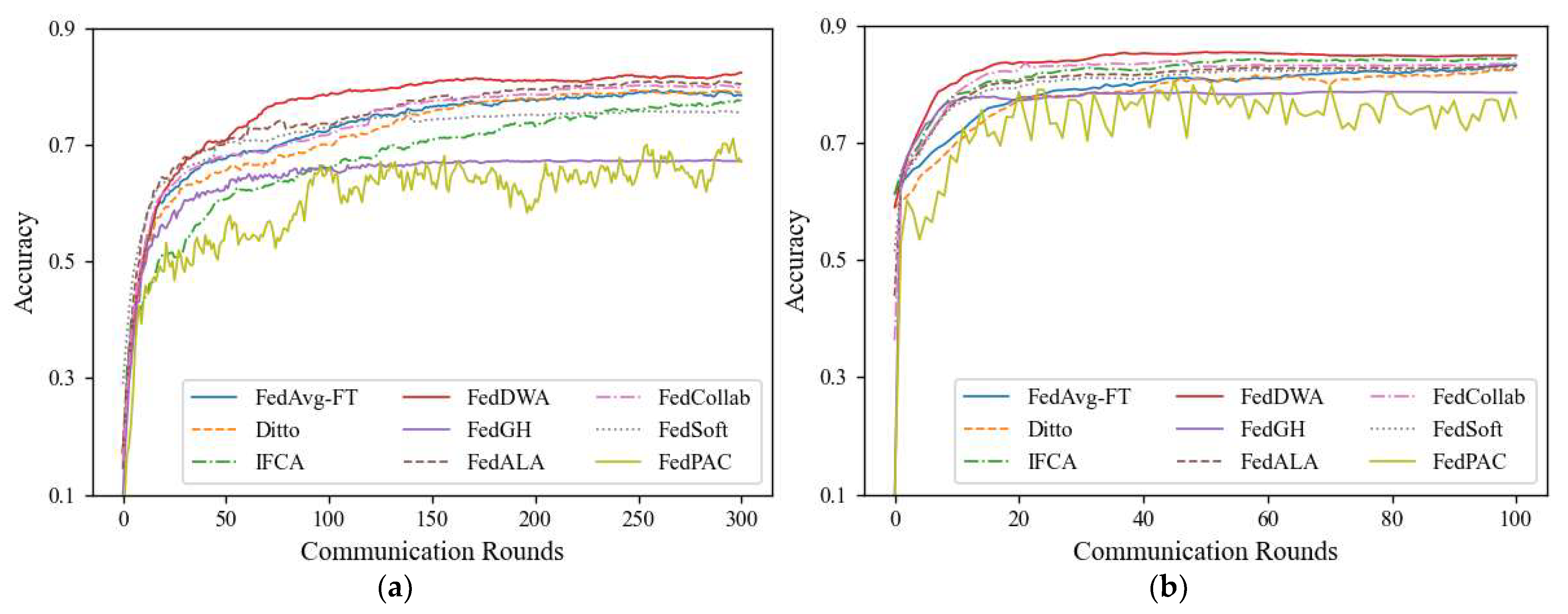
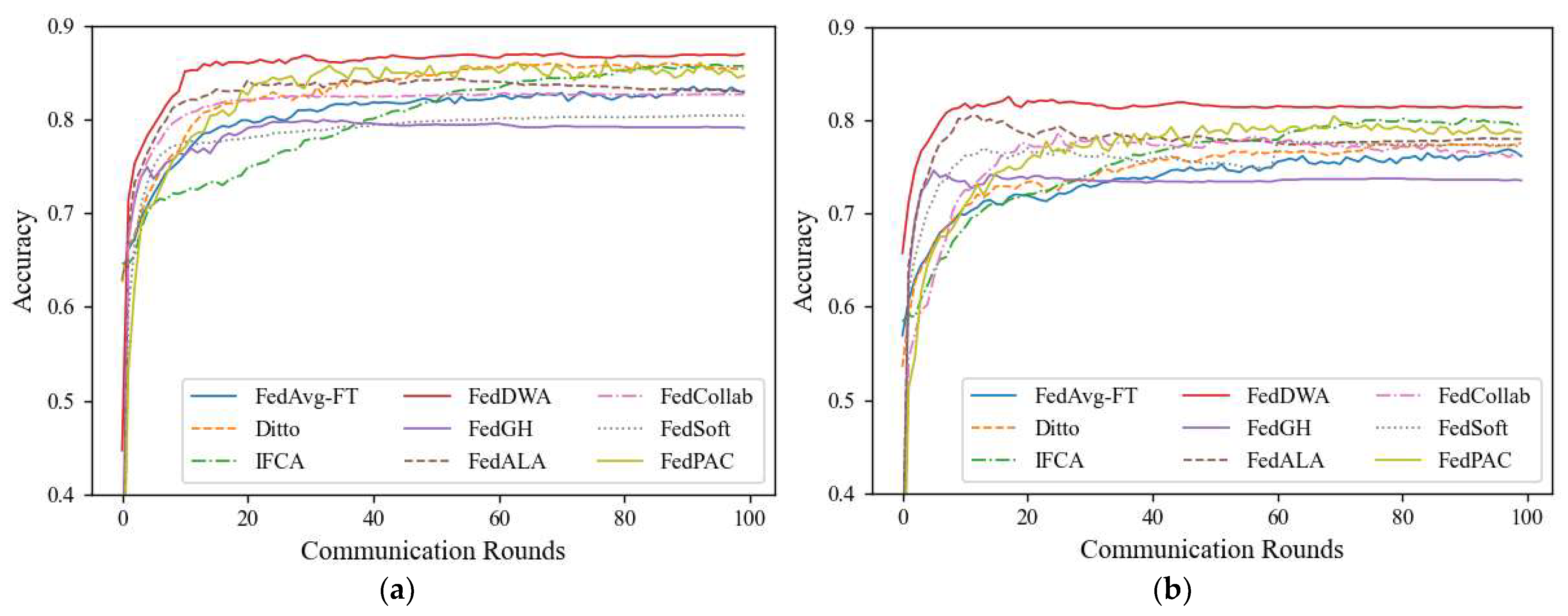
5.5. Results and Discussion
5.6. Hyperparametric Analysis
5.7. Impact of Participating Rates
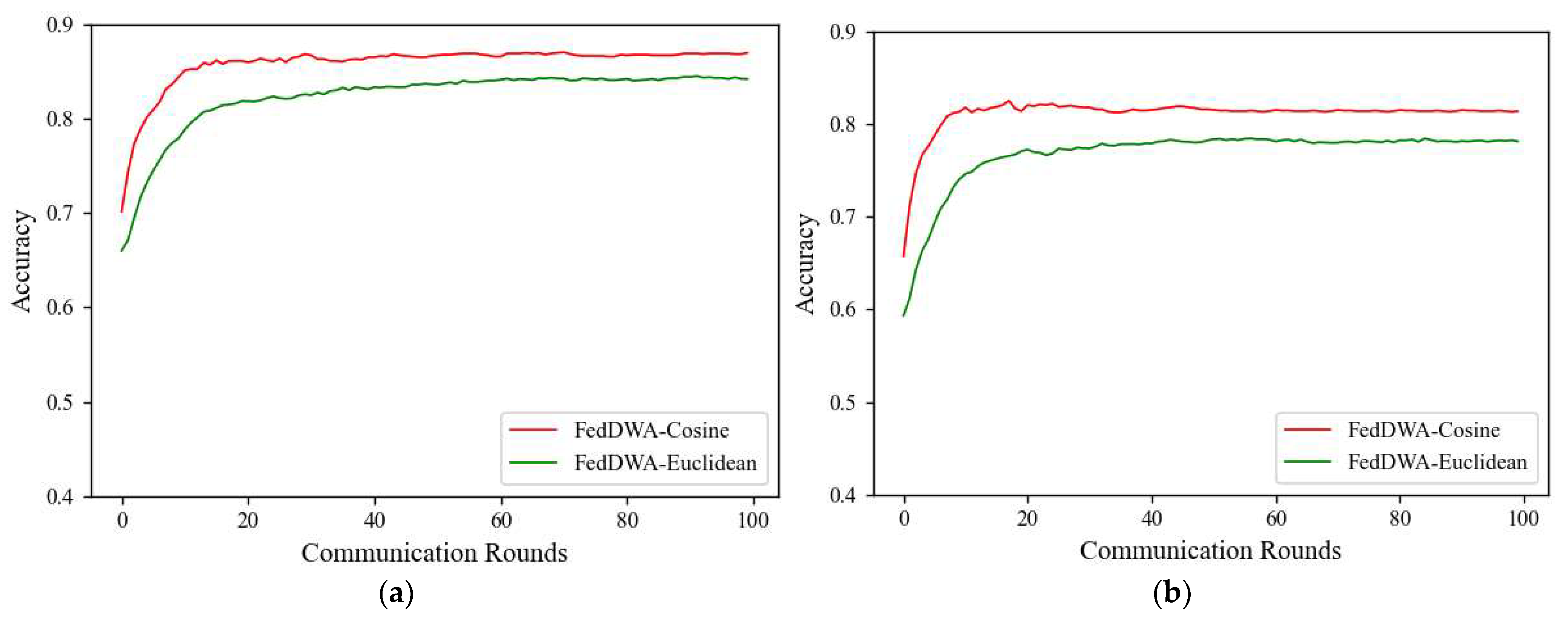
5.8. Discussion on Model Similarity Measures
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
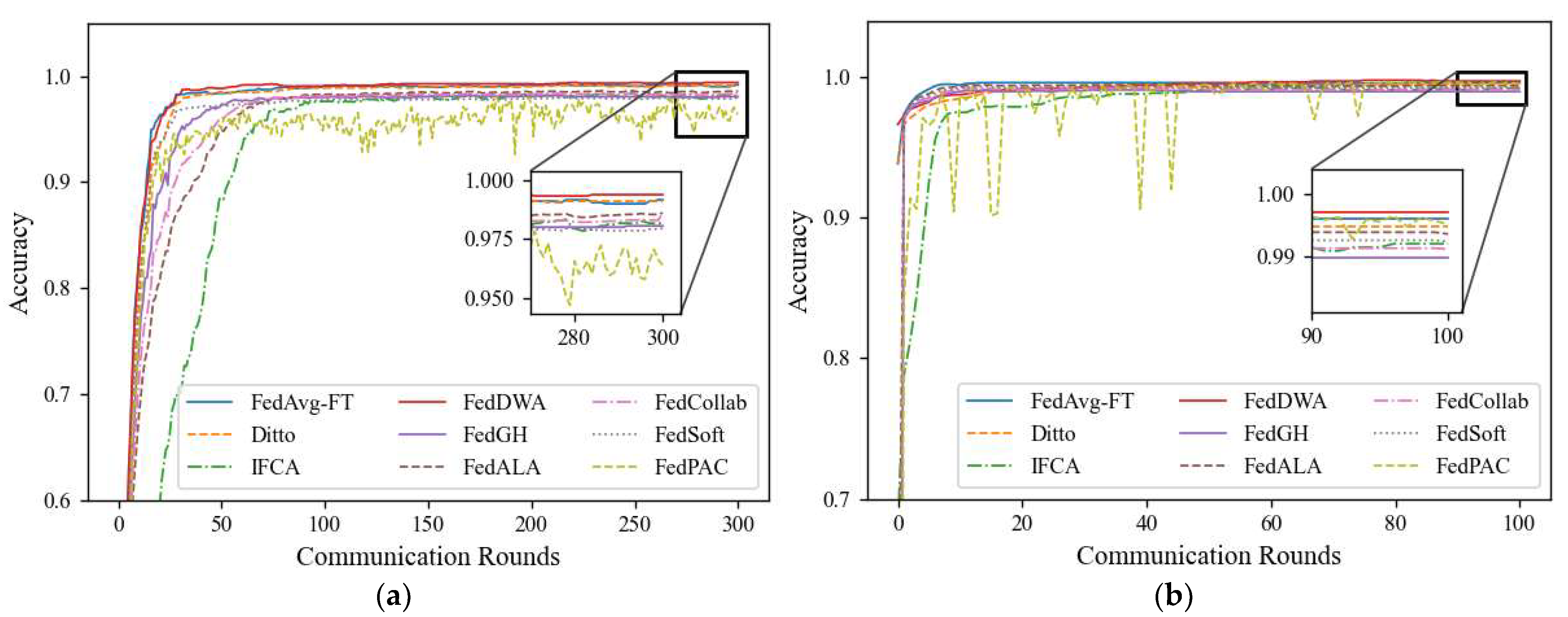
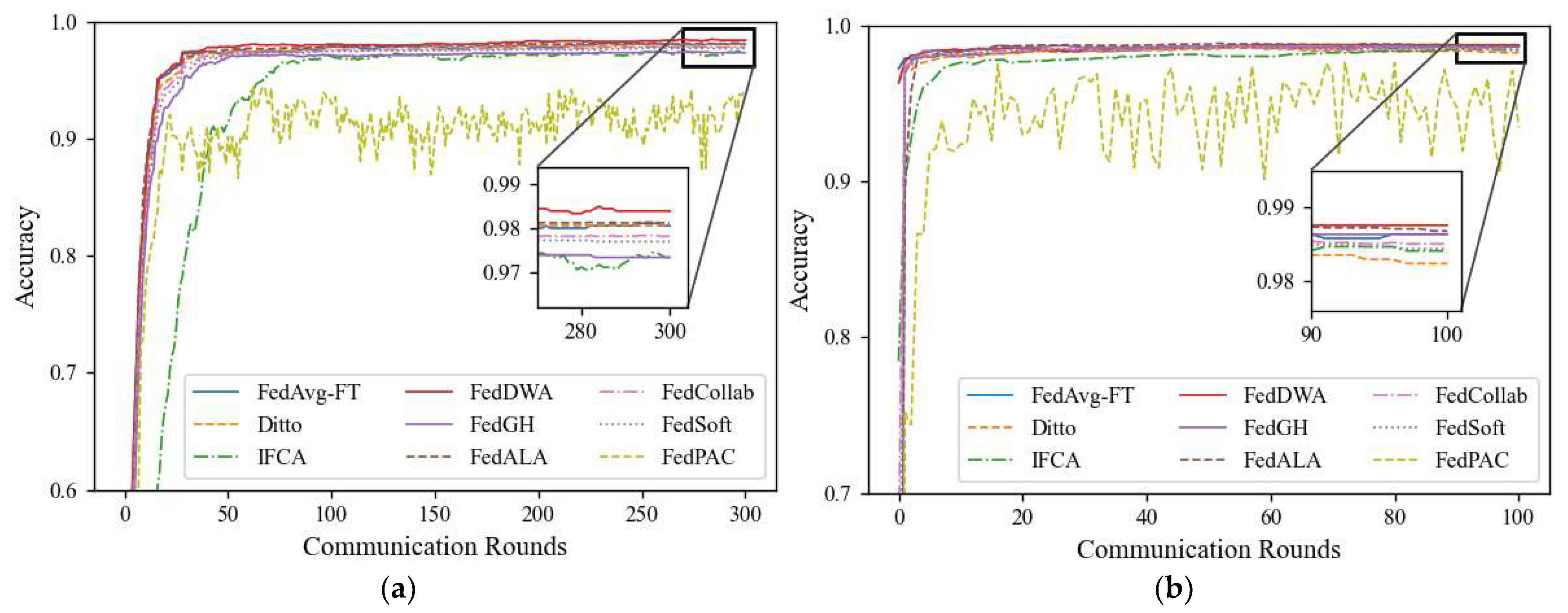
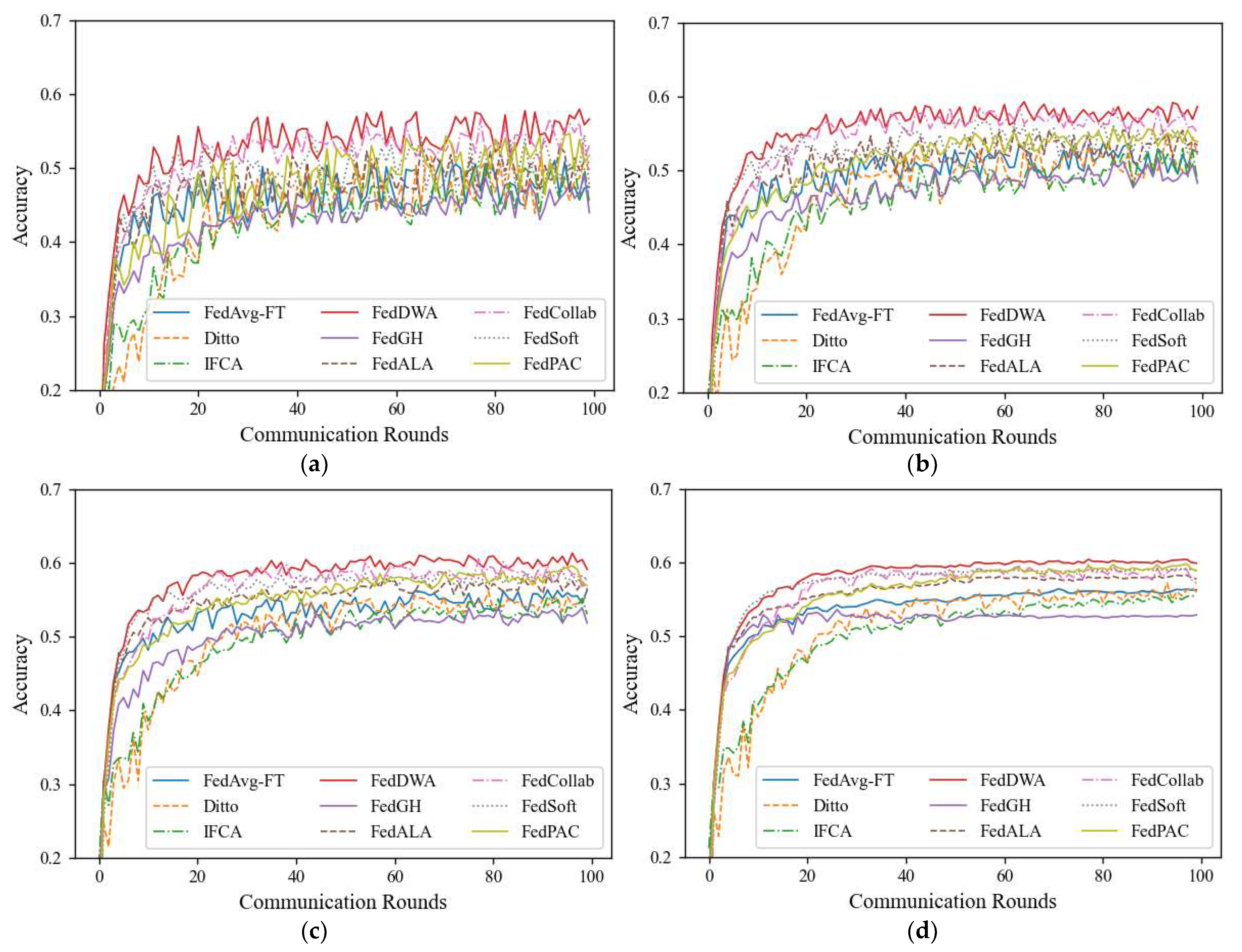
Appendix A. Experimental Settings Under Pathological Heterogeneous Data Distribution
Appendix B. Simulation Experimental Results Under Pathological Heterogeneous Data Distribution
| Algorithm | CIFAR-10 | MNIST | FMNIST | |||
|---|---|---|---|---|---|---|
| 20% | 100% | 20% | 100% | 20% | 100% | |
| FedAvg | 37.47 | 39.53 | 92.9 | 88.95 | 75.44 | 75.28 |
| FedAvg-FT | 78.63 | 83.13 | 99.17 | 99.52 | 98.06 | 98.64 |
| Ditto | 78.9 | 82.93 | 99.11 | 99.49 | 98.06 | 98.24 |
| IFCA | 77.6 | 84.4 | 98.17 | 99.2 | 97.33 | 98.41 |
| FedGH | 67.13 | 78.53 | 98.06 | 98.97 | 97.33 | 98.64 |
| FedPAC | 67.13 | 74.2 | 96.4 | 99.51 | 93.94 | 93.47 |
| FedCollab | 79.82 | 83.47 | 98.45 | 99.12 | 97.81 | 98.5 |
| FedSoft | 75.52 | 82.61 | 97.94 | 99.24 | 97.69 | 98.44 |
| FedALA | 80.4 | 83.01 | 98.61 | 99.41 | 98.12 | 98.68 |
| FedDWA (Ours) | 82.33 | 85.2 | 99.39 | 99.6 | 98.39 | 98.75 |
References
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 22 April 2017; pp. 1273–1282. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Poor, H.V. Federated learning for internet of things: A comprehensive survey. IEEE Commun. Surv. Tutor. 2021, 23, 1622–1658. [Google Scholar] [CrossRef]
- Lu, Z.; Pan, H.; Dai, Y.; Si, X.; Zhang, Y. Federated learning with non-iid data: A survey. IEEE Internet Things J. 2024, 11, 19188–19209. [Google Scholar] [CrossRef]
- Lee, R.; Kim, M.; Li, D.; Qiu, X.; Hospedales, T.; Huszár, F.; Lane, N. Fedl2p: Federated learning to personalize. In Proceedings of the 37th Conference on Neural Information Processing Systems (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023; p. 36. [Google Scholar]
- Sabah, F.; Chen, Y.; Yang, Z.; Azam, M.; Ahmad, N.; Sarwar, R. Model optimization techniques in personalized federated learning: A survey. Expert Syst. Appl. 2024, 243, 122874. [Google Scholar] [CrossRef]
- Ruan, Y.; Joe-Wong, C. Fedsoft: Soft clustered federated learning with proximal local updating. In Proceedings of the 36th AAAI Conference on Artificial Intelligence, 22 February–1 March 2022; pp. 8124–8131. [Google Scholar]
- Li, C.; Li, G.; Varshney, P.K. Federated learning with soft clustering. IEEE Internet Things J. 2021, 9, 7773–7782. [Google Scholar] [CrossRef]
- Ghosh, A.; Chung, J.; Yin, D.; Ramchandran, K. An efficient framework for clustered federated learning. In Proceedings of the 34th Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; Volume 33, pp. 19586–19597. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. In Proceedings of the 3rd Machine Learning and Systems Conference, Austin, TX, USA, 2–4 March 2020; Volume 2, pp. 429–450. [Google Scholar]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. Scaffold: Stochastic controlled averaging for federated learning. In Proceedings of the 37th International Conference on Machine Learning, Online, 13–18 July 2020; pp. 5132–5143. [Google Scholar]
- Hsu, T.-M.H.; Qi, H.; Brown, M. Measuring the effects of non-identical data distribution for federated visual classification. arXiv 2019, arXiv:1909.06335. [Google Scholar]
- Chen, H.-Y.; Chao, W.-L. On bridging generic and personalized federated learning for image classification. arXiv 2021, arXiv:2107.00778. [Google Scholar]
- Collins, L.; Hassani, H.; Mokhtari, A.; Shakkottai, S. Fedavg with fine tuning: Local updates lead to representation learning. In Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS 2022), New Orleans, LA, USA, 28 November–9 December 2022; Volume 35, pp. 10572–10586. [Google Scholar]
- Li, T.; Hu, S.; Beirami, A.; Smith, V. Ditto: Fair and robust federated learning through personalization. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 6357–6368. [Google Scholar]
- Panchal, K.; Choudhary, S.; Parikh, N.; Zhang, L.; Guan, H. Flow: Per-instance personalized federated learning. In Proceedings of the 37th Neural Information Processing Systems (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023; p. 36. [Google Scholar]
- Sattler, F.; Müller, K.-R.; Samek, W. Clustered federated learning: Model-agnostic distributed multitask optimization under privacy constraints. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3710–3722. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.; Hong, J.; Yin, D.; Ramchandran, K. Robust federated learning in a heterogeneous environment. arXiv 2019, arXiv:1906.06629. [Google Scholar]
- Briggs, C.; Fan, Z.; Andras, P. Federated learning with hierarchical clustering of local updates to improve training on non-IID data. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–9. [Google Scholar]
- Liu, B.; Guo, Y.; Chen, X. Pfa: Privacy-preserving federated adaptation for effective model personalization. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 923–934. [Google Scholar]
- Yang, L.; Huang, J.; Lin, W.; Cao, J. Personalized federated learning on non-IID data via group-based meta-learning. ACM Trans. Knowl. Discov. Data 2023, 17, 1–20. [Google Scholar] [CrossRef]
- Huang, Y.; Chu, L.; Zhou, Z.; Wang, L.; Liu, J.; Pei, J.; Zhang, Y. Personalized cross-silo federated learning on non-iid data. In Proceedings of the 35th AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; pp. 7865–7873. [Google Scholar]
- Wang, Z.; Fan, X.; Qi, J.; Jin, H.; Yang, P.; Shen, S.; Wang, C. Fedgs: Federated graph-based sampling with arbitrary client availability. In Proceedings of the 37th AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 10271–10278. [Google Scholar]
- Xu, X.; Duan, S.; Zhang, J.; Luo, Y.; Zhang, D. Optimizing federated learning on device heterogeneity with a sampling strategy. In Proceedings of the 2021 IEEE/ACM 29th International Symposium on Quality of Service (IWQOS), Tokyo, Japan, 25–28 June 2021; pp. 1–10. [Google Scholar]
- Zhu, D.; Lu, S.; Wang, M.; Lin, J.; Wang, Z. Efficient precision-adjustable architecture for softmax function in deep learning. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3382–3386. [Google Scholar] [CrossRef]
- Yi, L.; Wang, G.; Liu, X.; Shi, Z.; Yu, H. FedGH: Heterogeneous federated learning with generalized global header. In Proceedings of the Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 8686–8696. [Google Scholar]
- Xu, J.; Tong, X.; Huang, S.-L. Personalized federated learning with feature alignment and classifier collaboration. arXiv 2023, arXiv:2306.11867. [Google Scholar]
- Bao, W.; Wang, H.; Wu, J.; He, J. Optimizing the collaboration structure in cross-silo federated learning. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 1718–1736. [Google Scholar]
- Zhang, J.; Hua, Y.; Wang, H.; Song, T.; Xue, Z.; Ma, R.; Guan, H. Fedala: Adaptive local aggregation for personalized federated learning. In Proceedings of the 37th AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 11237–11244. [Google Scholar]






| Algorithm | CIFAR-10 | CIFAR-100 | Tiny-ImageNet | |||
|---|---|---|---|---|---|---|
| dir = 0.3 | dir = 0.5 | dir = 0.3 | dir = 0.5 | dir = 0.3 | dir = 0.5 | |
| FedAvg | 53.44 | 58.32 | 22.46 | 26.13 | 16.37 | 18.06 |
| FedAvg-FT | 82.87 | 76.14 | 42.95 | 29.09 | 39.79 | 31.28 |
| Ditto | 85.41 | 77.53 | 39.66 | 28.36 | 39.71 | 33.12 |
| IFCA | 85.84 | 79.7 | 42.9 | 30.05 | 36.76 | 33.28 |
| FedGH | 79.07 | 73.56 | 41.31 | 36.69 | 39.71 | 31.87 |
| FedPAC | 84.67 | 78.65 | 42.28 | 34.77 | 39.54 | 33.86 |
| FedCollab | 82.66 | 76.34 | 43.84 | 36.64 | 36.21 | 31.17 |
| FedSoft | 80.4 | 77.24 | 40.58 | 33.21 | 36.36 | 33.37 |
| FedALA | 83.05 | 77.97 | 42.18 | 36.3 | 34.79 | 33.32 |
| FedDWA (Ours) | 86.97 | 81.74 | 45.63 | 38.13 | 41.83 | 35.23 |
| Algorithm | Non-IID (dir = 0.3) | Non-IID (dir = 0.5) |
|---|---|---|
| Caac (36%) | Caac (30%) | |
| Round | Round | |
| FedAvg-FT | 82 | 149 |
| Ditto | 106 | 62 |
| IFCA | 125 | 72 |
| FedGH | 131 | 192 |
| FedPAC | 110 | 91 |
| FedCollab | 153 | 198 |
| FedSoft | 183 | 85 |
| FedALA | - | 84 |
| FedDWA (Ours) | 51 | 48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, S.; Li, W.; Qian, H.; Xia, H. A Personalized Federated Learning Algorithm Based on Dynamic Weight Allocation. Electronics 2025, 14, 484. https://doi.org/10.3390/electronics14030484
Liu Y, Li S, Li W, Qian H, Xia H. A Personalized Federated Learning Algorithm Based on Dynamic Weight Allocation. Electronics. 2025; 14(3):484. https://doi.org/10.3390/electronics14030484
Chicago/Turabian StyleLiu, Yazhi, Siwei Li, Wei Li, Hui Qian, and Haonan Xia. 2025. "A Personalized Federated Learning Algorithm Based on Dynamic Weight Allocation" Electronics 14, no. 3: 484. https://doi.org/10.3390/electronics14030484
APA StyleLiu, Y., Li, S., Li, W., Qian, H., & Xia, H. (2025). A Personalized Federated Learning Algorithm Based on Dynamic Weight Allocation. Electronics, 14(3), 484. https://doi.org/10.3390/electronics14030484







