Optimization Model-Based Robust Method and Performance Evaluation of GNSS/INS Integrated Navigation for Urban Scenes
Abstract
1. Introduction
2. Models and Methods
2.1. Robust Extended Kalman Filter Loosely Coupled GNSS PPP/INS Models
2.1.1. State Model
2.1.2. Observation Model
2.1.3. Robust EKF Based on the Observation Residuals
2.2. Loosely Integrated GNSS PPP/INS Model Based on Factor Graph Optimization
2.2.1. GNSS PPP Factor
2.2.2. INS Factor
2.2.3. Factor Graph Optimization Model
3. Experimental Analysis
3.1. High-Precision Sensor On-Vehicle Experiment
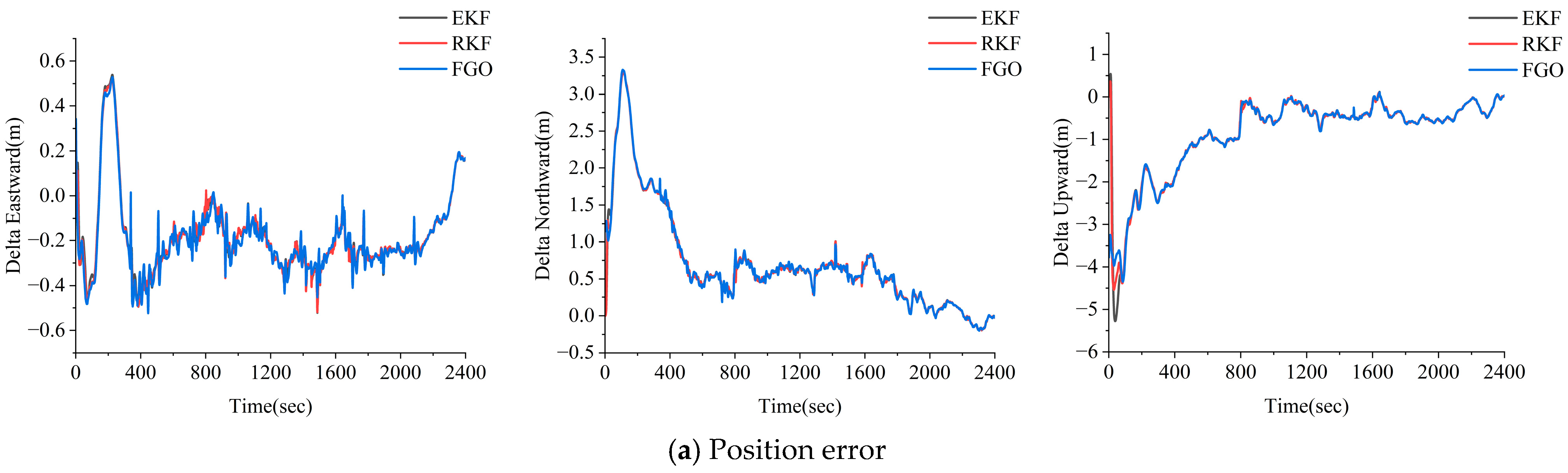
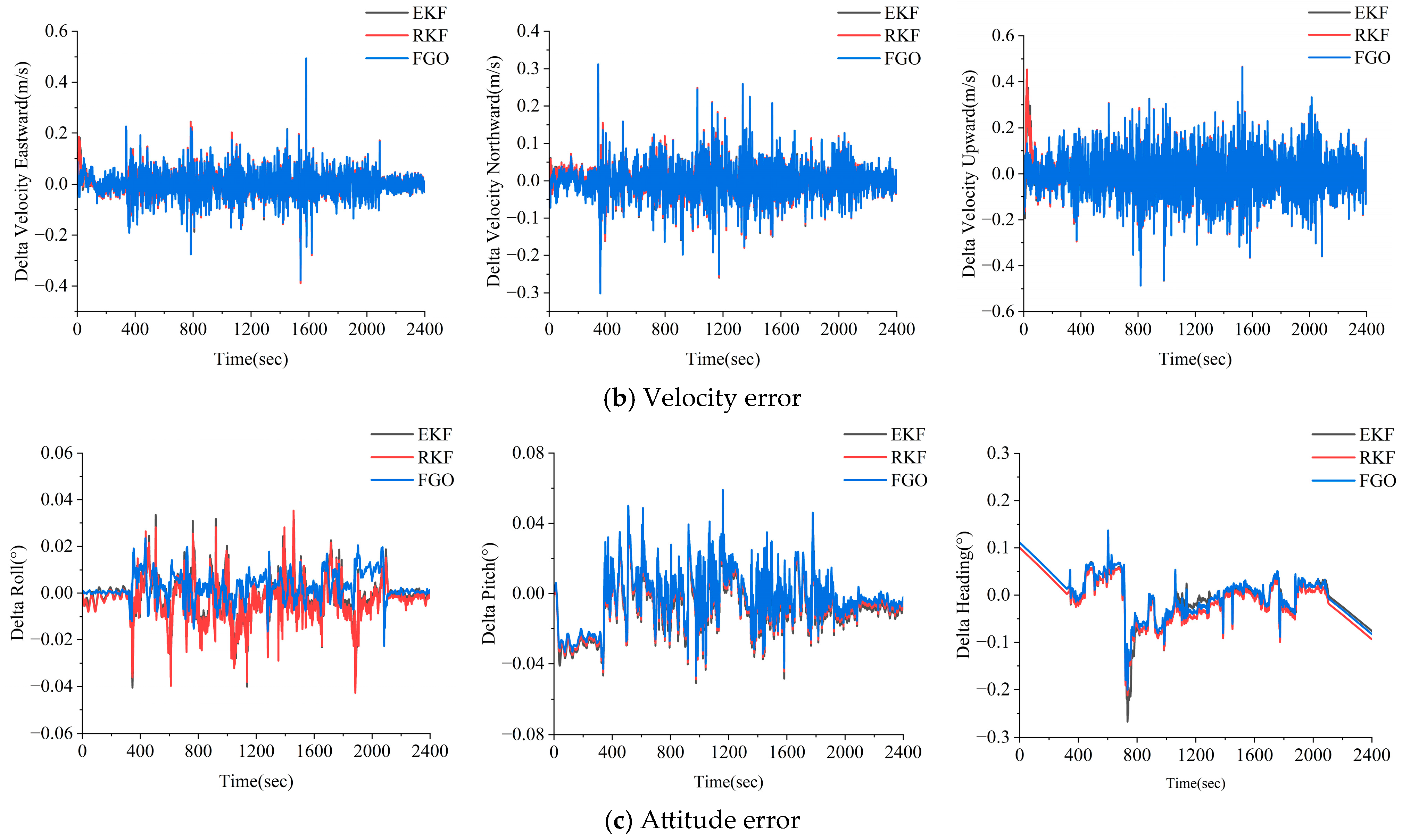
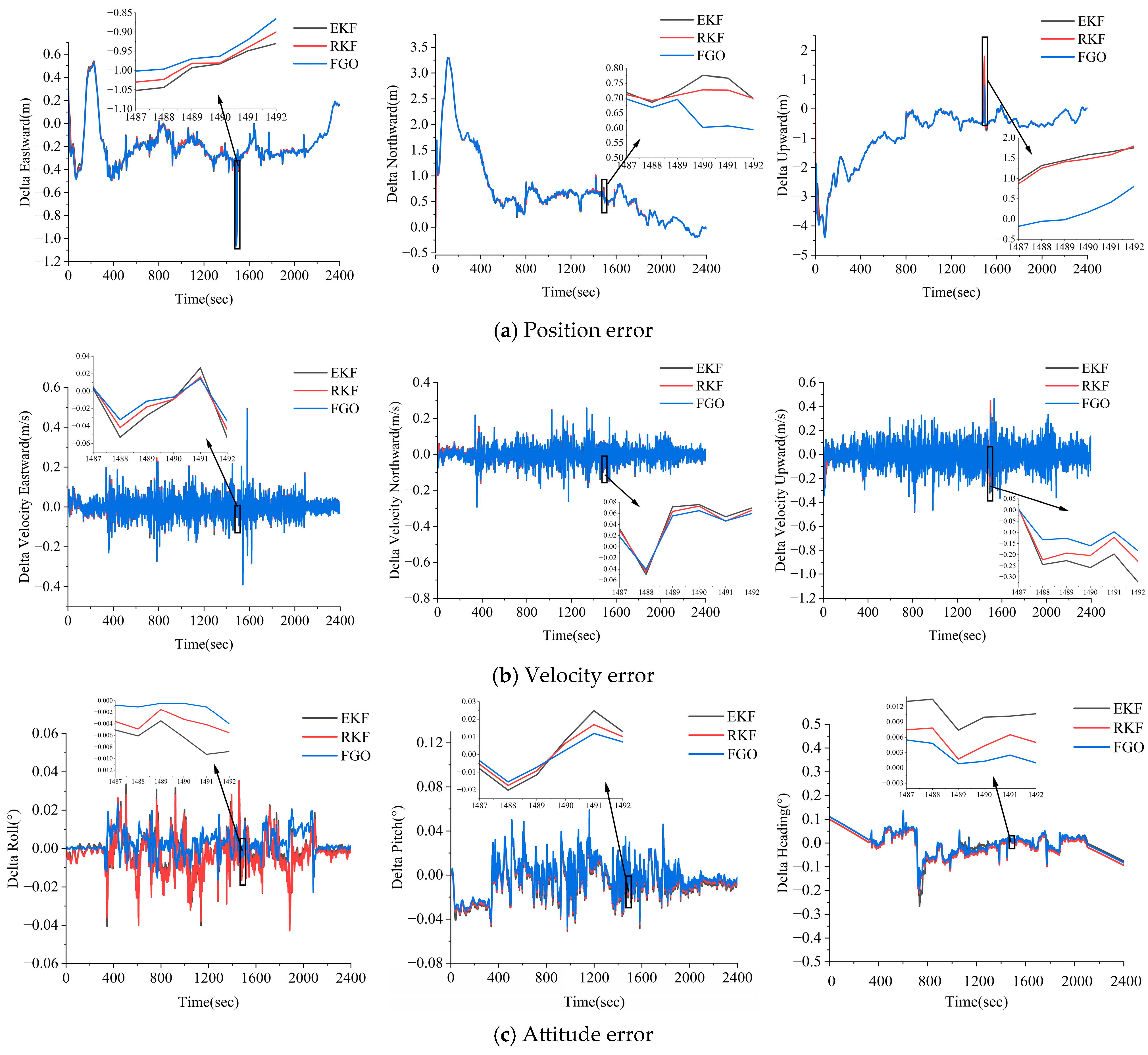
3.1.1. GNSS PPP/INS Combined Performance Analysis
3.1.2. Simulated Gross GNSS PPP/INS Combined Navigation Performance Analysis
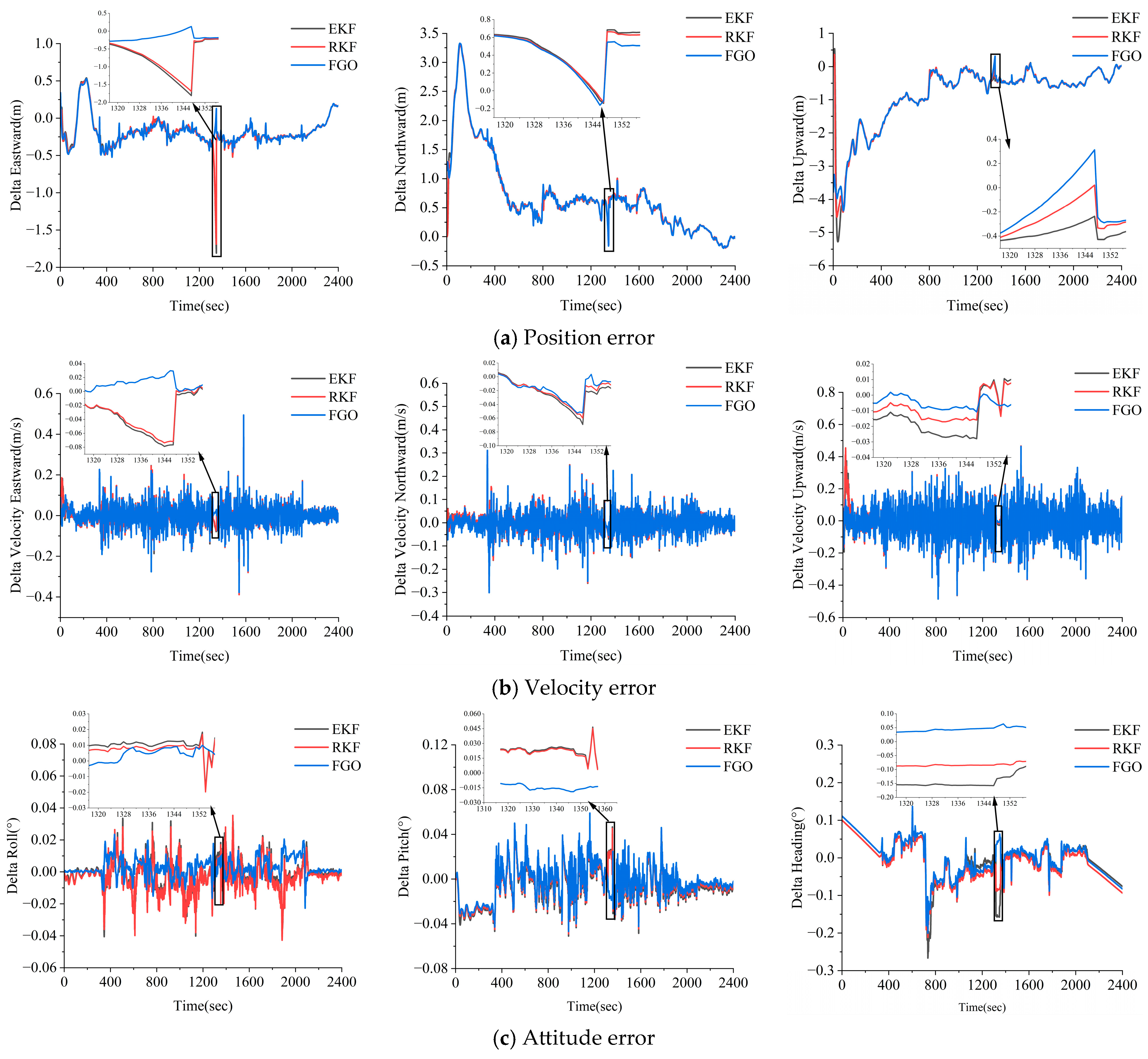
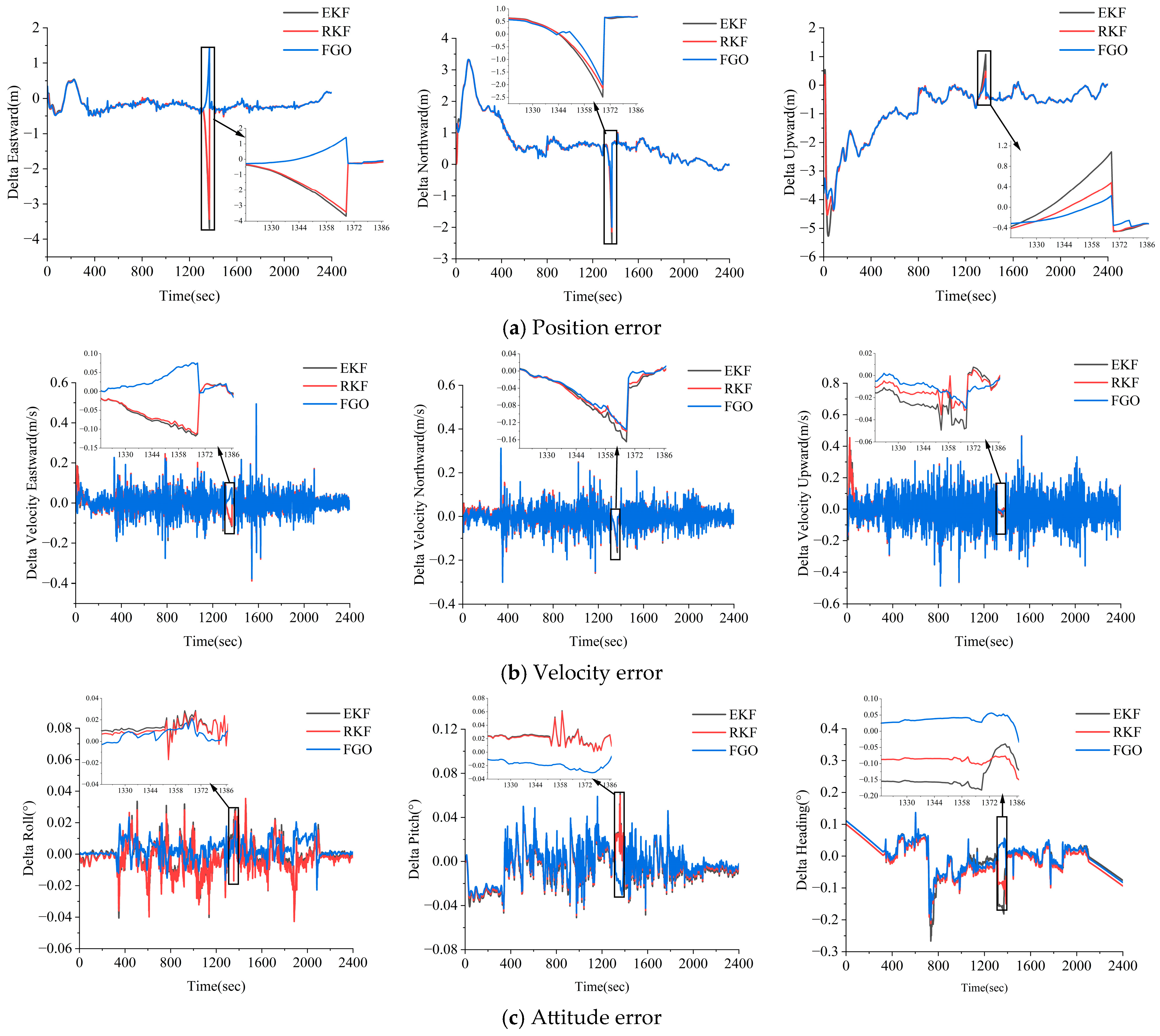
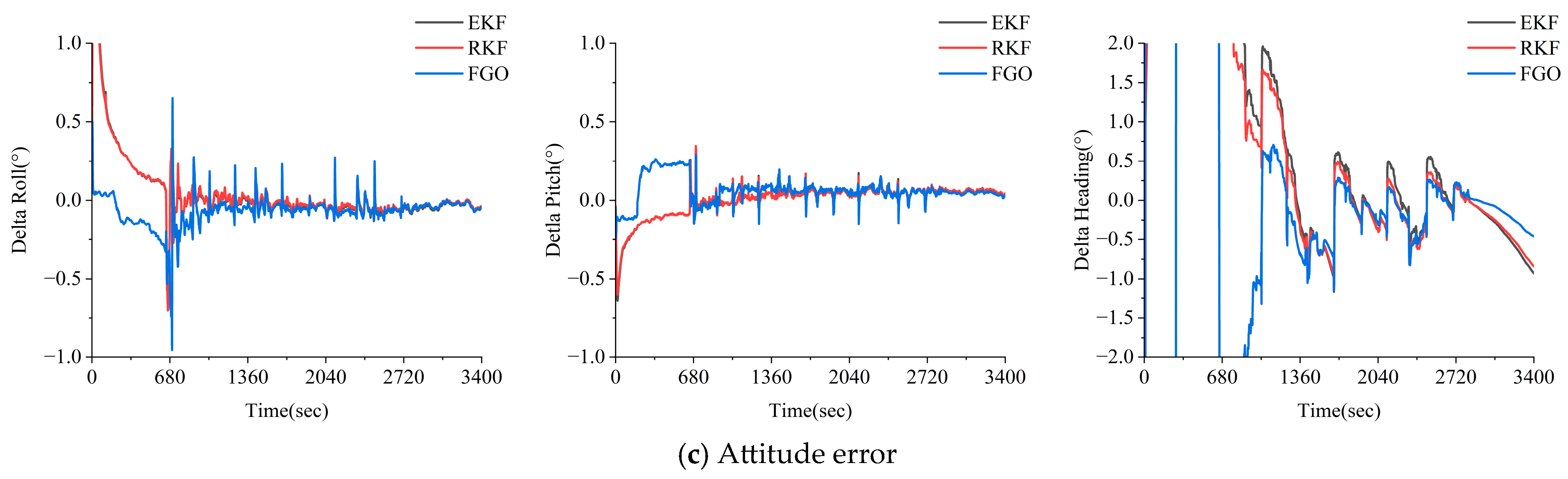
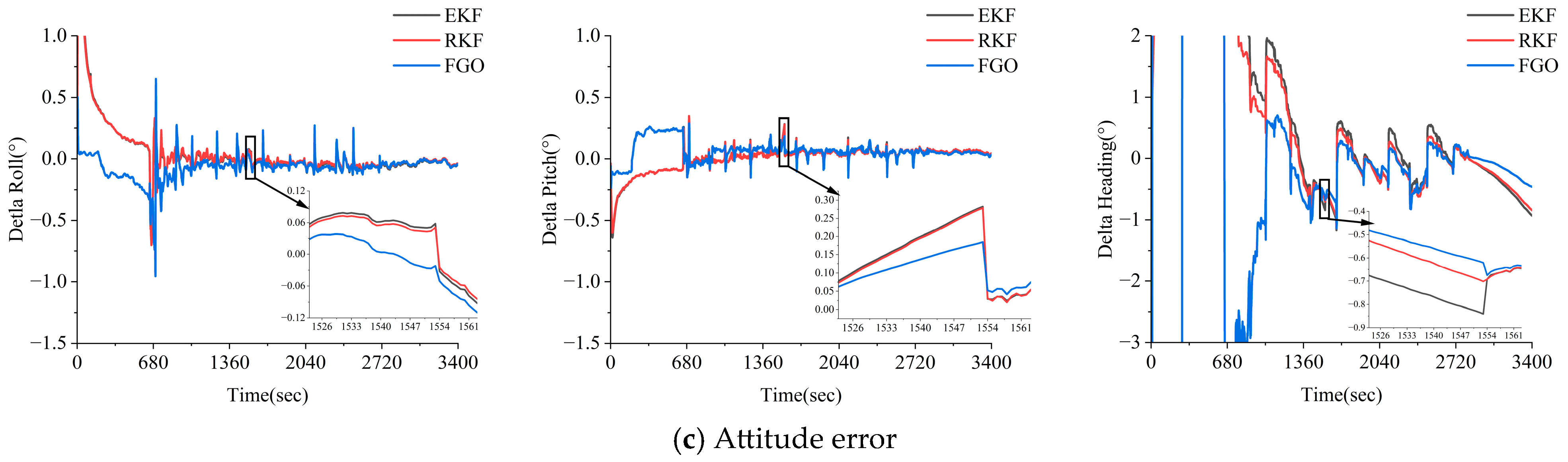
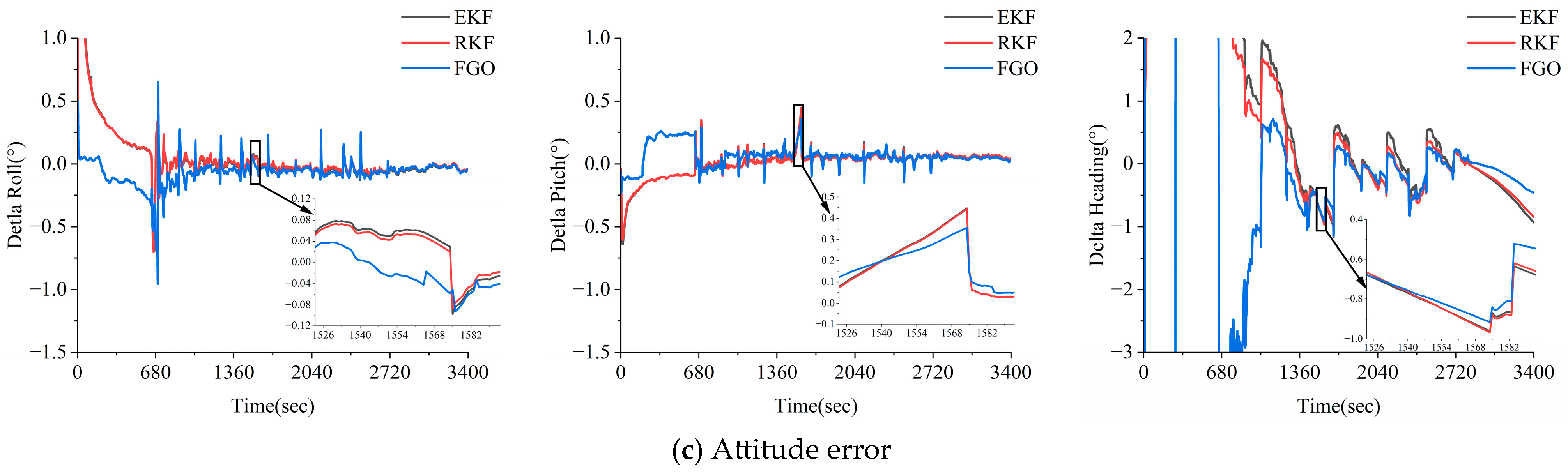
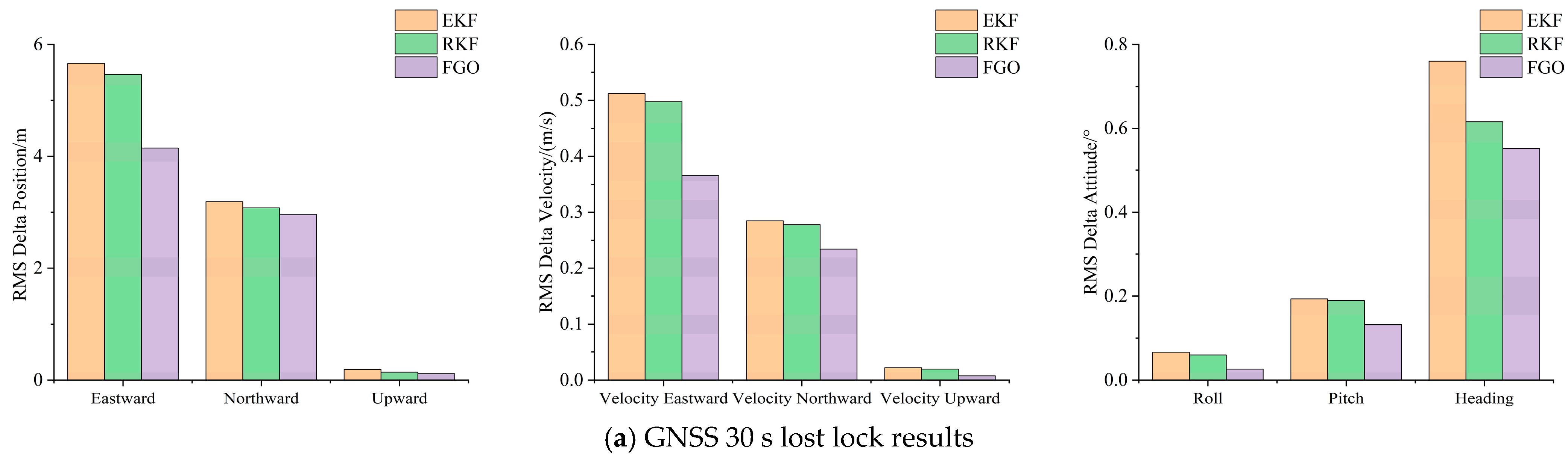
3.1.3. Performance Analysis of the GNSS PPP/INS Combination for Three Methods of GNSS Loss of Lock Scenarios
3.2. In-Vehicle Experiments with Consumer Grade Sensors
3.2.1. GNSS PPP/INS Combination Performance Analysis
3.2.2. Simulated Gross GNSS PPP/INS Combined Navigation Performance Analysis
3.2.3. Analysis of GNSS PPP/INS Combined Performance Under GNSS Loss-of-Lock Conditions
4. Conclusions
- (1)
- Compared to the EKF and RKF methods, the FGO strategy has a good anti-discrepancy effect and stability. The FGO method utilizes IMU factors and GNSS factors to construct a sliding window solution, which can better utilize the constraints between the calendar elements within the window and the redundant observation information to suppress the effect of the coarseness.
- (2)
- In the simulated gross errors experiments, the FGO method yielded a better resistance to errors compared to the EKF and RKF methods. In the high-precision inertial guidance experiments, the FGO model yielded maximum improvements of 74.2% and 73.0% in the positions, 43.3% and 27.6% in the velocity, and 73.5% and 55.0% in the attitude compared to the EKF and RKF models. In the consumer grade inertial guidance experiments, the FGO model yielded maximum improvements of 36.4% and 24.1% in the position, the maximum improvements of 73.8% and 72.1% in the velocity, and = maximum improvement of 62.3% and 53.3% in the attitude.
- (3)
- In the simulated GNSS loss experiments, the GNSS/INS integration system based on the FGO method yielded a higher parameter estimation accuracy. In the high-precision inertial guidance experiments, the FGO model yielded maximum improvements of 81.1% and 79.8% in the position, 69.8% and 67.6% in the velocity, and 75.1% and 56.7% in the attitude compared to the EKF and RKF models, and the FGO model yielded maximum improvements of 39.2% and 27.6% in the position, 65.6% and 60.7% in the velocity, and 61.2% and 57.1% in the attitude compared to the EKF and RKF models. In the consumer grade inertial guidance experiments, the FGO model yielded maximum improvements of 65.6% and 60.7% in the velocity and maximum improvements of 61.2% and 57.1% in the attitude.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pan, L.; Zhang, X.; Liu, J.; Li, X.; Li, X. Performance Evaluation of Single-frequency Precise Point Positioning with GPS, GLONASS, BeiDou and Galileo. J. Navig. 2017, 70, 465–482. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Zhu, F.J.G. Factor graph optimization for urban environment GNSS positioning and robust performance analysis. Geomat. Inf. Sci. Wuhan Univ. 2023, 48, 1050–1057. [Google Scholar]
- Zhang, X.; Tao, X.; Wang, Y.; Liu, W.; Zhu, F.J.G. MEMS-Enhanced Smartphone GNSS High-Precision Positioning for Vehicular Navigation in Urban Conditions. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 1740–1749. [Google Scholar]
- Wang, D.; Dong, Y.; Li, Z.; Li, Q.; Wu, J. Constrained MEMS-based GNSS/INS tightly coupled system with robust Kalman filter for accurate land vehicular navigation. IEEE Trans. Instrum. Meas. 2019, 69, 5138–5148. [Google Scholar] [CrossRef]
- Shi, B.; Wang, M.; Wang, Y.; Bai, Y.; Lin, K.; Yang, F. Effect analysis of GNSS/INS processing strategy for sufficient utilization of urban environment observations. Sensors 2021, 21, 620. [Google Scholar] [CrossRef] [PubMed]
- Takasu, T.; Yasuda, A. Development of the low-cost RTK-GPS receiver with an open source program package RTKLIB. In Proceedings of the International Symposium on GPS/GNSS, Seoul, Republic of Korea, 1–3 December 2009. [Google Scholar]
- Chai, D.; Chen, G.; Wang, S.J. A Novel Method of Adaptive Kalman Filter for Heading Estimation Based on an Autoregressive Model. Appl. Sci. 2019, 9, 3727. [Google Scholar] [CrossRef]
- Hajiyev, C.; Soken, H.E. Robust adaptive Kalman filter for estimation of UAV dynamics in the presence of sensor/actuator faults. Aerosp. Sci. Technol. 2013, 28, 376–383. [Google Scholar] [CrossRef]
- Gao, W.; Li, J. Adaptive Kalman filtering for the integrated SINS/DVL system. J. Comput. Inf. Syst. 2013, 9, 6443–6450. [Google Scholar]
- Sage, A.P.; Husa, G.W. Adaptive filtering with unknown prior statistics. In Proceedings of the Joint Automatic Control Conference, Boulder, CO, USA, 12–15 August 1969. [Google Scholar]
- Ma, L.; Li, X. Improved Algorithmof Adaptive Fading Kalman Filtering Based on GPS/INS Integrated Navigation. Sci. Technol. Eng 2013, 13, 9973–9977. [Google Scholar]
- Godha, S.; Cannon, M. GPS/MEMS INS integrated system for navigation in urban areas. GPS Solut. 2007, 11, 193–203. [Google Scholar] [CrossRef]
- Huber, P.J. Robust estimation of a location parameter. In Breakthroughs in Statistics: Methodology and Distribution; Springer: Berlin/Heidelberg, Germany, 1992; pp. 492–518. [Google Scholar]
- Yang, Y.; Gao, W.-G.; Zhang, X.-D. Robust Kalman filtering with constraints: A case study for integrated navigation. J. Geod. 2010, 84, 373–381. [Google Scholar] [CrossRef]
- Gao, S.; Zhong, Y.; Li, W. Robust adaptive filtering method for SINS/SAR integrated navigation system. Aerosp. Sci. Technol. 2011, 15, 425–430. [Google Scholar] [CrossRef]
- Guo, Y.; Li, X.; Meng, Q. A runs test-based Kalman filter with both adaptability and robustness with application to INS/GNSS integration. IEEE Sens. J. 2022, 22, 22919–22930. [Google Scholar] [CrossRef]
- Yin, Z.; Yang, J.; Ma, Y.; Wang, S.; Chai, D.; Cui, H.J.R.S. A Robust Adaptive Extended Kalman Filter Based on an Improved Measurement Noise Covariance Matrix for the Monitoring and Isolation of Abnormal Disturbances in GNSS/INS Vehicle Navigation. Remote Sens. 2023, 15, 4125. [Google Scholar] [CrossRef]
- Watson, R.M.; Gross, J.N. Robust navigation in GNSS degraded environment using graph optimization. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017. [Google Scholar]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.-A. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Dellaert, F.; Kaess, M. Square Root SAM: Simultaneous localization and mapping via square root information smoothing. Int. J. Robot. Res. 2006, 25, 1181–1203. [Google Scholar] [CrossRef]
- Jinke, W.; Xingxing, Z.; Xiangrui, Z.; Jiajun, L.; Yong, L. Review of multi-source fusion SLAM: Current status and challenges. J. Image Graph. 2022, 27, 368–389. [Google Scholar]
- Suzuki, T. First place award winner of the smartphone decimeter challenge: Global optimization of position and velocity by factor graph optimization. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), Nashville, TN, USA, 20–24 September 2021. [Google Scholar]
- Suzuki, T. 1st place winner of the smartphone decimeter challenge: Two-step optimization of velocity and position using smartphone’s carrier phase observations. In Proceedings of the 35th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022. [Google Scholar]
- Xin, S.; Wang, X.; Zhang, J.; Zhou, K.; Chen, Y. A Comparative Study of Factor Graph Optimization-Based and Extended Kalman Filter-Based PPP-B2b/INS Integrated Navigation. Remote Sens. 2023, 15, 5144. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, F.; Zhang, X. Improving Gnss Positioning Reliability and Accuracy Based on Factor Graph Optimization in Urban Environment. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 48, 1179–1184. [Google Scholar] [CrossRef]
- Wen, W.; Pfeifer, T.; Bai, X.; Hsu, L.T. Factor graph optimization for GNSS/INS integration: A comparison with the extended Kalman filter. Navigation 2021, 68, 315–331. [Google Scholar] [CrossRef]
- Li, Z.; Lee, P.-H.; Hung, T.H.M.; Zhang, G.; Hsu, L.-T. Intelligent Environment-Adaptive GNSS/INS Integrated Positioning with Factor Graph Optimization. Remote Sens. 2023, 16, 181. [Google Scholar] [CrossRef]
- Hu, Y.; Li, H.; Liu, W. Robust factor graph optimisation method for shipborne GNSS/INS integrated navigation system. IET Radar Sonar Navig. 2024, 18, 782–798. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, C.; Zhang, Y.; Song, H. Inertial-Navigation-Aided Single-Satellite Highly Dynamic Positioning Algorithm. Sensors 2019, 19, 4196. [Google Scholar] [CrossRef] [PubMed]
- Wen, W.; Kan, Y.C.; Hsu, L.-T. Performance comparison of GNSS/INS integrations based on EKF and factor graph optimization. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Mao, Y.; Sun, R.; Wang, J.; Cheng, Q.; Kiong, L.C.; Ochieng, W.Y. New time-differenced carrier phase approach to GNSS/INS integration. GPS Solut. 2022, 26, 122. [Google Scholar] [CrossRef]
- Barfoot, T.D. State Estimation for Robotics; Cambridge University Press: Cambridge, UK, 2024. [Google Scholar]
- Kaess, M.; Johannsson, H.; Roberts, R.; Ila, V.; Leonard, J.J.; Dellaert, F. iSAM2: Incremental smoothing and mapping using the Bayes tree. Int. J. Robot. Res. 2012, 31, 216–235. [Google Scholar] [CrossRef]
- Zhang, S.; Tu, R.; Gao, Z.; Zou, D.; Wang, S.; Lu, X. LEO-Enhanced GNSS/INS Tightly Coupled Integration Based on Factor Graph Optimization in the Urban Environment. Remote Sens. 2024, 16, 1782. [Google Scholar] [CrossRef]
- Tang, H.; Zhang, T.; Niu, X.; Fan, J.; Liu, J. Impact of the earth rotation compensation on MEMS-IMU preintegration of factor graph optimization. IEEE Sens. J. 2022, 22, 17194–17204. [Google Scholar] [CrossRef]

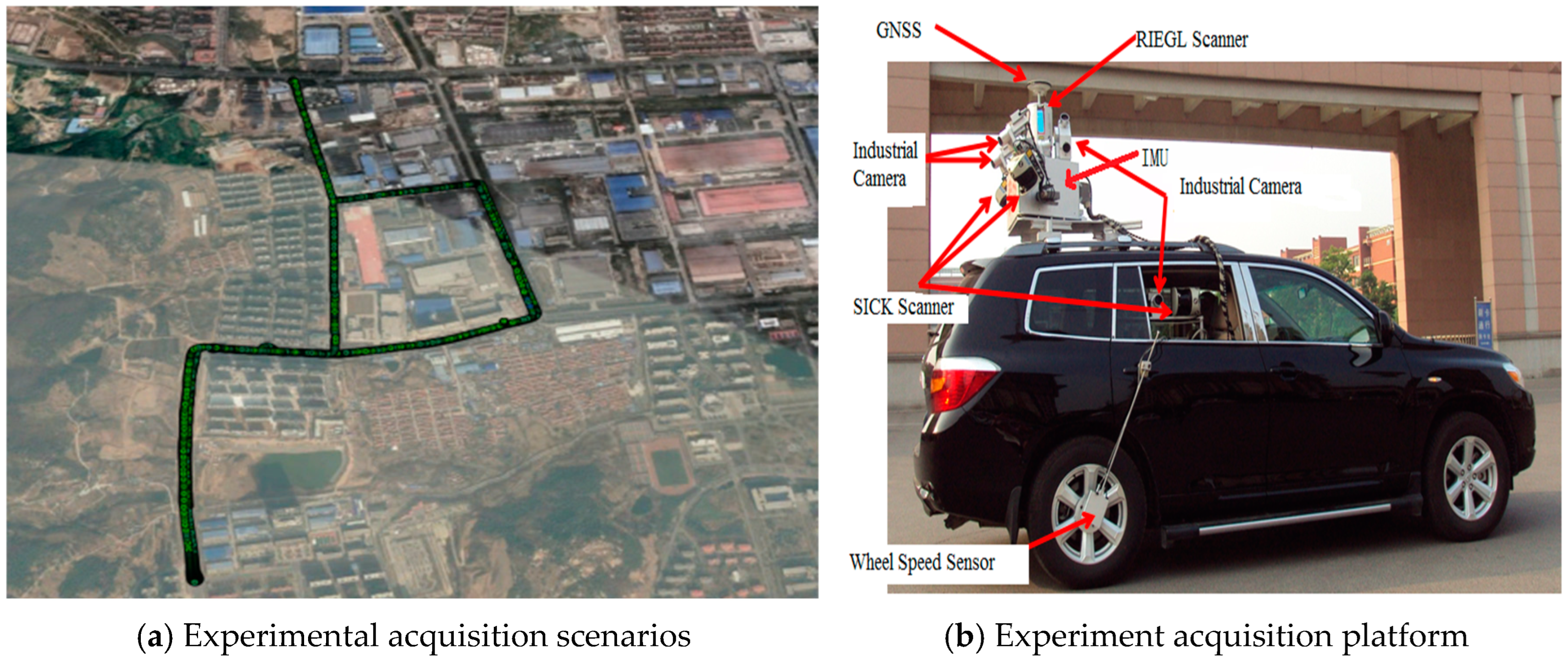







| Type of IMU | High-Precision IMU | |
|---|---|---|
| Gyroscope Performance | Rate bias | <0.25°/h |
| Angular random walk | <0.04°/ | |
| Accelerometer Performance | Bias | <1 mg |
| Random walk | <0.03 m/s/ | |
| Collection Frequency | 200 Hz | |
| ERROR | EKF | RKF | FGO | |
|---|---|---|---|---|
| Position (m) | E | 0.259 | 0.256 | 0.256 |
| N | 0.507 | 0.507 | 0.506 | |
| U | 0.525 | 0.524 | 0.524 | |
| Velocity (m/s) | E | 0.051 | 0.049 | 0.049 |
| N | 0.045 | 0.043 | 0.043 | |
| U | 0.101 | 0.100 | 0.095 | |
| Attitude (deg) | Roll | 0.010 | 0.009 | 0.006 |
| Pitch | 0.021 | 0.017 | 0.015 | |
| Heading | 0.065 | 0.050 | 0.048 | |
| ERROR | EKF | RKF | FGO | |
|---|---|---|---|---|
| Position (m) | E | 0.993 | 0.977 | 0.954 |
| N | 0.729 | 0.711 | 0.654 | |
| U | 1.476 | 1.418 | 0.383 | |
| Velocity (m/s) | E | 0.035 | 0.027 | 0.021 |
| N | 0.061 | 0.056 | 0.050 | |
| U | 0.232 | 0.181 | 0.131 | |
| Attitude (deg) | Roll | 0.007 | 0.005 | 0.002 |
| Pitch | 0.016 | 0.012 | 0.009 | |
| Heading | 0.011 | 0.006 | 0.003 | |
| Type of IMU | Consumer-Grade IMU | |
|---|---|---|
| Gyroscope Performance | Rate bias | <2.7°/h |
| Angular random walk | <0.2°/ | |
| Accelerometer Performance | Bias | <2 mg |
| Random walk | <0.3 m/s/ | |
| Collection Frequency | 100 Hz | |
| ERROR | EKF | RKF | FGO | |
|---|---|---|---|---|
| Position (m) | E | 0.283 | 0.281 | 0.280 |
| N | 0.132 | 0.116 | 0.114 | |
| U | 0.343 | 0.343 | 0.343 | |
| Velocity (m/s) | E | 0.031 | 0.027 | 0.022 |
| N | 0.131 | 0.108 | 0.020 | |
| U | 0.020 | 0.018 | 0.011 | |
| Attitude (deg) | Roll | 0.162 | 0.158 | 0.119 |
| Pitch | 0.103 | 0.101 | 0.095 | |
| Heading | 0.421 | 0.392 | 0.290 | |
| ERROR | EKF | RKF | FGO | |
|---|---|---|---|---|
| Position (m) | E | 0.337 | 0.317 | 0.286 |
| N | 0.190 | 0.159 | 0.121 | |
| U | 0.522 | 0.458 | 0.403 | |
| Velocity (m/s) | E | 0.186 | 0.174 | 0.049 |
| N | 0.127 | 0.106 | 0.080 | |
| U | 0.372 | 0.303 | 0.102 | |
| Attitude (deg) | Roll | 0.100 | 0.085 | 0.072 |
| Pitch | 0.140 | 0.112 | 0.067 | |
| Heading | 0.392 | 0.317 | 0.148 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, D.; Song, S.; Wang, K.; Bi, J.; Zhang, Y.; Ning, Y.; Yan, R. Optimization Model-Based Robust Method and Performance Evaluation of GNSS/INS Integrated Navigation for Urban Scenes. Electronics 2025, 14, 660. https://doi.org/10.3390/electronics14040660
Chai D, Song S, Wang K, Bi J, Zhang Y, Ning Y, Yan R. Optimization Model-Based Robust Method and Performance Evaluation of GNSS/INS Integrated Navigation for Urban Scenes. Electronics. 2025; 14(4):660. https://doi.org/10.3390/electronics14040660
Chicago/Turabian StyleChai, Dashuai, Shijie Song, Kunlin Wang, Jingxue Bi, Yunlong Zhang, Yipeng Ning, and Ruijie Yan. 2025. "Optimization Model-Based Robust Method and Performance Evaluation of GNSS/INS Integrated Navigation for Urban Scenes" Electronics 14, no. 4: 660. https://doi.org/10.3390/electronics14040660
APA StyleChai, D., Song, S., Wang, K., Bi, J., Zhang, Y., Ning, Y., & Yan, R. (2025). Optimization Model-Based Robust Method and Performance Evaluation of GNSS/INS Integrated Navigation for Urban Scenes. Electronics, 14(4), 660. https://doi.org/10.3390/electronics14040660







