Smart Tuning of Control System Parameters for a Grid Connected Converter: A Robust Artificial Neural Network Approach
Abstract
1. Introduction
1.1. Grid-Forming Converter
1.2. Data-Driven and Neural Network-Based Tuning Methods
1.3. Research Gaps and Challenges
1.4. Objectives and Contributions
- ▪
- Developing a comprehensive framework for integrating the RANN-based tuning methods into the existing control structures of the GFM converters.
- ▪
- Investigating the potential of NNs in improving the transient and steady-state performance of the GFM converters, particularly in response to variations in grid inertia, load demand, and renewable energy fluctuations.
- ▪
- A novel RANN-based stabilizing tuning framework: proposing a systematic approach for embedding the RANNs into the GFM converter control loops, enabling the dynamic and adaptive tuning of control parameters.
- ▪
- Enhanced control performance: demonstrating improved transient response, steady-state accuracy, and robustness against system uncertainties compared to traditional controllers.
2. System Modeling and Problem Formulation
3. Robust Neural Network-Based Tuning Framework
3.1. Neural Network Architecture and Training Strategy
3.2. Robust Neural Network
3.2.1. Deadzone Technique
3.2.2. E-Modification Technique
3.3. Input Features and Output Parameters
3.4. Performance Metrics
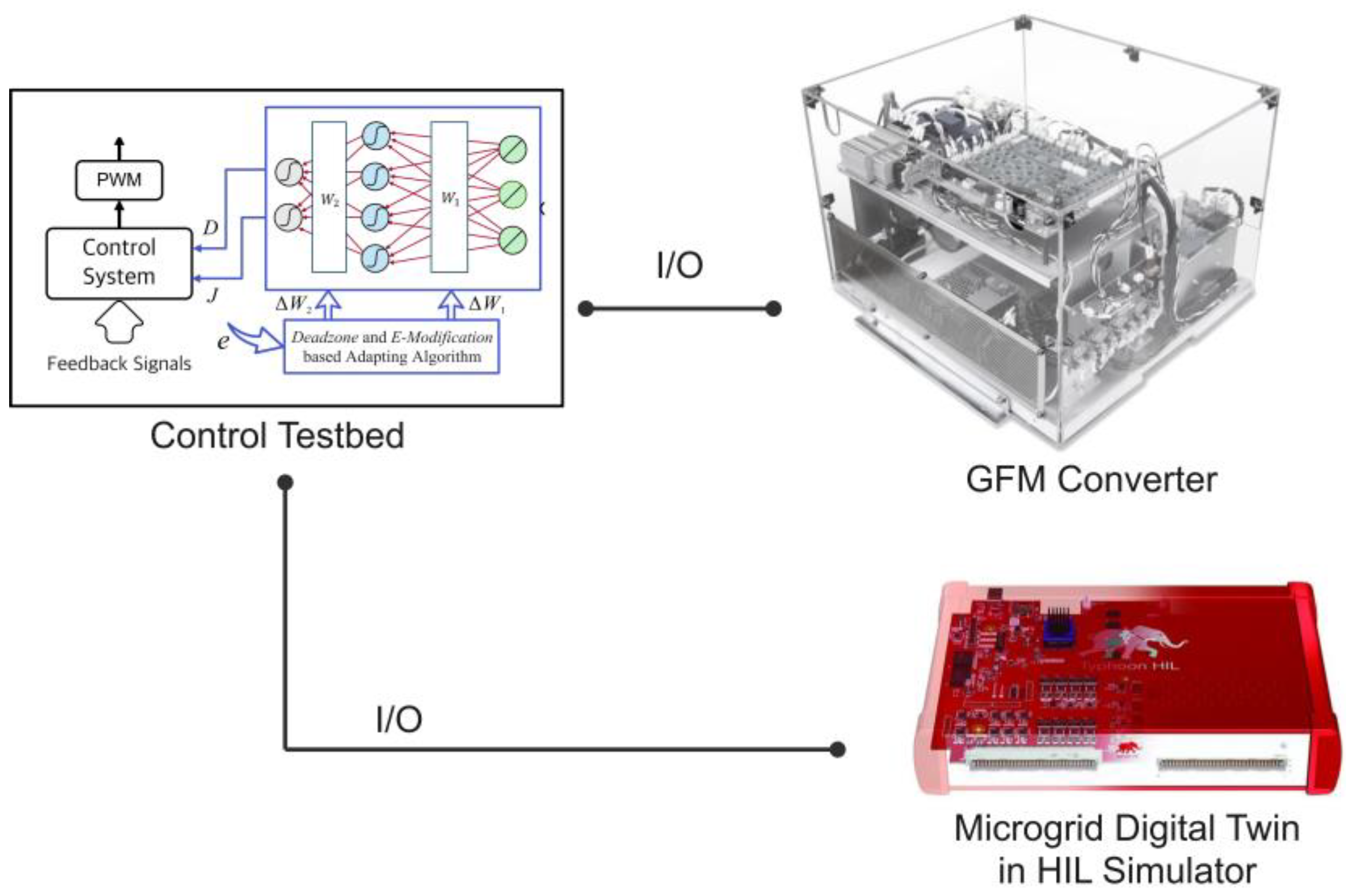
4. Simulation and HIL-Based Real-Time Results
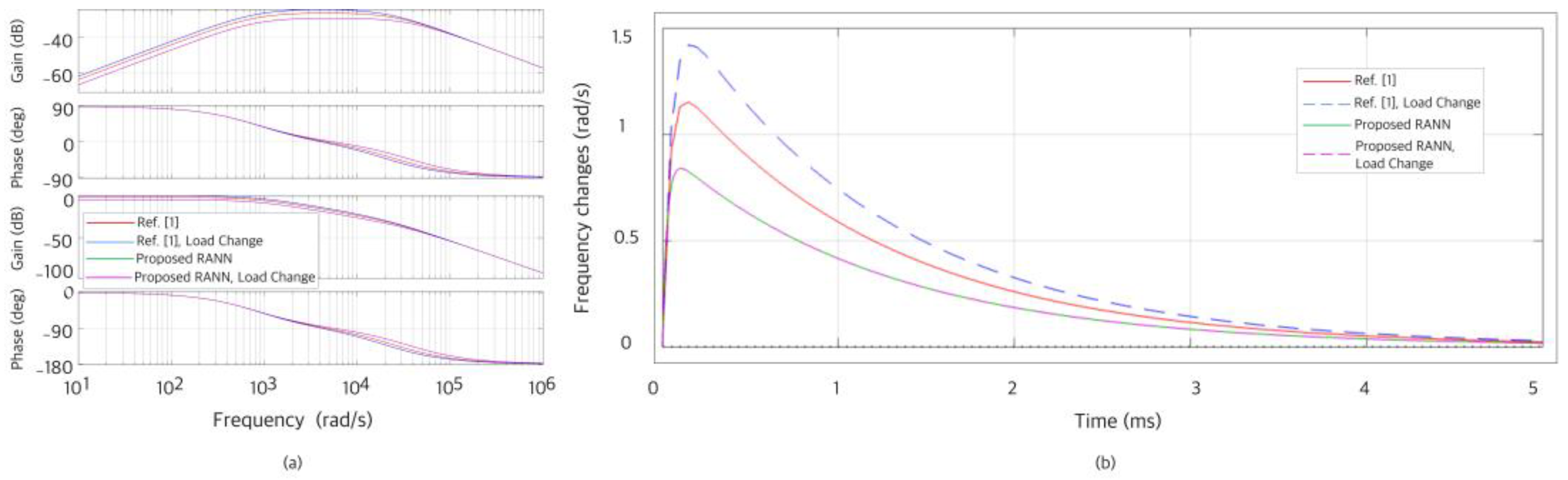
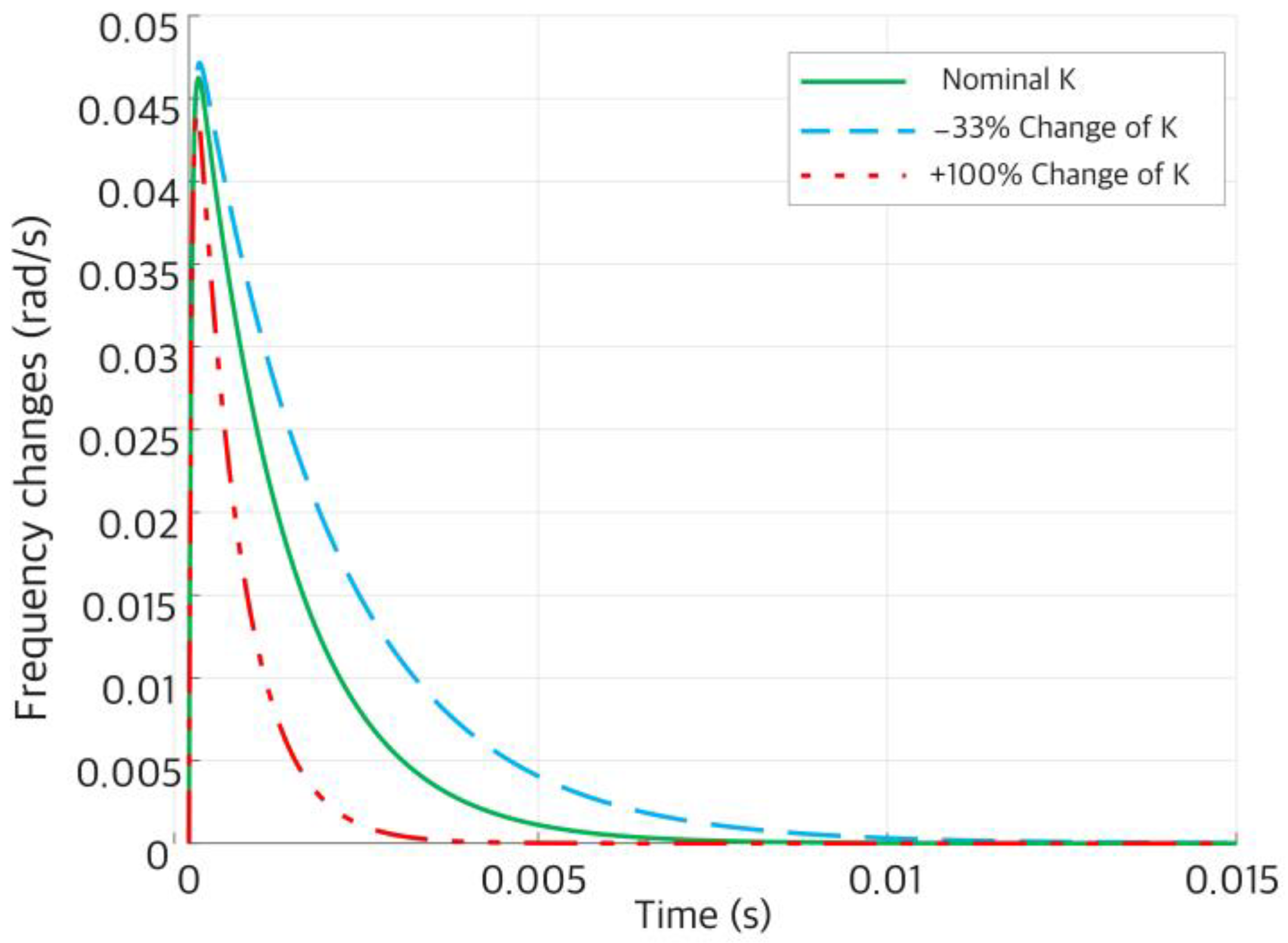
4.1. Simulation Results
4.2. Laboratory Real-Time Results
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bevrani, H.; Kato, T.; Ise, T.; Inoue, K. Grid Connected Converters: Modeling, Stability and Control; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Lasseter, R.H. MicroGrids. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.02CH37309), New York, NY, USA, 27–31 January 2002. [Google Scholar]
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the art in research on modern power grids: A review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Rosso, R.; Engelken, S.; Liserre, M. Robust stability investigation of the interactions among grid-forming and grid-following converters. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 991–1003. [Google Scholar] [CrossRef]
- Gao, X.; Zhou, D.; Anvari-Moghaddam, A.; Blaabjerg, F. Grid-following and grid-forming control in power electronic based power systems: A comparative study. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021. [Google Scholar]
- Tayyebi, A.; Dörfler, F.; Kupzog, F.; Miletic, Z.; Hribernik, W. Grid-Forming Converters–Inevitability, Control Strategies and Challenges in Future Grids Application, 2018, CIRED Workshop—Ljubljana. Available online: https://www.cired-repository.org/bitstream/handle/20.500.12455/1249/CIRED%202018%20Ljubljana%20WS%20-%200236%20-%2021086.pdf?sequence=1 (accessed on 10 January 2025).
- Tayyebi, A.; Groß, D.; Anta, A.; Kupzog, F.; Dörfler, F. Frequency stability of synchronous machines and grid-forming power converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1004–1018. [Google Scholar] [CrossRef]
- Fu, X.; Sun, J.; Huang, M.; Tian, Z.; Yan, H.; Iu, H.H.C.; Hu, P.; Zha, X. Large-signal stability of grid-forming and grid-following controls in voltage source converter: A comparative study. IEEE Trans. Power Electron. 2020, 36, 7832–7840. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Current limiting control with enhanced dynamics of grid-forming converters during fault conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 1062–1073. [Google Scholar] [CrossRef]
- Khan, S.A.; Wang, M.; Su, W.; Liu, G.; Chaturvedi, S. Grid-forming converters for stability issues in future power grids. Energies 2022, 15, 4937. [Google Scholar] [CrossRef]
- Arghir, C.; Jouini, T.; Dörfler, F. Grid-forming control for power converters based on matching of synchronous machines. Automatica 2018, 95, 273–282. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-forming converters: An overview of control approaches and future trends. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020. [Google Scholar]
- Chen, M.; Zhou, D.; Tayyebi, A.; Prieto-Araujo, E.; Dörfler, F.; Blaabjerg, F. Generalized multivariable grid-forming control design for power converters. IEEE Trans. Smart Grid 2022, 13, 2873–2885. [Google Scholar] [CrossRef]
- Gao, Y.; Ren, H.P.; Li, J. Grid-forming converters control based on dc voltage feedback. arXiv 2020, arXiv:2009.05759. [Google Scholar]
- Alshahrani, S.; Khan, K.; Abido, M.; Khalid, M. Grid-forming converter and stability aspects of renewable-based low-inertia power networks: Modern trends and challenges. Arab. J. Sci. Eng. 2024, 49, 6187–6216. [Google Scholar] [CrossRef]
- Nurminen, T.; Mourouvin, R.; Hinkkanen, M.; Kukkola, J. Multifunctional grid-forming converter control based on a disturbance observer. IEEE Trans. Power Electron. 2024, 39, 13023–13032. [Google Scholar] [CrossRef]
- Ning, K. Data driven artificial intelligence techniques in renewable energy system. Doctoral dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 2021. [Google Scholar]
- Karimi, A.; Bahrani, B.; Zheng, D.; Madani, S.S. Data-Driven Control and Its Applications to Modern power grids. In Proceedings of the 2022 IEEE Conference on Control Technology and Applications (CCTA), Trieste, Italy, 23–25 August 2022. [Google Scholar]
- Soliman, A.S.; Amin, M.M.; El-Sousy, F.F.; Mohammad, O.A. A data-driven based online learning control of voltage source converter for DC modern power grids. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Bari, Italy, 7–10 September 2021. [Google Scholar]
- Issa, H.; Debusschere, V.; Garbuio, L.; Lalanda, P.; Hadjsaid, N. Artificial intelligence-based controller for grid-forming inverter-based generators. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Novi Sad, Serbia, 10–12 October 2022. [Google Scholar]
- Li, Y.; Liao, Y.; Zhao, L.; Chen, M.; Wang, X.; Nordström, L.; Mittal, P.; Poor, H.V. Machine Learning at the Grid Edge: Data-Driven Impedance Models for Model-Free Inverters. IEEE Trans. Power Electron. 2024, 39, 10465–10481. [Google Scholar] [CrossRef]
- Silva-Vera, E.D.; Valdez-Resendiz, J.E.; Escobar, G.; Guillen, D.; Rosas-Caro, J.C.; Sosa, J.M. Data-Driven Modeling of DC–DC Power Converters. Electronics 2024, 13, 3890. [Google Scholar] [CrossRef]
- Qin, C.; Gao, F.; Zhou, K. Data-Driven Online Adaptive Parameters Adjustment for Output Quality of Grid-Connected Converters. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023. [Google Scholar]
- Bana, P.R.; Amin, M. Control for grid-connected VSC with improved damping based on physics-informed neural network. IEEE J. Emerg. Sel. Top. Ind. Electron. 2023, 4, 878–888. [Google Scholar] [CrossRef]
- Santos, L.E.; Bernardo, R.T.; Alcahuaman, H.; Ota, J.I.; Pomilio, J.A.; Dotta, D. An Online Data-Driven Tuning of Control Parameters for a Grid-Forming Inverter. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022. [Google Scholar]
- Pinthurat, W.; Kongsuk, P.; Surinkaew, T.; Marungsri, B. An Adaptive Data-Driven-Based Control for Voltage Control Loop of Grid-Forming Converters in Variable Inertia MGs; IEEE Access: Piscataway, NJ, USA, 2024. [Google Scholar]
- Soliman, A.S.; Amin, M.M.; El-Sousy, F.F.; Mohammad, O.A. Experimental validation for artificial data-driven tracking control for enhanced three-phase grid-connected boost rectifier in DC modern power grids. IEEE Trans. Ind. Appl. 2022, 59, 2563–2580. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, S.; Dragicevic, T.; Wheeler, P.; Zanchetta, P. Artificial Intelligence Techniques for Enhancing the Performance of Controllers in Power Converter-based Systems—An Overview. IEEE Open J. Ind. Appl. 2023, 4, 366–375. [Google Scholar] [CrossRef]
- Zeng, Y. Data-Driven Control Methods of Dual-Active-Bridge-Based grid-Connected Battery Energy Storage System. Ph.D. Thesis, Nanyang Technological University, Singapore, 2023. [Google Scholar]
- Fathollahi, A.; Gheisarnejad, M.; Andresen, B.; Farsizadeh, H.; Khooban, M.H. Robust artificial intelligence controller for stabilization of full-bridge converters feeding constant power loads. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3504–3508. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Fathollahi, A.; Sharifzadeh, M.; Laurendeau, E.; Al-Haddad, K. Data-driven switching control technique based on deep reinforcement learning for packed E-Cell as smart ev charger. In IEEE Transactions on Transportation Electrification; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Nicol, C.; Macnab, C.J.B.; Ramirez-Serrano, A. Robust neural network control of a quadrotor helicopter. In Proceedings of the 2008 Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 4–7 May 2008. [Google Scholar]
- Rehimi, S.; Bevrani, H.; Urabe, C.T.; Kato, T. Microgrid Control Assessment Using Advanced Hardware in the Loop Technologies. In Microgrids and Virtual Power Plants; Springer Nature: Singapore, 2024. [Google Scholar]
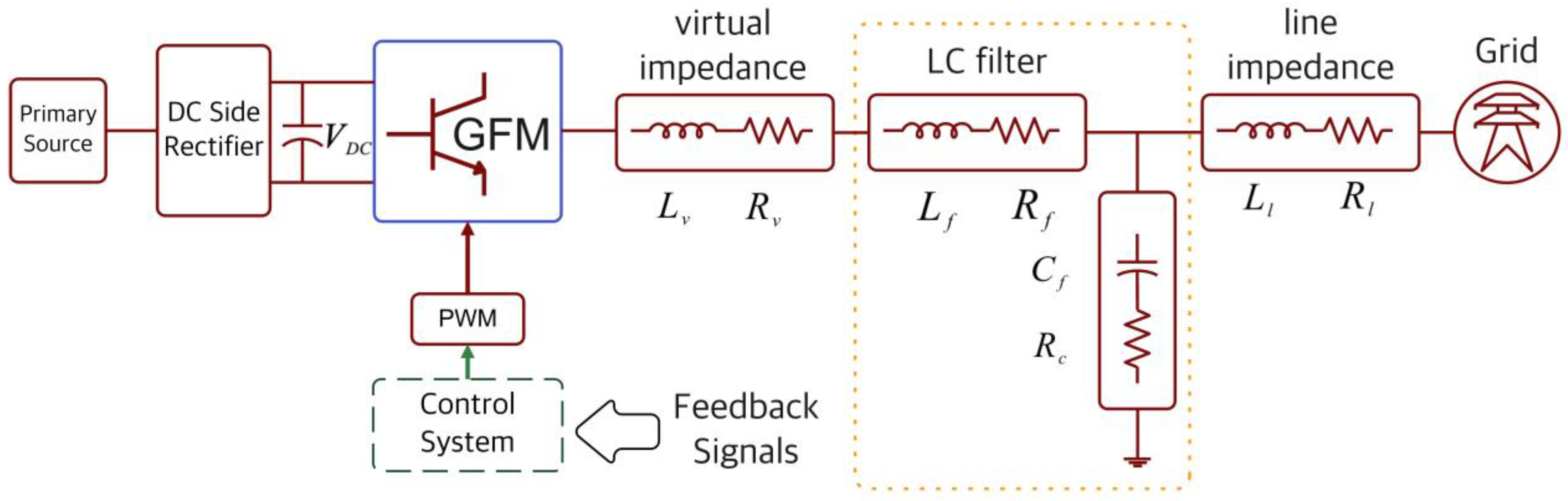



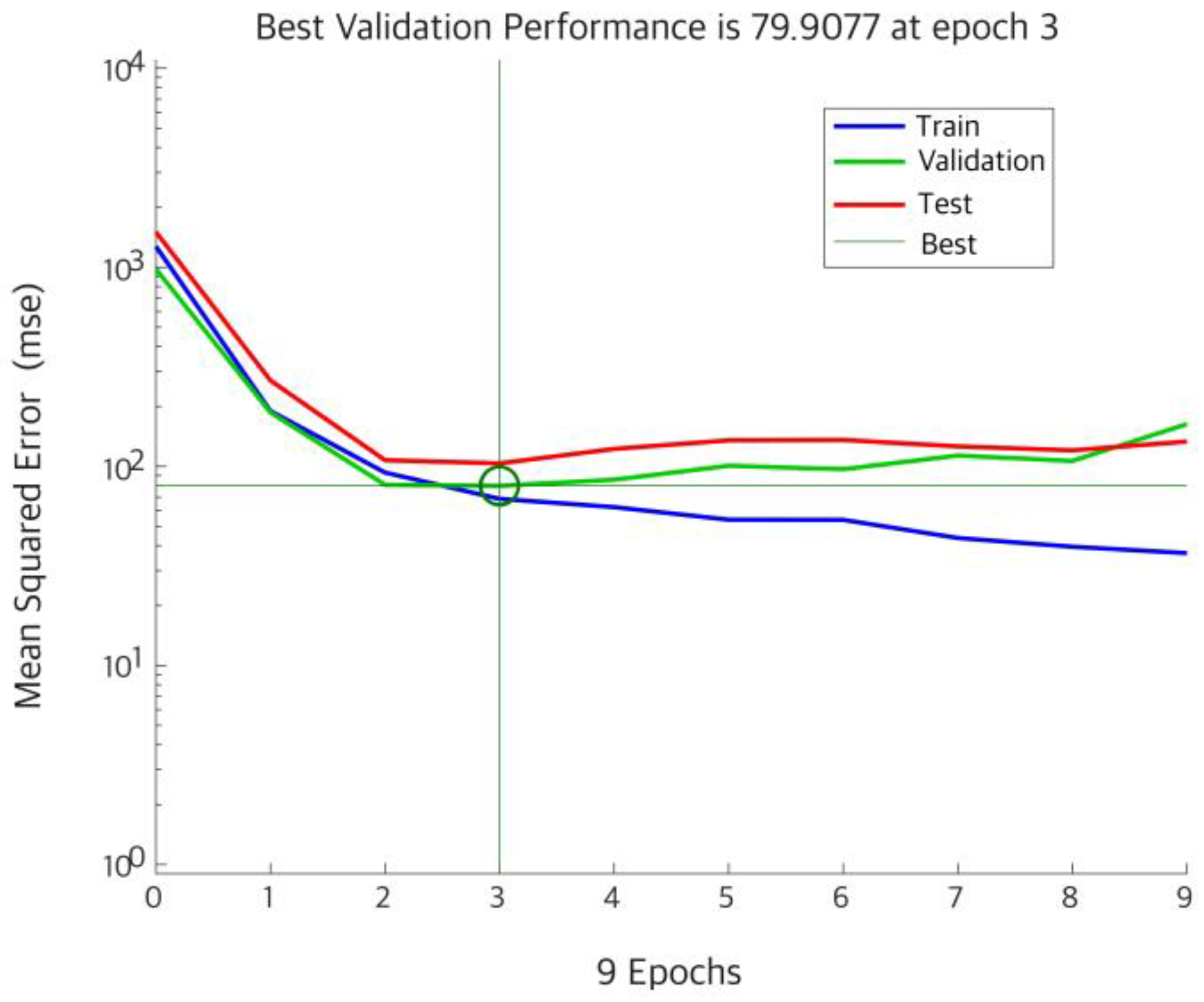
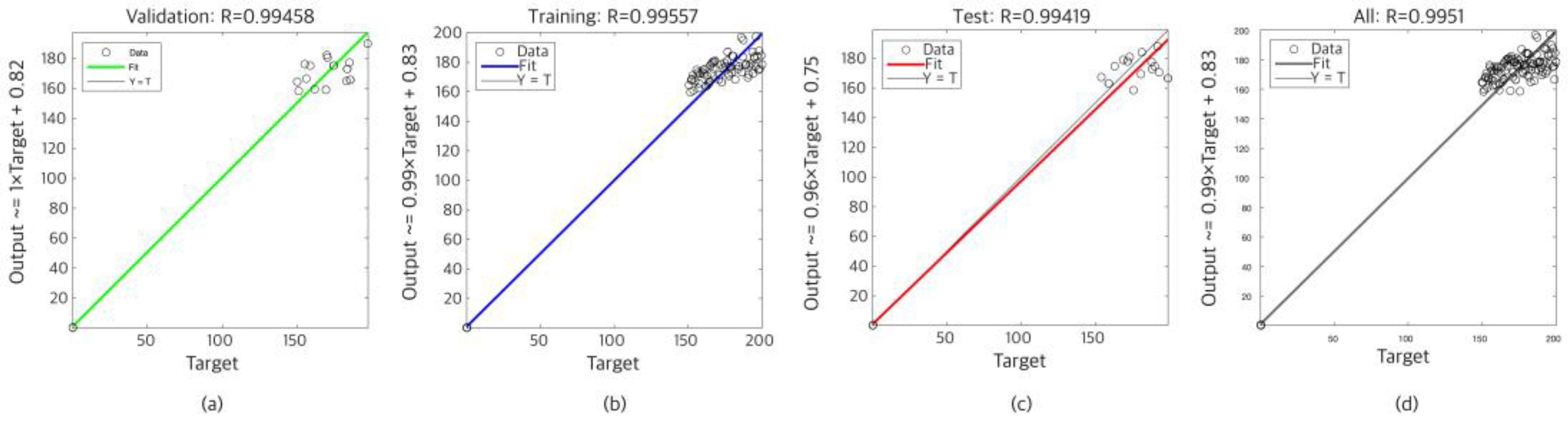
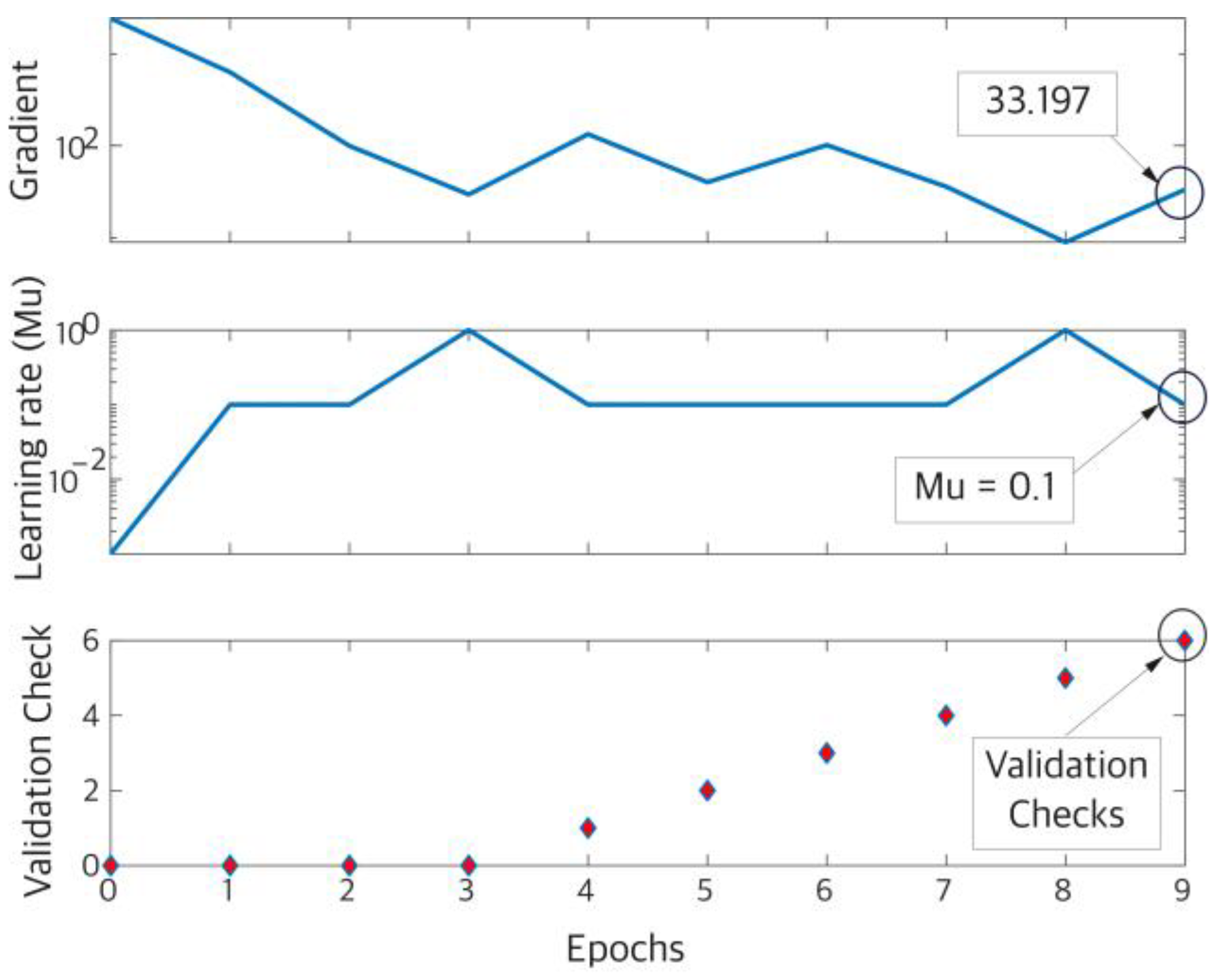

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| pu | |||
| pu | |||
| rad/s | pu | ||
| pu | pu | ||
| pu | pu | ||
| pu | pu | ||
| kVA | V |
| Proposed Method | Nonlinear and Data-Driven Method, e.g., [32] | Deep Reinforcement Learning Method, e.g., [31] | |
|---|---|---|---|
| Advantages | Simple ANN structure, less computational complexity, simple learning algorithm, solves the tuning problem | Handles variable DC loads, uses proximal policy optimization to design control coefficients, reduces hardware requirements | Solves the tuning problem considering challenging conditions |
| Disadvantages | Model-based | High computational complexity, estimation requirements | High computational demand from deep reinforcement learning requires extensive training and reward signal definition |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehimi, S.; Bevrani, H.; Urabe, C.T.; Kato, T.; Kato, T. Smart Tuning of Control System Parameters for a Grid Connected Converter: A Robust Artificial Neural Network Approach. Electronics 2025, 14, 699. https://doi.org/10.3390/electronics14040699
Rehimi S, Bevrani H, Urabe CT, Kato T, Kato T. Smart Tuning of Control System Parameters for a Grid Connected Converter: A Robust Artificial Neural Network Approach. Electronics. 2025; 14(4):699. https://doi.org/10.3390/electronics14040699
Chicago/Turabian StyleRehimi, Sharara, Hassan Bevrani, Chiyori T. Urabe, Takeyoshi Kato, and Toshiji Kato. 2025. "Smart Tuning of Control System Parameters for a Grid Connected Converter: A Robust Artificial Neural Network Approach" Electronics 14, no. 4: 699. https://doi.org/10.3390/electronics14040699
APA StyleRehimi, S., Bevrani, H., Urabe, C. T., Kato, T., & Kato, T. (2025). Smart Tuning of Control System Parameters for a Grid Connected Converter: A Robust Artificial Neural Network Approach. Electronics, 14(4), 699. https://doi.org/10.3390/electronics14040699






