Yolov8s-DDC: A Deep Neural Network for Surface Defect Detection of Bearing Ring
Abstract
1. Introduction
2. Related Work
2.1. Traditional Bearing Defect Detection Algorithms
2.2. Deep Learning-Based Bearing Defect Detection Algorithms
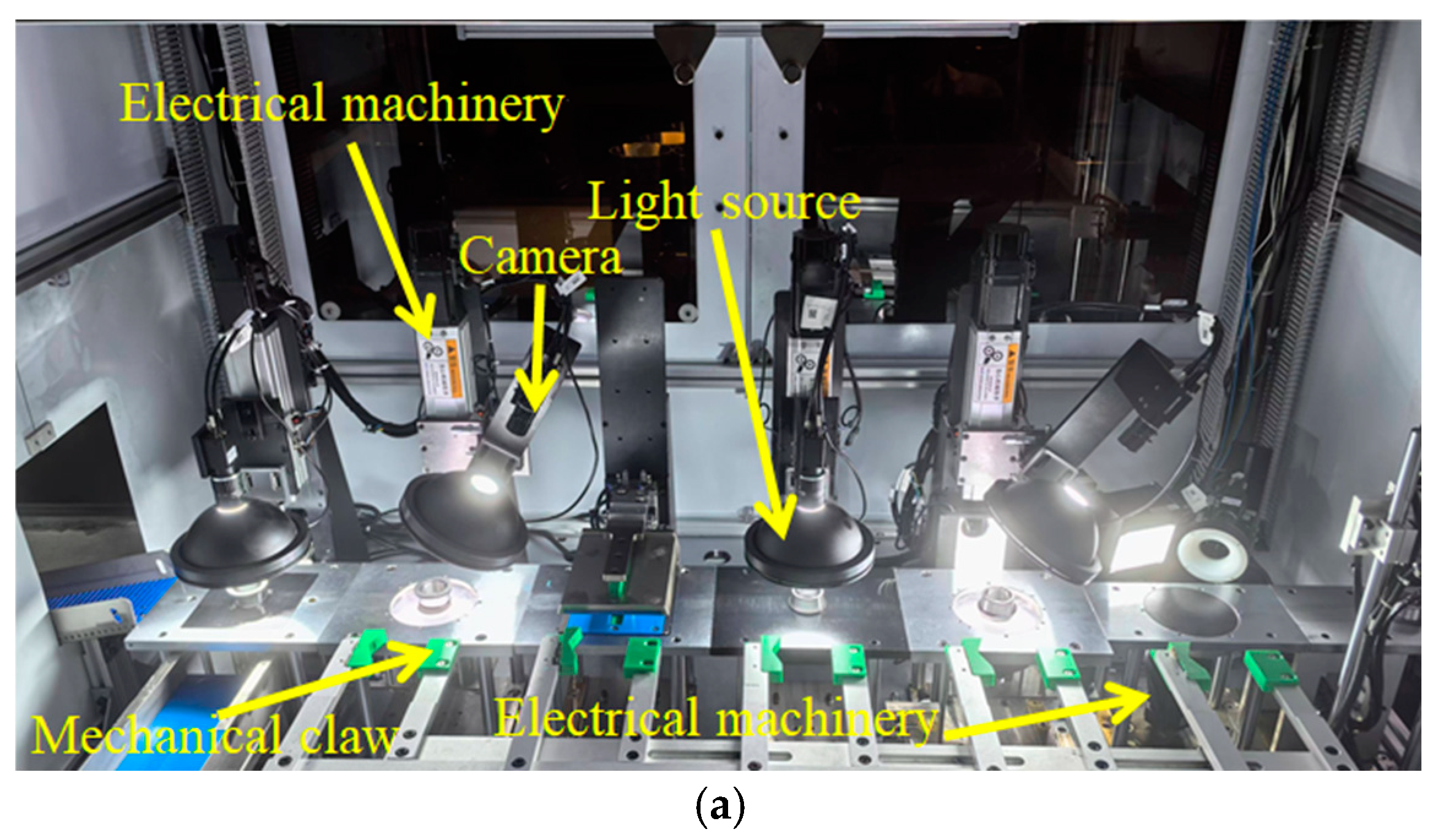
3. Bearing Surface Defect Detection Device
3.1. Principle of Bearing Surface Defect Detection Device
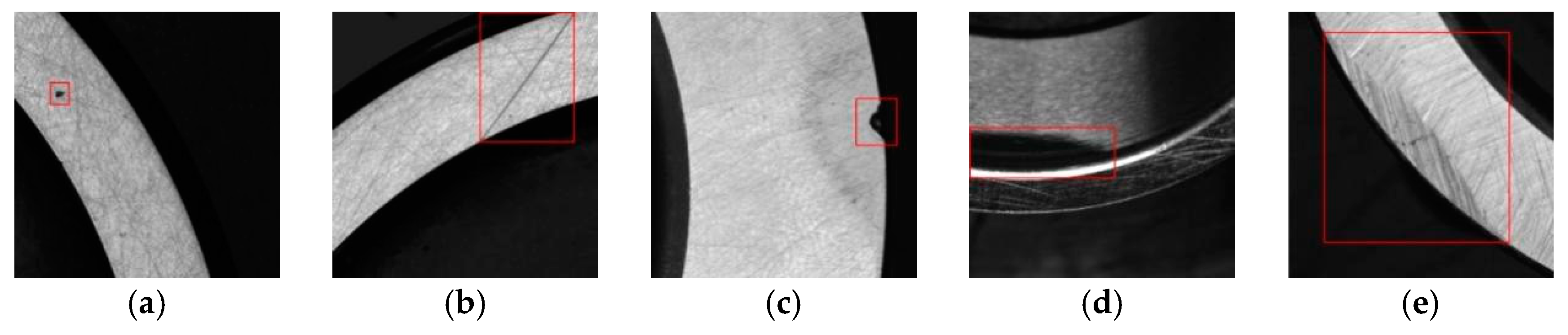
3.2. Types of Bearing Defects
- (1)
- Black spots
- (2)
- Scratches
- (3)
- Dents
- (4)
- Material waste
- (5)
- Wear
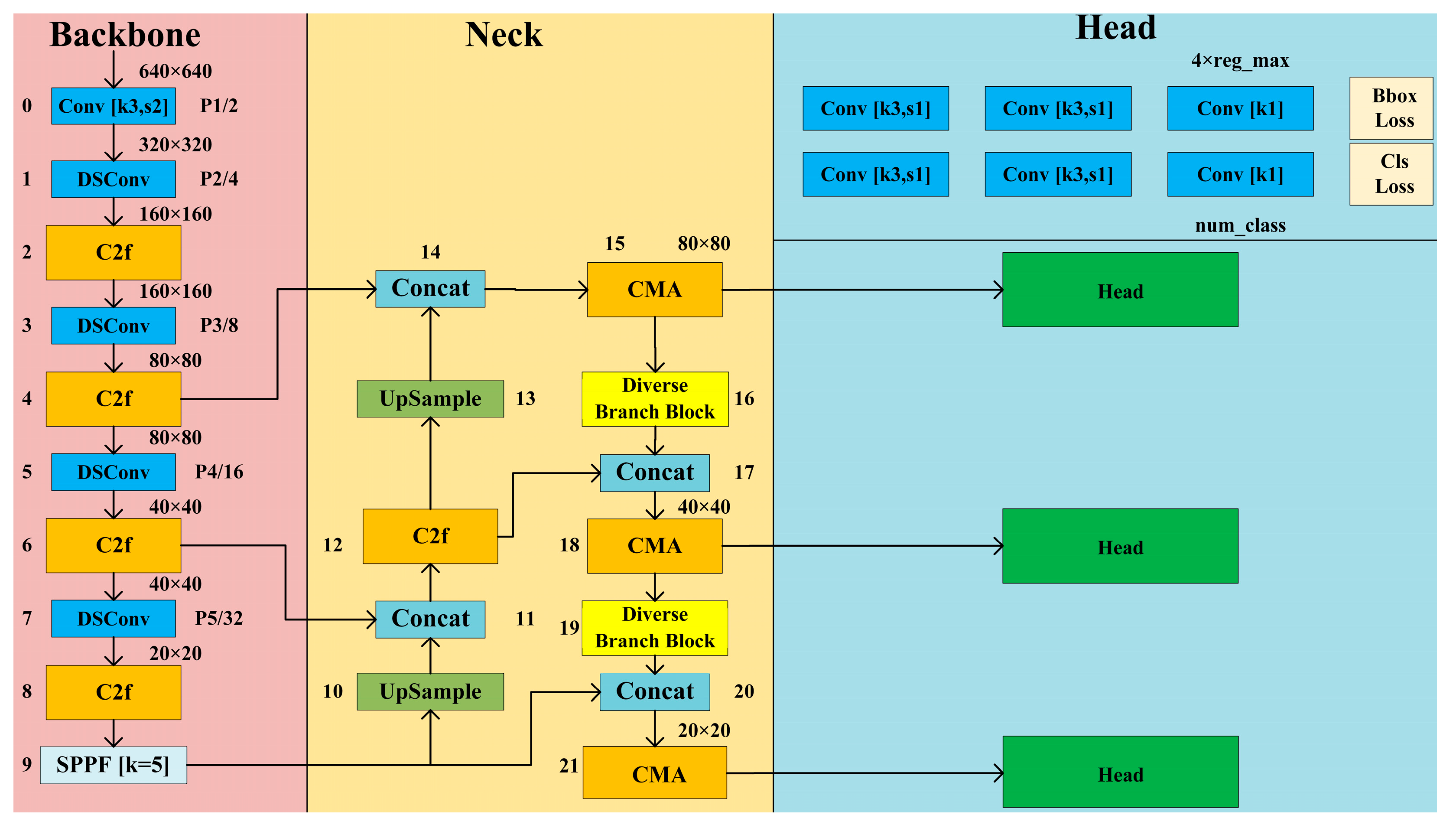
4. Algorithm Improvement
4.1. Yolov8s-DDC
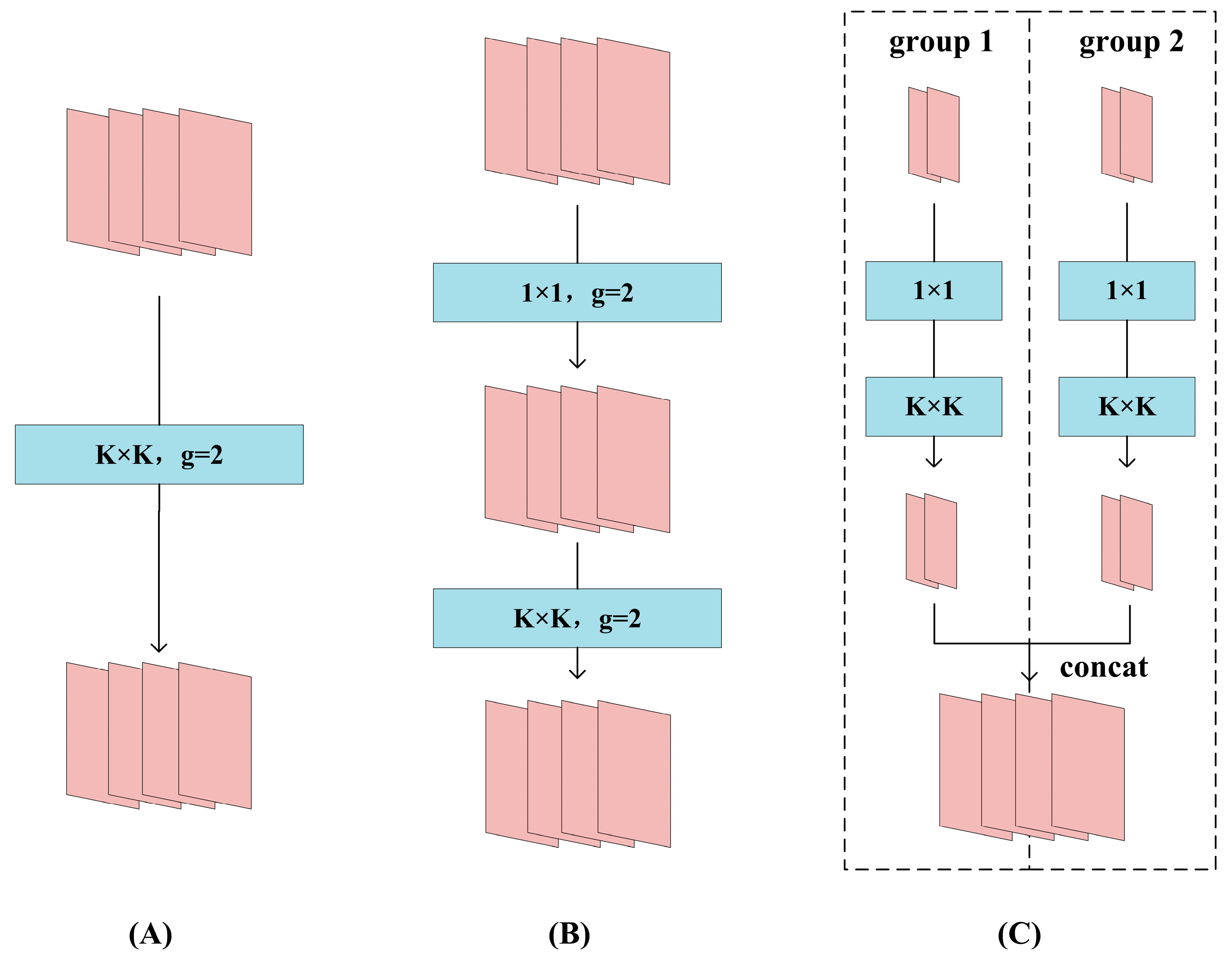
4.2. Depthwise Separable Convolution
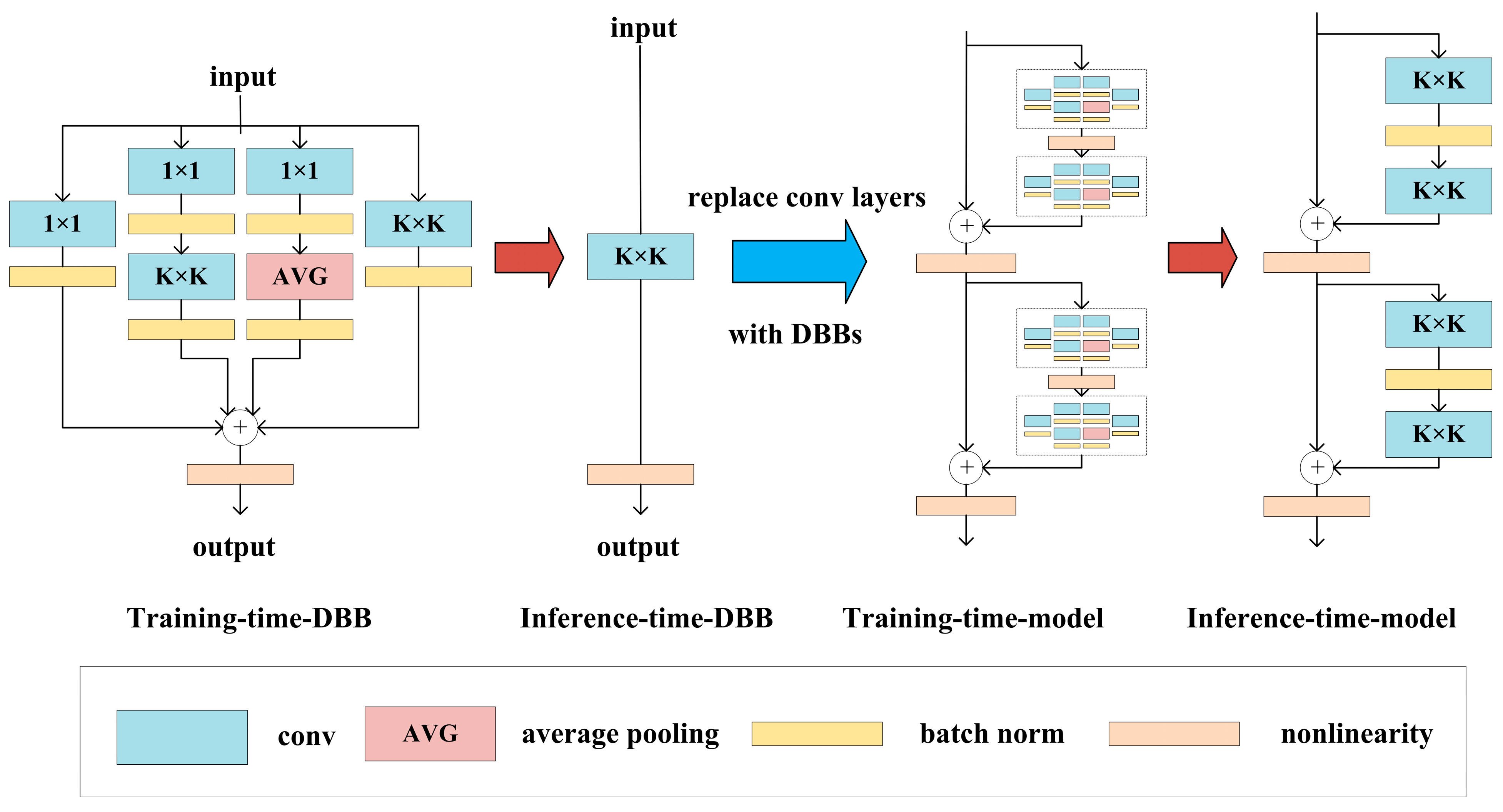
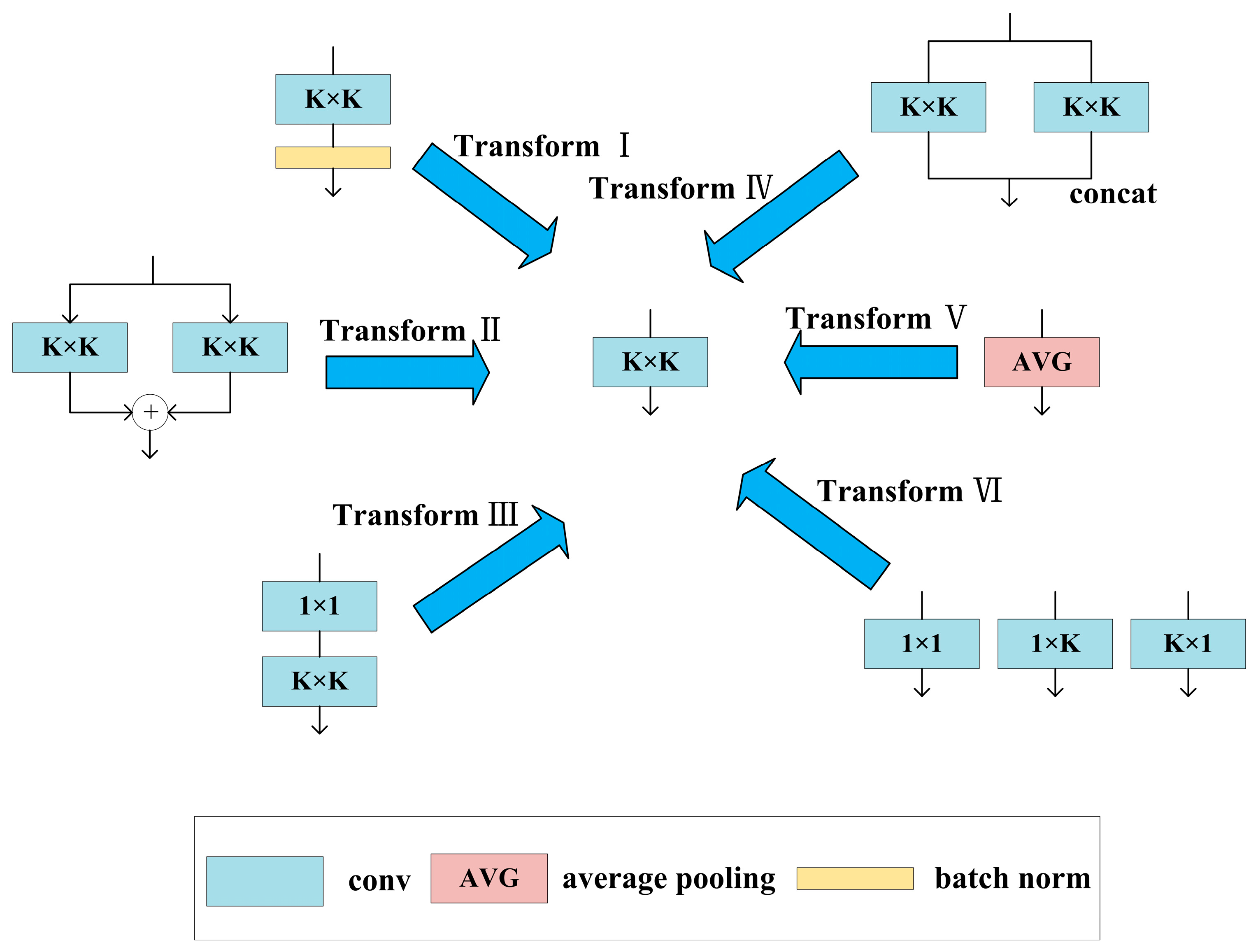
4.3. Diverse Branch Block
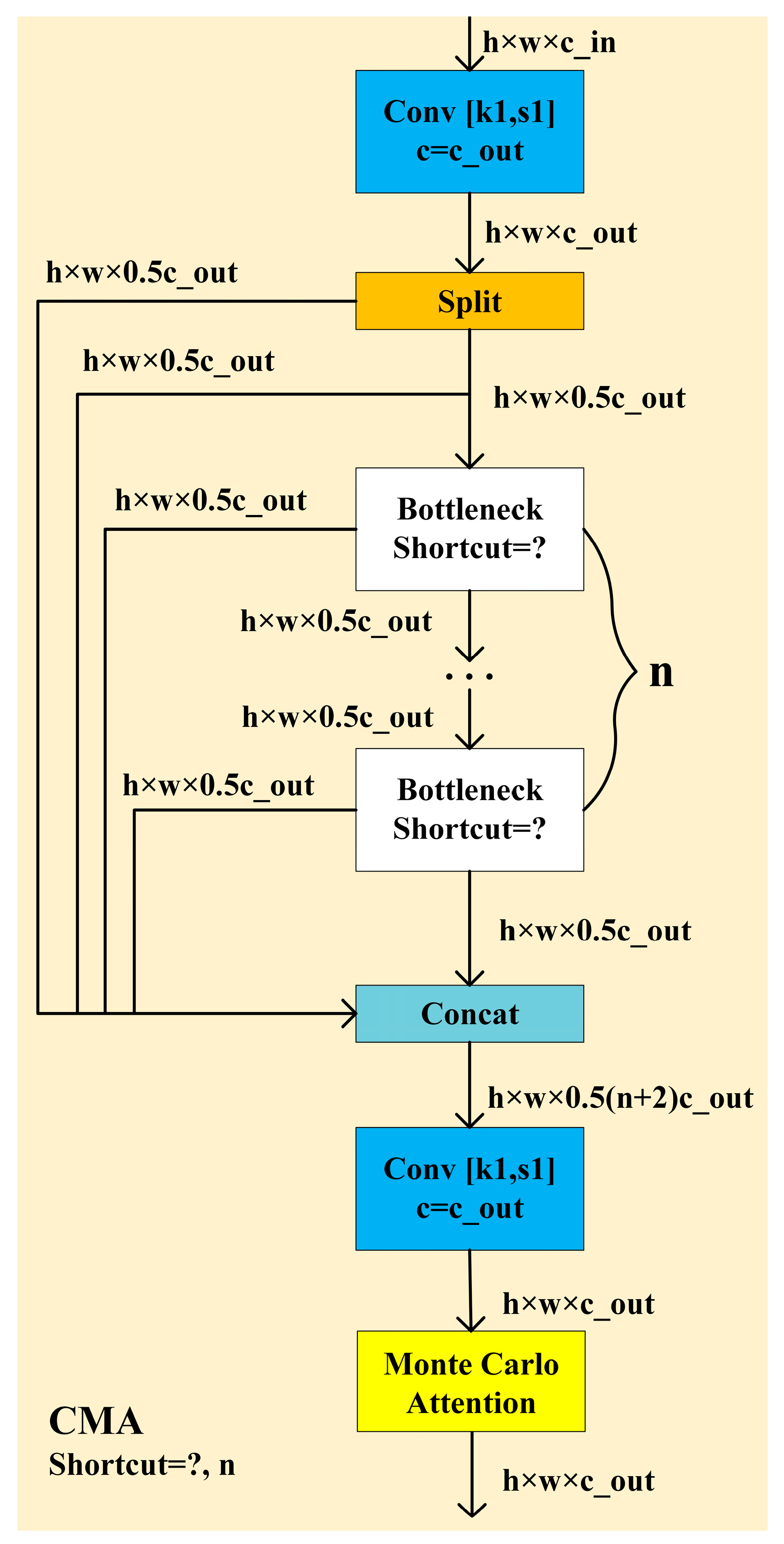
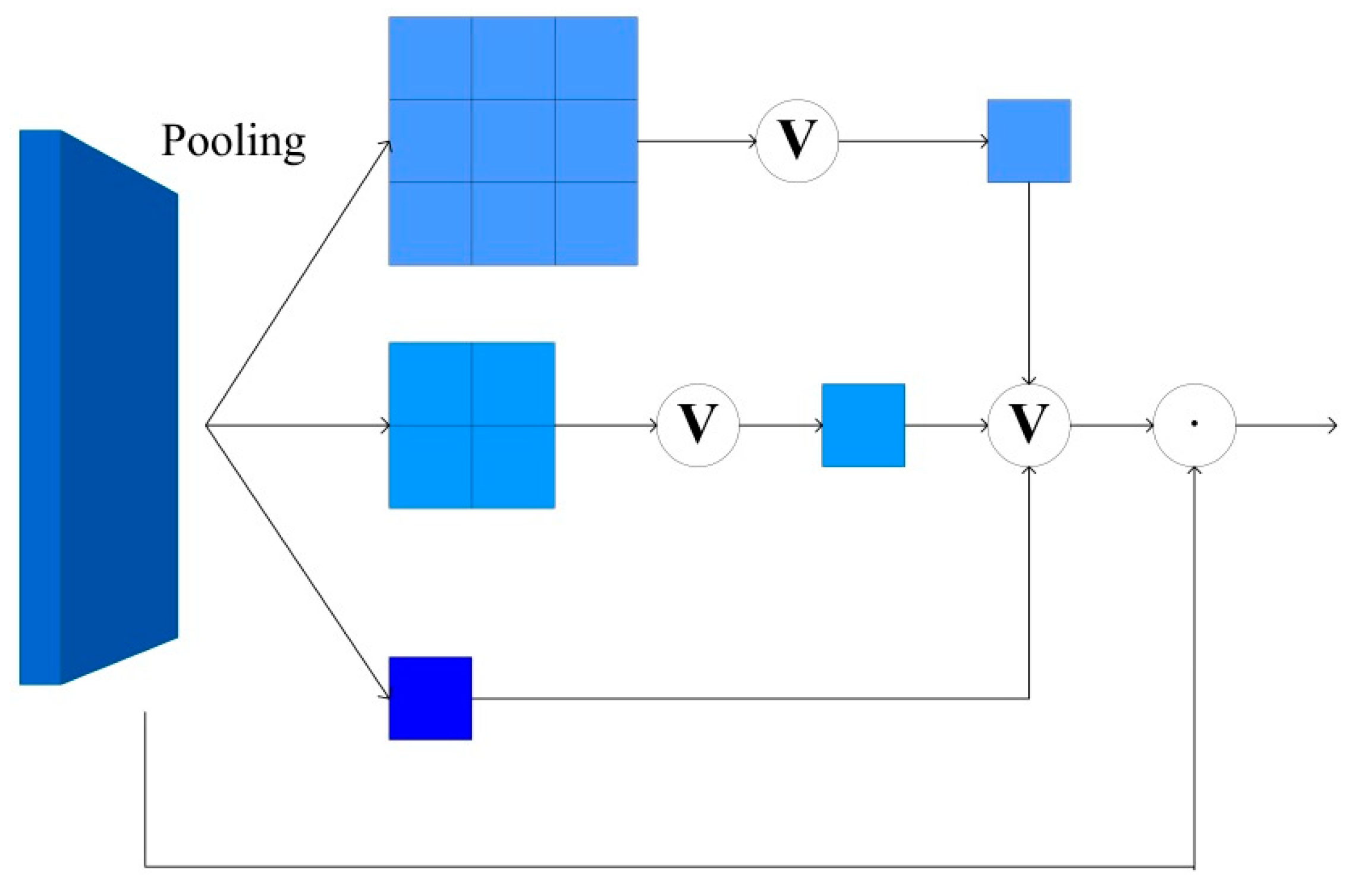
4.4. CMA
5. Experimental Verification
5.1. Dataset of Bearing Surface Defects
5.2. Experimental Setup and Performance Indicators
5.2.1. Experimental Setup
5.2.2. Performance Indicators
5.3. Ablation Experiment
5.4. Feature Visualization Analysis
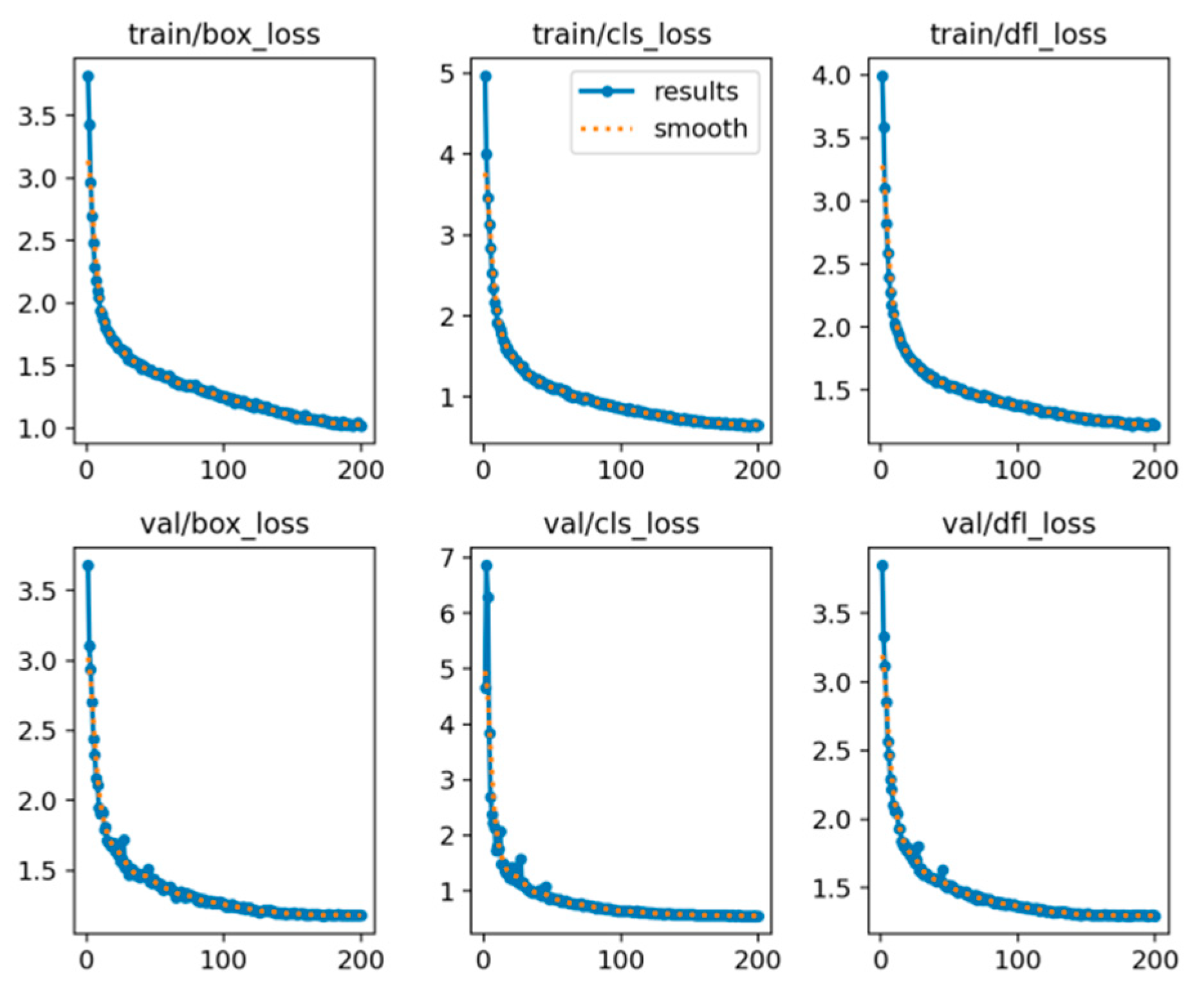
5.5. Experimental Results and Comparative Experiments
- (1)
- train/box_loss: This indicates the loss for bounding box prediction during training, reflecting the model’s error in localizing target objects.
- (2)
- train/cls_loss: This represents the classification loss during training, reflecting the model’s error in classifying target categories.
- (3)
- train/dfl_loss: This denotes the distribution focal loss during training, which optimizes the distribution prediction in object detection.
- (4)
- val/box_loss, val/cls_loss, val/dfl_loss: These represent the corresponding losses on the validation set, used to evaluate the model’s performance on unseen data.
5.6. Causes of False Positives and False Negatives
5.7. Detection Results of the Public Datasets
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; pp. 21–37. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Liang, Y.; Xu, K.; Zhou, P. Mask gradient response-based threshold segmentation for surface defect detection of milled aluminum ingot. Sensors 2020, 20, 4519. [Google Scholar] [CrossRef] [PubMed]
- Zhang, E.; Ma, Q.; Chen, Y.; Duan, J.; Shao, L. EGD-Net: Edge-guided and differential attention network for surface defect detection. J. Ind. Inf. Integr. 2022, 30, 100403. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Z.; Jiao, T.; Wang, M. Defect detection of aluminum alloy wheels in radiography images using adaptive threshold and morphological reconstruction. Appl. Sci. 2018, 8, 2365. [Google Scholar] [CrossRef]
- Cheng, B.; Li, B.; Ye, L. Defect detection of photovoltaic panel based on morphological segmentation. In Proceedings of the MIPPR 2023: Automatic Target Recognition and Navigation, Wuhan, China, 10–12 November 2023. [Google Scholar]
- Zhou, P.; Zhou, G.; Li, Y.; He, Z.; Liu, Y. A hybrid data-driven method for wire rope surface defect detection. IEEE Sens. J. 2020, 20, 8297–8306. [Google Scholar] [CrossRef]
- Hua, J.; Zhiquan, W. Resolving mode mixing in wheel–rail surface defect detection using EMD based on binary time scale. Meas. Sci. Technol. 2023, 35, 035015. [Google Scholar] [CrossRef]
- Lan, S.; Li, J.; Hu, S.; Fan, H.; Pan, Z. A neighbourhood feature-based local binary pattern for texture classification. Vis. Comput. 2024, 40, 3385–3409. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, J.; Tian, Y.; Chen, H.; Sun, H.; Liu, K. A simple guidance template-based defect detection method for strip steel surfaces. IEEE Trans. Ind. Inform. 2018, 15, 2798–2809. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Zhang, X.; Yang, Z. Multi-view based template matching method for surface defect detection of circuit board. J. Phys. Conf. Ser. 2021, 1983, 012063. [Google Scholar] [CrossRef]
- Pastor-López, I.; Sanz, B.; de la Puerta, J.G.; Bringas, P.G. Surface defect modelling using co-occurrence matrix and fast fourier transformation. In Proceedings of the Hybrid Artificial Intelligent Systems: 14th International Conference, HAIS 2019, León, Spain, 4–6 September 2019. Proceedings 14. [Google Scholar]
- Wang, F.-l.; Zuo, B. Detection of surface cutting defect on magnet using Fourier image reconstruction. J. Cent. South Univ. 2016, 23, 1123–1131. [Google Scholar] [CrossRef]
- Rostami, B.; Shanehsazzadeh, F.; Fardmanesh, M. Fast fourier transform based NDT approach for depth detection of hidden defects using HTS rf-SQUID. IEEE Trans. Appl. Supercond. 2018, 28, 1–6. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, M.; Chen, Y.; Hu, N.; Gao, L.; Liu, L.; Ping, E.; Song, J.I. Surface defect detection method for air rudder based on positive samples. J. Intell. Manuf. 2024, 35, 95–113. [Google Scholar] [CrossRef]
- Zhang, Q.; Lai, J.; Zhu, J.; Xie, X. Wavelet-guided promotion-suppression transformer for surface-defect detection. IEEE Trans. Image Process. 2023, 32, 4517–4528. [Google Scholar] [CrossRef]
- Liu, H.; Ma, R.; Li, Y. Asphalt Pavement Image Segmentation Method Based on Optimized Markov Random Field. In Proceedings of the 2021 6th International Conference on Transportation Information and Safety (ICTIS), Wuhan, China, 22–24 October 2021. [Google Scholar]
- Xu, J.; Zuo, Z.; Wu, D.; Li, B.; Li, X.; Kong, D. Bearing Defect Detection with Unsupervised Neural Networks. Shock. Vib. 2021, 2021, 9544809. [Google Scholar] [CrossRef]
- Wu, Y.; Lu, Y. An intelligent machine vision system for detecting surface defects on packing boxes based on support vector machine. Meas. Control. 2019, 52, 1102–1110. [Google Scholar] [CrossRef]
- Ghiasi, R.; Khan, M.A.; Sorrentino, D.; Diaine, C.; Malekjafarian, A. An unsupervised anomaly detection framework for onboard monitoring of railway track geometrical defects using one-class support vector machine. Eng. Appl. Artif. Intell. 2024, 133, 108167. [Google Scholar] [CrossRef]
- Kumar, A.; Zhou, Y.; Gandhi, C.; Kumar, R.; Xiang, J. Bearing defect size assessment using wavelet transform based Deep Convolutional Neural Network (DCNN). Alex. Eng. J. 2020, 59, 999–1012. [Google Scholar] [CrossRef]
- Lu, M.; Mou, Y. Bearing defect classification algorithm based on autoencoder neural network. Adv. Civ. Eng. 2020, 2020, 6680315. [Google Scholar] [CrossRef]
- Lei, L.; Sun, S.; Zhang, Y.; Liu, H.; Xie, H. Segmented embedded rapid defect detection method for bearing surface defects. Machines 2021, 9, 40. [Google Scholar] [CrossRef]
- Ping, Z.; Chuangchuang, Z.; Gongbo, Z.; Zhenzhi, H.; Xiaodong, Y.; Shihao, W.; Meng, S.; Bing, H. Whole surface defect detection method for bearing rings based on machine vision. Meas. Sci. Technol. 2022, 34, 015017. [Google Scholar] [CrossRef]
- Jia, H.; Zhou, H.; Chen, Z.; Gao, R.; Lu, Y.; Yu, L. Research on Bearing Surface Scratch Detection Based on Improved YOLOV5. Sensors 2024, 24, 3002. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Chen, B.; Liu, B.; Yu, C.; Wang, L.; Wang, S. GRP-YOLOv5: An improved bearing defect detection algorithm based on YOLOv5. Sensors 2023, 23, 7437. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Song, Z.; Abdullahi, H.S.; Gao, S.; Zhang, H.; Zhou, L.; Li, Y. A Lightweight Detection Algorithm for Surface Defects in Small-Sized Bearings. Electronics 2024, 13, 2614. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, M.; Chen, X.; Zheng, C.; Wang, H. YOLOv8-LMG: An Improved Bearing Defect Detection Algorithm Based on YOLOv8. Processes 2024, 12, 930. [Google Scholar] [CrossRef]
- Nie, W.; Ju, Z. Lightweight bearing defect detection method based on collaborative attention and domain adaptive technology. J. Phys. Conf. Ser. 2024, 2858, 012018. [Google Scholar] [CrossRef]
- Han, T.; Dong, Q.; Wang, X.; Sun, L. BED-YOLO: An Enhanced YOLOv8 for High-Precision Real-Time Bearing Defect Detection. IEEE Trans. Instrum. Meas. 2024, 73, 1–13. [Google Scholar] [CrossRef]
- Li, J.; Cheng, M. FBS-YOLO: An improved lightweight bearing defect detection algorithm based on YOLOv8. Phys. Scr. 2025, 100, 025016. [Google Scholar] [CrossRef]
- Howard, A.G. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Ding, X.; Zhang, X.; Han, J.; Ding, G. Diverse branch block: Building a convolution as an inception-like unit. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Li, C.; Li, L.; Jiang, H.; Weng, K.; Geng, Y.; Li, L.; Ke, Z.; Li, Q.; Cheng, M.; Nie, W. YOLOv6: A single-stage object detection framework for industrial applications. arXiv 2022, arXiv:2209.02976. [Google Scholar]
- Wang, A.; Chen, H.; Liu, L.; Chen, K.; Lin, Z.; Han, J.; Ding, G. Yolov10: Real-time end-to-end object detection. arXiv 2024, arXiv:2405.14458. [Google Scholar]






| Black Spots | Scratches | Dents | Material Waste | Wear | |
|---|---|---|---|---|---|
| Number | 1049 | 1029 | 1023 | 1020 | 1027 |
| Training Set | Verification Set | Test Set | Total Quantity | |
|---|---|---|---|---|
| Black spots | 626 | 205 | 218 | 1049 |
| Scratches | 593 | 211 | 225 | 1029 |
| Dents | 610 | 204 | 209 | 1023 |
| Material waste | 620 | 206 | 194 | 1020 |
| Wear | 639 | 204 | 184 | 1027 |
| DSC | DBB | MCA | mAP | FPS | Parameters | GFlOPs | |
|---|---|---|---|---|---|---|---|
| Yolov8s | 95.4% | 128 | 11.13 M | 28.7 | |||
| DSC | √ | 95.9% | 131 | 9.74 M | 25.1 | ||
| DBB | √ | 96% | 113 | 12.11 M | 29.9 | ||
| CMA | √ | 96% | 124 | 11.81 M | 28.4 | ||
| DSC + DBB | √ | √ | 96.3% | 115 | 10.72 M | 26.6 | |
| DSC + CMA | √ | √ | 96.5% | 123 | 10.43 M | 25.7 | |
| DBB + CMA | √ | √ | 96.5% | 105 | 12.8 M | 30.5 | |
| Ours | √ | √ | √ | 96.9% | 106 | 11.41 M | 26.6 |
| Yolov5s | Yolov6s | Yolov8s | LSS-Yolov8s | Yolov10s | Our | |
|---|---|---|---|---|---|---|
| Black spots | 95.4% | 93.5% | 92.9% | 82.9% | 91.2% | 96.7% |
| Scratches | 96.2% | 99% | 97.3% | 92.3% | 94.5% | 98.5% |
| Dents | 88.4% | 84.9% | 88.5% | 87% | 86.9% | 90.4% |
| Material waste | 98.5% | 98.4% | 99.5% | 99.5% | 99% | 99.5% |
| Wear | 93.5% | 95.8% | 98.6% | 98.5% | 97.4% | 99.5% |
| P | 92.5% | 90.4% | 94.9% | 95.6% | 91.2% | 96.8% |
| R | 89.9% | 86% | 92.4% | 85.6% | 87.2% | 93.6% |
| mAP | 94.4% | 94.3% | 95.4% | 92% | 93.8% | 96.9% |
| FPS | 122 | 115 | 128 | 113 | 80 | 106 |
| Yolov5s | Yolov6s | Yolov8s | LSS-Yolov8s | Yolov10s | Our | |
|---|---|---|---|---|---|---|
| crazing | 38.7% | 35.8% | 42.9% | 37.8% | 35% | 42.3% |
| inclusion | 77.9% | 79.4% | 84.5% | 59.5% | 79.4% | 84.5% |
| patches | 89.8% | 90.3% | 94.2% | 63.8% | 88.7% | 93.8% |
| Pitted surface | 78% | 82.9% | 89.7% | 83.1% | 73.4% | 84.2% |
| rolled-in scale | 49.5% | 56.2% | 60.4% | 54.1% | 55.3% | 65.6% |
| scratches | 92.9% | 95.3% | 84.9% | 73.7% | 80.8% | 90.3% |
| mAP | 71.1% | 73.3% | 76.1% | 62% | 68.8% | 76.8% |
| FPS | 115 | 113 | 135 | 110 | 76 | 102 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liang, S.; Li, J.; Pan, H. Yolov8s-DDC: A Deep Neural Network for Surface Defect Detection of Bearing Ring. Electronics 2025, 14, 1079. https://doi.org/10.3390/electronics14061079
Zhang Y, Liang S, Li J, Pan H. Yolov8s-DDC: A Deep Neural Network for Surface Defect Detection of Bearing Ring. Electronics. 2025; 14(6):1079. https://doi.org/10.3390/electronics14061079
Chicago/Turabian StyleZhang, Yikang, Shijun Liang, Junfeng Li, and Haipeng Pan. 2025. "Yolov8s-DDC: A Deep Neural Network for Surface Defect Detection of Bearing Ring" Electronics 14, no. 6: 1079. https://doi.org/10.3390/electronics14061079
APA StyleZhang, Y., Liang, S., Li, J., & Pan, H. (2025). Yolov8s-DDC: A Deep Neural Network for Surface Defect Detection of Bearing Ring. Electronics, 14(6), 1079. https://doi.org/10.3390/electronics14061079






