An In-Depth Analysis of 2D and 3D Pose Estimation Techniques in Deep Learning: Methodologies and Advances
Abstract
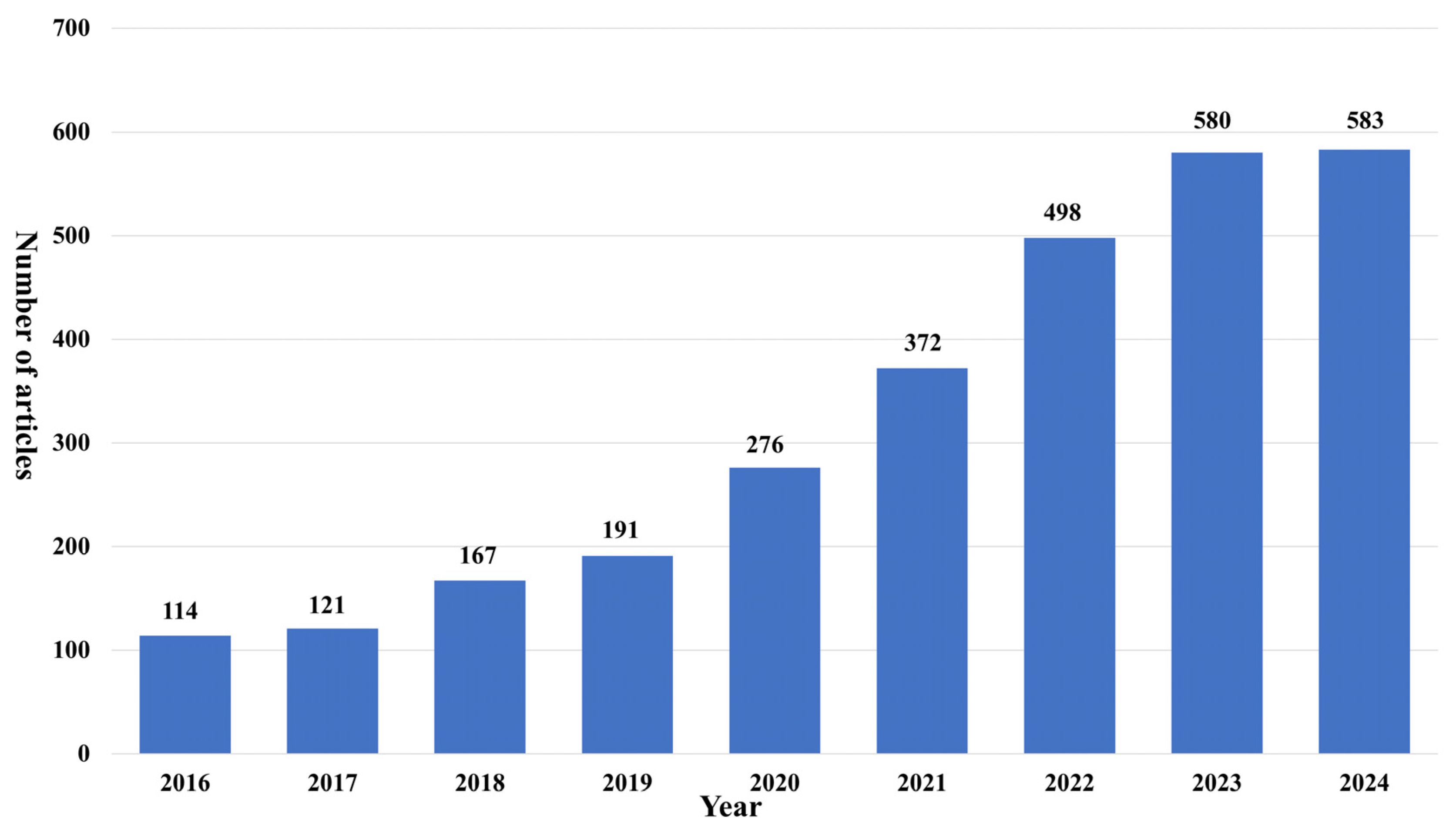
1. Introduction
- A comprehensive review of PE techniques, encompassing both 2D and 3D estimation, including single-view, multi-view, and dynamic video-based PE.
- An exhaustive summary of 2D and 3D datasets and evaluation metrics, offering detailed performance comparisons of prominent algorithms across standard datasets.
- An overview of practical applications in motion analysis, sports and training, human–computer interaction, entertainment and the arts, and health monitoring and rehabilitation.
- An in-depth analysis of various algorithms, examining their internal structures and application domains. This analysis highlights key challenges in PE and explores potential future developments based on practical application demands.
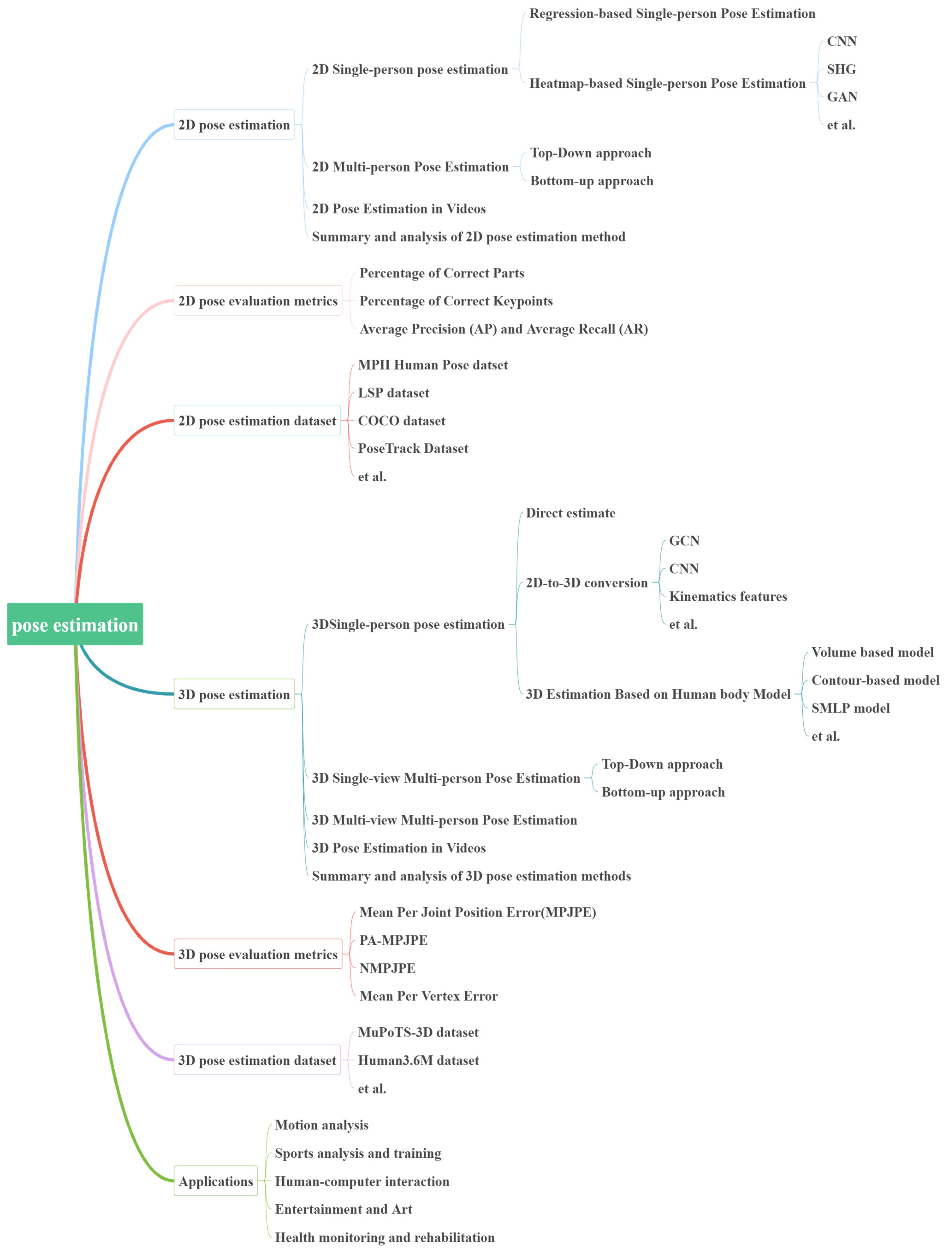
2. Two-Dimensional Pose Estimation
2.1. Two-Dimensional Single-Person Pose Estimation
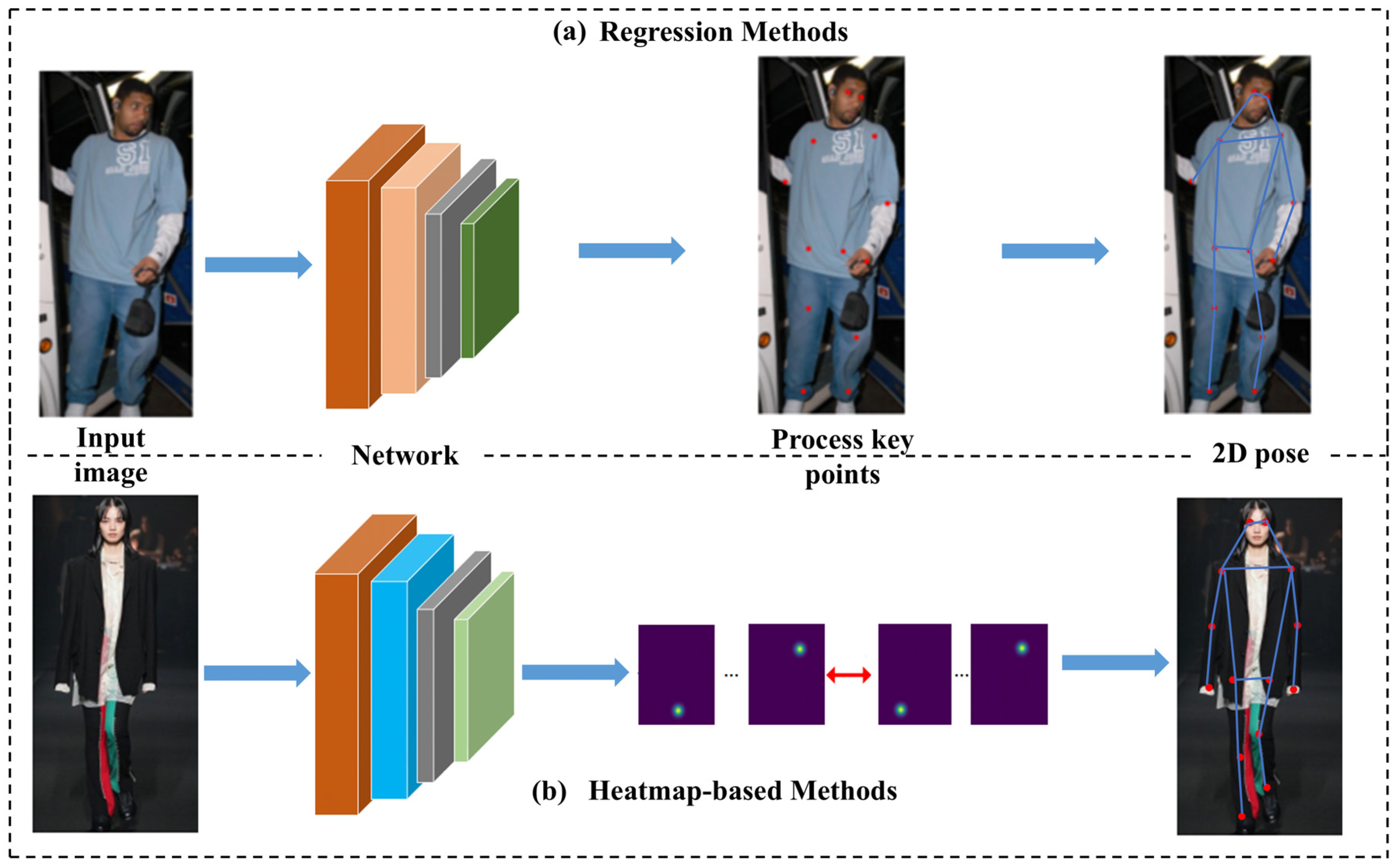
2.1.1. Regression-Based Single-Person Pose Estimation
2.1.2. Heatmap-Based Single-Person Pose Estimation
2.2. Two-Dimensional Multi-Person Pose Estimation
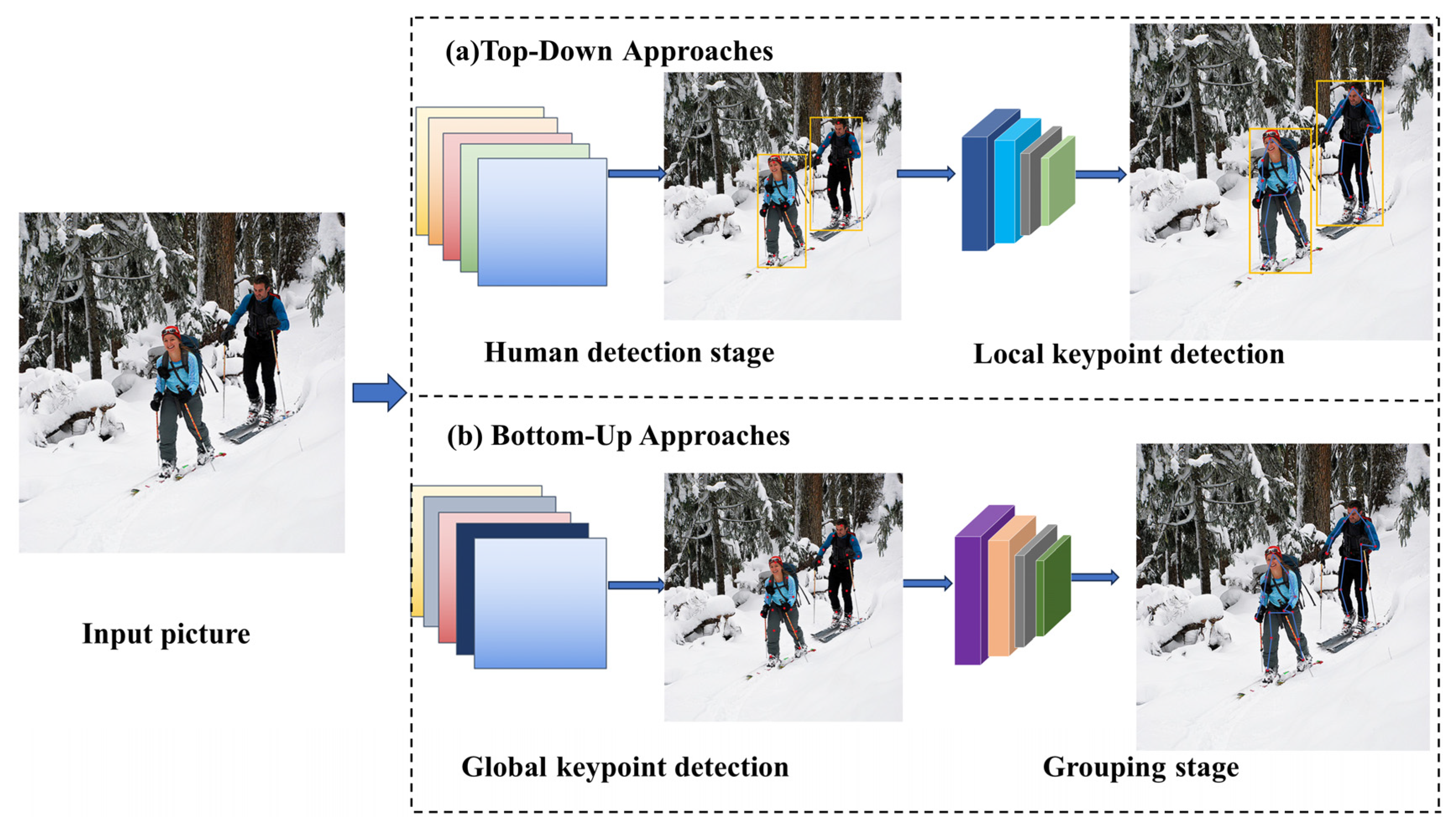
2.2.1. Top-Down Approach of Two-Dimensional Multi-Person Pose Estimation
2.2.2. Bottom-Up Approach of Two-Dimensional Multi-Person Pose Estimation
2.3. Two-Dimensional Pose Estimation in Videos
2.4. Summary and Analysis of 2D Pose Estimation Methods
3. Three-Dimensional Pose Estimation
3.1. 3D Single-Person Pose Estimation
3.1.1. Direct Estimation
3.1.2. Two-Dimensional-to-Three-Dimensional Conversion
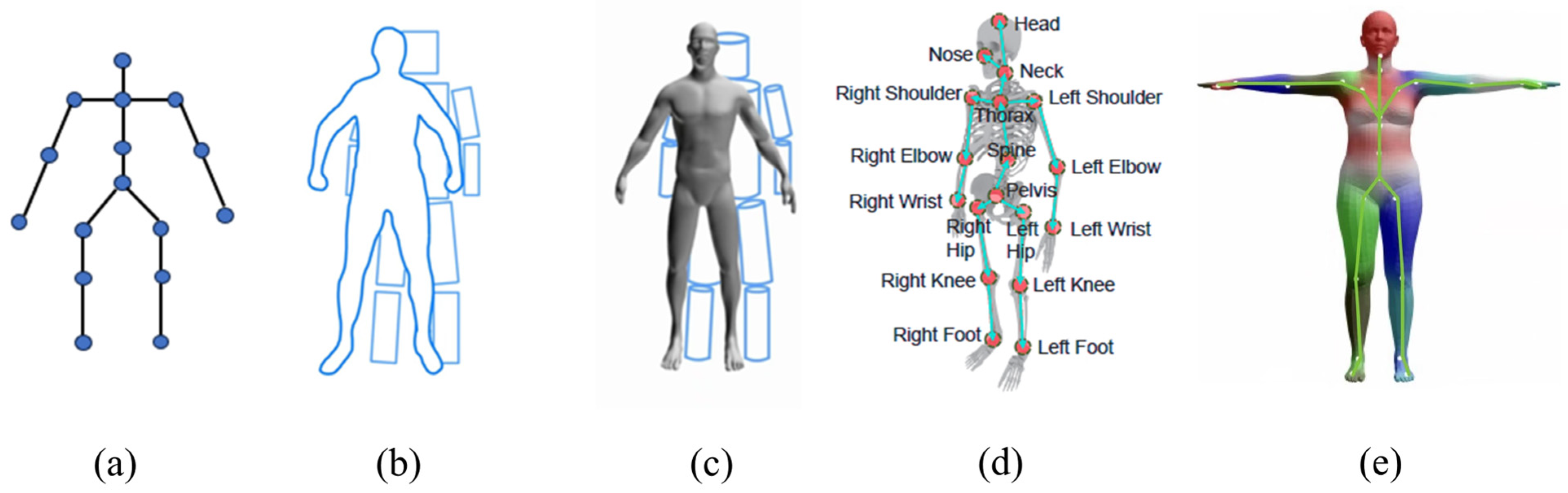
3.1.3. Three-Dimensional Estimation Based on Human Body Model
3.2. Three-Dimensional Single-View Multi-Person Pose Estimation
3.2.1. Top-Down Approach of Three-Dimensional Multi-Person Pose Estimation
3.2.2. Bottom-Up Approach of Three-Dimensional Multi-Person Pose Estimation
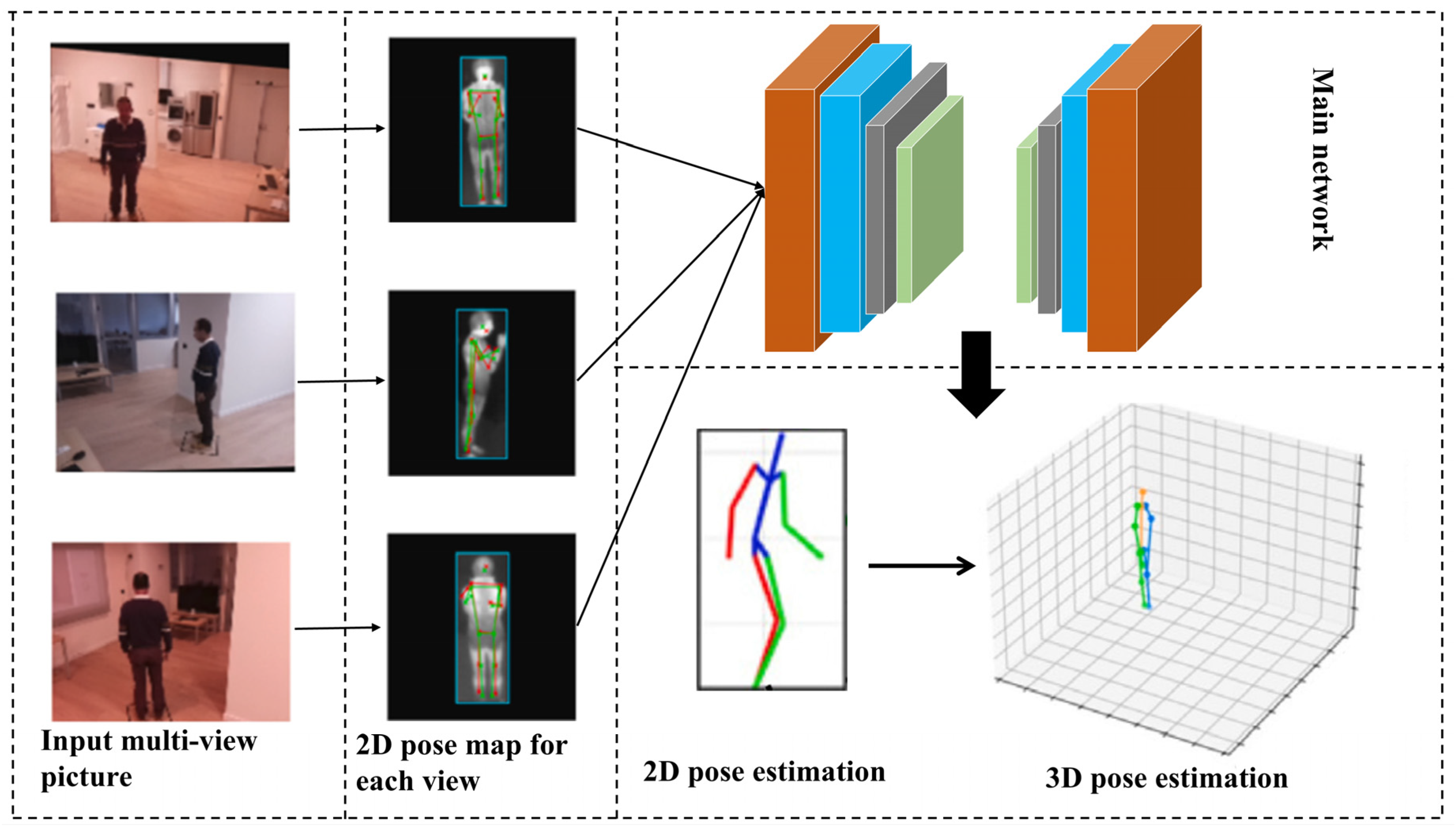
3.3. Three-Dimensional Multi-View Multi-Person Pose Estimation
3.4. Three-Dimensional Pose Estimation in Videos
3.5. Summary and Analysis of 3D Pose Estimation Methods
4. Evaluation Metrics, Datasets, and Comparative Analysis
4.1. Evaluation Metrics
4.1.1. Two-Dimensional Pose Evaluation Metrics
- Percentage of correct parts (PCP).
- 2.
- Percentage of correct keypoints (PCK).
- 3.
- Average precision (AP) and average recall (AR).
4.1.2. Three-Dimensional Pose Evaluation Metrics
- MPJPE (Mean Per Joint Position Error)
- 2.
- MPVE (Mean Per Vertex Error)
4.2. Dataset and Comparative Analysis
4.2.1. Two-Dimensional Datasets and Performance Comparison
4.2.2. Three-Dimensional Datasets and Performance Comparison
5. Practical Applications of Pose Estimation
- Motion analysis.
- 2.
- Sport analysis and training.
- 3.
- Human–computer interaction.
- 4.
- Entertainment and art.
- 5.
- Health monitoring and rehabilitation.
- 6.
- Performing arts.
6. Challenges, Outlook, and Conclusions
6.1. Challenges
- The problem of occlusion.
- 2.
- Not enough available data.
- 3.
- Computational efficiency and real-time performance.
6.2. Outlook
6.3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, X.; Geng, X.; Nie, G.; Wang, T.; Zhang, J.; You, J. Normative Evaluation Method of Long Jump Action Based on Human Pose Estimation. IEEE Access 2023, 11, 125452–125459. [Google Scholar] [CrossRef]
- Li, H.; Guo, H.; Huang, H. Analytical Model of Action Fusion in Sports Tennis Teaching by Convolutional Neural Networks. Comput. Intell. Neurosci. 2022, 2022, 7835241. [Google Scholar] [PubMed]
- Du, W.; Wang, Y.; Qiao, Y. Rpan: An end-to-end recurrent pose-attention network for action recognition in videos. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Wei, L.; Yu, X.; Liu, Z. Human pose estimation in crowded scenes using Keypoint Likelihood Variance Reduction. Displays 2024, 83, 102675. [Google Scholar]
- Juraev, S.; Ghimire, A.; Alikhanov, J.; Kakani, V.; Kim, H. Exploring Human Pose Estimation and the Usage of Synthetic Data for Elderly Fall Detection in Real-World Surveillance. IEEE Access 2022, 10, 94249–94261. [Google Scholar]
- Yu, X.; Zhang, X.; Xu, C.; Ou, L. Human-robot collaborative interaction with human perception and action recognition. Neurocomputing 2024, 563, 126827. [Google Scholar]
- Weng, C.-Y.; Curless, B.; Kemelmacher-Shlizerman, I. Photo wake-up: 3d character animation from a single photo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Lan, G.; De Vries, L.; Wang, S. Evolving efficient deep neural networks for real-time object recognition. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Zhou, D.; He, Q. PoSeg: Pose-Aware Refinement Network for Human Instance Segmentation. IEEE Access 2020, 8, 15007–15016. [Google Scholar]
- Niu, Z.; Lu, K.; Xue, J.; Wang, J. Skeleton Cluster Tracking for robust multi-view multi-person 3D human pose estimation. Comput. Vis. Image Underst. 2024, 246, 104059. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; Springer: Berlin/Heidelberg, Germany, 2012; p. 25. [Google Scholar]
- Toshev, A.; Szegedy, C. DeepPose: Human Pose Estimation via Deep Neural Networks. In Proceedings of the 27th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Mehta, D.; Sridhar, S.; Sotnychenko, O.; Rhodin, H.; Shafiei, M.; Seidel, H.P.; Theobalt, C. VNect: Real-time 3D Human Pose Estimation with a Single RGB Camera. ACM Trans. Graph. 2017, 36, 1–14. [Google Scholar]
- Poppe, R. Vision-based human motion analysis: An overview. Comput. Vis. Image Underst. 2007, 108, 4–18. [Google Scholar]
- Yue, R.; Tian, Z.; Du, S. Action recognition based on RGB and skeleton data sets: A survey. Neurocomputing 2022, 512, 287–306. [Google Scholar]
- Wang, C.; Yan, J. A Comprehensive Survey of RGB-Based and Skeleton-Based Human Action Recognition. IEEE Access 2023, 11, 53880–53898. [Google Scholar]
- Liu, Z.; Zhu, J.; Bu, J.; Chen, C. A survey of human pose estimation: The body parts parsing based methods. J. Vis. Commun. Image Represent. 2015, 32, 10–19. [Google Scholar] [CrossRef]
- Gong, W.; Zhang, X.; Gonzàlez, J.; Sobral, A.; Bouwmans, T.; Tu, C.; Zahzah, E.-H. Human Pose Estimation from Monocular Images: A Comprehensive Survey. Sensors 2016, 16, 1966. [Google Scholar] [CrossRef] [PubMed]
- Munea, T.L.; Jembre, Y.Z.; Weldegebriel, H.T.; Chen, L.; Huang, C.; Yang, C. The Progress of Human Pose Estimation: A Survey and Taxonomy of Models Applied in 2D Human Pose Estimation. IEEE Access 2020, 8, 133330–133348. [Google Scholar]
- Dang, Q.; Yin, J.; Wang, B.; Zheng, W. Deep Learning Based 2D Human Pose Estimation: A Survey. Tsinghua Sci. Technol. 2019, 24, 663–676. [Google Scholar]
- El Kaid, A.; Baina, K. A Systematic Review of Recent Deep Learning Approaches for 3D Human Pose Estimation. J. Imaging 2023, 9, 275. [Google Scholar] [CrossRef]
- Wang, J.; Tan, S.; Zhen, X.; Xu, S.; Zheng, F.; He, Z.; Shao, L. Deep 3D human pose estimation: A review. Comput. Vis. Image Underst. 2021, 210, 103225. [Google Scholar]
- Sarafianos, N.; Boteanu, B.; Ionescu, B.; Kakadiaris, I.A. 3D Human pose estimation: A review of the literature and analysis of covariates. Comput. Vis. Image Underst. 2016, 152, 1–20. [Google Scholar]
- Liu, W.; Bao, Q.; Sun, Y.; Mei, T. Recent Advances of Monocular 2D and 3D Human Pose Estimation: A Deep Learning Perspective. Acm Comput. Surv. 2023, 55, 1–41. [Google Scholar]
- Chen, Y.; Tian, Y.; He, M. Monocular human pose estimation: A survey of deep learning-based methods. Comput. Vis. Image Underst. 2020, 192, 102897. [Google Scholar]
- Sun, X.; Xiao, B.; Wei, F.; Liang, S.; Wei, Y. Integral Human Pose Regression. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- He, K.M.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 27–30 June 2016. [Google Scholar]
- Gu, K.; Yang, L.; Mi, M.B.; Yao, A. Bias-Compensated Integral Regression for Human Pose Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10687–10702. [Google Scholar] [PubMed]
- Su, S.; She, B.; Zhu, Y.; Fang, X.; Xu, Y. RCENet: An efficient pose estimation network based on regression correction. Multimed. Syst. 2024, 30, 1–13. [Google Scholar]
- Kumar, P.; Chauhan, S. Towards improvement of baseline performance for regression based human pose estimation. Evol. Syst. 2024, 15, 659–667. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Tompson, J.; Goroshin, R.; Jain, A.; LeCun, Y.; Bregler, C. Efficient Object Localization Using Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Newell, A.; Yang, K.; Deng, J. Stacked Hourglass Networks for Human Pose Estimation. In Proceedings of the 14th European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Zou, X.; Bi, X.; Yu, C. Improving Human Pose Estimation Based on Stacked Hourglass Network. Neural Process. Lett. 2023, 55, 9521–9544. [Google Scholar]
- Dong, X.; Yu, J.; Zhang, J. Joint usage of global and local attentions in hourglass network for human pose estimation. Neurocomputing 2022, 472, 95–102. [Google Scholar]
- Kamel, A.; Sheng, B.; Li, P.; Kim, J.; Feng, D.D. Hybrid Refinement-Correction Heatmaps for Human Pose Estimation. IEEE Trans. Multimed. 2021, 23, 1330–1342. [Google Scholar]
- Kim, S.-T.; Lee, H.J. Lightweight Stacked Hourglass Network for Human Pose Estimation. Appl. Sci. 2020, 10, 6497. [Google Scholar] [CrossRef]
- Qin, X.; Guo, H.; He, C.; Zhang, X. Lightweight human pose estimation: CVC-net. Multimed. Tools Appl. 2022, 81, 17615–17637. [Google Scholar]
- Yang, W.; Li, S.; Ouyang, W.; Li, H.; Wang, X. Learning Feature Pyramids for Human Pose Estimation. In Proceedings of the 16th IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the 28th Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Chen, Y.; Shen, C.; Wei, X.; Liu, L.; Yang, J. Adversarial PoseNet: A Structure-aware Convolutional Network for Human Pose Estimation. In Proceedings of the 16th IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Zhu, A.; Zhang, S.; Huang, Y.; Hu, F.; Cui, R.; Hua, G. Exploring hard joints mining via hourglass-based generative adversarial network for human pose estimation. AIP Adv. 2019, 9, 035321. [Google Scholar]
- Tian, L.; Wang, P.; Liang, G.; Shen, C. An adversarial human pose estimation network injected with graph structure. Pattern Recognit. 2021, 115, 107863. [Google Scholar]
- Malakshan, S.R.; Saadabadi, M.S.E.; Mostofa, M.; Soleymani, S.; Nasrabadi, N.M. Joint Super-Resolution and Head Pose Estimation for Extreme Low-Resolution Faces. IEEE Access 2023, 11, 11238–11253. [Google Scholar] [CrossRef]
- Xiao, B.; Wu, H.; Wei, Y. Simple Baselines for Human Pose Estimation and Tracking. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Chen, K.; Wu, Z.; Huang, J.; Su, Y. Self-Attention Mechanism-Based Head Pose Estimation Network with Fusion of Point Cloud and Image Features. Sensors 2023, 23, 9894. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Tong, J.; Wang, R.J.N.P.L. Attention refined network for human pose estimation. Neural Process. Lett. 2021, 53, 2853–2872. [Google Scholar] [CrossRef]
- Wang, J.; Long, X.; Gao, Y.; Ding, E.; Wen, S. Graph-pcnn: Two stage human pose estimation with graph pose refinement. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XI 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Cai, Y.; Wang, Z.; Luo, Z.; Yin, B.; Du, A.; Wang, H.; Sun, J. Learning delicate local representations for multi-person pose estimation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part III 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Xu, L.; Jin, S.; Liu, W.; Qian, C.; Ouyang, W.; Luo, P.; Wang, X. ZoomNAS: Searching for Whole-Body Human Pose Estimation in the Wild. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 5296–5313. [Google Scholar]
- Artacho, B.; Savakis, A. UniPose plus: A Unified Framework for 2D and 3D Human Pose Estimation in Images and Videos. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 9641–9653. [Google Scholar] [CrossRef]
- Wang, J.; Sun, K.; Cheng, T.; Jiang, B.; Deng, C.; Zhao, Y.; Liu, D.; Mu, Y.; Tan, M.; Wang, X.; et al. Deep High-Resolution Representation Learning for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3349–3364. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, X.; He, M.; Jin, L.; Song, M.; Zhao, J. A Compact and Powerful Single-Stage Network for Multi-Person Pose Estimation. Electronics 2023, 12, 857. [Google Scholar] [CrossRef]
- Cheng, Y.; Ai, Y.; Wang, B.; Wang, X.; Tan, R.T. Bottom-up 2D pose estimation via dual anatomical centers for small-scale persons. Pattern Recognit. 2023, 139, 109403. [Google Scholar] [CrossRef]
- Newell, A.; Huang, Z.; Deng, J. Associative embedding: End-to-end learning for joint detection and grouping. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Jin, S.; Liu, W.; Xie, E.; Wang, W.; Qian, C.; Ouyang, W.; Luo, P. Differentiable hierarchical graph grouping for multi-person pose estimation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part VII 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Zeng, Q.; Hu, Y.; Li, D.; Sun, D. Multi-person pose estimation based on graph grouping optimization. Multimed. Tools Appl. 2023, 82, 7039–7053. [Google Scholar] [CrossRef]
- Jin, L.; Wang, X.; Nie, X.; Liu, L.; Guo, Y.; Zhao, J. Grouping by Center: Predicting Centripetal Offsets for the Bottom-up Human Pose Estimation. IEEE Trans. Multimed. 2023, 25, 3364–3374. [Google Scholar]
- Chen, X.; Yang, G. Multi-person pose estimation with limb detection heatmaps. In Proceedings of the 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018. [Google Scholar]
- Luo, Y.; Ren, J.; Wang, Z.; Sun, W.; Pan, J.; Liu, J.; Lin, L. LSTM Pose Machines. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Nie, X.; Li, Y.; Luo, L.; Zhang, N.; Feng, J. Dynamic kernel distillation for efficient pose estimation in videos. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Lee, J.; Kim, T.-Y.; Beak, S.; Moon, Y.; Jeong, J. Real-Time Pose Estimation Based on ResNet-50 for Rapid Safety Prevention and Accident Detection for Field Workers. Electronics 2023, 12, 3513. [Google Scholar] [CrossRef]
- Bertasius, G.; Feichtenhofer, C.; Tran, D.; Shi, J.; Torresani, L. Learning temporal pose estimation from sparsely-labeled videos. Adv. Neural Inf. Process. Syst. 2019, 32, 3027–3038. [Google Scholar]
- Dong, X.; Wang, X.; Li, B.; Wang, H.; Chen, G.; Cai, M. YH-Pose: Human pose estimation in complex coal mine scenarios. Eng. Appl. Artif. Intell. 2024, 127, 107338. [Google Scholar]
- Liu, H.; Liu, W.; Chi, Z.; Wang, Y.; Yu, Y.; Chen, J.; Tang, J. Fast Human Pose Estimation in Compressed Videos. IEEE Trans. Multimed. 2023, 25, 1390–1400. [Google Scholar]
- Liu, Z.; Feng, R.; Chen, H.; Wu, S.; Gao, Y.; Gao, Y.; Wang, X. Temporal feature alignment and mutual information maximization for video-based human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21–24 June 2022. [Google Scholar]
- Zhou, Q.; Shi, H.; Xiang, W.; Kang, B.; Latecki, L.J. DPNet: Dual-Path Network for Real-Time Object Detection with Lightweight Attention. IEEE Trans. Neural Netw. Learn. Syst. 2024, 25, 1390–1400. [Google Scholar]
- Ravi, N.; Gabeur, V.; Hu, Y.T.; Hu, R.; Ryali, C.; Ma, T.; Feichtenhofer, C. Sam 2: Segment anything in images and videos. arXiv 2024, arXiv:2408.00714. [Google Scholar]
- Chen, Y.; Wang, Z.; Peng, Y.; Zhang, Z.; Yu, G.; Sun, J. Cascaded Pyramid Network for Multi-Person Pose Estimation. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Li, S.; Chan, A.B. 3D Human Pose Estimation from Monocular Images with Deep Convolutional Neural Network. In Proceedings of the 12th Asian Conference on Computer Vision (ACCV), Singapore, 1–5 November 2014. [Google Scholar]
- Liang, S.; Sun, X.; Wei, Y. Compositional Human Pose Regression. Comput. Vis. Image Underst. 2018, 176, 1–8. [Google Scholar]
- Luvizon, D.C.; Picard, D.; Tabia, H. 2D/3D Pose Estimation and Action Recognition using Multitask Deep Learning. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Nibali, A.; He, Z.; Morgan, S.; Prendergast, L. 3d human pose estimation with 2d marginal heatmaps. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Pavlakos, G.; Zhou, X.; Derpanis, K.G.; Daniilidis, K. Coarse-to-Fine Volumetric Prediction for Single-Image 3D Human Pose. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 22–25 July 2017. [Google Scholar]
- Pavlakos, G.; Zhou, X.; Daniilidis, K. Ordinal Depth Supervision for 3D Human Pose Estimation. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Martinez, J.; Hossain, R.; Romero, J.; Little, J.J. A simple yet effective baseline for 3d human pose estimation. In Proceedings of the 16th IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Chen, C.-H.; Ramanan, D. 3D Human Pose Estimation=2D Pose Estimation plus Matching. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 22–25 July 2017. [Google Scholar]
- Hwang, T.; Kim, J.; Kim, M. A Distributed Real-time 3D Pose Estimation Framework based on Asynchronous Multiviews. Br. Ksii Trans. Internet Inf. Syst. 2023, 17, 559–575. [Google Scholar]
- Yang, J.; Ma, Y.; Zuo, X.; Wang, S.; Gong, M.; Cheng, L. 3D pose estimation and future motion prediction from 2D images. Pattern Recognit. 2022, 124, 108439. [Google Scholar]
- Ghafoor, M.; Mahmood, A. Quantification of Occlusion Handling Capability of a 3D Human Pose Estimation Framework. IEEE Trans. Multimed. 2023, 25, 3311–3318. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, D. A CNN-based 3D human pose estimation based on projection of depth and ridge data. Pattern Recognit. 2020, 106, 107462. [Google Scholar] [CrossRef]
- Yan, J.; Zhou, M.L.; Fang, B.; Xu, K. 3D Human Pose Estimation via Spatio-Temporal Matching from Monocular RGB Images. Int. J. Pattern Recognit. Artif. Intell. 2022, 36, 2255017. [Google Scholar] [CrossRef]
- Zou, L.; Huang, Z.; Gu, N.; Wang, F.; Yang, Z.; Wang, G. GMDN: A lightweight graph-based mixture density network for 3D human pose regression. Comput. Graph. 2021, 95, 115–122. [Google Scholar] [CrossRef]
- Yu, B.; Huang, Y.; Cheng, G.; Huang, D.; Ding, Y. Graph U-Shaped Network with Mapping-Aware Local Enhancement for Single-Frame 3D Human Pose Estimation. Electronics 2023, 12, 4120. [Google Scholar] [CrossRef]
- Hua, G.; Liu, H.; Li, W.; Zhang, Q.; Ding, R.; Xu, X. Weakly-Supervised 3D Human Pose Estimation with Cross-View U-Shaped Graph Convolutional Network. IEEE Trans. Multimed. 2023, 25, 1832–1843. [Google Scholar] [CrossRef]
- Wang, H.; Bai, B.; Li, J.; Ke, H.; Xiang, W. 3D human pose estimation method based on multi-constrained dilated convolutions. Multimed. Syst. 2024, 30, 1–17. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Q. Relation-balanced graph convolutional network for 3D human pose estimation. Image Vis. Comput. 2023, 140, 104841. [Google Scholar] [CrossRef]
- Wu, Y.; Kong, D.; Wang, S.; Li, J.; Yin, B. HPGCN: Hierarchical poselet-guided graph convolutional network for 3D pose estimation. Neurocomputing 2022, 487, 243–256. [Google Scholar] [CrossRef]
- Zanfir, A.; Bazavan, E.G.; Xu, H.; Freeman, W.T.; Sukthankar, R.; Sminchisescu, C. Weakly supervised 3d human pose and shape reconstruction with normalizing flows. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part VI 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Xu, J.; Yu, Z.; Ni, B.; Yang, J.; Yang, X.; Zhang, W. Deep kinematics analysis for monocular 3d human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Jiang, L.; Wang, Y.; Li, W. Regress 3D human pose from 2D skeleton with kinematics knowledge. Electron. Res. Arch. 2023, 31, 1485–1497. [Google Scholar] [CrossRef]
- Liao, X.; Dong, J.; Song, K.; Xiao, J. Three-Dimensional Human Pose Estimation from Sparse IMUs through Temporal Encoder and Regression Decoder. Sensors 2023, 23, 3547. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, Z.; Han, Y.; Meng, H.; Yang, M.; Rajasegarar, S. Deep learning-based real-time 3D human pose estimation. Eng. Appl. Artif. Intell. 2023, 119, 105813. [Google Scholar]
- Martini, E.; Boldo, M.; Bombieri, N. FLK: A filter with learned kinematics for real-time 3D human pose estimation. Signal Process. 2024, 224, 109598. [Google Scholar] [CrossRef]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A Skinned Multi-Person Linear Model. ACM Trans. Graph. 2015, 34, 851–866. [Google Scholar]
- Zhou, K.; Han, X.; Jiang, N.; Jia, K.; Lu, J. HEMlets PoSh: Learning Part-Centric Heatmap Triplets for 3D Human Pose and Shape Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3000–3014. [Google Scholar]
- Gilbert, A.; Trumble, M.; Malleson, C.; Hilton, A.; Collomosse, J. Fusing Visual and Inertial Sensors with Semantics for 3D Human Pose Estimation. Int. J. Comput. Vis. 2019, 127, 381–397. [Google Scholar] [CrossRef]
- Zheng, C.; Mendieta, M.; Wang, P.; Lu, A.; Chen, C. A lightweight graph transformer network for human mesh reconstruction from 2d human pose. In Proceedings of the 30th ACM international Conference on Multimedia, Lisbon, Portugal, 10–14 October 2022. [Google Scholar]
- Choi, H.; Moon, G.; Lee, K.M. Pose2mesh: Graph convolutional network for 3d human pose and mesh recovery from a 2d human pose. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part VII 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Zhang, Y.; Wang, C.; Wang, X.; Liu, W.; Zeng, W. VoxelTrack: Multi-Person 3D Human Pose Estimation and Tracking in the Wild. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 2613–2626. [Google Scholar]
- Zhang, H.; Tian, Y.; Zhou, X.; Ouyang, W.; Liu, Y.; Wang, L.; Sun, Z. Pymaf: 3d human pose and shape regression with pyramidal mesh alignment feedback loop. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021. [Google Scholar]
- Xu, X.; Chen, H.; Moreno-Noguer, F.; Jeni, L.A.; De la Torre, F. 3d human shape and pose from a single low-resolution image with self-supervised learning. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part IX 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Li, J.; Xu, C.; Chen, Z.; Bian, S.; Yang, L.; Lu, C. Hybrik: A hybrid analytical-neural inverse kinematics solution for 3d human pose and shape estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Wang, S.; Leroy, V.; Cabon, Y.; Chidlovskii, B.; Revaud, J. Dust3r: Geometric 3d vision made easy. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 11–15 June 2024. [Google Scholar]
- Heo, J.; Hu, G.; Wang, Z.; Yeung-Levy, S. DeforHMR: Vision Transformer with Deformable Cross-Attention for 3D Human Mesh Recovery. arXiv 2024, arXiv:2411.11214. [Google Scholar]
- Stathopoulos, A.; Han, L.; Metaxas, D. Score-guided diffusion for 3d human recovery. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024. [Google Scholar]
- Xie, P.; Xu, W.; Tang, T.; Yu, Z.; Lu, C. MS-MANO: Enabling hand pose tracking with biomechanical constraints. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024. [Google Scholar]
- Sárándi, I.; Pons-Moll, G.J.A.P.A. Neural Localizer Fields for Continuous 3D Human Pose and Shape Estimation. Adv. Neural Inf. Process. Syst. 2025, 37, 140032–140065. [Google Scholar]
- Cai, Z.; Yin, W.; Zeng, A.; Wei, C.; Sun, Q.; Yanjun, W.; Liu, Z. Smpler-x: Scaling up expressive human pose and shape estimation. Adv. Neural Inf. Process. Syst. 2023, 36, 11454–11468. [Google Scholar]
- Choutas, V.; Pavlakos, G.; Bolkart, T.; Tzionas, D.; Black, M.J. Monocular expressive body regression through body-driven attention. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part X 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Lassner, C.; Romero, J.; Kiefel, M.; Bogo, F.; Black, M.J.; Gehler, P.V. Unite the People: Closing the Loop Between 3D and 2D Human Representations. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Kolotouros, N.; Pavlakos, G.; Black, M.; Daniilidis, K. Learning to reconstruct 3D human pose and shape via model-fitting in the loop. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Madadi, M.; Bertiche, H.; Escalera, S. SMPLR: Deep learning based SMPL reverse for 3D human pose and shape recovery. Pattern Recognit. 2020, 106, 107472. [Google Scholar]
- Xu, X.; Liu, L.; Yan, S. SMPLer: Taming Transformers for Monocular 3D Human Shape and Pose Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 3275–3289. [Google Scholar] [PubMed]
- Kolotouros, N.; Pavlakos, G.; Daniilidis, K. Convolutional mesh regression for single-image human shape reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Mahmood, N.; Ghorbani, N.; Troje, N.F.; Pons-Moll, G.; Black, M.J. AMASS: Archive of motion capture as surface shapes. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Baradel, F.; Armando, M.; Galaaoui, S.; Brégier, R.; Weinzaepfel, P.; Rogez, G.; Lucas, T. Multi-hmr: Multi-person whole-body human mesh recovery in a single shot. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Wang, H.; Güler, R.A.; Kokkinos, I.; Papandreou, G.; Zafeiriou, S. BLSM: A bone-level skinned model of the human mesh. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part V 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Cheng, Y.; Yang, B.; Wang, B.; Yan, W.; Tan, R.T. Occlusion-aware networks for 3d human pose estimation in video. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Xiang, D.; Joo, H.; Sheikh, Y. Monocular total capture: Posing face, body, and hands in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Dwivedi, S.K.; Sun, Y.; Patel, P.; Feng, Y.; Black, M.J. Tokenhmr: Advancing human mesh recovery with a tokenized pose representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 17–21 June 2024. [Google Scholar]
- Song, Y.; Zhou, H. 3D Human Mesh Recovery with Learned Gradient. 2024; in press. [Google Scholar]
- Patel, P.; Black, M.J.J.A.P.A. CameraHMR: Aligning People with Perspective. arXiv 2024, arXiv:2411.08128. [Google Scholar]
- Zhang, Y.; Nie, L.J.S.R. Human motion similarity evaluation based on deep metric learning. Sci. Rep. 2024, 14, 30908. [Google Scholar]
- Rogez, G.; Weinzaepfel, P.; Schmid, C. LCR-Net: Localization-Classification-Regression for Human Pose. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 22–25 July 2017. [Google Scholar]
- Rogez, G.; Weinzaepfel, P.; Schmid, C. LCR-Net plus plus: Multi-Person 2D and 3D Pose Detection in Natural Images. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 1146–1161. [Google Scholar]
- Seo, K.; Cho, H.; Choi, D.; Heo, T. Stereo Feature Learning Based on Attention and Geometry for Absolute Hand Pose Estimation in Egocentric Stereo Views. IEEE Access 2021, 9, 116083–116093. [Google Scholar]
- Moon, G.; Chang, J.Y.; Lee, K.M. Camera distance-aware top-down approach for 3d multi-person pose estimation from a single rgb image. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- El Kaid, A.; Brazey, D.; Barra, V.; Baïna, K. Top-Down System for Multi-Person 3D Absolute Pose Estimation from Monocular Videos. Sensors 2022, 22, 4109. [Google Scholar] [CrossRef]
- Shen, T.; Li, D.; Wang, F.-Y.; Huang, H. Depth-Aware Multi-Person 3D Pose Estimation with Multi-Scale Waterfall Representations. IEEE Trans. Multimed. 2023, 25, 1439–1451. [Google Scholar]
- Paudel, P.; Kwon, Y.-J.; Kim, D.-H.; Choi, K.-H. Industrial Ergonomics Risk Analysis Based on 3D-Human Pose Estimation. Electronics 2022, 11, 3403. [Google Scholar] [CrossRef]
- Zhen, J.; Fang, Q.; Sun, J.; Liu, W.; Jiang, W.; Bao, H.; Zhou, X. Smap: Single-shot multi-person absolute 3d pose estimation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XV 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Mehta, D.; Sotnychenko, O.; Mueller, F.; Xu, W.; Elgharib, M.; Fua, P.; Theobalt, C. XNect: Real-time Multi-Person 3D Motion Capture with a Single RGB Camera. ACM Trans. Graph. 2020, 39, 17. [Google Scholar]
- Vasileiadis, M.; Bouganis, C.-S.; Tzovaras, D. Multi-person 3D pose estimation from 3D cloud data using 3D convolutional neural networks. Comput. Vis. Image Underst. 2019, 185, 12–23. [Google Scholar]
- Fabbri, M.; Lanzi, F.; Calderara, S.; Alletto, S.; Cucchiara, R. Compressed volumetric heatmaps for multi-person 3d pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Li, M.; Zhou, Z.; Liu, X. 3D hypothesis clustering for cross-view matching in multi-person motion capture. Comput. Vis. Media 2020, 6, 147–156. [Google Scholar] [CrossRef]
- Omran, M.; Lassner, C.; Pons-Moll, G.; Gehler, P.; Schiele, B. Neural Body Fitting: Unifying Deep Learning and Model Based Human Pose and Shape Estimation. In Proceedings of the 6th International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018. [Google Scholar]
- Tian, Y.; Hu, W.; Jiang, H.; Wu, J. Densely connected attentional pyramid residual network for human pose estimation. Neurocomputing 2019, 347, 13–23. [Google Scholar]
- Cheng, Y.; Wang, B.; Tan, R.T.T. Dual Networks Based 3D Multi-Person Pose Estimation from Monocular Video. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 1636–1651. [Google Scholar] [CrossRef]
- Rhodin, H.; Spörri, J.; Katircioglu, I.; Constantin, V.; Meyer, F.; Müller, E.; Fua, P. Learning Monocular 3D Human Pose Estimation from Multi-view Images. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Rhodin, H.; Salzmann, M.; Fua, P. Unsupervised Geometry-Aware Representation for 3D Human Pose Estimation. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 12 June 2018. [Google Scholar]
- Dong, J.; Jiang, W.; Huang, Q.; Bao, H.; Zhou, X. Fast and robust multi-person 3d pose estimation from multiple views. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Tian, L.; Cheng, X.; Honda, M.; Ikenaga, T. Multi-view 3D human pose reconstruction based on spatial confidence point group for jump analysis in figure skating. Complex Intell. Syst. 2023, 9, 865–879. [Google Scholar]
- Lupion, M.; Polo-Rodríguez, A.; Medina-Quero, J.; Sanjuan, J.F.; Ortigosa, P.M. 3D Human Pose Estimation from multi-view thermal vision sensors. Inf. Fusion 2024, 104, 102154. [Google Scholar]
- Ershadi-Nasab, S.; Kasaei, S.; Sanaei, E. Uncalibrated multi-view multiple humans association and 3D pose estimation by adversarial learning. Multimed. Tools Appl. 2021, 80, 2461–2488. [Google Scholar]
- Wang, H.; Sun, M.-H.; Zhang, H.; Dong, L.-Y. LHPE-nets: A lightweight 2D and 3D human pose estimation model with well-structural deep networks and multi-view pose sample simplification method. PLoS ONE 2022, 17, e0264302. [Google Scholar]
- Zhang, Y.; Zhang, J.; Xu, S.; Xiao, J. Multi-view human pose and shape estimation via mesh-aligned voxel interpolation. Inf. Fusion 2025, 114, 102651. [Google Scholar]
- Wang, J.; Yan, S.; Xiong, Y.; Lin, D. Motion guided 3d pose estimation from videos. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Liu, R.; Shen, J.; Wang, H.; Chen, C.; Cheung, S.-C.; Asari, V. Attention mechanism exploits temporal contexts: Real-time 3d human pose reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Dabral, R.; Mundhada, A.; Kusupati, U.; Afaque, S.; Sharma, A.; Jain, A. Learning 3D Human Pose from Structure and Motion. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Li, Z.; Wang, X.; Wang, F.; Jiang, P. On boosting single-frame 3d human pose estimation via monocular videos. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Pavllo, D.; Feichtenhofer, C.; Grangier, D.; Auli, M. 3d human pose estimation in video with temporal convolutions and semi-supervised training. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Hong, J.W.; Yoon, S.; Kim, J.; Yoo, C.D. Joint Path Alignment Framework for 3D Human Pose and Shape Estimation from Video. IEEE Access 2023, 11, 43267–43275. [Google Scholar]
- Hossain, M.R.I.; Little, J.J. Exploiting Temporal Information for 3D Human Pose Estimation. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Chen, T.; Fang, C.; Shen, X.; Zhu, Y.; Chen, Z.; Luo, J. Anatomy-Aware 3D Human Pose Estimation with Bone-Based Pose Decomposition. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 198–209. [Google Scholar] [CrossRef]
- Zhang, J.; Gong, K.; Wang, X.; Feng, J. Learning to Augment Poses for 3D Human Pose Estimation in Images and Videos. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10012–10026. [Google Scholar] [CrossRef] [PubMed]
- Eichner, M.; Marin-Jimenez, M.; Zisserman, A.; Ferrari, V. 2D Articulated Human Pose Estimation and Retrieval in (Almost) Unconstrained Still Images. Int. J. Comput. Vis. 2012, 99, 190–214. [Google Scholar] [CrossRef]
- Yang, Y.; Ramanan, D. Articulated Human Detection with Flexible Mixtures of Parts. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2878–2890. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the 13th European Conference on Computer Vision (ECCV), Zurich, Switzerland, 22 June 2014. [Google Scholar]
- Zhang, W.; Zhu, M.; Derpanis, K.G. From Actemes to Action: A Strongly-supervised Representation for Detailed Action Understanding. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Sapp, B.; Taskar, B. MODEC: Multimodal Decomposable Models for Human Pose Estimation. In Proceedings of the 26th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Jhuang, H.; Gall, J.; Zuffi, S.; Schmid, C.; Black, M.J. Towards understanding action recognition. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Li, J.; Wang, C.; Zhu, H.; Mao, Y.; Fang, H.S.; Lu, C. Crowdpose: Efficient crowded scenes pose estimation and a new benchmark. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Lin, W.; Liu, H.; Liu, S.; Li, Y.; Xiong, H.; Qi, G.; Sebe, N. HiEve: A Large-Scale Benchmark for Human-Centric Video Analysis in Complex Events. Int. J. Comput. Vis. 2023, 131, 2994–3018. [Google Scholar] [CrossRef]
- Andriluka, M.; Pishchulin, L.; Gehler, P.; Schiele, B. 2D Human Pose Estimation: New Benchmark and State of the Art Analysis. In Proceedings of the 27th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 24–27 June 2014. [Google Scholar]
- Johnson, S.; Everingham, M. Clustered Pose and Nonlinear Appearance Models for Human Pose Estimation; University of Leeds: Aberystwyth, UK, 2010. [Google Scholar]
- Andriluka, M.; Iqbal, U.; Insafutdinov, E.; Pishchulin, L.; Milan, A.; Gall, J.; Schiele, B. PoseTrack: A Benchmark for Human Pose Estimation and Tracking. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3.6M: Large Scale Datasets and Predictive Methods for 3D Human Sensing in Natural Environments. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1325–1339. [Google Scholar] [CrossRef]
- Mehta, D.; Sotnychenko, O.; Mueller, F.; Xu, W.; Sridhar, S.; Pons-Moll, G.; Theobalt, C. Single-Shot Multi-Person 3D Pose Estimation from Monocular RGB. In Proceedings of the 6th International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018. [Google Scholar]
- von Marcard, T.; Henschel, R.; Black, M.J.; Rosenhahn, B.; Pons-Moll, G. Recovering Accurate 3D Human Pose in the Wild Using IMUs and a Moving Camera. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Zhu, L.; Rematas, K.; Curless, B.; Seitz, S.M.; Kemelmacher-Shlizerman, I. Reconstructing nba players. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part V 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Cao, Z.; Gao, H.; Mangalam, K.; Cai, Q.Z.; Vo, M.; Malik, J. Long-term human motion prediction with scene context. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part I 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Zhang, Z.; Wang, C.; Qiu, W.; Qin, W.; Zeng, W. AdaFuse: Adaptive Multiview Fusion for Accurate Human Pose Estimation in the Wild. Int. J. Comput. Vis. 2021, 129, 703–718. [Google Scholar]
- Duan, H.; Zhao, Y.; Chen, K.; Lin, D.; Dai, B. Revisiting skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21–24 June 2022. [Google Scholar]
- Das, S.; Sharma, S.; Dai, R.; Bremond, F.; Thonnat, M. Vpn: Learning video-pose embedding for activities of daily living. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part IX 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Hbali, Y.; Hbali, S.; Ballihi, L.; Sadgal, M. Skeleton-based human activity recognition for elderly monitoring systems. IET Comput. Vis. 2018, 12, 16–26. [Google Scholar] [CrossRef]
- Guo, H.; Yu, Y.; Ding, Q.; Skitmore, M. Image-and-skeleton-based parameterized approach to real-time identification of construction workers’ unsafe behaviors. J. Constr. Eng. Manag. 2018, 144, 04018042. [Google Scholar]
- Duan, C.; Hu, B.; Liu, W.; Song, J. Motion Capture for Sporting Events Based on Graph Convolutional Neural Networks and Single Target Pose Estimation Algorithms. Appl. Sci. 2023, 13, 7611. [Google Scholar] [CrossRef]
- Swain, D.; Satapathy, S.; Acharya, B.; Shukla, M.; Gerogiannis, V.C.; Kanavos, A.; Giakovis, D. Deep learning models for yoga pose monitoring. Algorithms 2022, 15, 403. [Google Scholar] [CrossRef]
- Kulkarni, K.M.; Shenoy, S. Table tennis stroke recognition using two-dimensional human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Giulietti, N.; Caputo, A.; Chiariotti, P.; Castellini, P. SwimmerNET: Underwater 2D Swimmer Pose Estimation Exploiting Fully Convolutional Neural Networks. Sensors 2023, 23, 2364. [Google Scholar] [CrossRef] [PubMed]
- Baumgartner, T.; Paassen, B.; Klatt, S. Extracting spatial knowledge from track and field broadcasts for monocular 3D human pose estimation. Sci. Rep. 2023, 13, 1–11. [Google Scholar]
- Sajina, R.; Ivasic-Kos, M. 3D Pose Estimation and Tracking in Handball Actions Using a Monocular Camera. J. Imaging 2022, 8, 308. [Google Scholar] [CrossRef]
- Qian, X.; He, F.; Hu, X.; Wang, T.; Ramani, K. Arnnotate: An augmented reality interface for collecting custom dataset of 3d hand-object interaction pose estimation. In Proceedings of the 35th Annual ACM Symposium on User Interface Software and Technology, Bend, OR, USA, 29 October–2 November 2022. [Google Scholar]
- Anvari, T.; Park, K.; Kim, G.J.A.S. Upper body pose estimation using deep learning for a virtual reality avatar. Appl. Sci. 2023, 13, 2460. [Google Scholar] [CrossRef]
- Scherfgen, D.; Schild, J. Estimating the pose of a medical manikin for haptic augmentation of a virtual patient in mixed reality training. In Proceedings of the 23rd Symposium on Virtual and Augmented Reality, Virtual, Brazil, 18–21 October 2021. [Google Scholar]
- Willett, N.S.; Shin, H.V.; Jin, Z.; Li, W.; Finkelstein, A. Pose2Pose: Pose selection and transfer for 2D character animation. In Proceedings of the 25th International Conference on Intelligent User Interfaces, Greenville, SC, USA, 18–21 March 2020. [Google Scholar]
- Xia, G.; Ma, F.; Liu, Q.; Zhang, D. Pose-Driven Realistic 2-D Motion Synthesis. IEEE Trans. Cybern. 2023, 53, 2412–2425. [Google Scholar]
- Seth, A.; James, A.; Mukhopadhyay, S. Wearable Sensing System to perform Realtime 3D posture estimation for lower back healthcare. In Proceedings of the 2021 IEEE International Symposium on Robotic and Sensors Environments (ROSE), Virtual, 28–29 October 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Guo, H.; Liu, X.; Liu, H. Research on Athlete Posture Monitoring and Correction Technology Based on Wireless Sensing and Computer Vision Algorithms. Mob. Netw. Appl. 2024, 2024, 1–12. [Google Scholar]
- Chen, W.; Jiang, Z.; Guo, H.; Ni, X. Fall Detection Based on Key Points of Human-Skeleton Using OpenPose. Symmetry 2020, 12, 744. [Google Scholar] [CrossRef]
- Baker, B.; Liu, T.; Matelsky, J.; Parodi, F.; Mensh, B.; Krakauer, J.W.; Kording, K. Computational kinematics of dance: Distinguishing hip hop genres. Front. Robot. AI 2024, 11, 1295308. [Google Scholar]
- Leroy, V.; Cabon, Y.; Revaud, J. Grounding image matching in 3d with mast3r. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]

| Dataset | Year | Size | Single/Multi-Person | Joints | Metrics |
|---|---|---|---|---|---|
| MPII | 2014 | 25K images | A | 16 | PCK/ mAP |
| LSP | 2010 | 2K images | S | 14 | PCP/ PCK |
| COCO | 2017 | 330K images | M | 17 | AP/AR |
| PoseTrack Dataset | 2017 | 46K frames | M | 15 | mAP |
| PoseTrack Dataset | 2018 | 46K frames | M | 15 | mAP |
| Penn Action | 2013 | 2326 video clips | S | 13 | PCK |
| FLIC | 2013 | 5K images | S | 10 | PCP PCK |
| J-HMDB | 2013 | 5K images | S | 15 | PCK |
| CrowdPose | 2017 | 20K images | M | 14 | mAP |
| HiEve | 2017 | 50k frames | M | 14 | mAP |
| Method | Head | Shoulder | Elbow | Wrist | Hip | Knee | Ankle | Total |
|---|---|---|---|---|---|---|---|---|
| [36] | 97.5 | 96.2 | 90.8 | 86.6 | 89.3 | 87.1 | 83.4 | 90.4 |
| [33] | 98.2 | 96.3 | 91.2 | 87.1 | 90.1 | 87.4 | 83.6 | 90.9 |
| [38] | 98.3 | 96.5 | 91.8 | 82.9 | 90.7 | 88.4 | 85.2 | 91.6 |
| [39] | 98.5 | 96.7 | 92.5 | 88.7 | 91.1 | 88.6 | 86.0 | 92.0 |
| [37] | 98.1 | 96.2 | 90.9 | 87.2 | 89.8 | 87.3 | 83.5 | 90.8 |
| [42] | 98.1 | 96.7 | 92.5 | 88.4 | 90.8 | 88.8 | 85.3 | 91.8 |
| [34] | 97.1 | 96.2 | 91.6 | 86.1 | 90.4 | 87.7 | 83.9 | 90.9 |
| [43] | 97.1 | 95.9 | 90.4 | 85.1 | 89.1 | 85.8 | 81.5 | 89.8 |
| [49] | 98.5 | 97.3 | 93.9 | 89.9 | 90.2 | 90.6 | 86.8 | 93.0 |
| Method | Head | Shoulder | Elbow | Wrist | Hip | Knee | Ankle | Total |
|---|---|---|---|---|---|---|---|---|
| [43] | 97.8 | 95.5 | 94.4 | 92.9 | 94.7 | 95.6 | 94.3 | 95.1 |
| [37] | 98.1 | 93.1 | 89.2 | 86.1 | 92.7 | 92.8 | 90.4 | 91.7 |
| [38] | 98.2 | 93.8 | 90.6 | 89.3 | 93.6 | 94.4 | 93.8 | 88.6 |
| [39] | 98.3 | 94.5 | 92.2 | 88.9 | 94.4 | 95.0 | 93.7 | 93.9 |
| [42] | 98.3 | 94.7 | 92.3 | 89.7 | 94.3 | 95.4 | 94.1 | 92.9 |
| Method | AP | AP50 | AP75 | APM | APL | AR |
|---|---|---|---|---|---|---|
| [53] | 70.5 | 88.5 | 76.7 | 64.5 | 79.4 | - |
| [52] | 77.0 | 92.7 | 84.5 | 73.4 | 83.1 | 82.0 |
| [48] | 76.8 | 92.6 | 84.3 | 73.3 | 82.7 | 81.6 |
| [49] | 78.6 | 94.3 | 86.6 | 75.5 | 83.3 | 83.8 |
| [55] | 65.5 | 86.8 | 72.3 | 60.6 | 82.6 | - |
| [56] | 67.6 | 85.1 | 73.7 | 62.7 | 74.6 | - |
| [54] | 71.5 | 89.1 | 78.5 | 67.2 | 18.1 | - |
| [58] | 70.6 | 89.9 | 77.2 | 69.3 | 75.3 | 76.2 |
| Method | Head | Shoulder | Elbow | Wrist | Hip | Knee | Ankle | Total |
|---|---|---|---|---|---|---|---|---|
| PoseTrack2017 | ||||||||
| [63] | 79.5 | 84.3 | 80.1 | 75.8 | 77.6 | 76.8 | 70.8 | 77.9 |
| [65] | 79.9 | 87.6 | 82.8 | 76.7 | 80.7 | 79.4 | 72.8 | 80.0 |
| [66] | 86.1 | 86.1 | 81.8 | 77.4 | 79.5 | 79.1 | 73.6 | 80.9 |
| PoseTrack2018 | ||||||||
| [63] | 78.9 | 84.4 | 80.9 | 76.8 | 75.6 | 77.5 | 71.8 | 78.0 |
| [65] | 78.8 | 84.8 | 79.8 | 73.2 | 76.2 | 75.6 | 69.9 | 77.2 |
| [66] | 83.6 | 84.5 | 81.4 | 77.9 | 76.8 | 78.3 | 72.9 | 79.6 |
| Dataset | Year | Size | Environment | Single/ Multi-Person | Subject |
|---|---|---|---|---|---|
| Human3.6M | 2014 | 3.6 M frames | I | M | 11 |
| MuCo-3DHP | 2017 | n/a | A | S | 8 |
| 3DPW | 2018 | 60 sequences | O | M | 7 |
| MuPoTs-3D | 2018 | 8 k frames | A | A | 8 |
| AMASS | 2019 | 9 M frames | A | S | 300 |
| GTA-IM | 2020 | 1 M frames | I | S | n/a |
| NBA2K | 2020 | 27 k poses | O | S | 27 |
| Occlusion-Person | 2020 | 7.3 M frames | I | A | 13 |
| Methods/Index | [74] | [75] | [79] | [84] | [86] | [87] | [90] | [148] | [149] | [155] |
|---|---|---|---|---|---|---|---|---|---|---|
| MPJPE | 71.9 | 56.2 | 44.3 | 49.7 | 44.1 | 50.1 | 45.6 | 42.6 | 45.1 | 44.1 |
| PA-MPJPE | 51.9 | 41.8 | 34.7 | - | 34.7 | 39.3 | 36.2 | 32.7 | 35.6 | 35.0 |
| Method | MuPoTS-3D | Human3.6M | ||||
|---|---|---|---|---|---|---|
| 3DPCKrel | 3DPCKabs | MPJPE | ||||
| All People | Matched People | All People | Matched People | p1 | p2 | |
| [128] | 81.8 | 82.5 | - | - | - | 54.4 |
| [129] | - | - | - | 56.8 | - | - |
| [130] | 75.2 | 83.2 | 39.2 | 39.7 | - | - |
| [133] | 72.1 | 78.0 | - | - | 63.6 | - |
| [135] | - | - | - | - | 43.4 | 49.1 |
| [132] | 73.5 | 80.5 | 35.4 | 38.7 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, R.; Lin, Z.; Leng, S.; Wang, A.; Zhao, L. An In-Depth Analysis of 2D and 3D Pose Estimation Techniques in Deep Learning: Methodologies and Advances. Electronics 2025, 14, 1307. https://doi.org/10.3390/electronics14071307
Sun R, Lin Z, Leng S, Wang A, Zhao L. An In-Depth Analysis of 2D and 3D Pose Estimation Techniques in Deep Learning: Methodologies and Advances. Electronics. 2025; 14(7):1307. https://doi.org/10.3390/electronics14071307
Chicago/Turabian StyleSun, Ruiyang, Zixiang Lin, Song Leng, Aili Wang, and Lanfei Zhao. 2025. "An In-Depth Analysis of 2D and 3D Pose Estimation Techniques in Deep Learning: Methodologies and Advances" Electronics 14, no. 7: 1307. https://doi.org/10.3390/electronics14071307
APA StyleSun, R., Lin, Z., Leng, S., Wang, A., & Zhao, L. (2025). An In-Depth Analysis of 2D and 3D Pose Estimation Techniques in Deep Learning: Methodologies and Advances. Electronics, 14(7), 1307. https://doi.org/10.3390/electronics14071307









