A Novel Two-Stage Superpixel CFAR Method Based on Truncated KDE Model for Target Detection in SAR Images

Abstract

Target detection in synthetic aperture radar (SAR) imagery remains a significant technical challenge, particularly in scenarios involving multi-target interference and clutter edge effects that cannot be disregarded, notably in high-resolution imaging applications. To tackle this issue, a novel two-stage superpixel-level constant false-alarm rate (CFAR) detection method based on a truncated kernel density estimation (KDE) model is proposed in this article. The contribution mainly lies in three aspects. First, a truncated KDE model is used to fit the statistical distribution of clutter in the detection window, and adaptive thresholding is used for clutter truncation to remove outliers from the clutter samples while preserving the real clutter. Second, based on the clutter statistics, the KDE model is accurately constructed using the quartile based on the truncated clutter statistics. Third, target superpixel detection is performed using a two-stage CFAR detection scheme enhanced with local contrast measure (LCM), consisting of a global stage followed by a local stage. In the global detection phase, we identify candidate target superpixels (CTSs) based on the superpixel segmentation results. In the local detection phase, a local CFAR detector using a truncated KDE model is employed to improve the detection process, and further screening is performed on the global detection results combined with local contrast. Experimental results show that the proposed method achieves excellent detection performance, while significantly reducing detection time compared to current popular methods.

1. Introduction

Synthetic Aperture Radar (SAR) achieves high-resolution imaging by synthesizing echo signals received from different positions through radar platform movement and coherent processing techniques, effectively emulating a large-aperture antenna configuration to enhance azimuthal resolution [1,2,3,4]. Ship detection under complex SAR conditions has garnered significant attention in both marine monitoring and emergency response applications. While conventional ship detection methods predominantly rely on constant false-alarm rate (CFAR) detectors, achieving robust detection performance in dynamic scenarios characterized by non-stationary sea clutter, multi-scale target signatures, and speckle noise contamination poses significant technical challenges, especially under low signal-clutter-ratio (SCR) conditions.

The well-known CFAR detection method has been extensively studied for its computational simplicity, adaptive thresholding, and effectiveness in detecting targets against complex scenarios. Among the commonly used CFAR detection schemes, Cell Averaging CFAR (CA-CFAR), Greatest of CFAR (GO-CFAR), Smallest of CFAR (SO-CFAR), and Order Statistic CFAR (OS-CFAR) are popular choices [5,6,7,8]. Unfortunately, the effectiveness of CFAR detectors critically relies on precise statistical characterization of background clutter, and the aforementioned methods are unable to maintain good performance in the presence of large variations in clutter levels.

In recent years, several classical models have been proposed for modeling background clutter [9], such as Weibull, log-normal, K, and G0 distribution. The sliding-window technique is commonly used to estimate the above model parameters within a certain local reference window. However, in the crowded multi-target area, interference from the clutter edge and the multi-target environment frequently induces biased parameter estimation and degraded modeling accuracy. To decrease the multitarget impact, outliers can be evacuated through two plans with distinctive criteria, which are data censoring and data truncation. In terms of data censoring, Gao et al. [10] introduced an adaptive CFAR algorithm based on automatic censoring (AC), in which the index matrix automatically censors the clutter pixels in the sliding window to adaptively determine the clutter environment of detection. However, its censoring depth can only be determined empirically, making it difficult to effectively remove outliers. In the literature [11,12], improvements have been made by using an iterative censoring scheme, which effectively achieves simultaneous target detection and outlier rejection, resulting in a higher detection rate in a multi-target environment. For the detection environment with multiple targets, the truncated statistic CFAR (TS-CFAR) method proposed by Tao et al. [13] provided a truncation of clutter based on the gamma statistical model. Then, Yang et al. [14] put forth a novel two-parameter CFAR detector, designated as the adaptively truncated clutter statistics CFAR (TS-LNCFAR). This method employs a log-normal statistical model, with the model being precisely established through adaptive threshold-based clutter truncation within the background window. Compared to data censoring, data truncation enhances the stability of statistical models by removing extreme values or noise, making predictions and inferences more reliable. However, the aforementioned methods still require many cycles and long calculation times due to using pixel-level sliding windows.

Considering that pixel-level CFAR sliding window could cost a significant computational loss, changing it to superpixel-level is a feasible strategy. Several CFAR detection methods have already achieved some promising results by employing superpixels as the processing unit [15,16,17,18]. However, all of them employ parametric estimation models due to the influence of noise and local fluctuations in the clutter, the actual distribution deviates from the theoretical assumption, leading to a decline in the fitting accuracy of parametric models, and, in contrast to them, the kernel density estimation (KDE) model exhibits greater flexibility in adapting to various shapes of probability distributions, particularly in an environment where the clutter distribution is unknown or complex [19]. To combine the advantages of both superpixels and statistical models, a novel two-stage superpixel-level CFAR detection method based on a truncated KDE model is proposed in this article. In addition, the interquartiler range (IQR) is introduced to obtain the optimal bandwidth of the KDE model, while simultaneously using them to truncate clutter within the detection window. The proposed method consists of three steps. First, segment the SAR image into different superpixel regions by employing the Simple Linear Iterative Clustering (SLIC) algorithm [20]. Then, in the global detection, find out candidate target superpixels (CTSs) based on superpixel intensities. Finally, in the local detection, a local CFAR detector employs a truncated kernel density estimation (KDE) model to refine the detection process. The local contrast measure is subsequently defined to enhance the global detection results through further optimization, effectively suppressing land-based false alarms. The experiment demonstrates that the proposed method is capable of achieving a high detection rate while simultaneously maintaining a low false-alarm rate. The two-stage detection scheme, by globally indexing superpixels, achieves significant improvements in computational efficiency compared to current mainstream algorithms, while also demonstrating enhanced suppression capability for land-based backgrounds.

2. Truncated KDE Modeling

For an unknown probability density function (PDF) by the clutter samples X₁, X₂, …, X_N, the KDE is defined as

$$p_X\left(\mathrm{x}\right)={\displaystyle \frac{1}{Nh}}{\displaystyle \sum _{i=1}^{N}K\left(\frac{x-X_i}{h}\right)}$$

(1)

where $K\left(•\right)$ is the Gaussian kernel smoothing function and h is the bandwidth, which controls the width of $K\left(•\right)$. Then, the cumulative distribution function (CDF) for KDE is defined as

$$F_X\left(\mathrm{x}\right)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\varnothing \left(\frac{x-X_i}{h}\right)}$$

(2)

where $\varnothing \left(•\right)$ is the standard normal cumulative distribution function (CDF). Once the CDF has been defined, a truncated version is used to model the clutter within a specified range. This truncation ensures that the probability distribution adequately represents the observed clutter, while avoiding extreme values or outliers outside the specified range. With the truncated depth t, the truncated PDF of KDE is provided by

$${\stackrel{\sim }{p}}_X\left(x;t\right)=\left\{\begin{array}{l}{\displaystyle \frac{p_X\left(x\right)}{F_X\left(t\right)}},x\le t\\ 0, \mathrm{x}>t\end{array}\right.$$

(3)

For non-parametric KDE models, the option of bandwidth h is crucial. For clutter in SAR images, an excessively large h may obscure local details and statistical characteristics within the clutter, resulting in the KDE model underfitting, while an overly small h causes the kernel function to focus narrowly on local data points, rendering the density estimate overly sensitive to noise and introducing spurious peaks and fluctuations, resulting in the KDE model overfitting. According to [19], with the log reference criterion, the optical h can be calculated as

$$h=1.06\sigma N^{-1/5}$$

(4)

where $\sigma$ is the standard deviation. However, when the background clutter contains outliers or exhibits a heavy-tailed distribution, $\sigma$ is significantly overestimated, resulting in over-smoothing of the estimation. Considering that outliers cannot be completely removed due to the different settings of the truncation depth, the robustness of IQR should be included to make it more stable, which is defined as

$$I_{qr}=Q_3-Q_1$$

(5)

For a standard normal distribution, the first quartile Q₁ and third quartile Q₃ correspond to the 25th and 75th percentiles of the distribution, respectively. The interquartile range (IQR) is a measure of the spread of the middle 50% of a data set, effectively reflecting both the central tendency and dispersion of the clutter.

For a normal distribution $X\sim N\left(u,{\sigma }^2\right)$, the standardized variable $Z={\displaystyle \frac{x-\mu }{\sigma }}\sim N\left(0,1\right)$, ${\stackrel{\sim }{Q}}_1$ and ${\stackrel{\sim }{Q}}_3$ can be obtained by numerical solution. Therefore, for a general normal distribution $N\left(u,{\sigma }^2\right)$, the quartiles scale linearly with $\sigma$: $Q_N=u+{\stackrel{\sim }{Q}}_N$, the IQR can be computed as $I_{qr}=\mathit{\sigma }\cdot \left(Q_3-Q_1\right)$, then, we use I_qr to replace $\sigma$, the local optimal bandwidth $h_{opt}$ can be defined as

$$h_{opt}=1.06\min \left(\mathit{\sigma },I_{qr}/1.34\right)N^{-1/5}$$

(6)

3. Superpixel CFAR Based on Truncated KDE Model

Considering the advantages of the superpixel processing, a two-stage framework CFAR method was proposed in this section. The algorithm is composed of the following three steps:

(1)

SLIC segmentation;

(2)

Global CFAR detection;

(3)

Local CFAR detection.

First, superpixels are generated employing the Simple Linear Iterative Cluster (SLIC) algorithm.

Then, a global detection is performed based on the statistical features of the KDE model-fitted superpixels to obtain CTSs.

Finally, we use a local CFAR detector based on a truncated KDE model to achieve further screening, the CTSs will be refined. It is discussed in the following sections.

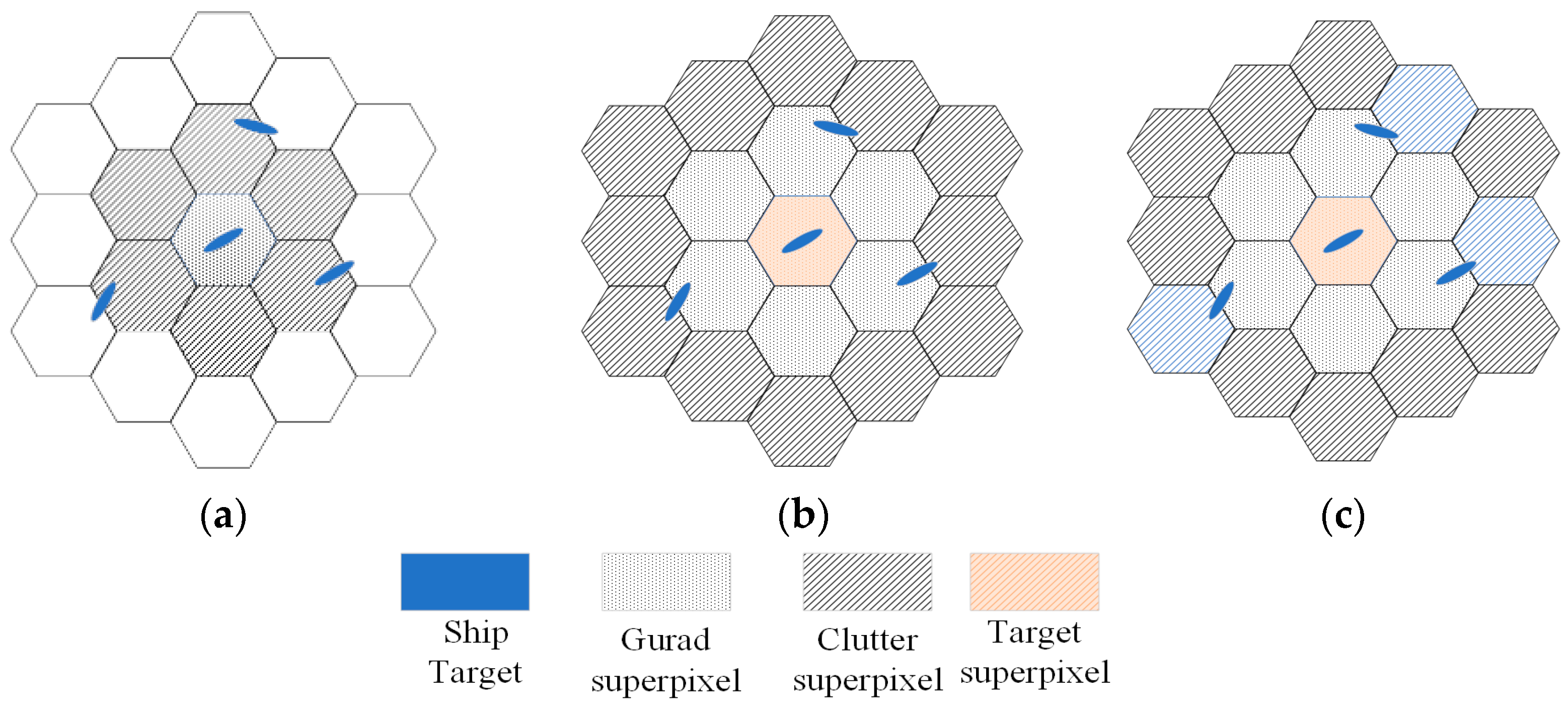
3.1. Superpixel Segmentation

Simple Linear Iterative Clustering (SLIC) is used to generate superpixels by the clustering of similarity between pixels in the image to achieve fast clustering. To suppress the influence of speckle noise, the intensity dissimilarity of two pixels is obtained by measuring the dissimilarity of the two local patches centering them [15,16]. Hence, the dissimilarity of the two patches can be defined as follows:

$$\zeta \left(u_{\mathrm{i}},u_j\right)=2M\cdot \ln {\displaystyle \frac{\stackrel{-}{I_{u_i}}+\stackrel{-}{I_{u_j}}}{2\sqrt{\stackrel{-}{I_{u_i}}\cdot \stackrel{-}{I_{u_j}}}}}$$

(7)

where ${\stackrel{-}{I}}_{u_k}$ denotes the average intensity in the patch $u_k$, and M is the number of pixels in the region $u_i$ or $u_j$. Then, the dissimilarity of pixels i and j can be measured as

$$D(i,j)=\zeta (u_i,u_j)+\lambda \cdot d(i,j)$$

(8)

where $d(i,j)={\left({\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2\right)}^{1/2}$ denotes the spatial distance between the pixel pair (i, j), and the tradeoff factor $\lambda$, also known as the compactness parameter, weighs the relative importance between the pixel intensity and the spatial dissimilarity. A smaller $\lambda$ places greater weight on spatial distance, resulting in more regular superpixels with smoother boundaries. Another important factor influencing segmentation results is the size of superpixels, as denoted by S. Figure 1 shows the effect of different settings of S on the superpixel segmentation results. A larger S would result in fewer superpixels, yielding reduced computational complexity for the consequent detection process. However, as illustrated in Figure 1d, excessive S setting may compromise pixel uniformity within superpixels. When the superpixel search domain extends beyond appropriate scales, its coverage could potentially overlap multiple object boundaries, ultimately leading to suboptimal segmentation outcomes characterized by region under-segmentation. In practice, the superpixels’ sizes should be set according to the smallest target size in multitarget situations.

Assuming that the SAR image with N pixels in the CIE-Lab space is uniformly segmented into K superpixel blocks with the same size $S=\sqrt{N/K}$. Then, for a single-channel SAR image, the details of the SLIC algorithm process can be summarized as follows.

Step 1: Initialize the clustering centers $C_m={[I_{u_m},x_m,y_m]}^T$$(m=1,2,3,\dots )$ by sampling on a rectangle grid with S × S.

Step 2: Label assignments. Within the 2S × 2S region of each cluster center, pixels are assigned to the nearest cluster center according to the distance metric $D(i,j)$.

Step 3: Update the position of each cluster center with the mean pixels belonging to the same cluster center.

Step 4: The adjacent merging method is adopted to eliminate the isolated superpixels with small sizes, which enhances the connectivity of the result.

3.2. Global CFAR

Due to the significant difference in intensity between clutter and target superpixels, a global threshold T can be calculated to identify CTSs according to the following equation.

$$P_G=1-{\displaystyle {\int }_0^{T}p\left(x\right)} d_x$$

(9)

where $p_G$ is the false-alarm-rate probability and p(x) is the probability density function (PDF) of superpixel intensity. Based on the CDF of the improved KDE model, T can be derived as

$$P_G=1-{\displaystyle {\int }_0^{T}p\left(x\right)} d_x=1-{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\varnothing \left(\frac{T-X_i}{h_{opt}}\right)}$$

(10)

Since the above equation is difficult to solve, we use the trapezoidal rule for cumulative integration. Assuming that X is the intensity of the superpixel, i.e., $X=\left[M_1,M_2,\dots ,M_N\right]$, N represents the total number of superpixels. As a result, superpixel intensity values can be divided into L equal intervals, i.e., $\tilde{X}=\left\{x_1 , x_2 ,\dots ,x_l,\dots ,x_L\right\}$, and the CDF values for $\tilde{X}$ are calculated as follows:

$$\hat{F}\left(x_l\right)={\displaystyle \sum _{k=1}^{l-1}\frac{x_{i+1}-x_i}{2}}\left(P_{x_{i+1}}+P_{x_i}\right)$$

(11)

The global T can be calculated through $1-\hat{F}\left(x_l\right)>P_G>1-\hat{F}\left(x_{l+1}\right)$. Then, the CTSs can be distinguished by the following equation:

$$C{T}_N=\left\{\begin{array}{l}1, M_N\ge T,S_N \mathrm{is} \mathrm{CTS}\\ 0, M_N<T,S_N \mathrm{is} \mathrm{clutter}\end{array}\right.$$

(12)

Here, $C{T}_N$ represents the binary classification index for the n-th superpixel, where $C{T}_N$ = 0 denotes clutter superpixels and $C{T}_N$ = 1 identifies candidate targets (CTSs). An adaptive classification mechanism is implemented based on intensity thresholds: superpixels with intensities exceeding T are assigned to the CTS set ${\left\{\cdot \right\}}_{candidate}$, while others are categorized into the clutter set ${\left\{\cdot \right\}}_{clutter}$, ensuring robust separation for subsequent CFAR parameter calibration.

3.3. Local CFAR

After global CFAR detection, the superpixels in ${\left\{\cdot \right\}}_{candidate}$ may contain significant terrestrial regions, leading to land-based false alarms. To address this, this article proposes a superpixel-driven local contrast measurement method, subsequently enabling adaptive local CFAR detection.

3.3.1. Local Contrast

The local contrast measure (LCM) algorithm enhances target detection by amplifying target saliency within local regions. As illustrated in Figure 2, target superpixels demonstrate higher saliency in local contexts while background superpixels exhibit lower saliency. Leveraging this localized saliency characteristic of superpixels, this paper proposes a superpixel-based local contrast measurement method that effectively differentiates targets from their surrounding backgrounds through regional significance analysis. Drawing inspiration from the literature [15], which achieves adaptive selection of clutter superpixels for parameter estimation through similarity-based clustering, we integrated pixel-wise and superpixel-wise analyses, a local superpixel contrast metric was designed to amplify discriminative features between maritime targets and complex backgrounds, thereby optimizing CFAR detection performance through enhanced separability in heterogeneous marine environments. For each pixel i within the superpixel in ${\left\{\cdot \right\}}_{candidate}$, its local contrast is calculated as follows:

$$\left\{\begin{array}{l}Q\left(i\right)=\eta (i)·{\displaystyle \sum _{S_n\in {\left\{\cdot \right\}}_{clutter}}\zeta (S_m,S_n)}\\ \eta =e^{\frac{-{{\sigma }^2}_{local}}{{{\mu }^2}_{local}\cdot k}}\\ \zeta \left(S_m,S_n\right)=2\min \left(size\left(S_m\right),size\left(S_n\right)\right)\cdot \ln {\displaystyle \frac{\stackrel{-}{I_{S_m}}+\stackrel{-}{I_{S_n}}}{2\sqrt{\stackrel{-}{I_{S_m}}\cdot \stackrel{-}{I_{S_n}}}}}\end{array}\right.$$

(13)

The definition follows a similar form to Equation (2), substituting the original patches u₁ and u₂ with the target superpixel S_m and its neighboring S_n, and $\zeta (S_m,S_n)$ represents the dissimilarity between superpixels. Here, $\eta (x)$ represents the pixel’s local variability, where ${{\sigma }^2}_{local}$ and ${\mu }_{local}$ represent the variance and mean of the region, respectively, while k is the spatial factor, which is set to 0.6, and local area size is set to 5 pixels × 5 pixels. According to Equation (13), for true target superpixels in ${\left\{\cdot \right\}}_{candidate}$, both $\zeta (S_m,S_n)$ and $\eta (i)$ exhibit larger values, resulting in a higher Q. Conversely, for land superpixels in ${\left\{\cdot \right\}}_{candidate}$, smaller $\zeta (S_m,S_n)$ and $\eta (i)$ lead to a reduced Q. For the issue of reduced local contrast in target superpixels in ${\left\{\cdot \right\}}_{candidate}$ caused by high-intensity neighboring superpixels in ${\left\{\cdot \right\}}_{candidate}$, we remove these interfering superpixels based on their index identified through global CFAR detection, thereby preserving the local saliency of target superpixels. It demonstrates that local contrast significantly enhances the detectability of potential ship targets by amplifying their distinctiveness against complex backgrounds.

3.3.2. Superpixel-Based Detection

During the local CFAR phase, it is essential to accurately identify and eliminate the clutter superpixels that persist after the global CFAR detection. In order to estimate the clutter parameters, a local CFAR detector should be constructed first to identify the background superpixels. Two popular approaches for acquiring background superpixels for threshold estimation are shown in Figure 2: the neighborhood superpixel approach suggested in [12] and the superpixel-level sliding-window technique detailed in [11]. A comparison of Figure 2a,b shows that the sliding-window strategy demonstrates superior mitigation of cross-contamination risks from neighboring target superpixels, despite its requirement for extended computational resources. While the neighborhood approach maintains computational efficiency through limited superpixel engagement, this approach may introduce bias in clutter characterization, particularly in complex environments with heterogeneous clutter distributions. Conversely, the sliding-window technique enhances environmental representation by adjusting the size of the window, thereby improving the robustness of the model at the cost of increased algorithmic complexity.

Considering that all CTSs are labeled in the global detection phase, the adoption of a sliding-window scheme can not only reduce the influence of the target backscattering effect, but also effectively improve the computational efficiency by screening CTSs. Additionally, low-intensity CTSs may be misclassified into superpixels in ${\left\{\cdot \right\}}_{candidate}$. This low-intensity CTS can contaminate the statistical characteristics of the clutter regions, leading to excessive kurtosis and elongated tails in the outlier histogram. If these CTSs are excluded from the neighborhood based on index values to mitigate local interference, it risks discarding true clutter information embedded in their spatial dependencies, thereby compromising the accuracy of clutter modeling.

Therefore, it is essential to truncate the clutter samples within the background window to eliminate outliers effectively, with the truncation depth being a crucial parameter. In [10], the truncated log normal is introduced to improve the impact of multi-target effects and outliers, with the model represented as $\mathit{ln}\left(x\right)>{\mu }_{\mathit{ln}}+t_1{\sigma }_{\mathit{ln}}$, where ${\mu }_{\mathit{ln}}$ denotes the mean and ${\sigma }_{\mathit{ln}}$ signifies the standard deviation. However, truncated log-normal is highly sensitive to outliers. Taking into account that the majority of pixels in the high-value section of the histogram belong to the target, while the majority of pixels in the low-value area are real clutter, the following formula can be used to truncate clutter samples for all pixels in the background detection window.

$$I_B-Q_{0.75}\ge t_2·I_{qr}$$

(14)

where I_B is the intensity of a pixel in the background window, and the truncation depth can be computed as $t=Q_{0.75}+t_2·I_{qr}$, where t₂ is set 1.9 in this article. Then, according to the proposed CFAR detection, the local detection threshold T_l is derived from the following formula, which ensures a predefined false-alarm rate Pfa.

$$p_{fa}=1-{\displaystyle \frac{\frac{1}{N}{\displaystyle \sum _{i=1}^N\varnothing \left(\frac{T_{\mathrm{l}}-X_i}{h_{opt}}\right)}}{F_X\left(Q_{0.75}+t_2·I_{qr}\right)}}$$

(15)

Since superpixels provide a more stable background estimate than a single pixel by aggregating similar pixels, the pixel being evaluated in the CTS can be determined using the following formula.

$$\left\{\begin{array}{l}{I}_N\left(k\right)\ge T_l, \mathrm{the} \mathrm{Nth} \mathrm{pixel} \mathrm{is} \mathrm{a} \mathrm{target} \mathrm{pixel}\\ I_N\left(k\right)<T_l, \mathrm{the} \mathrm{Nth} \mathrm{pixel} \mathrm{is} \mathrm{a} \mathrm{clutter} \mathrm{pixel}\end{array}\right.$$

(16)

To mitigate land false alarms, we implement a synergistic framework that integrates local contrast enhancement with adaptive CFAR detection. The optimization proceeds as follows:

$$\left\{\begin{array}{l}{I}_N\left(i\right)\cdot Q(i)\ge T_l, \mathrm{the} \mathrm{Nth} \mathrm{pixel} \mathrm{is} \mathrm{a} \mathrm{target} \mathrm{pixel}\\ I_N\left(i\right)\cdot Q(i)<T_l, \mathrm{the} \mathrm{Nth} \mathrm{pixel} \mathrm{is} \mathrm{a} \mathrm{clutter} \mathrm{pixel}\end{array}\right.$$

(17)

To prevent the target superpixels from being filtered out, the Pfa of global detection T should be set higher, and the Pfa of local detection T_l should be set lower.

4. Results and Discussion

4.1. Experiment 1

To assess the fitting accuracy of the KDE model, we first perform superpixel segmentation on the input SAR image from the RSDD-SAR images, followed by extraction of clutter regions within target-adjacent neighborhoods, and tests the clutter fit to this region, as shown in Figure 3.

From a visual assessment, some high-intensity scattering pixels lead to a heavy-tailed distribution in the histogram. The truncated KDE model demonstrates superior performance in comparison to the other models. Furthermore, the effectiveness of clutter-fitting is quantitatively evaluated using KL divergence [19]. As presented in

Table 1. Fitting performance comparison.

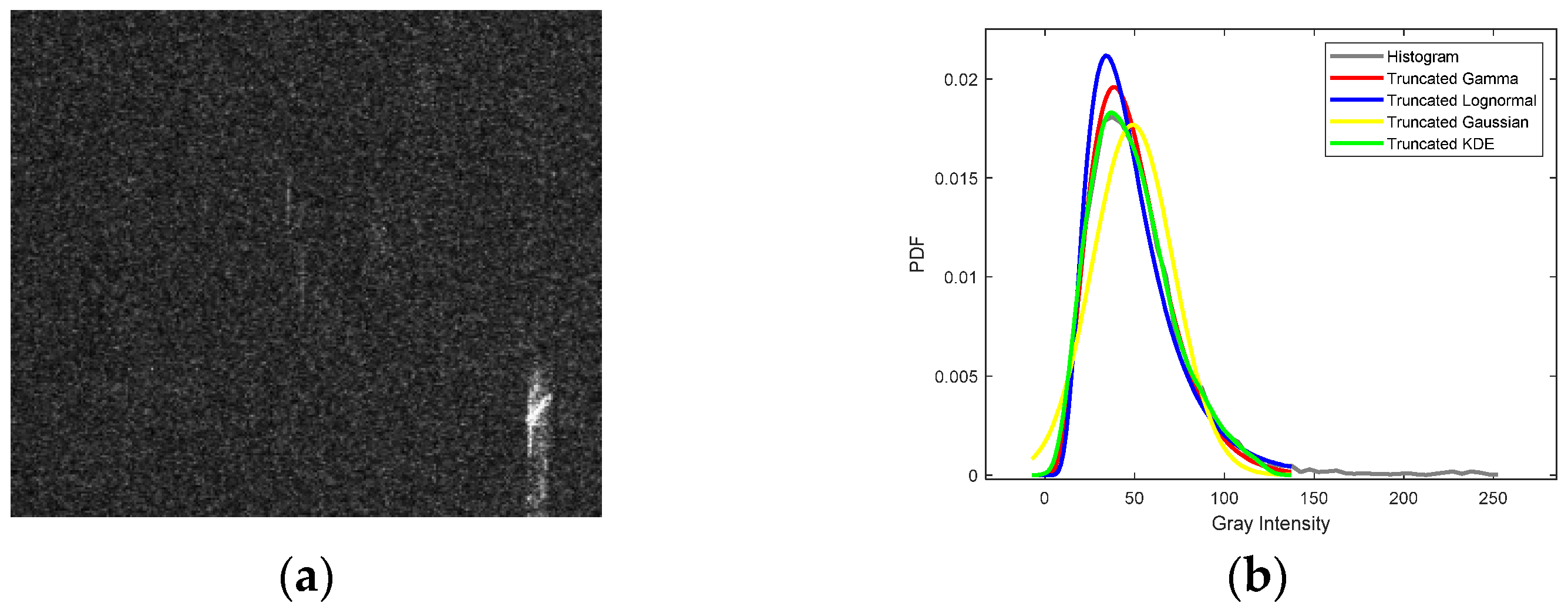
	KL Distance	KL Distance
Truncated Model
Truncated Gamma		0.0239
Truncated Lognormal		0.0447
Truncated Gaussian		0.1611
Truncated KDE		0.0024

, the truncated KDE model achieves the lowest KL divergence value, underscoring its efficacy in modeling sea clutter.

4.2. Experiment 2

To verify the performance improvement of the proposed method across various scenarios, detection results are compared with the ordered statistic CFAR (OS-CFAR) [8], the superpixel-level CFAR (SP-CFAR) [16], and the superpixel-level CFAR detector based on truncated gamma distribution (TS-SP-CFAR) [17]. The tested SAR images are all selected from the RSDD-SAR data set with a size of 512 × 512 pixels and a resolution of 10 m, which allow a detailed analysis of target detection and clutter estimation in different scenarios and are used to carry out this experiment. The RSDD-SAR data from high-resolution SAR satellites, including the Gaofen-3 data and the TerraSAR-X data. Imaging modes include Spotlight Mode, StripMap Mode, and ScanSAR Mode, with resolution ranges from 0.5 m to 40 m, covering various scales of ship detection needs.

One common instrument for the quantitative evaluation of SAR pictures is the receiver operating characteristic (ROC) curve. The ROC curves for various CFAR detection methods are displayed in Figure 4. The probability of detection (PD) is the proportion of target pixels detected out of all target pixels in the image, while the probability of false alarm (Pfa) is the proportion of clutter pixels detected out of all clutter pixels.

Figure 4a presents an image of eight offshore ships, while Figure 4b shows the ROC curve, which reveals that the superpixel-level CFAR detection method outperforms the performance of the pixel-level CFAR, with our method achieving the highest detection rate at the same false alarm probability (Pfa). This indicates that the superpixel-level method is more effective in distinguishing targets from clutter while maintaining low false-alarm rates. For a more quantitative comparison of the curve intersections, the AUC values of each method are listed in

Table 2. AUC comparison of the ROC curve.

Method	Algorithm	AUC Value
Method 1	OS-CFAR	0.7621
Method 2	SP-CFAR	0.8123
Method 3	TS-SP-CFAR	0.8674
Method 4	The proposed	0.8918

.

As shown in Table 2, the detection performance of pixel-level OS-CFAR is relatively modest. In comparison, the superpixel-based CFAR detection algorithms demonstrate significantly higher AUC values, all exceeding 0.85. Notably, the proposed method achieves the highest AUC value, indicating optimal detection performance.

4.3. Experiment 3

The third experiment was conducted on real SAR images, containing maritime ship targets and land areas. First, 20 SAR images were randomly selected to evaluate the detection performance of the proposed method, comprising a total of 81 ship targets. In this experiment, the above four detection methods were compared in terms of detection accuracy, with a default false-alarm rate of 0.1. The experimental results are summarized in

Table 3. Four methods of ship-detection accuracy.

Method	Algorithm	ACC
Method 1	OS-CFAR	0.7867
Method 2	SP-CFAR	0.8512
Method 3	TS-SP-CFAR	0.8893
Method 4	The proposed	0.9315

.

As shown in Table 3, OS-CFAR exhibits the lowest accuracy due to its susceptibility to noise and clutter regions contaminated by the outliers. In contrast, superpixel-based methods achieve significantly higher performance: SP-CFAR demonstrates an accuracy of 0.85, while TS-SP-CFAR reaches 0.88. The proposed method effectively fits the clutter and reduces interference from neighboring targets and clutter regions contaminated by the outliers, making it highly suitable for SAR image target detection in various scenarios. Next, two classical SAR images were chosen to analyze the details of target detection. The sizes of the superpixel S are, respectively, set to 20 and 40.

Figure 5c,d demonstrates the segmentation results of the SLIC algorithm on SAR images. For single-channel SAR images, the superpixels generated by the SLIC algorithm effectively adhere to image boundaries, with targets and coastlines being accurately segmented. Moreover, most of the superpixels are homogeneous. As shown in Figure 5e,f, the local contrast analysis demonstrates that the target is enhanced due to its local saliency, while both land regions and highlighted background areas are completely suppressed. The comparative results are shown in Figure 5g–n. The detection results for OS-CFAR are shown in Figure 5g,h, where it is observed that the target area contains fractures and holes, together with a significant amount of noise in the background. Similarly, the detection results for SP-CFAR are shown in Figure 5i,j, where speckle noise is suppressed, but the target boundaries are not well preserved, especially at the boundaries. Figure 5k,l show the detection results of the TS-SP-CFAR. Although all targets are correctly detected, there are still some false alarm pixels present. Compared to the detection results of the aforementioned methods, the performance of the proposed method shows a significant improvement, as illustrated in Figure 5m,n. It can be seen that false alarms, primarily caused by the presence of reefs, are consistent across all detection results. However, the proposed method has the lowest false detections with the same Pfa while also preserving the shape of the targets effectively.

4.4. Experiment 4

In Section 3.1, we briefly discussed the influence of the superpixel size S on the SLIC segmentation. Since the number of image pixels N is fixed, the size of S can be adjusted by inputting the number of superpixels K. In this section, we first select the real SAR image in Figure 5a, conduct superpixel segmentation, with the number of superpixels being 1000, 1500, 2000, and 2500, respectively, and then use the proposed method for ship detection and calculate the corresponding PD and Pfa values. The results are shown in

Table 4. Quantitative measures for Figure 5a with different superpixel numbers.

Number of Superpixels (K)
S = 1000		S = 1500		S = 2000		S = 2500
PD (%)	Pfa (%)	PD (%)	Pfa (%)	PD (%)	Pfa (%)	PD (%)	Pfa (%)
87.31	0.34	91.24	0.35	92.72	0.32	92.32	0.36

.

From the table, it can be observed that when the number of superpixels increases from 1000 to 1500, the Pfa slightly decreases, while the PD rises from 87.31% to 91.24%. This indicates that appropriately increasing the number of superpixels can enhance detection accuracy and reduce the false-alarm rate. However, when the number of superpixels reaches 2500, the PD decreases and the Pfa increases. The reason for this deterioration is that excessive superpixels may lead to over-segmentation of targets, thereby degrading the detection result.

The computational time required by the algorithms is presented in

Table 5. Detecting time(s) of four algorithms.

	Figure 5a (K = 1000)	Figure 5a (K = 2000)
OS-CFAR	24.94	24.68
SP-CFAR	4.95	7.50
TS-SP-CFAR	7.84	14.37
The proposed	3.93	5.95

. The experiments were carried out on a 64-bit Windows system with an Intel Core i7 CPU (produced by Intel Corporation, Santa Clara, CA, USA), 16 GB of RAM, and MATLAB 2019b as the software platform.

It is noted that the detection efficiency of the superpixel-level sliding window is obviously higher than that of the pixel-level sliding window, as shown in Table 5. The SP-CFAR and TS-SP-CFAR are both implemented with the superpixel-level sliding window. Therefore, compared with SP-CFAR and TS-SP-CFAR, the proposed two-stage method takes the lowest possible detection time, its computational efficiency is largely unaffected by image scale, primarily depending on the number of CTS, and it compensates for the long fitting time of KDE.

5. Conclusions

In this article, a two-stage superpixel-level CFAR detector based on adaptive truncated clutter statistics for SAR imagery is proposed. The proposed method utilizes truncated KDE as the statistical model for sea clutter, which is accurately determined by adaptive threshold-based clutter truncation within the background window; then, the detection results are further optimized by integrating local contrast measures. Through efficient outlier elimination and accurate clutter fitting, the method maintains a low false-alarm rate while increasing detection rates in multitarget situations.

Furthermore, this article adopts a two-stage detection framework and applies it to clutter fitting with the truncated model. By preserving authentic clutter characteristics while effectively eliminating outlier interference, the proposed method mitigates information loss in clutter modeling. Experimental results demonstrate that compared to other mainstream superpixel-level detection approaches, our framework achieves superior clutter-fitting accuracy alongside a high computational efficiency, particularly in large-scale SAR image processing. The proposed method realizes accurate modeling and lightweight processing, though challenges remain in adapting it to broader applications like land object detection, change detection, or disaster monitoring. For instance, performance may vary when processing complex polarimetric features due to increased computational demands and feature heterogeneity. Especially when adapting to optical or hyperspectral imagery, the high-dimensional spectral features may necessitate significant structural adaptations to the statistical framework, since the proposed method is specifically designed for single-channel intensity characteristics of SAR data. In the future, we aim to extend the framework to dual-polarization and fully polarimetric SAR ship detection by exploiting polarization features to enhance target discrimination capabilities.