DIMK-GCN: A Dynamic Interactive Multi-Channel Graph Convolutional Network Model for Intrusion Detection
Abstract
1. Introduction
- (1)
- Proposal of the DIMK-GCN Model: We introduce the dynamic interaction multi-channel graph convolutional network (DIMK-GCN), which consists of a spatiotemporal feature weighting module, an interactive graph feature fusion module, and a temporal feature learning module, enhancing the model’s adaptability to spatiotemporal evolution data.
- (2)
- Construction of a Spatiotemporal Graph Structure: By integrating cosine similarity and a self-attention mechanism, we propose a precise feature weight allocation method to address the challenges of static connections and dynamic feature distribution, thereby improving the expressiveness of spatiotemporal features.
- (3)
- Optimization of Edge Weights in Graph Structures: We incorporate graph attention networks (GATs) and multi-kernel graph convolutional networks (MK-GCNs) to refine edge weights, enhance the capture of node interaction relationships, and improve the compactness and robustness of feature representation.
- (4)
- Introduction of GRUs for Temporal Feature Learning: By integrating gated recurrent units (GRUs), we overcome the limitations of traditional methods in capturing long-term dependencies and handling non-stationary time-series data, enhancing the model’s adaptability to evolving temporal patterns.
2. Materials
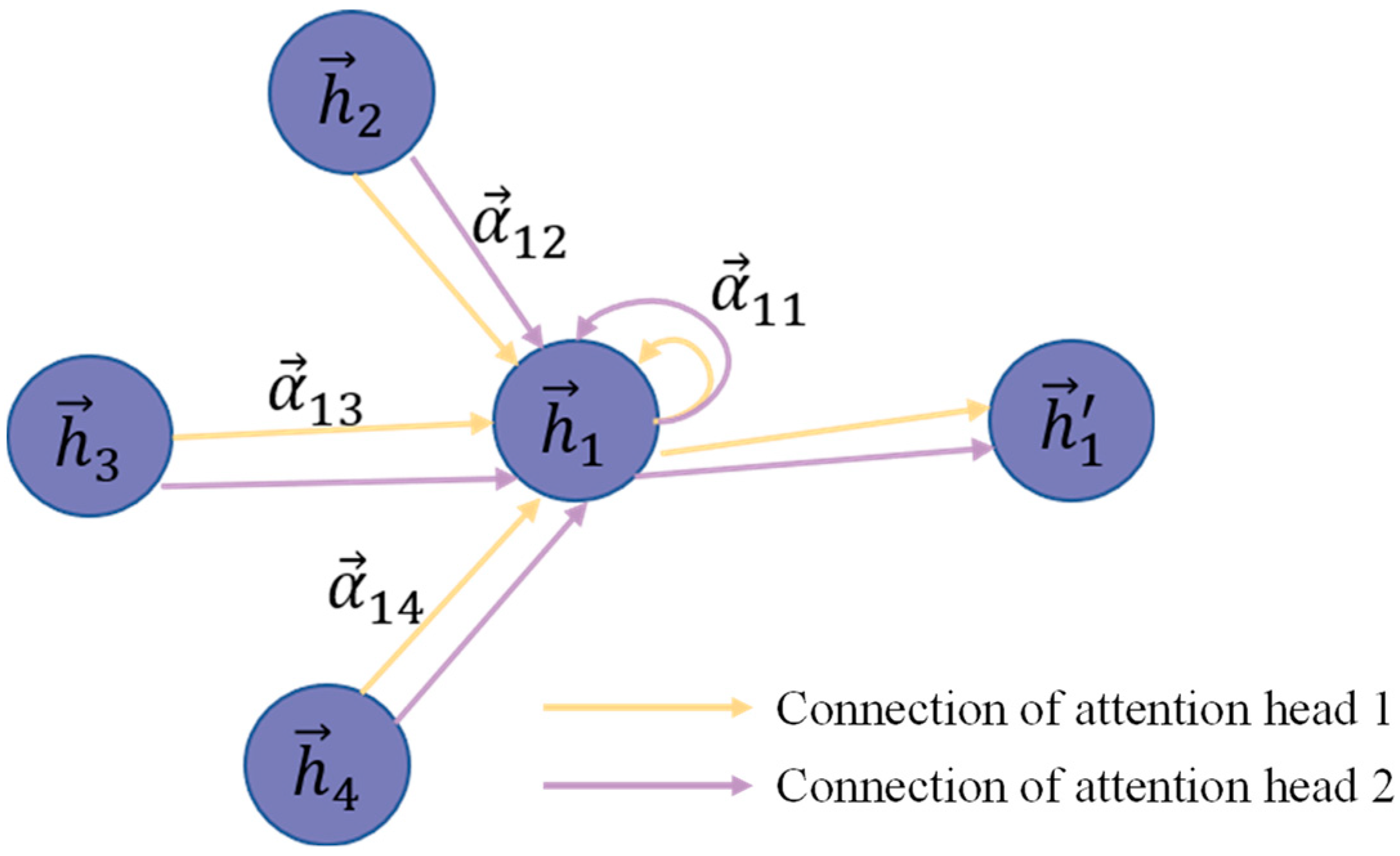
2.1. Graph Attention Networks
2.2. Graph Convolutional Neural Networks
2.3. Gated Recurrent Neural Network
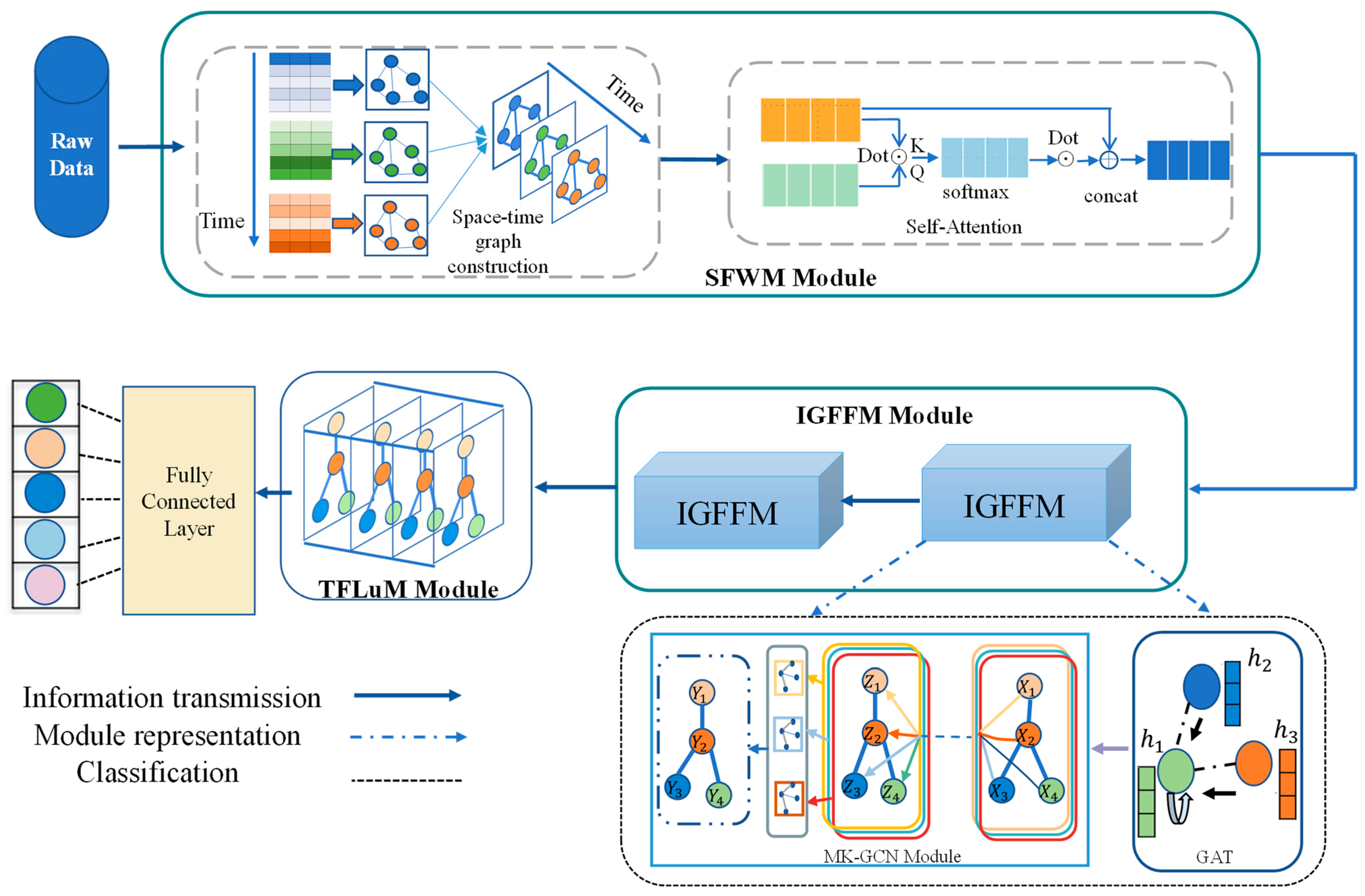
3. DIMK-GCN Network Model
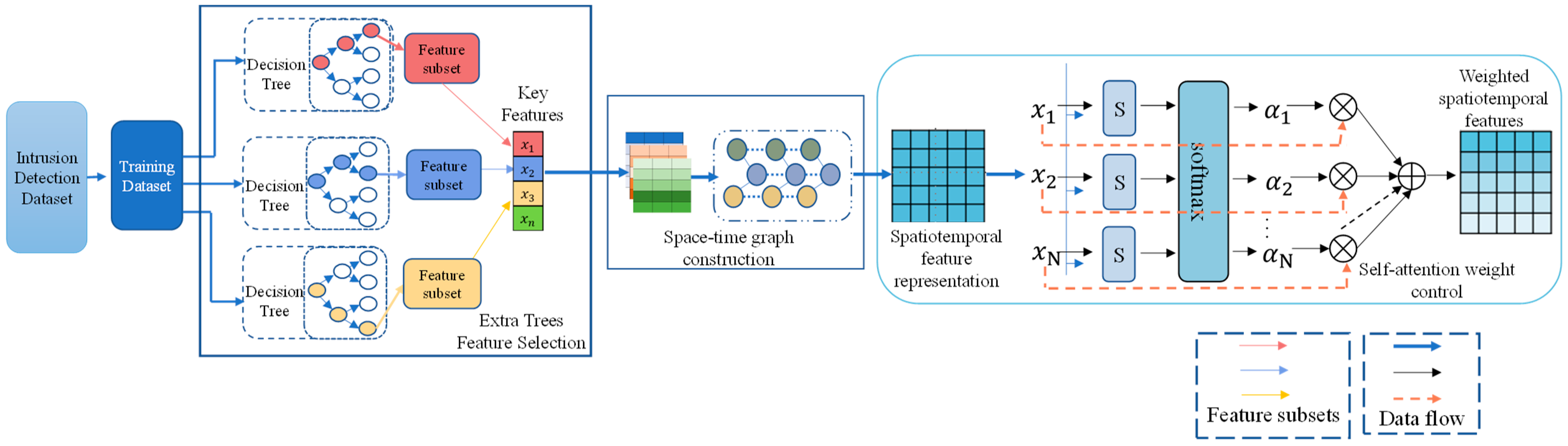
3.1. Spatiotemporal Feature Weighting Module
- is the impurity of the node before splitting;
- represents the impurity of the j-th child node after the split;
- N is the total number of samples in the node before splitting;
- is the number of samples with impurity in the child node.
| Algorithm 1: Spatiotemporal Graph Construction Algorithm |
| Input: X: Node feature matrix for all time steps, T: Time step length : Similarity threshold Output: A: Adjacency matrix for each time step, Steps:
|
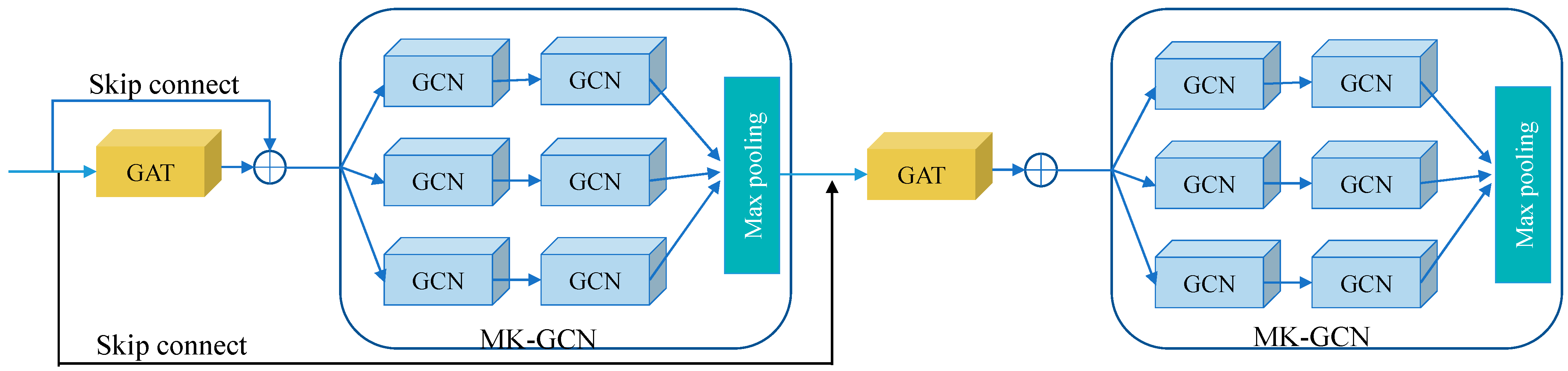
3.2. Interactive Graph Feature Fusion Module
3.2.1. Interactive Graph Feature Fusion
- Step 1.
- Initial feature extraction. First, GAT extracts initial node features from the input graph and calculates weights between nodes using the attention mechanism, emphasizing key neighboring node information.
- Step 2.
- Feature transmission. The node features calculated by GAT are passed to MK-GCN, which uses this information to extract rich representations of nodes from multiple feature spaces.
- Step 3.
- Feature feedback. The node representations extracted by MK-GCN are fed back to GAT, which recalculates attention weights based on the new node representations to refine node relationships.
- Step 4.
- Iterative optimization. The above process is iterated multiple times, with GAT and MK-GCN mutually enhancing each other, progressively optimizing node feature representations and node weights.
| Algorithm 2: Interactive Graph Feature Fusion Module |
| Input: X: Initial node feature matrix; A: Adjacency matrix; : Weight parameters for GAT; : Weight matrix collection for MK-GCN; activation_GAT: Activation function type for GAT; activation_MKGCN: Activation function type for MK-GCN; num_iterations: Number of interaction iterations. Output: X_refined: Final refined node feature matrix Steps:
|
3.2.2. Edge Weight Learning with Graph Attention
3.2.3. Node Feature Learning with Multi-Channel Graph Convolution
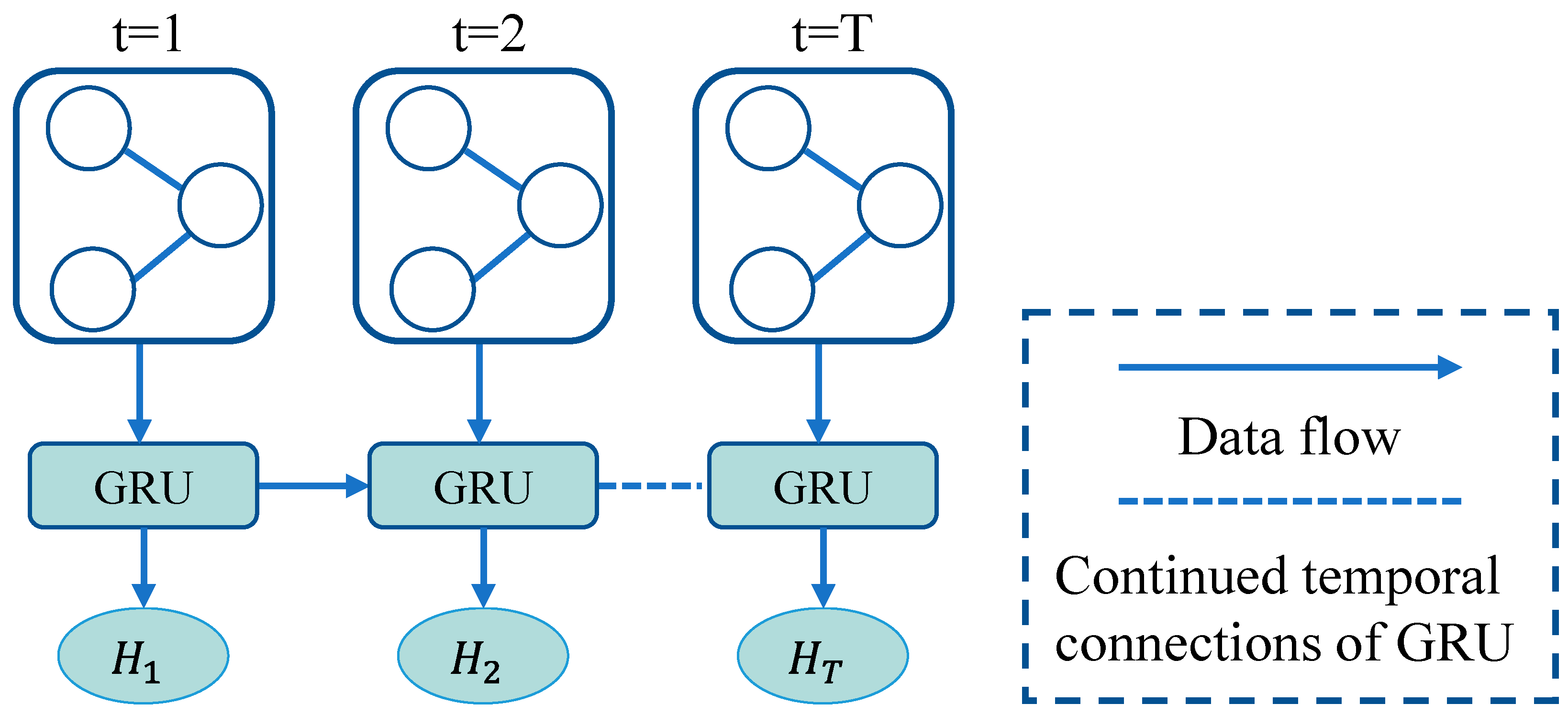
3.3. Temporal Feature Learning Module
4. Experiment
4.1. Evaluation Metrics
4.2. Dataset Description
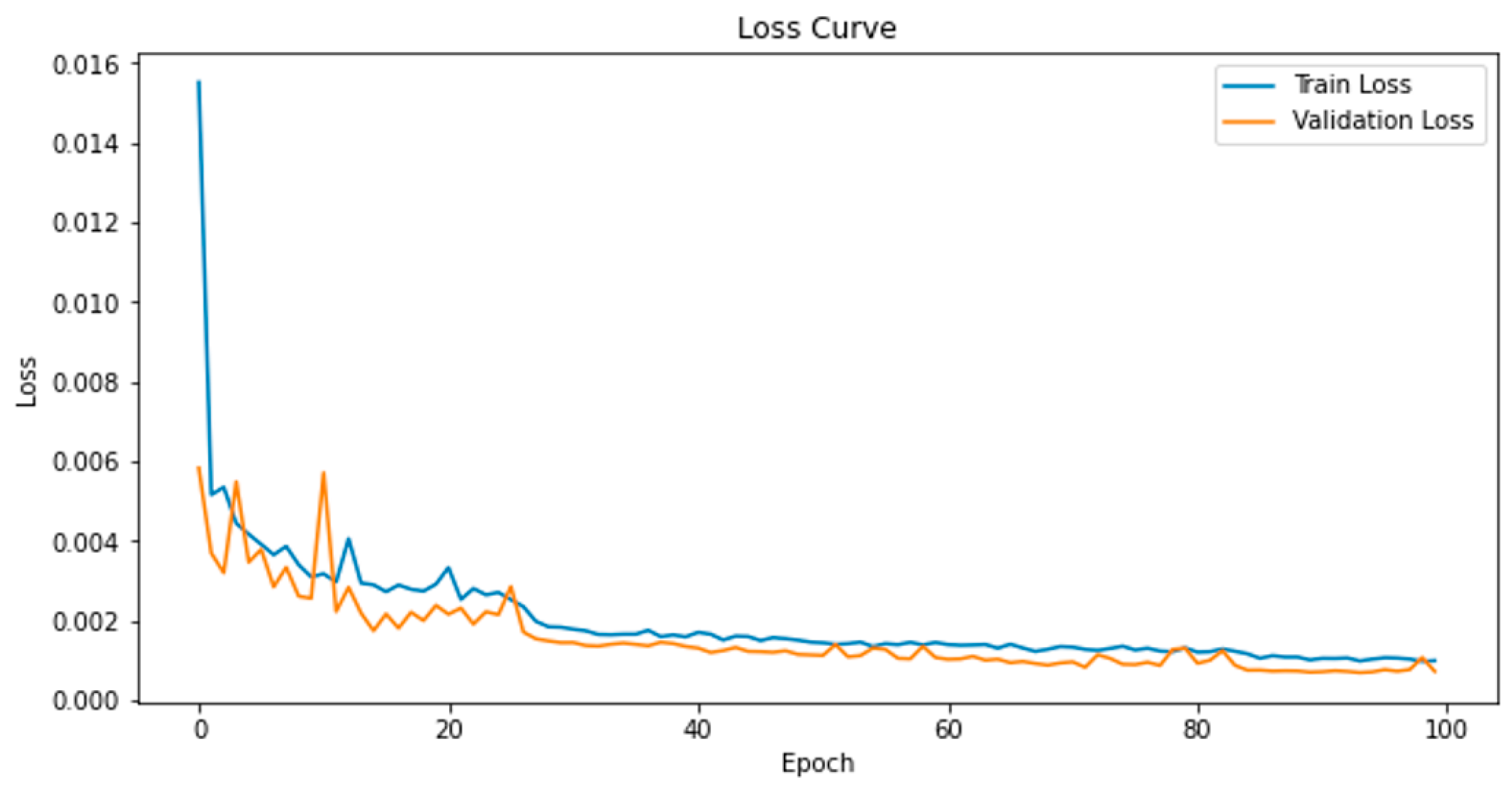
4.3. Parameter Settings
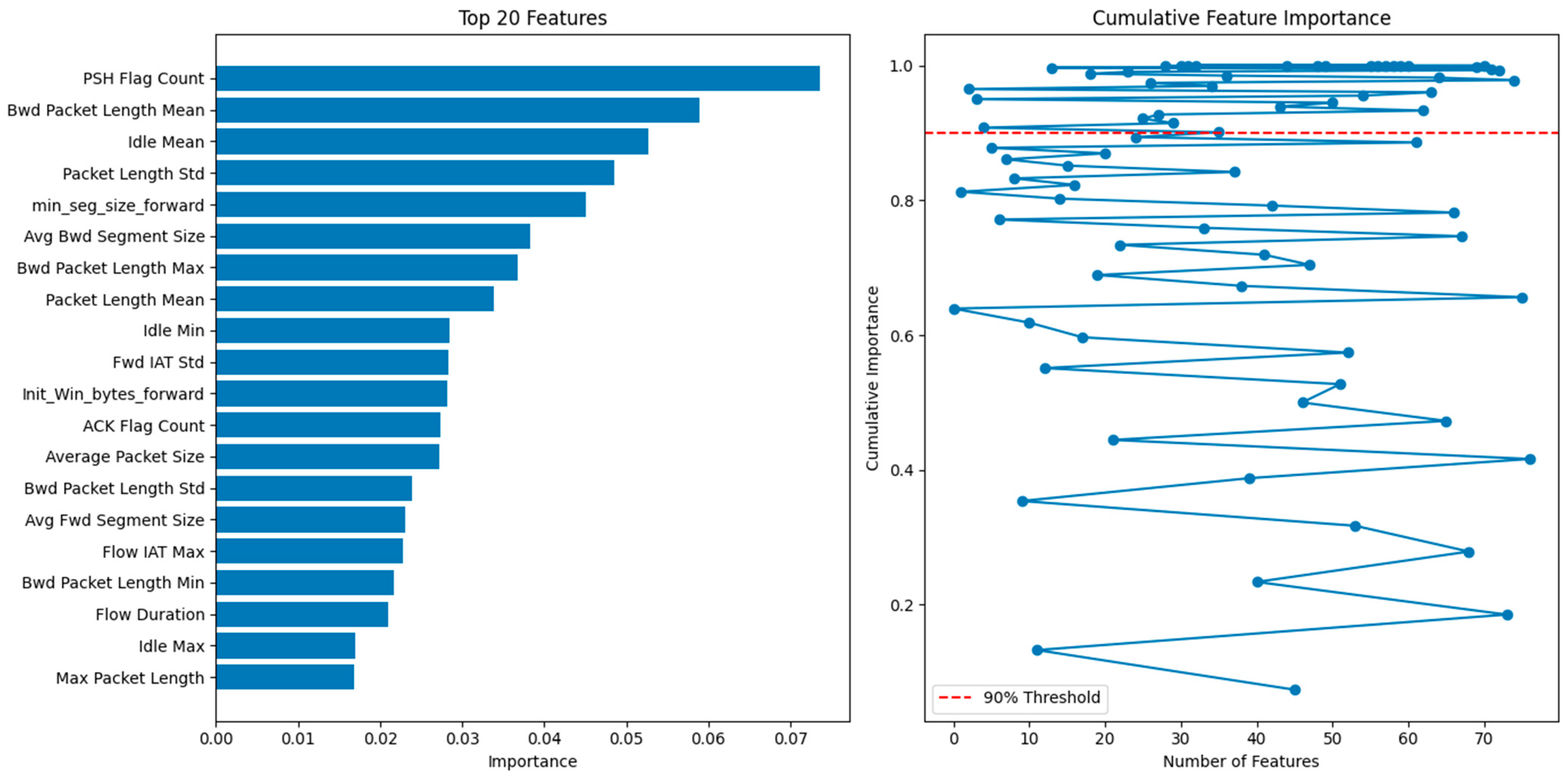
4.4. Dataset Preprocessing
- Data Cleaning: Records with missing values, infinite values, or insufficient labels were removed to enhance dataset integrity and reliability.
- Data Numerization: Non-numeric features such as protocol type, flag, and service were converted into numeric values using label encoding.
- Data Normalization: Min–max normalization was applied to scale all features into a similar range while preserving the relative positions of data points.
- Class Imbalance Handling: The SMOTE algorithm was used to synthesize minority-class samples and balance the dataset, improving the model’s learning and generalization capabilities.
4.5. Ablation Study
4.6. Impact of DIMK-GCN Channels
4.7. Model Performance Analysis
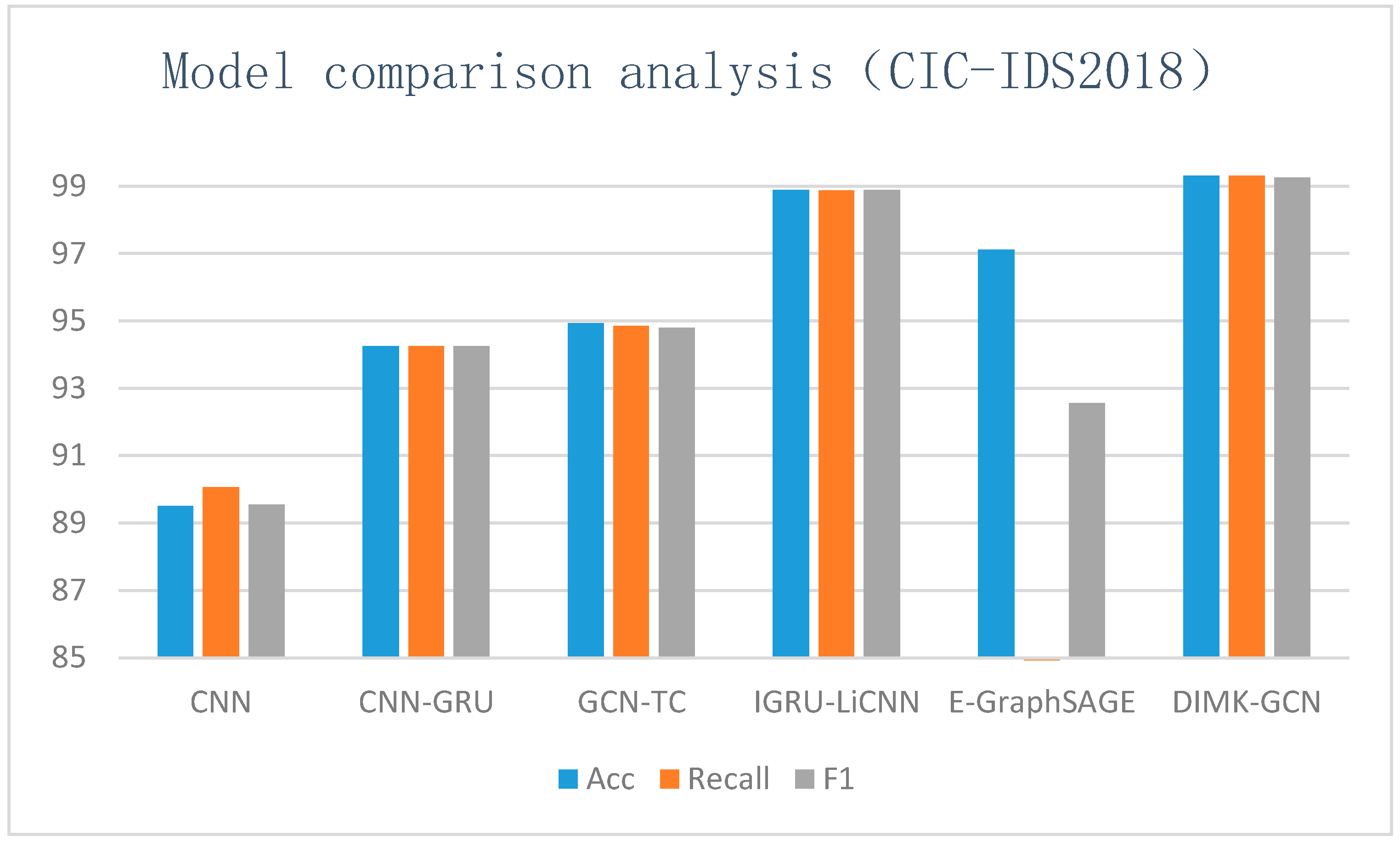
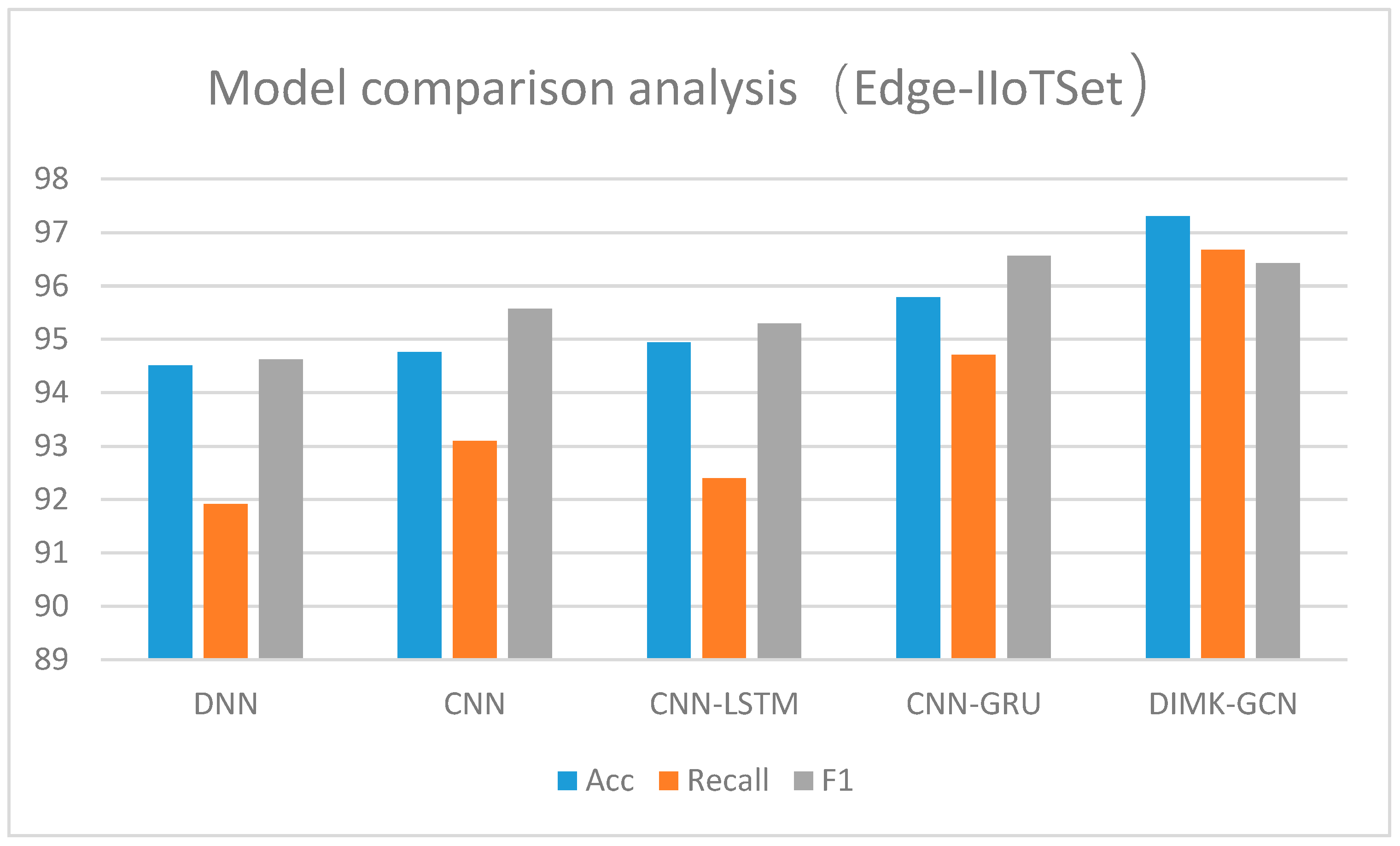
4.8. Comparative Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ren, K.; Yuan, S.; Zhang, C.; Shi, Y.; Huang, Z. CANET: A hierarchical cnn-attention model for network intrusion detection. Comput. Commun. 2023, 205, 170–181. [Google Scholar]
- Qazi, E.U.; Faheem, M.H.; Zia, T. HDLNIDS: Hybrid deep-learning-based network intrusion detection system. Appl. Sci. 2023, 13, 4921. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, J. CNID: Research of network intrusion detection based on convolutional neural network. Discret. Dyn. Nat. Soc. 2020, 2020, 4705982. [Google Scholar]
- Xu, H.; Sun, L.; Fan, G.; Li, W.; Kuang, G. A hierarchical intrusion detection model combining multiple deep learning models with attention mechanism. IEEE Access 2023, 11, 66212–66226. [Google Scholar]
- Zhou, C.; Yang, D.; Wei, S.J. Lightweight Network Intrusion Detection Model Integrating GRU and CNN. Comput. Syst. Appl. 2023, 32, 162–170. [Google Scholar]
- Mittal, K.; Khurana Batra, P. Graph-ensemble fusion for enhanced IoT intrusion detection: Leveraging GCN and deep learning. Clust. Comput. 2024, 27, 10525–10552. [Google Scholar]
- Lin, L.; Zhong, Q.; Qiu, J.; Liang, Z. E-GRACL: An IoT intrusion detection system based on graph neural networks. J. Supercomput. 2025, 81, 42. [Google Scholar]
- Jahin, M.A.; Soudeep, S.; Mridha, M.F.; Kabir, R.; Islam, M.R.; Watanobe, Y. CAGN-GAT Fusion: A Hybrid Contrastive Attentive Graph Neural Network for Network Intrusion Detection. arXiv 2025, arXiv:2503.00961. [Google Scholar]
- Tran, D.H.; Park, M. FN-GNN: A novel graph embedding approach for enhancing graph neural networks in network intrusion detection systems. Appl. Sci. 2024, 14, 6932. [Google Scholar] [CrossRef]
- Abdullayeva, F.; Suleymanzade, S. Cyber security attack recognition on cloud computing networks based on graph convolutional neural network and graphsage models. Results Control Optim. 2024, 15, 100423. [Google Scholar] [CrossRef]
- Nowroozi, E.; Taheri, R.; Hajizadeh, M.; Bauschert, T. Verifying the Robustness of Machine Learning based Intrusion Detection Against Adversarial Perturbation. In Proceedings of the 2024 IEEE International Conference on Cyber Security and Resilience (CSR), IEEE, London, UK, 2–4 September 2024; pp. 9–15. [Google Scholar]
- Shojafar, M.; Taheri, R.; Pooranian, Z.; Javidan, R.; Miri, A.; Jararweh, Y. Automatic clustering of attacks in intrusion detection systems. In Proceedings of the 2019 IEEE/ACS 16th International Conference on Computer Systems and Applications (AICCSA), IEEE, Abu Dhabi, United Arab Emirates, 3–7 November 2019; pp. 1–8. [Google Scholar]
- Reka, R.; Karthick, R.; Ram, R.S.; Singh, G. Multi head self-attention gated graph convolutional network based multi-attack intrusion detection in MANET. Comput. Secur. 2024, 136, 103526. [Google Scholar] [CrossRef]
- Altaf, T.; Wang, X.; Ni, W.; Liu, R.P.; Braun, R. NE-GConv: A lightweight node edge graph convolutional network for intrusion detection. Comput. Secur. 2023, 130, 103285. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, Y.; Lan, J. Intrusion detection using few-shot learning based on triplet graph convolutional network. J. Web Eng. 2021, 20, 1527–1552. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Cho, K. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Shang, R.; Ma, Y. Electric Vehicle Charging Load Forecasting Based on K-Means++-GRU-KSVR. World Electr. Veh. J. 2024, 15, 582. [Google Scholar] [CrossRef]
- Sharafaldin, I.; Lashkari, A.H.; Ghorbani, A.A. Toward generating a new intrusion detection dataset and intrusion traffic characterization. ICISSp 2018, 1, 108–116. [Google Scholar]
- Leevy, J.L.; Khoshgoftaar, T.M. A survey and analysis of intrusion detection models based on cse-cic-ids2018 big data. J. Big Data 2020, 7, 1–19. [Google Scholar] [CrossRef]
- Ferrag, M.A.; Friha, O.; Hamouda, D.; Maglaras, L.; Janicke, H. Edge-IIoTset: A new comprehensive realistic cyber security dataset of IoT and IIoT applications for centralized and federated learning. IEEE Access 2022, 10, 40281–40306. [Google Scholar] [CrossRef]
- Lanvin, M.; Gimenez, P.F.; Han, Y.; Majorczyk, F.; Mé, L.; Totel, É. Errors in the CICIDS2017 dataset and the significant differences in detection performances it makes. In Proceedings of the International Conference on Risks and Security of Internet and Systems, Sousse, Tunisia, 7–9 December 2022; Springer Nature: Cham, Switzerland, 2022; pp. 18–33. [Google Scholar]
- Liu, L.; Engelen, G.; Lynar, T.; Essam, D.; Joosen, W. Error prevalence in nids datasets: A case study on cic-ids-2017 and cse-cic-ids-2018. In Proceedings of the 2022 IEEE Conference on Communications and Network Security (CNS), IEEE, Virtually, 3–5 October 2022; pp. 254–262. [Google Scholar]
- Mohammadian, H.; Ghorbani, A.A.; Lashkari, A.H. A gradient-based approach for adversarial attack on deep learning-based network intrusion detection systems. Appl. Soft Comput. 2023, 137, 110173. [Google Scholar]
- Idrissi, M.J.; Alami, H.; El Mahdaouy, A.; El Mekki, A.; Oualil, S.; Yartaoui, Z.; Berrada, I. Fed-anids: Federated learning for anomaly-based network intrusion detection systems. Expert Syst. Appl. 2023, 234, 121000. [Google Scholar]
- Cao, B.; Li, C.; Song, Y.; Qin, Y.; Chen, C. Network intrusion detection model based on CNN and GRU. Appl. Sci. 2022, 12, 4184. [Google Scholar] [CrossRef]
- Zheng, J.; Li, D. GCN-TC: Combining trace graph with statistical features for network traffic classification. In Proceedings of the ICC 2019-2019 IEEE International Conference on Communications (ICC), IEEE, Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Lo, W.W.; Layeghy, S.; Sarhan, M.; Gallagher, M.; Portmann, M. E-graphsage: A graph neural network based intrusion detection system for iot. In Proceedings of the NOMS 2022-2022 IEEE/IFIP Network Operations and Management Symposium, IEEE, Budapest, Hungary, 25–29 April 2022; pp. 1–9. [Google Scholar]









| Confusion Matrix | Predicted Value | ||
|---|---|---|---|
| Attack | Normal | ||
| True Value | Attack | TN | FP |
| Normal | FN | TP | |
| Label Type | Count |
|---|---|
| BENIGN | 1,553,795 |
| DoS Hulk | 230,124 |
| PortScan | 158,930 |
| DDoS | 128,027 |
| DoS GoldenEye | 10,293 |
| FTP-Patator | 7894 |
| SSH-Patator | 5897 |
| DoS slowloris | 5796 |
| DoS Slowhttptest | 5499 |
| Web Attack -Brute Force | 1507 |
| Web Attack -XSS | 652 |
| Infiltration | 36 |
| Web Attack -Sql Injection | 21 |
| Heartbleed | 11 |
| Label Type | Count |
|---|---|
| Benign | 6,078,004 |
| DDOS attack-HOIC | 686,012 |
| DoS attacks-Hulk | 461,912 |
| Bot | 286,191 |
| FTP-BruteForce | 193,354 |
| SSH-Bruteforce | 187,589 |
| Infilteration | 160,726 |
| DoS attacks-SlowHTTPTest | 139,890 |
| DoS attacks-GoldenEye | 41,508 |
| DoS attacks-Slowloris | 10,990 |
| DDOS attack-LOIC-UDP | 1730 |
| Brute Force -Web | 611 |
| Brute Force -XSS | 230 |
| SQL Injection | 87 |
| Label Type | Count |
|---|---|
| Normal | 1,242,299 |
| DOS/DDOS | 260,161 |
| Information gathering | 63,729 |
| Injection attacks | 92,611 |
| MITM | 324 |
| Malware attacks | 75,450 |
| Parameter Name | Parameter Value |
|---|---|
| Optimizer | Adam |
| Initial Learning Rate | 0.001 |
| Weight Decay | 1.00 × 10−4 |
| Dropout Rate | 0.6 |
| Max Gradient Norm | 5 |
| Learning Rate Scheduler | ReduceLROnPlateau |
| Loss Function | Cross-Entropy Loss |
| Label Type | Evaluation Indicators | ||
|---|---|---|---|
| ACC | Recall | F1 | |
| BENIGN | 99.55 | 99.57 | 99.56 |
| DoS Hulk | 97.83 | 99.29 | 98.56 |
| PortScan | 99.34 | 99.93 | 99.65 |
| DDoS | 99.82 | 99.85 | 99.88 |
| DoS GoldenEye | 99.43 | 98.88 | 99.17 |
| FTP-Patator | 99.17 | 97.98 | 98.57 |
| SSH-Patator | 99.53 | 99.03 | 99.12 |
| DoS slowloris | 98.62 | 98.79 | 98.71 |
| DoS Slowhttptest | 92.30 | 98.09 | 95.11 |
| Web Attack -Brute Force | 96.72 | 94.21 | 94.25 |
| Web Attack -XSS | 93.22 | 96.85 | 96.87 |
| Infiltration | 94.36 | 95.89 | 95.82 |
| Web Attack -Sql Injection | 92.23 | 93.56 | 93.54 |
| Heartbleed | 93.15 | 94.21 | 94.23 |
| Label Type | Evaluation Indicators | ||
|---|---|---|---|
| ACC | Recall | F1 | |
| Benign | 99.68 | 99.63 | 99.62 |
| DDOS attack-HOIC | 99.12 | 99.18 | 99.18 |
| DoS attacks-Hulk | 99.26 | 99.10 | 99.20 |
| Bot | 99.63 | 99.40 | 99.42 |
| FTP-BruteForce | 98.61 | 96.71 | 97.43 |
| SSH-Bruteforce | 98.17 | 98.72 | 98.97 |
| Infilteration | 98.23 | 98.32 | 98.35 |
| DoS attacks-SlowHTTPTest | 98.72 | 98.94 | 98.95 |
| DoS attacks-GoldenEye | 97.20 | 97.59 | 97.61 |
| DoS attacks-Slowloris | 96.83 | 96.92 | 96.92 |
| DDOS attack-LOIC-UDP | 93.12 | 93.81 | 93.83 |
| Brute Force -Web | 94.42 | 95.10 | 95.12 |
| Brute Force -XSS | 92.23 | 93.56 | 93.54 |
| SQL Injection | 91.85 | 91.93 | 91.93 |
| Label Type | Evaluation Indicators | ||
|---|---|---|---|
| ACC | Recall | F1 | |
| Normal | 99.21 | 99.32 | 99.32 |
| DOS/DDOS | 96.06 | 97.10 | 97.10 |
| Information gathering | 98.13 | 97.11 | 96.50 |
| Injection attacks | 97.35 | 97.22 | 96.82 |
| MITM | 95.21 | 94.82 | 94.82 |
| Malware attacks | 97.21 | 96.12 | 95.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Zhang, C.; Yang, G.; Yang, P.; Ren, J.; Liu, L. DIMK-GCN: A Dynamic Interactive Multi-Channel Graph Convolutional Network Model for Intrusion Detection. Electronics 2025, 14, 1391. https://doi.org/10.3390/electronics14071391
Han Z, Zhang C, Yang G, Yang P, Ren J, Liu L. DIMK-GCN: A Dynamic Interactive Multi-Channel Graph Convolutional Network Model for Intrusion Detection. Electronics. 2025; 14(7):1391. https://doi.org/10.3390/electronics14071391
Chicago/Turabian StyleHan, Zhilin, Chunying Zhang, Guanghui Yang, Pengchao Yang, Jing Ren, and Lu Liu. 2025. "DIMK-GCN: A Dynamic Interactive Multi-Channel Graph Convolutional Network Model for Intrusion Detection" Electronics 14, no. 7: 1391. https://doi.org/10.3390/electronics14071391
APA StyleHan, Z., Zhang, C., Yang, G., Yang, P., Ren, J., & Liu, L. (2025). DIMK-GCN: A Dynamic Interactive Multi-Channel Graph Convolutional Network Model for Intrusion Detection. Electronics, 14(7), 1391. https://doi.org/10.3390/electronics14071391





