Recursive PID-NT Estimation-Based Second-Order SMC Strategy for Knee Exoskeleton Robots: A Focus on Uncertainty Mitigation
Abstract
:1. Introduction
2. Modeling of Exoskeleton Dynamics
3. Main Results
3.1. Mathematical Foundation
- I
- For every non-zero vector , ;
- II
- For zero vector , ;
- III
- for a symmetric matrix .
3.2. Proposed Rescursive PID NT Estimation-Based SOSMC
3.2.1. Sliding Variable Design
3.2.2. Reaching Controller Design
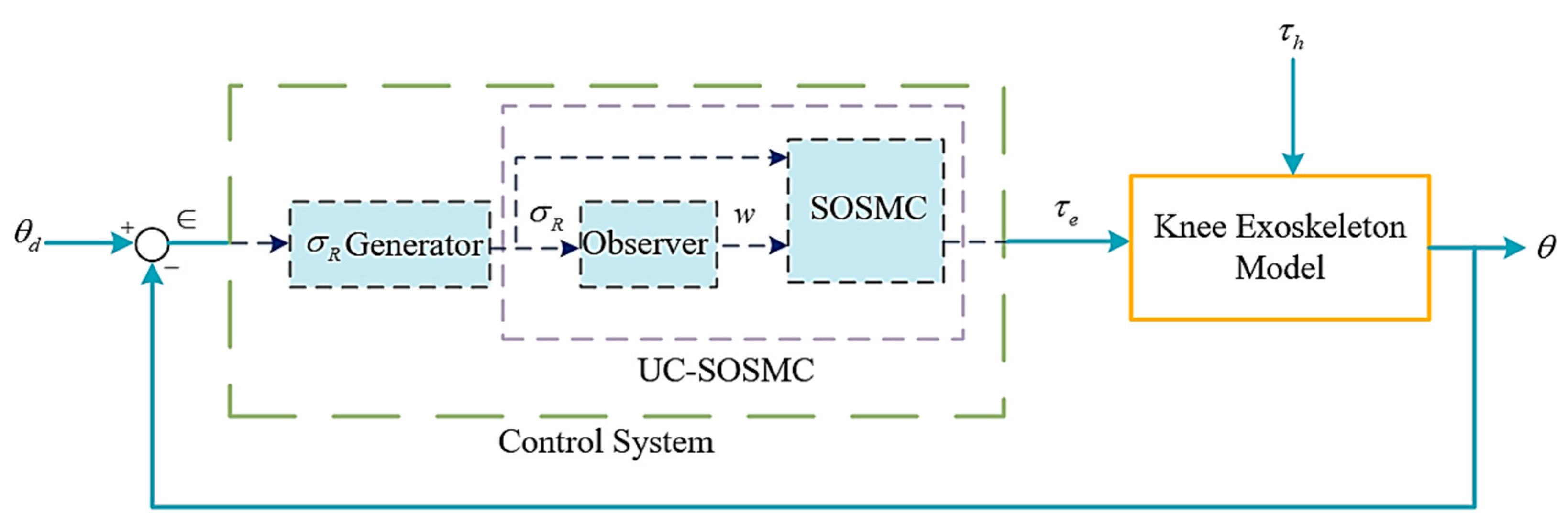
3.3. Knee Exoskeleton Control Using Proposed Controller
4. Results
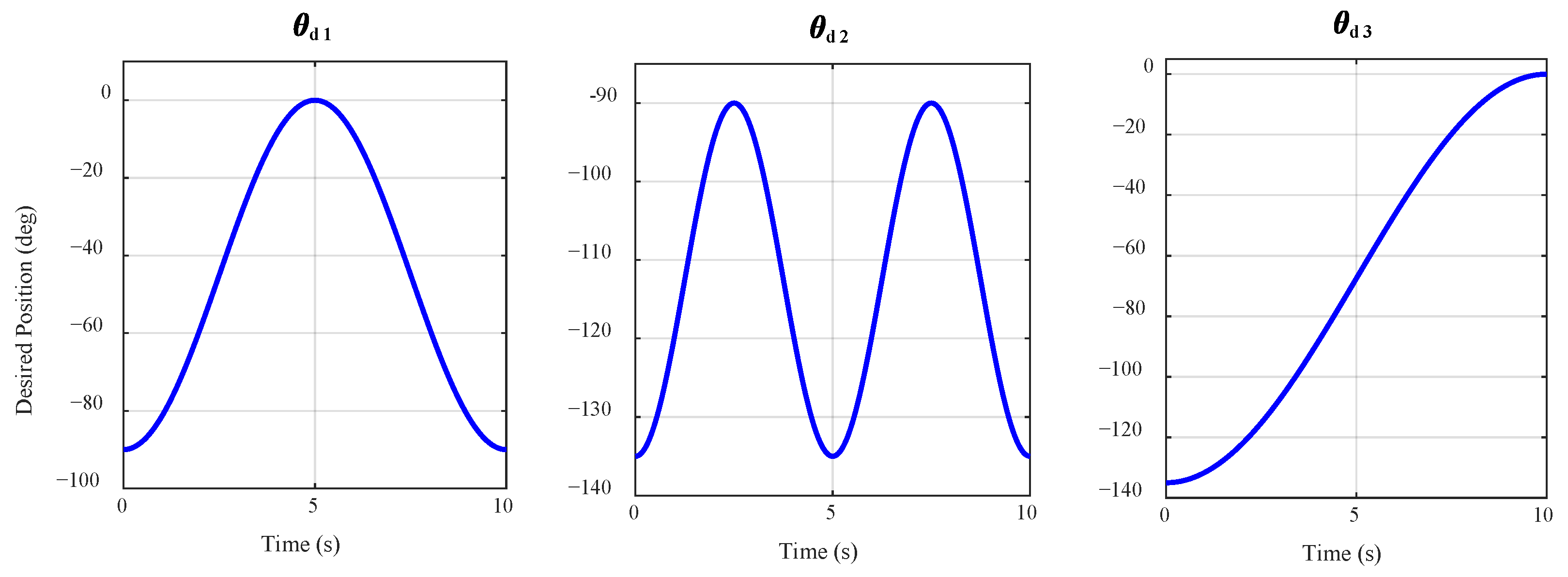
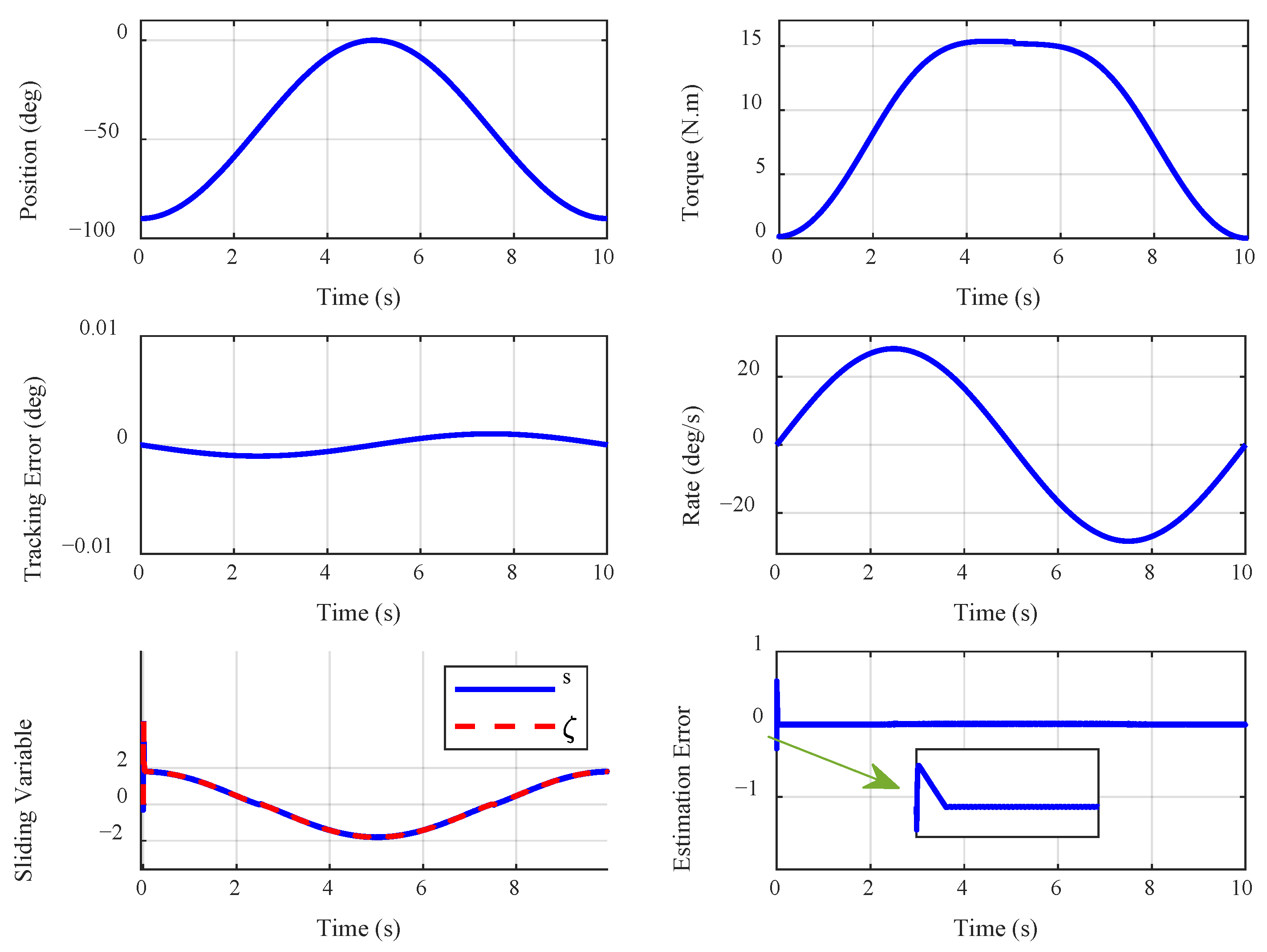
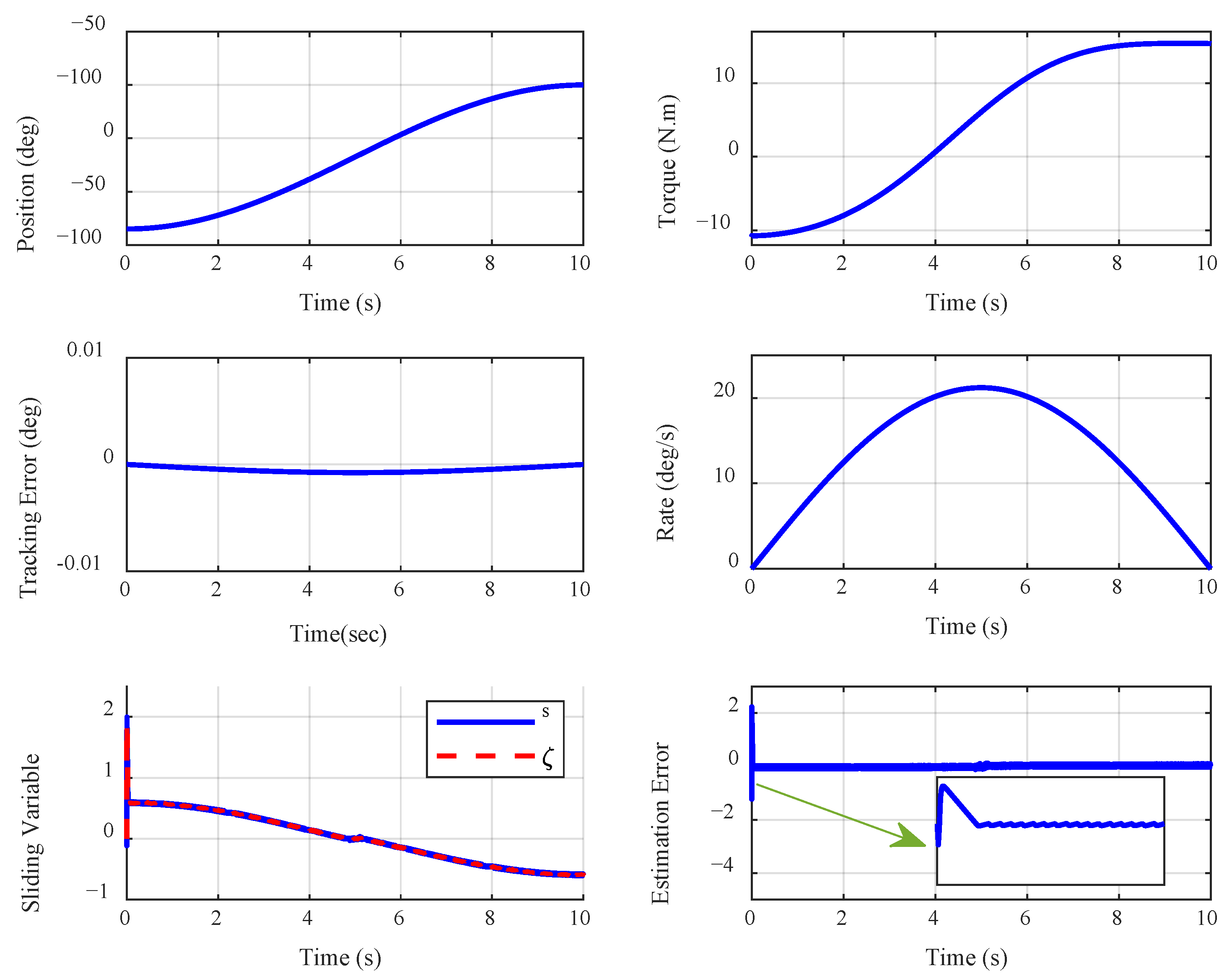
4.1. Examining the Impact of Knee Position Variation
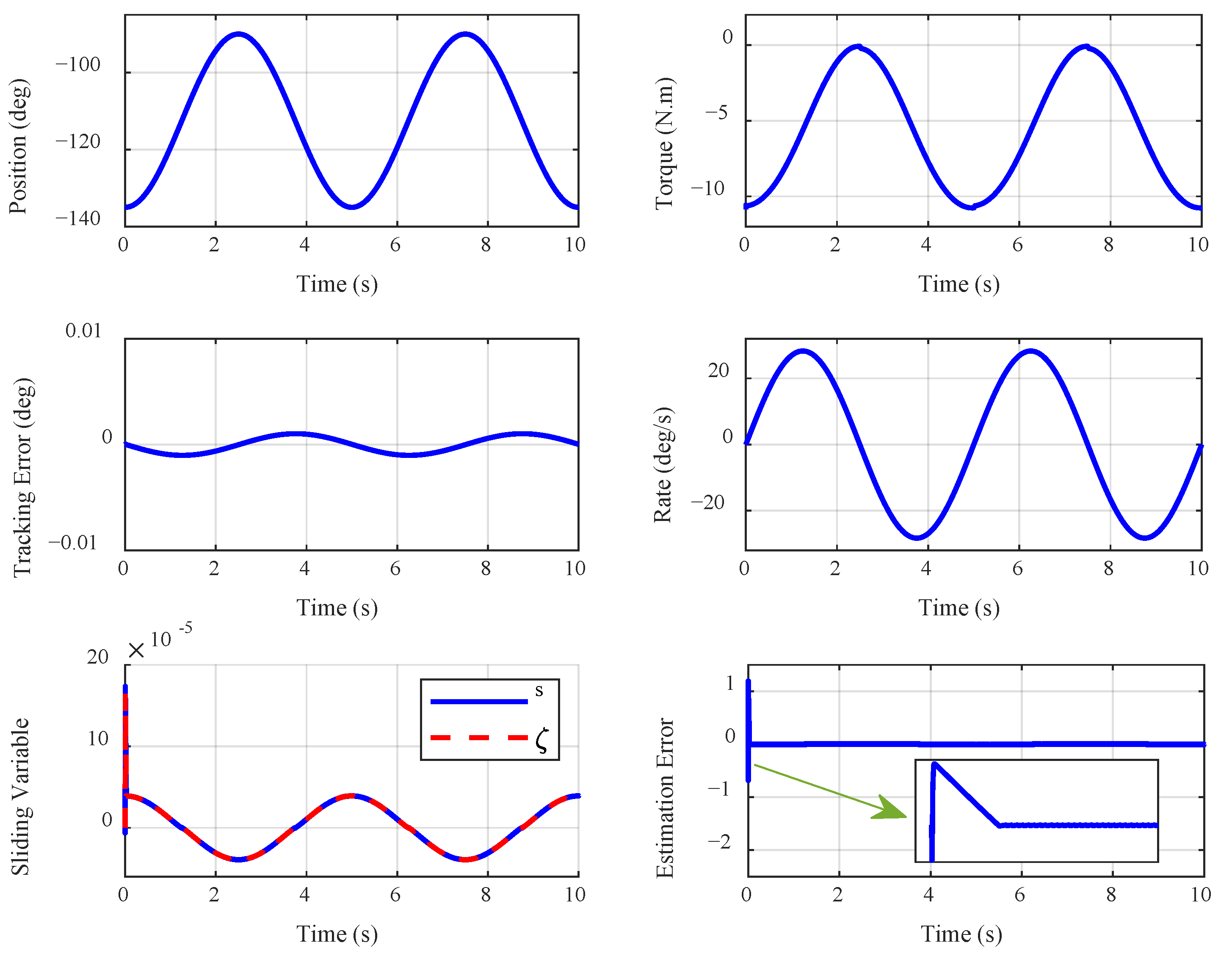
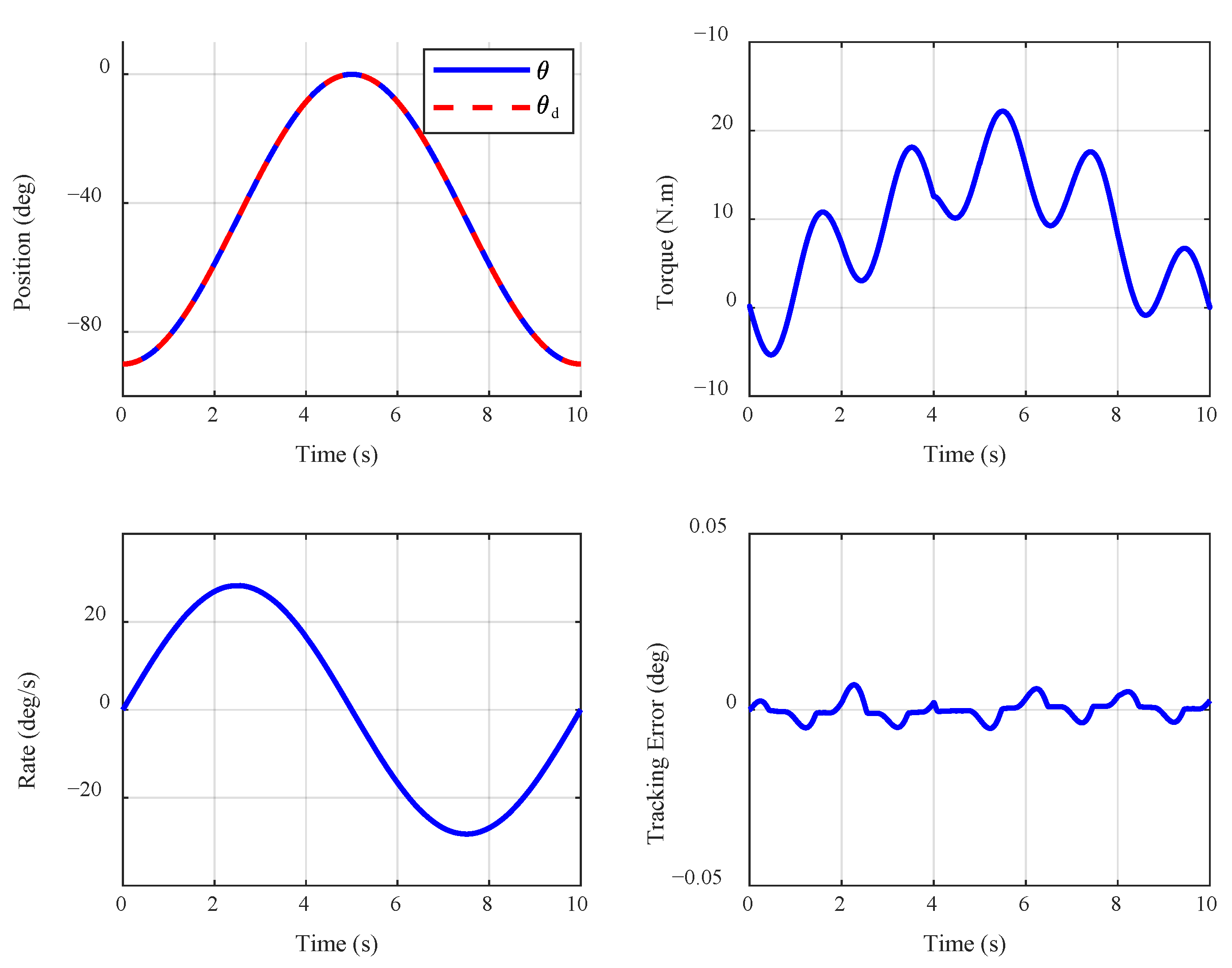
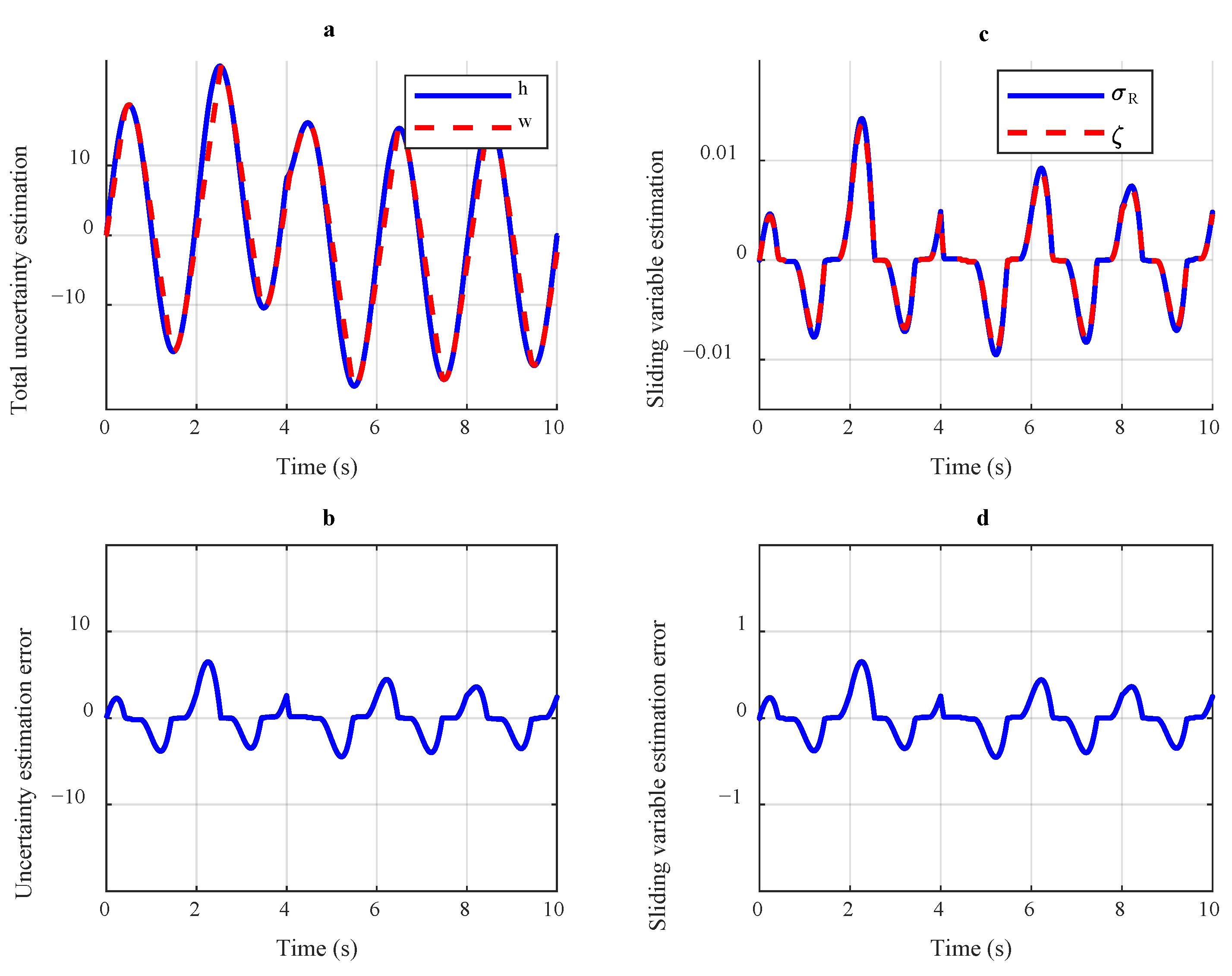
4.2. Analysis of the Impact of Human Torque Variation
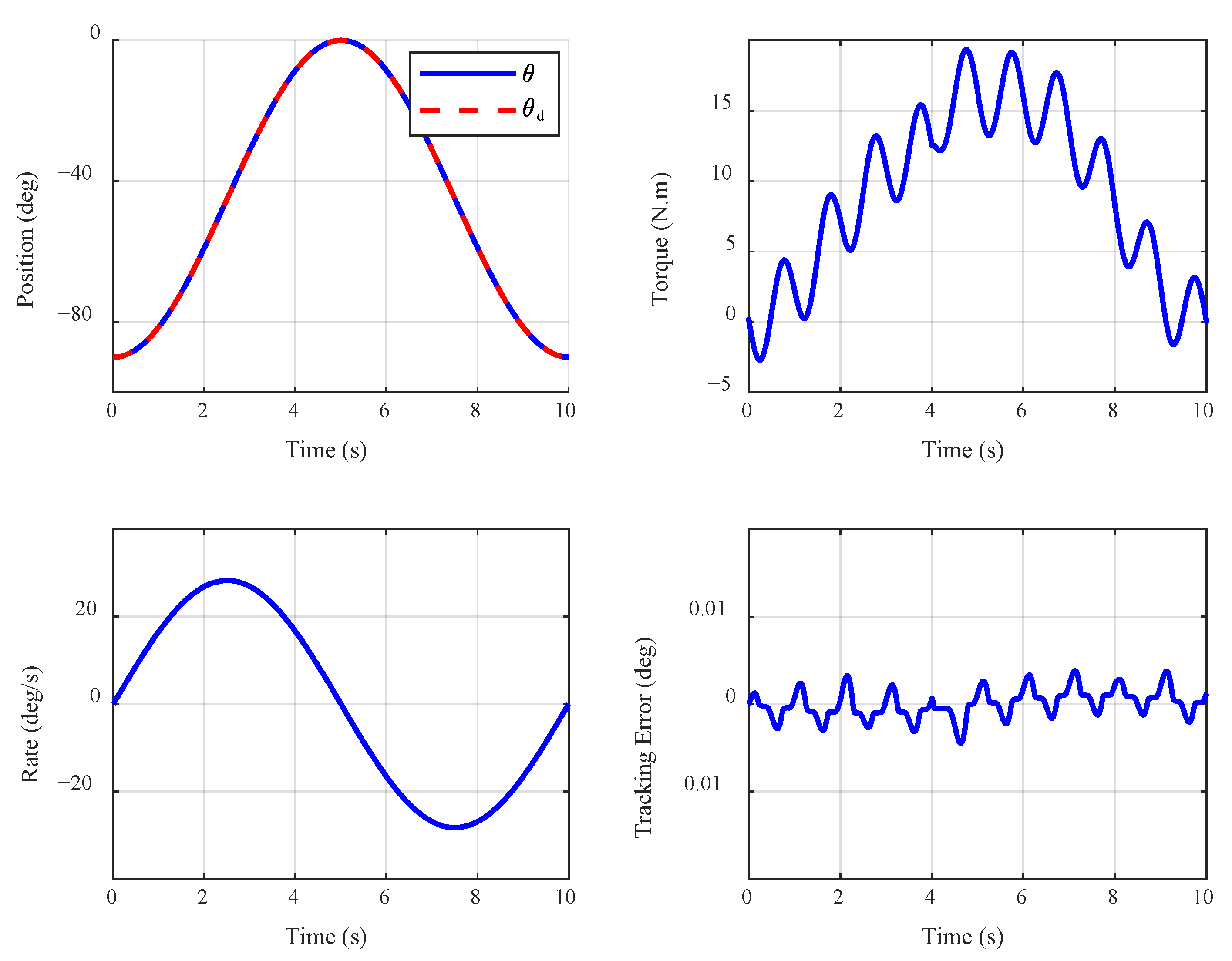
4.3. Investigation of System Behavior for Three Different Subjects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| DOF | Degree of freedom |
| HOSMC | High-order sliding mode control |
| ISE | Integral of Squared Error |
| ITSE | Integral of Time-weighted Squared Error |
| NT-SMC | Non-singular terminal sliding mode control |
| OB-SMC | Observer-based sliding mode control |
| PID | Proportional–Integral–Derivative |
| PI | Proportional–Integral |
| PD | Proportional–Derivative |
| SMC | Sliding mode control |
| SOSMC | Second-order sliding mode control |
| ST | Super twisting |
| T-SMC | Terminal sliding mode control |
References
- Yang, X.; Guo, S.; Wang, P.; Wu, Y.; Niu, L.; Liu, D. Design and Optimization Analysis of an Adaptive Knee Exoskeleton. Chin. J. Mech. Eng. 2024, 37, 104. [Google Scholar]
- Iqbal, J.; Tsagarakis, N.; Fiorilla, A.E.; Caldwell, D. Design requirements of a hand exoskeleton robotic device. In Proceedings of the 14th IASTED International Conference on Robotics and Applications (RA), Cambridge, MA, USA, 2–4 November 2009; pp. 44–51. [Google Scholar]
- Yan, M.; Gao, G.; Chen, X.; Xing, Y.; Lu, S. Human-Mechanical Biomechanical Analysis of a Novel Knee Exoskeleton Robot for Rehabilitation Training. In Proceedings of the The International Conference on Applied Nonlinear Dynamics, Vibration and Control, Hong Kong, China, 4–6 December 2023; pp. 390–402. [Google Scholar]
- Wu, Z.; Yang, M.; Xia, Y.; Wang, L. Mechanical structural design and actuation technologies of powered knee exoskeletons: A review. Appl. Sci. 2023, 13, 1064. [Google Scholar] [CrossRef]
- Iqbal, J.; Tsagarakis, N.G.; Caldwell, D.G. A human hand compatible optimised exoskeleton system. In Proceedings of the 2010 IEEE International Conference on Robotics and Biomimetics, Tianjin, China, 14–18 December 2010; pp. 685–690. [Google Scholar]
- Preethichandra, D.; Piyathilaka, L.; Sul, J.-H.; Izhar, U.; Samarasinghe, R.; Arachchige, S.D.; de Silva, L.C. Passive and Active Exoskeleton Solutions: Sensors, Actuators, Applications, and Recent Trends. Sensors 2024, 24, 7095. [Google Scholar] [CrossRef] [PubMed]
- Arefeen, A.; Xiang, Y. Subject specific optimal control of powered knee exoskeleton to assist human lifting tasks under controlled environment. Robotica 2023, 41, 2809–2828. [Google Scholar]
- Iqbal, J.; Ahmad, O.; Malik, A. HEXOSYS II-towards realization of light mass robotics for the hand. In Proceedings of the 2011 IEEE 14th International Multitopic Conference, Karachi, Pakistan, 22–24 December 2011; pp. 115–119. [Google Scholar]
- Chen, Z.; Guo, Q.; Li, T.; Yan, Y. Output constrained control of lower limb exoskeleton based on knee motion probabilistic model with finite-time extended state observer. IEEE/ASME Trans. Mechatron. 2023, 28, 2305–2316. [Google Scholar]
- Yao, Y.; Shao, D.; Tarabini, M.; Moezi, S.A.; Li, K.; Saccomandi, P. Advancements in Sensor Technologies and Control Strategies for Lower-Limb Rehabilitation Exoskeletons: A Comprehensive Review. Micromachines 2024, 15, 489. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.; Zhu, X.; Wang, R.; Gutierrez-Farewik, E.M. Neuromusculoskeletal model-informed machine learning-based control of a knee exoskeleton with uncertainties quantification. Front. Neurosci. 2023, 17, 1254088. [Google Scholar]
- Kuber, P.M.; Rashedi, E. Training and Familiarization with Industrial Exoskeletons: A Review of Considerations, Protocols, and Approaches for Effective Implementation. Biomimetics 2024, 9, 520. [Google Scholar] [CrossRef]
- Barkataki, R.; Kalita, Z.; Kirtania, S. Anthropomorphic design and control of a polycentric knee exoskeleton for improved lower limb assistance. Intell. Serv. Robot. 2024, 17, 555–577. [Google Scholar]
- Lin, C.-J.; Sie, T.-Y. Design and experimental characterization of artificial neural network controller for a lower limb robotic exoskeleton. Actuators 2023, 12, 55. [Google Scholar] [CrossRef]
- Masengo, G.; Zhang, X.; Dong, R.; Alhassan, A.B.; Hamza, K.; Mudaheranwa, E. Lower limb exoskeleton robot and its cooperative control: A review, trends, and challenges for future research. Front. Neurorobot. 2023, 16, 913748. [Google Scholar]
- Ehsani, M.; Oraee, A.; Abdi, B.; Behnamgol, V.; Hakimi, S. Adaptive Dynamic Sliding Mode Algorithm for BDFIG Control. Iran. J. Electr. Electron. Eng. 2023, 19, 2405. [Google Scholar]
- Liu, J.; Zhang, Y.; Wang, J.; Chen, W. Adaptive sliding mode control for a lower-limb exoskeleton rehabilitation robot. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 1481–1486. [Google Scholar]
- Mefoued, S. A second order sliding mode control and a neural network to drive a knee joint actuated orthosis. Neurocomputing 2015, 155, 71–79. [Google Scholar]
- Gol, V.B.; Ghahramani, N. Design of a New Proportional Guidance Algorithm Using Sliding Mode Control. Aerosp. Mech. J. 2014, 10, 77–86. [Google Scholar]
- Utkin, V.; Poznyak, A.; Orlov, Y.; Polyakov, A. Conventional and high order sliding mode control. J. Frankl. Inst. 2020, 357, 10244–10261. [Google Scholar]
- Khamar, M.; Edrisi, M. Designing a backstepping sliding mode controller for an assistant human knee exoskeleton based on nonlinear disturbance observer. Mechatronics 2018, 54, 121–132. [Google Scholar]
- Gogani, N.S.; Behnamgol, V.; Hakimi, S.; Derakhshan, G. Finite time back stepping supper twisting controller design for a quadrotor. Eng. Lett. 2022, 30, 674–680. [Google Scholar]
- Alouane, S.; Djeghali, N.; Bettayeb, M.; Hamoudi, A. High-order sliding mode-based robust active disturbance rejection control for uncertain fractional-order nonlinear systems. Int. J. Syst. Sci. 2025, 1–21. [Google Scholar] [CrossRef]
- Ehsani, M.; Oraee, A.; Abdi, B.; Behnamgol, V.; Hakimi, M. Adaptive dynamic sliding mode controller based on extended state observer for brushless doubly fed induction generator. Int. J. Dyn. Control. 2024, 12, 3719–3732. [Google Scholar] [CrossRef]
- Zhufu, G.; Wang, S.; Wang, X. Finite time disturbance observer based sliding mode control for PMSM with unknown disturbances. Int. J. Robust Nonlinear Control 2024, 34, 7547–7564. [Google Scholar] [CrossRef]
- Mefoued, S.; Belkhiat, D.E.C. A robust control scheme based on sliding mode observer to drive a knee-exoskeleton. Asian J. Control. 2019, 21, 439–455. [Google Scholar]
- Behnamgol, V.; Asadi, M.; Mohamed, M.A.A.; Aphale, S.S.; Niri, M.F. Comprehensive review of lithium-ion battery state of charge estimation by sliding mode observers. Energies 2024, 17, 5754. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, W.; Guo, Q. Extended State Observer-Based Sliding Mode Control Design of Two-DOF Lower Limb Exoskeleton. Actuators 2023, 12, 402. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, G.; Ouyang, H.; Mei, L. An adaptive super twisting nonlinear fractional order PID sliding mode control of permanent magnet synchronous motor speed regulation system based on extended state observer. IEEE Access 2020, 8, 53498–53510. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Y.; Man, Z. Terminal sliding mode control–an overview. IEEE Open J. Ind. Electron. Soc. 2020, 2, 36–52. [Google Scholar]
- Behnamgol, V.; Vali, A.R. Terminal sliding mode control for nonlinear systems with both matched and unmatched uncertainties. Iran. J. Electr. Electron. Eng. 2015, 11, 109–117. [Google Scholar]
- Mao, Y.; Chen, J. Nonsingular Fast Terminal Sliding Mode Neural Network Decentralized Control of a Quadrotor Unmanned Aerial Vehicle. Complexity 2023, 2023, 3288944. [Google Scholar]
- Sohani, B.; Rahmani, A.; Mercer, K.; Nelson-Smith, O.; Butcher, C.; Hazell, S.; Ren, Y.; Aliyu, A.; Goher, K. Optimising Knee Replacement Surgery: Development and Assessment of a Parallel Kinematic Machine for Precise Positioning in Knee Arthroplasty. In Proceedings of the Climbing and Walking Robots Conference, Kaiserslautern, Germany, 4–6 September 2024; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Mohammed, S.; Huo, W.; Huang, J.; Rifaï, H.; Amirat, Y. Nonlinear disturbance observer based sliding mode control of a human-driven knee joint orthosis. Robot. Auton. Syst. 2016, 75, 41–49. [Google Scholar]
- Mahdi, S.M.; Yousif, N.Q.; Oglah, A.A.; Sadiq, M.E.; Humaidi, A.J.; Azar, A.T. Adaptive synergetic motion control for wearable knee-assistive system: A rehabilitation of disabled patients. Actuators 2022, 11, 176. [Google Scholar] [CrossRef]
- Rifaï, H.; Mohammed, S.; Hassani, W.; Amirat, Y. Nested saturation based control of an actuated knee joint orthosis. Mechatronics 2013, 23, 1141–1149. [Google Scholar]
- Khan, A.H.; Li, S. Sliding mode control with PID sliding surface for active vibration damping of pneumatically actuated soft robots. IEEE Access 2020, 8, 88793–88800. [Google Scholar]
- Shao, X.; Sun, G.; Xue, C.; Li, X. Nonsingular terminal sliding mode control for free-floating space manipulator with disturbance. Acta Astronaut. 2021, 181, 396–404. [Google Scholar]
- Plestan, F.; Shtessel, Y.; Bregeault, V.; Poznyak, A. New methodologies for adaptive sliding mode control. Int. J. Control 2010, 83, 1907–1919. [Google Scholar]
- Shtessel, Y.B.; Shkolnikov, I.A.; Levant, A. Smooth second-order sliding modes: Missile guidance application. Automatica 2007, 43, 1470–1476. [Google Scholar]
- Behnamgol, V.; Vali, A.R.; Mohammadi, A. A new adaptive finite time nonlinear guidance law to intercept maneuvering targets. Aerosp. Sci. Technol. 2017, 68, 416–421. [Google Scholar] [CrossRef]
- Yang, J.; Yu, X.; Zhang, L.; Li, S. A Lyapunov-based approach for recursive continuous higher order nonsingular terminal sliding-mode control. IEEE Trans. Autom. Control 2020, 66, 4424–4431. [Google Scholar]
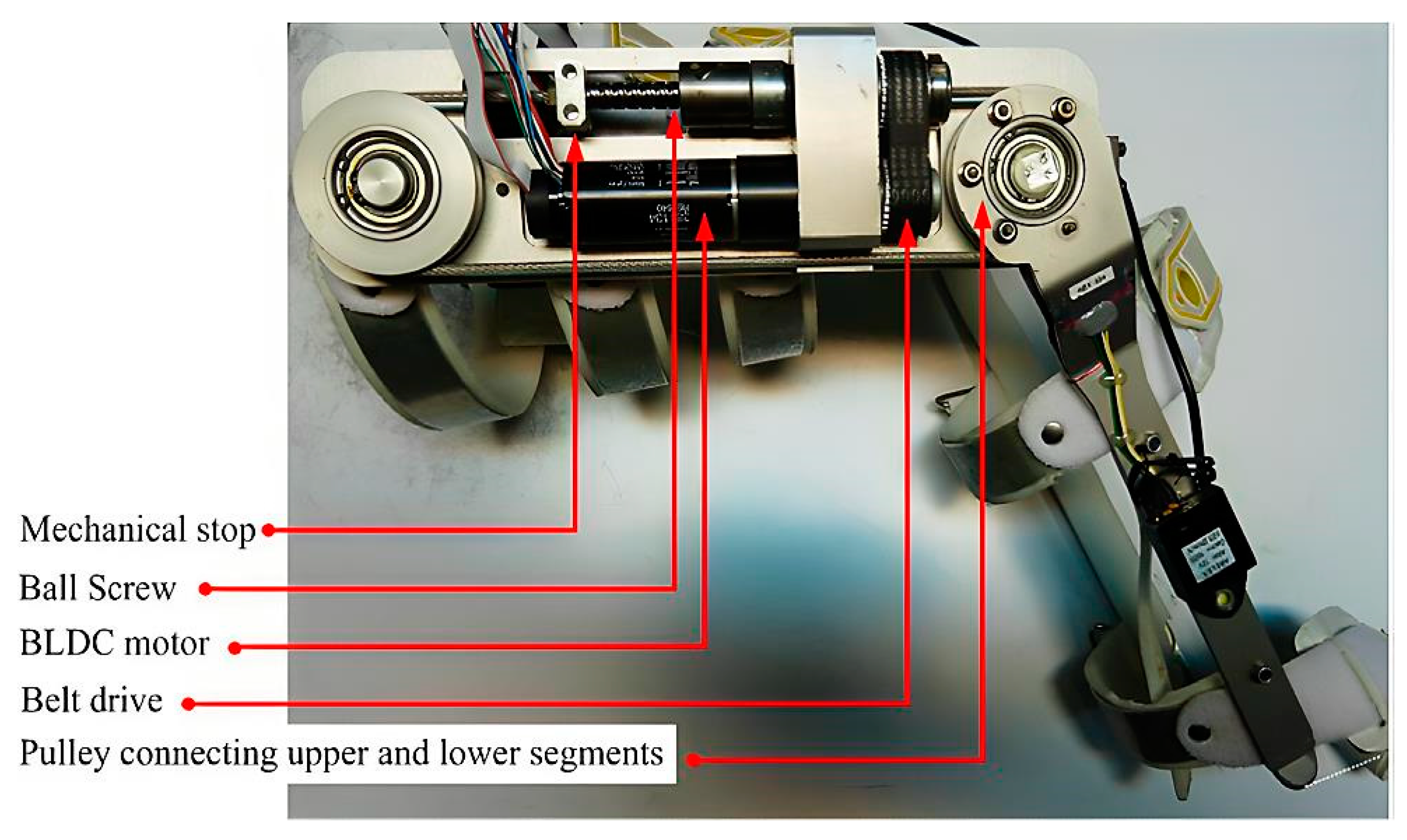
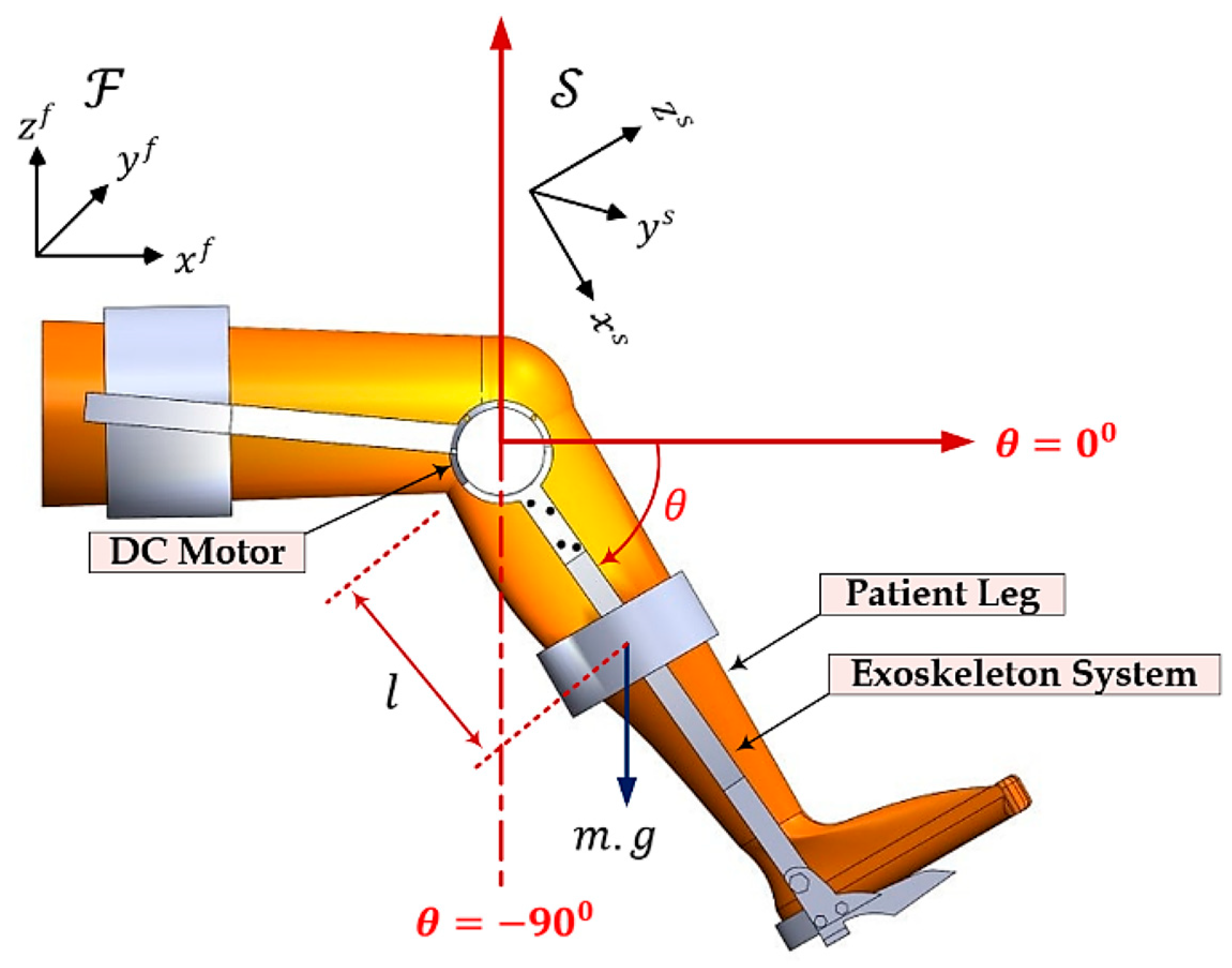

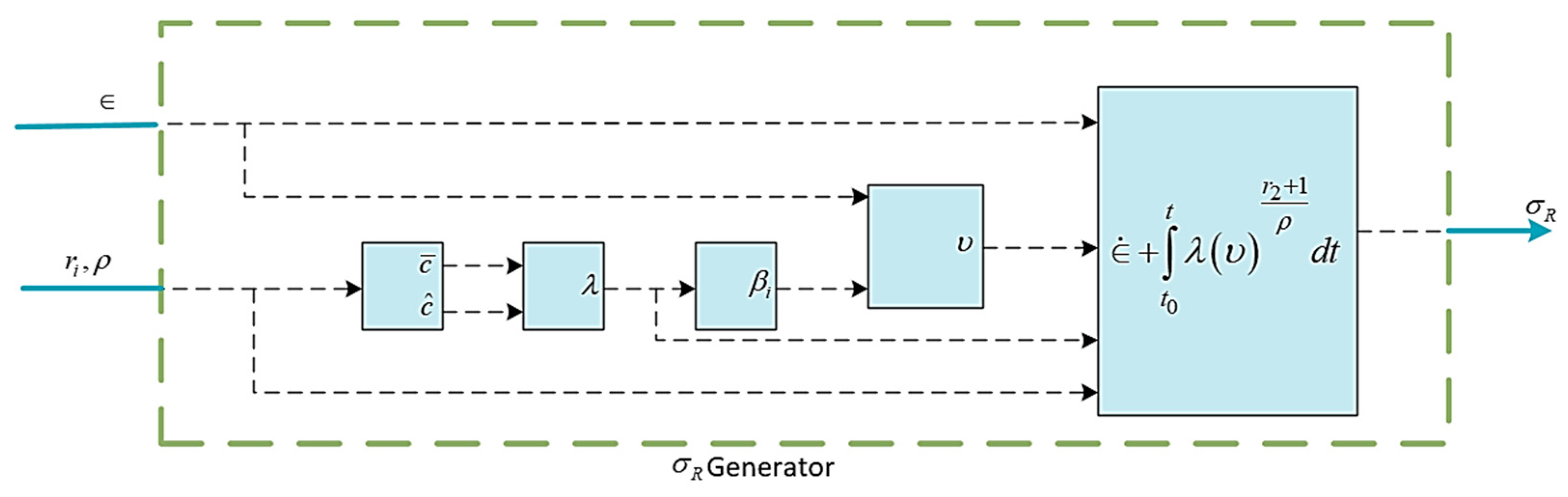
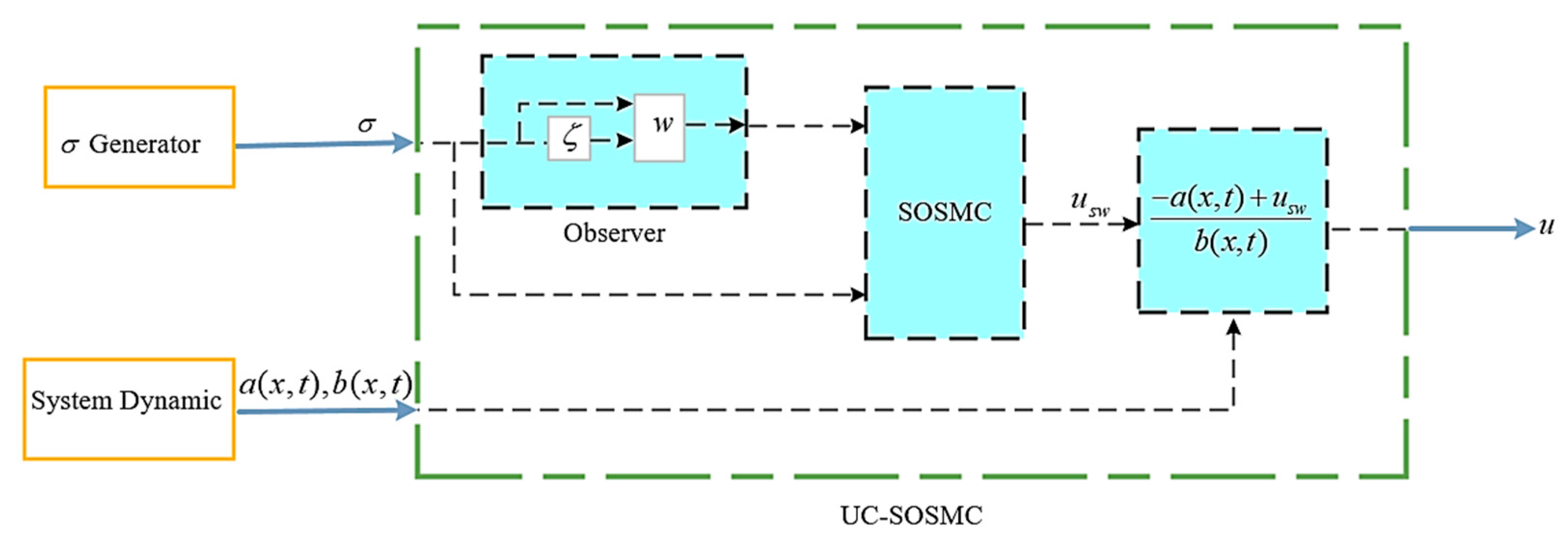




| Parameters | Value | Unit |
|---|---|---|
| 0.326 | ||
| 15.341 | ||
| K | 0.114 | |
| B | 0.064 | |
| A | 0.354 |
| Parameter | Value |
|---|---|
| 300 | |
| 20 | |
| 20 | |
| 10,000 | |
| 0.9 | |
| 0.3 |
| 0.326 | 15.39 | 0.354 | 0.064 | |
| 0.359 | 13.23 | 0.361 | 0.085 | |
| 0.314 | 17.59 | 0.387 | 0.041 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behnamgol, V.; Asadi, M.; Aphale, S.S.; Sohani, B. Recursive PID-NT Estimation-Based Second-Order SMC Strategy for Knee Exoskeleton Robots: A Focus on Uncertainty Mitigation. Electronics 2025, 14, 1455. https://doi.org/10.3390/electronics14071455
Behnamgol V, Asadi M, Aphale SS, Sohani B. Recursive PID-NT Estimation-Based Second-Order SMC Strategy for Knee Exoskeleton Robots: A Focus on Uncertainty Mitigation. Electronics. 2025; 14(7):1455. https://doi.org/10.3390/electronics14071455
Chicago/Turabian StyleBehnamgol, Vahid, Mohamad Asadi, Sumeet S. Aphale, and Behnaz Sohani. 2025. "Recursive PID-NT Estimation-Based Second-Order SMC Strategy for Knee Exoskeleton Robots: A Focus on Uncertainty Mitigation" Electronics 14, no. 7: 1455. https://doi.org/10.3390/electronics14071455
APA StyleBehnamgol, V., Asadi, M., Aphale, S. S., & Sohani, B. (2025). Recursive PID-NT Estimation-Based Second-Order SMC Strategy for Knee Exoskeleton Robots: A Focus on Uncertainty Mitigation. Electronics, 14(7), 1455. https://doi.org/10.3390/electronics14071455









