Integrated Sliding Mode Control for Permanent Magnet Synchronous Motor Drives Based on Second-Order Disturbance Observer and Low-Pass Filter
Abstract
:1. Introduction
- A novel sliding-mode control strategy is put forward, which integrates an improved reaching law and a new-type sliding-mode surface. This unique sliding-mode surface has the ability to adapt to changes in both the sliding surface itself and the system states. Through this adaptation, the control strategy intends to minimize chattering and shorten the reaching time.
- To improve the disturbance rejection and robustness of the new sliding-mode control, especially when a reference speed jump occurs, an improvement to the DOB mitigates the impact of disturbances and reduces system overshoot.
- Additionally, the DOB and LPF filter work together to enhance the system’s characteristics and make the transient characteristics smoother than before.
2. Novel Slide Mode Controller Design
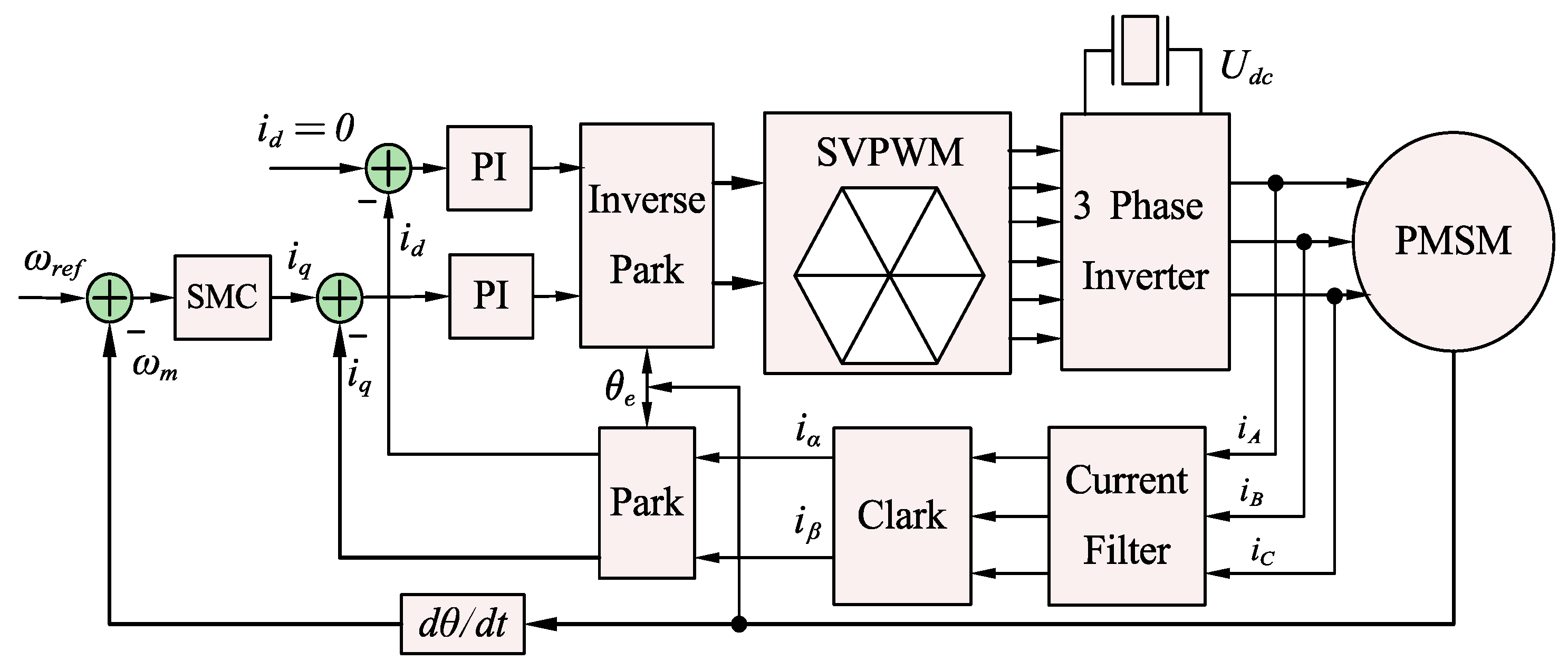
2.1. The Mathematical Model of PMSM
2.2. Proposed NSMCEAL Design
2.3. Performance Analysis of NSMCEAL
2.4. Analysis and Selection of a Novel Sliding-Mode Surface
2.5. Stability Proof
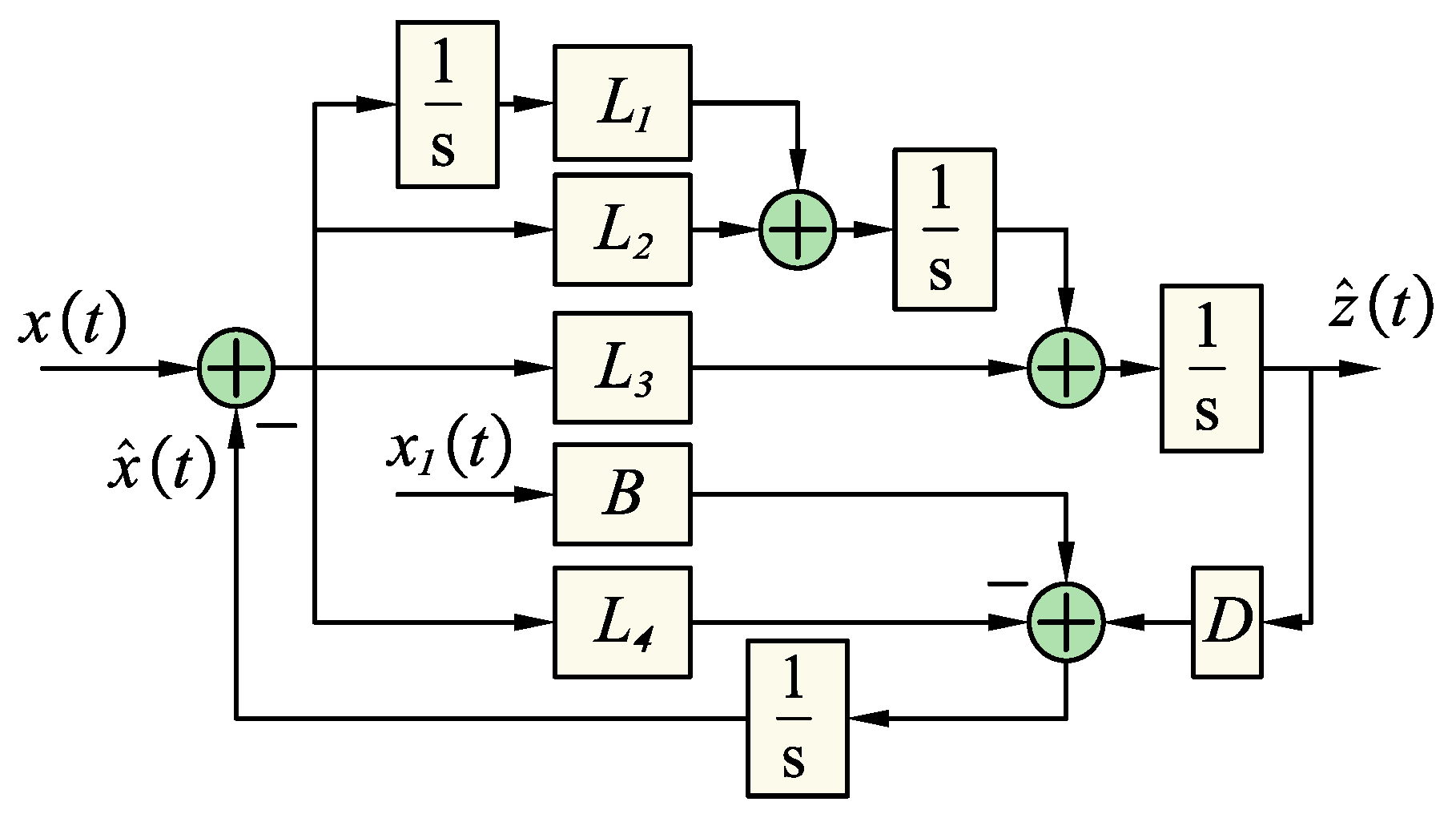
3. LPF Filter Gets Integrated into the High-Order Disturbance Observer
4. Simulation Analysis
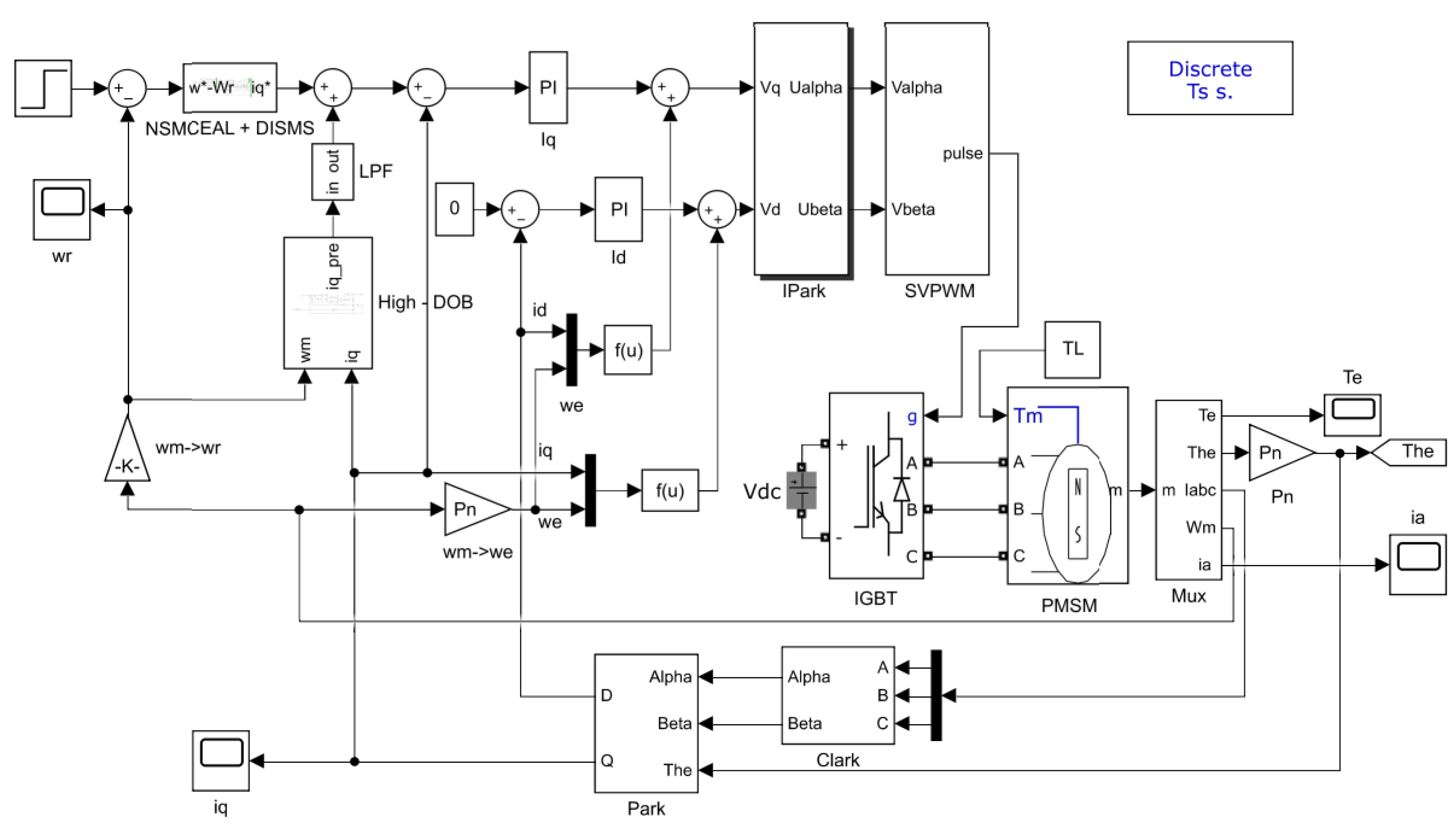
4.1. Set Up a Simulation Model
4.2. Simulation Results
4.2.1. Performance Analysis of Traditional Sliding-Mode Surface
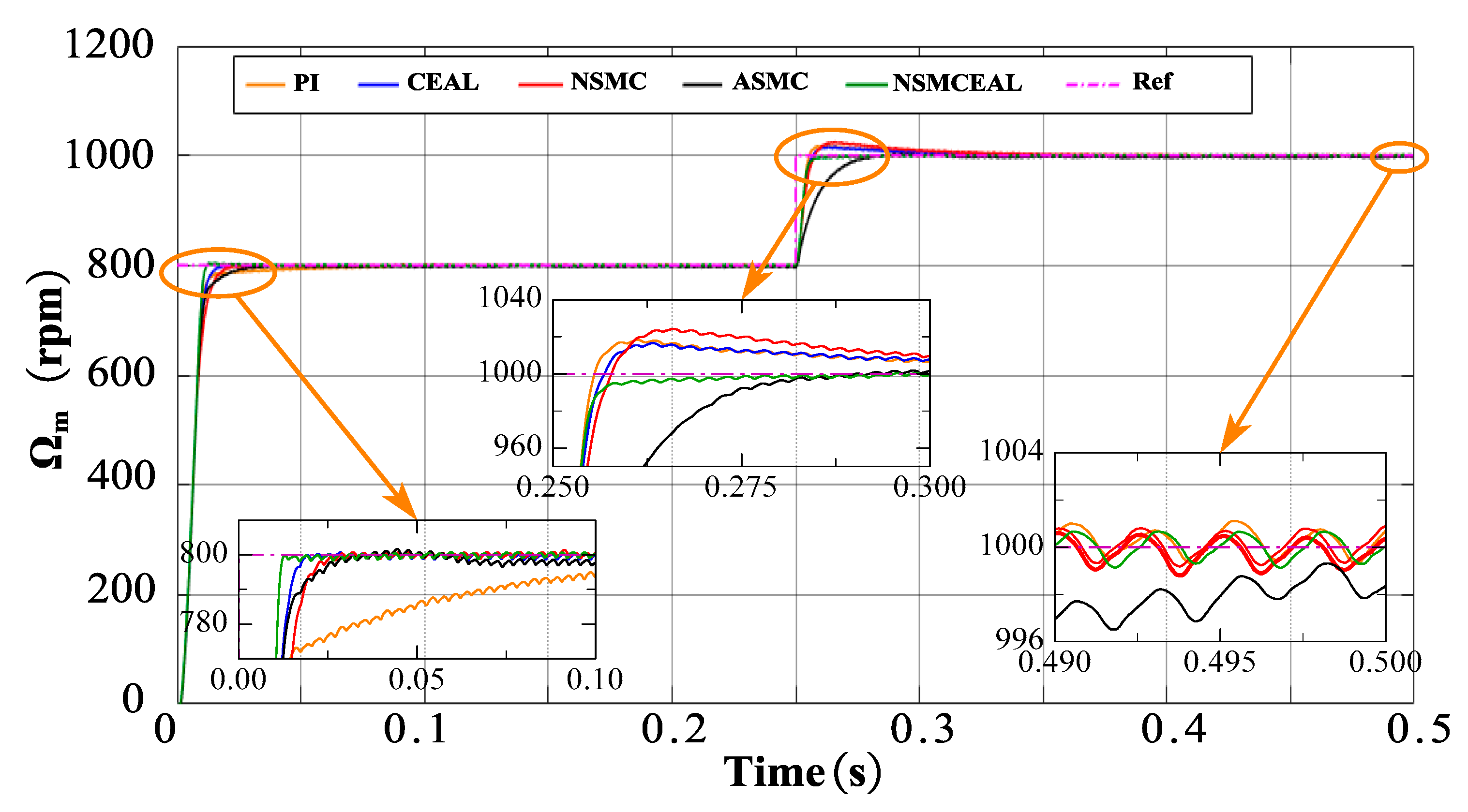
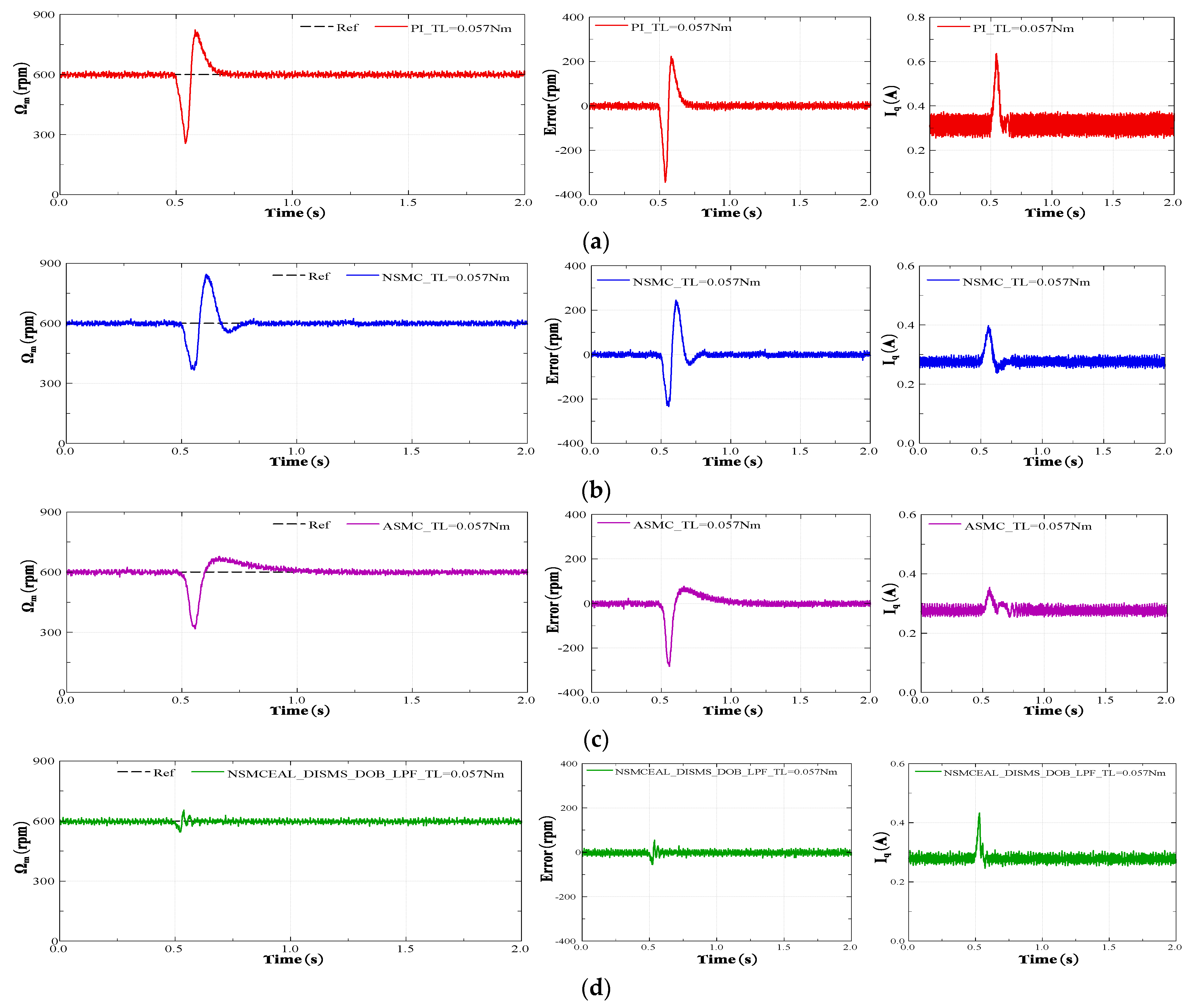
4.2.2. Evaluating and Comparing the Dynamic Performance of Sliding Surfaces
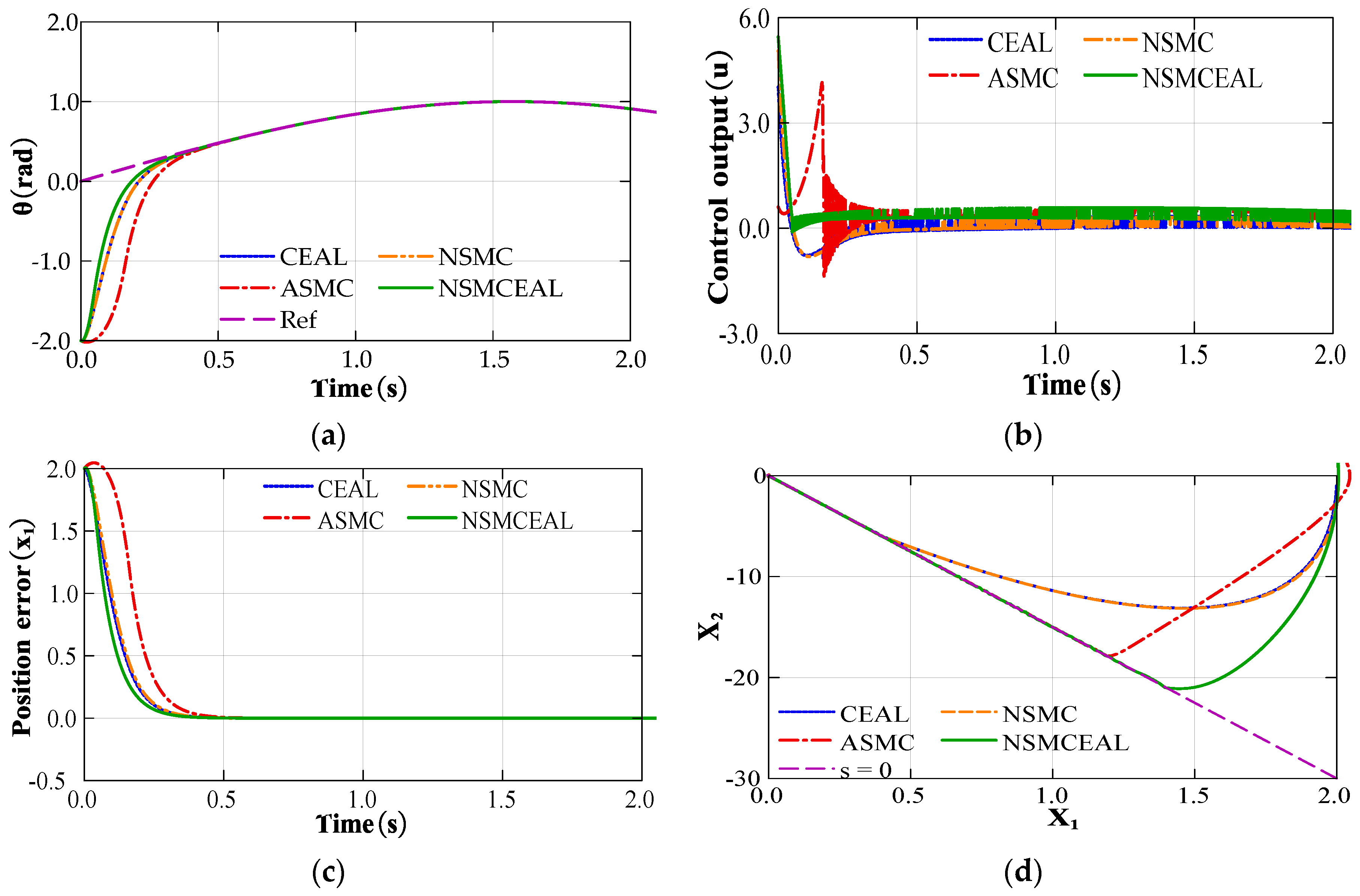
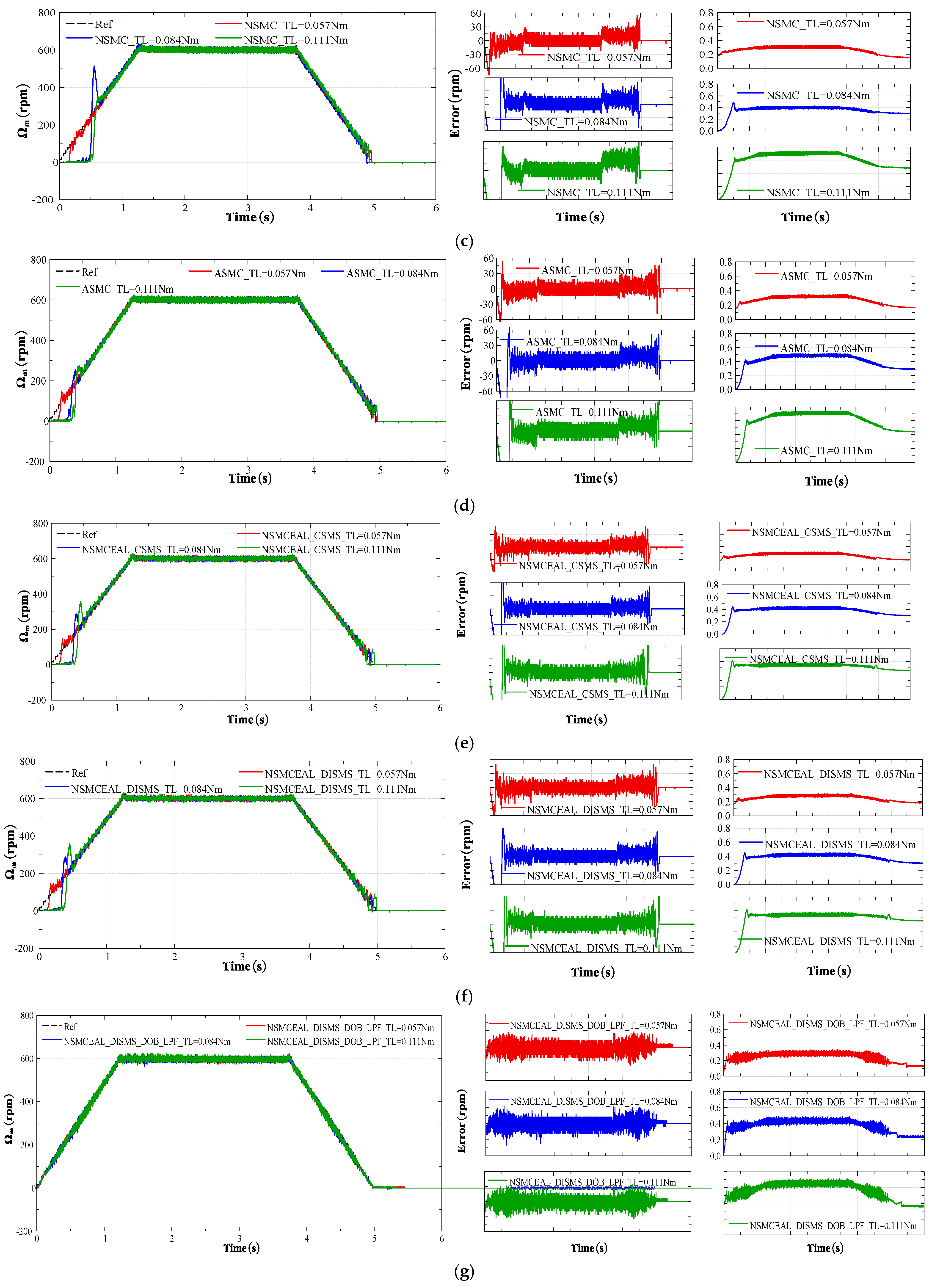
4.2.3. Performance Analysis of Various Response Methods
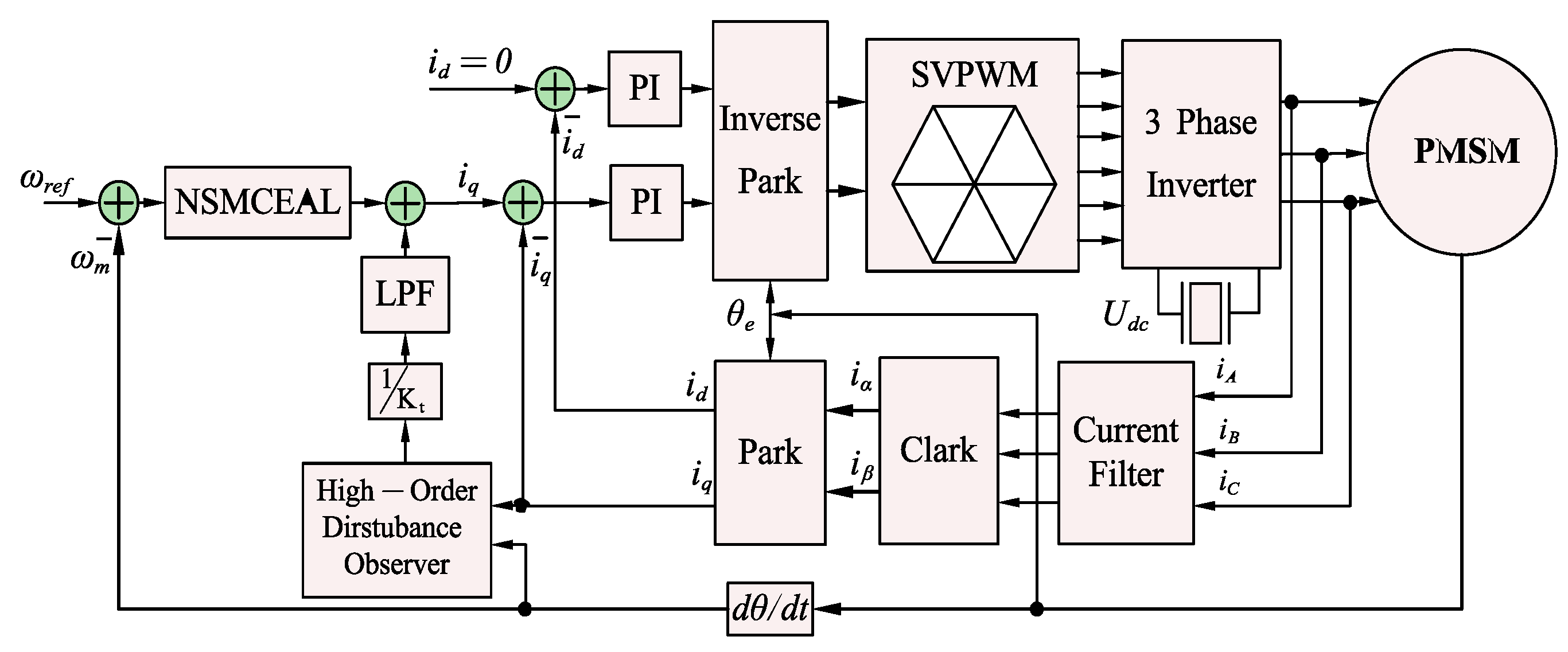
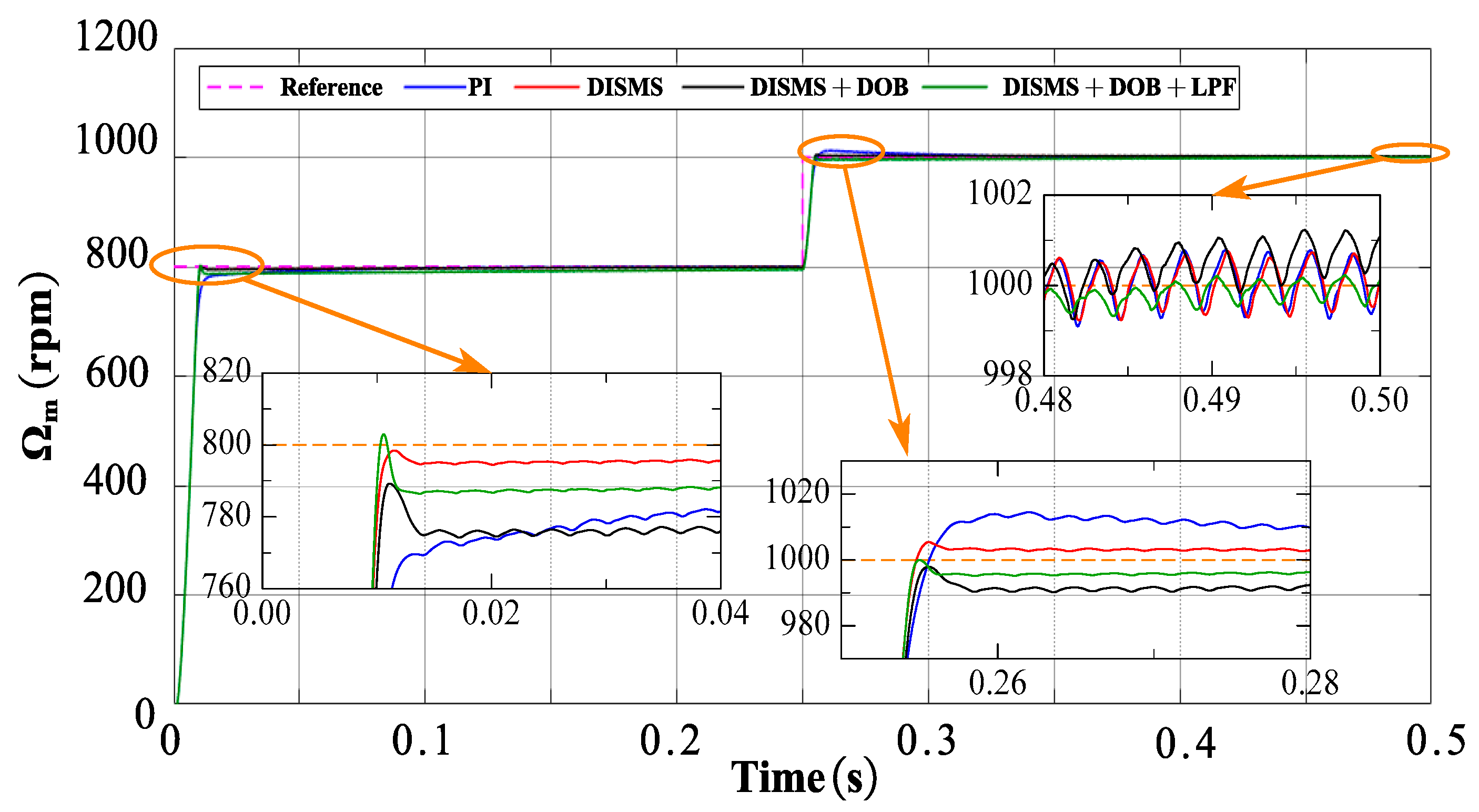
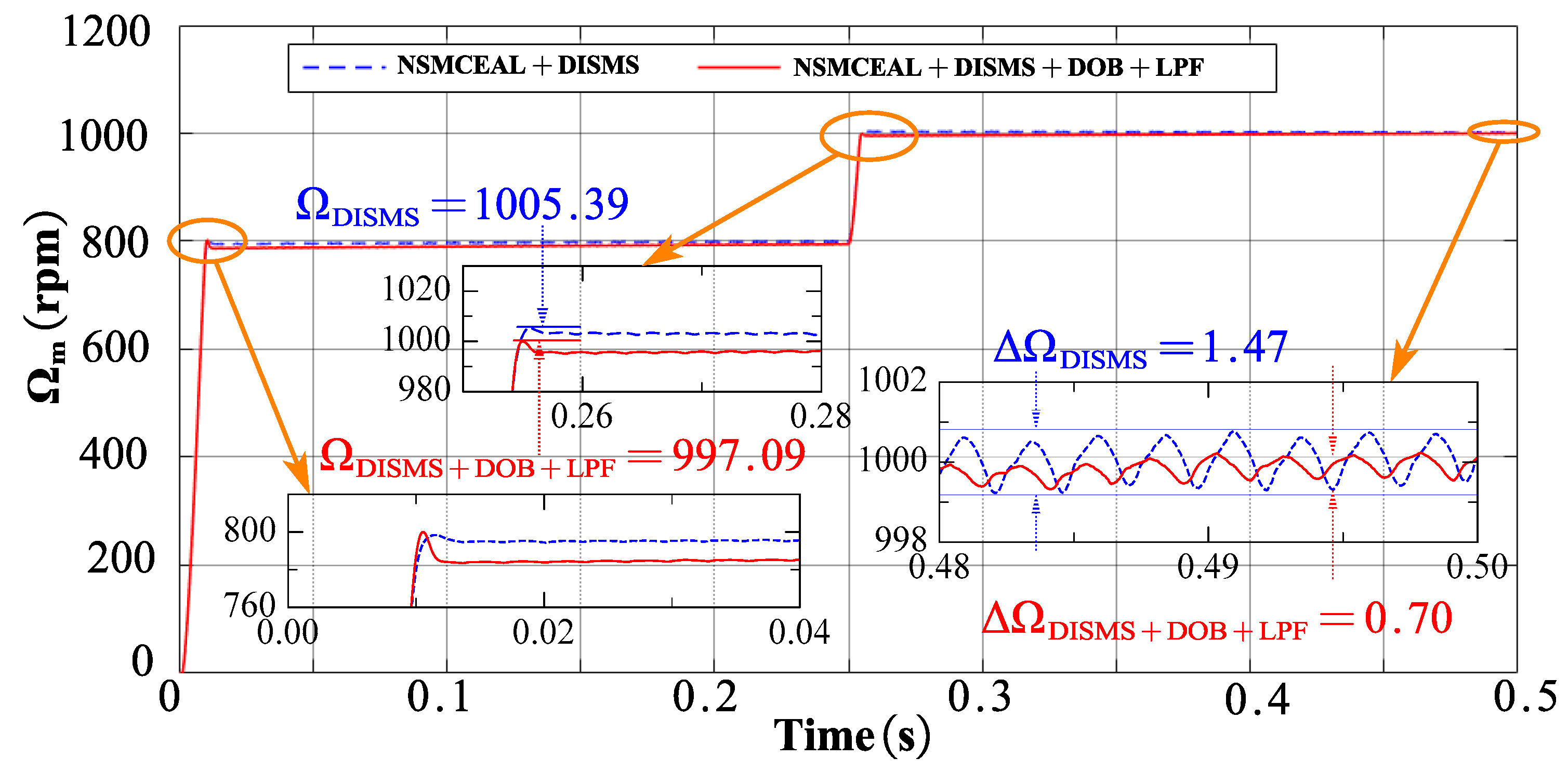
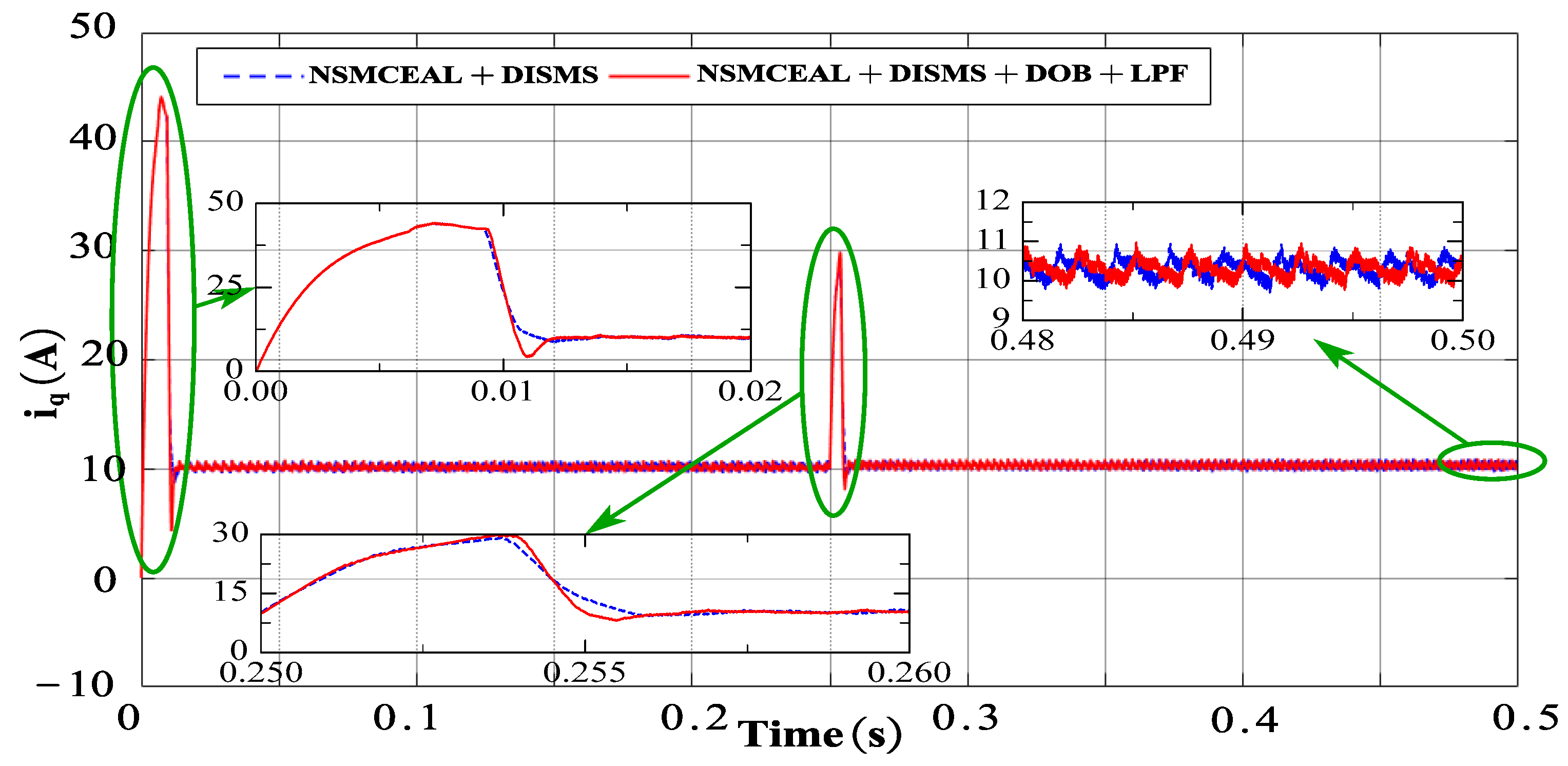
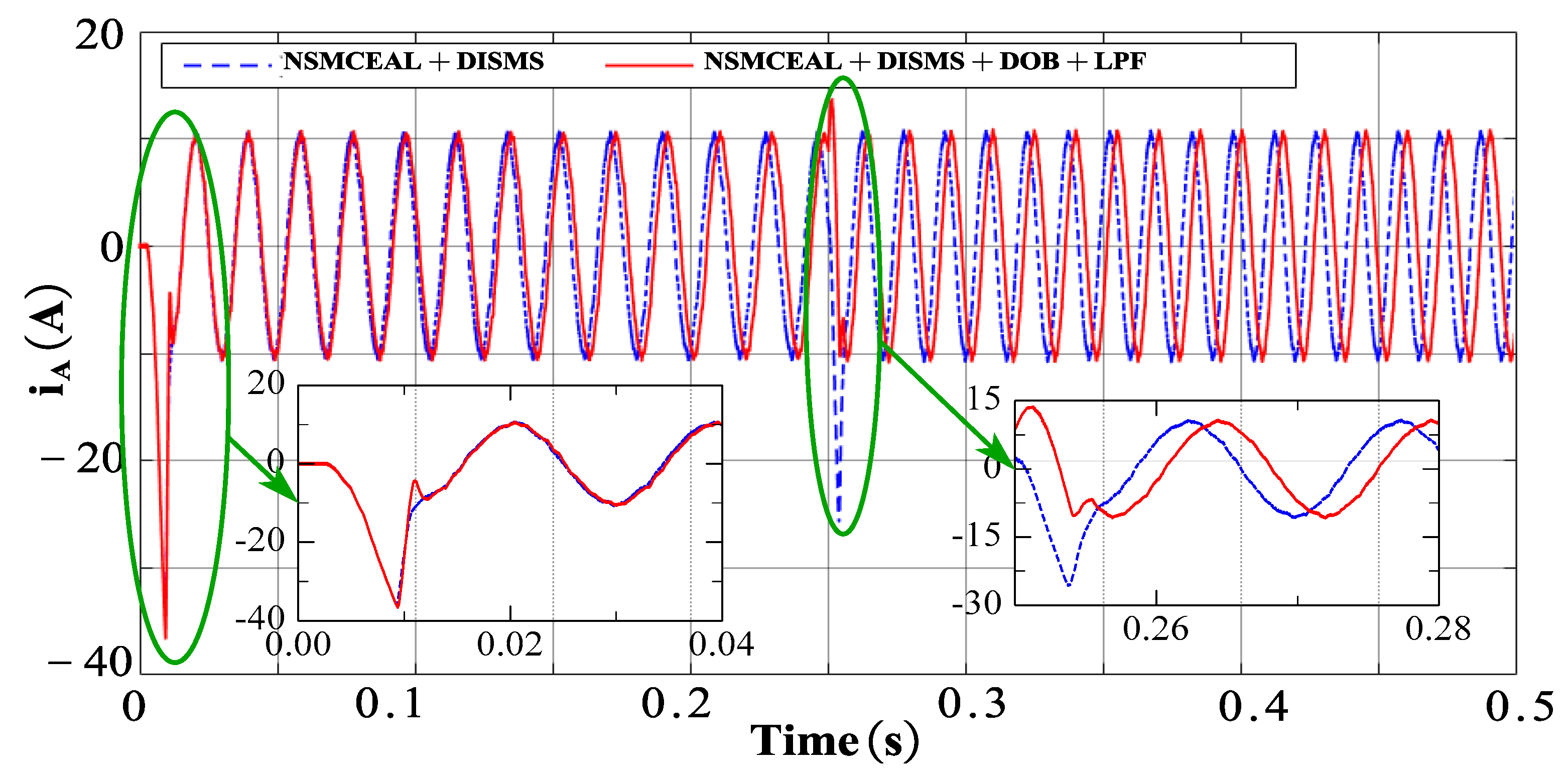
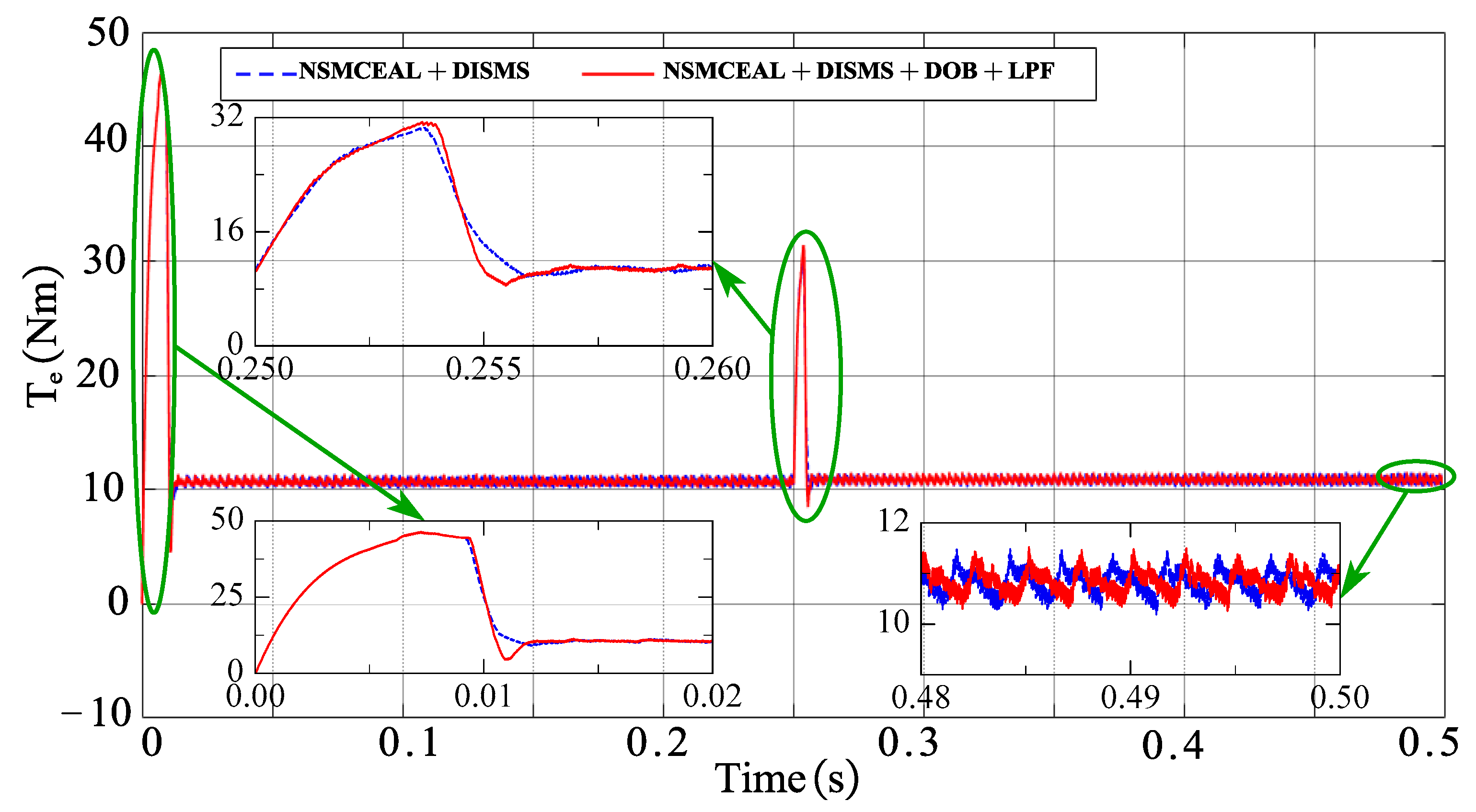
4.2.4. Response Performance of Novel NSMCEAL + DISMS and Proposed NSMCEAL + DISMS + DOB + LPF
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Z.; Zhou, D.; Wang, L.; Shen, Z.; Li, Y. A Review of Single-Stage Multiport Inverters for Multisource Applications. IEEE Trans. Power Electron. 2023, 38, 6566–6584. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, Q.; Li, Y.; Lin, Z.; Yang, M. Temperature Dependence of Powder Cores Magnetic Properties for Medium-Frequency Applications. IEEE Trans. Magn. 2022, 58, 2300505. [Google Scholar] [CrossRef]
- Husain, I.; Ozpineci, B.; Islam, M.S.; Gurpinar, E.; Su, G.J.; Yu, W.; Chowdhury, S.; Xue, L.; Rahman, D.; Sahu, R. Electric Drive Technology Trends, Challenges, and Opportunities for Future Electric Vehicles. Proc. IEEE 2021, 109, 1039–1059. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Chen, Z.; Jiao, N. An Overall System Delay Compensation Method for IPMSM Sensorless Drives in Rail Transit Applications. IEEE Trans. Power Electron. 2021, 36, 1316–1329. [Google Scholar]
- Hang, J.; Xia, M.; Ding, S.; Li, Y.; Sun, L.; Wang, Q. Research on Vector Control Strategy of Surface-Mounted Permanent Magnet Synchronous Machine Drive System with High-Resistance Connection. IEEE Trans. Power Electron. 2020, 35, 2023–2033. [Google Scholar]
- Tursini, M.; Parasiliti, F.; Zhang, D. Real-Time Gain Tuning of PI Controllers for High-Performance PMSM Drives. IEEE Trans. Ind. Appl. 2002, 38, 1018–1026. [Google Scholar]
- Maghfiroh, H.; Nizam, M. Improved LQR Control Using PSO Optimization and Kalman Filter Estimator. IEEE Access 2022, 10, 18330–18337. [Google Scholar]
- Systems, M. The Exact Model Matching of Linear Multivariable Systems. IEEE Trans. Automat. Contr. 1971, 17, 347–349. [Google Scholar]
- Tan, L.N.; Cong, T.P.; Cong, D.P. Neural Network Observers and Sensorless Robust Optimal Control for Partially Unknown PMSM with Disturbances and Saturating Voltages. IEEE Trans. Power Electron. 2021, 36, 12045–12056. [Google Scholar] [CrossRef]
- Shao, Y.; Yu, Y.; Chai, F.; Chen, T. A Two-Degree-of-Freedom Structure-Based Backstepping Observer for DC Error Suppression in Sensorless PMSM Drives. IEEE Trans. Ind. Electron. 2022, 69, 10846–10858. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, S.; Hu, J. Active Disturbance Rejection Control Based on Deep Reinforcement Learning of PMSM for More Electric Aircraft. IEEE Trans. Power Electron. 2023, 38, 406–416. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, Z.Q. Fuzzy Logic Speed Control of Permanent Magnet Synchronous Machine and Feedback Voltage Ripple Reduction in Flux-Weakening Operation Region. IEEE Trans. Ind. Appl. 2020, 56, 1505–1517. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Tran, H.N.; Nguyen, T.H.; Jeon, J.W. Recurrent Neural Network-Based Robust Adaptive Model Predictive Speed Control for PMSM with Parameter Mismatch. IEEE Trans. Ind. Electron. 2023, 70, 6219–6228. [Google Scholar] [CrossRef]
- Lang, W.; Hu, Y.; Gong, C.; Zhang, X.; Xu, H.; Deng, J. Artificial Intelligence-Based Technique for Fault Detection and Diagnosis of EV Motors: A Review. IEEE Trans. Transp. Electrif. 2022, 8, 384–406. [Google Scholar] [CrossRef]
- Tang, B.; Lu, W.; Yan, B.; Lu, K.; Feng, J.; Guo, L. A Novel Position Speed Integrated Sliding Mode Variable Structure Controller for Position Control of PMSM. IEEE Trans. Ind. Electron. 2022, 69, 12621–12631. [Google Scholar] [CrossRef]
- Li, H.X.; Gatland, H.B.; Green, A.W. Fuzzy Variable Structure Control. IEEE Trans. Syst. Man. Cybern. Part B Cybern. 1997, 27, 306–312. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Huang, L. Generalized Multiple-Vector-Based Model Predictive Control for PMSM Drives. IEEE Trans. Ind. Electron. 2018, 65, 9356–9366. [Google Scholar] [CrossRef]
- Dai, C.; Guo, T.; Yang, J.; Li, S. A Disturbance Observer-Based Current-Constrained Controller for Speed Regulation of PMSM Systems Subject to Unmatched Disturbances. IEEE Trans. Ind. Electron. 2021, 68, 767–775. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Huang, L. Model-Free Predictive Current Control of PMSM Drives Based on Extended State Observer Using Ultralocal Model. IEEE Trans. Ind. Electron. 2021, 68, 993–1003. [Google Scholar]
- Feng, L.; Deng, M.; Xu, S.; Huang, D. Speed Regulation for PMSM Drives Based on a Novel Sliding Mode Controller. IEEE Access 2020, 8, 63577–63584. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.T.; Nguyen, V.Q.; Le, K.M.; Tran, H.N.; Jeon, J.W. An Adaptive Sliding-Mode Controller with a Modified Reduced-Order Proportional Integral Observer for Speed Regulation of a Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2022, 69, 7181–7191. [Google Scholar] [CrossRef]
- Liu, T.T.; Tan, Y.; Wu, G.; Wang, S.M. Simulation of PMSM Vector Control System Based on Matlab/Simulink. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, ICMTMA, Zhangjiajie, China, 11–12 April 2009; Volume 2, pp. 343–346. [Google Scholar] [CrossRef]
- Suleimenov, K.; Do, T.D. Design and Analysis of a Generalized High-Order Disturbance Observer for PMSMs with a Fuzy-PI Speed Controller. IEEE Access 2022, 10, 42238–42246. [Google Scholar] [CrossRef]
- Seryasat, O.R.; Aliyari Shoorehdeli, M.; Honarvar, F.; Rahmani, A. Multi-Fault Diagnosis of Ball Bearing Using FFT, Wavelet Energy Entropy Mean and root Mean Square (RMS). In Proceedings of the 2010 IEEE International Conference on Systems, Man and Cybernetics, Istanbul, Turkey, 10–13 October 2010; pp. 4295–4299. [Google Scholar]
- Yang, J.; Zhou, J.; Zhou, H.; Yi, F.; Song, D.; Dong, M. High-Precision Harmonic Current Extraction for PMSM Based on Multiple Reference Frames Considering Speed Harmonics. IEEE Trans. Ind. Electron. 2023, 70, 9764–9776. [Google Scholar] [CrossRef]








| Description | Value | Description | Value |
|---|---|---|---|
| Pole pairs | 4 | Resistance | 2.875 Ω |
| PM flux | 0.175 Wb | DC voltage | 311 V |
| Rate power | 750 W | Rated speed | 3000 rpm |
| Rotor inertia | 0.003 g·m2 | Viscous damping | 0.008 N·mm·s |
| d-q axis inductance | 8.5 mH | Switching frequency | 10 kHz |
| Sampling cycle | 10 μs |
| Description | Value | Description | Value |
|---|---|---|---|
| kp (Current loop) | 10 | C_NSMCEAL | 52.75 |
| ki (Current loop) | 20 | ε_NSMCEAL | 5 × 103 |
| C_NSMC | 25 | q_NSMCEAL | 6.8 × 102 |
| ε_NSMC | 5 × 102 | α_NSMCEAL | 9.3 × 10−2 |
| q_NSMC | 3.3 × 102 | β_NSMCEAL | 3.89 × 10−1 |
| λ_NSMC | 1 | λ_NSMCEAL | 1 |
| Kiw (PI) | 20 | C_CEAL | 20 |
| Kpw (PI) | 0.16 | ε_CEAL | 1 × 104 |
| ωc | 100 | q_CEAL | 4.5 × 102 |
| C_ASMC | 120 | η_ASMC | 5.95 × 102 |
| ε_ASMC | 1 × 105 | λ_ASMC | 1 |
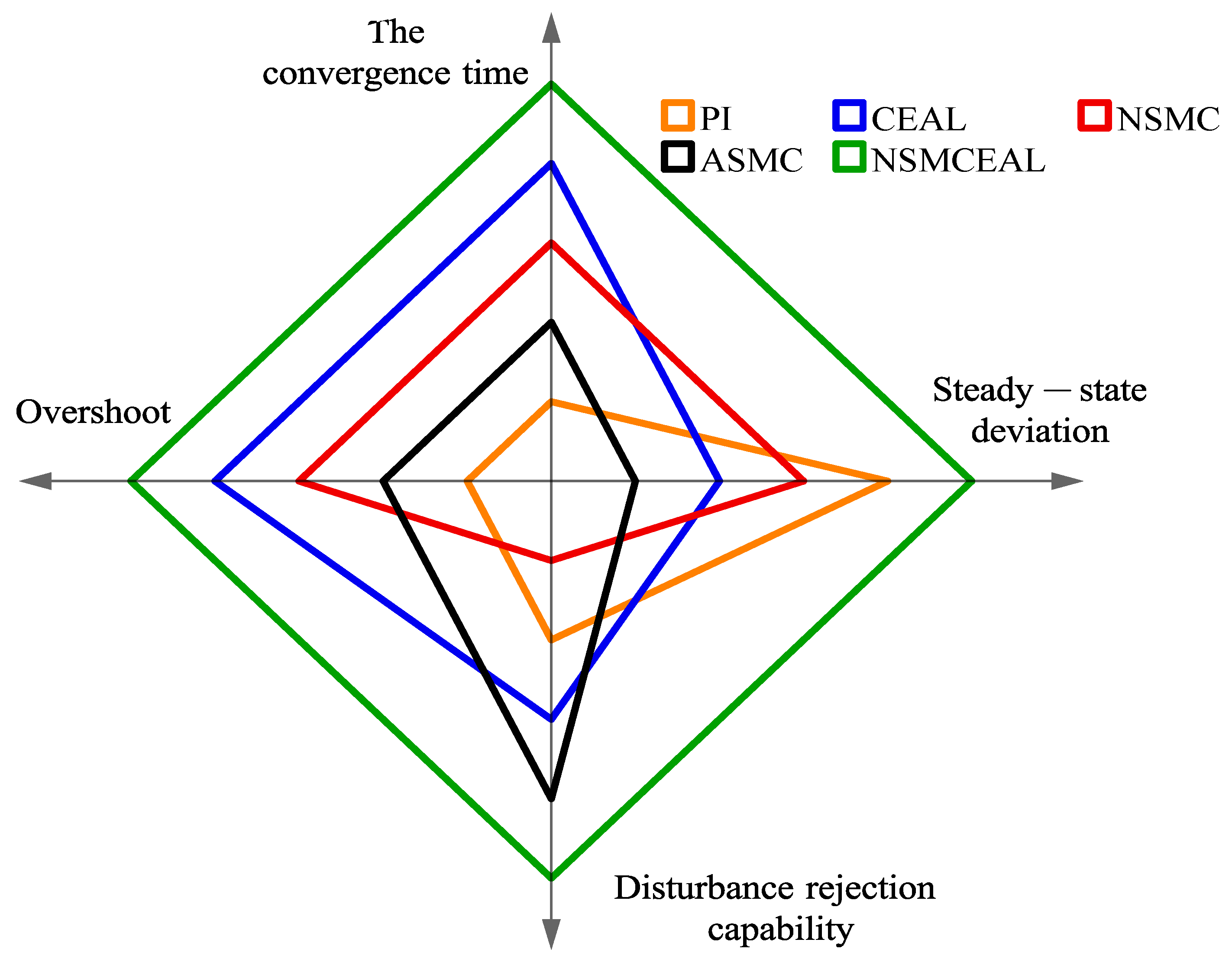
| Control Scheme | Steady-State Deviation (RMSE) | The Convergence Time | Over Shoot | Disturbance Rejection Capability | ||
|---|---|---|---|---|---|---|
| Index (%) | Score | Index (ms) | Score | Score | Score | |
| PI | 0.0525 | 4 | 77.52 | 1 | 1 | 2 |
| CEAL | 0.0610 | 2 | 16.16 | 4 | 4 | 3 |
| NSMC | 0.0557 | 3 | 21.61 | 3 | 3 | 1 |
| ASMC | 0.1321 | 1 | 24.39 | 2 | 2 | 4 |
| NSMCEAL | 0.0489 | 5 | 11.85 | 5 | 5 | 5 |
| Control Scheme | Steady-State Deviation (RMSE) | The Convergence Time | Over Shoot | Disturbance Rejection Capability | ||
|---|---|---|---|---|---|---|
| Index (%) | Score | Index (ms) | Score | Score | Score | |
| PI | 0.0525 | 1 | 77.52 | 1 | 1 | 1 |
| CSMS | 0.0489 | 2 | 11.85 | 2 | 3 | 3 |
| DISMS | 0.0438 | 3 | 10.42 | 3 | 2 | 2 |
| Control Scheme | Steady-State Deviation (RMSE) | The Convergence Time | Over Shoot | Disturbance Rejection Capability | ||
|---|---|---|---|---|---|---|
| Index (%) | Score | Index (ms) | Score | Score | Score | |
| PI | 0.0525 | 2 | 77.52 | 2 | 1 | 1 |
| DISMS | 0.0438 | 3 | 10.42 | 3 | 2 | 2 |
| NSMCEAL + DOB | 0.0652 | 1 | 118.31 | 1 | 3 | 3 |
| NSMCEAL + DOB + LPF | 0.0421 | 4 | 2.60 | 4 | 4 | 4 |
| Description | Value | Description | Value |
|---|---|---|---|
| Pole pairs | 5 | Resistance | 0.44 Ω |
| PM flux | 0.02 Wb | DC voltage | 36 V |
| Rate power | 200 W | Rated speed | 3000 rpm |
| Rotor inertia | 0.5 g·m2 | Viscous damping | 0.2 N·mm·s |
| D-Q axis inductance | 4.5 mH | Switching frequency | 10 kHz |
| Sampling cycle | 10 μs | Rated torque | 0.64 Nm |
| Description | Value | Description | Value |
|---|---|---|---|
| kp (Current loop) | 0.6 | C_NSMCEAL_CSMS | 5 × 104 |
| ki (Current loop) | 0.07 | ε_NSMCEAL | 1 × 103 |
| C_NSMC | 1000 | q_NSMCEAL | 5 × 100 |
| ε_NSMC | 2 × 101 | α_NSMCEAL | 5 × 10−1 |
| q_NSMC | 5 × 103 | β_NSMCEAL | 5 × 10−1 |
| λ_NSMC | 1 | λ_NSMCEAL | 1 |
| Kiw (PI) | 0.01 | C1_NSMCEAL_DISMS | 1 × 106 |
| Kpw (PI) | 1.5 | C2_NSMCEAL_DISMS | 5 × 100 |
| ωc | 10 | C3_NSMCEAL_DISMS | 1 × 106 |
| C_ASMC | 1 × 104 | C_CEAL | 1000 |
| q_ASMC | 10 | ε_CEAL | 2 × 101 |
| η_ASMC | 5 × 10−1 | q_CEAL | 5 × 102 |
| λ_ASMC | 1 |
| Parameters | PI | SMC in [21] | SMC in [20] | Proposed Control |
|---|---|---|---|---|
| Steady-state deviation | Moderate | Moderate | Moderate | Minimum |
| Spead overshoot (%) | Less | Less | Less | Medium |
| Speed settling time | Medium | High | High | Less |
| Current harmonics | Medium | Medium | Medium | Less |
| Chattering analysis | Moderate | Moderate | Moderate | Less |
| Disturbance rejection capability | Lower | Medium | Lower | Higher |
| Chattering analysis | Severe chatteing | Moderate chatteing | Moderate chatteing | Minimum chatteing |
| Control efficieancy | Moderate | Good | Moderate | Excellent |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuyen, T.T.; Yang, J.; Liao, L.; Zhou, J. Integrated Sliding Mode Control for Permanent Magnet Synchronous Motor Drives Based on Second-Order Disturbance Observer and Low-Pass Filter. Electronics 2025, 14, 1466. https://doi.org/10.3390/electronics14071466
Tuyen TT, Yang J, Liao L, Zhou J. Integrated Sliding Mode Control for Permanent Magnet Synchronous Motor Drives Based on Second-Order Disturbance Observer and Low-Pass Filter. Electronics. 2025; 14(7):1466. https://doi.org/10.3390/electronics14071466
Chicago/Turabian StyleTuyen, Tran Thanh, Jian Yang, Liqing Liao, and Jingyang Zhou. 2025. "Integrated Sliding Mode Control for Permanent Magnet Synchronous Motor Drives Based on Second-Order Disturbance Observer and Low-Pass Filter" Electronics 14, no. 7: 1466. https://doi.org/10.3390/electronics14071466
APA StyleTuyen, T. T., Yang, J., Liao, L., & Zhou, J. (2025). Integrated Sliding Mode Control for Permanent Magnet Synchronous Motor Drives Based on Second-Order Disturbance Observer and Low-Pass Filter. Electronics, 14(7), 1466. https://doi.org/10.3390/electronics14071466






