ShipMOT: A Robust and Reliable CNN-NSA Filter Framework for Marine Radar Target Tracking
Abstract
1. Introduction
- (1)
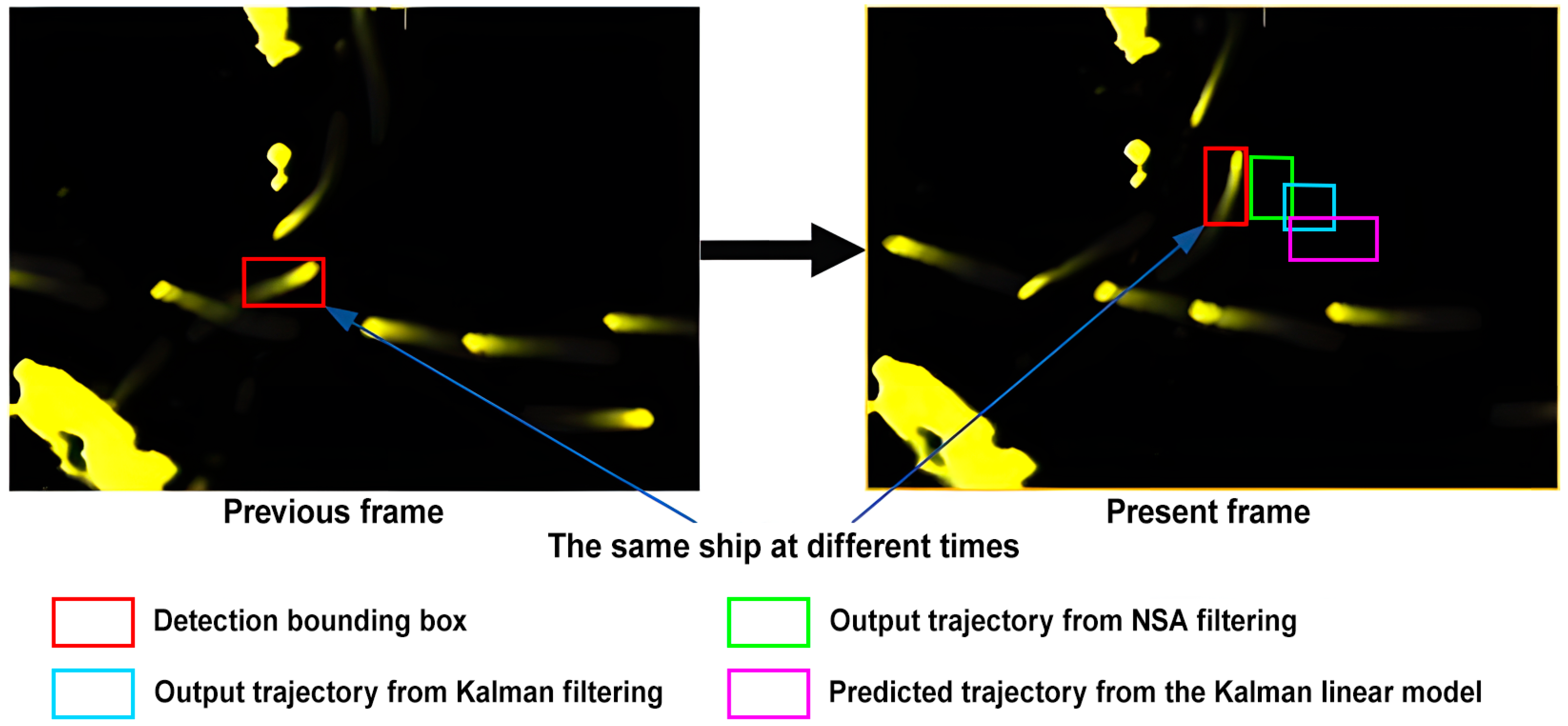
- In the aspect of motion prediction in the tracker, this approach introduces a new motion filtering prediction method. Compared to the traditional Kalman filter (KF), it can incorporate the detection confidence of bounding boxes, adaptively adjusting the observation noise of the filter to reduce the offset error between the filtered output trajectory and the actual trajectory, thereby decreasing the number of ship ID switches.
- (2)
- In the data association part of the tracker, this algorithm employs a Bounding Box Similarity Index (BBSI) to replace the traditional Intersection over Union (IoU) cost, reducing ID switches during dense and crossing ship navigation.
- (3)
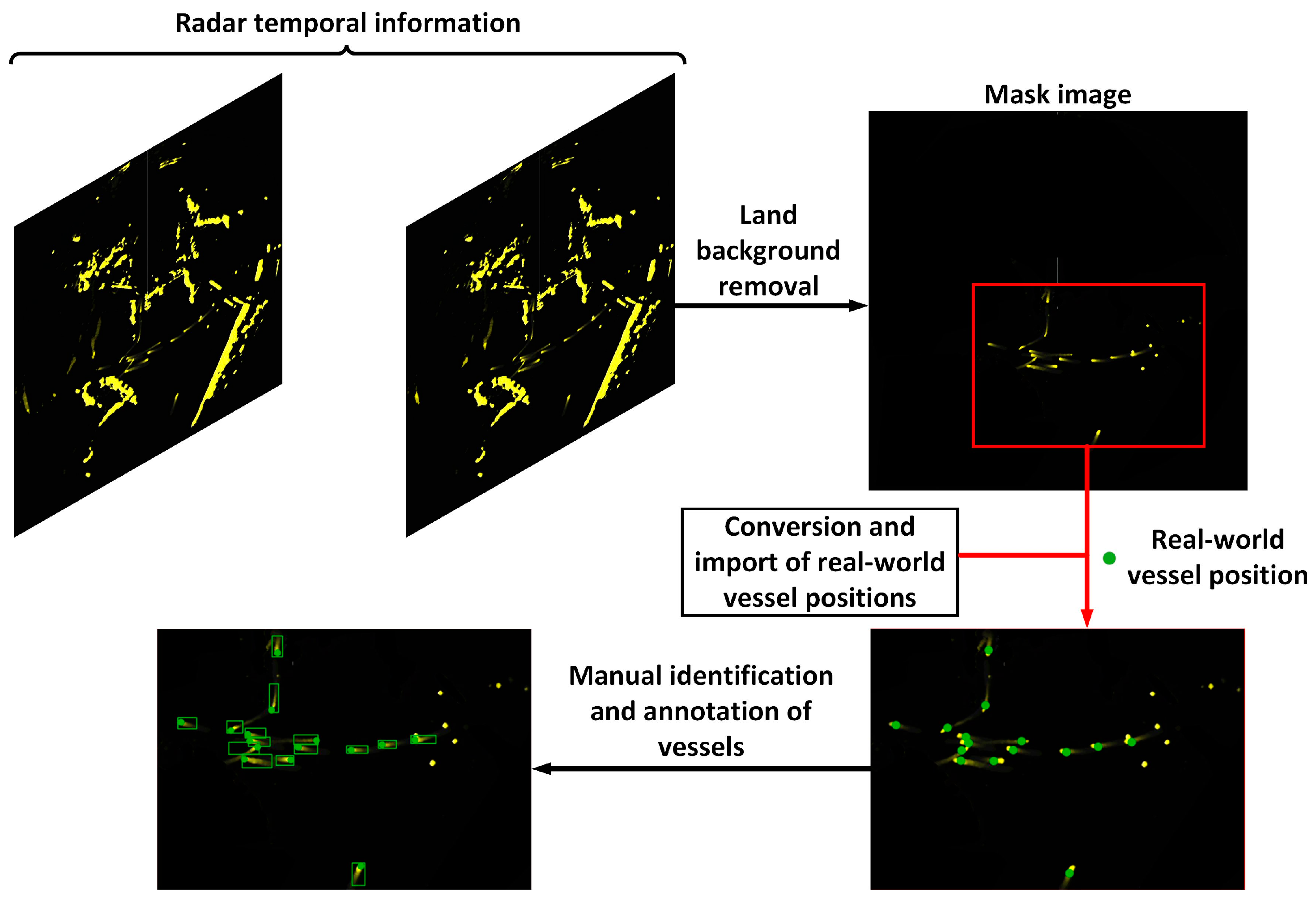
- To evaluate the practical effectiveness of the algorithm, this research establishes the Radar-Track dataset, consisting of 4816 real-world MR images. Scene generalization is performed on this dataset to facilitate the training and validation of various types of algorithms.
2. Literature Review
2.1. Multi-Object Tracking Methods Based on MR Images
2.2. Image-Based Deep Learning Multi-Object Tracking Methods
2.3. Nonlinear State Augmentation (NSA) Filter
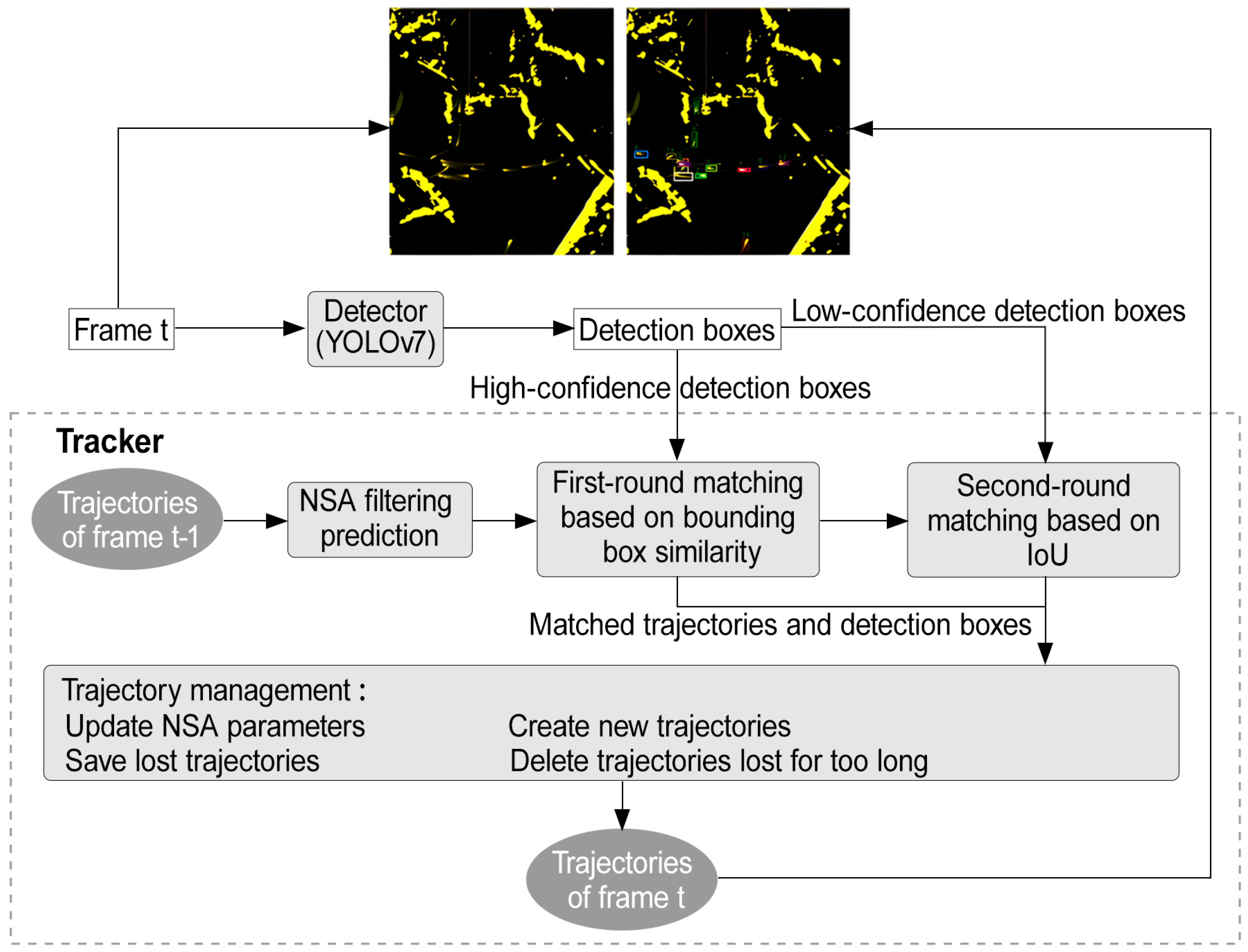
3. A Proposed Approach
3.1. Nonlinear State Augmentation (NSA) Filtering
3.2. The Bounding Box Similarity Index (BBSI)
4. A Case Study
4.1. Experiment Preparation
4.1.1. A Dataset
4.1.2. Experiment Platform
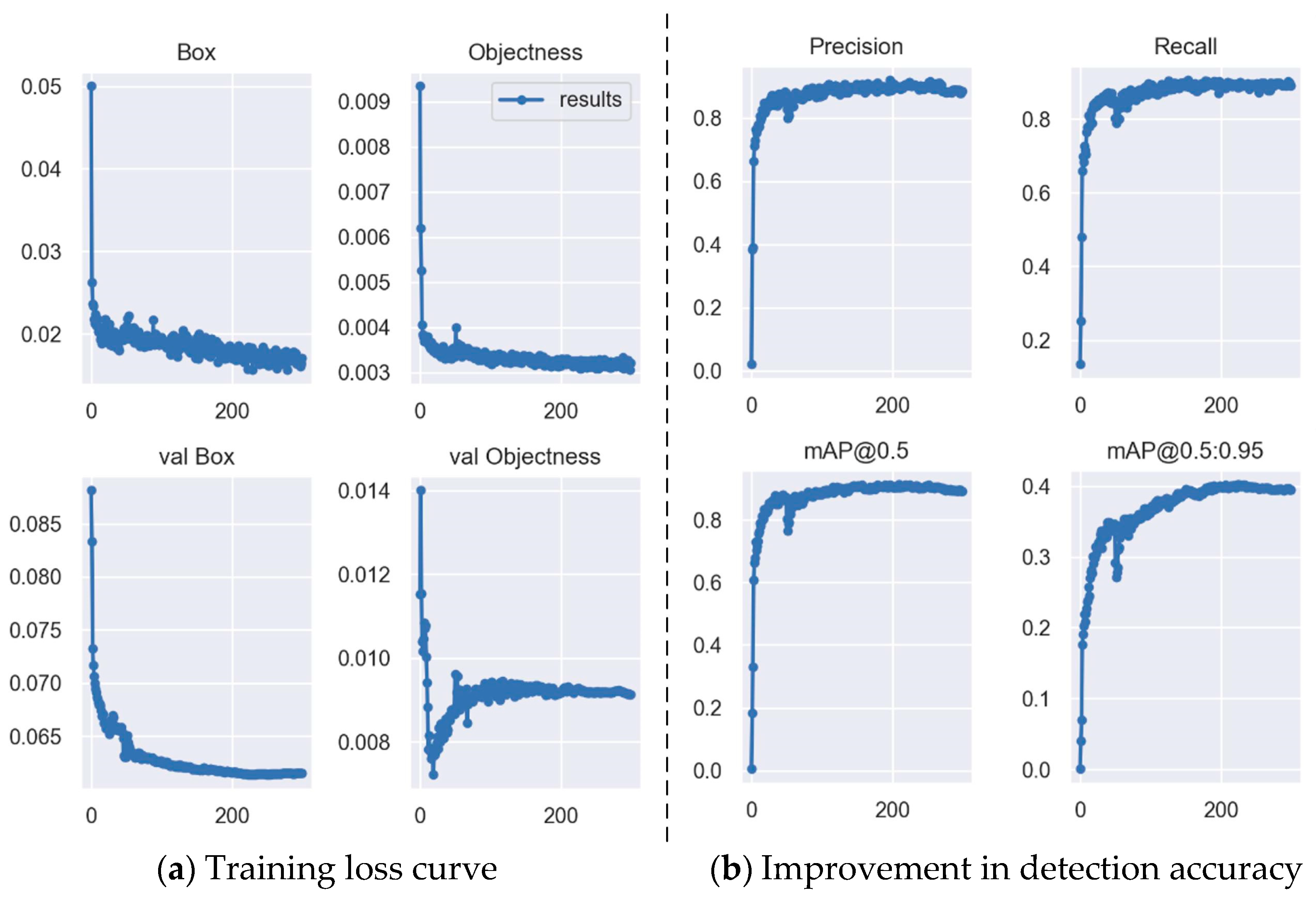
4.1.3. Target Detection
4.2. Experiment Results
4.2.1. Target Tracking
4.2.2. Ablation Study
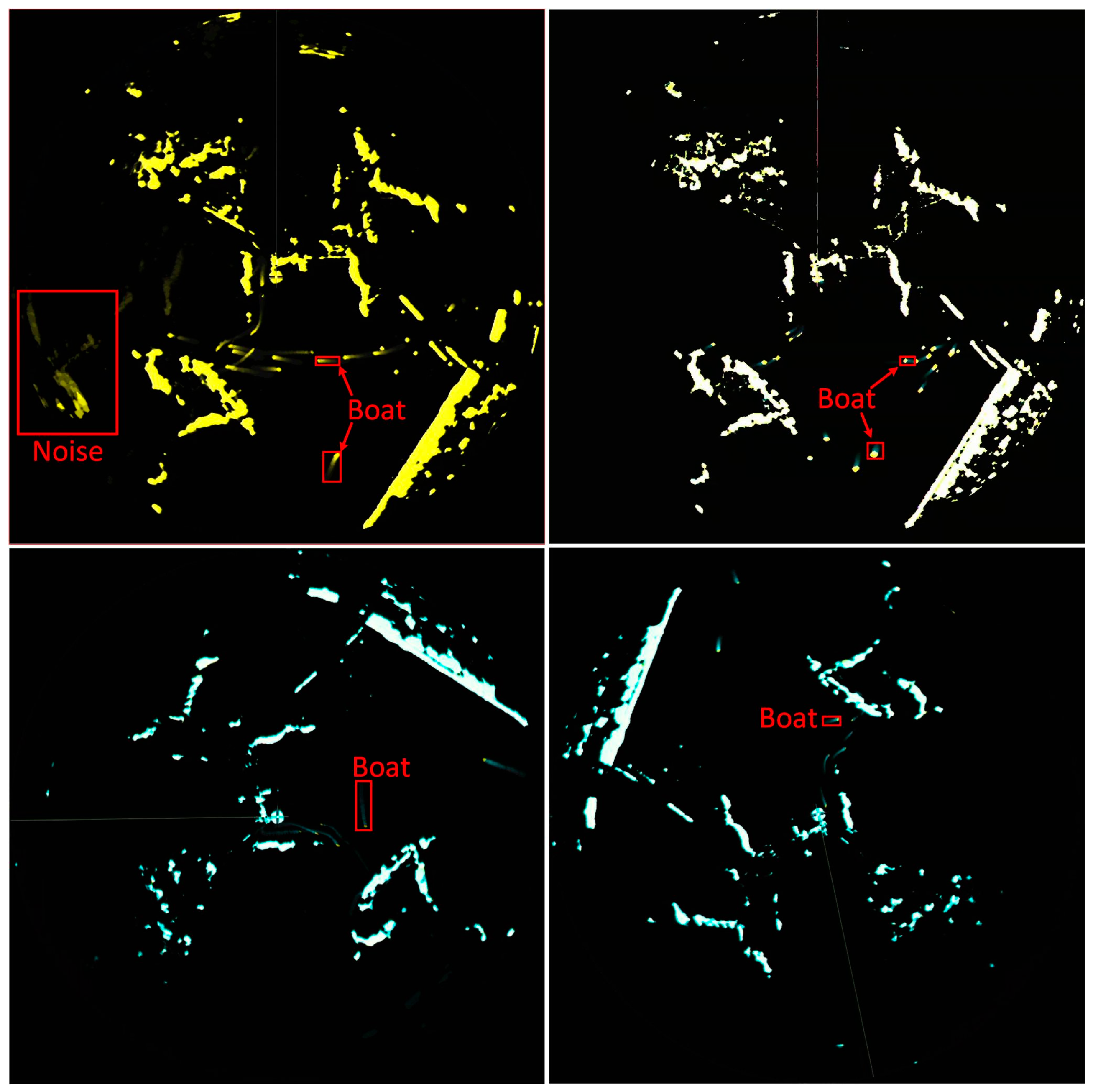
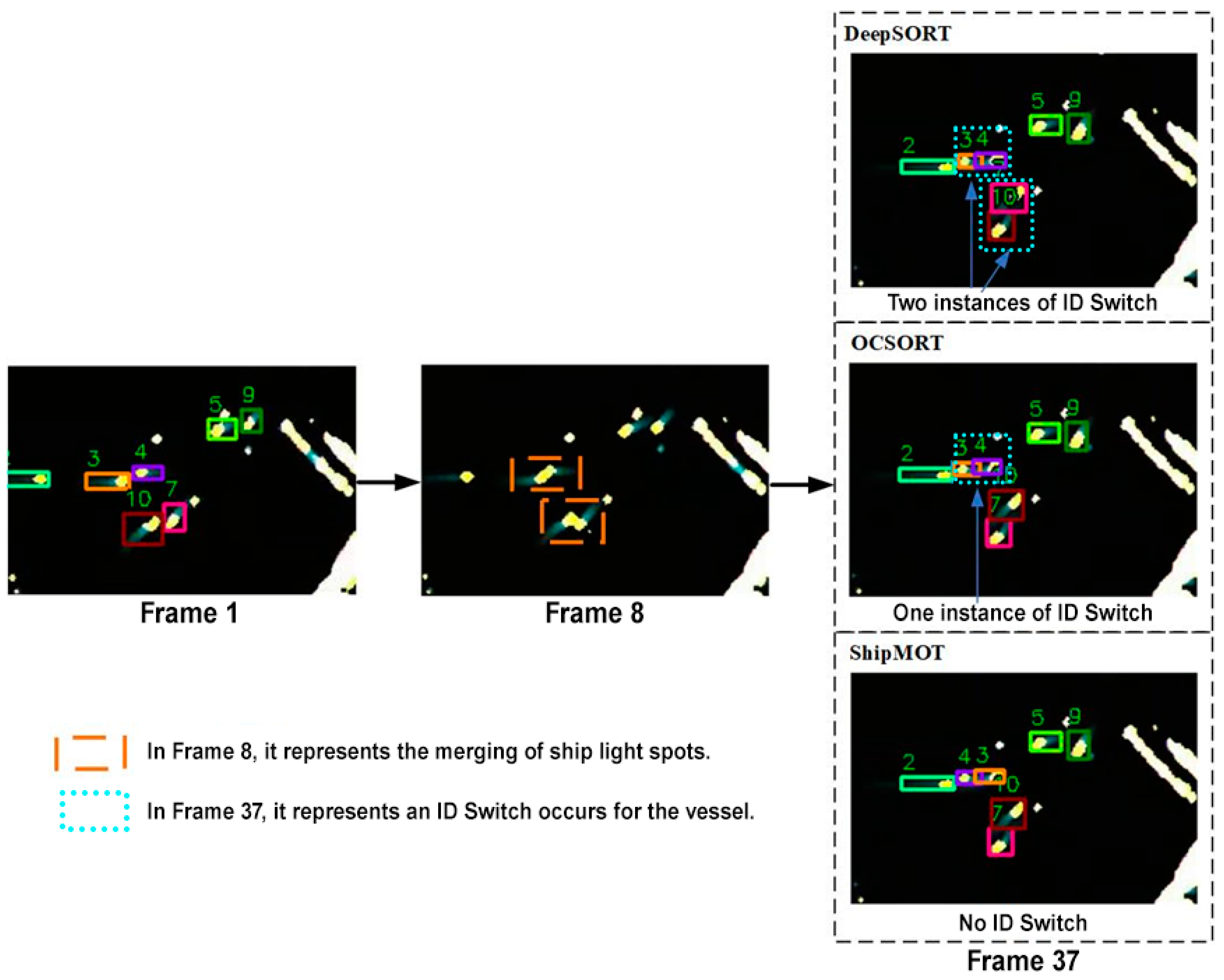
4.2.3. Ship Tracking in Different Scenarios
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, B.; Xu, J.; Pan, X.; Chen, R.; Ma, L.; Yin, J.; Liao, Z.; Chu, L.; Zhao, Z.; Lian, J.; et al. Preliminary Investigation on Marine Radar Oil Spill Monitoring Method Using YOLO Model. J. Mar. Sci. Eng. 2023, 11, 670. [Google Scholar] [CrossRef]
- Wei, Y.; Liu, Y.; Lei, Y.; Lian, R.; Lu, Z.; Sun, L. A New Method of Rainfall Detection from the Collected X-Band Marine Radar Images. Remote Sens. 2022, 14, 3600. [Google Scholar] [CrossRef]
- Do, C.-T.; Van Nguyen, H. Multistatic Doppler-Based Marine Ships Tracking. In Proceedings of the 2018 International Conference on Control, Automation and Information Sciences (ICCAIS), Hangzhou, China, 9 December 2018; pp. 151–156. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, J.; Cheng, D.; Chen, C.; Chen, W. Motion-Regularized Background-Aware Correlation Filter for Marine Radar Target Tracking. In IEEE Geoscience and Remote Sensing Letters; IEEE: New York, NY, USA, 2023; Volume 20. [Google Scholar]
- Guerraou, Z.; Khenchaf, A.; Comblet, F.; Leouffre, M.; Lacrouts, O. Particle Filter Track-Before-Detect for Target Detection and Tracking from Marine Radar Data. In Proceedings of the 2019 IEEE Conference on Antenna Measurements & Applications (CAMA), Kuta, Bali, Indonesia, 23–25 October 2019; pp. 304–307. [Google Scholar] [CrossRef]
- Fowdur, J.S.; Baum, M.; Heymann, F.; Banys, P. An Overview of the PAKF-JPDA Approach for Elliptical Multiple Extended Target Tracking Using High-Resolution Marine Radar Data. Remote Sens. 2023, 15, 2503. [Google Scholar] [CrossRef]
- Kim, E.; Kim, J.; Kim, J. Multi-Target Tracking Considering the Uncertainty of Deep Learning-based Object Detection of Marine Radar Images. In Proceedings of the 20th International Conference on Ubiquitous Robots (UR), Honolulu, HI, USA, 25–28 June 2023; pp. 191–194. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Lee, S.-M. Marine Object Segmentation and Tracking by Learning Marine Radar Images for Autonomous Surface Vehicles. IEEE Sens. J. 2023, 23, 10062–10070. [Google Scholar]
- Hao, Z.; Qiu, J.; Zhang, H.; Ren, G.; Liu, C. Umotma: Underwater multiple object tracking with memory aggregation. Front. Mar. Sci. 2022, 9, 1071618. [Google Scholar]
- Li, W.; Liu, Y.; Wang, W.; Li, Z.; Yue, J. TFMFT: Transformer-based multiple fish tracking. Comput. Electron. Agric. 2024, 217, 108600. [Google Scholar]
- Din, M.U.; Bakht, A.B.; Akram, W.; Dong, Y.; Seneviratne, L.; Hussain, I. Benchmarking Vision-Based Object Tracking for USVs in Complex Maritime Environments. IEEE Access 2025, 13, 15014–15027. [Google Scholar]
- Bewley, A.; Ge, Z.; Ott, L.; Ramos, F.; Upcroft, B. Simple Online and Realtime Tracking. In Proceedings of the 23rd IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 3464–3468. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar]
- Wojke, N.; Bewley, A.; Paulus, D. Simple Online and Realtime Tracking with a Deep Association Metric. In Proceedings of the 24th IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3645–3649. [Google Scholar]
- Zhang, Y.; Sun, P.; Jiang, Y.; Yu, D.; Weng, F.; Yuan, Z.; Luo, P.; Liu, W.; Wang, X. ByteTrack: Multi-object Tracking by Associating Every Detection Box. In Proceedings of the 17th European Conference on Computer Vision (ECCV), Tel Aviv, Isreal, 23–27 October 2022; pp. 1–21. [Google Scholar]
- Cao, J.; Pang, J.; Weng, X.; Khirodkar, R.; Kitani, K. Observation-Centric SORT: Rethinking SORT for Robust Multi-Object Tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 9686–9696. [Google Scholar]
- Du, Y.; Zhao, Z.; Song, Y.; Zhao, Y.; Su, F.; Gong, T.; Meng, H. StrongSORT: Make DeepSORT Great Again. IEEE Trans. Multimed. 2023, 25, 8725–8737. [Google Scholar] [CrossRef]
- Luo, H.; Jiang, W.; Gu, Y.; Liu, F.; Liao, X.; Lai, S.; Gu, J. A Strong Baseline and Batch Normalization Neck for Deep Person Re-Identification. IEEE Trans. Multimed. 2020, 22, 2597–2609. [Google Scholar] [CrossRef]
- Evangelidis, G.D.; Psarakis, E.Z. Parametric image alignment using enhanced correlation coefficient maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1858–1865. [Google Scholar]
- Dendorfer, P.; Rezatofighi, H.; Milan, A.; Shi, J.; Cremers, D.; Reid, I.; Roth, S.; Schindler, K.; Leal-Taixé, L. Mot20: A benchmark for multi object tracking in crowded scenes. arXiv 2020, arXiv:2003.09003. [Google Scholar]
- Milan, A.; Leal-Taixé, L.; Reid, I.; Roth, S.; Schindler, K. MOT16: A benchmark for multi-object tracking. arXiv 2016, arXiv:1603.00831. [Google Scholar]
- Chen, B.; Hu, G. Nonlinear state estimation under bounded noises. Automatica 2018, 98, 159–168. [Google Scholar] [CrossRef]
- Müller, M.A. Nonlinear moving horizon estimation in the presence of bounded disturbances. Automatica 2017, 79, 306–314. [Google Scholar] [CrossRef]
- Du, Y.; Wan, J.; Zhao, Y.; Zhang, B.; Tong, Z.; Dong, J. GIAOTracker: A comprehensive framework for MCMOT with global information and optimizing strategies in VisDrone. In Proceedings of the 18th IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 2809–2819. [Google Scholar]
- Ma, F.; Kang, Z.; Chen, C.; Sun, J.; Xu, X.-B.; Wang, J. Identifying Ships from Radar Blips Like Humans Using a Customized Neural Network. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7187–7205. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 7464–7475. [Google Scholar]
- Morsali, M.M.; Sharifi, Z.; Fallah, F.; Hashembeiki, S.; Mohammadzade, H.; Shouraki, S.B. SFSORT: Scene Features-based Simple Online Real-Time Tracker. arXiv 2024, arXiv:2404.07553. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Lapaine, M.; Frančula, N. Web mercator projection-one of cylindrical projections of an ellipsoid to a plane. Kartogr. I Geoinformacije 2021, 20, 31–47. [Google Scholar] [CrossRef]
- Yang, F.; Odashima, S.; Masui, S.; Jiang, S. Hard to Track Objects with Irregular Motions and Similar Appearances? Make It Easier by Buffering the Matching Space. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 2–7 January 2023; pp. 4788–4797. [Google Scholar] [CrossRef]





| Algorithm | HOTA (%) ↑ | MOTA (%) ↑ | ID Switch ↓ | FPS ↑ |
|---|---|---|---|---|
| DeepSORT | 59.84 | 80.13 | 345 | 18.4 |
| StrongSORT | 68.65 | 81.83 | 265 | 15.6 |
| C-BIoU | 72.13 | 88.34 | 68 | 35.83 |
| ByteTrack | 75.31 | 87.43 | 82 | 34.86 |
| OC-SORT | 77.27 | 87.89 | 65 | 31.25 |
| ShipMOT | 79.01 | 88.58 | 40 | 32.36 |
| Method | ByteTrack | +NSA | +BBSI | HOTA | MOTA | ID Switch ↓ | FPS |
|---|---|---|---|---|---|---|---|
| M1 | √ | 75.31 | 87.43 | 82 | 34.86 | ||
| M2 | √ | √ | 78.01 | 88.07 | 65 | 34.66 | |
| M3 | √ | √ | 77.57 | 88.03 | 55 | 32.56 | |
| M4 | √ | √ | √ | 79.01 | 88.58 | 40 | 32.36 |
| Filter | HOTA (%) ↑ | MOTA (%) ↑ | ID Switch ↓ | FPS ↑ |
|---|---|---|---|---|
| EKF | 77.31 | 87.83 | 70 | 31.23 |
| UKF | 78.45 | 88.23 | 62 | 23.47 |
| NSA | 78.01 | 88.07 | 65 | 34.66 |
| Detector | mAP@50 ↑ | mAP@50-95 ↑ | ID Switch ↓ | HOTA ↑ |
|---|---|---|---|---|
| SSD | 0.76 | 0.22 | 85 | 74.35 |
| YOLOv5 | 0.89 | 0.38 | 52 | 77.23 |
| YOLOv7 | 0.93 | 0.41 | 40 | 79.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Ma, F.; Wang, K.-L.; Liu, H.-H.; Zeng, D.-H.; Lu, P. ShipMOT: A Robust and Reliable CNN-NSA Filter Framework for Marine Radar Target Tracking. Electronics 2025, 14, 1492. https://doi.org/10.3390/electronics14081492
Chen C, Ma F, Wang K-L, Liu H-H, Zeng D-H, Lu P. ShipMOT: A Robust and Reliable CNN-NSA Filter Framework for Marine Radar Target Tracking. Electronics. 2025; 14(8):1492. https://doi.org/10.3390/electronics14081492
Chicago/Turabian StyleChen, Chen, Feng Ma, Kai-Li Wang, Hong-Hong Liu, Dong-Hai Zeng, and Peng Lu. 2025. "ShipMOT: A Robust and Reliable CNN-NSA Filter Framework for Marine Radar Target Tracking" Electronics 14, no. 8: 1492. https://doi.org/10.3390/electronics14081492
APA StyleChen, C., Ma, F., Wang, K.-L., Liu, H.-H., Zeng, D.-H., & Lu, P. (2025). ShipMOT: A Robust and Reliable CNN-NSA Filter Framework for Marine Radar Target Tracking. Electronics, 14(8), 1492. https://doi.org/10.3390/electronics14081492






