Problem of Supraharmonic Diagnostics in Power Networks
Abstract
1. Introduction
2. Description of the Research Subject
- Stage I
- Research in a controlled environment using a symmetric 3-phase low-voltage (LV) power grid model with a branching radial topology. The nominal values of resistances and inductances, connected in series to constitute subsequent sections in the power grid model, are presented in Table 1. The criteria for selecting the parameters specified in Table 1 was to recreate an example power grid with parameters corresponding to an example of a real LV network with overhead lines (parameters selected as for the configuration in the real power system in Poland). The research at this stage concerns the analysis of propagation in the selected phase of the 3-phase system and at assessing the propagation of supraharmonic components in the LV radial network.
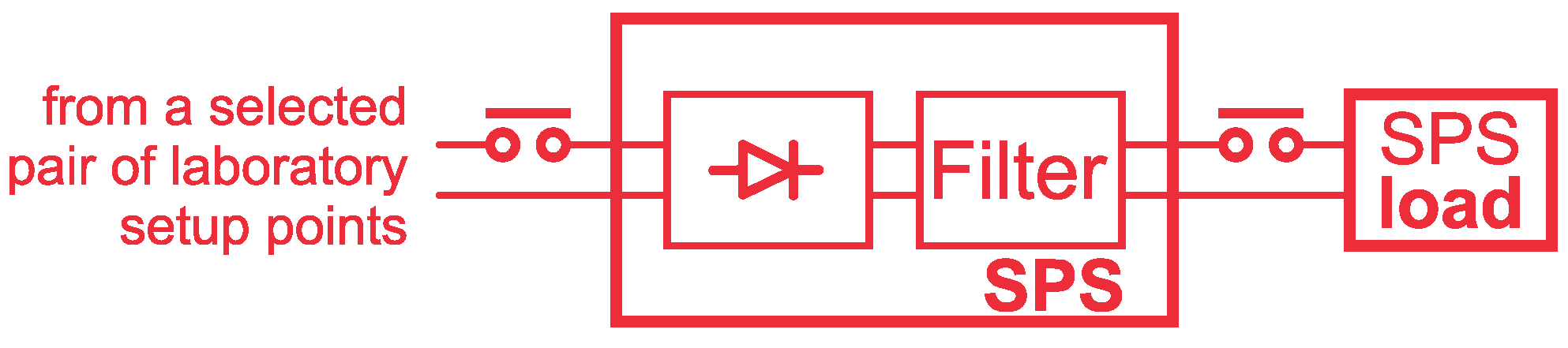
- Stage II
- Research carried out in the same environment as in Stage I. The research at this stage also concerns the analysis of propagation in the selected phase of the 3-phase system. The research aimed to assess the impact of typical loads in an LV power grid on the propagation of supraharmonics in the LV radial network.
- Stage III
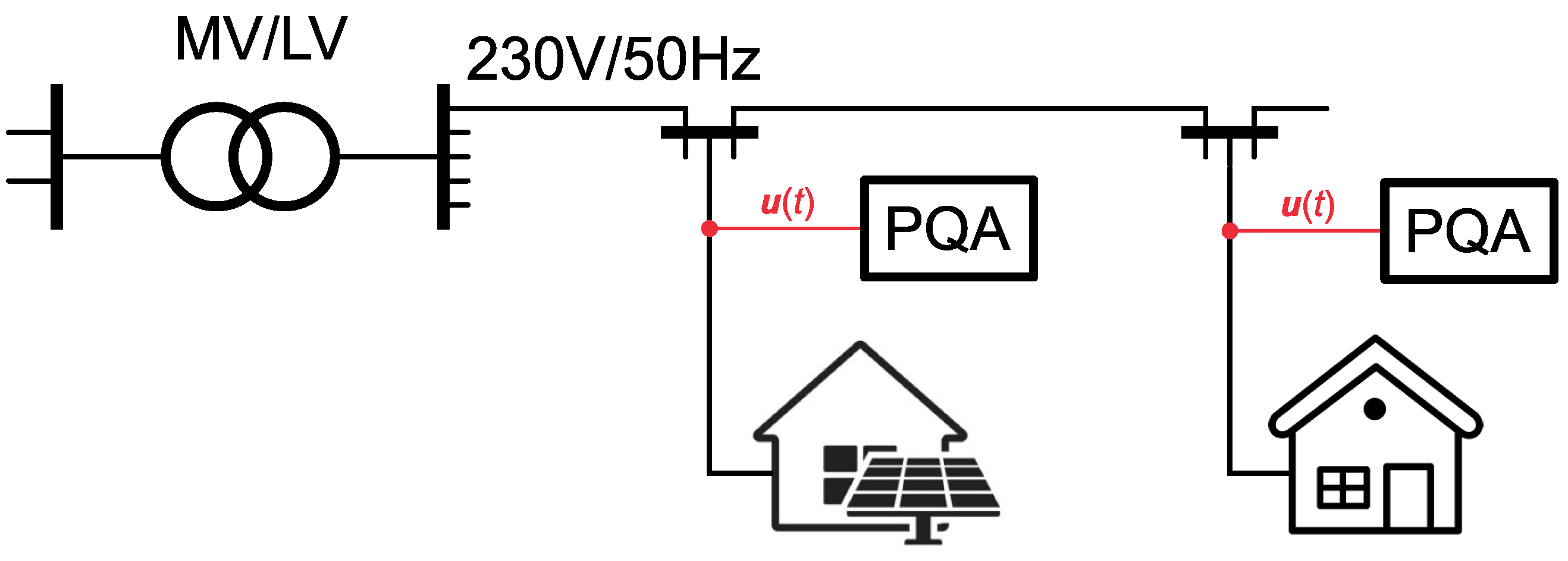
- Industrial research carried out in a real 3-phase LV power grid.
3. Research Results and Discussion
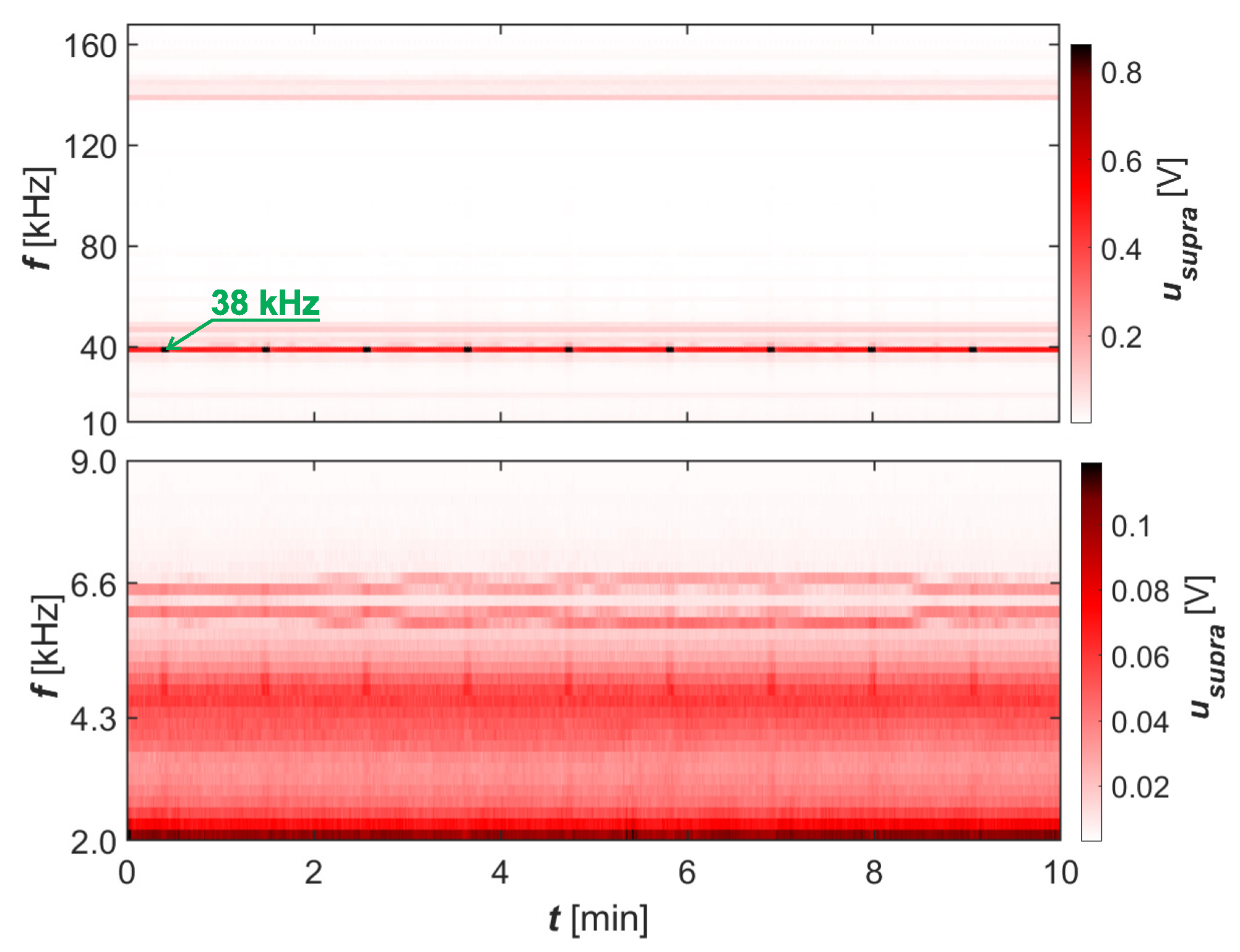
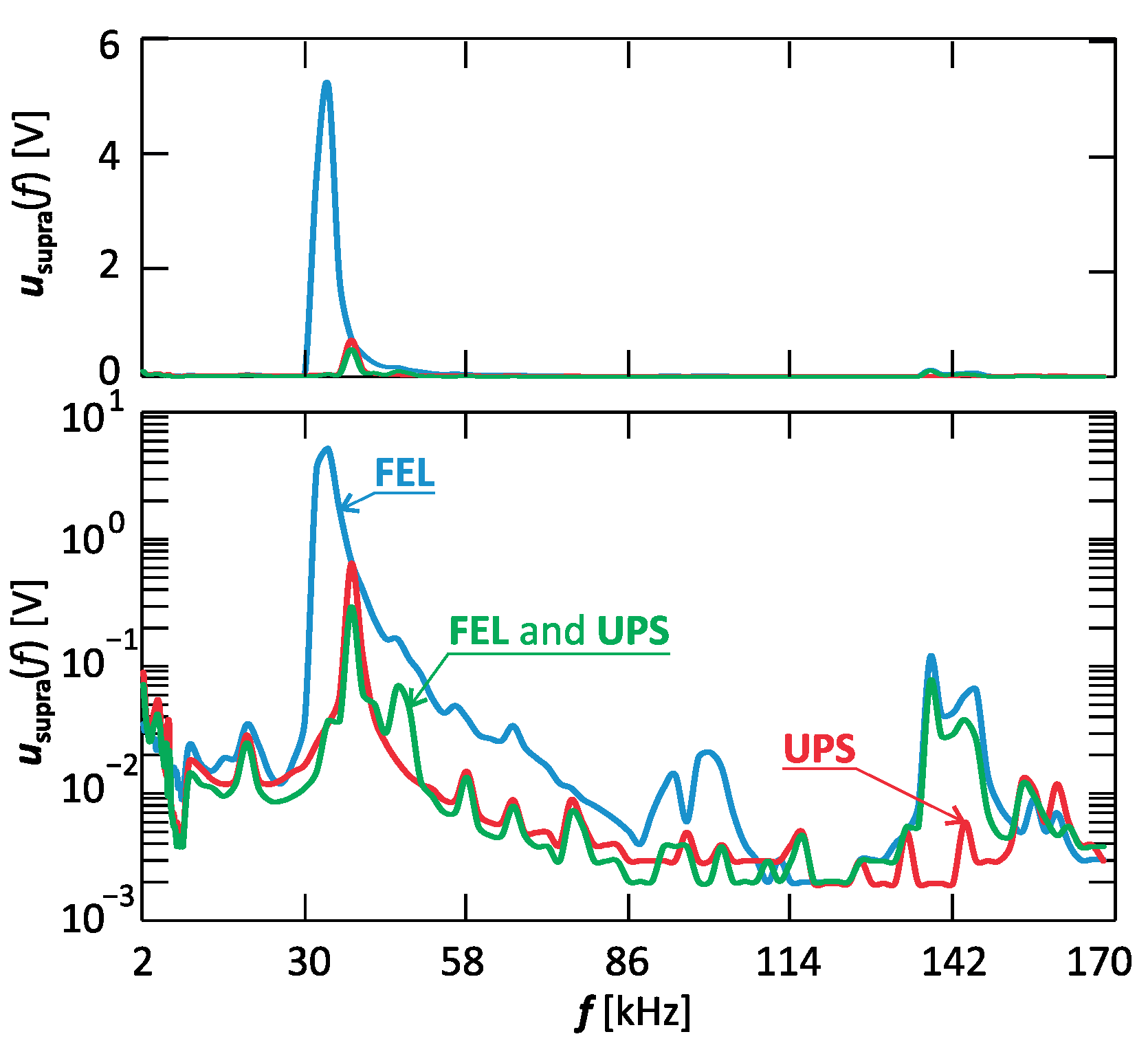
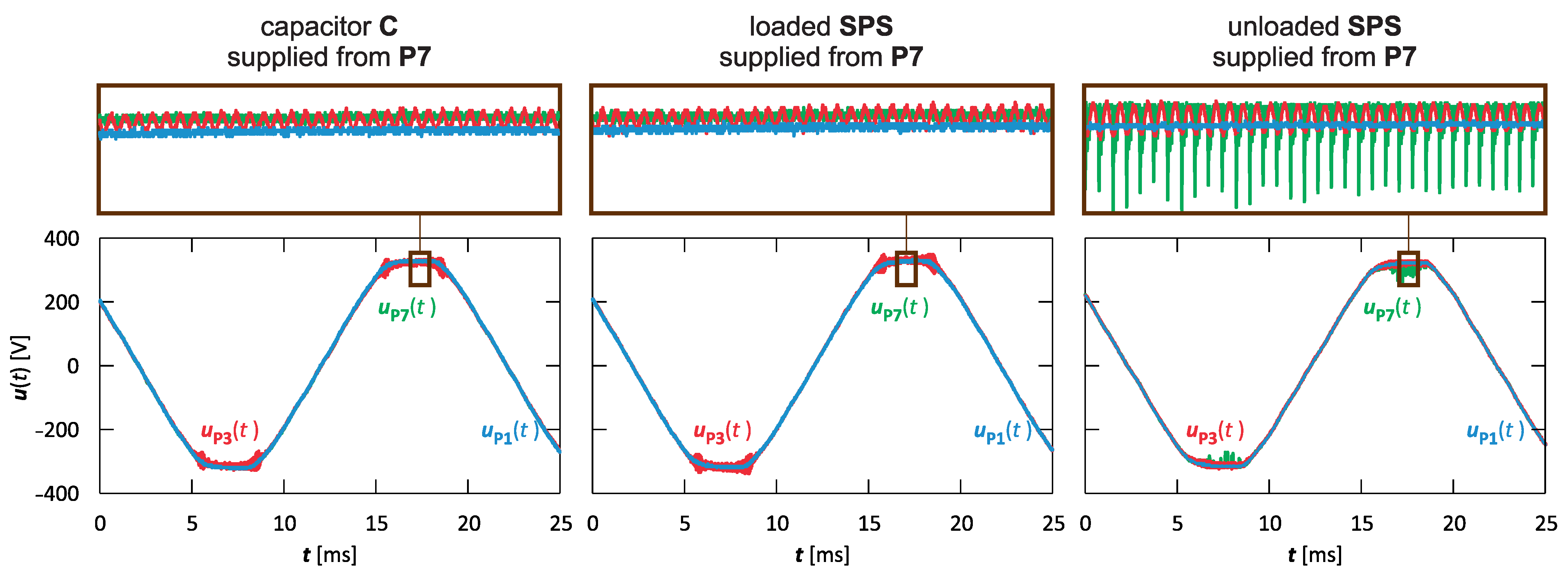
3.1. Stage I—Assessment of Supraharmonic Propagation in the Radial Low-Voltage Network
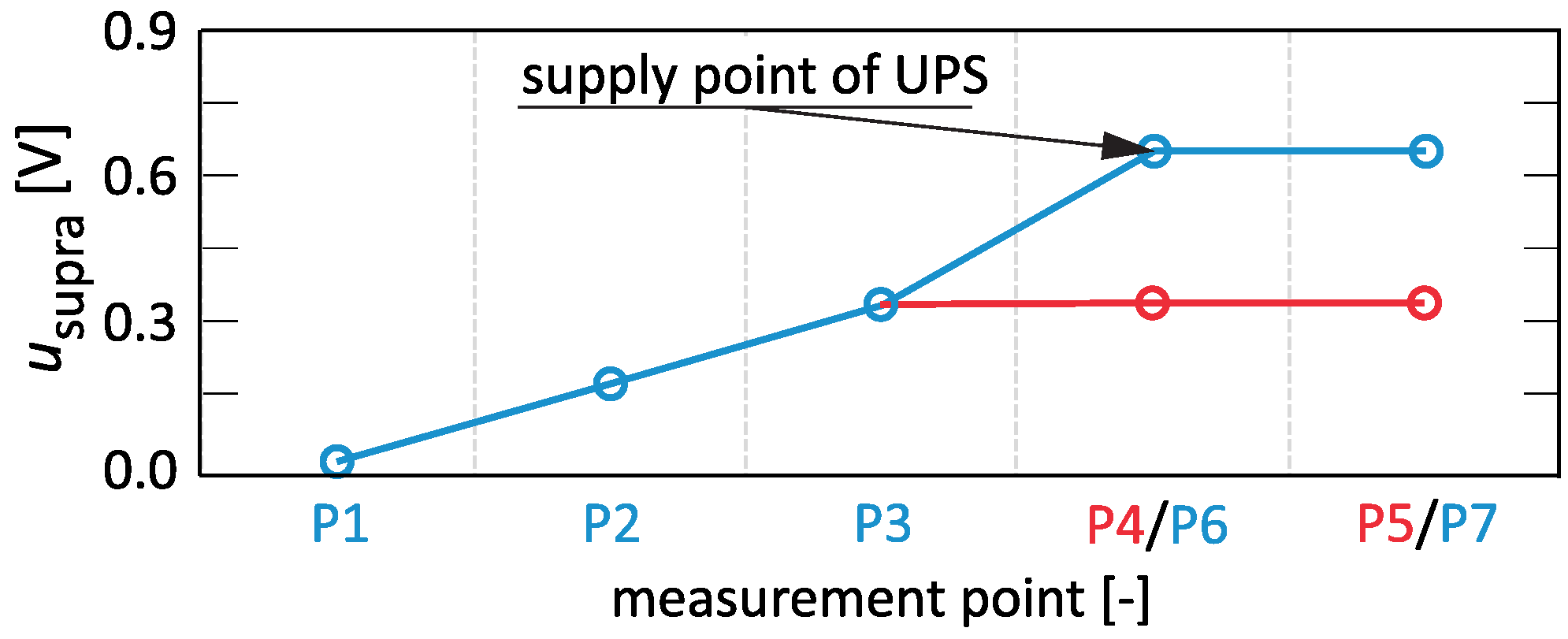
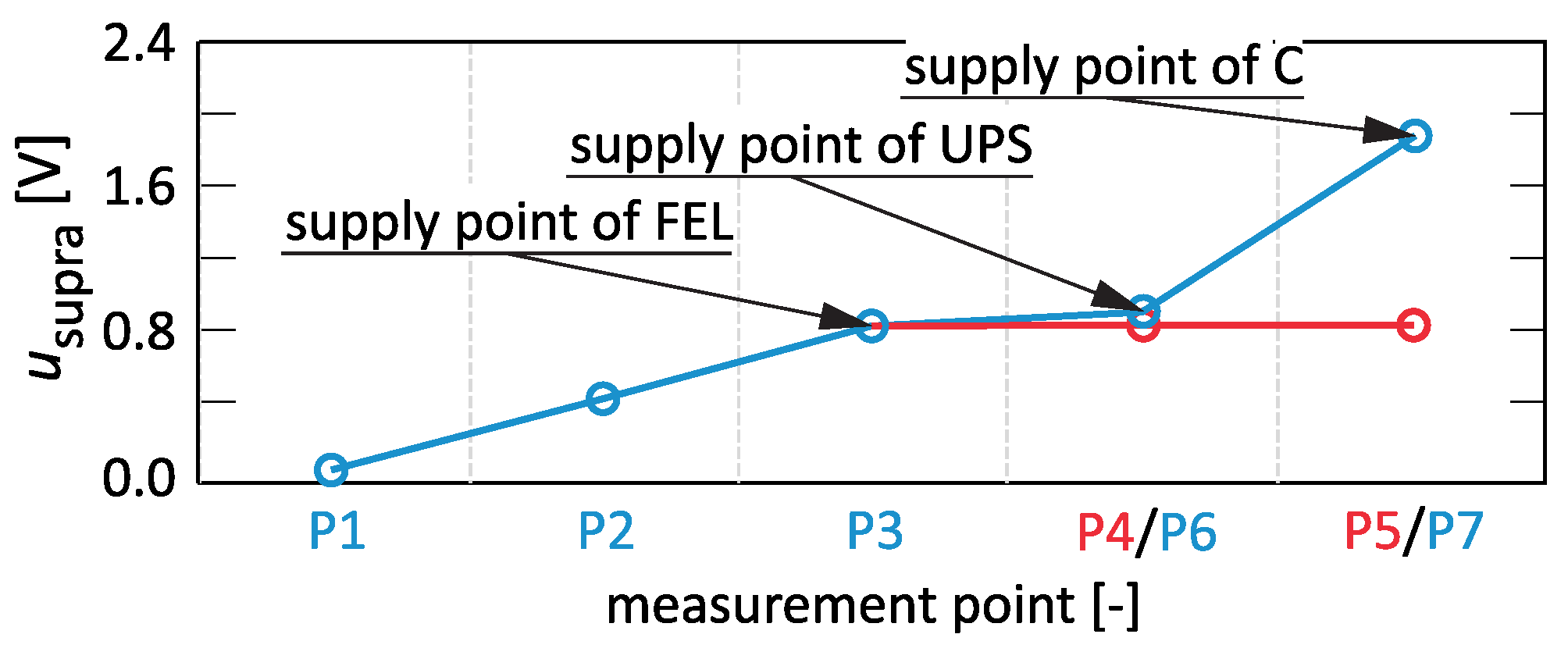
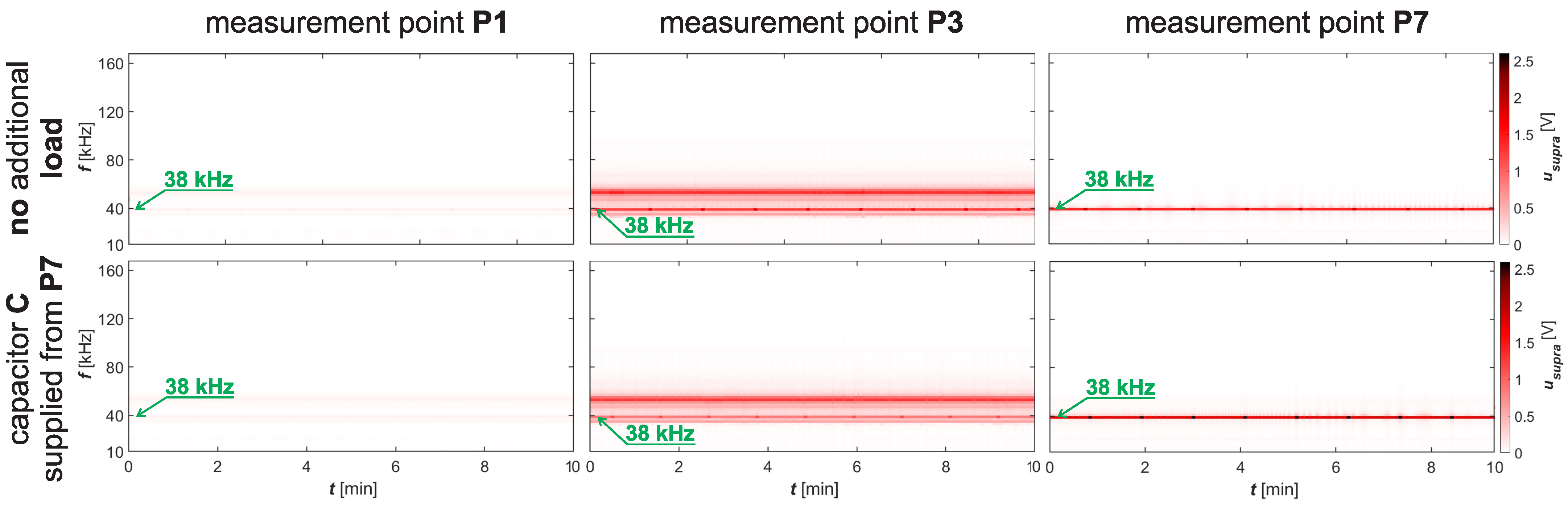
3.2. Stage II—Assessment of Supraharmonic Propagation in the Radial Low-Voltage Network with Additional Loads
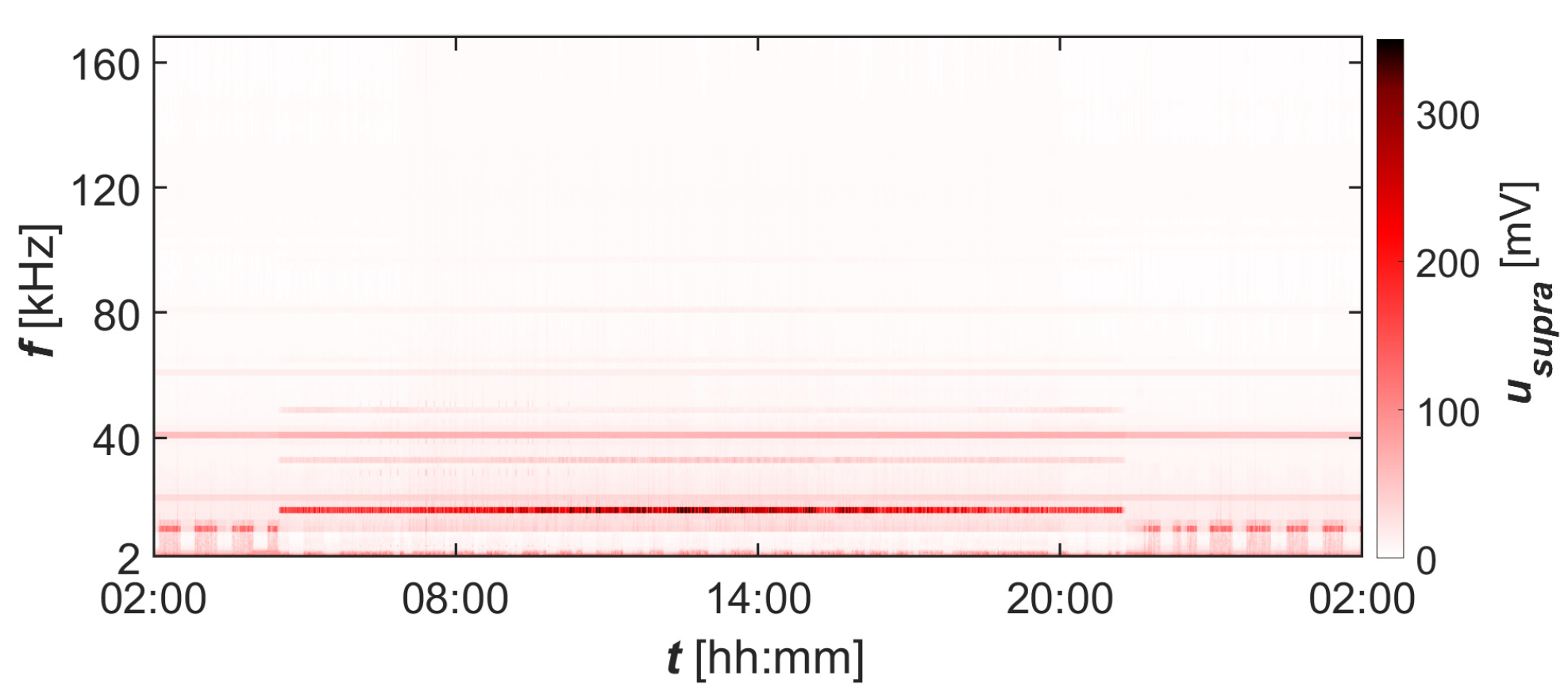
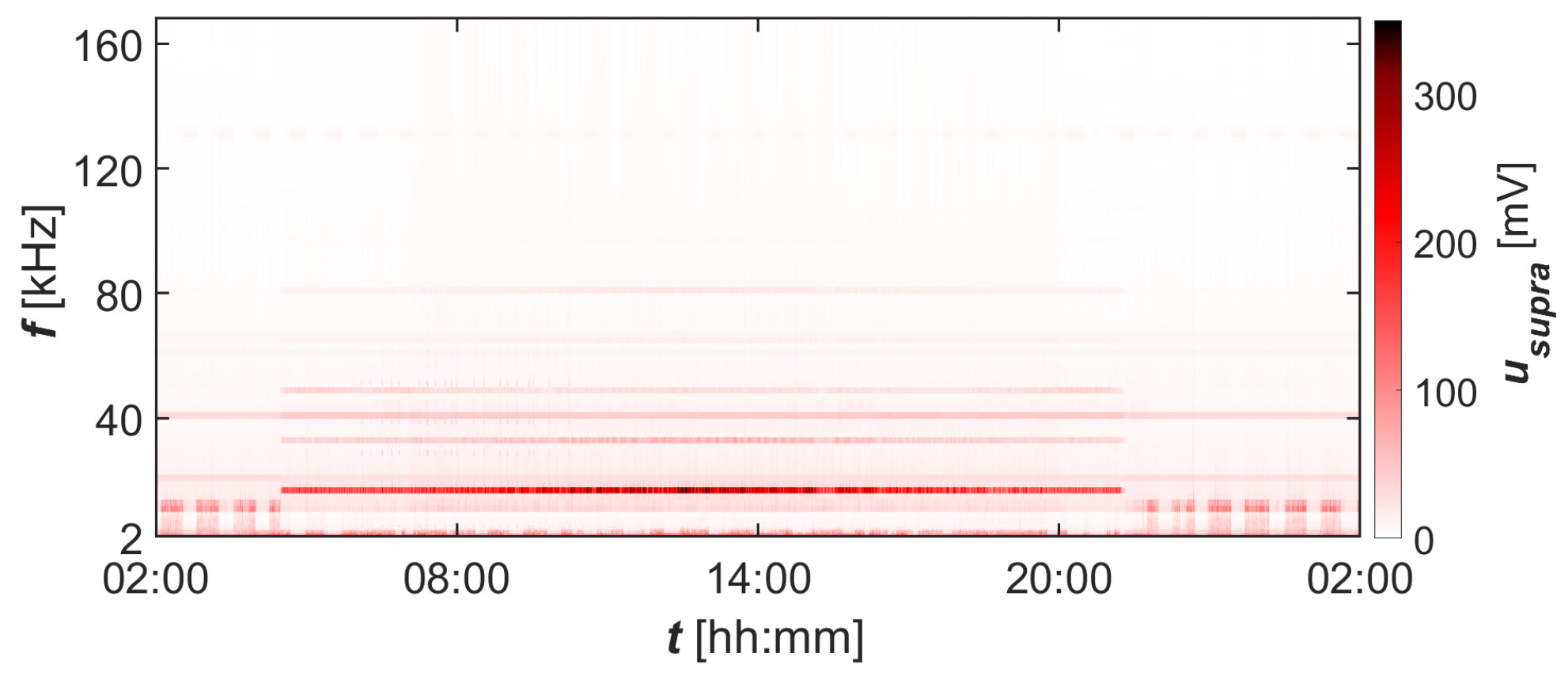
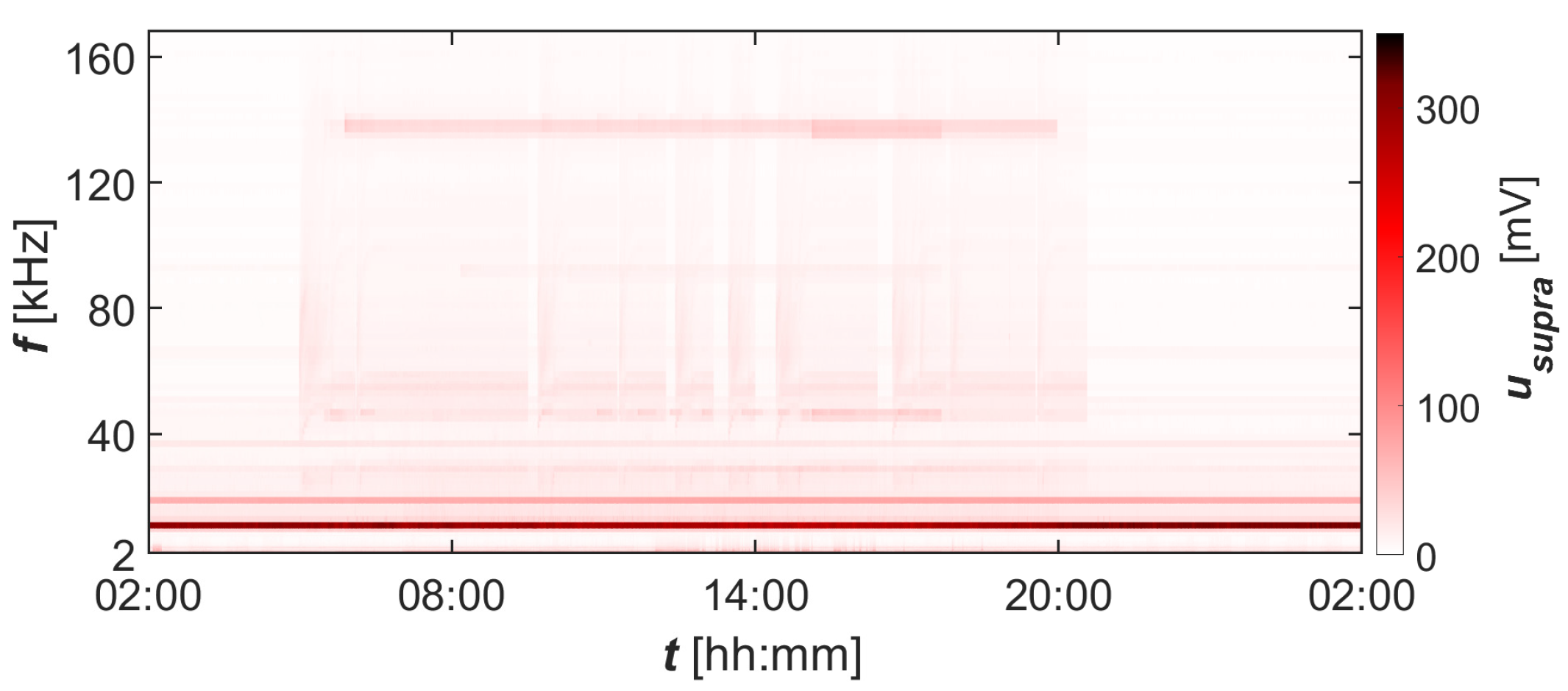
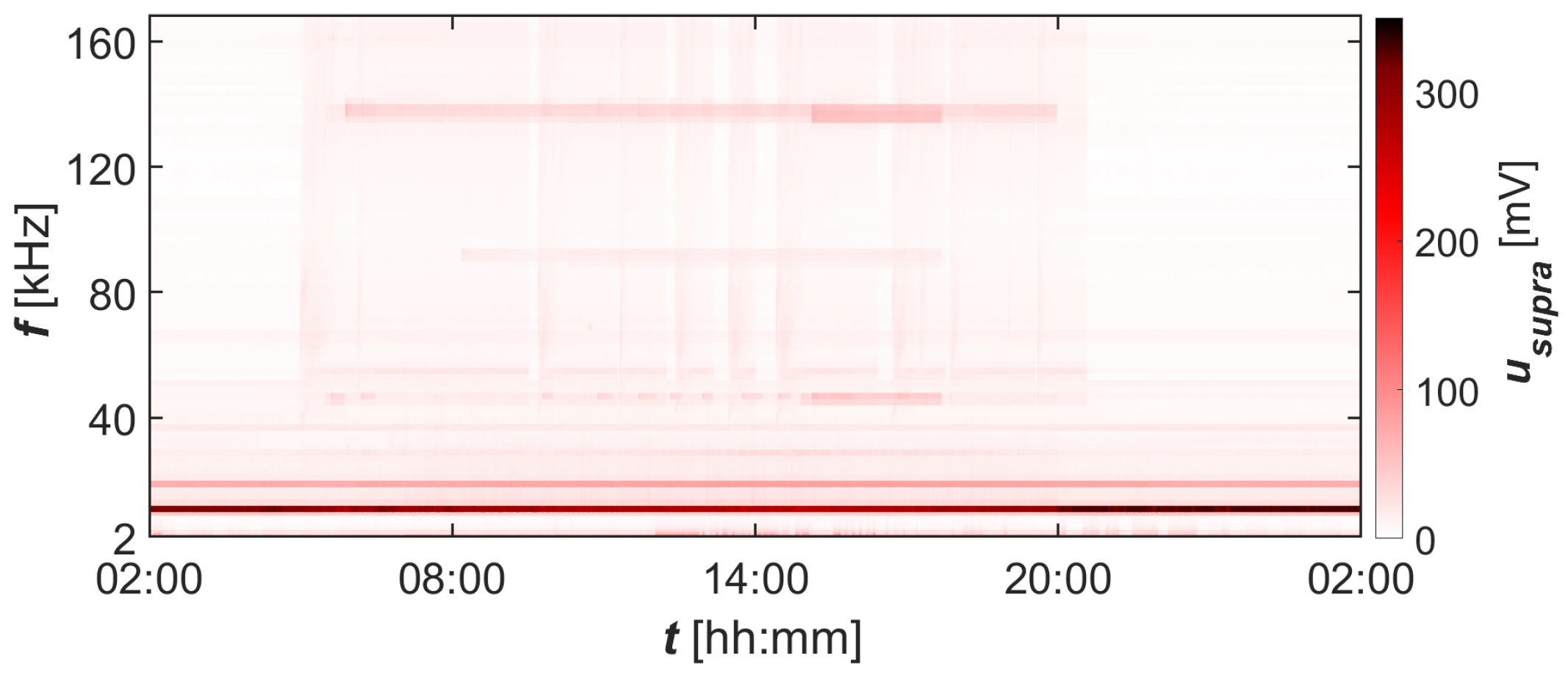
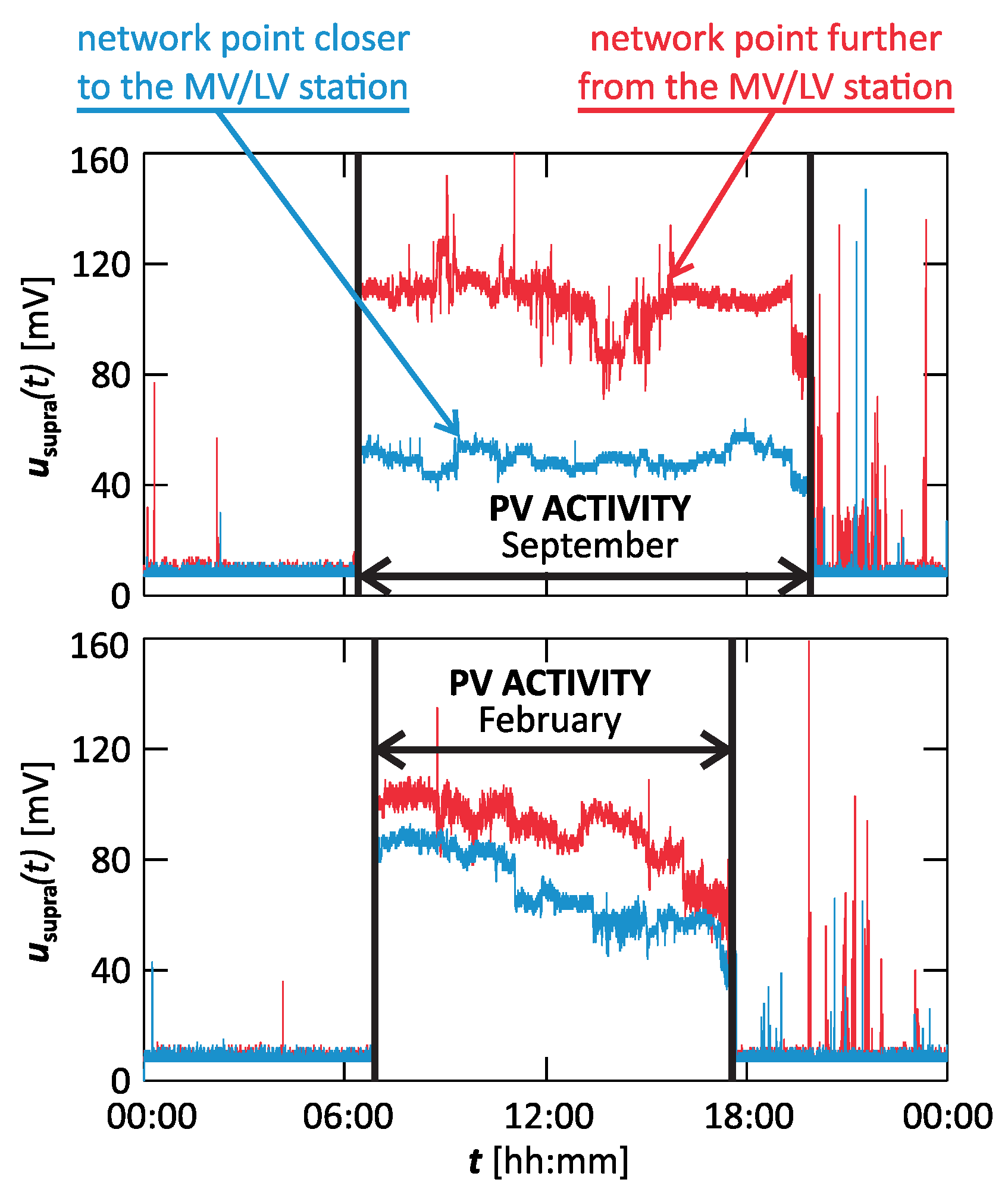
3.3. Stage III—Measurement Results from Industrial Research
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Standard EN 50160:2010/A2:2019; Voltage Characteristics of Electricity Supplied by Public Electricity Networks. CENELEC: Brussels, Belgium, 2017.
- Fuchs, E.; Masoum, M. Power Quality in Power Systems, Electrical Machines, and Power-Electronic Drives, 3rd ed.; Academic Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Sitki Akkaya, E.Y.; Akgun, H.M. A New Comparative Approach Based on Features of Subcomponents and Machine Learning Algorithms to Detect and Classify Power Quality Disturbances. Electr. Power Compon. Syst. 2024, 52, 1269–1292. [Google Scholar] [CrossRef]
- Donolo, P.D.; Pezzani, C.M.; Bossio, G.R.; De Angelo, C.H.; Donolo, M.A. Derating of Induction Motors Due to Power Quality Issues Considering the Motor Efficiency Class. IEEE Trans. Ind. Appl. 2020, 56, 961–969. [Google Scholar] [CrossRef]
- Gnacinski, P.; Hallmann, D.; Peplinski, M.; Jankowski, P. The effects of voltage subharmonics on cage induction machine. Int. J. Electr. Power Energy Syst. 2019, 111, 125–131. [Google Scholar] [CrossRef]
- Gnacinski, P.; Peplinski, M.; Muc, A.; Hallmann, D.; Klimczak, P. Induction Motors Under Voltage Fluctuations and Power Quality Standards. IEEE Trans. Energy Convers. 2024, 39, 1255–1264. [Google Scholar] [CrossRef]
- Gnacinski, P.; Hallmann, D.; Muc, A.; Klimczak, P.; Peplinski, M. Induction Motor Supplied with Voltage Containing Symmetrical Subharmonics and Interharmonics. Energies 2022, 15, 7712. [Google Scholar] [CrossRef]
- Langella, R.; Testa, A.; Vendemia, V.; Drapela, J. New Comprehensive Analytical Model of Single-Phase AC/DC Diode Rectifiers in the Presence of Interharmonics in Supply Voltage. In Proceedings of the 2022 20th International Conference on Harmonics and Quality of Power (ICHQP 2022), Naples, Italy, 29 May–1 June 2022. [Google Scholar] [CrossRef]
- 6th CEER Benchmarking Report on All the Quality of Electricity and Gas Supply 2016. 2016. Available online: https://www.ceer.eu/ (accessed on 1 September 2021).
- Enslin, J.; Heskes, P. Harmonic interaction between a large number of distributed power inverters and the distribution network. IEEE Trans. Power Electron. 2004, 19, 1586–1593. [Google Scholar] [CrossRef]
- Siostrzonek, T.; Chmielowiec, K.; Firlit, A.; Barczentewicz, S. Advantages and disadvantages of using multi-pulse systems in the electric drive of hoisting machines. Prz. Elektrotechniczny 2020, 96, 43–46. [Google Scholar] [CrossRef]
- Teng, F.; Ding, Z.; Hu, Z.; Sarikprueck, P. Technical Review on Advanced Approaches for Electric Vehicle Charging Demand Management, Part I: Applications in Electric Power Market and Renewable Energy Integration. IEEE Trans. Ind. Appl. 2020, 56, 5684–5694. [Google Scholar] [CrossRef]
- Kuwalek, P.; Wiczynski, G. Dependence of Voltage Fluctuation Severity on Clipped Sinewave Distortion of Voltage. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Kuwalek, P. Decomposition by Approximation With Pulse Waves Allowing Further Research on Sources of Voltage Fluctuations. IEEE Trans. Ind. Electron. 2024, 71, 5263–5273. [Google Scholar] [CrossRef]
- Gonzalez-Abreu, A.D.; Osornio-Rios, R.A.; Jaen-Cuellar, A.Y.; Delgado-Prieto, M.; Antonino-Daviu, J.A.; Karlis, A. Advances in Power Quality Analysis Techniques for Electrical Machines and Drives: A Review. Energies 2022, 15, 1909. [Google Scholar] [CrossRef]
- Nandi, R.; Tripathy, M.; Gupta, C.P. Multi-Objective Optimization Based Voltage Injection Technique for Minimizing Imbalance and Harmonics in AC Microgrid. IEEE Trans. Sustain. Energy 2024, 15, 1269–1287. [Google Scholar] [CrossRef]
- Chmielowiec, K.; Topolski, L.; Dutka, M.; Piszczek, A.; Hanzelka, Z.; Rodziewicz, T. Technical Requirements of Photovoltaic Inverters for Low Voltage Distribution Networks. Inventions 2024, 9, 91. [Google Scholar] [CrossRef]
- Bollen, M.; Olofsson, M.; Larsson, A.; Ronnberg, S.; Lundmark, M. Standards for supraharmonics (2 to 150 kHz). IEEE Electromagn. Compat. Mag. 2014, 3, 114–119. [Google Scholar] [CrossRef]
- Standard IEC 61000-4-30:2015/AMD1:2021; Testing and Measurement Techniques—Power Quality Measurement Methods. IEC: Geneva, Switzerland, 2021.
- Standard IEC 61000-4-7:2002/A1:2008; Testing and Measurement Techniques—General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto. IEC: Geneva, Switzerland, 2009.
- Kuwalek, P.; Otomanski, P.; Wandachowicz, K. Influence of the Phenomenon of Spectrum Leakage on the Evaluation Process of Metrological Properties of Power Quality Analyser. Energies 2020, 13, 5338. [Google Scholar] [CrossRef]
- Kuwalek, P.; Bracale, A.; Sikorski, T.; Rezmer, J. Synchronized Approach Based on Empirical Fourier Decomposition for Accurate Assessment of Harmonics and Specific Supraharmonics. IEEE Trans. Ind. Electron. 2025, 72, 992–1002. [Google Scholar] [CrossRef]
- Frigo, G.; Braun, J. Supraharmonic Dynamic Phasors: Estimation of Time-Varying Emissions. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Mendes, T.M.; Ferreira, D.D.; Silva, L.R.M.; Ribeiro, P.F.; Meyer, J.; Duque, C.A. PLL Based Method for Supraharmonics Emission Assessment. IEEE Trans. Power Deliv. 2022, 37, 2610–2620. [Google Scholar] [CrossRef]
- Carpinelli, G.; Bracale, A.; Varilone, P.; Sikorski, T.; Kostyla, P.; Leonowicz, Z. A New Advanced Method for an Accurate Assessment of Harmonic and Supraharmonic Distortion in Power System Waveforms. IEEE Access 2021, 9, 88685–88698. [Google Scholar] [CrossRef]
- Akkaya, S.; Yuksek, E.; Akgun, H. A comprehensive research of machine learning algorithms for power quality disturbances classifier based on time-series window. Electr. Eng. 2024, 106, 3983–4001. [Google Scholar] [CrossRef]
- Ritzmann, D.; Lodetti, S.; de la Vega, D.; Khokhlov, V.; Gallarreta, A.; Wright, P.; Meyer, J.; Fernández, I.; Klingbeil, D. Comparison of Measurement Methods for 2–150-kHz Conducted Emissions in Power Networks. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Zhuang, S.; Zhao, W.; Wang, R.; Wang, Q.; Huang, S. New Measurement Algorithm for Supraharmonics Based on Multiple Measurement Vectors Model and Orthogonal Matching Pursuit. IEEE Trans. Instrum. Meas. 2019, 68, 1671–1679. [Google Scholar] [CrossRef]
- Lodetti, S.; Bruna, J.; Melero, J.J.; Khokhlov, V.; Meyer, J. A Robust Wavelet-Based Hybrid Method for the Simultaneous Measurement of Harmonic and Supraharmonic Distortion. IEEE Trans. Instrum. Meas. 2020, 69, 6704–6712. [Google Scholar] [CrossRef]
- IEEE Std 519-2022 (Revision of IEEE Std 519-2014); IEEE Standard for Harmonic Control in Electric Power Systems. IEEE: New York, NY, USA, 2022; pp. 1–31. [CrossRef]
- Powell, J.; McCafferty-Leroux, A.; Hilal, W.; Gadsden, S.A. Smart grids: A comprehensive survey of challenges, industry applications, and future trends. Energy Rep. 2024, 11, 5760–5785. [Google Scholar] [CrossRef]
- Frydlewicz, W.; Michalec, L.; Kostyla, P.; Kaczorowska, D.; Sikorski, T. Influence of the Supply Voltage Variation on the Conducted Emission in the Frequency Range up to 150 kHz Injected into the Power Grid by CFL and LED Lamps—Case Study. Appl. Sci. 2024, 14, 2590. [Google Scholar] [CrossRef]
- Mariscotti, A.; Mingotti, A. The Effects of Supraharmonic Distortion in MV and LV AC Grids. Sensors 2024, 24, 2465. [Google Scholar] [CrossRef] [PubMed]
- Barczentewicz, S.; Rodziewicz, T.; Bien, A.; Firlit, A. Individual emission assessment of harmonics in DSO environment. Int. J. Electron. Telecommun. 2024, 70, 169–174. [Google Scholar] [CrossRef]
- Alfalahi, S.T.Y.; Alkahtani, A.A.; Al-Shetwi, A.Q.; Al-Ogaili, A.S.; Abbood, A.A.; Mansor, M.B.; Fazea, Y. Supraharmonics in Power Grid: Identification, Standards, and Measurement Techniques. IEEE Access 2021, 9, 103677–103690. [Google Scholar] [CrossRef]
- Kuwalek, P.; Wiczynski, G. Preliminary Observations of Supraharmonics in Low Voltage Networks. In Proceedings of the 2023 IEEE International Conference on Energy Technologies for Future Grids (ETFG), Wollongong, Australia, 3–6 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Sakar, S.; Rönnberg, S.K.; Bollen, M. Interharmonic Emission in AC–DC Converters Exposed to Nonsynchronized High-Frequency Voltage Above 2 kHz. IEEE Trans. Power Electron. 2021, 36, 7705–7715. [Google Scholar] [CrossRef]
- Sakar, S.; Rönnberg, S. Modeling and Analysis of DC-Link Capacitors Subjected to High Frequency Conducted Disturbances in Electronic Equipment. IEEE Trans. Power Electron. 2022, 37, 5949–5956. [Google Scholar] [CrossRef]
- Sanchez-Herrera, R.; Clavijo-Camacho, J.; Gomez-Ruiz, G.; Vazquez, J.R. Identification of Both Distortion and Imbalance Sources in Electrical Installations: A Comparative Assessment. Energies 2024, 17, 2536. [Google Scholar] [CrossRef]
- Mariscotti, A.; Sandrolini, L.; Pasini, G. Variability Caused by Setup and Operating Conditions for Conducted EMI of Switched Mode Power Supplies Over the 2–1000 kHz Interval. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Espin-Delgado, A.; Ronnberg, S.; Sudha Letha, S.; Bollen, M. Diagnosis of supraharmonics-related problems based on the effects on electrical equipment. Electr. Power Syst. Res. 2021, 195, 107179. [Google Scholar] [CrossRef]
- Espin-Delgado, A.; Ronnberg, S. Modeling and Analysis of Supraharmonic Propagation for Stochastic Studies. IEEE Trans. Power Deliv. 2022, 37, 4899–4910. [Google Scholar] [CrossRef]
- Pinto, J.; Grasel, B.; Baptista, J. Analysis of Supraharmonics Emission in Power Grids: A Case Study of Photovoltaic Inverters. Electronics 2024, 13, 4880. [Google Scholar] [CrossRef]
- Osheba, M.S.; Aboutaleb, A.M.; Desmet, J.; Knockaert, J. The Impact of Grid Distortion on the Power Conversion Harmonics of AC/DC Converters in the Supraharmonic Range. Electronics 2024, 13, 2244. [Google Scholar] [CrossRef]
- Aboutaleb, A.M.; Desmet, J.; Knockaert, J. Impact of Grid-Connected Inverter Parameters on the Supraharmonic Emissions in Distributed Power Generation Systems. Machines 2023, 11, 1014. [Google Scholar] [CrossRef]
- Tebexreni, I.S.L.; Duque, C.A.; Seixas, J.M.d. Separation and Identification of Sources of Supraharmonic Signals Using Complex ICA. In Proceedings of the 2023 IEEE Power and Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Tao, S.; Siddique, A.; Dong, X. A Flexible Supraharmonic Group Method Based on Switching Frequency Identification. IEEE Access 2020, 8, 39491–39501. [Google Scholar] [CrossRef]
- Xu, L.; He, Y.; Lei, C.; Qiu, J.; Deng, Q. Research on Active Filter for Supraharmonics Suppression of Power Grid. In Proceedings of the 2020 IEEE 3rd Student Conference on Electrical Machines and Systems (SCEMS), Jinan, China, 4–6 December 2020; pp. 735–740. [Google Scholar] [CrossRef]
- Ronnberg, S.K.; Castro, A.G.d.; Moreno-Munoz, A.; Bollen, M.H.; Garrido, J. Solar PV inverter supraharmonics reduction with random PWM. In Proceedings of the 2017 11th IEEE International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Cadiz, Spain, 4–6 April 2017; pp. 644–649. [Google Scholar] [CrossRef]
- Garrido-Zafra, J.; Moreno-Munoz, A.; Gil-De-Castro, A.; Ortiz-Lopez, M.A.; Morales, T. Supraharmonics reduction in LED drivers via random pulse-position modulation. Int. J. Electron. 2018, 105, 2128–2143. [Google Scholar] [CrossRef]
- Garrido, J.; Moreno-Munoz, A.; de Castro, A.G.; Pallares-Lopez, V.; Morales-Leal, T. Supraharmonics emission from LED lamps: A reduction proposal based on random pulse-width modulation. Electr. Power Syst. Res. 2018, 164, 11–19. [Google Scholar] [CrossRef]
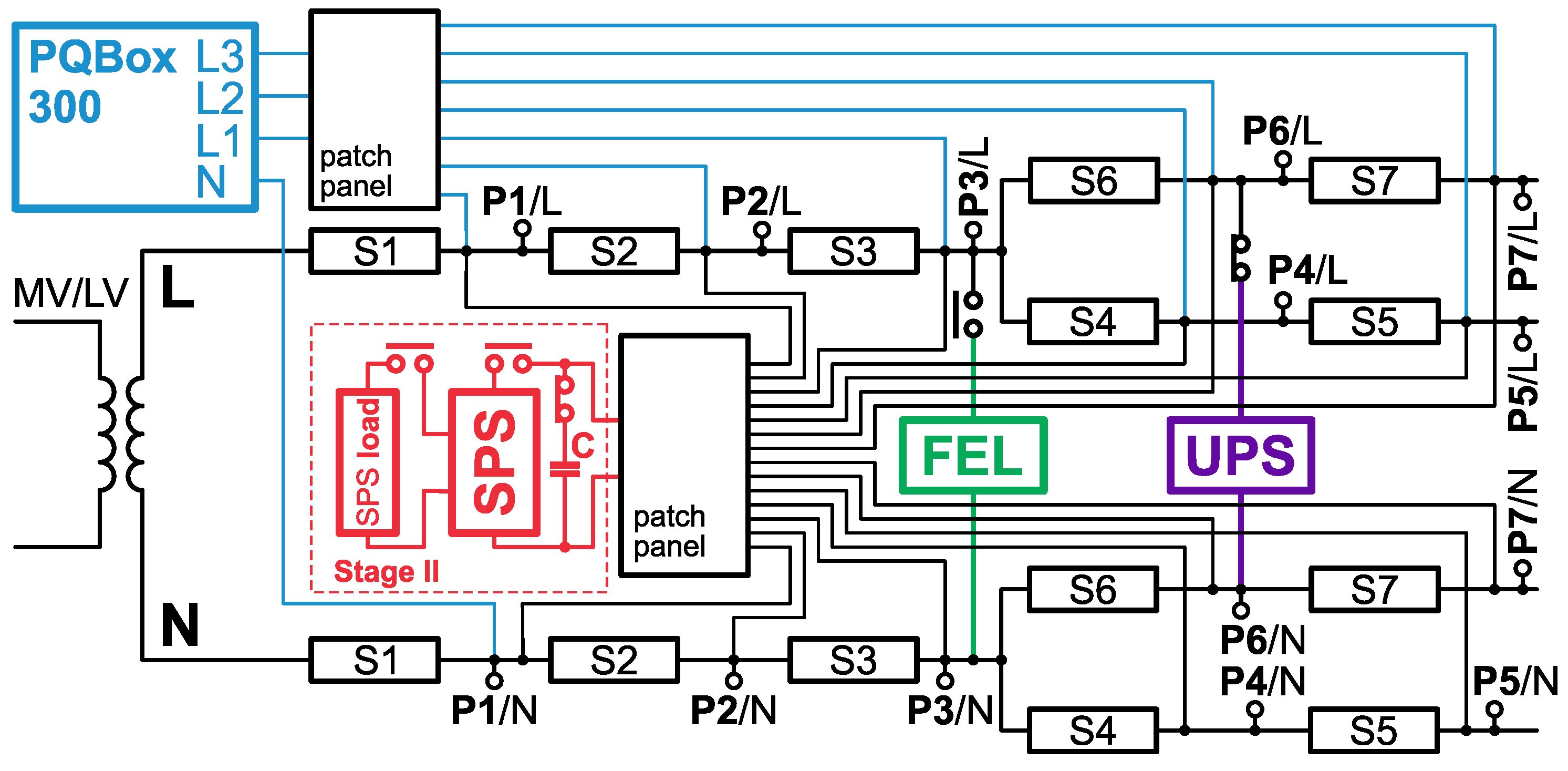








| Section No. | R [m] | L [H] |
|---|---|---|
| S1 | 3.8 | 34.4 |
| S2 | 150.0 | 100.0 |
| S3 | 150.0 | 100.0 |
| S4 | 100.0 | 220.0 |
| S5 | 50.0 | 6.8 |
| S6 | 100.0 | 220.0 |
| S7 | 50.0 | 6.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuwałek, P.; Wiczyński, G. Problem of Supraharmonic Diagnostics in Power Networks. Electronics 2025, 14, 1609. https://doi.org/10.3390/electronics14081609
Kuwałek P, Wiczyński G. Problem of Supraharmonic Diagnostics in Power Networks. Electronics. 2025; 14(8):1609. https://doi.org/10.3390/electronics14081609
Chicago/Turabian StyleKuwałek, Piotr, and Grzegorz Wiczyński. 2025. "Problem of Supraharmonic Diagnostics in Power Networks" Electronics 14, no. 8: 1609. https://doi.org/10.3390/electronics14081609
APA StyleKuwałek, P., & Wiczyński, G. (2025). Problem of Supraharmonic Diagnostics in Power Networks. Electronics, 14(8), 1609. https://doi.org/10.3390/electronics14081609







