Optimizing the Operational Process of a Social Robot for Elderly Assistance: Enhancing Reliability and Readiness
Abstract
1. Introduction
- −
- Increase the reliability of social robots;
- −
- Enhance the safety of services provided by social robots by introducing solutions that increase resistance to adverse factors;
- −
- Improve the safety of social robots through proper operational process planning.
2. State of the Art
3. Modeling the Operation Process of a Social Robot Dedicated to the Elderly
- −
- Weibull models, used to analyze time to failure, but which do not take into account the operational context of the robot.
- −
- Markov processes, which allow for the modeling of robot transients, but are often based on a limited number of states and assume stationarity.
- −
- Redundancy-based models, typical for critical systems, but difficult to apply to light mobile robotics.
- −
- classification of robot states based on the robot’s actual activity in the user environment;
- −
- the dynamics of transitions between states (activity–inactivity–failure);
- −
- integration with an optimization function for operational decision-making.
- −
- SPZ (S0)—state of full fitness of all robots employed within a limited space of a patient care facility. All assumed robot functionalities are implemented on an ongoing basis. Control and safety monitoring systems covering individual robots are functional. All primary and redundant power supply sources are fit for use and ready to accept the load associated with the operation of robots S01, S02,…, S0n. Robot power supply systems are always diagnosed online due to the technical parameters of battery bank charging voltage.
- −
- SZB (SD1, SD2,…, SDn−1)—state of safety hazard for the implementation of specific functionalities in robots used in relation to monitoring and care for hospitalized patients. Out of the available robot functionalities, only selected functions are implemented, which enable providing patient care at a pre-set safety level. This is marked in Figure 1 by distinguished, technically permissible, appropriate technical states; SD1—state of safety hazard No. 1 (unfitness of selected functionalities in robots No. S0, SD1, SD2,…, SDn−1, SD), which is the unfitness of functionalities, No. S012, S021, respectively, (marked in red in Figure 1). In a state of safety hazard, SD2 No. 2 (unfitness of selected functionalities in robots No. S0, SD1, SD2,…, SDn−1, SD) is the respective unfitness of a greater number of functionalities in individual robots numbered S011, S012, S021, S0n−1 (red in Figure 1). The last permissible state in space SZB is SDn−1 is the state of safety hazard n-1 in robots No. S0, SD1, SD2, SDn−1). Is the unfitness for selected robots, marked, respectively, in the context of implementing functionalities as No. S011, S012, S01n, S021, S022, S0n−1, in red in Figure 1. Ensuring the continuity and quality of healthcare implemented by robot groups S0, SD1, SD2,…, SDn−1, SD requires selecting only the most important function for implementation, to guarantee continued technical quality of the technical system. The available local maintenance personnel immediately takes repair action associated with recovering all robots implementing custom programmed functions, including the guarantee of electricity supply by power supply systems. In the case of extensive technical systems of such a type, remote services that are not located within the facility should be taken into account. Such personnel may be located at a remote center, monitoring the operation process. Remote service receives all information on unfitness and has a specified time to intervene to improve all functionalities, taking into account the priorities of implementing the entire healthcare process. Robot battery bank charging stations are always diagnosed online due to the technical parameters of battery bank charging output voltage. Such information on the unfitness states of stations for robots with specific functionalities is sent to a collective receiving center that manages the technical system.
- −
- SB (SD)—state of safety unreliability for the technical healthcare system in question implemented by robots. All states in Figure 1 were marked in red accordingly. Individual technical states within the healthcare system operation process graph that prevent the implementation of all system functionalities were marked. However, technical discussions are required to ensure the functionality of the care provided by robots designated to guarantee operational continuity in the aspect of its safety and implement assumed operational tasks, taking into account elemental and informational redundancy, including permissible failures in accordance with the safe-failure principle. Task implementation by individual robots within a technical system is independent. A state of safety unreliability, SD, for the technical system in question is a function of many variables, with power supply being one of them. It is a very technical function due to the ability of all robots to implement operational tasks.
- −
- Research duration—1 year (time in hours [h]):
- −
- Intensity of a transition from a state of full fitness SPZ to a state of safety hazard SZB1:
- −
- Intensity of a transition from a state of safety hazard SZB1 to a state of safety hazard SZB2:
- −
- Intensity of a transition from a state of safety hazard SZB2 to a state of safety unreliability SB:
- −
- Intensity of a transition from a state of full fitness SPZ a state of safety unreliability SB;
- −
- Intensity of a transition from a state of full fitness SPZ to a state of safety hazard SZB2:
- −
- Intensity of a transition from a state of safety hazard SZB1 to a state of safety unreliability SB:
- −
- Intensity of a transition from a state of safety hazard SZB1 to a state of full fitness SPZ:
- −
- Intensity of a transition from a state of safety hazard SZB2 to a state of safety hazard ZB1,
- −
- Intensity of a transition from a state of safety unreliability SB to a state of safety hazard SZB2:
- −
- Intensity of a transition from a state of safety unreliability SB to a state of full fitness SPZ:
- −
- Intensity of a transition from a state of safety hazard SZB2 to a state of full fitness SPZ,
- −
- Intensity of a transition from a state of safety unreliability SB to a state of safety hazard SZB1:
- ;
- ;
- ;
- .
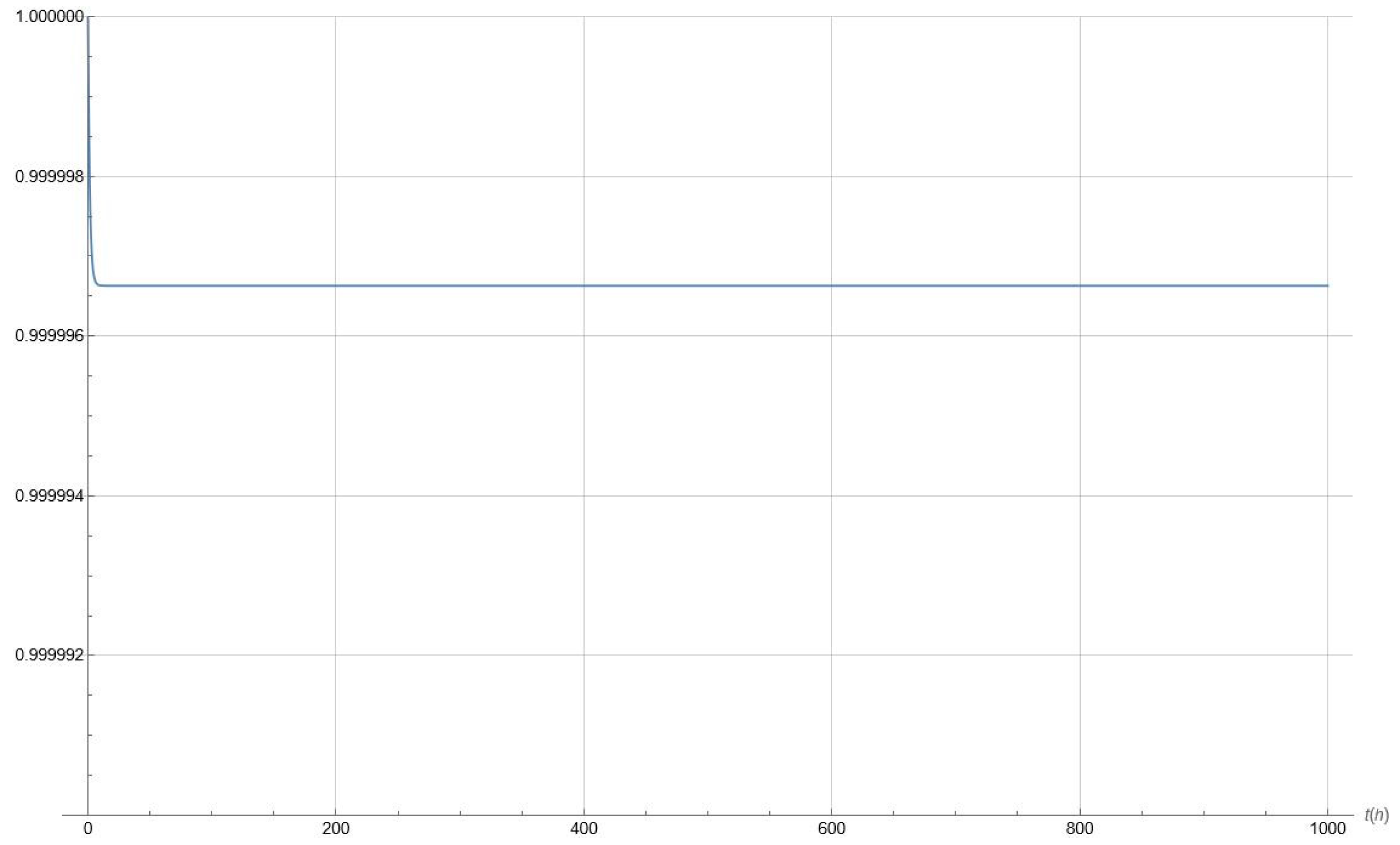
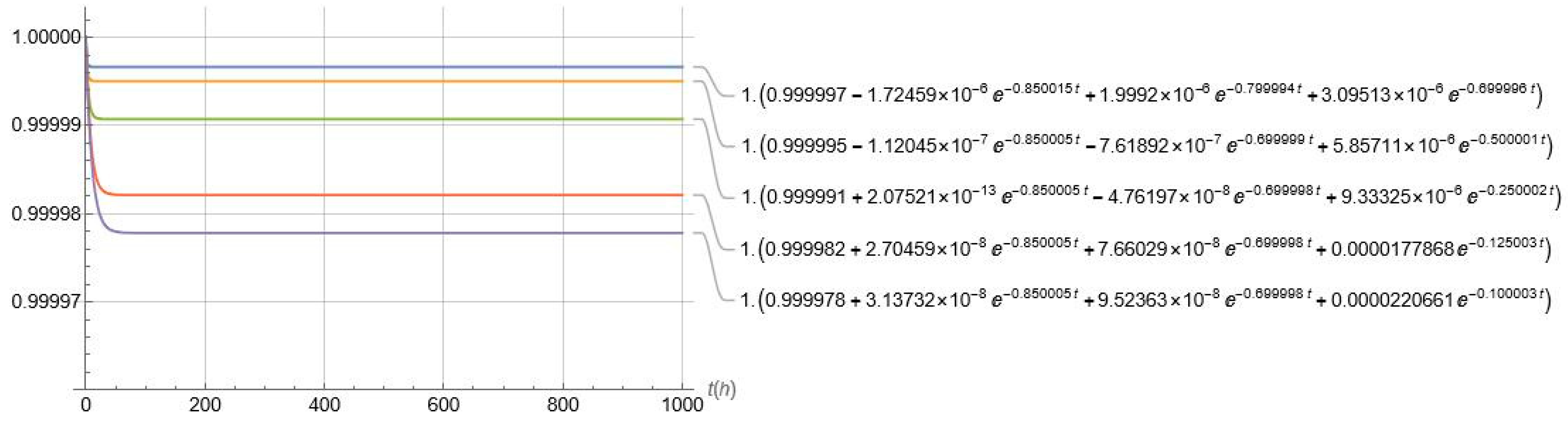
- for :
- for :
- for :
- for :
- −
- Multimodal data validation (sensor fusion)—combining data from different sources (camera, microphone, LIDAR, tactile sensors) allows the detection of inconsistencies typical of adversary attacks;
- −
- Real-time anomaly detection—the use of statistical monitoring methods (e.g., deviation from patterns) allows early detection of suspicious changes in robot behavior,
- −
- Estimating the level of confidence in the input data—by analyzing the stability of the signals and their compatibility with the operational context (e.g., location of the robot vs. expected area of operation);
- −
- Resilient learning methods (adversarial training)—future versions of the model may be extended to include mechanisms for resilient learning (e.g., augmentation of data with simulated errors).
4. Discussion About the Practical Application of Research
5. Conclusions
- −
- Acceptable response time determined by the average response time observed in human–robot interaction;
- −
- Social interaction weighting based on user surveys: the higher the expectation towards the interactivity of the robot, the more weight should be given to this component;
- −
- An inactivity penalty estimated based on the frequency and length of inactivity episodes during testing.
- Development of a dedicated operational model for social robots that considers reliability, safety, and partial usability states, providing a more accurate representation of real-world operating conditions;
- Integration of Markov processes to mathematically model transitions between usability states, enabling precise predictions of a robot’s operational readiness;
- Proposal of optimization methods for the operation process to improve the readiness index of social robots, specifically tailored to the needs of elderly and disabled users.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Piotrowski, M. (Ed.) Użyteczność Robota Kompana w Świetle Determinant Wpływających na Jakość Życia Osób z Ograniczoną Sprawnością Ruchową; Uniwersytet Warmińsko-Mazurski w Olsztynie: Olsztyn, Poland, 2024; 166p, ISBN 978-83-8100-399-5. [Google Scholar]
- Seewald, A. Revisiting End-to-end Deep Learning for Obstacle Avoidance: Replication and Open Issues. In Proceedings of the 12th International Conference on Agents and Artificial Intelligence, ICAART 2020, Valletta, Malta, 22–24 February 2020; SciTePress: Setúbal, Portugal, 2020; Volume 2, pp. 652–659, ISBN 978-989-758-395-7, ISSN 2184-433X. [Google Scholar] [CrossRef]
- Rychlicki, M.; Kasprzyk, Z.; Rosiński, A. Analysis of Accuracy and Reliability of Different Types of GPS Receivers. Sensors 2020, 20, 6498. [Google Scholar] [CrossRef] [PubMed]
- Siva, J.; Poellabauer, C. Robot and Drone Localization in GPS-Denied Areas. In Mission-Oriented Sensor Networks and Systems: Art and Science; Ammari, H., Ed.; Springer: Cham, Switzerland, 2019; pp. 597–631. [Google Scholar] [CrossRef]
- Broekens, J.; Heerink, M.; Rosendal, H. Assistive Social Robots in Elderly Care: A Review. Gerontechnology 2009, 8, 94–103. [Google Scholar] [CrossRef]
- Santhanaraj, K.K.; Ramya, M.M. A Survey of Assistive Robots and Systems for Elderly Care. J. Enabling Technol. 2021, 15, 66–72. [Google Scholar] [CrossRef]
- Martinez-Martin, E.; del Pobil, A.P. Personal Robot Assistants for Elderly Care: An Overview. In Personal Assistants: Emerging Computational Technologies; Springer: Cham, Switzerland, 2018; pp. 77–91. [Google Scholar] [CrossRef]
- Hersh, M. Overcoming Barriers and Increasing Independence–Service Robots for Elderly and Disabled People. Int. J. Adv. Robot. Syst. 2015, 12, 114. [Google Scholar] [CrossRef]
- Koh, W.Q.; Felding, S.A.; Budak, K.B.; Toomey, E.; Casey, D. Barriers and Facilitators to the Implementation of Social Robots for Older Adults and People with Dementia: A Scoping Review. BMC Geriatr. 2021, 21, 351. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulos, I.; Koulouglioti, C.; Lazzarino, R.; Ali, S. Enablers and Barriers to the Implementation of Socially Assistive Humanoid Robots in Health and Social Care: A Systematic Review. BMJ Open 2020, 10, e033096. [Google Scholar] [CrossRef]
- Servaty, R.; Kersten, A.; Brukamp, K.; Möhler, R.; Mueller, M. Implementation of Robotic Devices in Nursing Care. Barriers and Facilitators: An Integrative Review. BMJ Open 2020, 10, e038650. [Google Scholar] [CrossRef]
- Rigaud, A.S.; Dacunha, S.; Harzo, C.; Lenoir, H.; Sfeir, I.; Piccoli, M.; Pino, M. Implementation of Socially Assistive Robots in Geriatric Care Institutions: Healthcare Professionals’ Perspectives and Identification of Facilitating Factors and Barriers. J. Rehabil. Assist. Technol. Eng. 2024, 11, 20556683241284765. [Google Scholar]
- Luo, C.; Yang, C.; Yuan, R.; Liu, Q.; Li, P.; He, Y. Barriers and Facilitators to Technology Acceptance of Socially Assistive Robots in Older Adults—A Qualitative Study Based on the Capability, Opportunity, and Motivation Behavior Model (COM-B) and Stakeholder Perspectives. Geriatr. Nurs. 2024, 58, 162–170. [Google Scholar] [CrossRef]
- Sharkey, A.; Sharkey, N. Children, the Elderly, and Interactive Robots. IEEE Robot. Autom. Mag. 2011, 18, 32–38. [Google Scholar] [CrossRef]
- Kidd, C.D.; Taggart, W.; Turkle, S. A Sociable Robot to Encourage Social Interaction Among the Elderly. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation (ICRA 2006), Orlando, FL, USA, 15–19 May 2006; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Sharkey, A.; Sharkey, N. Granny and the Robots: Ethical Issues in Robot Care for the Elderly. Ethics Inf. Technol. 2012, 14, 27–40. [Google Scholar] [CrossRef]
- Oh, S.; Oh, Y.H.; Ju, D.Y. Understanding the Preference of the Elderly for Companion Robot Design. In Advances in Human Factors in Robots and Unmanned Systems: Proceedings of the AHFE 2019 International Conference on Human Factors in Robots and Unmanned Systems, Washington, DC, USA, 24–28 July 2019; Springer International Publishing: Cham, Switzerland, 2020; Volume 10, pp. 67–78. [Google Scholar] [CrossRef]
- Sun, X.; Chen, Z.; Jiang, Q. An Empirical Study on the Willingness of Young Elderly to Use Elderly Companion Robot. Int. J. Hum. Comput. Interact. 2024, 40, 1–22. [Google Scholar] [CrossRef]
- Kwiatkowska, E.; Janusz, M.; Piotrowski, M.; Krzykowska-Piotrowska, K.; Dileo, I. The Social Awareness Index as a Tool to Determine the Role of a Companion Robot in the Lives of People with Reduced Mobility. Sustainability 2024, 16, 9744. [Google Scholar] [CrossRef]
- Vercelli, A.; Rainero, I.; Ciferri, L.; Boido, M.; Pirri, F. Robots in Elderly Care. Digit.-Sci. J. Digit. Cult. 2018, 2, 37–50. [Google Scholar] [CrossRef]
- Chen, N.; Song, J.; Li, B. Providing Aging Adults Social Robots’ Companionship in Home-Based Elder Care. J. Healthc. Eng. 2019, 2019, 2726837. [Google Scholar] [CrossRef]
- Liang, F.; Hernandez, R.; Sheng, W. A Collaborative Elderly Care System Using a Companion Robot and a Wearable Device. In Proceedings of the 2022 IEEE 17th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 16–19 December 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Bardaro, G.; Antonini, A.; Motta, E. Robots for Elderly Care in the Home: A Landscape Analysis and Co-Design Toolkit. Int. J. Soc. Robot. 2022, 14, 657–681. [Google Scholar] [CrossRef]
- Fosch-Villaronga, E.; Mahler, T. Cybersecurity, Safety and Robots: Strengthening the Link between Cybersecurity and Safety in the Context of Care Robots. Comput. Law Secur. Rev. 2021, 41, 105528. [Google Scholar] [CrossRef]
- Asgharian, P.; Panchea, A.M.; Ferland, F. A Review on the Use of Mobile Service Robots in Elderly Care. Robotics 2022, 11, 127. [Google Scholar] [CrossRef]
- Arents, J.; Abolins, V.; Judvaitis, J.; Vismanis, O.; Oraby, A.; Ozols, K. Human–Robot Collaboration Trends and Safety Aspects: A Systematic Review. J. Sens. Actuator Netw. 2021, 10, 48. [Google Scholar] [CrossRef]
- Miyagawa, M.; Kai, Y.; Yasuhara, Y.; Ito, H.; Betriana, F.; Tanioka, T.; Locsin, R. Consideration of Safety Management When Using Pepper, a Humanoid Robot for Care of Older Adults. Intell. Control Autom. 2019, 11, 15–24. [Google Scholar] [CrossRef]
- Ahn, S.; Moon, I. A Study on Standard for Safety Requirements for Care Robots. In Assistive Technology: Shaping a Sustainable and Inclusive World; IOS Press: Amsterdam, The Netherlands, 2023; pp. 57–62. [Google Scholar] [CrossRef]
- Kuncara, I.A.; Widyotriatmo, A.; Hasan, A.; Nazaruddin, Y.Y. Enhancing accuracy in field mobile robot state estimation with GNSS and encoders. Measurement 2024, 235, 114903, ISSN 0263-2241. [Google Scholar] [CrossRef]
- Massa, F.; Bonamini, L.; Settimi, A.; Pallottino, L.; Caporale, D. LiDAR-Based GNSS Denied Localization for Autonomous Racing Cars. Sensors 2020, 20, 3992. [Google Scholar] [CrossRef] [PubMed]
- Matveev, A.S.; Savkin, A.V.; Hoy, M.; Wang, C. Safe Robot Navigation Among Moving and Steady Obstacles; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Möller, R.; Furnari, A.; Battiato, S.; Härmä, A.; Farinella, G.M. A survey on human-aware robot navigation. Robot. Auton. Syst. 2021, 145, 103837. [Google Scholar] [CrossRef]
- Calderita, L.V.; Vega, A.; Bustos, P.; Núñez, P. A new human-aware robot navigation framework based on time-dependent social interaction spaces: An application to assistive robots in caregiving centers. Robot. Auton. Syst. 2021, 145, 103873. [Google Scholar] [CrossRef]
- Cavallo, F.; Aquilano, M.; Bonaccorsi, M.; Limosani, R.; Manzi, A.; Carrozza, M.C.; Dario, P. Improving Domiciliary Robotic Services by Integrating the ASTRO Robot in an AMI Infrastructure. In Gearing Up and Accelerating Cross-Fertilization Between Academic and Industrial Robotics Research in Europe; Röhrbein, F., Veiga, G., Natale, C., Eds.; Springer: Cham, Switzerland, 2014; pp. 267–282. [Google Scholar] [CrossRef]
- Costa, A.; Martinez-Martin, E.; Cazorla, M.; Julian, V. PHAROS—PHysical Assistant RObot System. Sensors 2018, 18, 2633. [Google Scholar] [CrossRef]
- Kanda, T. Enabling Harmonized Human-Robot Interaction in a Public Space. In Human-Harmonized Information Technology; Nishida, T., Ed.; Springer: Tokyo, Japan, 2017; pp. 115–137. [Google Scholar] [CrossRef]
- Mikołajczyk, T.; Mikołajewski, D.; Kłodowski, A.; Łukaszewicz, A.; Mikołajewska, E.; Paczkowski, T.; Macko, M.; Skornia, M. Energy Sources of Mobile Robot Power Systems: A Systematic Review and Comparison of Efficiency. Appl. Sci. 2023, 13, 7547. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, G. Experimental Study on a Semi-Active Battery-Supercapacitor Hybrid Energy Storage System for Electric Vehicle Application. IEEE Trans. Power Electron. 2020, 35, 1014–1021. [Google Scholar] [CrossRef]
- Marzougui, H.; Kadri, A.; Martin, J.-P.; Amari, M.; Pierfederici, S.; Bacha, F. Implementation of energy management strategy of hybrid power source for electrical vehicle. Energy Convers. Manag. 2019, 195, 830–843. [Google Scholar] [CrossRef]
- Krot, K.; Iskierka, G.; Poskart, B.; Gola, A. Predictive Monitoring System for Autonomous Mobile Robots Battery Management Using the Industrial Internet of Things Technology. Materials 2022, 15, 6561. [Google Scholar] [CrossRef]
- Xie, S.B.; Hu, X.S.; Qi, S.W.; Tang, X.L.; Lang, K.; Xin, Z.K.; Brighton, J. Model predictive management for plug-in hybird electric vehicles considering optimal battery depth of discharge. Energy 2019, 173, 667–678. [Google Scholar] [CrossRef]
- Góra, K.; Granosik, G.; Cybulski, B. Energy Utilization Prediction Techniques for Heterogeneous Mobile Robots: A Review. Energies 2024, 17, 3256. [Google Scholar] [CrossRef]
- Szeląg, P.; Dudzik, S.; Podsiedlik, A. Investigation on the Mobile Wheeled Robot in Terms of Energy Consumption, Travelling Time and Path Matching Accuracy. Energies 2023, 16, 1210. [Google Scholar] [CrossRef]
- Hou, L.; Zhang, L.; Kim, J. Energy Modeling and Power Measurement for Mobile Robots. Energies 2019, 12, 27. [Google Scholar] [CrossRef]
- Haug, E.J.; De Sapio, V.; Peidro, A. Extended Operational Space Kinematics, Dynamics, and Control of Redundant Serial Robots. Robotics 2024, 13, 170. [Google Scholar] [CrossRef]
- Młynarski, S.; Pilch, R.; Smolnik, M.; Szybka, J.; Wiązania, G. A model of an adaptive strategy of preventive maintenance of complex technical objects. Eksploat. Niezawodn. Maint. Reliab. 2020, 22, 35–41. [Google Scholar] [CrossRef]
- Luo, J.; Guo, P.; Lin, Y. A Novel Modular Biomimetic Live Working Robot for Power Distribution Line. Machines 2022, 10, 195. [Google Scholar] [CrossRef]
- Sharma, A.; Rathi, Y.; Patni, V.; Sinha, D.K. A systematic review of assistance robots for elderly care. In Proceedings of the 2021 International Conference on Communication information and Computing Technology (ICCICT), Mumbai, India, 25–27 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Sawik, B.; Tobis, S.; Baum, E.; Suwalska, A.; Kropińska, S.; Stachnik, K.; Pérez-Bernabeu, E.; Cildoz, M.; Agustin, A.; Wieczorowska-Tobis, K. Robots for Elderly Care: Review, Multi-Criteria Optimization Model and Qualitative Case Study. Healthcare 2023, 11, 1286. [Google Scholar] [CrossRef]
- Wu, J.; Tian, P.; Wang, S.; Tao, Y. A Multi-Fidelity Integration Method for Reliability Analysis of Industrial Robots. J. Mech. Des. 2024, 146, 011703. [Google Scholar] [CrossRef]
- Ma, R.; Vanstrum, E.B.; Lee, R.; Chen, J.; Hung, A.J. Machine learning in the optimization of robotics in the operative field. Curr. Opin. Urol. 2020, 30, 808–816. [Google Scholar] [CrossRef]
- Jalili, P.; Ziaei-Rad, S.; Keshmiri, M. Dynamic modeling and simulation of a new conceptual design of a magnetic capsule robot by application of endoscopic capsule. J. Magn. Magn. Mater. 2024, 610, 172567, ISSN 0304-8853. [Google Scholar] [CrossRef]
- Ezra, N.; Cohen, A.; Zarrouk, D. Modeling, simulation, and experiments of a flexible track robot over rigid horizontal and inclined surfaces. Mech. Mach. Theory 2024, 199, 105689, ISSN 0094-114X. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krzykowska-Piotrowska, K.; Rosiński, A.; Paś, J.; Piotrowski, M.; Siergiejczyk, M. Optimizing the Operational Process of a Social Robot for Elderly Assistance: Enhancing Reliability and Readiness. Electronics 2025, 14, 1630. https://doi.org/10.3390/electronics14081630
Krzykowska-Piotrowska K, Rosiński A, Paś J, Piotrowski M, Siergiejczyk M. Optimizing the Operational Process of a Social Robot for Elderly Assistance: Enhancing Reliability and Readiness. Electronics. 2025; 14(8):1630. https://doi.org/10.3390/electronics14081630
Chicago/Turabian StyleKrzykowska-Piotrowska, Karolina, Adam Rosiński, Jacek Paś, Marek Piotrowski, and Mirosław Siergiejczyk. 2025. "Optimizing the Operational Process of a Social Robot for Elderly Assistance: Enhancing Reliability and Readiness" Electronics 14, no. 8: 1630. https://doi.org/10.3390/electronics14081630
APA StyleKrzykowska-Piotrowska, K., Rosiński, A., Paś, J., Piotrowski, M., & Siergiejczyk, M. (2025). Optimizing the Operational Process of a Social Robot for Elderly Assistance: Enhancing Reliability and Readiness. Electronics, 14(8), 1630. https://doi.org/10.3390/electronics14081630







