Next Article in Journal
An Adaptive Signal Control Model for Intersection Based on Deep Reinforcement Learning Considering Carbon Emissions
Previous Article in Journal
Length Instruction Fine-Tuning with Chain-of-Thought (LIFT-COT): Enhancing Length Control and Reasoning in Edge-Deployed Large Language Models
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Electronics
Volume 14
Issue 8
10.3390/electronics14081663
electronics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Intelligent Scheduling Methods for Optimisation of Job Shop Scheduling Problems in the Manufacturing Sector: A Systematic Review

by
Atefeh Momenikorbekandi
and
Tatiana Kalganova
*
Department of Electronic and Electrical Engineering, Brunel University of London, Uxbridge UB8 3PH, UK
*
Author to whom correspondence should be addressed.
Electronics 2025, 14(8), 1663; https://doi.org/10.3390/electronics14081663
Submission received: 28 February 2025 / Revised: 4 April 2025 / Accepted: 15 April 2025 / Published: 19 April 2025
Browse Figures
Versions Notes

Abstract

:
This article aims to review the industrial applications of AI-based intelligent system algorithms in the manufacturing sector to find the latest methods used for sustainability and optimisation. In contrast to previous review articles that broadly summarised existing methods, this paper specifically emphasises the most recent techniques, providing a systematic and structured evaluation of their practical applications within the sector. The primary objective of this study is to review the applications of intelligent system algorithms, including metaheuristics, evolutionary algorithms, and learning-based methods within the manufacturing sector, particularly through the lens of optimisation of workflow in the production lines, specifically Job Shop Scheduling Problems (JSSPs). It critically evaluates various algorithms for solving JSSPs, with a particular focus on Flexible Job Shop Scheduling Problems (FJSPs), a more advanced form of JSSPs. The manufacturing process consists of several intricate operations that must be meticulously planned and scheduled to be executed effectively. In this regard, Production scheduling aims to find the best possible schedule to maximise one or more performance parameters. An integral part of production scheduling is JSSP in both traditional and smart manufacturing; however, this research focuses on this concept in general, which pertains to industrial system scheduling and concerns the aim of maximising operational efficiency by reducing production time and costs. A common feature among research studies on optimisation is the lack of consistent and more effective solution algorithms that minimise time and energy consumption, thus accelerating optimisation with minimal resources.

1. Introduction

Manufacturing is seen as the source of all products used for production purposes and is entirely dependent on contemporary technologies [1,2]. Manufacturing is critical since it contributes significantly to the global economy [3,4]. It is strategically necessary to shift the current manufacturing paradigm to one that emphasises sustainability and energy reduction [1,5,6,7,8]. To achieve sustainability, manufacturers are rethinking and changing their manufacturing processes. Given that natural resources are finite and cannot meet future generations’ demands, manufacturing sustainability is a crucial concern [1,4,5,6,9].
An essential element of any manufacturing setup is scheduling, which directly affects the system’s efficiency, productivity, and cost-effectiveness [10,11]. Scheduling allocates, manages, and optimises task execution. Scheduling is a crucial technique to assign machinery and equipment effectively and optimise production processes by focusing on time and energy reduction. In manufacturing, scheduling provides the objective of simultaneously optimising production time and cost; it is a strategic process that seeks to minimise the makespan [10,11]. Production scheduling has several types of machine environments, such as Single-Machines (SM) and Multi-Machines (MM), parallel machines, flow shops, and flexible job shops. These types depend on the jobs’ technological needs and the type of facilities available [12,13]. Studies on JSSP used to be primarily oriented on a single target, such as completion time, but modern scheduling considers multiple objectives [14]. For instance, there may be a focus on JSSP’s energy and environmental aspects and makespan [15], or more academic inquiries, such as applying improved optimisation algorithms [16].
Although traditional scheduling methods have contributed significantly to this domain, they often need to handle complex and dynamic environments encountered in contemporary industrial settings [1,10,11,17,18,19]. Artificial Intelligence (AI) has brought about substantial changes to the domain of JSSPs, which has historically faced challenges related to efficiency in the manufacturing and service sectors. AI offers a cutting-edge answer to these difficulties by its capacity to effectively process extensive datasets and intricate algorithms. This improves operational effectiveness and enables the implementation of flexible and responsive scheduling approaches, essential in settings marked by unpredictability and swift fluctuations in demand [20].
In this paper, the term Artificial Intelligence (AI) is broadly used to encompass intelligent scheduling systems, including metaheuristic optimisation, learning-based algorithms, and reinforcement learning models. These are collectively referred to as AI-based approaches throughout the study [18,20,21,22]. The application of AI in the domain of JSSPs is readily apparent through the advancement of intricate models and algorithms. These models and algorithms can acquire knowledge from data, identify trends, and enhance scheduling decisions in real time. These innovations improve operational efficiency, enhance resource utilisation, and decrease lead times. Industries’ increasing automation and intelligence have significantly impacted JSSPs [20]. Despite numerous research on JSSPs, there is still a need to find an improved and advanced model to optimise JSSPs. As a result, emphasis is now being placed on more capable and modern technology. Various scheduling methods have been applied to solve JSSPs, and there are encouraging indicators of the current spike in interest in Metaheuristic (MH) algorithms. These high-level algorithmic frameworks give developers a set of rules or approaches to follow. They are a desirable solution for scheduling problems due to their proficiency in navigating challenging search spaces [18,21,23].
The main contribution of this paper lies in its structured and comparative review of AI-based intelligent scheduling methods specifically applied to job shop and flexible job shop scheduling problems. Unlike prior surveys focusing on algorithm classes in isolation, this review synthesises methods across metaheuristics, evolutionary computation, and reinforcement learning, offering insight into their adaptability, performance, and practical relevance. This paper also identifies trends in hybridisation and highlights underexplored integration paths between AI and traditional scheduling models. This synthesis supports researchers and practitioners in selecting or designing appropriate scheduling strategies for modern, dynamic manufacturing systems.

Methodology of the Systematic Review

This paper adopts a systematic review approach to evaluate the application of AI-based intelligent scheduling techniques for solving Job Shop Scheduling Problems (JSSPs), focusing on Flexible Job Shop Scheduling Problems (FJSPs). The review process included peer-reviewed articles published between 2000 and 2024 retrieved from scientific databases such as Scopus, IEEE Xplore, Web of Science, and Google Scholar.
The search strategy used combinations of keywords, including “job shop scheduling”, “FJSP”, “metaheuristics”, “artificial intelligence in manufacturing”, “intelligent scheduling”, “reinforcement learning”, and “evolutionary optimisation”.
Studies were included if they (i) focused on JSSPs or FJSPs in manufacturing contexts, (ii) utilised AI-based or intelligent optimisation algorithms, and (iii) reported on performance, applications, or comparative results. Papers were excluded if they lacked a practical scheduling focus or did not apply intelligent or AI-based techniques.
After an initial screening of titles and abstracts, relevant full-text articles were reviewed in detail. The selected literature was then synthesised based on their algorithmic category (e.g., evolutionary, swarm-based, learning-based), scheduling objectives (e.g., makespan, energy consumption), and industrial application. This systematic analysis informed the taxonomy and comparative insights developed throughout this review.
It explores the strengths and weaknesses of these methods, aiming to identify potential improvements. While all approaches demonstrate accuracy, there is always room for enhancement, which remains challenging. Metaheuristic models are promising in this field; however, integrating them with advanced machine learning and deep learning techniques could further enhance their effectiveness. The structure of this article is as follows: Section 2 reviews definitions of JSSPs and establishes the description that will be used for this study. Section 3 discusses the different types of job shops and justifies the rationale for selecting those appropriate for this project. Section 4 reviews optimisation algorithms and scheduling methods pertinent to this research. Section 5 examines scheduling using learning-based methods and Reinforcement Learning (RL). Section 6 discusses the existing research gap and analyses different scheduling methods, and finally, Section 7 summarises the review paper.

2. Job Shop Scheduling Problems

Job shop scheduling problems involve scheduling operations across multiple machines or workstations [24]. The standard JSSP can be characterised as a collection of jobs to be carried out on various machines, whereby each job consists of many processes carried out in a predetermined order and on particular machines [25,26]. JSSPs are categorised as non-deterministic polynomial-time hardness (NP-hard problems), which is the most complex problem class according to the computational complexity theory. These are challenging to solve and usually pertain to sophisticated optimisation problems [27,28,29].

3. Job Shop Types

Manufacturing systems encompass several job shop configurations, which are reviewed in the following sections.

3.1. Single-Machine Job Shop Scheduling

Single-machine (SM) job shop scheduling is the simplest form of JSSP, in which one workstation is used to complete all jobs, each of which consists of a sequence of operations with a specific duration. SM job shop scheduling aims to minimise total completion time (i.e., the time taken to complete all jobs) [30].
SM scheduling and its learning effects have been the subject of numerous studies. For instance, Wang et al. [31] analysed an SM scheduling problem with the time-dependent learning effect to minimise the weighted sum of completion times, the maximum lateness. A job’s computation time is a function of the total average processing time of all the other jobs scheduled upfront in the job. In addition, Lee et al. [32] studied SM problems, including the learning effect and released time, to reduce the makespan. A branch-and-bound algorithm was also created to find the best answer [33,34].
SM job shop scheduling can be solved using various algorithms, including the Shortest Processing Time (SPT) and the Earliest Due Date (EDD) algorithms. As their names imply, the SPT and EDD algorithms prioritise jobs with the fastest processing time and earliest due date, respectively [30,35]. One of the main advantages of SM job shop scheduling is its simplicity, which requires less computational power and can be solved using basic algorithms.
Challenges: This characteristic makes it an attractive option for small-scale manufacturing industries with limited resources. However, it is hampered by its fundamental inefficiency, including long waiting times, resulting in low productivity and increased production costs. Furthermore, it is unsuitable for large-scale manufacturing industries requiring high-volume production. Therefore, SM scheduling is commonly used in small-scale manufacturing industries such as job and repair shops and maintenance workshops [30]. In contrast to SM, Multi Machines (MM) job shops have several workstations to be executed, which will be discussed later in the following sections

3.2. Parallel Job Shop Scheduling

Parallel job shop scheduling is used when multiple machines or workstations work to complete jobs simultaneously. In this type of scheduling, each job consists of a sequence of operations performed simultaneously on different machines or workstations. Parallel job shop scheduling aims to minimise total completion time (i.e., the time taken to complete all jobs). It can be solved using various algorithms, such as the branch-and-bound algorithm, the Genetic Algorithm (GA), and the Simulated Annealing algorithm (SA). The branch-and-bound algorithm systematically explores all possible solutions to find the optimal solution. GA is based on natural selection and evolution and is used to find near-optimal answers [30,36].
One of the main advantages of parallel job shop scheduling is its efficiency, as jobs are performed on different machines simultaneously [30]. It can significantly reduce waiting times, increase productivity, and lower production costs. Furthermore, it suits large-scale manufacturing industries requiring high-volume production.
Challenges: However, its disadvantage is its complexity. It requires significant computational power, and large-scale problems can be challenging. Furthermore, using multiple machines and workstations can increase the risk of machine breakdowns, leading to production delays [30,36].

3.3. Flexible Job Shop Scheduling Problem

In a practical model of JSSPs, a machine may perform more than one type of operation, and every procedure may then be performed on various machines, giving it greater flexibility than a standard JSSP; this problem is referred to as FJSP [25,26,37]. (FJSP) is an extension of the traditional JSSP, which reduces constraints on machine selection by allowing each operation to be processed on many machines within its alternative machine set. Due to the addition of new choice content to the sequencing and the fact that it comprises more problems than JSSP, FJSPs are more difficult combinatorial optimisation problems. In FJSPs, the objective is to solve two subproblems: operation sequencing and machine assignment. The goal of the FJSP is to obtain an allocation for each operation and define the order of operations on each machine to reduce the maximum processing workload time (makespan) [28,37,38,39,40].
FJSPs, which are specific kinds of JSSPs, may be formulated as described below:
  • In FJSP, there is a set of independent jobs J = J1, J2, …, Jn.
  • Each job Ji is formed by a sequence O1, O2, …, Oni of operations to be processed one after the other.
  • There is a set U = M1, M2, …, Mm of machines as well.
  • Each operation Oij is executed among a subset Uij ⊂ U of compatible machines.
  • Each operation has to be executed to complete the job.
Each operation j of job i (Oij) needs one machine from a set of given machines, Mij.
In general, the following assumptions are considered in FJSSP:
  • Machines are available at time t = 0.
  • Jobs are available at time t = 0.
  • Each operation can be executed only by one machine at a time.
  • There are no precedence constraints in executing different jobs, and jobs are independent of each other.
  • Pre-emption of operations is not allowed; an action, once begun, cannot be interrupted.
  • Transportation time of jobs between available machines and the time required to set up the machine for processing the operations are included in the processing time [28,37,41,42].
Many optimisation techniques have been devised to address FJSPs. Table 1 presents the chronological application of optimisation methods to FJSPs, listing each algorithm, year of publication, and primary scheduling approach. As shown in Table 1, numerous optimisation techniques have been applied to FJSPs over the past two decades. These range from early hybrid PSO methods to recent reinforcement learning and hyper-heuristic strategies.

3.4. Flow Shop Scheduling

Flow shop scheduling is a particular example of job shop scheduling in which every operation must be done in a specific order. In specific flow shop scheduling, no machine can carry out more than one task at once, and an execution time is given for each job’s operation. There has been much research into the flow shop scheduling problem. For example, Lin et al. [66] solved the flow shop scheduling problem for changeable processing parameters and low carbon emissions, thoroughly examining the effects of machines and scheduling levels on production throughput and the environment. Wu et al. [67] developed a mathematical model of multi-objective optimal scheduling using renewable energy and processing time as constraints. Lu et al. [68] investigated the energy consumption of the flow shop scheduling problem with the sequence-dependent setup, and controlled transit time was investigated. Figure 1 depicts some fundamental categories of job shop scheduling methods reviewed in this study.
JSSP, the primary production and manufacturing system’s topic, has been discussed in the previous sections. Based on the above review of job shop types, this article focuses on FJSPs due to their flexibility in the scheduling process. Due to the features of FJSPs and their importance in production scheduling and manufacturing, much research has been done in this field [69]; however, there is still a need to improve and find advanced models.
Challenges: The review of prior research indicates that the central emphasis on improving JSSPs and introducing novel models mainly focuses on verifying and evaluating the performance of optimisation algorithms. The following sections review the application of various intelligent methods in solving FJSPs

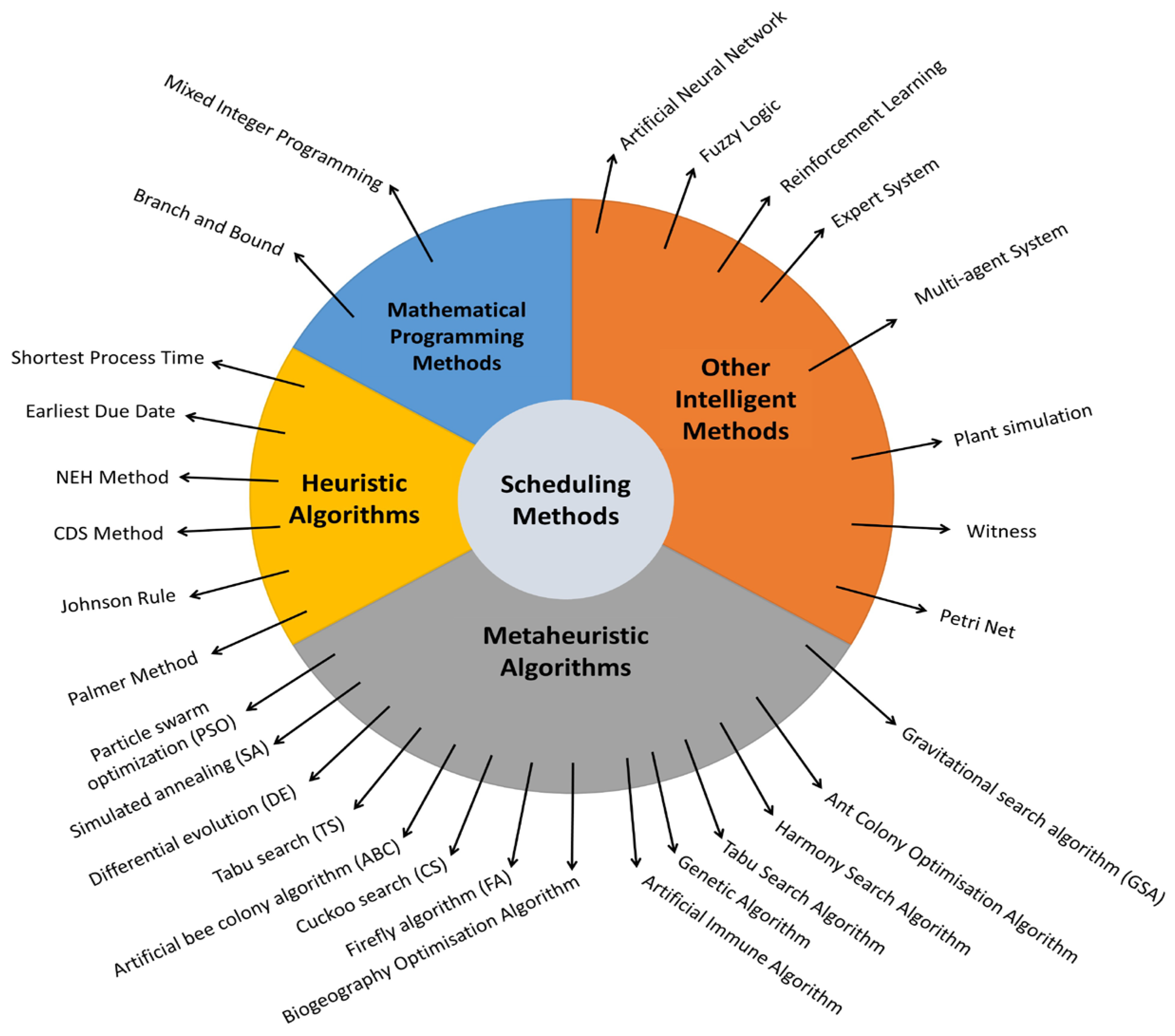
4. Optimisation Algorithms and Scheduling Methods

In relation to the JSSPs, four distinct activities can be undertaken to address an optimisation problem effectively. The first step is identifying the problem’s parameters. The optimisation problem can be categorised as continuous or discrete based on these parameters. The second step involves distinguishing between a constrained and an unconstrained optimisation problem by deciding what limitations should be placed on the parameters. Thirdly, the problem’s goals must be carefully examined and incorporated. Optimisation problems may be classified as single-objective problems (having one objective) or multi-objective problems (having multiple objectives). Lastly, a compatible optimiser should be selected to solve the problem depending on the parameters, constraints, and number of objectives [21,70,71].
Many optimisation challenges are inherently complicated, and traditional mathematical optimisation techniques cannot quickly identify optimal solutions. Current studies demonstrate a growing demand for optimisation techniques that are more accurate and efficient in terms of associated time and financial costs. Metaheuristics (MH) is one of these optimisation techniques [21,72]. Different scheduling methods are used to optimise JSSPs. Figure 2 [73,74] indicates popular scheduling methods (i.e., MH, heuristic, simulation, and mathematical programming). Each category includes models using discrete and continuous problems; this paper focuses on FJSPs and constant problems. This section will discuss various scheduling methods based on MH algorithms, which are the most popular techniques for scheduling problems.

4.1. Metaheuristics and AI Techniques for Optimisation

Glover [75] proposed the term “metaheuristic” in the 1980s, derived from “meta” (indicating something superseding the usual or natural bounds) and “heuristics” (“to discover”), referring to the methodology of solving problems within systems. MH optimisation seeks to identify the best solutions to defined problems while avoiding local optima. MHs are optimisation solution techniques incorporating higher-level strategies within search procedures [75,76,77].
Challenges: Metaheuristic methods (MH) have gained prominence in optimisation due to their ability to find near-optimal solutions while avoiding local optima. However, several challenges remain in applying MH techniques effectively. One significant challenge is the difficulty in selecting the most suitable metaheuristic for a given problem, as various algorithms may perform differently depending on the problem’s complexity and structure. Moreover, the computational cost and time required to run these methods, especially for large-scale problems, can limit their practical implementation [75,76,77].
The history of MH usage is categorised into five main periods [72,75]. MH approaches were not formally introduced during the first period, prior to the 1940s, and only straightforward optimisation problems were resolved using these techniques. MH was first formally used during the second period, from 1940 to 1980. Many MHs were used for various applications during the third phase (1980 to 2000). This approach was effectively introduced in the fourth period, which spans from 2000 to the present. In the fifth phase, the scientific period, the creation of new MHs will become an increasingly specialised scientific endeavour [72,75]. MHs fall into four primary categories: The first group is Evolutionary Algorithms (EAs), which include GAs [78], memetic algorithms, Differential Evolution (DE) [79], and evolution methods [80], all of which are based on biological evolution [72,81]. Darwinian principles (i.e., natural selection) to solve scientific problems first emerged in the 1940s, before computers were developed [72].
The cooperative behaviour of decentralised and self-organised natural or artificial systems provides the basis for the second category of swarm intelligence-based algorithms, including ACO [82], PSO [83], ABC [84], and Cuckoo Search (CS) [85].
The following section reviews and discusses the application of the most popular MH algorithms in scheduling problems.

4.2. Evolutionary Algorithms

Evolutionary Algorithm (EA) is a fundamental population-based optimisation algorithm and a subset of the MH evolution account. EA uses biologically inspired mechanisms, including selection, recombination, mutation, and reproduction. The fitness function establishes the quality of the candidate solutions, which act as members of a population in the improvement issue. Population growth occurs after the relevant operators are applied repeatedly.
Challenges: Computational complexity is a prohibited element in most real-world EA applications. The evaluation of the fitness function causes this computational complexity; simple EAs can frequently handle complicated issues. Application areas for EAs include planning, design, and simulation. Different types of EAs, including GA and DE, are discussed in the subsections [21,86].

4.3. Genetic Algorithm

Among EAs, GA is a popular optimiser scheduling system. John Holland created the first GA in 1975 [80,87]. It is a well-known optimisation technique that uses the theories of evolution and natural selection to address challenging optimisation problems [88]. It begins with a random initial population in which each member is referred to as a chromosome (potential solution). Evaluating an individual’s performance using an objective function initiates the algorithm’s primary iterative cycle. Higher fitness values are given a higher likelihood of selection for creating a new generation (offspring) than lower fitness values since they represent better solutions. The most promising individuals are likelier to be chosen for reproduction, while individuals with low fitness scores are commensurately eliminated. As a result, the performance of the new generation of individuals is expected to improve. The selected individuals are then recombined to create offspring by sharing information. After reproduction, mutation further messes with the progeny [89]. A new generation will subsequently emerge based on the fitness of these new offspring. This selection, reproduction, mutation, and evaluation cycle continues until the optimisation requirement is met.
GAs have been widely employed to address challenging JSSPs [80]. GAs encourage solution space exploration through crossover and mutation operators [80]. Furthermore, GAs can become trapped in local optimums and are susceptible to premature convergence. They also need the parameters for population size, mutation rate, and crossover rate to be carefully tuned. The size and complexity of the task can significantly lengthen the computing time [90]. The following are some salient features of GA:
1. 
Optimisation: Natural selection and genetics are the foundations of GAs, making them effective at finding the best solutions in vast and complex problem spaces, such as those seen in scheduling difficulties [89].
2. 
Adaptability: GAs are suitable for flexible scheduling problems where conditions can change over time because they can handle changes in the problem environment [89]. Selection is the core part of the GA process, and there are different types of selections, such as elitism, fittest, sexual, tournament, and roulette wheel selection. Table 2 summarises key literature published from 1996 to 2023 concerning different GA selection types applied in optimising FJSPs, which is the principal aim of this research. This review demonstrates the potential of GAs to address FJSPs by employing a range of selection types, as displayed in Table 2. Table 2 provides a detailed overview of Genetic Algorithm (GA) selection strategies applied to Flexible Job Shop Scheduling Problems (FJSPs) across various studies. Since GAs are population-based metaheuristic algorithms, the choice of selection mechanism, such as elitism, tournament selection, or roulette wheel, significantly influences the performance and convergence speed of the algorithm.
This table highlights the diversity of approaches researchers have used to fine-tune GA performance for FJSPs. It also illustrates how GA research has evolved from basic selection strategies to more adaptive, hybrid, and problem-specific methods in recent years. By summarising this historical progression, the table demonstrates the critical role of selection strategy in determining the effectiveness of GA-based scheduling, especially in complex, multi-objective optimisation settings like FJSPs.

4.4. Particle Swarm Optimisation

Particle Swarm Optimisation (PSO) is a well-known swarm intelligence model created by Eberhart and Kennedy [83], based on the social behaviour of swarming birds and fish. Swarm intelligence models refer to computational algorithms that take inspiration from the collective behaviour observed in natural systems, such as the coordinated movements of bird flocks or the organised activities of ant colonies. These models employ basic principles for individual agents to engage with their surroundings and one another, resulting in the formation of intricate, intelligent global patterns that are advantageous for addressing optimisation challenges. In PSO, the agent known as particles represents the candidate solution to the optimisation problem. Position and velocity describe particles that are free to move about the search space.
In the startup phase of PSO, each particle is given a randomly chosen initial position and velocity. The following iteration will change the particle’s position depending on its rate [83]. By comparing the particle’s present fitness to both its past best placements and its neighbour’s best solution, the PSO technique determines the particle’s new position. To solve JSSPs, PSO is frequently taken into consideration by researchers in hybridisation with other MH algorithms, including TS [135], ACO [136], harmony search (HE) [137], and CS [138].
Unlike GA, PSO lacks a systematic calculation approach and evolutionary operators like crossover, selection, and mutation. Consequently, PSO models are more straightforward to build and have fewer parameters to alter [73]. Fontes et al. [139] proposed a hybrid PS and SA algorithm for the JSSPs. PSO, which has unique advantages for resolving issues with FJSP, has a quick search speed and a limited number of parameters [140]. Furthermore, in another study by [40], the scheduling of embedded real-time production systems was categorised as an FJSP, and a distributed PSO approach was proposed as a solution. In this work, the elements affecting speed, position, and learning remained the same. Notably, the PSO algorithm’s ability to balance local search with global exploration largely depends on the control settings that the algorithm uses [141].

4.5. Differential Evolution

Differential Evolution (DE) is a global optimisation algorithm developed by Storn and Price [78]. It can be considered an EA, which solves optimisation problems by evolving a population of candidate solutions using biology-inspired crossover, mutation, and selection operations [78]. The DE approach provides better results for multi-dimensional optimisation problems, including neural network learning, than other EAs, such as GA. In addition, DE methods have been suggested to solve Holland’s primary problem of poor local search performance [80].

4.6. Simulated Annealing

Simulated Annealing (SA) is a local and random search MH algorithm [85]. This algorithm mimics the annealing process in metallurgy. During an annealing process, a metal is heated to a specified temperature and then cools and freezes at a determined cooling rate into a crystalline state with minimum energy to avoid defects. The optimisation procedures of SA always start by generating an initial solution space, after which a proper initial value of the annealing parameter is set. In each iteration step, the algorithm determines whether the neighbouring solution is better or worse than the current solution. The adjacent solution will be accepted if it improves the cost function value, and only specific worse points will be taken based on an acceptance function. After that, the temperature decreases slowly, and the probability of accepting a worse solution is the same. Lastly, the iteration ends while a stopping criterion is met.
A significant advantage of SA is that it is highly flexible and robust and can approach global optimality compared to other local search methods [85]. Its key drawback is that the computation time tends to grow dramatically with the size of the problem. Furthermore, picking a suitable cooling schedule is a crucial SA parameter, but it can be difficult and significantly affect the algorithm’s performance. Zhang and Wu [142] proposed a functional SA model for JSSPs.
The selection operations used by GA and DE algorithms differ markedly [78]. One of the advantages of the DE approach is its simplicity because the search process is only controlled by three input parameters: size of the population, scale factor, and crossover parameter. However, its efficiency depends on the control parameter [143]. In addition, obtaining the optimum operations, such as crossover and mutation, in the DE approach is usually time-consuming [143]. Different variants of DE have been implemented in various industrial applications for better performance [144,145,146].

4.7. Tabu Search

Glover created Tabu Search (TS), an MH algorithm to solve optimisation problems [75]. This method employs responsive exploration and memory structures to find an optimisation solution. Memory structures like the tabu list can effectively search the solution space by specifying the visited solutions. Responsive exploration provides a fundamentally enhanced technique employing the search history in TS.
The tabu list prevents the seen solutions and directs the search towards the undiscovered solution space for possible solutions. It stores the keys studied throughout the search space. TS effectively solves larger and more complex problems. Numerous control parameters should be established, and the parameter setting significantly impacts achieving a global optimum [75]. TS has been applied in hybridisations with other optimisation techniques for scheduling, including SA [147,148] and ABC [149].

4.8. Artificial Bee Colony Algorithm

The Artificial Bee Colony (ABC) algorithm is an MH algorithm based on bees’ foraging behaviour [150]. A food source’s position and nectar content symbolise a potential solution to a problem and the fitness that goes along with it. The program uses three types of artificial bees: employed, bystander, and scout bees. The available food and the number of bees at work are equal. All employed bees belong to groups that use dancing to find, transport, and communicate information about food sources. Scout and observer bees are always looking for new food sources. Scout bees only blindly explore the search area, while spectator bees can gather information from employed bees by remaining in the dance area while searching for a food source [151].
The ABC method solves issues in various applications, such as improving wireless sensor networks, maximising heat transfer rates, power plant optimisation, machining process improvement, and JSSPs [146]. Compared to other MH algorithms, the ABC method has been shown to tackle engineering problems with high dimensionality [152] efficiently. To improve performance, the ABC algorithm has also been combined with other algorithms, including the hill-climbing [153], ACO [154], and DE [155,156] algorithms. As a result, in recent years, JSSP has been solved using ABC and its advancements [157]. Problems including no-wait constraints [158,159], rescheduling strategy [47], or FSSP [160] have been addressed using deteriorated or hybrid versions. However, due to the search process, ABC has shortcomings in solving the scheduling problems [161].

4.9. Harmony Search

The intriguing Harmony Search (HS) algorithm is designed to overcome problems according to the inspirations of musical performances [162,163]. Musicians constantly seek the ideal harmony, and the search process in HS is modelled on their behaviour while seeking the optimal balance to improve their melodies. The HS iteratively improves the solutions during optimisation to optimise the objective function. Initialising the HS parameter, which includes the amount of harmony memory, harmony considering rate, and pitch adjusting rate, is the first step in the HS algorithm technique.
Three different iterative techniques must be used to improvise and update the new solution to reach the best outcome [162]: (a) Consideration of memory: to use HM, a new solution is created from an old one; (b) Considering memory, a new solution is devised by slightly changing the pitch; (c) Randomisation process: a new, improvised solution is constructed. The subsequent HM acceptance rate determines its strength. These three factors can thus be used to achieve good performance in HS with a balance of intensification and diversification.
HS is straightforward to implement because it does not involve complicated calculations. The HS method has also been modified to enhance its convergence capabilities. This approach is frequently used in many applications, including scheduling in manufacturing processes [164] and medical applications [165]. Owing to these benefits, HS has been effectively adapted to address many optimisation issues in various domains [166]. Despite its benefits for solving JSSPs, HS can experience stagnation throughout the optimisation process, resulting in less-than-ideal solutions [167]. The algorithm’s complexity rises due to the requirement for precise parameter adjustment to produce the best results [168].

4.10. Cuckoo Search

According to Yang and Deb [169], the Cuckoo Search (CS) optimisation MH algorithm imitates the cuckoo’s breeding habits, which are defined by laying fertilised eggs to be hatched in the nests of other birds. Cuckoos typically prefer newly produced nests to enhance the likelihood of hatching eggs; consequently, the host birds will care for the cuckoo offspring. To increase their access to food delivered by the foster parents, the cuckoo chick pushes the native eggs out of the nest after hatching. The host bird either destroys or quits the nest and creates a new one elsewhere if it learns that the egg that has been hatched is alien [169]. As a result, the cuckoo chick has a unique ability to imitate the look and sound of its host bird to maximise its reproductive success and prevent abandonment.
To solve the JSSP, Singh et al. [170] suggested CSO with several individual enhancement schemes. In terms of finding the global optimum, CS has a faster convergence speed in finding optimal solutions. Compared to other algorithms, it simplifies the tuning process because there are fewer parameters to change [169,171]. CS excels at solving continuous or combinatorial problems, making it adaptable to various JSSPs. However, it is exposed to premature convergence in areas with complicated problems [172].

4.11. Firefly Algorithm

The Firefly Algorithm (FA) is an MH algorithm inspired by the flashing behaviour of fireflies [173]. A firefly is a species of bug that may emit natural light to entice a mate or ward off predators. The FA generally follows three guidelines: 1. Since fireflies are unisex, they usually gravitate toward the brighter and more appealing mating partner. 2. Since air absorbs light, the attraction is inversely related to brightness and diminishes as the distance between two fireflies grows. 3. The brightness of a firefly will depend on the geography of the objective function.
FA is a simpler algorithm compared to other swarm-based algorithms. Additionally, the benefits of the autonomous subdivision have improved its effectiveness [173]. As documented in the literature [173,174,175,176], this approach has been used in numerous applications since the inception of the firefly algorithm. Studies have shown that FA outperforms algorithms like ABC and PSO and can obtain the world’s best solutions [174].
FA has been used effectively in a variety of applications, but in contrast to other MHs, not much study has been done on applying the FA with regard to the FJSP [177]. In the study by [177], an integrated approach using FA has been proposed to solve FJSPs. In the scheduling field, an FA was provided by [178] to minimise makespan in the workflow scheduling problem with deadline constraints. Recently, ref. [179] applied improved FA for FJSPs.

4.12. Gravitational Search Algorithm

The Gravitational Search Algorithm (GSA) is a physical-based heuristic search algorithm that draws inspiration from the Newtonian principle of mass interaction [180]. It is widely used to solve nonlinear optimisation problems. According to Newton’s gravity equation, any two particles will be attracted to one another by a gravitational force [181]. The gravitational force varies inversely with the square distance between the particles and directly with the product of the particle masses. A group of agents in search space are drawn together by gravity in GSA. While their performance is correlated with their packs, these agents behave as objects. Due to the pull of gravity, all things in the search space gravitate toward those with heavier masses [73].
Researchers’ interest in this algorithm is growing because it can produce better results than other nature-inspired algorithms and identify solutions close to the global optimum. In various applications, it is useful when combined with other computational techniques to overcome its slow convergence and searching speed [73].
Based on current knowledge, the GSA has many reported applications for scheduling problems. For instance, ref. [182] introduced a highly efficient GSA for addressing the study’s permutation flow shop scheduling problem. In another study, ref. [183] proposed an enhanced GSA for addressing the scheduling problem in hybrid flow shop environments with parallel machines. Furthermore, ref. [184] suggested discrete GSA for a kind of flow shop problem with total flow time minimisation.

4.13. Ant Colony Optimisation

Ant Colony Optimisation (ACO) is another effective swarm intelligence method, first put forth to categorise problems in the medical industry and achieve success in continuous optimisation [185]. The ACO algorithm’s application to scheduling problems, such as SM scheduling problems, was the subject of preliminary studies [186], or JSSP in general [187]. Researchers have employed strategies for combining the ACO algorithm with specific JSSPs, such as local searches [188,189].
JSSPs have been successfully solved using ACO [190]. Heuristics customised to a particular situation can be incorporated into ACO algorithms to improve the search process [191]. ACO’s distributed computing model makes parallel processing possible, speeding up the problem-solving process [192]. One of the disadvantages of ACO is that the algorithm needs to be fine-tuned to perform well because it is highly sensitive to parameter adjustments [193]. ACO performance degrades with more significant problems [190].

4.14. Comparative Discussion and Insights

Despite the advancements of metaheuristic and learning-based algorithms, several limitations remain in their practical application to JSSPs and FJSPs. Many metaheuristics, such as Genetic Algorithms (GA), require extensive parameter tuning (e.g., population size, mutation rate) and are susceptible to premature convergence. Algorithms like Particle Swarm Optimisation (PSO) often struggle with local optima and scalability in large problem spaces. Reinforcement Learning (RL) methods offer adaptability but can suffer from slow convergence and instability during training. Hybrid methods show promise but add complexity, and their integration often lacks generalisability across various manufacturing contexts. Moreover, real-time application of these algorithms remains limited due to high computational demands and the need for large datasets or simulation environments [169,170,171,172,173,174,175,176,177,178,179].

5. AI-Driven Learning-Based Scheduling and Reinforcement Learning Approaches

One of the promising models for JSSPs and FJSPs is RL [24,194], wherein agents make decisions while receiving little input, and each decision is rewarded or penalised based on a given reward policy. RL is the subfield of machine learning (ML) in which the agent aims to maximise the reward by starting with arbitrary trials [195]. A Markov decision process has been used to model the primary reinforcement [195]. RL is frequently employed in autonomous robotic operation manufacturing [196]; furthermore, Q-learning and deep learning are often used to create RL agents [197].
An emerging trend in scheduling research is the integration of AI and Machine Learning (ML) techniques with traditional scheduling methods. For instance, machine learning models can be used to predict job processing times or machine availability, which can feed into deterministic scheduling algorithms for more dynamic performance. AI-based optimisers, such as genetic algorithms or RL agents, can enhance heuristic rules by learning from past scheduling scenarios. This hybridisation can enable real-time adaptability and improve robustness in uncertain environments. However, the integration requires careful design to maintain interpretability and ensure computational efficiency, especially in industrial settings where response time is critical [22,37,198].
Many RL techniques are being used to improve JSSPs [22]. For instance, Shahrabi et al. [199] created an RL with the Q-factor method to solve JSSP. Shen et al. [200] suggested a multi-objective dynamic software project scheduling based on Q-learning. Chen et al. [37] proposed a self-learning GA for addressing the FJSP. This method incorporates both the state-action-reward-state-action (SARSA) algorithm and Q-learning within the self-learning framework. Shi et al. [198] adopted a DRL strategy for intelligently scheduling discrete automated production lines. In another study, Chen et al. [37] suggested using a self-learning genetic algorithm (SLGA) based on RL to reduce the FJSP makespan.

6. Research Gap in the Current State of Knowledge

6.1. Identifying the Knowledge Gap

Various intelligent optimisation methodologies have been discussed in this paper, including GA, PSO, SA, DE, TS, ABC, CS, GSA, ACO, and RL. After reviewing the relevant literature on JSSPs, and specifically FJSPs, it is evident that there are distinct differences and challenges in each model. This highlights a research gap, underscoring the need for greater clarity on the effectiveness of intelligent algorithms in optimizing job shop scheduling. This article focuses specifically on FJSPs because of their flexibility in the production process, particularly in the allocation of machines and resources. Numerous algorithms have been used to solve FJSPs. However, the effectiveness and quality of the solutions can be improved by parameter modifications in the algorithms. The key features of the knowledge gap in this area are outlined below.
1. 
Scheduling using MH algorithms: MH algorithms are promising methods for locating excellent answers to optimisation issues. JSSPs are ideally suited to them, mainly when the solution space is large and complex. However, depending on the problem’s features and the particular settings of the algorithm, the efficacy of MH can vary dramatically. They are mostly slow, which is why there is a need to find more advanced solutions [18,21,23,201,202,203,204].
2. 
Hybrid models: There are numerous methods for solving scheduling problems, each with their own benefits and drawbacks. However, there is limited research on hybrid models that combine multiple methods to enhance performance. These models offer potential benefits but also present certain challenges. It would be valuable to focus on addressing these challenges to fully harness the advantages of hybrid approaches. For instance, a hybrid model combining genetic algorithms and simulated annealing could optimise job shop scheduling by leveraging both the exploration capabilities of genetic algorithms and the refinement abilities of simulated annealing. While these hybrid approaches show promise, they also present challenges, such as finding the best way to integrate the methods and avoid excessive computational complexity. Addressing these challenges could unlock the full potential of hybrid models. The following section compares the advantages and disadvantages of some popular MHs discussed earlier.
Compared to ACO and GA, CS and HS could be more straightforward to deploy and require less parameter adjustment [162,169]. Unlike the more recent CS and HS, GA and ACO have been extensively used for job shop scheduling and are backed by substantial research outlining strategies to improve their performance [80,190]. GA and ACO are known to be computationally expensive because of their complicated processes, such as crossover and mutation [90,190].
Careful parameter tuning is necessary for GA and ACO to work properly [193]. Comparing CS to other algorithms, the tuning procedure is more straightforward because there are fewer parameters to change [171]. Additionally, HS needs precise parameter tweaking [168]. Moving on to PSO, it offers several advantages over other algorithms, such as being easy to create, fast on computers, and requiring fewer changes to its parameters [83]. However, it frequently becomes trapped in local optima, and the quality of the solutions may decline as the size of the problem grows [140]. Regarding DE, like many EAs, they tend to be slow, particularly for challenging problems. Additionally, it can be difficult to determine the ideal control parameters for DE [143].
  • Scheduling using RL models: RL effectively solves job shop schedulings. The most significant advantage of developing RL models is their ability to enhance the system’s performance without using many EA functions [24]. It is noted that the RL technique in the literature has been applied to fewer studies of FJSP. As a result, it is possible to determine the best FJSP scheme via RL.

A Unifying Framework for AI-Based Scheduling Methods

To organise the diversity of approaches covered in this review, a unifying framework is proposed that classifies the algorithms into three broad categories:
  • Metaheuristic Algorithms: This group includes Evolutionary Algorithms (e.g., GA, DE), Simulated Annealing (SA), and Tabu Search (TS). These methods typically rely on biologically or physically inspired rules to search for global optima across complex problem spaces.
  • Swarm Intelligence Methods: Algorithms like Particle Swarm Optimisation (PSO), Ant Colony Optimisation (ACO), Artificial Bee Colony (ABC), and Cuckoo Search (CS) fall under this category. Inspired by collective behaviours in nature, these methods are suitable for distributed and multi-agent scheduling environments.
  • Learning-Based Approaches: This includes traditional Machine Learning (ML) techniques, Reinforcement Learning (RL), and Deep Learning (DL). These models aim to learn scheduling strategies from historical data and are increasingly used in real-time, adaptive scheduling systems.

7. Conclusions

This article reviewed a comprehensive review of various types of Job JSSPs, including (SM) job shops, parallel job shop scheduling, FJSPs, and flow shop scheduling. JSSPs are typically categorized as NP-hard problems, highlighting their inherent complexity, which stems from multiple constraints, diverse sets of objectives, and expansive search spaces.
JSSPs require meticulous planning and optimization. They involve scheduling a sequence of jobs on a set of machines, each job consisting of a series of operations that must be completed in a predefined order. The complexity of these scheduling problems is exacerbated by constraints such as task non-preemption, machine availability, and operation sequences, making efficient scheduling challenging.
Among the different types, FJSPs stand out due to their flexibility in handling operations. Unlike traditional job shops, FJSPs allow an operation to be processed by any machine from a given set, increasing the complexity of the problem but also providing a greater scope for optimization. This flexibility results in a larger search space, requiring more advanced and efficient optimization techniques.
In the later part of this paper, the most popular approaches to addressing these varied scheduling challenges were explored. In conclusion, advancing algorithmic approaches in JSSPs, particularly for FJSPs, indicates a promising direction for future research. With the ongoing advancement of computational capabilities and AI-based algorithmic frameworks, there is strong potential to develop more robust and scalable scheduling solutions. These will be essential for meeting the dynamic and complex demands of smart and sustainable manufacturing systems.
Future Research Directions:
  • Develop hybrid AI models that combine learning-based and rule-based approaches for enhanced generalisability.
  • Explore lightweight, real-time RL agents for industrial deployment, especially in energy-aware and multi-objective scheduling.
  • Investigate transfer learning and meta-learning techniques to apply trained models across different job shop scenarios.
  • Design benchmark datasets and simulation environments that reflect realistic job shop constraints (e.g., machine breakdowns, dynamic job arrivals).
  • Evaluate explainable AI methods for scheduling decisions to increase transparency in industrial adoption.

Author Contributions

A.M. substantial contributions to the conception and design of the work; or the acquisition, analysis, or interpretation of data for the work. A.M. drafting the work or reviewing it critically for important intellectual content. T.K. final approval of the version to be published. T.K. agreement to be accountable for all aspects of the work, ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

There are no data associated with this paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Waltersmann, L.; Kiemel, S.; Stuhlsatz, J.; Sauer, A.; Miehe, R. Artificial intelligence applications for increasing resource efficiency in manufacturing companies—A comprehensive review. Sustainability 2021, 13, 6689. [Google Scholar] [CrossRef]
  2. Ahuja, J.; Panda, T.K.; Luthra, S.; Kumar, A.; Choudhary, S.; GarzaReyes, J.A. Do human critical success factors matter in adoption of sustainable manufacturing practices an influential mapping analysis of multicompany perspective. J. Clean. Prod. 2019, 239, 117981. [Google Scholar] [CrossRef]
  3. Seliger, G.; Kim, H.J.; Kernbaum, S.; Zettl, M. Approaches to sustainable manufacturing. Int. J. Sustain. Manuf. 2008, 1, 58–77. [Google Scholar] [CrossRef]
  4. Renna, P.; Sciences, S.M.A. A literature review of energy efficiency and sustainability in manufacturing systems. Appl. Sci. 2021, 8, 7366. [Google Scholar] [CrossRef]
  5. Machado, C.G.; Winroth, M.P.; da Silva, E.H.D.R. Sustainable manufacturing in industry 4.0: An emerging research agenda. Int. J. Prod. Res. 2020, 58, 1462–1484. [Google Scholar] [CrossRef]
  6. Malek, J.; Desai, T.N. A systematic literature review to map literature focus of sustainable manufacturing. J. Clean. Prod. 2020, 256, 120345. [Google Scholar] [CrossRef]
  7. Li, J.-Q.; Du, Y.; Gao, K.-Z.; Duan, P.-Y.; Gong, D.-W.; Pan, Q.-K.; Suganthan, P.N. A hybrid iterated greedy algorithm for a crane transportation flexible job shop problem. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2153–2170. [Google Scholar] [CrossRef]
  8. Meng, L.; Ren, Y.; Zhang, B.; Li, J.-Q.; Sang, H.; Zhang, C. Milp modeling and optimization of energy-efficient distributed flexible job shop scheduling problem. IEEE Access 2020, 8, 191191–191203. [Google Scholar] [CrossRef]
  9. Stock, T.; Seliger, G. Opportunities of sustainable manufacturing in industry 4.0. Procedia CIRP 2016, 40, 536–541. [Google Scholar] [CrossRef]
  10. Fernandes, J.M.; Homayouni, S.M.; Fontes, D.B. Energy-efficient scheduling in job shop manufacturing systems: A literature review. Sustainability 2022, 14, 6264. [Google Scholar] [CrossRef]
  11. Xu, Q.; Zhang, L.; Yu, W. A localization method of ant colony optimization in nonuniform space. Sensors 2022, 22, 7389. [Google Scholar] [CrossRef] [PubMed]
  12. Chang, Z.; Song, S.; Zhang, Y.; Ding, J.Y.; Zhang, R.; Chiong, R. Distributionally robust single machine scheduling with risk aversion. Eur. J. Oper. Res. 2017, 256, 261–274. [Google Scholar] [CrossRef]
  13. Xiong, H.; Shi, S.; Ren, D.; Hu, J. A survey of job shop scheduling problem: The types and models. Comput. Oper. Res. 2022, 142, 105731. [Google Scholar] [CrossRef]
  14. Ambrogio, G.; Guido, R.; Palaia, D.; Filice, L. Job shop scheduling model for a sustainable manufacturing. Procedia Manuf. 2020, 42, 538–541. [Google Scholar] [CrossRef]
  15. Ning, T.; Wang, Z.; Zhang, P.; Gou, T. Integrated optimization of disruption management and scheduling for reducing carbon emission in manufacturing. J. Clean. Prod. 2020, 263, 121449. [Google Scholar] [CrossRef]
  16. Fang, K.; Uhan, N.; Zhao, F.; Sutherland, J.W. A new approach to scheduling in manufacturing for power consumption and carbon footprint reduction. J. Manuf. Syst. 2011, 30, 234–240. [Google Scholar] [CrossRef]
  17. Giret, A.; Trentesaux, D.; Prabhu, V. Sustainability in manufacturing operations scheduling: A state of the art review. J. Manuf. Syst. 2015, 37, 126–140. [Google Scholar] [CrossRef]
  18. Maccarthy, B.L.; Liu, J. Addressing the gap in scheduling research: A review of optimization and heuristic methods in production scheduling. Int. J. Prod. Res. 2007, 31, 59–79. [Google Scholar] [CrossRef]
  19. Wei, Z.; Liao, W.; Zhang, L. Hybrid energy-efficient scheduling measures for flexible job-shop problem with variable machining speeds. Expert Syst. Appl. 2022, 7, 197. [Google Scholar] [CrossRef]
  20. Li, Y.; Liao, C.; Wang, L.; Xiao, Y.; Cao, Y.; Guo, S. A reinforcement learning-artificial bee colony algorithm for flexible job-shop scheduling problem with lot streaming. Appl. Soft Comput. 2023, 146, 110658. [Google Scholar] [CrossRef]
  21. Oliva, D.; Houssein, E.H.; Hinojosa, S. Studies in Computational Intelligence 967 Metaheuristics in Machine Learning: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2021; Available online: http://www.springer.com/series/7092 (accessed on 28 February 2025).
  22. Momenikorbekandi, A.; Abbod, M. Intelligent scheduling based on reinforcement learning approaches: Applying advanced q-learning and state–action–reward–state–action reinforcement learning models for the optimisation of job shop scheduling problems. Electronics 2023, 12, 4752. [Google Scholar] [CrossRef]
  23. Mauergauz, Y. Advanced Planning and Scheduling in Manufacturing and Supply Chains; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–570. [Google Scholar]
  24. Chen, R.; Li, W.; Yang, H. A deep reinforcement learning framework based on an attention mechanism and disjunctive graph embedding for the job-shop scheduling problem. IEEE Trans. Ind. Inform. 2023, 19, 1322–1331. [Google Scholar] [CrossRef]
  25. Brucker, P.; Schlie, R. Job-shop scheduling with multi-purpose machines. Computing 1990, 45, 369–375. [Google Scholar] [CrossRef]
  26. Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar] [CrossRef]
  27. Biskup, D. Single-machine scheduling with learning considerations. Eur. J. Oper. Res. 1999, 115, 173–178. [Google Scholar] [CrossRef]
  28. Garey, M.R.; Johnson, D.S.; Sethi, R. The complexity of flowshop and jobshop scheduling. Math. Oper. Res. 1976, 1, 117–129. [Google Scholar] [CrossRef]
  29. Wang, J.; Lei, D.; Li, M. A q-learning-based artificial bee colony algorithm for distributed three-stage assembly scheduling with factory eligibility and setup times. Machines 2022, 10, 661. [Google Scholar] [CrossRef]
  30. Pinedo, M.L. Scheduling: Theory, Algorithms, Systems, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–673. [Google Scholar] [CrossRef]
  31. Wang, J.B.; Ng, C.T.; Cheng, T.C.; Liu, L.L. Single-machine scheduling with a time-dependent learning effect. Int. J. Prod. Econ. 2008, 111, 802–811. [Google Scholar] [CrossRef]
  32. Lee, C.Y.; Piramuthu, S.; Tsai, Y.K. Job shop scheduling with a genetic algorithm and machine learning. Int. J. Prod. Res. 2010, 35, 1171–1191. [Google Scholar] [CrossRef]
  33. Lu, Y.Y.; Wei, C.M.; Wang, J.B. Several single-machine scheduling problems with general learning effects. Appl. Math. Model. 2012, 36, 5650–5656. [Google Scholar] [CrossRef]
  34. Cheng, C.Y.; Li, S.F.; Ying, K.C.; Liu, Y.H. Scheduling jobs of two competing agents on a single machine. IEEE Access 2019, 7, 98702–98714. [Google Scholar] [CrossRef]
  35. de Weerdt, M.; Baart, R.; He, L. Single-machine scheduling with release times, deadlines, setup times, and rejection. Eur. J. Oper. Res. 2021, 291, 629–639. [Google Scholar] [CrossRef]
  36. Lei, D.; He, S. An adaptive artificial bee colony for unrelated parallel machine scheduling with additional resource and maintenance. Expert Syst. Appl. 2022, 205, 117577. [Google Scholar] [CrossRef]
  37. Chen, R.; Yang, B.; Li, S.; Wang, S. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem. Comput. Ind. Eng. 2020, 149, 106778. [Google Scholar] [CrossRef]
  38. Al-Hinai, N.; Elmekkawy, T.Y. Robust and stable flexible job shop scheduling with random machine breakdowns using a hybrid genetic algorithm. Int. J. Prod. Econ. 2011, 132, 279–291. [Google Scholar] [CrossRef]
  39. Kacem, I.; Hammadi, S.; Borne, P. Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2002, 32, 1–13. [Google Scholar] [CrossRef]
  40. Nouiri, M.; Bekrar, A.; Abderezak; Smail, J.; Ahmed, N.; Ammari, C.; Nouiri, M.; Jemai, A.; Ammari, A.C.; Bekrar, A.; et al. An effective and distributed particle swarm optimization algorithm for flexible job-shop scheduling problem. J. Intell. Manuf. 2018, 29, 603–615. [Google Scholar]
  41. Yamada, T.; Nakano, R. A Fusion of crossover and local search. In Proceedings of the IEEE International Conference on Industrial Technology, Shanghai, China, 2–6 December 1996; pp. 426–430. [Google Scholar] [CrossRef]
  42. Yoshitomi, Y. A genetic algorithm approach to solving stochastic job-shop scheduling problems. Int. Trans. Oper. Res. 2002, 9, 479–495. [Google Scholar] [CrossRef]
  43. Zhang, G.; Shao, X.; Li, P.; Gao, L. An effective hybrid particle swarm optimization algorithm for multi-objective flexible job-shop scheduling problem. Comput. Ind. Eng. 2009, 56, 1309–1318. [Google Scholar] [CrossRef]
  44. Xing, L.N.; Chen, Y.W.; Wang, P.; Zhao, Q.S.; Xiong, J. A knowledge-based ant colony optimization for flexible job shop scheduling problems. Appl. Soft Comput. 2010, 10, 888–896. [Google Scholar] [CrossRef]
  45. Zhang, G.; Gao, L.; Shi, Y. An effective genetic algorithm for the flexible job-shop scheduling problem. Expert Syst. Appl. 2011, 38, 3563–3573. [Google Scholar] [CrossRef]
  46. Nouiri, M.; Bekrar, A.; Jemai, A.; Trentesaux, D.; Ammari, A.C.; Niar, S. Two stage particle swarm optimization to solve the flexible job shop predictive scheduling problem considering possible machine breakdowns. Comput. Ind. Eng. 2017, 112, 595–606. [Google Scholar] [CrossRef]
  47. Li, X.; Peng, Z.; Du, B.; Guo, J.; Xu, W.; Zhuang, K. Hybrid artificial bee colony algorithm with a rescheduling strategy for solving flexible job shop scheduling problems. Comput. Ind. Eng. 2017, 113, 10–26. [Google Scholar] [CrossRef]
  48. Jiang, E.-D.; Wang, L. An improved multi-objective evolutionary algorithm based on decomposition for energy-efficient permutation flow shop scheduling problem with sequence-dependent setup time. Int. J. Prod. Res. 2019, 57, 1756–1771. [Google Scholar] [CrossRef]
  49. Meng, L.; Zhang, C.; Shao, X.; Ren, Y. Milp models for energy-aware flexible job shop scheduling problem. J. Clean. Prod. 2019, 210, 710–723. [Google Scholar] [CrossRef]
  50. Gao, K.; Cao, Z.; Zhang, L.; Chen, Z.; Han, Y.; Pan, Q. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar] [CrossRef]
  51. Caldeira, R.H.; Gnanavelbabu, A.; Vaidyanathan, T. An effective backtracking search algorithm for multi-objective flexible job shop scheduling considering new job arrivals and energy consumption. Comput. Ind. Eng. 2020, 11, 149. [Google Scholar] [CrossRef]
  52. Li, B.; Zhang, H.; Ye, P.; Wang, J. Trajectory smoothing method using reinforcement learning for computer numerical control machine tools. Robot. Comput. -Integr. Manuf. 2020, 61, 101847. [Google Scholar] [CrossRef]
  53. Wei, H.; Li, S.; Quan, H.; Liu, D.; Rao, S.; Li, C.; Hu, J. Unified multi-objective genetic algorithm for energy efficient job shop scheduling. IEEE Access 2021, 9, 54542–54557. [Google Scholar] [CrossRef]
  54. Xu, W.; Hu, Y.; Luo, W.; Wang, L.; Wu, R. A multi-objective scheduling method for distributed and flexible job shop based on hybrid genetic algorithm and tabu search considering operation outsourcing and carbon emission. Comput. Ind. Eng. 2021, 7, 157. [Google Scholar] [CrossRef]
  55. Rakovitis, N.; Li, D.; Zhang, N.; Li, J.; Zhang, L.; Xiao, X. Novel approach to energy-efficient flexible job-shop scheduling problems. Energy 2022, 1, 238. [Google Scholar] [CrossRef]
  56. Fan, J.; Zhang, C.; Liu, Q.; Shen, W.; Gao, L. An improved genetic algorithm for flexible job shop scheduling problem considering reconfigurable machine tools with limited auxiliary modules. J. Manuf. Syst. 2022, 62, 650–667. [Google Scholar] [CrossRef]
  57. Fan, C.; Wang, W.; Tian, J. Flexible job shop scheduling with stochastic machine breakdowns by an improved tuna swarm optimization algorithm. J. Manuf. Syst. 2024, 74, 180–197. [Google Scholar] [CrossRef]
  58. Guo, H.; Liu, J.; Wang, Y.; Zhuang, C. An improved genetic programming hyper-heuristic for the dynamic flexible job shop scheduling problem with reconfigurable manufacturing cells. J. Manuf. Syst. 2024, 74, 252–263. [Google Scholar] [CrossRef]
  59. Liu, Z.; Zha, J.; Yan, J.; Zhang, Y.; Zhao, T.; Cheng, Q.; Cheng, C. An improved genetic algorithm with an overlapping strategy for solving a combination of order batching and flexible job shop scheduling problem. Eng. Appl. Artif. Intell. 2024, 127, 107321. [Google Scholar] [CrossRef]
  60. Khan, M.N.; Sinha, A.K. Whale optimization algorithm for scheduling and sequencing. In Handbook of Whale Optimization Algorithm: Variants, Hybrids, Improvements, and Applications; Academic Press: Cambridge, MA, USA, 2024; pp. 487–494. [Google Scholar] [CrossRef]
  61. Liao, X.; Zhang, R.; Chen, Y.; Song, S. A new artificial bee colony algorithm for the flexible job shop scheduling problem with extra resource constraints in numeric control centers. Expert Syst. Appl. 2024, 249, 123556. [Google Scholar] [CrossRef]
  62. Zhang, W.; Zhao, F.; Li, Y.; Du, C.; Feng, X.; Mei, X. A novel collaborative agent reinforcement learning framework based on an attention mechanism and disjunctive graph embedding for flexible job shop scheduling problem. J. Manuf. Syst. 2024, 74, 329–345. [Google Scholar] [CrossRef]
  63. Tiacci, L.; Rossi, A. A discrete event simulator to implement deep reinforcement learning for the dynamic flexible job shop scheduling problem. Simul. Model. Pract. Theory 2024, 134, 102948. [Google Scholar] [CrossRef]
  64. Liu, M.; Lv, J.; Du, S.; Deng, Y.; Shen, X.; Zhou, Y. Multi-resource constrained flexible job shop scheduling problem with fixture-pallet combinatorial optimisation. Comput. Ind. Eng. 2024, 188, 109903. [Google Scholar] [CrossRef]
  65. Zhang, G.; Yan, S.; Song, X.; Zhang, D.; Guo, S. Evolutionary algorithm incorporating reinforcement learning for energy-conscious flexible job-shop scheduling problem with transportation and setup times. Eng. Appl. Artif. Intell. 2024, 133, 107974. [Google Scholar] [CrossRef]
  66. Lin, W.; Tian, G.; Li, Z.; Zhang, Y.; Zhang, C. Flow shop scheduling with low carbon emission and variable machining parameters. Proc. Inst. Mech. Engineers. Part B J. Eng. Manuf. 2019, 233, 1561–1572. [Google Scholar] [CrossRef]
  67. Wu, X.; Zhao, J.; Tong, Y. Big data analysis and scheduling optimization system oriented assembly process for complex equipment. IEEE Access 2018, 6, 36479–36486. [Google Scholar] [CrossRef]
  68. Lu, C.; Gao, L.; Li, X.; Pan, Q.; Wang, Q. Energy-efficient permutation flow shop scheduling problem using a hybrid multi-objective backtracking search algorithm. J. Clean. Prod. 2017, 144, 228–238. [Google Scholar] [CrossRef]
  69. Ebrahimi, A.; Jeon, H.W.; Lee, S.; Wang, C. Minimizing total energy cost and tardiness penalty for a scheduling-layout problem in a flexible job shop system: A comparison of four metaheuristic algorithms. Comput. Ind. Eng. 2020, 141, 106295. [Google Scholar] [CrossRef]
  70. Momenikorbekandi, A.; Abbod, M.F. New Intelligent Optimisation Systems for Job Shop Scheduling Problems in the Manufacturing Industry; Brunel University London: London, UK, 2024; Available online: http://bura.brunel.ac.uk/handle/2438/29901 (accessed on 28 February 2025).
  71. Han, W.; Deng, Q.; Gong, G.; Zhang, L.; Luo, Q. Multi-objective evolutionary algorithms with heuristic decoding for hybrid flow shop scheduling problem with worker constraint. Expert Syst. Appl. 2021, 168, 114282. [Google Scholar] [CrossRef]
  72. Momenikorbekandi, A.; Abbod, M. A novel metaheuristic hybrid parthenogenetic algorithm for job shop scheduling problems: Applying optimization model. IEEE Access 2023, 11, 56027–56045. [Google Scholar] [CrossRef]
  73. Chong, H.Y.; Yap, H.J.; Tan, S.C.; Yap, K.S.; Wong, S.Y. Advances of metaheuristic algorithms in training neural networks for industrial applications. Soft Comput. 2021, 25, 11209–11233. [Google Scholar] [CrossRef]
  74. Jiang, Z.; Yuan, S.; Ma, J.; Wang, Q. The evolution of production scheduling from industry 3.0 through industry 4.0. Int. J. Prod. Res. 2021, 60, 3534–3554. [Google Scholar] [CrossRef]
  75. Glover, F. Future paths for integer programming and links to ar tifi cial intelligence. Comput. Ops. Res 1986, 13, 533–549. [Google Scholar] [CrossRef]
  76. Dang, Q.V.; van Diessen, T.; Martagan, T.; Adan, I. A matheuristic for parallel machine scheduling with tool replacements. Eur. J. Oper. Res. 2021, 291, 640–660. [Google Scholar] [CrossRef]
  77. Tamssaouet, K.; Dauz, S.; Yugma, C. Metaheuristics for the job-shop scheduling problem with machine availability constraints. Comput. Ind. Eng. 2018, 125, 1–8. [Google Scholar] [CrossRef]
  78. Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
  79. Beyer, H.-G.; Schwefel, H.-P. Evolution strategies a comprehensive introduction. ACM Comput. Classif. 2002, 1, 3–52. [Google Scholar] [CrossRef]
  80. Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
  81. Fogel, D.B. Evolutionary Computation: The Fossil Record; Selected Readings on the History of Evolutionary Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 1998; p. 641. [Google Scholar]
  82. Tiwari, M.K.; Chan, F.T. Swarm Intelligence, Focus on Ant and Particle Swarm Optimization; BoD–Books on Demand: Norderstedt, Germany, 2019; p. 548. [Google Scholar] [CrossRef]
  83. Eberhart, R.; Kennedy, J. New optimizer using particle swarm theory. In Proceedings of the International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
  84. Walton, S.; Hassan, O.; Morgan, K.; Brown, M.R. A review of the development and applications of the cuckoo search algorithm. Swarm Intell. BioInspired Comput. Theory Appl. 2013, 2013, 257–271. [Google Scholar]
  85. Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
  86. da Jiang, E.; Wang, L. Multi-objective optimization based on decomposition for flexible job shop scheduling under time-of-use electricity prices. Knowl. -Based Syst. 2020, 204, 106177. [Google Scholar] [CrossRef]
  87. Holland, J.H. Genetic algorithms and adaptation. In Adaptive Control of Ill-Defined Systems; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
  88. Momenikorbekandi, A.; Abbod, M.F. Multi-ethnicity genetic algorithm for job shop scheduling problems. Tech. Rep. 2022, 13.1–13.4. [Google Scholar]
  89. Goldberg, D.E.; Holland, J.H. Genetic algorithms in search, optimization, and machine learning david e. goldberg the university of alabama t. Mach. Learn. 1979, 3, 95–99. [Google Scholar] [CrossRef]
  90. Whitley, D. An overview of evolutionary algorithms: Practical issues and common pitfalls. Inf. Softw. Technol. 2001, 43, 817–831. [Google Scholar] [CrossRef]
  91. Ghosh, A.; Tsutsui, S.; Tanaka, H. Individual aging in genetic algorithms. In Proceedings of the Australian and New Zealand Conference on Intelligent Information Systems, Adelaide, Australia, 18–20 November 1996; pp. 276–279. [Google Scholar] [CrossRef]
  92. Zhao, C.; Wu, Z. A genetic algorithm approach to the scheduling of fmss with multiple routes. Int. J. Flex. Manuf. Syst. 2001, 13, 71–88. [Google Scholar] [CrossRef]
  93. Kacem, I. Genetic algorithm for the flexible job-shop scheduling problem. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics 4, Washington, DC, USA, 8 October 2003; pp. 3464–3469. [Google Scholar] [CrossRef]
  94. Goh, K.S.; Lim, A.; Rodrigues, B. Sexual selection for genetic algorithms. Artif. Intell. Rev. 2003, 19, 123–152. [Google Scholar] [CrossRef]
  95. Guimar, K.F.; Fernandes, M.A. An approach for flexible job-shop scheduling with separable sequence-dependent setup time. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006; Volume 5, pp. 3727–3731. [Google Scholar] [CrossRef]
  96. Chan, F.T.; Chung, S.H.; Chan, L.Y. An introduction of dominant genes in genetic algorithm for fms. Int. J. Prod. Res. 2008, 46, 4369–4389. [Google Scholar] [CrossRef]
  97. Pezzella, F.; Morganti, G.; Ciaschetti, G. A genetic algorithm for the flexible jobshop scheduling problem. Comput. Oper. Res. 2008, 35, 3202–3212. [Google Scholar] [CrossRef]
  98. Zhang, M.; Luo, W.; Wang, X. Differential evolution with dynamic stochastic selection for constrained optimization. Inf. Sci. 2008, 178, 3043–3074. [Google Scholar] [CrossRef]
  99. Giovanni, L.D.; Pezzella, F. An improved genetic algorithm for the distributed and flexible job-shop scheduling problem. Eur. J. Oper. Res. 2010, 200, 395–408. [Google Scholar] [CrossRef]
  100. Unachak, P.; Goodman, E. Solving multiobjective flexible job-shop scheduling using an adaptive representation. In Proceedings of the 12th Annual Genetic and Evolutionary Computation Conference, GECCO, Portland, OR, USA, 7–11 July 2010; Volume 10, pp. 737–742. [Google Scholar] [CrossRef]
  101. Xu, X.H.; Zeng, L.L.; Fu, Y.W. Hybrid particle swarm optimization for flexible job-shop scheduling problem and its implementation? In Proceedings of the 2010 IEEE International Conference on Information and Automation, ICIA, Harbin, China, 20–23 June 2010; pp. 1155–1159. [Google Scholar] [CrossRef]
  102. Zhang, G.; Gao, L.; Shi, Y. A genetic algorithm and tabu search for multi objective flexible job shop scheduling problems. In Proceedings of the 2010 International Conference on Computing, Control and Industrial Engineering, CCIE, Wuhan, China, 5–6 June 2010; pp. 251–254. [Google Scholar] [CrossRef]
  103. Hu, D.; Yao, Z. Stacker-reclaimer scheduling for raw material yard operation. In Proceedings of the 3rd International Workshop on Advanced Computational Intelligence, IWACI, Suzhou, China, 25–27 August 2010; pp. 432–436. [Google Scholar] [CrossRef]
  104. Wan, M.; Xu, X.; Nan, J. Flexible job-shop scheduling with integrated genetic algorithm. In Proceedings of the 4th International Workshop on Advanced Computational Intelligence, IWACI, Wuhan, China, 19–21 October 2011; pp. 13–16. [Google Scholar] [CrossRef]
  105. Jiang, J.; Wen, M.; Ma, K.; Long, X.; Li, J. Hybrid genetic algorithm for flexible job-shop scheduling with multi-objective. J. Inf. Comput. Sci. 2011, 8, 2197–2205. [Google Scholar]
  106. Xing, L.N.; Chen, Y.W.; Yang, K.W. Multi-population interactive coevolutionary algorithm for flexible job shop scheduling problems. Comput. Optim. Appl. 2011, 48, 139–155. [Google Scholar] [CrossRef]
  107. Phanden, R.K.; Jain, A.; Verma, R. A genetic algorithm-based approach for flexible job shop scheduling. Appl. Mech. Mater. 2012, 110–116, 3930–3937. [Google Scholar] [CrossRef]
  108. Lin, L. A hybrid ea for reactive flexible job-shop scheduling. Procedia Comput. Sci. 2012, 12, 110–115. [Google Scholar] [CrossRef]
  109. Na, H.; Park, J. Multi-level job scheduling in a flexible job shop environment. Int. J. Prod. Res. 2014, 52, 3877–3887. [Google Scholar] [CrossRef]
  110. Liu, T.K.; Chen, Y.P.; Chou, J.H. Solving distributed and flexible job-shop scheduling problems for a real-world fastener manufacturer. IEEE Access 2014, 2, 1598–1606. [Google Scholar] [CrossRef]
  111. Chang, H.C.; Chen, Y.P.; Liu, T.K.; Chou, J.H. Solving the flexible job shop scheduling problem with makespan optimization by using a hybrid taguchi-genetic algorithm. IEEE Access 2015, 3, 1740–1754. [Google Scholar] [CrossRef]
  112. Yang, X.; Wang, J.; Hou, M.; Fan, X. Job shop scheduling based on genetic algorithm using matlab. In Proceedings of the 2015 IEEE Advanced Information Technology. Electronic and Automation Control Conference, IAEAC, Chongqing, China, 19–20 December 2015; pp. 772–775. [Google Scholar] [CrossRef]
  113. Palacios, J.J.; Gonz, M.A.; Vela, C.R.; Gonz, I.; Puente, J. Genetic tabu search for the fuzzy flexible job shop problem. Comput. Oper. Res. 2015, 54, 74–89. [Google Scholar] [CrossRef]
  114. Wang, J.; Huang, W.; Ma, G.; Chen, S. An improved partheno genetic algorithm for multi-objective economic dispatch in cascaded hydropower systems. Int. J. Electr. Power Energy Syst. 2015, 67, 591–597. [Google Scholar] [CrossRef]
  115. Nouri, H.E.; Driss, O.B.; Gh, K. Simultaneous scheduling of machines and transport robots in flexible job shop environment using hybrid metaheuristics based on clustered holonic multiagent model. Comput. Ind. Eng. 2016, 102, 488–501. [Google Scholar] [CrossRef]
  116. Shi, C.; Li, T.; Bai, Y.; Zhao, F. A heuristics-based parthenogenetic algorithm for the vrp with potential demands and time windows. Sci. Program. 2016, 2016, 12. [Google Scholar] [CrossRef]
  117. He, Y.; Weng, W.; Fujimura, S. Improvements to genetic algorithm for flexible job shop scheduling with overlapping in operations. In Proceedings of the 16th IEEE/ACIS International Conference on Computer and Information Science, ICIS, Wuhan, China, 24–26 May 2017; pp. 791–796. [Google Scholar] [CrossRef]
  118. Costa, A.; Cappadonna, F.A.; Fichera, S. A hybrid genetic algorithm for minimizing makespan in a flow-shop sequence-dependent group scheduling problem. J. Intell. Manuf. 2017, 28, 1269–1283. [Google Scholar] [CrossRef]
  119. Yu, X.; Liao, X.; Li, W.; Liu, X.; Tao, Z. Logistics automation control based on machine learning algorithm. Clust. Comput. 2019, 22, 14003–14011. [Google Scholar] [CrossRef]
  120. Wang, B.; Wang, H. Multiobjective order acceptance and scheduling on unrelated parallel machines with machine eligibility constraints. Math. Probl. Eng. 2018, 2018, 6024631. [Google Scholar] [CrossRef]
  121. Biswas, T.; Kuila, P.; Ray, A.K. A novel scheduling with multi-criteria for highperformance computing systems: An improved genetic algorithm-based approach. Eng. Comput. 2019, 35, 1475–1490. [Google Scholar] [CrossRef]
  122. Bhosale, K.C.; Pawar, P.J. Material flow optimisation of production planning and scheduling problem in flexible manufacturing system by real coded genetic algorithm (rcga). Flex. Serv. Manuf. J. 2019, 31, 381–423. [Google Scholar] [CrossRef]
  123. Zhang, G.; Hu, Y.; Sun, J.; Zhang, W. An improved genetic algorithm for the flexible job shop scheduling problem with multiple time constraints. Swarm Evol. Comput. 2020, 54, 100664. [Google Scholar] [CrossRef]
  124. Yang, Z.; Jiacheng, L.; Lei, L. Time-dependent theme park routing problem by partheno-genetic algorithm. Mathematics 2020, 8, 2193. [Google Scholar] [CrossRef]
  125. Shi, S.; Xiong, H. A hybrid immune genetic algorithm with tabu search for minimizing the tool switch times in cnc milling batch-processing. Appl. Intell. 2022, 52, 7793–7807. [Google Scholar] [CrossRef]
  126. Guo, W.; Lei, Q.; Song, Y.; Lyu, X. A learning interactive genetic algorithm based on edge selection encoding for assembly job shop scheduling problem. Comput. Ind. Eng. 2021, 159, 107455. [Google Scholar] [CrossRef]
  127. Liang, X.; Chen, J.; Gu, X.; Huang, M. Improved adaptive non-dominated sorting genetic algorithm with elite strategy for solving multi-objective flexible job-shop scheduling problem. IEEE Access 2021, 9, 106352–106362. [Google Scholar] [CrossRef]
  128. Park, J.; Chun, J.; Kim, S.H.; Kim, Y.; Park, J. Learning to schedule job-shop problems: Representation and policy learning using graph neural network and reinforcement learning. Int. J. Prod. Res. 2021, 59, 3360–3377. [Google Scholar] [CrossRef]
  129. Viana, M.S.; Contreras, R.C.; Junior, O.M. A new frequency analysis operator for population improvement in genetic algorithms to solve the job shop scheduling problem. Sensors 2022, 22, 4561. [Google Scholar] [CrossRef]
  130. Saidat, S.; Junoh, A.K.; Muhamad, W.Z.A.W.; Yahya, Z. Modified job shop scheduling via taguchi method and genetic algorithm. Neural Comput. Appl. 2022, 34, 1963–1980. [Google Scholar] [CrossRef]
  131. Chen, N.; Xie, N.; Wang, Y. An elite genetic algorithm for flexible job shop scheduling problem with extracted grey processing time. Appl. Soft Comput. 2022, 131, 109783. [Google Scholar] [CrossRef]
  132. Tutumlu, B.; Sara, T. A mip model and a hybrid genetic algorithm for flexible job-shop scheduling problem with job-splitting. Comput. Oper. Res. 2023, 155, 106222. [Google Scholar] [CrossRef]
  133. Meng, L.; Cheng, W.; Zhang, B.; Zou, W.; Fang, W.; Duan, P. An improved genetic algorithm for solving the multi-agv flexible job shop scheduling problem. Sensors 2023, 23, 3815. [Google Scholar] [CrossRef] [PubMed]
  134. Homayouni, S.M.; Fontes, D.B.; Gon, J.F. A multistart biased random key genetic algorithm for the flexible job shop scheduling problem with transportation. Int. Trans. Oper. Res. 2023, 30, 688–716. [Google Scholar] [CrossRef]
  135. Shen, Q.; Shi, W.M.; Kong, W. Hybrid particle swarm optimization and tabu search approach for selecting genes for tumor classification using gene expression data. Comput. Biol. Chem. 2008, 32, 53–60. [Google Scholar] [CrossRef]
  136. Mandloi, M.; Bhatia, V. A low-complexity hybrid algorithm based on particle swarm and ant colony optimization for large-mimo detection. Expert Syst. Appl. 2016, 50, 66–74. [Google Scholar] [CrossRef]
  137. Ouyang, H.B.; Gao, L.Q.; Kong, X.Y.; Li, S.; Zou, D.X. Hybrid harmony search particle swarm optimization with global dimension selection. Inf. Sci. 2016, 346–347, 318–337. [Google Scholar] [CrossRef]
  138. Chen, J.; Do, Q.; Algorithms, H.H. Training artificial neural networks by a hybrid pso-cs algorithm. Algorithms 2015, 8, 292–308. [Google Scholar] [CrossRef]
  139. Fontes, D.B.; Homayouni, S.M.; Gon, J.F. A hybrid particle swarm optimization and simulated annealing algorithm for the job shop scheduling problem with transport resources. Eur. J. Oper. Res. 2023, 306, 1140–1157. [Google Scholar] [CrossRef]
  140. Bonyadi, M.R.; Michalewicz, Z. Particle swarm optimization for single objective continuous space problems: A review. Evol. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef]
  141. Wang, C.M.; Huang, Y.F. Self-adaptive harmony search algorithm for optimization. Expert Syst. Appl. 2010, 37, 2826–2837. [Google Scholar] [CrossRef]
  142. Zhang, H.; Deng, Z.; Fu, Y.; Lv, L.; Yan, C. A process parameters optimization method of multi-pass dry milling for high efficiency, low energy and low carbon emissions. J. Clean. Prod. 2017, 148, 174–184. [Google Scholar] [CrossRef]
  143. Das, S.; Suganthan, P.N. Differential evolution: A survey of the stateof-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
  144. Yi, W.; Zhou, Y.; Gao, L.; Li, X.; Mou, J. An improved adaptive differential evolution algorithm for continuous optimization. Expert Syst. Appl. 2016, 44, 1–12. [Google Scholar] [CrossRef]
  145. Fan, Q.; Zhang, Y. Self-adaptive differential evolution algorithm with crossover strategies adaptation and its application in parameter estimation. Chemom. Intell. Lab. Syst. 2016, 151, 164–171. [Google Scholar] [CrossRef]
  146. Das, S.; Mullick, S.S.; Suganthan, P.N. Recent advances in differential evolution—An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
  147. Lenin, K.; Reddy, B.R.; Suryakalavathi, M. Hybrid tabu search-simulated annealing method to solve optimal reactive power problem. Int. J. Electr. Power Energy Syst. 2016, 82, 87–91. [Google Scholar] [CrossRef]
  148. Sait, S.M.; Oughali, F.C.; Al-Asli, M.; Sait, S.M.; Oughali, F.C.; Al-Asli, M. Design partitioning and layer assignment for 3d integrated circuits using tabu search and simulated annealing. J. Appl. Res. Technol. 2016, 14, 67–76. [Google Scholar] [CrossRef]
  149. Buyukozkan, K.; Kucukkoc, I.; Satoglu, S.I.; Zhang, D.Z. Lexicographic bottleneck mixed-model assembly line balancing problem: Artificial bee colony and tabu search approaches with optimised parameters. Expert Syst. Appl. 2016, 50, 151–166. [Google Scholar] [CrossRef]
  150. Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization. 2005. Available online: https://www.researchgate.net/publication/255638348_An_Idea_Based_on_Honey_Bee_Swarm_for_Numerical_Optimization_Technical_Report_-_TR06 (accessed on 28 February 2025).
  151. Yuce, B.; Packianather, M.S.; Mastrocinque, E.; Pham, D.T.; Lambiase, A. Honey bees inspired optimization method: The bees algorithm. Insects 2013, 4, 646–662. [Google Scholar] [CrossRef]
  152. Karaboga, D.; Basturk, B. On the performance of artificial bee colony (abc) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
  153. Bolaji, A.L.A.; Khader, A.T.; Al-Betar, M.A.; Awadallah, M.A. University course timetabling using hybridized artificial bee colony with hill climbing optimizer. J. Comput. Sci. 2014, 5, 809–818. [Google Scholar] [CrossRef]
  154. Janakiraman, S. A hybrid ant colony and artificial bee colony optimization algorithm-based cluster head selection for iot. Procedia Comput. Sci. 2018, 143, 360–366. [Google Scholar] [CrossRef]
  155. ZorarpacI, E.; Ozel, S.A. A hybrid approach of differential evolution and artificial bee colony for feature selection. Expert Syst. Appl. 2016, 62, 91–103. [Google Scholar] [CrossRef]
  156. Jadon, S.S.; Tiwari, R.; Sharma, H.; Bansal, J.C. Hybrid artificial bee colony algorithm with differential evolution. Appl. Soft Comput. 2017, 58, 11–24. [Google Scholar] [CrossRef]
  157. Sharma, N.; Sharma, H.; Sharma, A. Beer froth artificial bee colony algorithm for job-shop scheduling problem. Appl. Soft Comput. 2018, 68, 507–524. [Google Scholar] [CrossRef]
  158. Gao, J.; Zhu, X.; Bai, K.; Zhang, R. New controllable processing time scheduling with subcontracting strategy for no-wait job shop problem. Int. J. Prod. Res. 2022, 60, 2254–2274. [Google Scholar] [CrossRef]
  159. Sundar, S.; Suganthan, P.N.; Jin, C.T.; Xiang, C.T.; Soon, C.C. A hybrid artificial bee colony algorithm for the job-shop scheduling problem with no-wait constraint. Soft Comput. 2017, 21, 1193–1202. [Google Scholar] [CrossRef]
  160. Pan, Q.-K.; Tasgetiren, M.F.; Suganthan, P.N.; Chua, T.J. A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem. Inf. Sci. 2011, 181, 2455–2468. [Google Scholar] [CrossRef]
  161. Pan, Q.K.; Wang, L.; Mao, K.; Zhao, J.H.; Zhang, M. An effective artificial bee colony algorithm for a real-world hybrid flowshop problem in steelmaking process. IEEE Trans. Autom. Sci. Eng. 2013, 10, 307–322. [Google Scholar] [CrossRef]
  162. Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
  163. Lee, K.S.; Geem, Z.W. A new structural optimization method based on the harmony search algorithm. Comput. Struct. 2004, 82, 781–798. [Google Scholar] [CrossRef]
  164. Awadallah, M.A.; Al-Betar, M.A.; Khader, A.T.; Bolaji, A.L.; Alkoffash, M. Hybridization of harmony search with hill climbing for highly constrained nurse rostering problem. Neural Comput. Appl. 2017, 28, 463–482. [Google Scholar] [CrossRef]
  165. Panchal, A. Harmony search in therapeutic medical physics. Stud. Comput. Intell. 2009, 191, 189–203. [Google Scholar]
  166. Manjarres, D.; Landa-Torres, I.; Gil-Lopez, S.; Ser, J.D.; Bilbao, M.N.; SalcedoSanz, S.; Geem, Z.W. Survey paper a survey on applications of the harmony search algorithm. Eng. Appl. Artif. Intell. 2013, 26, 1818–1831. [Google Scholar] [CrossRef]
  167. Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
  168. Alia, O.M.D.; Mandava, R. The variants of the harmony search algorithm: An overview. Artif. Intell. Rev. 2011, 36, 49–68. [Google Scholar] [CrossRef]
  169. Yang, X.S.; Deb, S. Cuckoo search via l’evy flights. In Proceedings of the 2009 World Congress on Nature and Biologically Inspired Computing, NABIC, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar] [CrossRef]
  170. Singh, S.; Singh, K.P. Cuckoo search optimization for job shop scheduling problem. Adv. Intell. Syst. Comput. 2015, 335, 99–111. [Google Scholar]
  171. Walton, S.; Hassan, O.; Morgan, K.; Brown, M.R. Modified cuckoo search: A new gradient free optimisation algorithm. Chaos. Solitons Fractals 2011, 44, 710–718. [Google Scholar] [CrossRef]
  172. Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
  173. Yang, X.-S. Nature-Inspired Metaheuristic Algorithms. 2010. Available online: https://www.researchgate.net/publication/235979455_Nature-Inspired_Metaheuristic_Algorithms (accessed on 28 February 2025).
  174. Chatterjee, A.; Mahanti, G.; Electromagnetics, A.C.P.I. Design of a fully digital controlled reconfigurable switched beam concentric ring array antenna using firefly and particle swarm optimization algorithm. Prog. Electromagn. Res. B 2012, 36, 113–131. [Google Scholar] [CrossRef]
  175. Apostolopoulos, T.; Vlachos, A. Application of the firefly algorithm for solving the economic emissions load dispatch problem. Int. J. Comb. 2010, 2011, 523806. [Google Scholar] [CrossRef]
  176. Horng, M.H. Vector quantization using the firefly algorithm for image compression. Expert Syst. Appl. 2012, 39, 1078–1091. [Google Scholar] [CrossRef]
  177. Gil, N.A.; Rosillo, R.; de la Fuente, D.; Pino, R. A discrete firefly algorithm for’ solving the flexible job-shop scheduling problem in a make-to-order manufacturing system. Cent. Eur. J. Oper. Res. 2021, 29, 1353–1374. [Google Scholar]
  178. Chakravarthi, K.K.; Shyamala, L.; Vaidehi, V. Cost-effective workflow scheduling approach on cloud under deadline constraint using firefly algorithm. Appl. Intell. 2021, 51, 1629–1644. [Google Scholar] [CrossRef]
  179. Xu, G.; Jiang, X.; Sun, D.; Yang, B.; Deng, R.; Fu, J. Flexible jobshop scheduling based on improved firefly algorithm. In Proceedings of the 2022 2nd International Conference on Computer, Control and Robotics, ICCCR, Shanghai, China, 18–20 March 2022; pp. 90–97. [Google Scholar] [CrossRef]
  180. Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. Gsa: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
  181. Schutz, B.; Schutz, D. Gravity from the Ground up: An Introductory Guide to Gravity and General Relativity. 2003. Available online: https://www.google.co.uk/books/edition/Gravity_from_the_Ground_Up/P_T0xxhDcsIC?hl=en (accessed on 28 February 2025).
  182. Li, X.; Wang, J.; Zhou, J.; Yin, M. An effective gsa based memetic algorithm for permutation flow shop scheduling. In Proceedings of the 2010 IEEE World Congress on Computational Intelligence, WCCI 2010—2010 IEEE Congress on Evolutionary Computation, CEC, Barcelona, Spain, 18–23 July 2010. [Google Scholar] [CrossRef]
  183. Cao, C.; Zhang, Y.; Gu, X.; Li, D.; Li, J. An improved gravitational search algorithm to the hybrid flowshop with unrelated parallel machines scheduling problem. Int. J. Prod. Res. 2021, 2021, 5592–5608. [Google Scholar] [CrossRef]
  184. Zhao, F.; Xue, F.; Zhang, Y.; Ma, W.; Zhang, C.; Song, H. A discrete gravitational search algorithm for the blocking flow shop problem with total flow time minimization. Appl. Intell. 2019, 49, 3362–3382. [Google Scholar] [CrossRef]
  185. Socha, K.; Blum, C. An ant colony optimization algorithm for continuous optimization: Application to feed-forward neural network training. Neural Comput. Appl. 2007, 16, 235–247. [Google Scholar] [CrossRef]
  186. Bauer, A.; Bullnheimer, B.; Hartl, R.F.; Strauss, C. An ant colony optimization approach for the single machine total tardiness problem. In Proceedings of the 1999 Congress on Evolutionary Computation, CEC, Washington, DC, USA, 6–9 July 1999; pp. 1445–1450. [Google Scholar] [CrossRef]
  187. Puris, A.; Bello, R.; Trujillo, Y.; Nowe, A.; Mart, Y. Two-stage aco to solve the job shop scheduling problem. In Proceedings of the 12th Iberoamerican Congress on Pattern Recognition, CIARP 2007, Valpariso, Chile, 13–16 November 2007; pp. 447–456. [Google Scholar]
  188. Chaouch, I.; Driss, O.B.; Ghedira, K. A modified ant colony optimization algorithm for the distributed job shop scheduling problem. Procedia Comput. Sci. 2017, 112, 296–305. [Google Scholar] [CrossRef]
  189. Eswaramurthy, V.P.; Tamilarasi, A. Hybridizing tabu search with ant colony optimization for solving job shop scheduling problems. Int. J. Adv. Manuf. Technol. 2009, 40, 1004–1015. [Google Scholar] [CrossRef]
  190. Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef]
  191. Blum, C. Beam-aco—Hybridizing ant colony optimization with beam search: An application to open shop scheduling. Comput. Oper. Res. 2005, 32, 1565–1591. [Google Scholar] [CrossRef]
  192. Gutjahr, W.J. Aco algorithms with guaranteed convergence to the optimal solution. Inf. Process. Lett. 2002, 82, 145–153. [Google Scholar] [CrossRef]
  193. Birattari, M.; Stu, T.; Stu, S.; Paquete, L.; Varrentrapp, K. A Racing Algorithm for Configuring Metaheuristics. 2002. Available online: https://www.researchgate.net/publication/220740639_A_Racing_Algorithm_for_Configuring_Metaheuristics (accessed on 28 February 2025).
  194. Liu, R.; Piplani, R.; Toro, C. Deep reinforcement learning for dynamic scheduling of a flexible job shop. Int. J. Prod. Res. 2022, 60, 4049–4069. [Google Scholar] [CrossRef]
  195. Bellman, R. A markovian decision process. Indiana Univ. Math. J. 1957, 6, 679–684. [Google Scholar] [CrossRef]
  196. Oliff, H.; Liu, Y.; Kumar, M.; Williams, M.; Ryan, M. Reinforcement learning for facilitating human-robot-interaction in manufacturing. J. Manuf. Syst. 2020, 56, 326–340. [Google Scholar] [CrossRef]
  197. Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
  198. Shi, D.; Fan, W.; Xiao, Y.; Lin, T.; Xing, C. Intelligent scheduling of discrete automated production line via deep reinforcement learning. Int. J. Prod. Res. 2020, 58, 3362–3380. [Google Scholar] [CrossRef]
  199. Shahrabi, J.; Adibi, M.A.; Mahootchi, M. A reinforcement learning approach to parameter estimation in dynamic job shop scheduling. Comput. Ind. Eng. 2017, 110, 75–82. [Google Scholar] [CrossRef]
  200. Shen, X.N.; Minku, L.L.; Marturi, N.; Guo, Y.N.; Han, Y. A q-learning-based memetic algorithm for multi-objective dynamic software project scheduling. Inf. Sci. 2018, 428, 1–29. [Google Scholar] [CrossRef]
  201. Alem, D.; Rocha, A.D.; Barata, J. Smart manufacturing scheduling approaches—Systematic review and future directions. Appl. Sci. 2021, 11, 2186. [Google Scholar] [CrossRef]
  202. Chaudhry, I.A.; Khan, A.A. A research survey: Review of flexible job shop scheduling techniques. Int. Trans. Oper. Res. 2016, 23, 551–591. [Google Scholar] [CrossRef]
  203. Karimi-Mamaghan, M.; Mohammadi, M.; Meyer, P.; Karimi-Mamaghan, A.M.; Talbi, E.G. Machine learning at the service of meta-heuristics for solving combinatorial optimization problems: A state-of-the-art. Eur. J. Oper. Res. 2022, 296, 393–422. [Google Scholar] [CrossRef]
  204. Rosen, M.A.; Kishawy, H.A. Sustainable manufacturing and design: Concepts, practices and needs. Sustainability 2012, 4, 154–174. [Google Scholar] [CrossRef]
Electronics 14 01663 g001
Figure 1. Categories of job shop scheduling problems (JSSPs), including single-machine, parallel machine, flexible job shop, and flow shop types.
Figure 1. Categories of job shop scheduling problems (JSSPs), including single-machine, parallel machine, flexible job shop, and flow shop types.
Electronics 14 01663 g001
Electronics 14 01663 g002
Figure 2. Summary of optimisation methods applied to scheduling problems.
Figure 2. Summary of optimisation methods applied to scheduling problems.
Electronics 14 01663 g002
Table 1. Application of different optimisation methods on FJSPs.
Table 1. Application of different optimisation methods on FJSPs.
ReferenceYearMethod
[43]2009Hybrid approach combining PSO and TS
[44]2010Knowledge-based ant colony optimisation
(ACO)
[45]2011GA
[46]2017Multi-agent-based Particle swarm optimisation (PSO) and a two-stage PSO
[47]2017Hybrid ABC based on Tabu Search (TS)
[48]2018Multi-objective evolutionary algorithm
[49]2019
[50]2019Novel Metaheuristic (MH) method
[51]2020Effective search algorithm
[52]2020RL (RL)
[37]2020Self-learning genetic algorithm (GA)
[53]2021Advanced GA
[54]2021Hybrid GA and TS
[55]2022Novel approach for FJSPs
[56]2022Improved GA
[7]2022A hybrid iterated greedy algorithm
[19]2022Hybrid scheduling measures
[57]2024stochastic machine breakdowns by an improved tuna swarm optimiser
[58]2024An improved genetic programming hyperheuristic
[59]2024An improved GA with an overlapping strategy
[60]2024Whale optimisation algorithm
[61]2024A new artificial bee colony algorithm
[62]2024A novel col-laboratory agent RL framework
[63]2024A discrete event simulator to implement deep re-RL
[64]2024Multi-resource constrained
[65]2024Evolutionary algorithm incorporating RL
Table 2. Application of different types of selections of GA on FJSPs.
Table 2. Application of different types of selections of GA on FJSPs.
ReferenceYearAlgorithmSelection Types
[91]1996GAAgeing
[92]2001GAFittest
[93]2003GAFittest
[94]2003GASexual selection
[95]2006GAElitism
[96]2005GAElitism
[97]2008GATournament
[98]2008GA + TSTournament selection
[99]2009GALinear ranking
[100]2010GARandom
[101]2010PSO + GAHybrid
[102]2010GA + TSHybrid
[103]2010ParthenogeneticRoulette wheel
[104]2011GATournament selection
[105]2011GA + SARoulette wheel
[106]2011GA + ACOLinear scaling, stochastic universal sampling
[107]2012GAElitism
[108]2012GA + PSORoulette wheel
[109]2014GATournament selection
[110]2014GARoulette wheel
[111]2015GARoulette wheel
[112]2015GARoulette wheel
[113]2015GA + TSTournament selection
[114]2015Improved parthenogeneticGreedy selection
[115]2016Neighbourhood GA + TSFitness neighbourhood selection operator
[116]2016A Heuristics-based
parthenogenetic		Roulette wheel selection
[117]2017GATournament selection
[118]2017A hybrid GAElitism
[119]2018ParthenogeneticParthenogenetic
[120]2018List-scheduling-based multiobjective parthenogenetic (LS-MPGA)Pareto-Ranking and Selection
[121]2019GATournament selection
[122]2019RCGARoulette wheel
[123]2020GATournament selection
[124]2020Parthenogenetic algorithmParthenogenetic
[125]2022Hybrid immune GA with
TS		Tournament, Roulette-wheel,
linear-rank
[123]2020IGAMaximum priority selection method for remaining processing time
[126]2021Learning interactive GAEdge selection encoding
[127]2021Adaptive GA based on individual similarityBinary tournament
[128]2021ParthenogeneticParthenogenetic
[129]2022GIFARanking based on Fitness
[130]2022Taguchi methodGA and Parthenogenetic
[56]2022MILP and IGATwo-vector encoding scheme to represent the configuration selection and operation sequencing
[131]2022Elite GABinary tournament selection and the elitism method
[132]2023HGAA hybrid selection of tournament selection and elite selection
[133]2023Improved GA with a population diversity check methodElitist selection and the binary tournament selection
[134]2023MGA multi-start GABased on random parthenogenetic algorithm
[58]2024An improved genetic programmingHyper-heuristic
[59]2024An improved GAAn overlapping strategy
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Momenikorbekandi, A.; Kalganova, T. Intelligent Scheduling Methods for Optimisation of Job Shop Scheduling Problems in the Manufacturing Sector: A Systematic Review. Electronics 2025, 14, 1663. https://doi.org/10.3390/electronics14081663

AMA Style

Momenikorbekandi A, Kalganova T. Intelligent Scheduling Methods for Optimisation of Job Shop Scheduling Problems in the Manufacturing Sector: A Systematic Review. Electronics. 2025; 14(8):1663. https://doi.org/10.3390/electronics14081663

Chicago/Turabian Style

Momenikorbekandi, Atefeh, and Tatiana Kalganova. 2025. "Intelligent Scheduling Methods for Optimisation of Job Shop Scheduling Problems in the Manufacturing Sector: A Systematic Review" Electronics 14, no. 8: 1663. https://doi.org/10.3390/electronics14081663

APA Style

Momenikorbekandi, A., & Kalganova, T. (2025). Intelligent Scheduling Methods for Optimisation of Job Shop Scheduling Problems in the Manufacturing Sector: A Systematic Review. Electronics, 14(8), 1663. https://doi.org/10.3390/electronics14081663

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop