A Review of Battery Electric Public Transport Timetabling and Scheduling: A 10 Year Retrospective and New Developments
Abstract
1. Introduction
2. Research Method
3. EV Timetabling
- Timetabling to meet specific demand patterns;
- Timetabling to minimize waiting times;
- Timetabling to maximize synchronous events;
- Timetabling with multi-objective optimization.
4. Electric Vehicle Scheduling
4.1. Exact Methods for Solving EVSPs
4.2. Heuristic Methods for Handling EVSPs
4.3. Machine Learning Methods Applied to EVSPs
4.4. Other Methods to Cope with EVSPs
4.5. Extended Research Directions to Optimize EVSPs
5. The Integration of Electric Vehicle Scheduling and Timetabling
5.1. Exact Methods
5.2. Heuristic Methods
6. Conclusions and Future Research Directions
6.1. Robust Scheduling and Dynamic Adjustment
6.2. Integration of Multiple Planning Processes
6.3. Application of Intelligent Algorithms and Techniques
6.4. Combined with New Traffic Modes
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Han, Y.; Peng, J.; Wang, Y. Vehicle and charging scheduling of electric bus fleets: A comprehensive review. J. Intell. Connect. Veh. 2023, 6, 116–124. [Google Scholar] [CrossRef]
- Häll, C.H.; Ceder, A.; Ekström, J.; Quttineh, N.H. Adjustments of public transit operations planning process for the use of electric buses. J. Intell. Transp. Syst. 2019, 23, 216–230. [Google Scholar] [CrossRef]
- Ibarra-Rojas, O.J.; Delgado, F.; Giesen, R.; Muñoz, J.C. Planning, operation, and control of bus transport systems: A literature review. Transp. Res. Part B Methodol. 2015, 77, 38–75. [Google Scholar] [CrossRef]
- Behnia, F.; Schuelke-Leech, B.A.; Mirhassani, M. Optimizing sustainable urban mobility: A comprehensive review of electric bus scheduling strategies and future directions. Sustain. Cities Soc. 2024, 105497. [Google Scholar] [CrossRef]
- Kalakanti, A.K.; Rao, S. Computational challenges and approaches for electric vehicles. ACM Comput. Surv. 2023, 55, 1–35. [Google Scholar] [CrossRef]
- Perumal, S.S.; Lusby, R.M.; Larsen, J. Electric bus planning & scheduling: A review of related problems and methodologies. Eur. J. Oper. Res. 2022, 301, 395–413. [Google Scholar]
- Liu, T.; Ceder, A. Synchronization of public transport timetabling with multiple vehicle types. Transp. Res. Rec. 2016, 2539, 84–93. [Google Scholar] [CrossRef]
- Zhang, S.; Ceder, A.; Cao, Z. Integrated optimization for feeder bus timetabling and procurement scheme with consideration of environmental impact. Comput. Ind. Eng. 2020, 145, 106501. [Google Scholar] [CrossRef]
- Hu, B.; Fu, Y.; Feng, S. Integrated optimization of multi-vehicle-type timetabling and scheduling to accommodate periodic passenger flow. Comput.-Aided Civ. Infrastruct. Eng. 2023, 38, 1973–1997. [Google Scholar] [CrossRef]
- Tang, C.; Ge, Y.E.; Xue, H.; Ceder, A.; Wang, X. Optimal selection of vehicle types for an electric bus route with shifting departure times. Int. J. Sustain. Transp. 2023, 17, 1217–1235. [Google Scholar] [CrossRef]
- Quttineh, N.H.; Häll, C.H.; Ekström, J.; Ceder, A.A. Integrated solution for electric bus timetabling and vehicle scheduling combined with choices of charging locations. J. Public Transp. 2023, 25, 100055. [Google Scholar] [CrossRef]
- Duan, M.; Liao, F.; Qi, G.; Guan, W. Integrated optimization of electric bus scheduling and charging planning incorporating flexible charging and timetable shifting strategies. Transp. Res. Part C Emerg. Technol. 2023, 152, 104175. [Google Scholar] [CrossRef]
- Liu, T.; Cats, O.; Gkiotsalitis, K. A review of public transport transfer coordination at the tactical planning phase. Transp. Res. Part C Emerg. Technol. 2021, 133, 103450. [Google Scholar] [CrossRef]
- Gkiotsalitis, K.; Alesiani, F. Robust timetable optimization for bus lines subject to resource and regulatory constraints. Transp. Res. Part E Logist. Transp. Rev. 2019, 128, 30–51. [Google Scholar] [CrossRef]
- Cao, Z.; Ceder, A.; Zhang, S. Real-time schedule adjustments for autonomous public transport vehicles. Transp. Res. Part C Emerg. Technol. 2019, 109, 60–78. [Google Scholar] [CrossRef]
- Cao, Z.; Ceder, A. Autonomous shuttle bus service timetabling and vehicle scheduling using skip-stop tactic. Transp. Res. Part C Emerg. Technol. 2019, 102, 370–395. [Google Scholar] [CrossRef]
- Zhang, W.; Xia, D.; Liu, T.; Fu, Y.; Ma, J. Optimization of single-line bus timetables considering time-dependent travel times: A case study of Beijing, China. Comput. Ind. Eng. 2021, 158, 107444. [Google Scholar] [CrossRef]
- Gkiotsalitis, K. Bus holding of electric buses with scheduled charging times. IEEE Trans. Intell. Transp. Syst. 2020, 22, 6760–6771. [Google Scholar] [CrossRef]
- Abdelwahed, A.; van den Berg, P.L.; Brandt, T.; Collins, J.; Ketter, W. Evaluating and optimizing opportunity fast-charging schedules in transit battery electric bus networks. Transp. Sci. 2020, 54, 1601–1615. [Google Scholar] [CrossRef]
- Abdelwahed, A.; van den Berg, P.L.; Brandt, T.; Ketter, W.; Mulder, J. A boost for urban sustainability: Optimizing electric transit bus networks in Rotterdam. Inf. J. Appl. Anal. 2021, 51, 391–407. [Google Scholar] [CrossRef]
- Raman, G.; Raman, G.; Peng, J.C.H. Resilience of urban public electric vehicle charging infrastructure to flooding. Nat. Commun. 2022, 13, 3213. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Chen, X. Optimizing battery electric bus transit vehicle scheduling with battery exchanging: Model and case study. Procedia Soc. Behav. Sci. 2013, 96, 2725–2736. [Google Scholar]
- Li, J.Q. Transit bus scheduling with limited energy. Transp. Sci. 2014, 48, 521–539. [Google Scholar] [CrossRef]
- Wen, M.; Linde, E.; Ropke, S.; Mirchandani, P.; Larsen, A. An adaptive large neighborhood search heuristic for the electric vehicle scheduling problem. Comput. Oper. Res. 2016, 76, 73–83. [Google Scholar] [CrossRef]
- Yao, E.; Liu, T.; Lu, T.; Yang, Y. Optimization of electric vehicle scheduling with multiple vehicle types in public transport. Sustain. Cities Soc. 2020, 52, 101862. [Google Scholar] [CrossRef]
- Alwesabi, Y.; Wang, Y.; Avalos, R.; Liu, Z. Electric bus scheduling under single depot dynamic wireless charging infrastructure planning. Energy 2020, 213, 118855. [Google Scholar] [CrossRef]
- Wang, J.; Kang, L.; Liu, Y. Optimal scheduling for electric bus fleets based on dynamic programming approach by considering battery capacity fade. Renew. Sustain. Energy Rev. 2020, 130, 109978. [Google Scholar] [CrossRef]
- Wang, C.; Guo, C.; Zuo, X. Solving multi-depot electric vehicle scheduling problem by column generation and genetic algorithm. Appl. Soft Comput. 2021, 112, 107774. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Qu, X. Optimal electric bus fleet scheduling considering battery degradation and non-linear charging profile. Transp. Res. Part E Logist. Transp. Rev. 2021, 154, 102445. [Google Scholar] [CrossRef]
- Lee, S.; Boomsma, T.K. An approximate dynamic programming algorithm for short-term electric vehicle fleet operation under uncertainty. Appl. Energy 2022, 325, 119793. [Google Scholar] [CrossRef]
- Guo, R.; Guan, W.; Vallati, M.; Zhang, W. Modular Autonomous Electric Vehicle Scheduling for Customized On-Demand Bus Services. IEEE Trans. Intell. Transport. Syst. 2023, 24, 10055–10066. [Google Scholar] [CrossRef]
- Shen, Y.; Li, Y.; Chen, C.; Li, J. Electric vehicle scheduling based on stochastic trip time and energy consumption. Comput. Ind. Eng. 2023, 177, 109071. [Google Scholar] [CrossRef]
- Vendé, P.; Desaulniers, G.; Kergosien, Y.; Mendoza, J.E. Matheuristics for a multi-day electric bus assignment and overnight recharge scheduling problem. Transp. Res. Part C Emerg. Technol. 2023, 156, 104360. [Google Scholar] [CrossRef]
- Cao, Z.; Mao, Z.; Wang, Y.; Zhang, S. Multi-type electric vehicle scheduling optimization considering load capacity, battery-allowed mileage, and recharging duration. Electronics 2023, 12, 4655. [Google Scholar] [CrossRef]
- Xie, D.F.; Yu, Y.P.; Zhou, G.J.; Zhao, X.M.; Chen, Y.J. Collaborative optimization of electric bus line scheduling with multiple charging modes. Transp. Res. Part D Transp. Environ. 2023, 114, 103551. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, H.; Xu, Y.; Sun, H. Learning-based real-time aggregate flexibility provision and scheduling of electric vehicles. IEEE Trans. Smart Grid 2024, 15, 5840–5852. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z. Distributionally robust evaluation for real-time flexibility of electric vehicles considering uncertain departure behavior and State-of-Charge. IEEE Trans. Smart Grid. 2024, 15, 4288–4291. [Google Scholar] [CrossRef]
- de Vos, M.H.; van Lieshout, R.N.; Dollevoet, T. Electric vehicle scheduling in public transit with capacitated charging stations. Transp. Sci. 2024, 58, 279–294. [Google Scholar] [CrossRef]
- Lu, Z.; Xing, T.; Li, Y. Optimization of electric bus vehicle scheduling and charging strategies under Time-of-Use electricity price. Transp. Res. Part E Logist. Transp. Rev. 2025, 196, 104021. [Google Scholar] [CrossRef]
- Ribeiro, C.C.; Soumis, F. A column generation approach to the multipledepot vehicle scheduling problem. Oper. Res. 1994, 42, 41–52. [Google Scholar] [CrossRef]
- Fescioglu-Unver, N.; Aktaş, M.Y. Electric vehicle charging service operations: A review of machine learning applications for infrastructure planning, control, pricing and routing. Renew. Sustain. Energy Rev. 2023, 188, 113873. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, C.K.; Yan, X.; Wang, H. Reinforcement learning for electric vehicle charging scheduling: A systematic review. Transp. Res. Part E Logist. Transp. Rev. 2024, 190, 103698. [Google Scholar] [CrossRef]
- Lu, Y.; Fang, S.; Niu, T.; Liao, R. Energy-transport scheduling for green vehicles in seaport areas: A review on operation models. Renew. Sustain. Energy Rev. 2023, 184, 113443. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Wang, Y.; Yu, B.; Tang, T. Charging facility planning and scheduling problems for battery electric bus systems: A comprehensive review. Transp. Res. Part E Logist. Transp. Rev. 2024, 183, 103463. [Google Scholar] [CrossRef]
- Shen, Y.; Li, Y. Minimum Cost Flow-Based Integrated Model for Electric Vehicle and Crew Scheduling. J. Adv. Transp. 2023, 2023, 6658030. [Google Scholar] [CrossRef]
- Jiang, Y.; He, T. Optimal Charging Scheduling and Management with Bus-Driver-Trip Assignment considering Mealtime Windows for an Electric Bus Line. Complexity 2022, 2022, 3087279. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Chang, A.; Song, C. Collaborative optimization of vehicle and crew scheduling for a mixed fleet with electric and conventional buses. Sustainability 2022, 14, 3627. [Google Scholar] [CrossRef]
- Perumal, S.S.; Dollevoet, T.; Huisman, D.; Lusby, R.M.; Larsen, J.; Riis, M. Solution approaches for integrated vehicle and crew scheduling with electric buses. Comput. Oper. Res. 2021, 132, 105268. [Google Scholar] [CrossRef]
- Sistig, H.M.; Sauer, D.U. Metaheuristic for the integrated electric vehicle and crew scheduling problem. Appl. Energy 2023, 339, 120915. [Google Scholar] [CrossRef]
- Cong, Y.; Bie, Y.; Liu, Z.; Zhu, A. Collaborative vehicle-crew scheduling for multiple routes with a mixed fleet of electric and fuel buses. Energy 2024, 298, 131400. [Google Scholar] [CrossRef]
- Govinda Raja Perumal, S.S.; Lusby, R.M.; Larsen, J. A Review of Integrated Approaches for Optimizing Electric Vehicle and Crew Schedules. 2020. Available online: https://orbit.dtu.dk/en/publications/a-review-of-integrated-approaches-for-optimizing-electric-vehicle (accessed on 17 April 2025).
- Schmid, V.; Ehmke, J.F. Integrated timetabling and vehicle scheduling with balanced departure times. OR Spectr. 2015, 37, 903–928. [Google Scholar] [CrossRef]
- Mertens, L.; Amberg, B.; Kliewer, N. Integrated Bus Timetabling, Vehicle Scheduling, and Crew Scheduling with a mutation-based evolutionary scheme. Transp. Res. Procedia 2024, 78, 7–15. [Google Scholar] [CrossRef]
- Gkiotsalitis, K.; Iliopoulou, C.; Kepaptsoglou, K. An exact approach for the multi-depot electric bus scheduling problem with time windows. Eur. J. Oper. Res. 2023, 306, 189–206. [Google Scholar] [CrossRef]
- Xu, X.; Yu, Y.; Long, J. Integrated electric bus timetabling and scheduling problem. Transp. Res. Part C Emerg. Technol. 2023, 149, 104057. [Google Scholar] [CrossRef]
- Teng, J.; Chen, T.; Fan, W. Integrated approach to vehicle scheduling and bus timetabling for an electric bus line. J. Transp. Eng. Part A Syst. 2020, 146. [Google Scholar]
- Qiao, J.; Li, S.; Liu, M.; Yang, Z.; Chen, J.; Liu, P.; Li, H.; Ma, C. A modified particle swarm optimization algorithm for a vehicle scheduling problem with soft time windows. Sci. Rep. 2023, 13, 18351. [Google Scholar] [CrossRef]
- Fan, D.; Feng, Q.; Zhang, A.; Liu, M.; Ren, Y.; Wang, Y. Optimization of scheduling and timetabling for multiple electric bus lines considering nonlinear energy consumption model. IEEE Trans. Intell. Transp. Syst. 2023, 25, 5342–5355. [Google Scholar] [CrossRef]
- Gao, W.; Lu, S.; Liu, K.; Li, D. Integrated optimization of timetabling and vehicle scheduling for pure electric buses considering multiple depots and vehicle types. Comput. Ind. Eng. 2025, 201, 110833. [Google Scholar] [CrossRef]
- Zattoni Scroccaro, P.; van Beek, P.; Mohajerin Esfahani, P.; Atasoy, B. Inverse optimization for routing problems. arXiv 2024, arXiv:2307.07357. [Google Scholar] [CrossRef]
- Molenbruch, Y.; Braekers, K.; Eisenhandler, O.; Kaspi, M. The electric dial-a-ride problem on a fixed circuit. Transp. Sci. 2023, 57, 594–612. [Google Scholar] [CrossRef]
- Cao, Z.; Zhang, S.; Ceder, A. Novel coupling–decoupling strategy for scheduling autonomous public transport vehicles in overcrowded corridors. Appl. Math. Model. 2022, 106, 299–324. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, Y.; Li, X. Modular Autonomous Electric Vehicle scheduling for demand-responsive transit services with modular charging strategy. Adv. Eng. Inform. 2025, 65, 103114. [Google Scholar] [CrossRef]
- Chang, A.; Cong, Y.; Wang, C.; Bie, Y. Optimal Vehicle Scheduling and Charging Infrastructure Planning for Autonomous Modular Transit System. Sustainability 2024, 16, 3316. [Google Scholar] [CrossRef]
- Oargă, I.T.; Prunean, G.; Varga, B.O.; Moldovanu, D.; Micu, D.D. Comparative Analysis of Energy Efficiency between Battery Electric Buses and Modular Autonomous Vehicles. Appl. Sci. 2024, 14, 4389. [Google Scholar] [CrossRef]
- Hong, Y.; Xu, M.; Jin, Y.; Wang, S. Data-Driven Modular Vehicle Scheduling in Scenic Areas. Appl. Sci. 2024, 15, 205. [Google Scholar] [CrossRef]
- Liu, T.; Ceder, A.; Rau, A. Using deficit function to determine the minimum fleet size of an autonomous modular public transit system. Transp. Res. Rec. 2020, 2674, 532–541. [Google Scholar] [CrossRef]
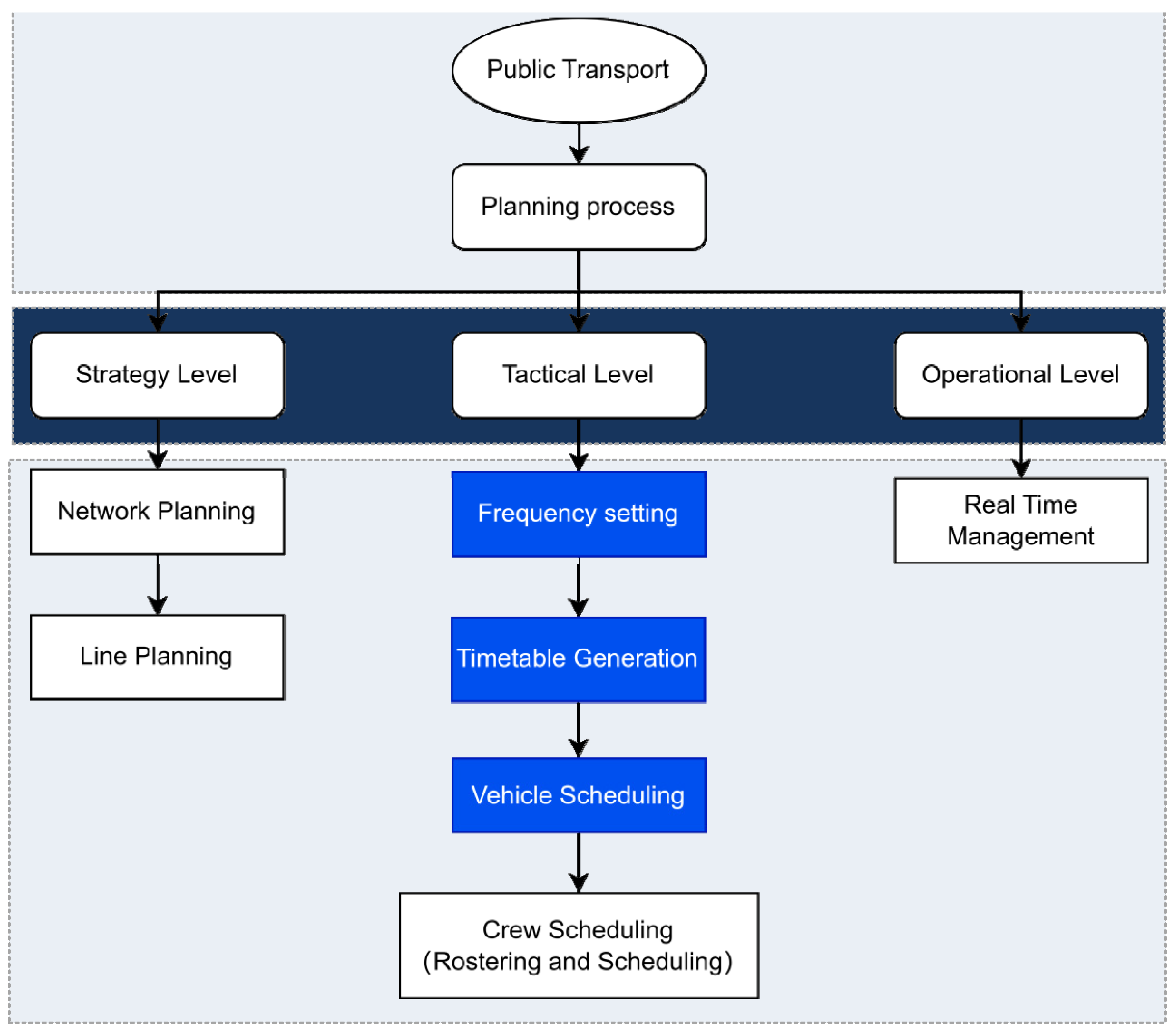

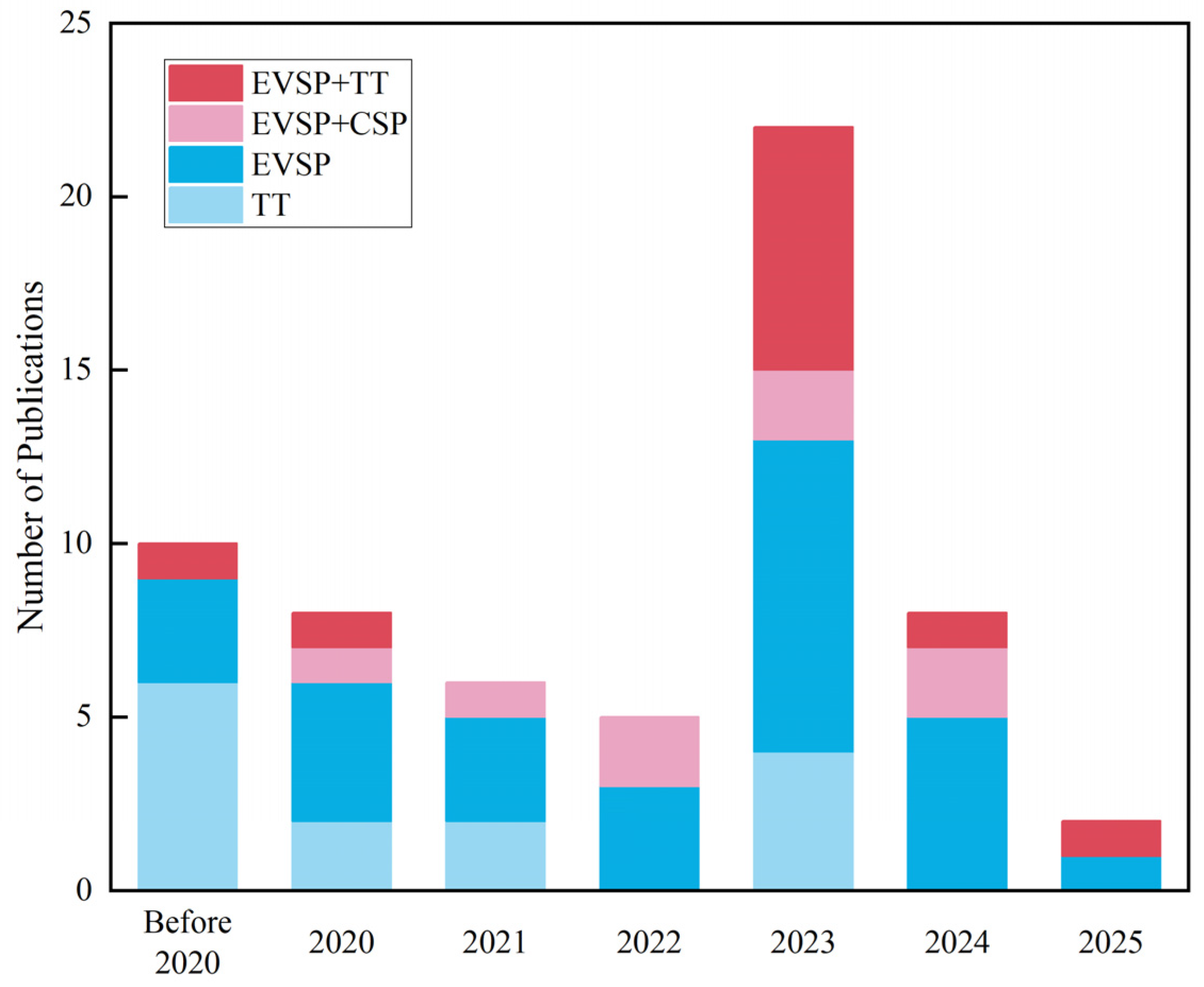


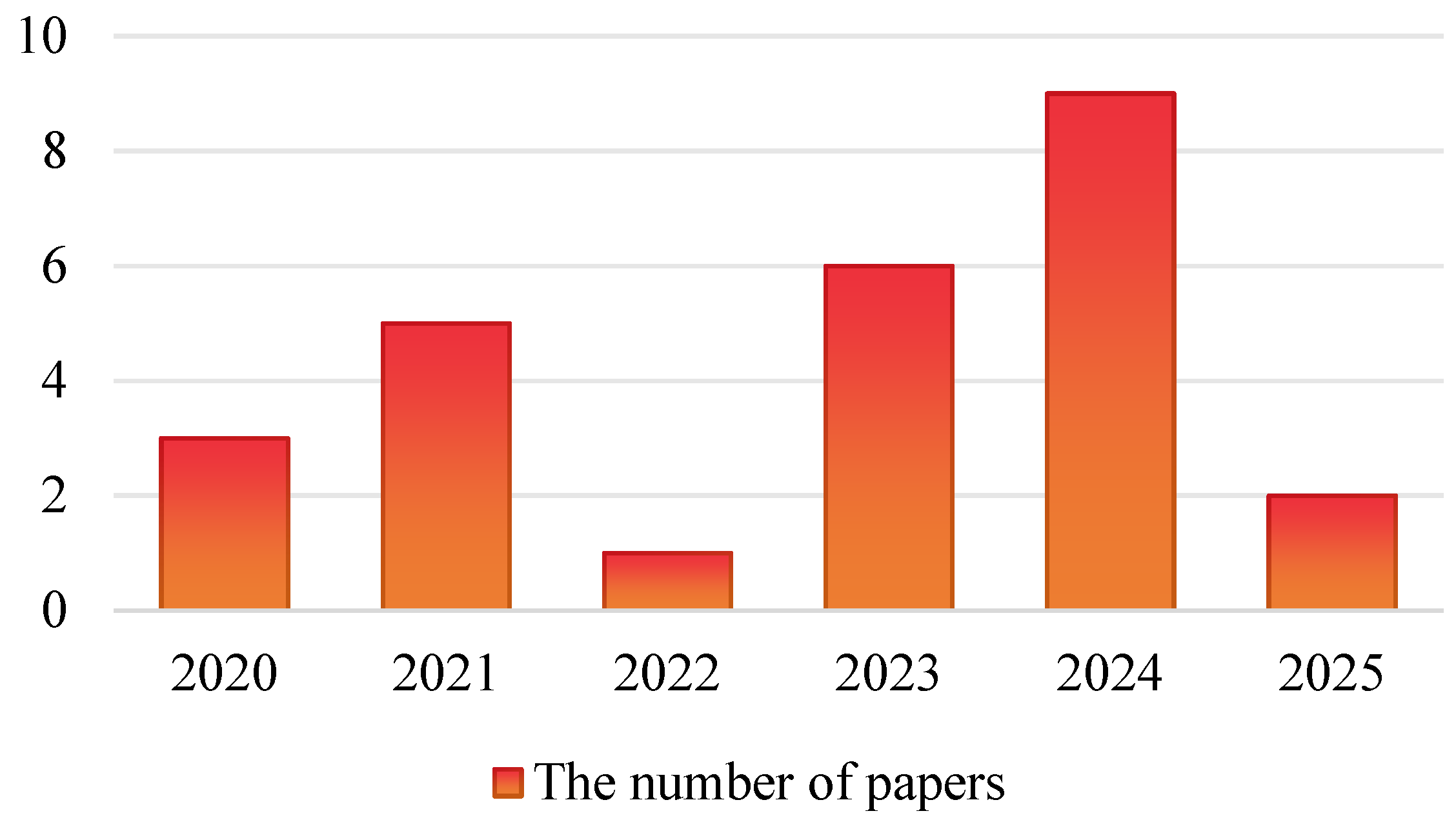
| Charging Modes | Timetabling | Vehicle Scheduling |
|---|---|---|
| Quick charging | √ | √ |
| Overnight charging | × | √ |
| Continuous charging (i.e., charging during driving) | × | × |
| Publication | Objective(s) | Model | Solution Type | Solution Method | |||
|---|---|---|---|---|---|---|---|
| Ex | Hu | ML | Others | ||||
| Zhu and Chen (2013) [22] | to minimize the capital investment for the electric fleet and the total charging demand in stations | A multi-objective model | √ | NSGA-II | |||
| Li (2014) [23] | to minimize total operational costs | ILP | √ | √ | BP+a truncated CG heuristic algorithm | ||
| Wen et al. (2016) [24] | to minimize the number of vehicles and the total traveling distance | MIP | √ | ALNS | |||
| Yao et al. (2020) [25] | to minimize annual total scheduling costs | MILP | √ | A heuristic procedure based on the GA | |||
| Alwesabi et al. (2020) [26] | to find the minimum total cost | MIQCP | √ | Julia–Gurobi solver | |||
| Wang et al. (2020) [27] | to minimize battery replacement costs | An optimal scheduling method based on dynamic programming | √ | Dynamic programming with a reverse-order matching strategy | |||
| Wang et al. (2021) [28] | to minimize the total cost | A connection network model | √ | GA + CG | |||
| Zhang et al. (2021) [29] | to minimize the total operational cost of the transit system | A set partitioning model | √ | BP | |||
| Lee and Boomsma (2022) [30] | to minimize the total cost | An MDP using DP | √ | ADP, the LSMC method | |||
| Guo et al. (2023) [31] | to minimize the operating costs | MIP based on space–time–state framework | √ | A Lagrangian relaxation algorithm and a dedicated dynamic dispatching procedure | |||
| Shen et al. (2023) [32] | to minimize the fleet size and operating cost and maximize on-time performance | A probabilistic model for EVSPs based on the probability density function of trip time | √ | ALNS | |||
| Vendé et al. (2023) [33] | to minimize the total charging costs | MIP | √ | AtS and D-AtS heuristic algorithm | |||
| Cao et al. (2023) [34] | to minimize the fleet size, idle mileage, and charging cost | MINLP | √ | A preprocessing-based GA | |||
| Xie et al. (2023) [35] | to minimize the total cost for bus companies | MINLP | √ | A two-stage solution algorithm based on ‘Generation and Selection’ | |||
| Zhang et al. (2024) [36] | to maximize the profit | —— | √ | M-SAC | |||
| Li and Li (2024) [37] | —— | A distributionally robust real-time flexibility evaluation model | √ | CPLEX or Gurobi | |||
| De Vos et al. (2024) [38] | to minimize the total costs | Path-based binary programming model based on a connected network | √ | Two heuristic algorithms based on CG (price and branch and diving heuristic) | |||
| Lu et al. (2025) [39] | to minimize the total cost | MIP model | √ | DLS-BP | |||
| Publication (Chronologically) | Objective(s) | Model | Solution Type | Solution Method | |
|---|---|---|---|---|---|
| Ex | Hu | ||||
| Teng et al. (2020) [56] | To minimize the number of vehicles and total charging costs | A multi-objective optimization model for a single bus line operated with electric buses | √ | MOPSO algorithm | |
| Gkiotsalitis et al. (2023) [54] | To minimize the total cost | MINLP | √ | Commericial solver with linearization and valid inequalities | |
| Duan et al. (2023) [12] | To minimize the total costs considering the power grid pressure cost | An integrated arc-based model | √ | CG and two timetable-shifting algorithms | |
| Quttineh et al. (2023) [11] | To minimize the number of buses (the number of arcs leaving the depot) | MIP | √ | MIP solver complex | |
| Tang et al. (2023) [10] | To minimize the total cost to users and operators | Nonlinear non-convex integer programming model | √ | GA associated with the right shifting of departure time | |
| Xu et al. (2023) [55] | To maximize the total profit | A multi-commodity network flow model based on a time–space network framework | √ | A Lagrangian relaxation heuristic algorithm | |
| Fan et al. (2023) [58] | To minimize the number of vehicles and total operation costs | Multi-objective MINLP | √ | An improved PSO algorithm | |
| Gao et al. (2025) [59] | To minimize the mixed cost, including passenger travel cost and bus enterprise operating cost | A data-driven multi-objective optimization model | √ | An improved NSGA-II algorithm | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, S.; Liu, L.; Gong, P.; Lu, W.; Wu, F.; Gu, J.; Li, Y.; Cao, Z. A Review of Battery Electric Public Transport Timetabling and Scheduling: A 10 Year Retrospective and New Developments. Electronics 2025, 14, 1694. https://doi.org/10.3390/electronics14091694
Wang Y, Zhang S, Liu L, Gong P, Lu W, Wu F, Gu J, Li Y, Cao Z. A Review of Battery Electric Public Transport Timetabling and Scheduling: A 10 Year Retrospective and New Developments. Electronics. 2025; 14(9):1694. https://doi.org/10.3390/electronics14091694
Chicago/Turabian StyleWang, Yaoyao, Shun Zhang, Liang Liu, Ping Gong, Weike Lu, Fuwei Wu, Jinggang Gu, Yuxuan Li, and Zhichao Cao. 2025. "A Review of Battery Electric Public Transport Timetabling and Scheduling: A 10 Year Retrospective and New Developments" Electronics 14, no. 9: 1694. https://doi.org/10.3390/electronics14091694
APA StyleWang, Y., Zhang, S., Liu, L., Gong, P., Lu, W., Wu, F., Gu, J., Li, Y., & Cao, Z. (2025). A Review of Battery Electric Public Transport Timetabling and Scheduling: A 10 Year Retrospective and New Developments. Electronics, 14(9), 1694. https://doi.org/10.3390/electronics14091694








