Ground-Moving Target Relocation for a Lightweight Unmanned Aerial Vehicle-Borne Radar System Based on Doppler Beam Sharpening Image Registration
Abstract
1. Introduction
- We construct a moving target relocation model that accounts for UAV platform errors.
- We first use the image registration method to register DBS images and SAR images for moving target relocation.
- We propose a new matching algorithm to compensate for the match error between DBS images and SAR images. In the algorithm, we first analyze the geometric distortions of DBS images and add a negative second-order term of distance in the matching algorithm. Experimental results demonstrate that the proposed algorithm can indeed improve the accuracy of moving target relocation.
2. Background
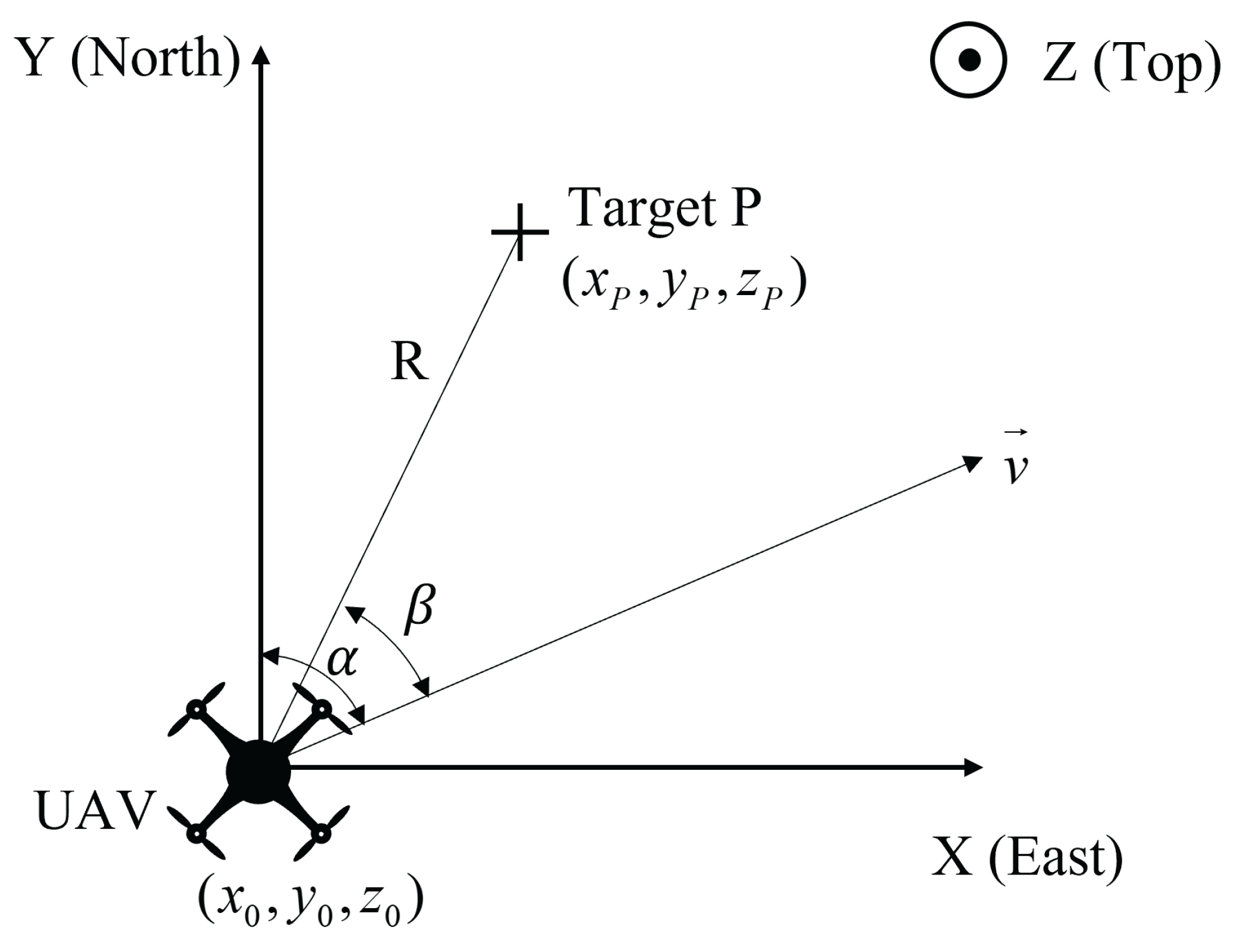
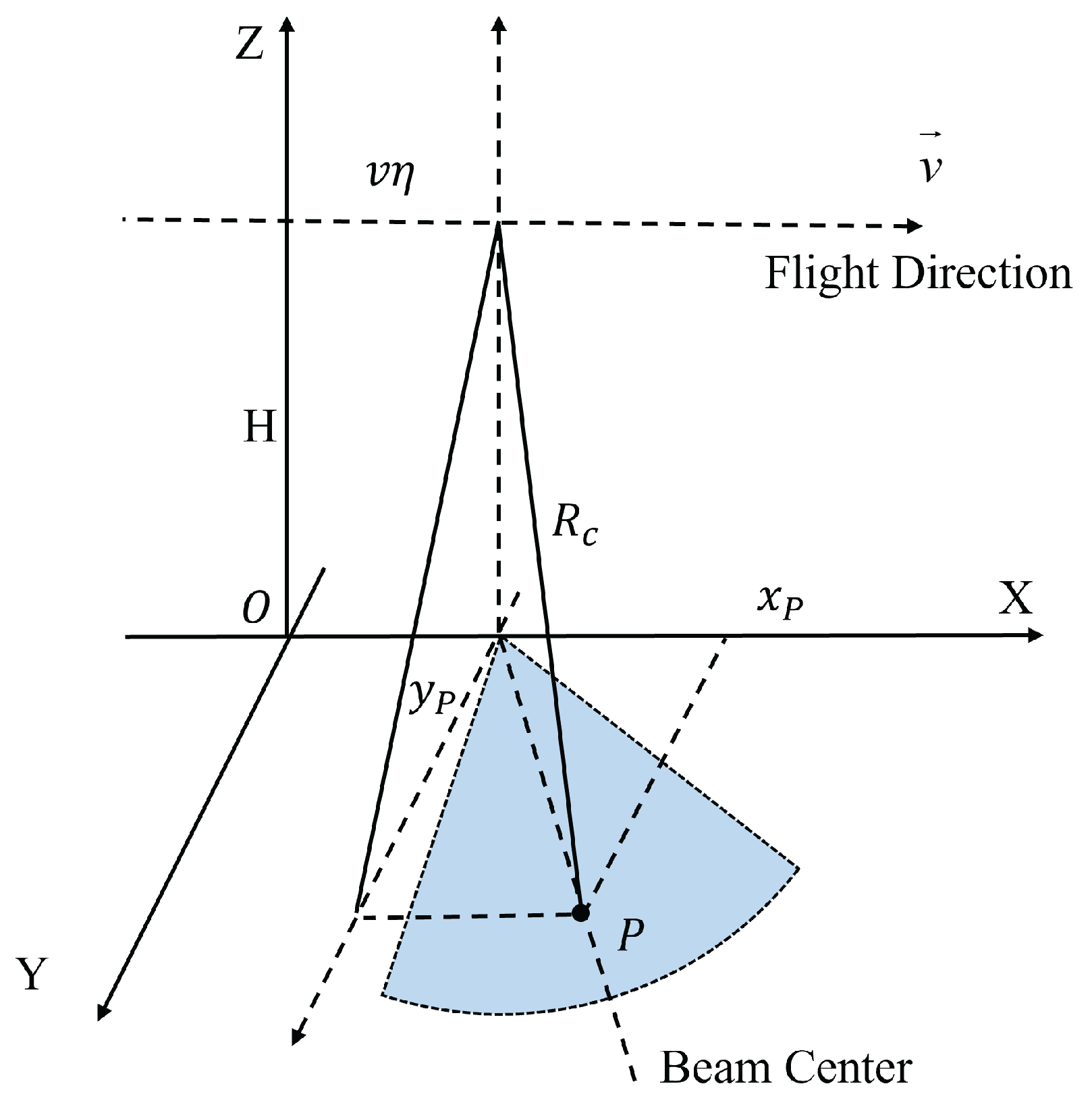
2.1. Moving Target Relocation Model
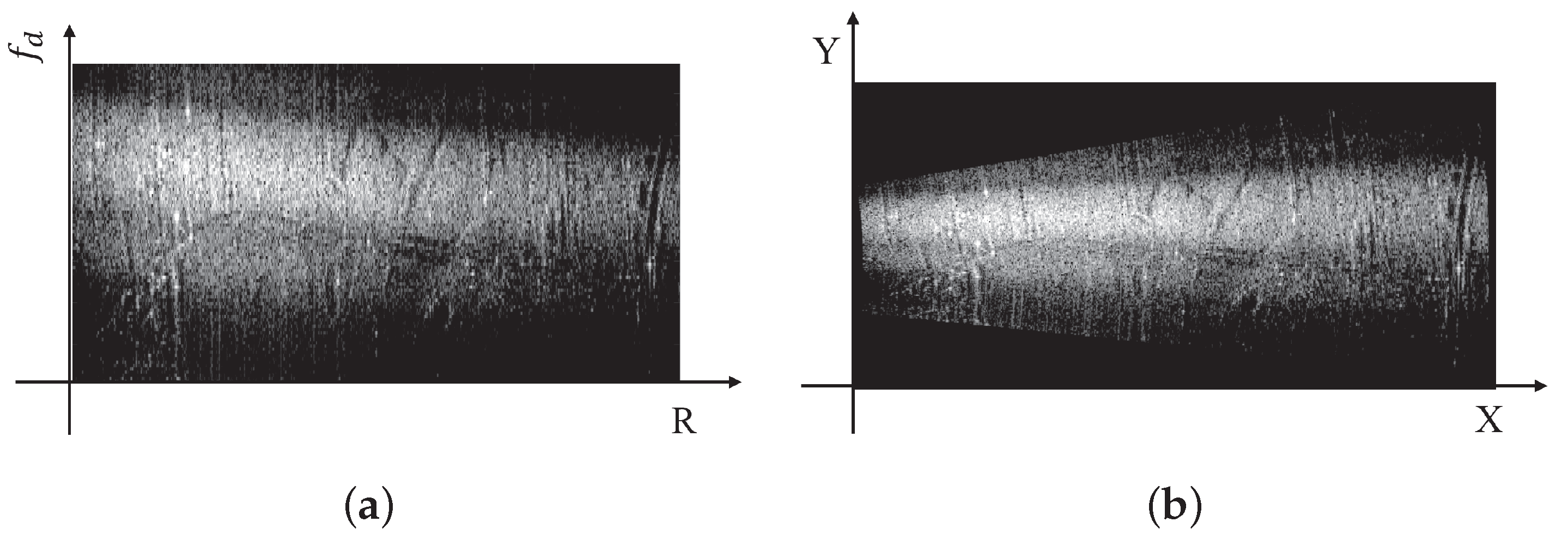
2.2. Doppler Beam Sharpening Image Acquisition and Stitching
2.3. Limitations in DBS-SAR Image Registration
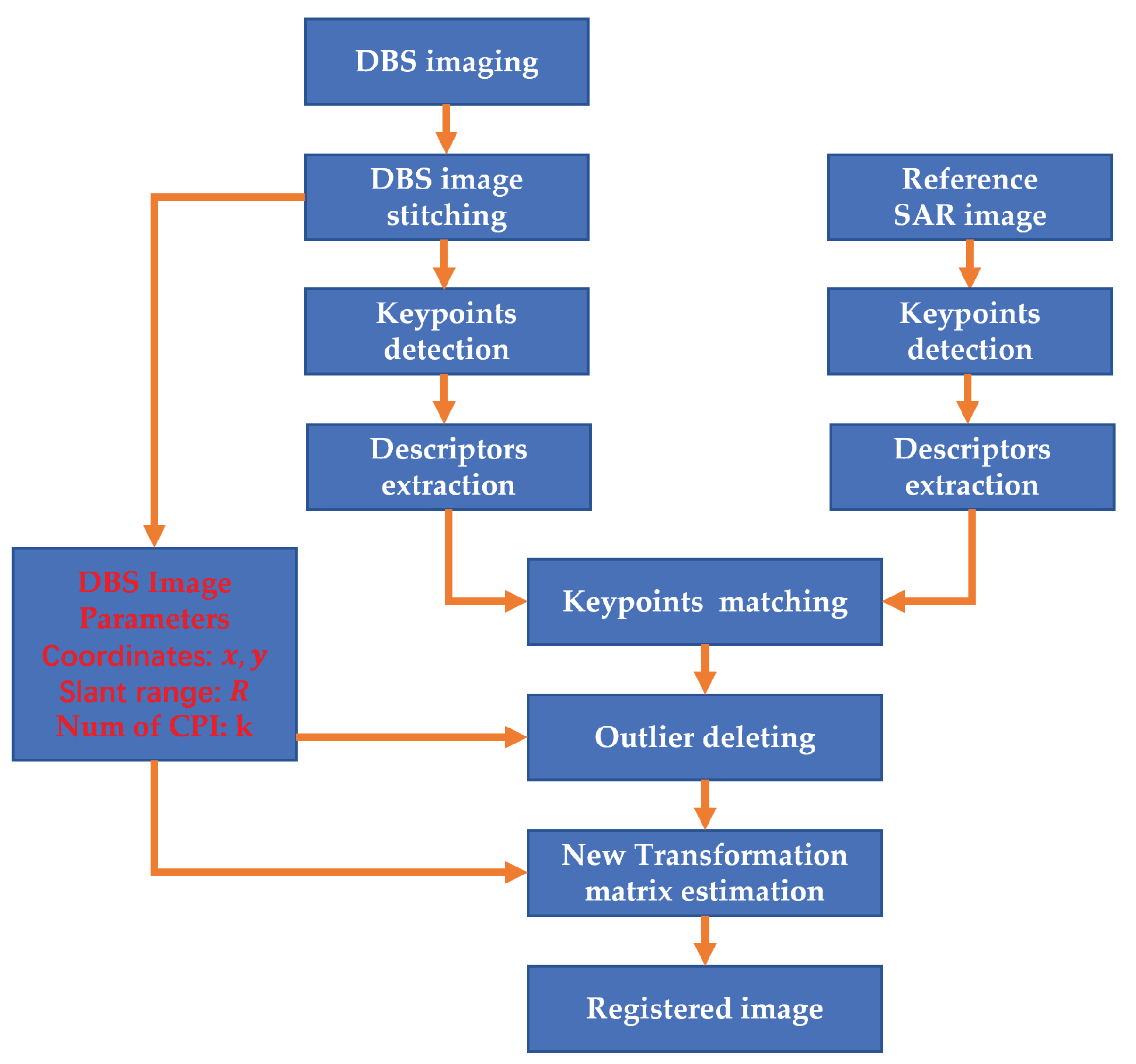
3. An Improved Matching Algorithm for DBS Images and SAR Images
3.1. Geometric Distortions in SAR Images and DBS Images
3.2. The New Matching Algorithm
4. Experimental Results
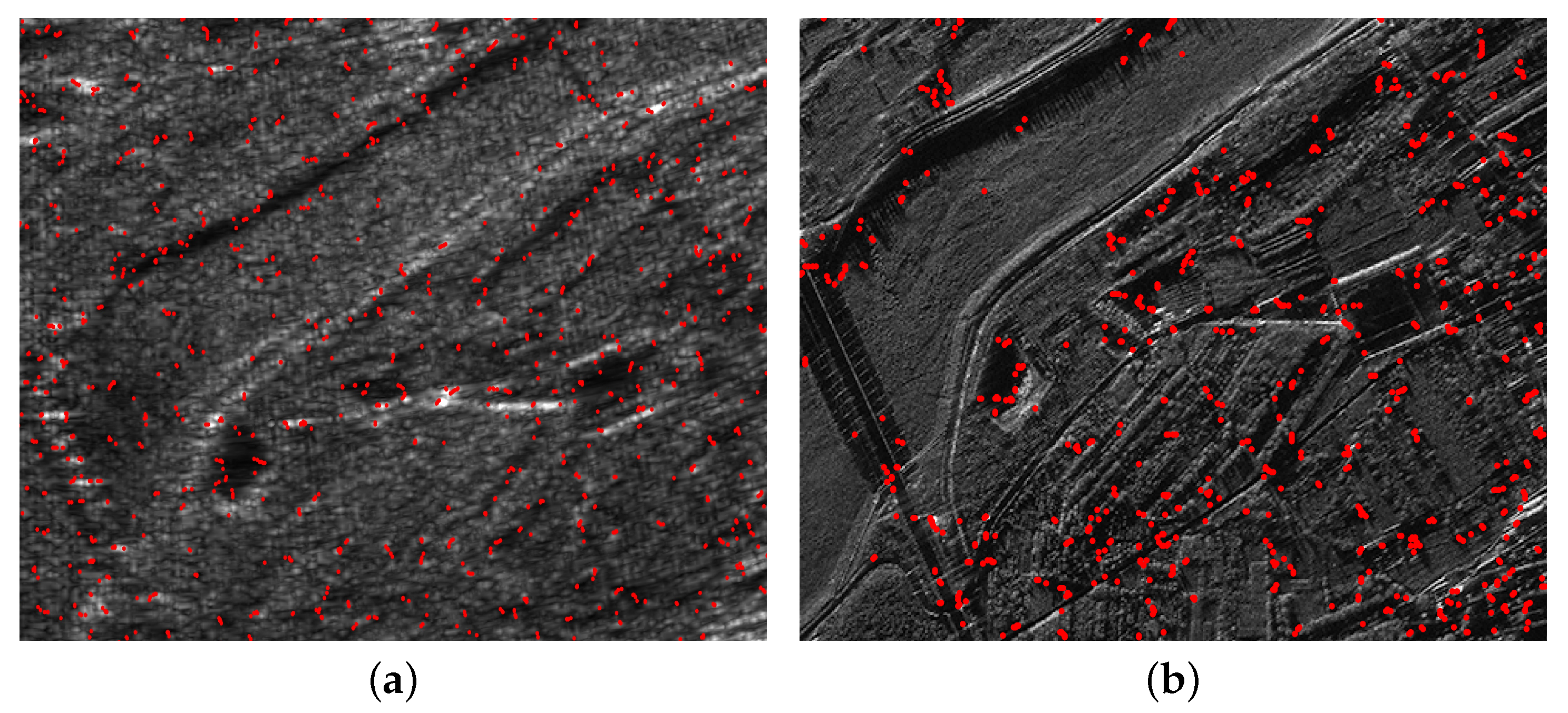
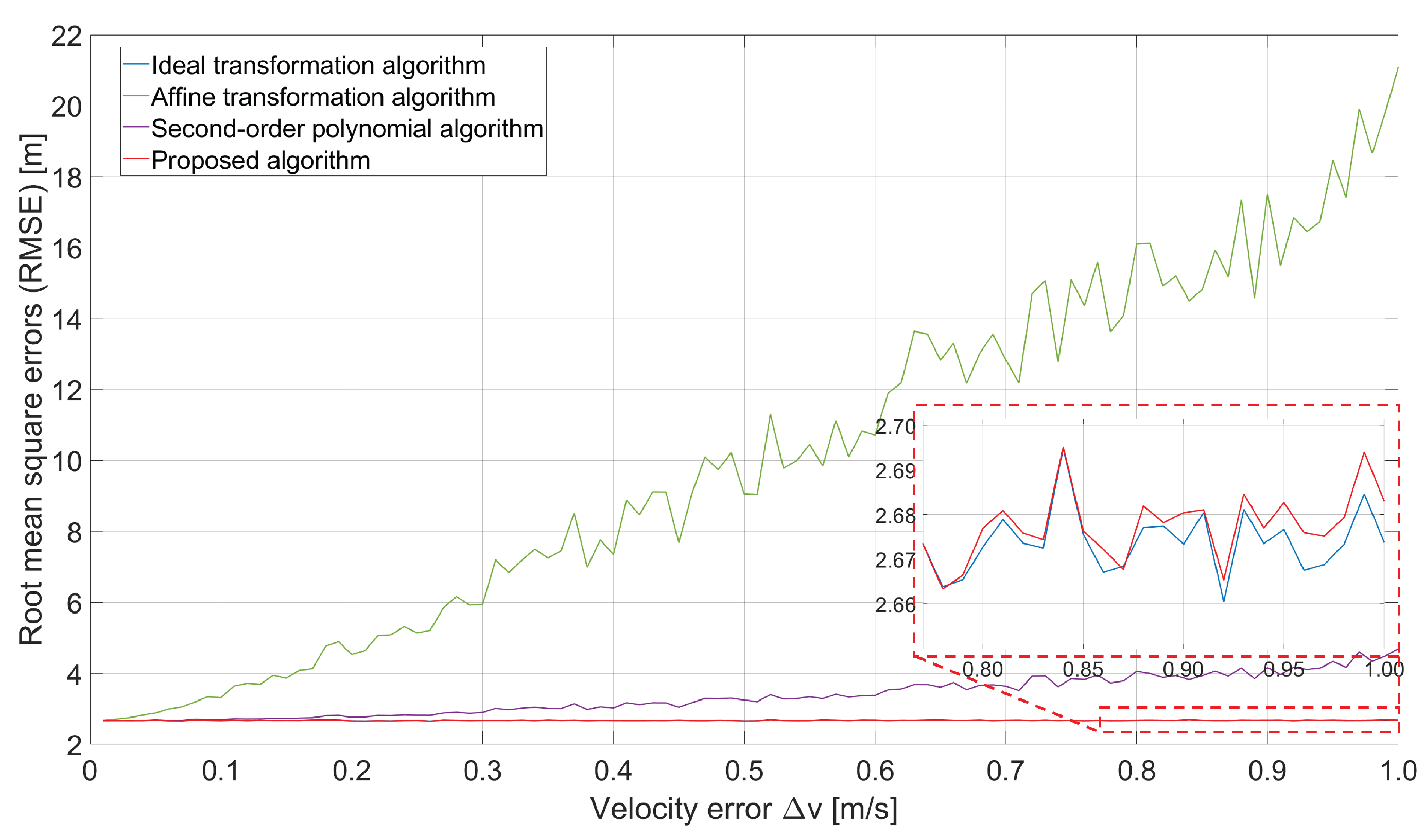
4.1. Simulated Image Registration Experiment
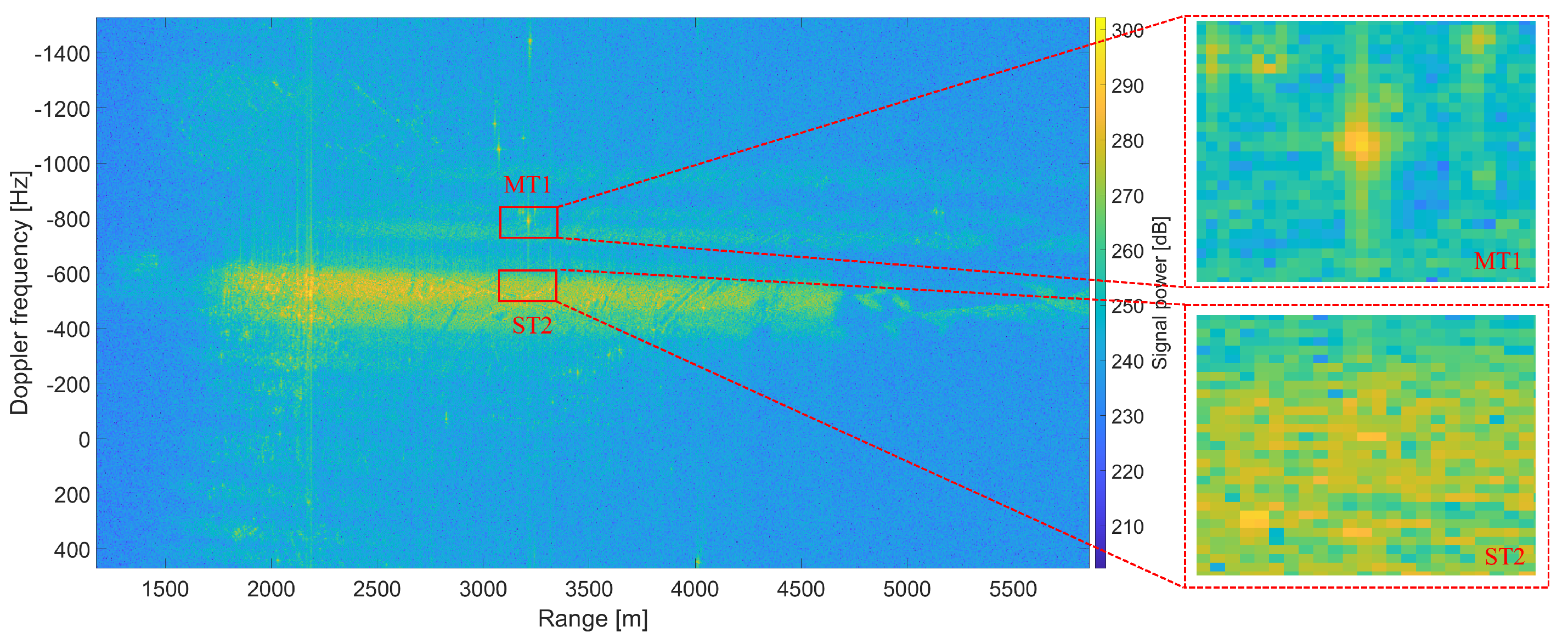
4.2. Comparison of the Algorithms Within a Real-World Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | unmanned aerial vehicle |
| GMTI | ground-moving target indication |
| SWaP | size, weight, and power |
| INS | inertial navigation system |
| DBS | Doppler beam sharpening |
| SAR | synthetic aperture radar |
| SIFT | scale-invariant feature transform |
| DOS | direction-of-arrival |
| DCB | digital channel balancing |
| KB | knowledge-based |
| PPS | polynomial phase signal |
| SWT | stationary wavelet transform |
| HORG | histogram of oriented ratio gradient |
| RCP | rational polynomial coefficient |
| MEMS | micro-electro-mechanical system |
| DGPS | differential global positioning system |
| CPI | coherent processing time |
| NNDR | nearest neighbor distance ratio |
| RANSAC | random sample consensus |
| LS | least square |
| DEM | digital elevation mode |
| ENU | East–North–Up |
| RMSE | root mean square error |
| ROI | region of interest |
| CSI | clutter suppression interferometry |
References
- Entzminger, J.N.; Fowler, C.A.; Kenneally, W.J. JointSTARS and GMTI: Past, present and future. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 748–761. [Google Scholar] [CrossRef]
- Chang, C.Y.; Woo, A.; Forry, H.; Sherman, J.; Recht, M.; Clark, R.; Levin, R. HISAR-300: An Advanced Airborne Multi-Mission Surveillance Radar. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Greenspan, M. Joint STARS—The Start of 50 Years of All Speed Surface Moving Target Detection and Tracking. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 32–37. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Klare, J.; Brenner, A.R.; Ender, J.H.G. Wide-Area Traffic Monitoring with the SAR/GMTI System PAMIR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3019–3030. [Google Scholar] [CrossRef]
- Silva, A.B.C.d.; Baumgartner, S.V. A Priori Knowledge-Based STAP for Traffic Monitoring Applications: First Results. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; pp. 1–5. [Google Scholar]
- Chen, J.; An, D.; Ge, B.; Zhou, Z. Detection, Parameters Estimation, and Imaging of Moving Targets Based on Extended Post-Doppler STAP in Multichannel WasSAR-GMTI. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5223515. [Google Scholar] [CrossRef]
- Budillon, A.; Pascazio, V.; Schirinzi, G. Estimation of Radial Velocity of Moving Targets by Along-Track Interferometric SAR Systems. IEEE Geosci. Remote Sens. Lett. 2008, 5, 349–353. [Google Scholar] [CrossRef]
- Barros Cardoso da Silva, A.; Baumgartner, S.V.; de Almeida, F.Q.; Krieger, G. In-Flight Multichannel Calibration for Along-Track Interferometric Airborne Radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3104–3121. [Google Scholar] [CrossRef]
- Barros Cardoso da Silva, A.; Joshi, S.K.; Baumgartner, S.V.; de Almeida, F.Q.; Krieger, G. Phase Correction for Accurate DOA Angle and Position Estimation of Ground-Moving Targets Using Multi-Channel Airborne Radar. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4021605. [Google Scholar] [CrossRef]
- Gierull, C.H. Digital Channel Balancing of Along-Track Interferometric SAR Data; Defence R & D Canada-Ottawa: Ottawa, ON, Canada, 2003. [Google Scholar]
- Ruixian, H.; Baochang, L.; Tong, W.; Dongdong, L.; Zheng, B. A Knowledge-Based Target Relocation Method for Wide-Area GMTI Mode. IEEE Geosci. Remote Sens. Lett. 2014, 11, 748–752. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.-G.; Wang, L.; Xu, H.; Liu, X.; Liao, G.; Jiang, X. Imaging and Relocation for Extended Ground Moving Targets in Multichannel SAR-GMTI Systems. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5214024. [Google Scholar] [CrossRef]
- Svedin, J.; Bernland, A.; Gustafsson, A.; Claar, E.; Luong, J. Small UAV-based SAR system using low-cost radar, position, and attitude sensors with onboard imaging capability. Int. J. Microw. Wirel. Technol. 2021, 13, 602–613. [Google Scholar] [CrossRef]
- Nitti, D.O.; Bovenga, F.; Chiaradia, M.T.; Greco, M.; Pinelli, G. Feasibility of Using Synthetic Aperture Radar to Aid UAV Navigation. Sensors 2015, 15, 18334–18359. [Google Scholar] [CrossRef] [PubMed]
- Wellig, P.; Speirs, P.; Schuepbach, C.; Oechslin, R.; Renker, M.; Boeniger, U.; Pratisto, H. Radar Systems and Challenges for C-UAV. In Proceedings of the 2018 19th International Radar Symposium (IRS), Bonn, Germany, 20–22 June 2018; pp. 1–8. [Google Scholar]
- Catapano, I.; Gennarelli, G.; Ludeno, G.; Noviello, C.; Esposito, G.; Renga, A.; Fasano, G.; Soldovieri, F. Small Multicopter-UAV-Based Radar Imaging: Performance Assessment for a Single Flight Track. Remote Sens. 2020, 12, 774. [Google Scholar] [CrossRef]
- Sun, B.M.; Kenney, R.H.; Yeary, M.B.; Sigmarsson, H.H.; McDaniel, J.W. Reduced Navigation Error Using a Multi-Sensor Fusion Technique and Its Application in Synthetic Aperture Radar. IEEE J. Microwaves 2024, 4, 86–100. [Google Scholar] [CrossRef]
- Meng, K.; Wu, Q.; Xu, J.; Chen, W.; Feng, Z.; Schober, R.; Swindlehurst, A.L. UAV-Enabled Integrated Sensing and Communication: Opportunities and Challenges. IEEE Wirel. Commun. 2024, 31, 97–104. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, W.; Chen, X.; Gao, Z.; Cai, Y. Terahertz Integrated Sensing and Communication-Empowered UAVs in 6G: A Transceiver Design Perspective. IEEE Veh. Technol. Mag. 2025, 2–11. [Google Scholar] [CrossRef]
- Šipoš, D.; Gleich, D. A Lightweight and Low-Power UAV-Borne Ground Penetrating Radar Design for Landmine Detection. Sensors 2020, 20, 2234. [Google Scholar] [CrossRef]
- Zhang, L.; Qiao, Z.; Xing, M.-D.; Yang, L.; Bao, Z. A Robust Motion Compensation Approach for UAV SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3202–3218. [Google Scholar] [CrossRef]
- Hu, X.; Ma, C.; Hu, R.; Yeo, T.S. Imaging for Small UAV-Borne FMCW SAR. Sensors 2019, 19, 87. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, F.; Chen, Z.; Li, J.; Hong, W. An Improved Map-Drift Algorithm for Unmanned Aerial Vehicle SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1–5. [Google Scholar] [CrossRef]
- Wang, G.; Feng, L.; Li, J.; Xing, T.; Ma, C.; Kang, C. A Robust Image Stitching and Geometric Correction Method for Doppler Beam Sharpening Imaging. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–4. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-Like Algorithm for SAR Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 453–466. [Google Scholar] [CrossRef]
- Jianwei, F.; Yan, W.; Fan, W.; Qiang, Z.; Guisheng, L.; Ming, L. SAR Image Registration Using Phase Congruency and Nonlinear Diffusion-Based SIFT. IEEE Geosci. Remote Sens. Lett. 2015, 12, 562–566. [Google Scholar] [CrossRef]
- Fan, J.; Wu, Y.; Li, M.; Liang, W.; Zhang, Q. SAR Image Registration Using Multiscale Image Patch Features With Sparse Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1483–1493. [Google Scholar] [CrossRef]
- Paul, S.; Pati, U.C. SAR Image Registration Using an Improved SAR-SIFT Algorithm and Delaunay-Triangulation-Based Local Matching. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2958–2966. [Google Scholar] [CrossRef]
- Chang, Y.; Xu, Q.; Xiong, X.; Jin, G.; Hou, H.; Man, D. SAR image matching based on rotation-invariant description. Sci. Rep. 2023, 13, 14510. [Google Scholar] [CrossRef] [PubMed]
- APX-15. Available online: https://www.applanix.com/cn/products/dg-uavs.htm (accessed on 23 February 2025).
- Wang, B.; Song, C.; Liu, N.; Liu, Z.; Zhou, L.; Xiang, M. An Advanced Lightweight Dual-Band Digital Array SAR System: Earth Observation Imaging and Moving Target Detection. IEEE Sens. J. 2023, 23, 21776–21786. [Google Scholar] [CrossRef]
- Chen, H.; Li, M.; Zhang, P.; Liu, G.; Jia, L.; Wu, Y. Resolution enhancement for Doppler beam sharpening imaging. Iet Radar Sonar Navig. 2015, 9, 843–851. [Google Scholar] [CrossRef]
- Mao, D.; Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J. Doppler Beam Sharpening Using Estimated Doppler Centroid Based on Edge Detection and Fitting. IEEE Access 2019, 7, 123604–123615. [Google Scholar] [CrossRef]
- Chen, H.; Li, M.; Lu, V.; Wu, Y. A DBS image stitching algorithm based on affine transformation. In Proceedings of the IET Conference Proceedings, Xi’an, China, 14–16 April 2013. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Smith, D.; Atkinson, S.F. Accuracy of rectification using topographic map versus GPS ground control points. Photogramm. Eng. Remote Sens. 2001, 67, 565–570. [Google Scholar]
- Deming, R.W.; MacIntosh, S.; Best, M. Three-channel processing for improved geo-location performance in SAR-based GMTI interferometry. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XIX, Baltimore, MD, USA, 23–26 April 2012; p. 83940F. [Google Scholar]
- Liu, W.; Zhang, Y.; Ge, X.; Li, Y.; Liu, Y.; Bu, X.; Liang, X. An Improved Knowledge-Based Ground Moving Target Relocation Algorithm for a Lightweight Unmanned Aerial Vehicle-Borne Radar System. Remote Sens. 2025, 17, 1182. [Google Scholar] [CrossRef]














| Quantity | Symbol | Value |
|---|---|---|
| Velocity of the platform | v | 14 m/s |
| Number of Tx/Rx channels | 1/2 | |
| Pulse repetition frequency | PRF | 2000 Hz |
| Number of pulses per burst | 512 | |
| Range bandwidth | BW | 40 MHz |
| Range resolution | 3.75 m | |
| Carrier frequency | 17 GHz | |
| Altitude of the platform | 800 m | |
| Nearest range | 1.98 km | |
| Scanning angle | −30~30° | |
| Number of look directions | 61 | |
| Beam width | 3.4° |
| Quantity | Symbol | Value |
|---|---|---|
| Accuracy of the range | 1.875 m | |
| Accuracy of the Doppler frequency | 2 Hz | |
| Accuracy of the platform’s position | 0.5 m | |
| Accuracy of the platform’s velocity | 0.1 m/s |
| Matching Algorithm | Correct Matched Key Points | RMSE (In Pixel) | ||
|---|---|---|---|---|
| SAR (2022) | SAR (2023) | SAR (2022) | SAR (2023) | |
| Affine transformation algorithm [26] | 34 | 5.22 | 16 | 14.89 |
| Second-order polynomial algorithm [37] | 47 | 4.94 | 17 | 13.75 |
| Proposed algorithm | 68 | 5.02 | 28 | 13.78 |
| Matching Algorithm | Correct Matched Key Points | RMSE (In Pixel) | ||
|---|---|---|---|---|
| SAR (2022) | SAR (2023) | SAR (2022) | SAR (2023) | |
| Affine transformation algorithm [26] | 110 | 2.13 | 10 | 14.89 |
| Second-order polynomial algorithm [37] | 147 | 1.88 | failed | failed |
| Proposed algorithm | 203 | 2.16 | 18 | 15.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Chen, Z.; Jiang, Z.; Li, Y.; Liu, Y.; Bu, X.; Liang, X. Ground-Moving Target Relocation for a Lightweight Unmanned Aerial Vehicle-Borne Radar System Based on Doppler Beam Sharpening Image Registration. Electronics 2025, 14, 1760. https://doi.org/10.3390/electronics14091760
Liu W, Chen Z, Jiang Z, Li Y, Liu Y, Bu X, Liang X. Ground-Moving Target Relocation for a Lightweight Unmanned Aerial Vehicle-Borne Radar System Based on Doppler Beam Sharpening Image Registration. Electronics. 2025; 14(9):1760. https://doi.org/10.3390/electronics14091760
Chicago/Turabian StyleLiu, Wencheng, Zhen Chen, Zhiyu Jiang, Yanlei Li, Yunlong Liu, Xiangxi Bu, and Xingdong Liang. 2025. "Ground-Moving Target Relocation for a Lightweight Unmanned Aerial Vehicle-Borne Radar System Based on Doppler Beam Sharpening Image Registration" Electronics 14, no. 9: 1760. https://doi.org/10.3390/electronics14091760
APA StyleLiu, W., Chen, Z., Jiang, Z., Li, Y., Liu, Y., Bu, X., & Liang, X. (2025). Ground-Moving Target Relocation for a Lightweight Unmanned Aerial Vehicle-Borne Radar System Based on Doppler Beam Sharpening Image Registration. Electronics, 14(9), 1760. https://doi.org/10.3390/electronics14091760






