Abstract
Many vision and graphics applications involve the efficient solving of various linear systems, which has been a popular topic for decades. With mobile devices arising and becoming popularized, designing a high-performance solver tailored for them, to ensure the smooth migration of various applications from PC to mobile devices, has become urgent. However, the unique features of mobile devices present new challenges. Mainstream mobile devices are equipped with so-called heterogeneous multiprocessor systems-on-chips (MPSoCs), which consist of processors with different architectures and performances. Designing algorithms to push the limits of of MPSoCs is attractive yet difficult. Different cores are suitable for different tasks. Further, data sharing among different cores can easily neutralize performance gains. Fortunately, the comparable performance of CPUs and GPUs on MPSoCs make the heterogeneous systems promising, compared to their counterparts on PCs. This paper is devoted to a high-performance mobile linear solver for a sparse system with a tailored asynchronous algorithm, to fully exploit the computing power of heterogeneous processors on mobile devices while alleviating the data-sharing overhead. Comprehensive evaluations are performed, with in-depth discussion to shed light on the future design of other numerical solvers.
1. Introduction
Mobile devices are dominating our daily life. More and more applications are being developed for mobile devices. Many of them, especially those related to computer graphics (CG) and computer vision (CV), involve tasks that can be formulated as energy-optimization problems. High performance is critical for interactive feedback in many of these applications. Thus, formulating these problems linearly is especially appreciated, as they can be solved rather quickly. Nevertheless, the limited computing power of CPUs on mobile devices still cannot meet the need for instant solving of linear systems in many applications.
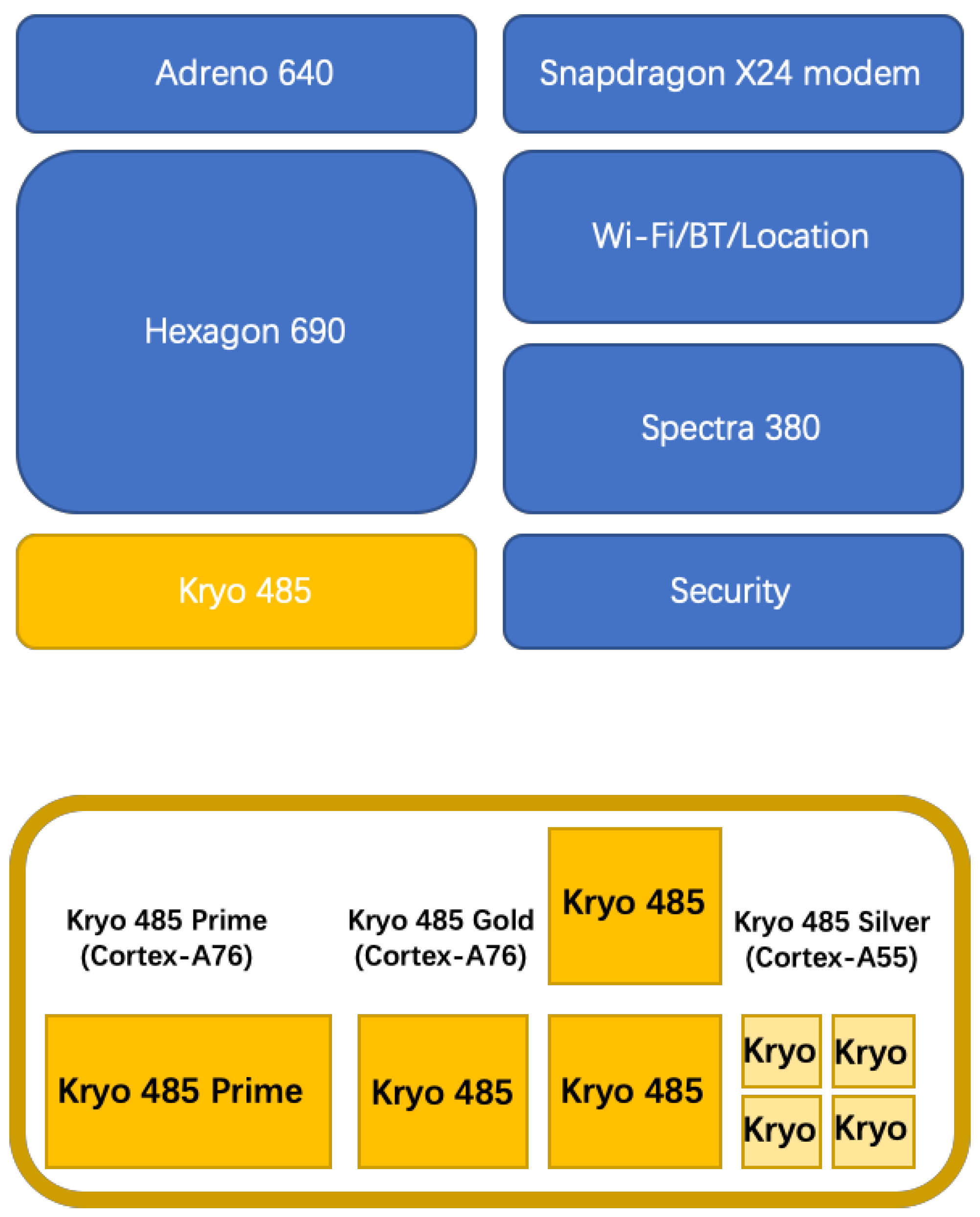
On the other hand, multi-core architecture is now the de-facto standard for processors on mobile devices, due to its effectiveness in eliminating thermal/power constraints, reliability issues and design complexity, etc. Most MPSoCs on current mobile devices adopt a heterogeneous architecture (containing a set of identical cores) to achieve superiority in size, performance and power against their homogeneous counterpart. Further, such heterogeneous multi-core architecture is more promising in the so-called dark silicon regime, which claims that the increasing on-chip power density will prevent all the cores from being switched on at the same time, as only the cores suited for an application need to be switched on. The heterogeneity of an MPSoC can be either in terms of performance or function. Taking the Qualcomm Snapdragon 855 as an example, which is designed with the ARM big.LITTLE architecture (a classic heterogeneous architecture in terms of performance), it integrates one Qualcomm Kryo 485 Gold @ 2841 MHz CPU (A76-based, high performance), three Qualcomm Kryo 485 Gold @ 2419 MHz CPUs (A76-based, medium performance CPU) and four Qualcomm Kryo 485 Silver @ 1785 MHz CPUs (A55-based, low performance). Moreover, it also has a GPU, the Adreno (TM) 640, with a totally different function (Figure 1 shows details on the specific architecture).
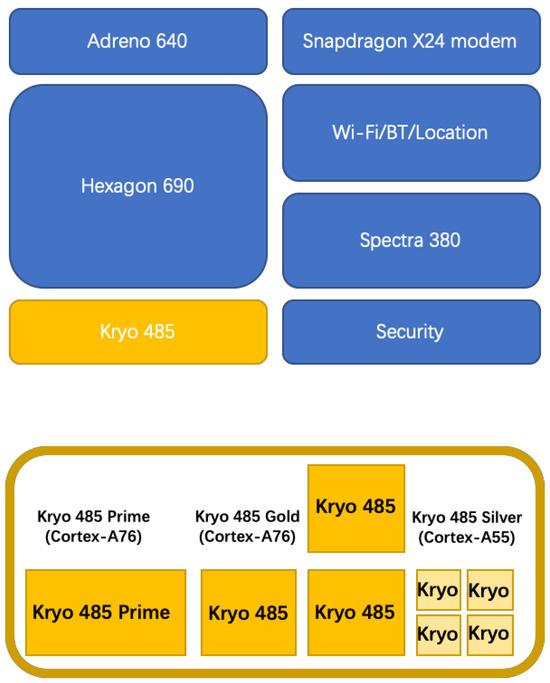
Figure 1.
The heterogeneity of an MPSoC, showing the heterogeneous processors and their numbers.
These MPSoCs show promise in delivering high performance in cases where the software can fully exploit all of the available resources in a manner that uses the most suitable cores for the current computing need. However, it is also challenging to design such algorithms. We need to select a suitable core type for the specific resource-demanded kernel, translate and optimize the corresponding kernel in a high-level language to an implementation suitable for the selected core type while carefully handling data sharing among processors to alleviate overheads such as synchronization, data transfer and mapping. The workload should be well-balanced among these heterogeneous cores with an accurate performance estimation of computing tasks on the different types of cores.
This paper investigates the high-performance design and implementation of a Jacobi solver on a heterogeneous MPSoC, aiming to lay a foundation for the smooth migration of various applications. Although not efficient as a stand-alone solver, Jacobi and other stationary iterations are often used as the basic primitives for complex algorithms such as multigrid methods. Jacobi iteration has a low computation complexity and is very suitable for parallel implementation. A number of studies [1,2] have been conducted on the GPU implementation of Jacobi iteration, achieving tens or even hundreds of times faster performance against the CPU counterpart. Other works investigated the heterogeneous implementation of a Jacobi solver on a desktop computer [3] or clusters [4]. However, there are few works targeting mobile MPSoCs, which have very different characteristics either in terms of processors or memory-sharing schemes, presenting new challenges. To be specific, the CPU and GPU on an MPSoC have comparable performance [5] (which is different from the PC platform) and thus the concurrent execution of an algorithm has the potential to gain apparent advantage against simply putting it purely on either the CPU or GPU. Furthermore, the CPU and GPU on an MPSoC share a unified memory [6], which can significantly reduce the data-sharing overhead, as copying data between different memories can be avoided and the heterogeneous Jacobi solver on the MPSoC can be designed differently than in the aforementioned methods. We firstly divided the workload of the Jacobi solver into roughly balanced parts and executed them concurrently on CPU and GPU of an MPSoC. To reduce the data-sharing overhead as much as possible, we implemented the Jacobi solver in an asynchronous manner and used appropriate memory storage for different data. Detailed experiments were conducted to validate the effectiveness of the method. In summary, the major contributions of this paper are:
- A complete paradigm for a heterogeneous Jacobi solver on a mobile MPSoC, with various schemes (data-sharing, load-balancing and asynchronous design, etc.) to fully exploit the capabilities of various processors on the MPSoC while alleviating the data-sharing overhead.
- A comprehensive evaluation and discussion of various aspects of the solver (time cost, processor utilization, energy consumption, etc.) with real applications, to shed light on the future design of other numerical solvers.
2. Related Work
2.1. Numerical Solver for CG
The pervasive usage of numerical solvers for linear or nonlinear problems in the computer graphics domain has strongly promoted research on efficient and accurate solvers. Earlier works were devoted to highly efficient [7] or high-level [8] CPU solvers. Later, researchers began to shift their attention to the acceleration of general or basic blocks on GPUs, such as sparse-matrix conjugate gradient solvers [9] and multigrid solvers [10]. Spontaneously, GPU-based non-linear solvers were developed to overcome the performance limitations of their CPU counterparts, tailored for specific applications such as deformable mesh tracking [11], shape-from-shading [12], computational imaging [13], model-to-frame camera tracking [14], face reconstruction [15] and cloth simulation [16], etc. To avoid the tedious hand-writing process, domain-specific languages [17,18] were designed to allow users to specify the high-level energy description only, with various solvers generated automatically. Thus, users can further explore tradeoffs in numerically precise, matrix-free methods and solver approaches. The recent work of Lai et al. [19] aimed at solving large-scale optimization problems with proximal algorithms and proposed a domain-specific modeling language and compiler, integrating differentiable proximal algorithms. Bangaru et al. [20] extended the Slang shading language to support class-one automatic differentiation.
This paper focuses on parallelization of Jacobi iteration on heterogeneous processors of mobile devices to gain performance improvements by overcoming the challenges of load imbalances and high data-sharing overhead with a tailor-designed asynchronous algorithm.
2.2. Mobile Graphics
Mobile graphics is increasingly gaining attention with the rapid popularization of mobile devices [21]. SeongKi Kim et al. [22] proposed a novel Dynamic Voltage and Frequency Scaling (DVFS) to control the balance between performance and energy consumption with new metrics for estimating the workload for GPUs as well as their memory workload. The works of Wang et al. [23,24,25] sought to find the optimal rendering configuration to maximize visual quality under the constraint of a specific power budget. While the work of Nah et al. [26] proposed a novel traversal order for tile-based mobile GPU architectures to reduce the computational cost of VR stereo rendering. Finally, the rise of neural rendering has also promoted research into its hardware acceleration [27].
While most research pays more attention to energy/power saving through DVFS, we have focused on how to improve the performance of numerical algorithms by mapping the algorithm onto the heterogeneous processors of mobile devices under the guidance of an accurate latency estimator, thus achieving a well-balanced workload among processors.
3. Background
The Open Computing Language is an open industry standard for programming on a well-organized heterogeneous collection of CPUs, GPUs and other discrete computing devices. There is a host (CPU) connecting to other devices and controlling the computation. Accordingly, a program is divided into a kernel and a host executed on devices and hosts, respectively. In each kernel instance, a work-item runs the kernel code on a single data point. A work-group consists of a user-defined number of work-items. Work-items in the same work-group share a local memory and execute concurrently on a single compute unit. Memory in OpenCL can be broadly divided into host memory and device memory. While the behavior of host memory is defined outside of OpenCL, the device memory is further divided into four regions according to their behaviors:
- Global memory permits read/write access to all work-items in all work-groups running on any device within a context.
- Constant memory is a region of global memory which remains constant during the execution of a kernel instance.
- Local memory is local to the work-group and can be used to allocate variables that are shared by all work-items in that work-group.
- Private memory is private to a work-item, where variables defined are not visible to another work-item.
The contents of global memory are memory objects, which are further categorized into three classes:
- Buffer is stored as a block of contiguous memory and used as a general-purpose object to hold data.
- Image holds one-, two- or three-dimensional images.
- Pipe is an ordered sequence of data items with a write endpoint where data items are inserted and a read endpoint where data items are removed.
Memory objects are made available to kernel instances running on one or more devices. There are four different ways of sharing between the host and devices:
- Read/Write/Fill commands explicitly read and write data associated with a memory object between the host and global memory regions.
- Map/Unmap commands map data from the memory object into a contiguous block of memory, which is accessed through a host-accessible pointer.
- Copy commands. The data associated with a memory object is copied between two buffers.
- Shared virtual memory provides a way for transparent data migration between a host and devices by extending the global memory region into the host memory region.
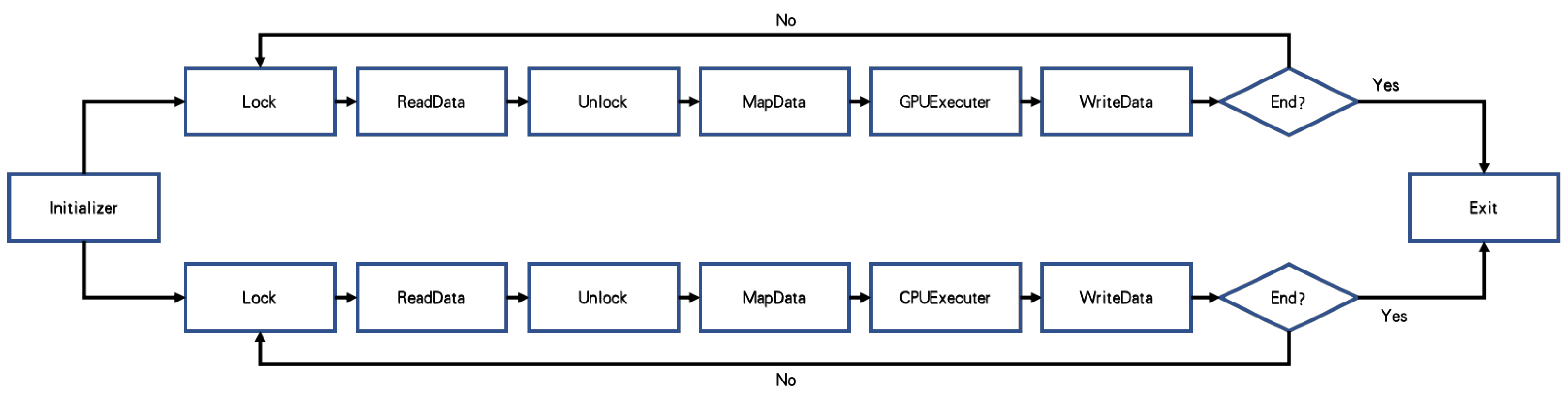
Runtime environment for mobile CPUs. The OpenCL runtime software for the Mali GPU is supplied by the vendor. However, current mobile MPSoCs typically do not include OpenCL support for the ARM CPU cores. Although there are some open-source solution such as FreeOCL [28], most of them are unmaintained and only suitable for very old platforms. We therefore designed and implemented an underlying architecture with OpenMP to utilize CPUs (except the one acting as the host) as computing devices. As shown in Figure 2, after setup of the execution environment in the initializer, CPU and GPU processors will lock and read data, map data to their own memory region, execute the task and write back.
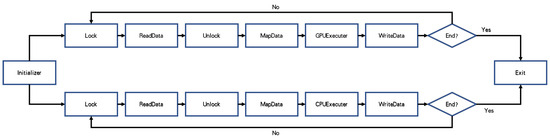
Figure 2.
Runtime architecture for heterogeneous computing with mobile CPUs and GPUs.
4. Asynchronized Jacobi Iteration
Let the linear system we want to solve be with and , we can find a non-singular splitting matrix such that . We can then formulate the stationary iteration as follow:
where the iteration matrix , and are the initial guess [29].
Generally, stationary iterations can be summarized in the form , and solved by an asynchronous iterative process with a sequence of updates as [30]:
where is the ith component of at time k. is the index set being updated at k and is the last update time of the component j of before the evaluation of at k.
For a linear system as in Equation (1), an asynchronous iteration converges for any initial condition if the spectral radius of the iteration matrix , is to be infinitely filled with each of and satisfies the following conditions:
5. Implementation
5.1. Solver
Algorithm 1 gives a heterogeneous version of a regular synchronous Jacobi iterator, which repeatedly computes the residual and updates the solution. We firstly divide the system matrix into small blocks by row. For a Jacobi iteration, we repeatedly assign an unprocessed block to an idle processor to calculate the corresponding residual. When all the blocks have been processed, we will go through a synchronization step to obtain the solution vector of the iteration and check for convergence to decide whether to continue the Jacobi iteration or to stop. As we can see, there will be a synchoronization after each iteration.
Algorithm 2 shows our asynchronous Jacobi iteration on a heterogeneous MPSoC. The basic idea is to divide the workload into pieces for the CPU and GPU to achieve a rough balance (Line 7–10). We then concurrently run Jacobi iterations on the CPU and GPU processors (Line 12–13). Each processor will update the corresponding part of the solution vector after iterates on it, and update its own version of the solution vector with the latest . However, processors do not need to be synchronized in this step. The total update time for all processors will be recorded. The system will check for convergence when the total time reaches a threshold to decide whether to terminate or continue. Note that we perform a roughly balanced workload division at the beginning, although it may not be necessary for the asynchronous algorithm. However, we believe it is beneficial in two aspects: (1) maintaining a rough consistency of pace between the CPU and GPU in Jacobi iteration is still beneficial although the solution update has been greatly relaxed with asynchronization; (2) in contrast to division during each iteration according to the dynamic change of the environment, pre-division of the workload can drastically reduce the data-sharing operations (data mapping, data transformation, etc., see Section 5.2 for more details), and thus reduce the data-sharing overhead. The asynchronous nature of the algorithm also reduces the requirement of a highly accurate performance predictor, which is challenging, especially in a dynamic environment. Compared to Algorithm 1, the number of synchronizations are greatly reduced.
| Algorithm 1: Synchronous Jacobi iteration on a Heterogeneous MPSoC |
 |
| Algorithm 2: Asynchronous Jacobi iteration on a Heterogeneous MPSoC |
 |
5.2. Data Storage and Sharing
We focused on a sparse linear system as they are frequently encountered in many applications, but the whole paradigm can be easily extended to dense cases. Another reason is that a large-scale dense system can easily exhaust the memory of mobile devices. A major challenge is that the irregularity of a sparse matrix will lead to non-contiguous memory access, reducing bandwidth efficiency and thus the performance algorithm. There have been various compact representations for sparse matrices with different sparsity patterns, such as the diagonal format (DIA) [31], the ELLpack (ELL) format [32], the compressessed sparse row (CSR) format [33] and the coordinate (COO) format [33]. We adopted a dynamic and potentially hybrid format. The whole linear system will be divided into two load-balanced parts for execution on the CPU and GPU concurrently. The division is guided by the performance-prediction models for the CPU and GPU, and the specific data-storage format will be determined for each part according to the performance prediction of these formats on the specific processor (see details in Section 5.3).
Apart from data representation, another critical issue is the type of memory used for storage of the system matrix and other data. Previous studies revealed that the image type can be much more efficient than the buffer on mobile GPUs. According to [34], using the image type on an Adreno GPU can achieve a 3.5× speedup compared to the buffer type for convolution. A similar conclusion was drawn for matrix operations (details can be found in Section 6). Based on these, we use the buffer to store the sub-part of the linear system matrix () on the CPU side, and image for that () on the GPU side. For the solution vector , the situation is a bit complicated. While and remain unchanged during the Jacobi iteration process, is frequently updated and shared between the CPU and GPU. Traditionally, developers need to explicitly copy data between the CPU and the GPU, which is tedious and error-prone. We adopted the shared virtual memory (SVM) for to achieve transparent migration of data between the CPU and GPU. This can also significantly enhance programming portability and productivity [35]. While such unified memory techniques have been investigated on the PC platform either for NVIDIA or AMD GPUs [36,37]. Some studies have been conducted on embedded GPUs, which have quite different characteristics compared to their PC counterparts.
5.3. Workload Distribution
Although the asynchronous nature of the solver has eliminated the need for synchronization of each Jacobi iteration, a rough matching of time costs on the CPU and GPU is still beneficial for the convergence of the whole solver as mentioned before.
We constructed models for performance prediction of Jacobi iterations on the CPU and GPU, respectively, which were then used to guide partitioning of the workload. Apparently, the most time-consuming aspect of a Jacobi iteration is sparse-matrix vector multiplication (SpMV), which is an essential operation in solving linear systems and partial differential equations. We chose a support vector machine for SpMV prediction on either the CPU or GPU, with the input feature listed in Table 1.

Table 1.
Matrix features used in the SpMV performance prediction model.
The performance of the SpMV depends on two parts: data transfer time and computing time. The former can be neglected in our asynchronous setting. While the latter can be further divided into computing time on cores and memory access time. Specifically, the performance of an SpMV operation is subjected to the sparse matrix’s size, non-zero skew and non-zero locality characteristics [38,39]. For the first factor, sparse-matrix size, we consider the number of rows, columns and non-zeros. The non-zero skewness distribution is characterized with R distribution, whose measurements are used as features. To capture non-zero locality, we logically break the matrix into tiles with rows and columns per tile. A row/column of tiles is called a row/column block. The distribution of tiles into row/column blocks is then characterized and the corresponding measurements are taken as features. Statistics including mean (), standard deviation (), variance (), min, max, Gini coefficient (G) and p-ratio (P) are used to characterize each distribution. The distribution of non-zeros across rows (R), columns (C), tiles (T), row blocks (RB) and column blocks (CB) is considered as listed in Table 1. Inspired by the work of [39], we trained decision trees for performance prediction of SpMV on the CPU and GPU of an MPSoC, respectively. The format with optimal performance will be chosen for the specific processor.
With the prediction models at hand, we can also perform workload distribution concurrently with linear programming to determine optimal row numbers on the CPU and GPU for the system matrix , so that the time costs of each Jacobi iteration on the CPU and GPU are roughly matched.
6. Experimental Results
We implemented the heterogeneous and asynchronous linear solver with OpenMP 5.0 (CPU-side) and OpenCL 2.0 (GPU-side). We ran various experiments on a Google Pixel 4, which contains a high-performance 2.84 GHz A76 core, three 2.41 GHz A76 cores, four high-efficiency 1.78 GHz A55 cores and an Adreno™ 640 GPU (Qualcomm, San Diego, CA, USA). The SpMV performance prediction models were trained with the Sparse Matrix collection from the University of Florida [40].
To distill the effect of different data types, we ran matrix multiplications on the GPU with buffer and image types, respectively. As shown in Table 2, the image type gains apparent advantages over the buffer type. The gains becomes greater with the increase of the matrix size. Note that the y-axis is log-scaled.

Table 2.
Timing statistics (in seconds) of matrix multiplication with different data types.
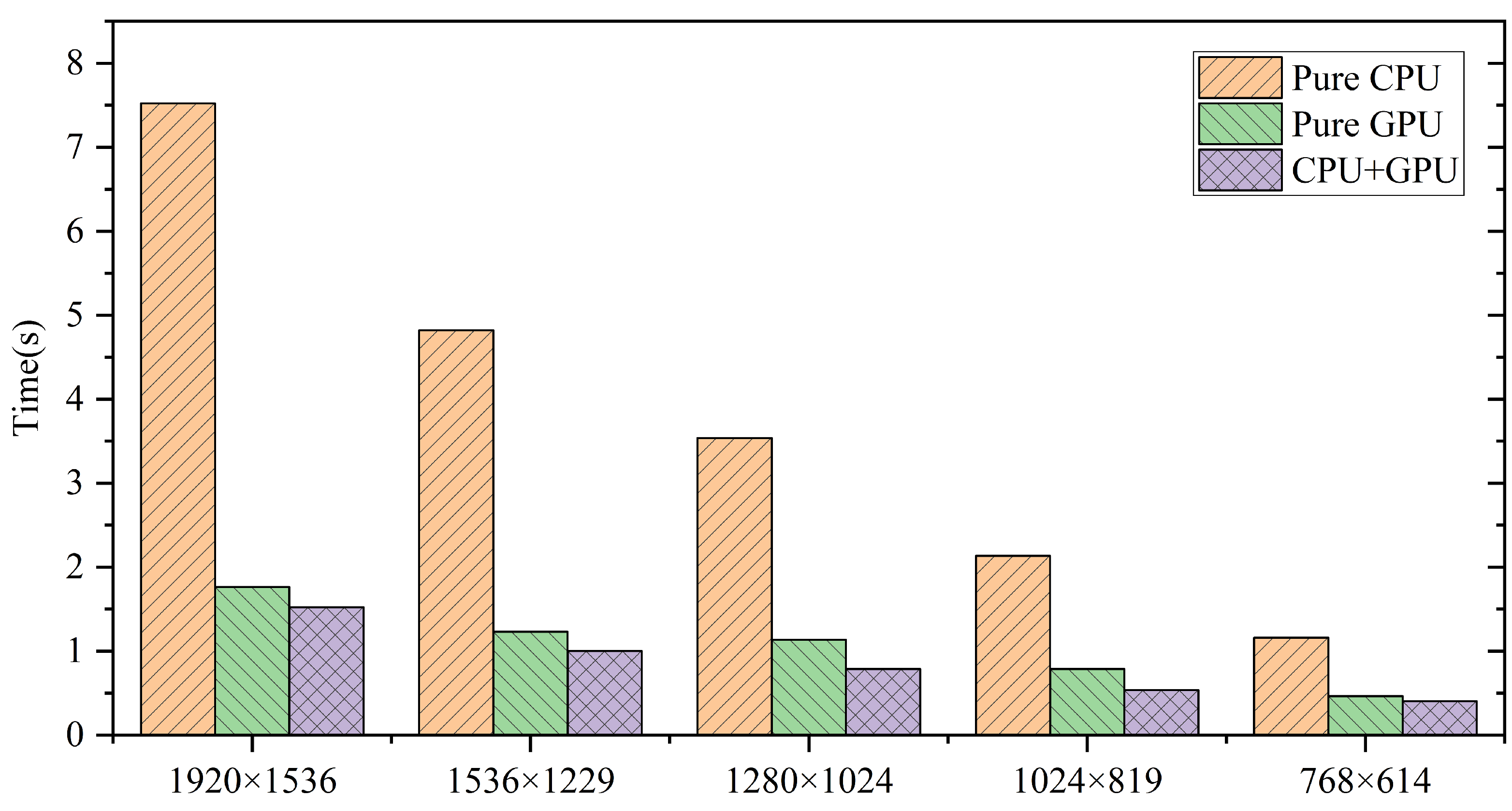
We conduct edvarious comparisons on solving a Laplacian problem. In Figure 3, we compare the heterogeneous asynchronous Jacobi iterator with a pure CPU algorithm and a pure GPU algorithm. The heterogeneous version gained and average improvements against the CPU and GPU, respectively.
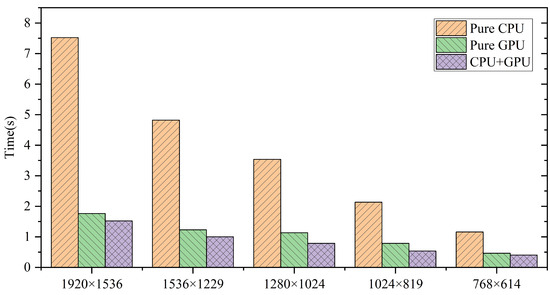
Figure 3.
Performance comparison of pure CPU, pure GPU and heterogeneous Jacobi sover. The label on the x-axis refers to the dimensions of the linear system.
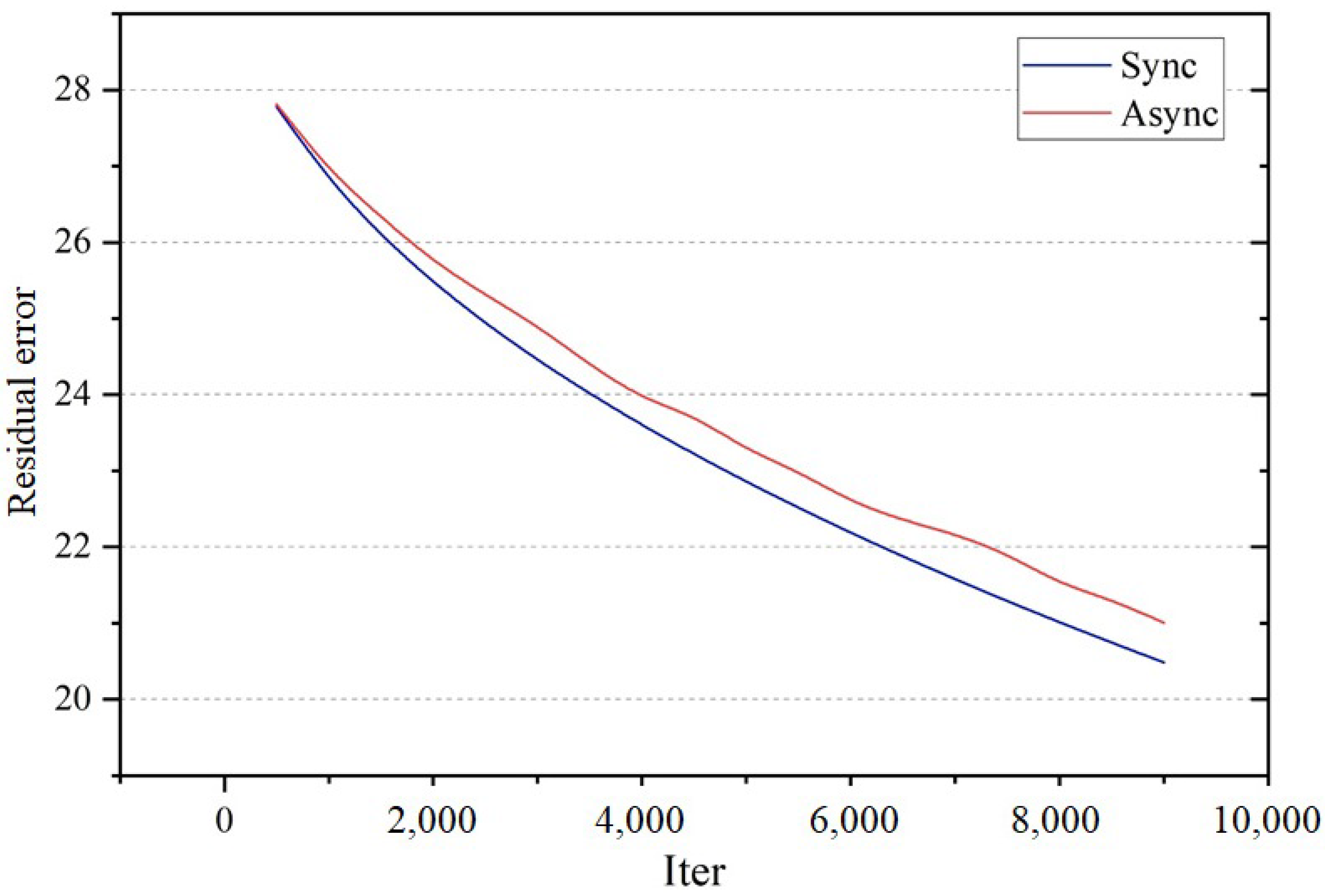
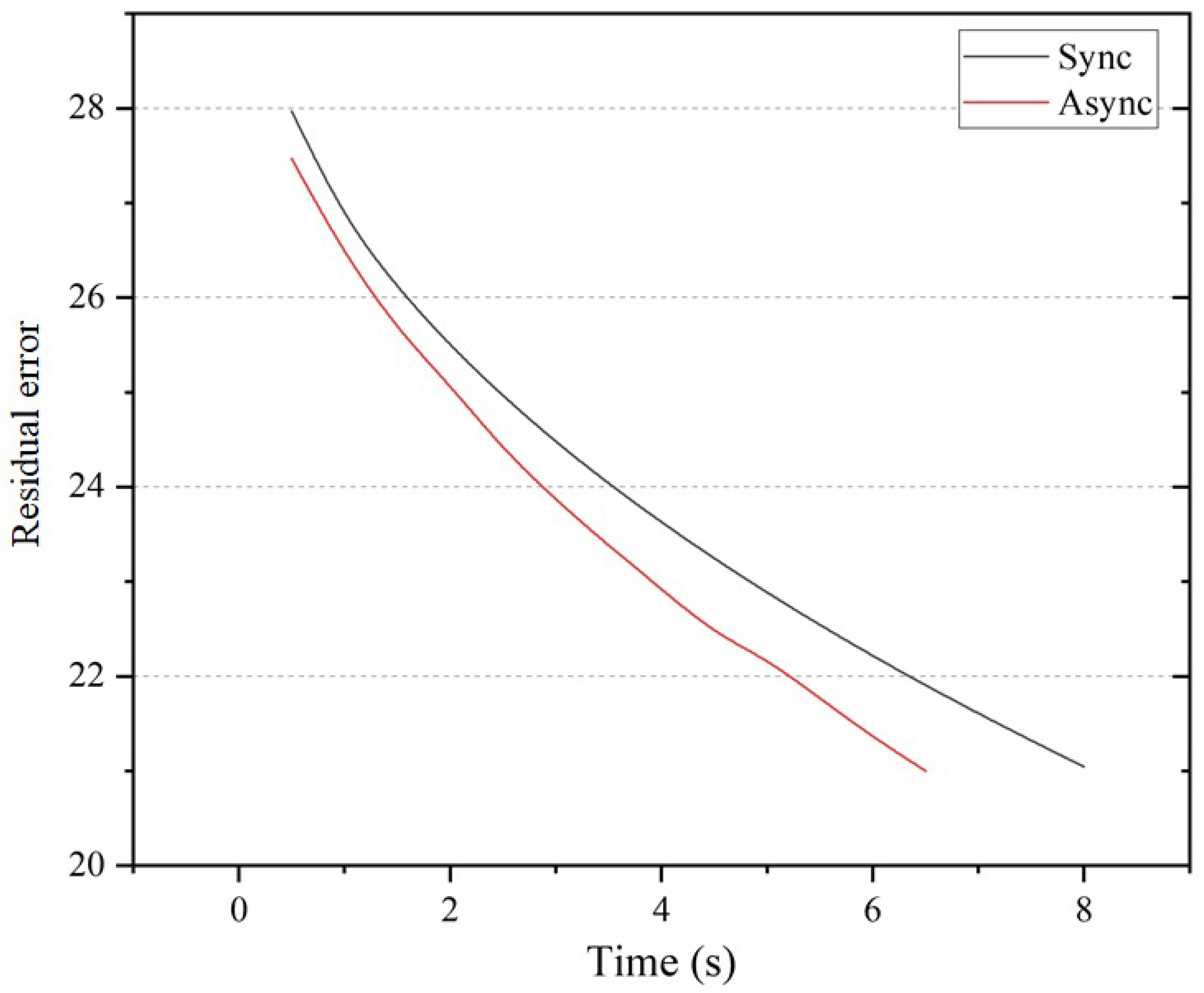
Figure 4 and Figure 5 show the convergence of the synchronous and asynchronous algorithms by iteration number and by time (with system size ), respectively. Although the asynchronous version converges somewhat slower in terms of iteration number, it is actually quite fast in respect of time cost.
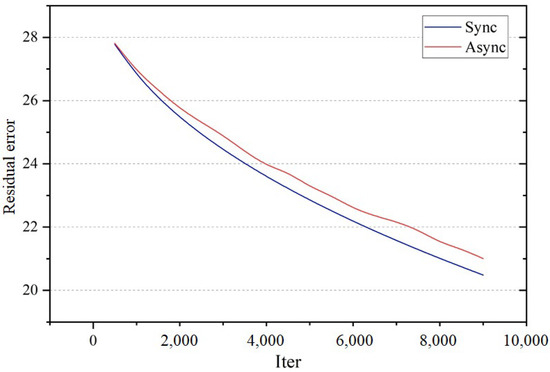
Figure 4.
Convergence of synchronous and asynchronous Jacobi iteration by iteration number. The residual error refers to the averaged pixel value (Laplacian coordinates, gradients, etc., depending on the specific editing operation) differences of the editing area.
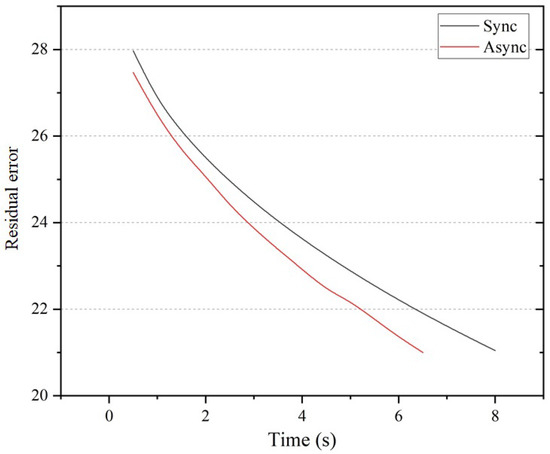
Figure 5.
Convergence of synchronous and asynchronous Jacobi iteration by time cost. The residual error refers to the averaged pixel value (Laplacian coordinates, gradients, etc., depending on the specific editing operation) differences of the editing area.
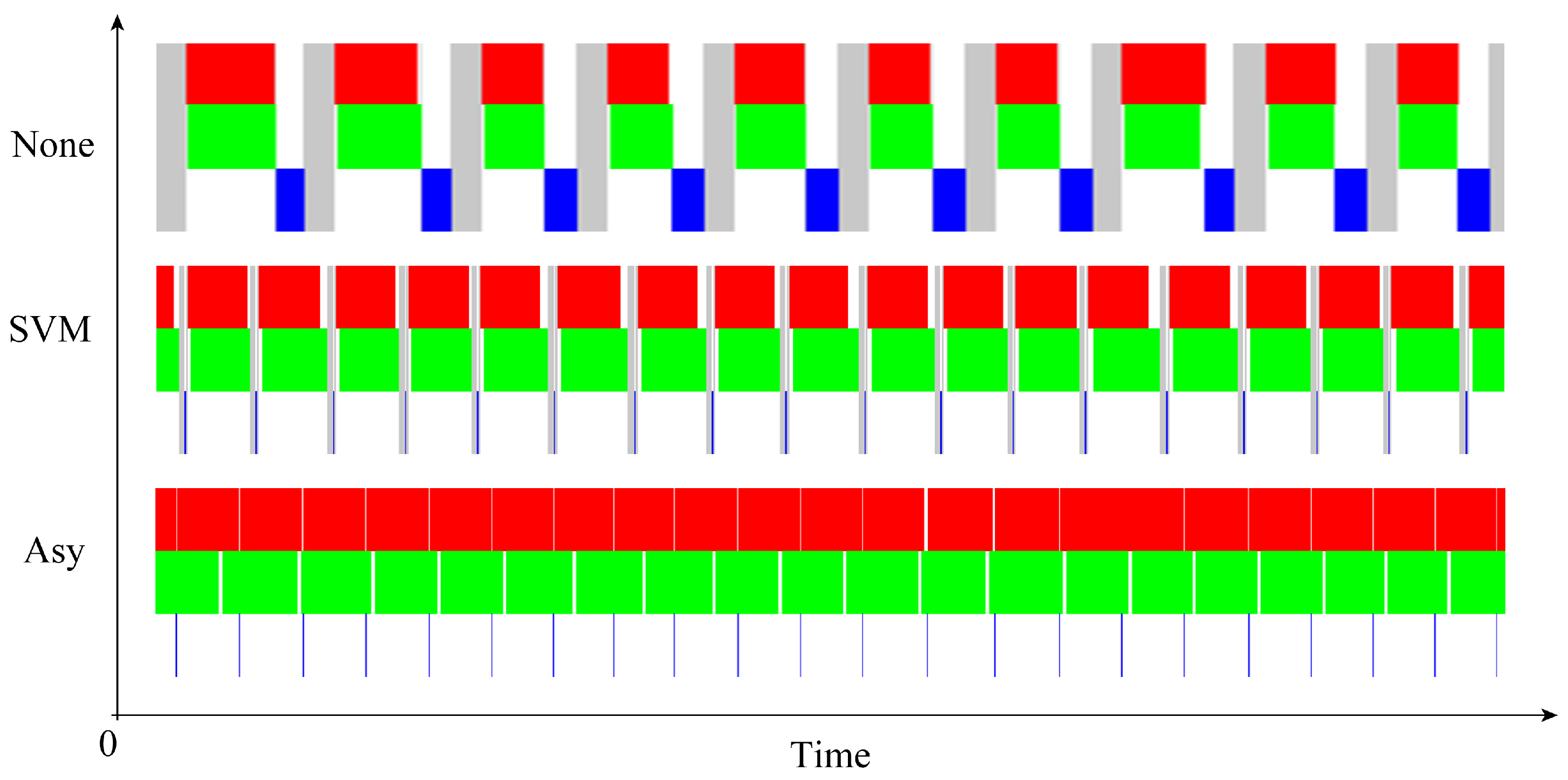
We further investigated the idle behavior of processors on the MPSoC. From Figure 6, we can observe an apparently idle condition. The introduction of the SVM technique drastically reduced idle time against direct data copying. With the algorithm changed to the asynchronous version, there are only negligible idle times.
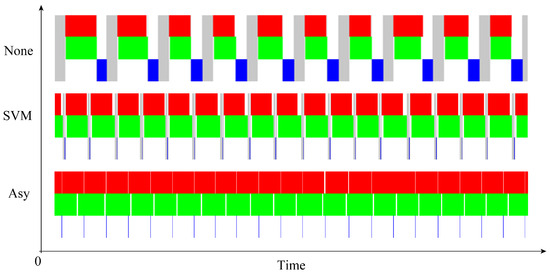
Figure 6.
Idle behavior of processors in the MPSoC during the Jacobi iteration process. Red refers to the running of the CPU, green refers to the running of the GPU and blue refers to data switching, while gray portions are idle periods. We can observe a minimal idle rate (minimal gray time slots) in the asynchronous case, indicating minimal waiting times for data synchronization.
Finally, we used the Jacobi solver in a classic image-editing framework, Poisson image editing [41], which involves solving a linear system consisting of Poisson equations. As shown in Figure 7, let
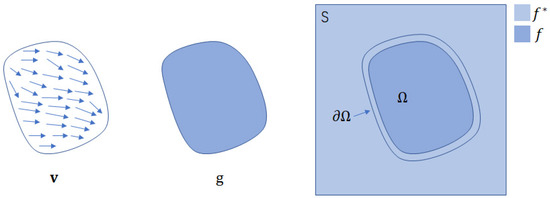
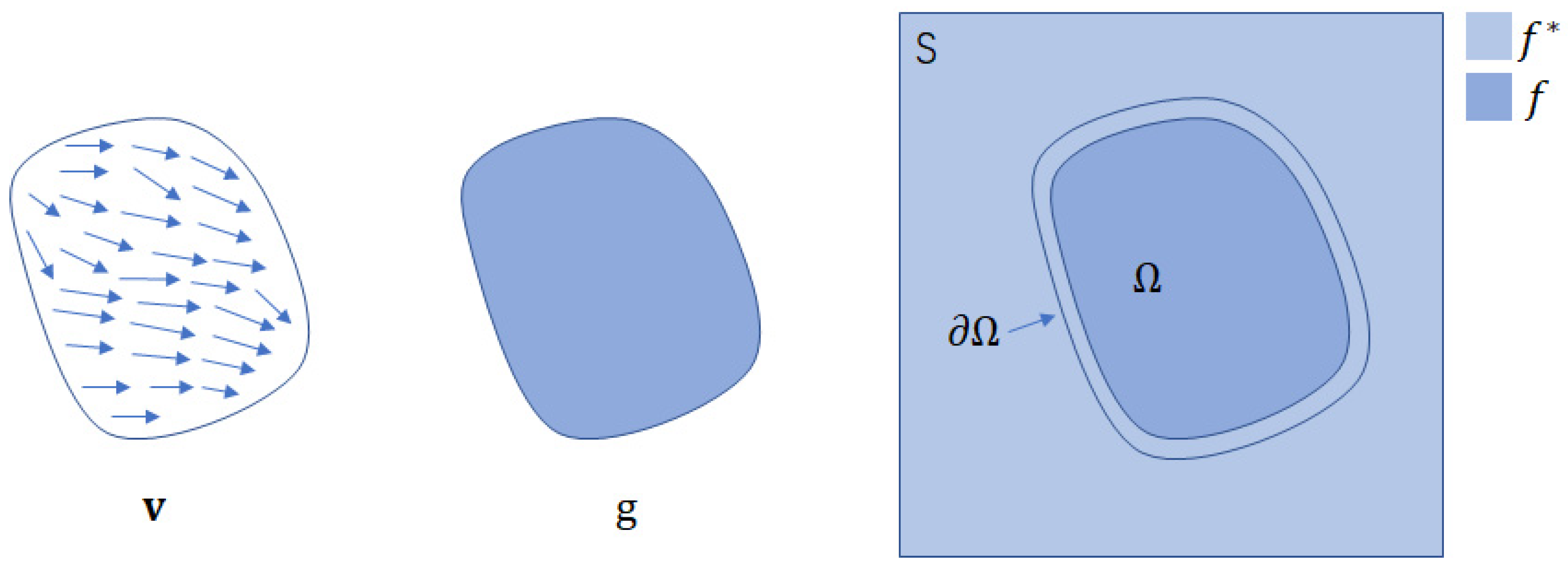
Figure 7.
Poisson image editing concept. Unknown function f interpolates in domain the destination function with boundary constraint , under the guidance of vector field , which might or might not be the gradient field of a source function .
be the image definition domain and be a closed region in S with boundary . Let be a known scalar function defined over and f be an unknown scalar function defined inside . Finally, let be a vector field defined over . The simplest interpolant f of over is the membrane interpolant defined as the solution of the following minimization problem:
where is the gradient operator. Minimizing Equation (2) is equivalent to solving the following Euler–Lagrange equation
where is the Laplacian operator. Equation (3) is a Laplace equation with Dirichlet boundary conditions. The naive application of the method in image editing leads to an unsatisfactory, blurred interpolant. It could be overcome by introducing further constraints in the form of a guidance field, which is a vector field used in an extended version of the minimization problem (Equation (2)) above:
whose solution is the unique solution of the following Poisson equation with Dirichlet boundary conditions:
where is the divergence of . This is the underlying principle of Poisson editing of color images: three Poisson equations of the form (Equation (5)) are solved independently in the three color channels of the chosen color space. The variational problem (Equation (4)), and the associated Poisson equation with Dirichlet boundary conditions (Equation (5)) can be discretized naturally using the underlying discrete pixel grid. Figure 8 gives some visual results during the converging process of Jacobi iteration.

Figure 8.
Applications of the Jacobi solver in Laplacican-based image editing. From left to right: 0 iterations, 100 iterations, 500 iterations and 1000 iterations. We can see that the newly attached patches (updated by a Poisson equation with boundary constraints) gradually merged into the whole image with the progress of Jacobi iteration.
7. Conclusions
This paper presents an asynchronous Jacobi iterator on a heterogneous MPSoC. Various tricks were used to fully exploit the computing power of different processors while reducing the data-sharing overhead. Apparent improvements in performance are achieved according to the experimental results. Generally, the heterogeneous computing scheme makes sense only when the CPU and GPU have comparable performance. In contrast to their PC counterparts, this requirement is satisfied for MPSoCs. Data-sharing overhead is critical in heterogeneous computing, which can easily neutralize performance gains. The asynchronous scheme helps to avoid such overhead by minimizing the frequency of data sharing. The in-depth analysis and discussion have shed some light on our future works. We will further investigate the effect of thermal condition on solver performance. The behavior of processors will change due to the change of thermal condition. Even worse, the long-time continuous execution of Jacobi iteration will make the MPSoC overheat and trigger throttling, which will greatly affect the performance. Furthermore, we will also investigate how to use Jacobi iteration as a pre-conditioner and combine it with other more efficient solvers under the heterogeneous setting. We may also explore how such an asynchronous scheme can be applied in other numerical problems.
Author Contributions
Conceptualization, J.L.; methodology, Z.L. and X.H.; software, Z.L. and. L.C.; validation, Y.C.; writing—original draft preparation, J.L. and Z.L.; writing—review and editing, X.C. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities, China (No. 20720230106), the Natural Science Foundation of Xiamen, China (No. 3502Z20227012) and the public technology service platform project of Xiamen City (No. 3502Z20231043).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Xiayun Hong and Yao Cheng were employed by the company China Mobile (Hangzhou) Information Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wang, T.; Yao, Y.; Han, L.; Zhang, D.; Zhang, Y. Implementation of Jacobi iterative method on graphics processor unit. In Proceedings of the 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems, Shanghai, China, 20–22 November 2009; IEEE: New York, NY, USA, 2009; Volume 3, pp. 324–327. [Google Scholar]
- Cheik Ahamed, A.K.; Magoulès, F. Efficient implementation of Jacobi iterative method for large sparse linear systems on graphic processing units. J. Supercomput. 2017, 73, 3411–3432. [Google Scholar] [CrossRef]
- Morris, G.R.; Abed, K.H. Mapping a jacobi iterative solver onto a high-performance heterogeneous computer. IEEE Trans. Parallel Distrib. Syst. 2012, 24, 85–91. [Google Scholar] [CrossRef]
- Cao, W.; Xu, C.F.; Wang, Z.H.; Yao, L.; Liu, H.Y. CPU/GPU computing for a multi-block structured grid based high-order flow solver on a large heterogeneous system. Clust. Comput. 2014, 17, 255–270. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, J.; Chae, D.; Kim, D.; Kim, J. ulayer: Low latency on-device inference using cooperative single-layer acceleration and processor-friendly quantization. In Proceedings of the Fourteenth EuroSys Conference 2019, Dresden, Germany, 25–28 March 2019; pp. 1–15. [Google Scholar]
- Jiang, S.; Ran, L.; Cao, T.; Xu, Y.; Liu, Y. Profiling and optimizing deep learning inference on mobile GPUs. In Proceedings of the 11th ACM SIGOPS Asia-Pacific Workshop on Systems, Tsukuba, Japan, 24–25 August 2020; pp. 75–81. [Google Scholar]
- Toledo, S. Taucs: A Library of Sparse Linear Solvers. 2003. Available online: https://www.tau.ac.il/~stoledo/taucs/ (accessed on 20 April 2025).
- Shearer, J.; Wolfe, M.A. ALGLIB, a simple symbol-manipulation package. Commun. ACM 1985, 28, 820–825. [Google Scholar] [CrossRef]
- Bolz, J.; Farmer, I.; Grinspun, E.; Schröder, P. Sparse matrix solvers on the GPU: Conjugate gradients and multigrid. ACM Trans. Graph. (TOG) 2003, 22, 917–924. [Google Scholar] [CrossRef]
- Goodnight, N.; Woolley, C.; Lewin, G.; Luebke, D.; Humphreys, G. A multigrid solver for boundary value problems using programmable graphics hardware. In Proceedings of the ACM SIGGRAPH 2005 Courses, Los Angeles, CA, USA, 31 July–4 August 2005; p. 193-es. [Google Scholar]
- Zollhöfer, M.; Nießner, M.; Izadi, S.; Rehmann, C.; Zach, C.; Fisher, M.; Wu, C.; Fitzgibbon, A.; Loop, C.; Theobalt, C.; et al. Real-time non-rigid reconstruction using an RGB-D camera. ACM Trans. Graph. (ToG) 2014, 33, 1–12. [Google Scholar] [CrossRef]
- Zollhöfer, M.; Dai, A.; Innmann, M.; Wu, C.; Stamminger, M.; Theobalt, C.; Nießner, M. Shading-based refinement on volumetric signed distance functions. ACM Trans. Graph. (ToG) 2015, 34, 1–14. [Google Scholar] [CrossRef]
- Heide, F.; Steinberger, M.; Tsai, Y.T.; Rouf, M.; Pająk, D.; Reddy, D.; Gallo, O.; Liu, J.; Heidrich, W.; Egiazarian, K.; et al. Flexisp: A flexible camera image processing framework. ACM Trans. Graph. (ToG) 2014, 33, 1–13. [Google Scholar] [CrossRef]
- Nießner, M.; Zollhöfer, M.; Izadi, S.; Stamminger, M. Real-time 3D reconstruction at scale using voxel hashing. ACM Trans. Graph. (ToG) 2013, 32, 1–11. [Google Scholar] [CrossRef]
- Thies, J.; Zollhofer, M.; Stamminger, M.; Theobalt, C.; Nießner, M. Face2face: Real-time face capture and reenactment of rgb videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2387–2395. [Google Scholar]
- Wu, B.; Wang, Z.; Wang, H. A GPU-based multilevel additive schwarz preconditioner for cloth and deformable body simulation. ACM Trans. Graph. (TOG) 2022, 41, 1–14. [Google Scholar] [CrossRef]
- DeVito, Z.; Mara, M.; Zollhöfer, M.; Bernstein, G.; Ragan-Kelley, J.; Theobalt, C.; Hanrahan, P.; Fisher, M.; Niessner, M. Opt: A domain specific language for non-linear least squares optimization in graphics and imaging. ACM Trans. Graph. (TOG) 2017, 36, 1–27. [Google Scholar] [CrossRef]
- Mara, M.; Heide, F.; Zollhöfer, M.; Nießner, M.; Hanrahan, P. Thallo–scheduling for high-performance large-scale non-linear least-squares solvers. ACM Trans. Graph. (TOG) 2021, 40, 1–14. [Google Scholar] [CrossRef]
- Lai, Z.; Wei, K.; Fu, Y.; Härtel, P.; Heide, F. ∇-Prox: Differentiable Proximal Algorithm Modeling for Large-Scale Optimization. ACM Trans. Graph. 2023, 42, 1–19. [Google Scholar] [CrossRef]
- Bangaru, S.P.; Wu, L.; Li, T.M.; Munkberg, J.; Bernstein, G.; Ragan-Kelley, J.; Durand, F.; Lefohn, A.; He, Y. SLANG.D: Fast, Modular and Differentiable Shader Programming. ACM Trans. Graph. 2023, 42, 1–28. [Google Scholar] [CrossRef]
- Barker, J.; Martin, S.; Guy, R.; Munoz-Lopez, J.E.; Kapoulkine, A.; Chang, K. Moving mobile graphics. In Proceedings of the SIGGRAPH Courses, Virtual, 17 August 2020; pp. 1–2. [Google Scholar]
- Kim, S.; Harada, T.; Kim, Y.J. Energy-efficient global illumination algorithms for mobile devices using dynamic voltage and frequency scaling. Comput. Graph. 2018, 70, 198–205. [Google Scholar] [CrossRef]
- Wang, R.; Yu, B.; Marco, J.; Hu, T.; Gutierrez, D.; Bao, H. Real-time rendering on a power budget. ACM Trans. Graph. (TOG) 2016, 35, 1–11. [Google Scholar] [CrossRef]
- Zhang, Y.; Ortin, M.; Arellano, V.; Wang, R.; Gutierrez, D.; Bao, H. On-the-Fly Power-Aware Rendering. Comput. Graph. Forum 2018, 37, 155–166. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, R.; Huo, Y.; Hua, W.; Bao, H. Powernet: Learning-based real-time power-budget rendering. IEEE Trans. Vis. Comput. Graph. 2021, 28, 3486–3498. [Google Scholar] [CrossRef]
- Nah, J.H.; Lim, Y.; Ki, S.; Shin, C. Z 2 traversal order: An interleaving approach for VR stereo rendering on tile-based GPUs. Comput. Vis. Media 2017, 3, 349–357. [Google Scholar] [CrossRef]
- Yan, X.; Xu, J.; Huo, Y.; Bao, H. Neural Rendering and Its Hardware Acceleration: A Review. arXiv 2024, arXiv:2402.00028. [Google Scholar]
- FreeOCL: Multi-Platform Implementation of OpenCL 1.2 Targeting CPUs. Available online: http://www.zuzuf.net/FreeOCL/ (accessed on 20 April 2025).
- Saad, Y. Iterative methods for linear systems of equations: A brief historical journey. In 75 Years of Mathematics of Computation; Contemporary Mathematics; Brenner, S.C., Shparlinski, I.E., Shu, C., Szyld, D.B., Eds.; American Mathematical Society: Providence, RI, USA, 2020; Volume 754, pp. 197–215. [Google Scholar]
- Chow, E.; Frommer, A.; Szyld, D.B. Asynchronous Richardson iterations: Theory and practice. Numer. Algorithms 2021, 87, 1635–1651. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; SIAM: Bangkok, Thailand, 2003. [Google Scholar]
- Kincaid, D.R.; Oppe, T.C.; Young, D.M. ITPACKV 2D User’s Guide; Technical Report; Texas University: Austin, TX, USA, 1989. [Google Scholar]
- Barrett, R.; Berry, M.; Chan, T.F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; Van der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods; SIAM: Bangkok, Thailand, 1994. [Google Scholar]
- Jia, F.; Zhang, D.; Cao, T.; Jiang, S.; Liu, Y.; Ren, J.; Zhang, Y. Codl: Efficient cpu-gpu co-execution for deep learning inference on mobile devices. In Proceedings of the 20th Annual International Conference on Mobile Systems, Applications and Services, Portland, OR, USA, 27 June–1 July 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 209–221. [Google Scholar]
- Cooper, B.; Scogland, T.R.W.; Ge, R. Shared Virtual Memory: Its Design and Performance Implications for Diverse Applications. In Proceedings of the 38th ACM International Conference on Supercomputing, Kyoto, Japan, 4–7 June 2024. [Google Scholar]
- Kim, H.; Sim, J.; Gera, P.; Hadidi, R.; Kim, H. Batch-aware unified memory management in GPUs for irregular workloads. In Proceedings of the Twenty-Fifth International Conference on Architectural Support for Programming Languages and Operating Systems, Lausanne, Switzerland, 16–20 March 2020; pp. 1357–1370. [Google Scholar]
- Jin, Z.; Vetter, J.S. Evaluating Unified Memory Performance in HIP. In Proceedings of the 2022 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Lyon, France, 30 May–3 June 2022; IEEE: New York, NY, USA, 2022; pp. 562–568. [Google Scholar]
- Kunegis, J.; Preusse, J. Fairness on the web: Alternatives to the power law. In Proceedings of the 4th Annual ACM Web Science Conference, Evanston, IL, USA, 22–24 June 2012; pp. 175–184. [Google Scholar]
- Yesil, S.; Heidarshenas, A.; Morrison, A.; Torrellas, J. WISE: Predicting the performance of sparse matrix vector multiplication with machine learning. In Proceedings of the 28th ACM SIGPLAN Annual Symposium on Principles and Practice of Parallel Programming, Montreal, QC, Canada, 25 February–1 March 2023; pp. 329–341. [Google Scholar]
- Davis, T.A.; Hu, Y. The university of Florida sparse matrix collection. ACM Trans. Math. Softw. 2011, 38, 1–25. [Google Scholar] [CrossRef]
- Pérez, P.; Gangnet, M.; Blake, A. Poisson image editing. ACM Trans. Graph. 2003, 22, 313–318. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).