Design and Modelling of a Bidirectional Front-End for Resonating Sensors Based on Pseudo Floating Gate Amplifier ^†

Abstract

In this paper, we characterize and model a bidirectional front-end based on pseudo-floating gate amplifier (PFGA) for actuation and read-out of resonating sensors. The basic idea consists of swapping the power supply of the PFGA in order to change the directionality of the front-end. A detailed description of the system has been discussed in this paper and supported by simulations and measurement results. A prototype has been fabricated using discrete components and tested with a real transducer (Murata MA40S4) and a Butterworth Van Dyke (BvD) load, which has proved to be proved to be a well approximated model for resonant sensors. The bidirectional amplifier has been implemented with the integrated circuit CD4007UB, which is a commercial discrete component containing low leakage MOSFET. The values chosen for the BvD load are $R_b=330$ $\mathsf{\Omega }$, $L_m=60$ mH, $C_s=450$ pF, $C_E=2.2$ nF, which are approximately the same values of the lumped parameters reported in the data-sheet of the real sensor. This transducer is characterized by a nominal resonant frequency of 40 kHz. Measurement results show good fitting with the models developed in this work and the possibility to predict the sensor response by using the BvD load.

1. Introduction

Resonant sensors are based on a vibrating structure, which changes their resonant frequency depending on the variations of a particular physical quantity in the surrounding environment [1]. The changing in the resonant frequency is due to variations of the stiffness or mass of the mechanical structure. Resonant sensors have great potential for numerous applications such as ultrasound, medical, military and many others. This is due to the fact that they offer high accuracy, high resolution and low drift [2,3]. In many of these fields, these types of sensors can be used to measure pressure, acceleration, rotation, etc. Different physical principles can be used to actuate a resonant sensor such as magnetic, piezoelectric, electrostatic, etc. [4,5]. Regardless of the technology utilized to realize this type of sensor, they have to be first activated and thereafter their response read-out. There are three common methods to perform these two operations: impedance analysis, oscillator-based read-out and ring-down measurement [6]. 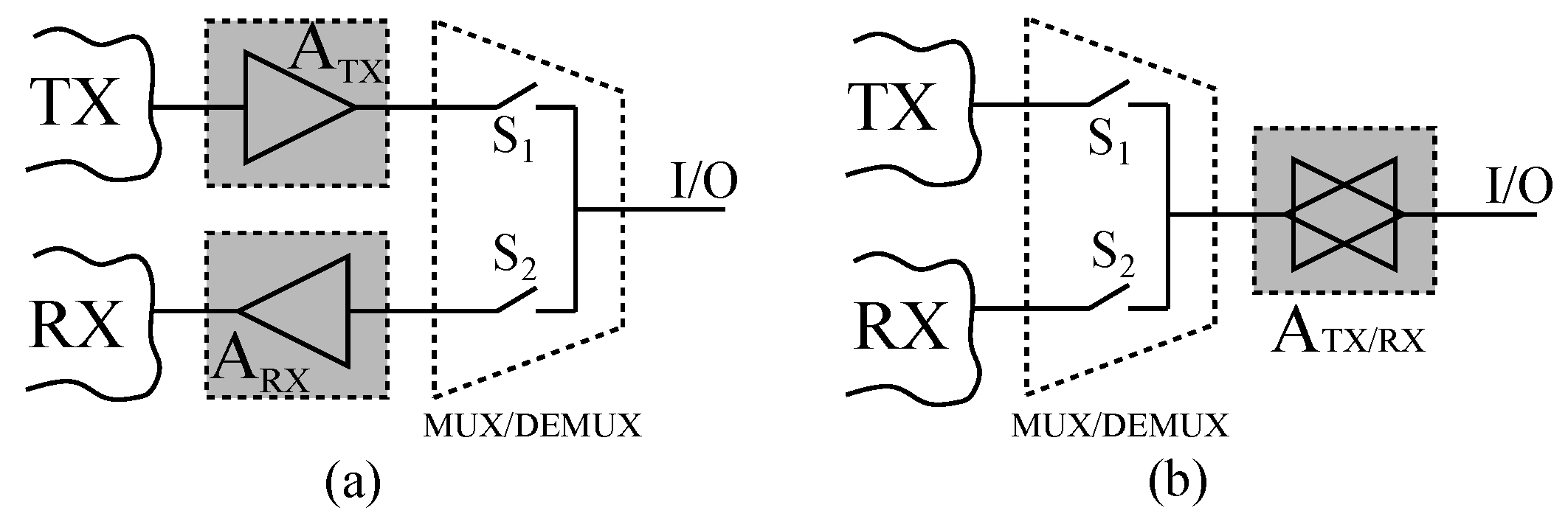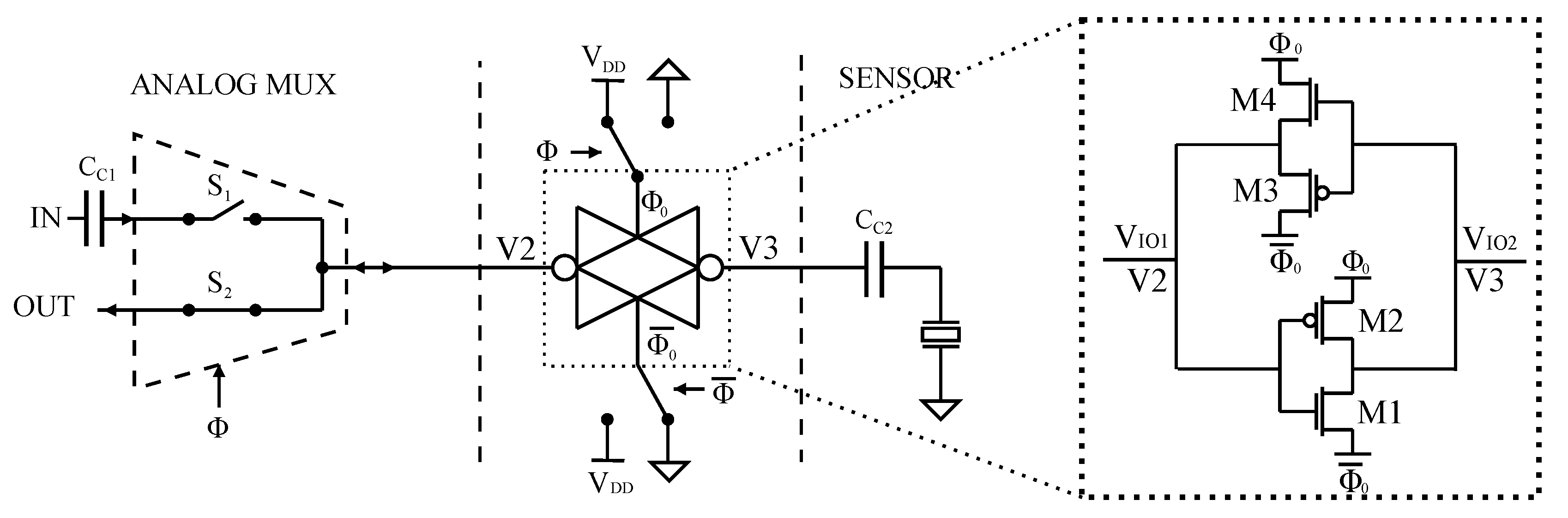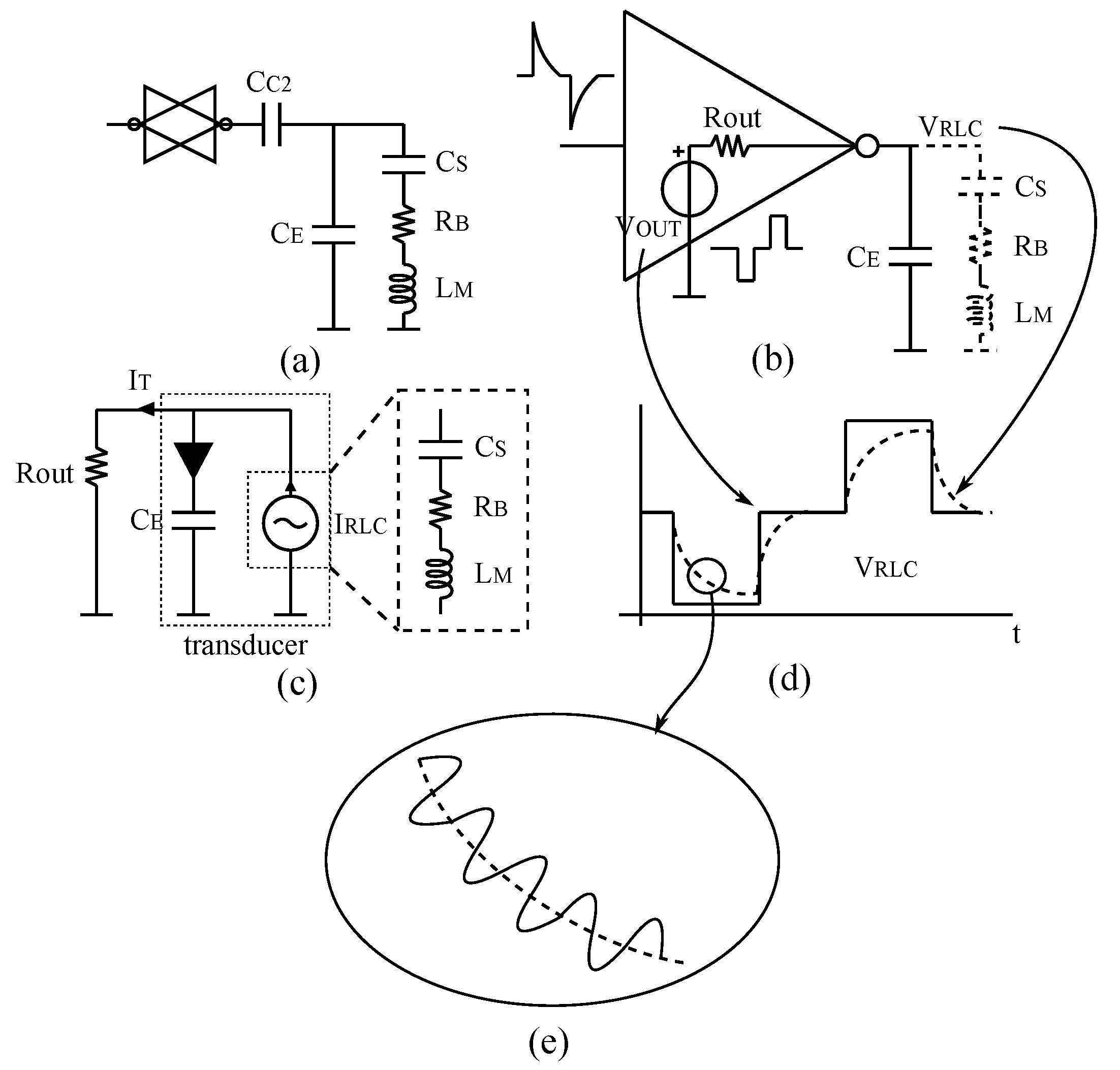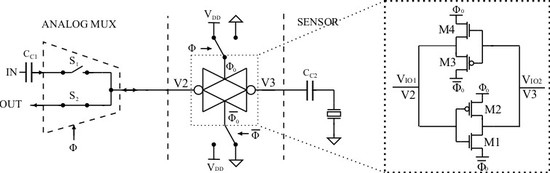The first method is in general time consuming because the reading operation is based on a sweep in frequency of the exciting source [7]; the second one is characterized by high power dissipation [8,9] mainly due the control system necessary to track the resonant frequency. Therefore, in this paper the third method will be applied to read-out the sensor. Typically, the measurement set-up for this technique requires two different circuits as shown in Figure 1a.

One is used to excite the sensor (TX) and the other to read the response (RX) but both use an amplifier as the main building block to implement the analogue front-end (${\mathrm{A}}_{\mathrm{TX}},{\mathrm{A}}_{\mathrm{RX}}$). These two front-ends work alternatively by means of a multiplexer/demultiplexer, which addresses correctly the flow of the signals. The sensor response read at the output terminal of the front-end consists in a sinusoidal oscillation, which decays exponentially due to the mechanical damping. It contains two types of information about the resonant sensor, i.e., the resonant frequency and the quality factor, the last one can be extracted by using a curve fitting method. The frequency of the output signal can be precisely measured by detecting, for example, the zero crossing points, which is usually performed by a digital system [10]. Thus, the output signal of the resonant sensor is often referred to as “quasi-digital”, which can be interpreted directly by digital electronics without the use of an analogue to digital (A/D) converter [11]. Due to the intrinsic digital nature of the output waveform, these types of sensors are suitable to realize precise control systems characterized by high reliability, low error rates and low susceptibility to the external interferences and noise [12]. Even though the information about the measurand is typically extracted from the resonant frequency of the output signal, the amplitude and the phase can be also used to carry information about the physical quantity under measurement in particular applications [13]. Nowadays, the design of electronic circuits used to implement sensor front-end is focused on compactness and low power consumption. In particular, in those applications where resonating sensors are utilized, a possible solution is to implement a bidirectional front-end based on pseudo floating gate amplifier (PFGA). PFGA has been widely applied to implement many and different types of electronic devices such as: multivalued gate (MV) [14], analog to digital converters [15], analog circuits such as band pass filters [16,17,18,19], tunable filters controlled with bulk voltages [20], tunable dual-band pass filters [21], filters based on current-starved PFGA [22,23], reconfigurable analogue circuits [24], to implement mixer and extractor [25], multiplexer/demultiplexer [26]. Furthermore, the bidirectionality of PFGA have been introduced in [19,24,25,26,27,28], but never deeply investigated. The first time the PFGA had been thought of as driver for resonant circuits was in Azadmehr et al. [27]. Such a system was simulated and proved to be, at least theoretically, a valid solution for the purpose. Later on, a prototype was developed to verify the concept with a resistance,inductance,capacitance (RLC) load [29] and a real piezoelectric sensor [30]. The aim of this paper consists of providing the design rules of the proposed front-end, which allow for optimizing this type of amplifier for driving and read-out resonating sensors.

The paper is organized as follows: Section 2 describes the basic concept used to extract a model of a resonating sensor. In Section 3, it is explained how to use PFGA to implement a bidirectional amplifier. In Section 4, the analysis and modelling of the bidirectional front-end is provided. Section 5 provides simulations results to verify the validity of the modelling discussed in the previous section and the design rules. Section 6 describes the measurement set-up used to perform the measurements. Section 7 presents the measurement results of the tests performed on the prototype. The paper terminates with the conclusions in Section 8.

2. Resonant Sensor Model

An electrical characterization of a resonant sensor is of fundamental importance to understand how it interacts with the electronic front-end. One of the most common methods to model a resonant sensor is based on LEM (Lumped Element Model) technique, which provides a good approximated way to predict the dynamic behaviour of this device [31] . This model describes a somewhat complex mechanical system in terms of mass-spring-damper elements, which are often referred to as the mechanical equivalent of the R-L-C elements in the electrical domain . This analogy is often used to extract the dynamic behaviour or the frequency response of a mechanical structure by means of the electrical circuit theory [32]. A general model of a resonant sensor is shown in Figure 2a.

Unfortunately, this model is not easy to apply in a first-hand design because it is highly nonlinear. However, this circuit can be simplified applying a linearization method, which leads to the model represented in Figure 2b. These parameters are often referred to as the motional resistance (${\mathrm{R}}_{\mathrm{b}}$), the motional capacitance (${\mathrm{C}}_{\mathrm{s}}$) and the motional inductance(${\mathrm{L}}_{\mathrm{m}}$) [33]. Therefore, the simplest model of a resonating sensor can be represented by a series RLC circuit in the electrical domain. Furthermore, when the parasitic capacitance between the electrodes of the transducer assumes relatively high values, then a capacitor (${\mathrm{C}}_{\mathrm{E}}$) must be added in parallel to the series RLC. This capacitor is known as feed-through capacitance. The effect of this parameter can be minimized reducing its geometrical dimensions, for instance implementing it in MEMS (Micro Electro-Mechanical Systems) technology. The whole model is often referred to as Butterworth Van Dyke (BvD) model, and it provides more accurate results than the only RLC series circuit. Alternative models, which take into account other non-idealities of the resonant device are: the Guan model [34] and the transmission line model for piezoelectric sensors [35]. In this paper, the accuracy of the BvD model will be proved to be sufficient for the purpose of this work.

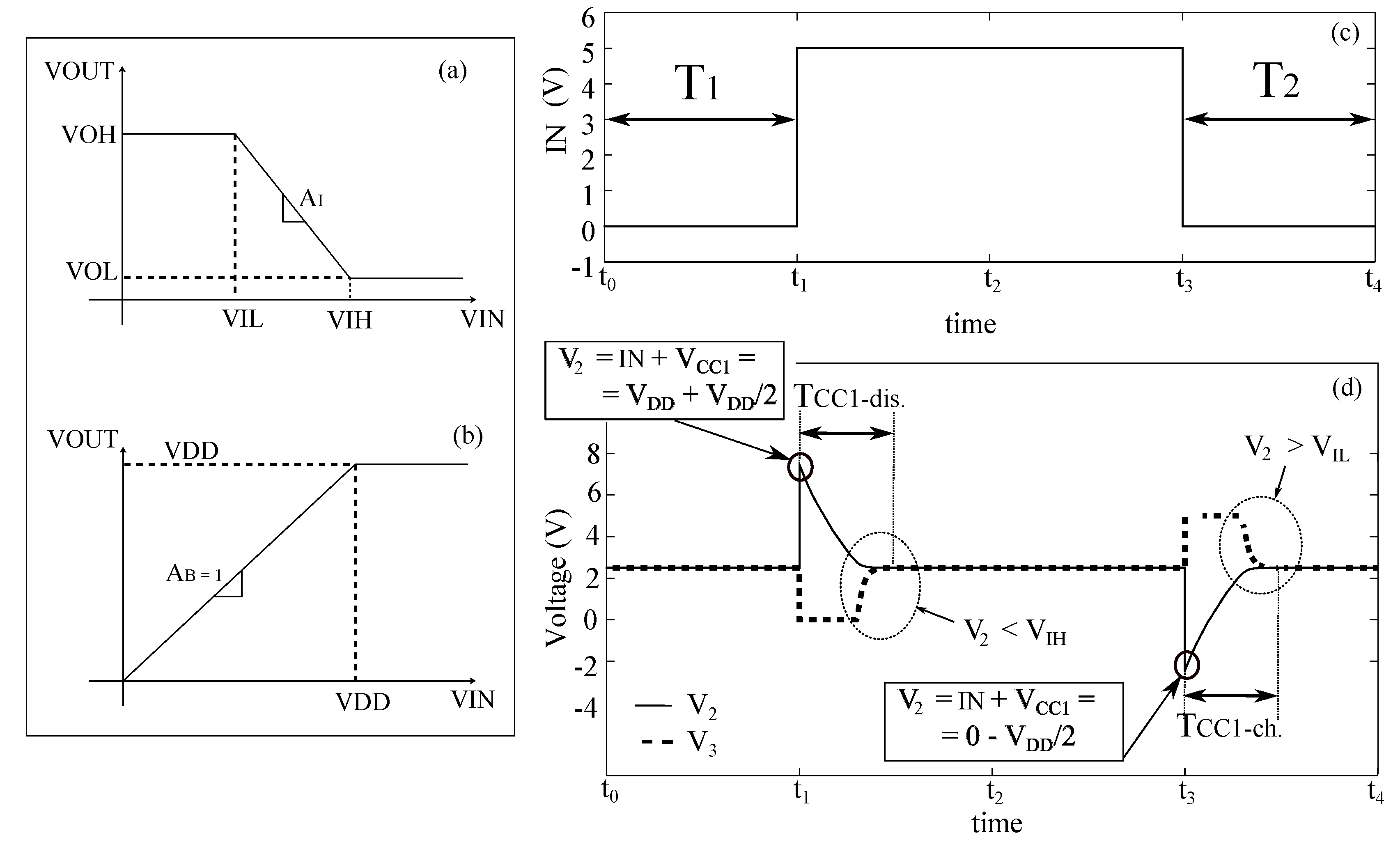
3. Bidirectional Amplifier Based on PFGA

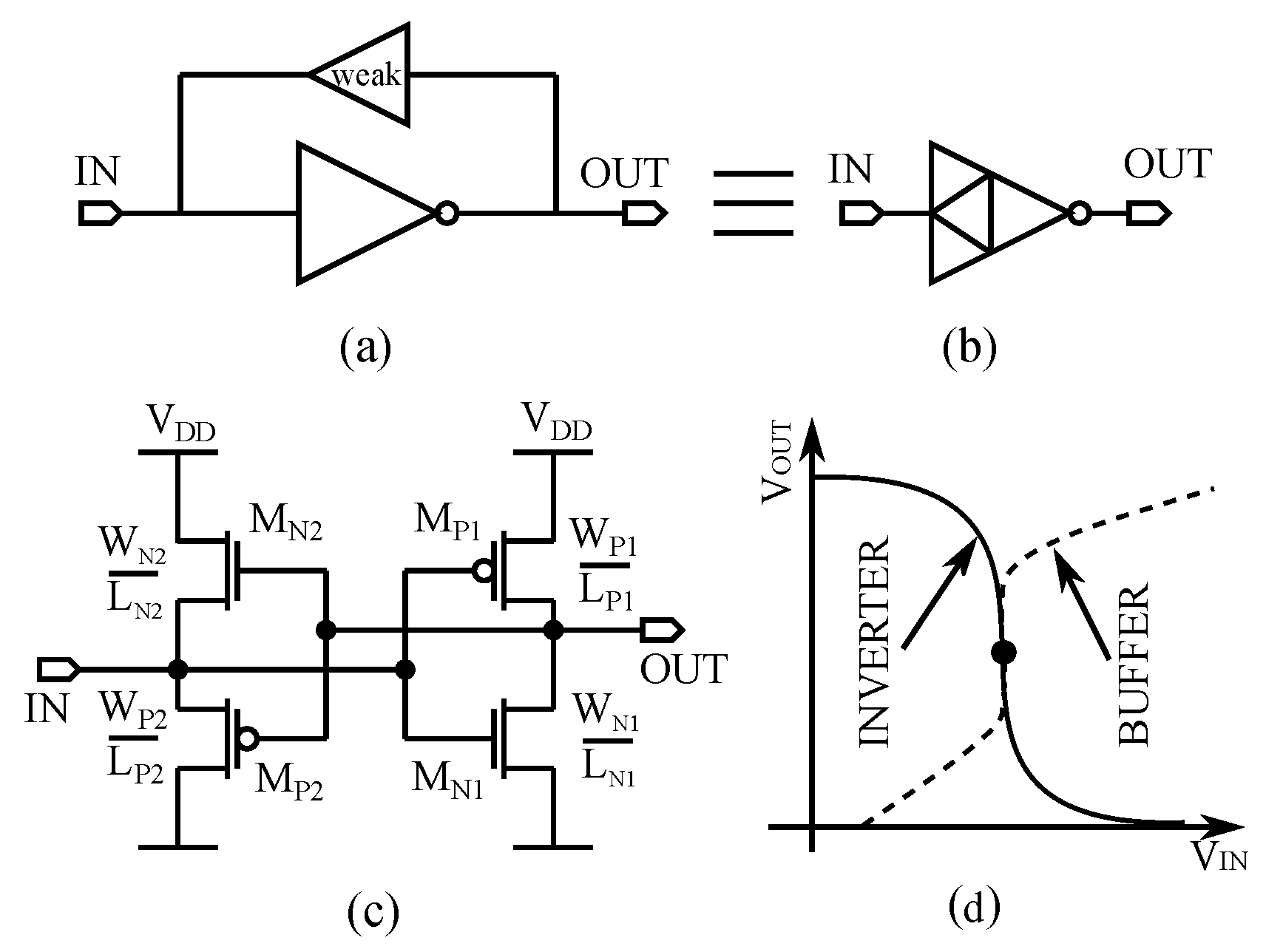
The Pseudo Floating gate Amplifier (PFGA) represented in Figure 3 is the building block of the proposed bidirectional front-end. It provides compactness and possibility of low power circuits implementation because of the small number of transistors. [20] provides a detailed description of the basic principle of the PFGA.

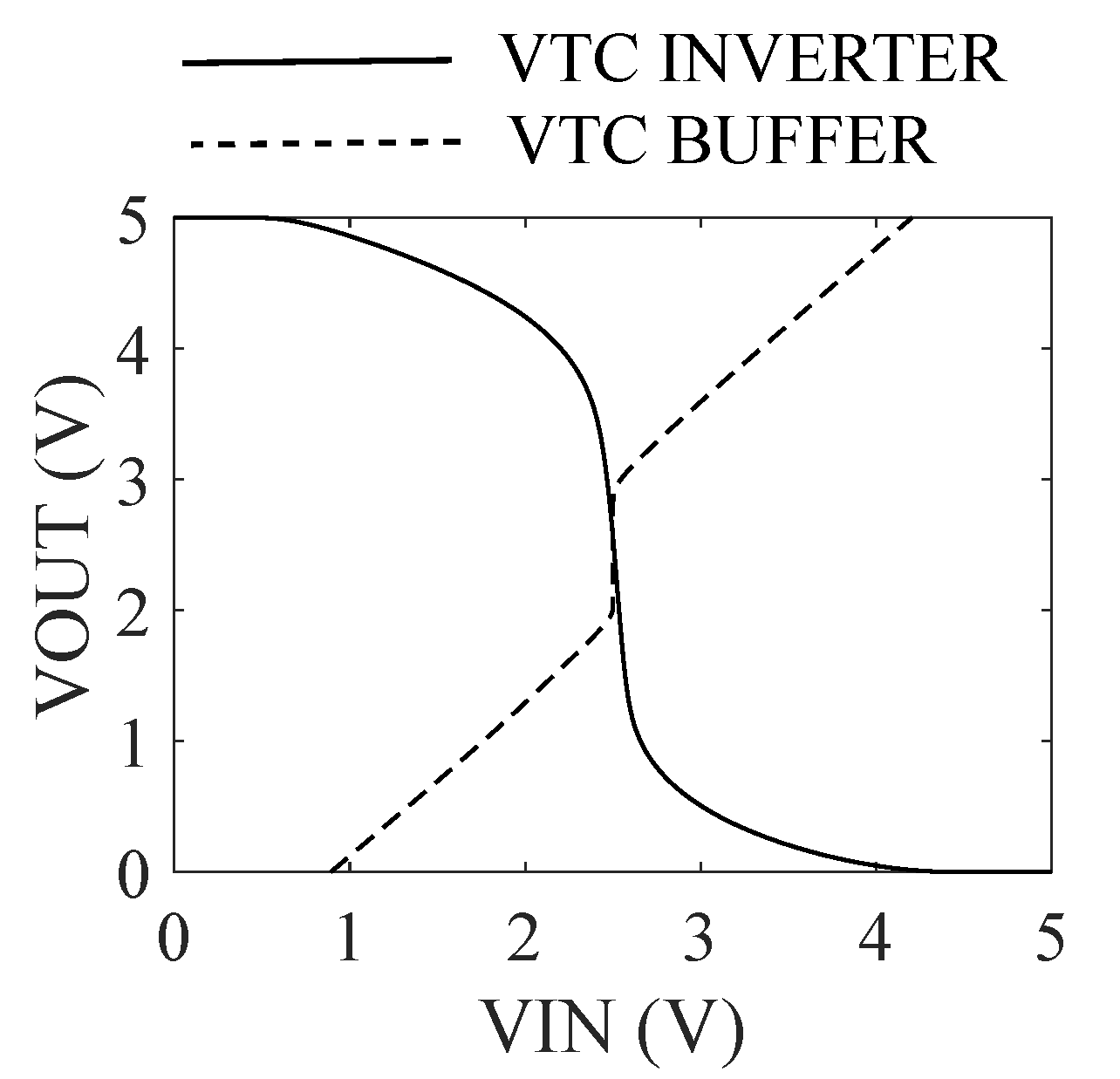
The PFGA is composed of a logic inverter closed in a negative feedback loop with a voltage buffer, which realizes the bias network of the inverter. The steady state of the PFGA is achieved, when both the inverter and the voltage buffer are in equilibrium. This situation can be graphically represented as the intersection of the voltage transfer characteristic curves of the inverter and the voltage buffer, as shown in Figure 3d, and it occurs ideally when ${\mathrm{V}}_{\mathrm{IN}}={\mathrm{V}}_{\mathrm{OUT}}={\mathrm{V}}_{\mathrm{DD}}/2$. The PFGA presents a band pass behaviour, where the low cut-off frequency depends on the capacitance at the input node and the output resistance of the voltage buffer, while the high cut-off frequency depends on the output resistance of the inverter and the load capacitance. Therefore, the design of these two elements set the bandwidth of the whole amplifier. Secondary effects such as offset, leakages and nonlinearities have been already discussed in literature, but they will be re-mentioned during this work to emphasize their effects in this application. The PFGA presents a small transconductance inherited by the logic inverter inside this structure, which lowers the gain of the amplifier. Nevertheless, the sensitivity of the amplifier can be increased by cascading more than one PFGA. This type of amplifier has already been proved to be functional if implemented in high leakage CMOS (Complementary metal oxide semiconductor) technologies because the biasing of the inverter is based on the channel leakages of the voltage buffer. However, an implementation in low leakage processes introduces new challenges. The most important is the inability of the system to reach the equilibrium state because the leakage currents are too low to drive the feedback reaction and bring back the system to the ideal state in a reasonable time. 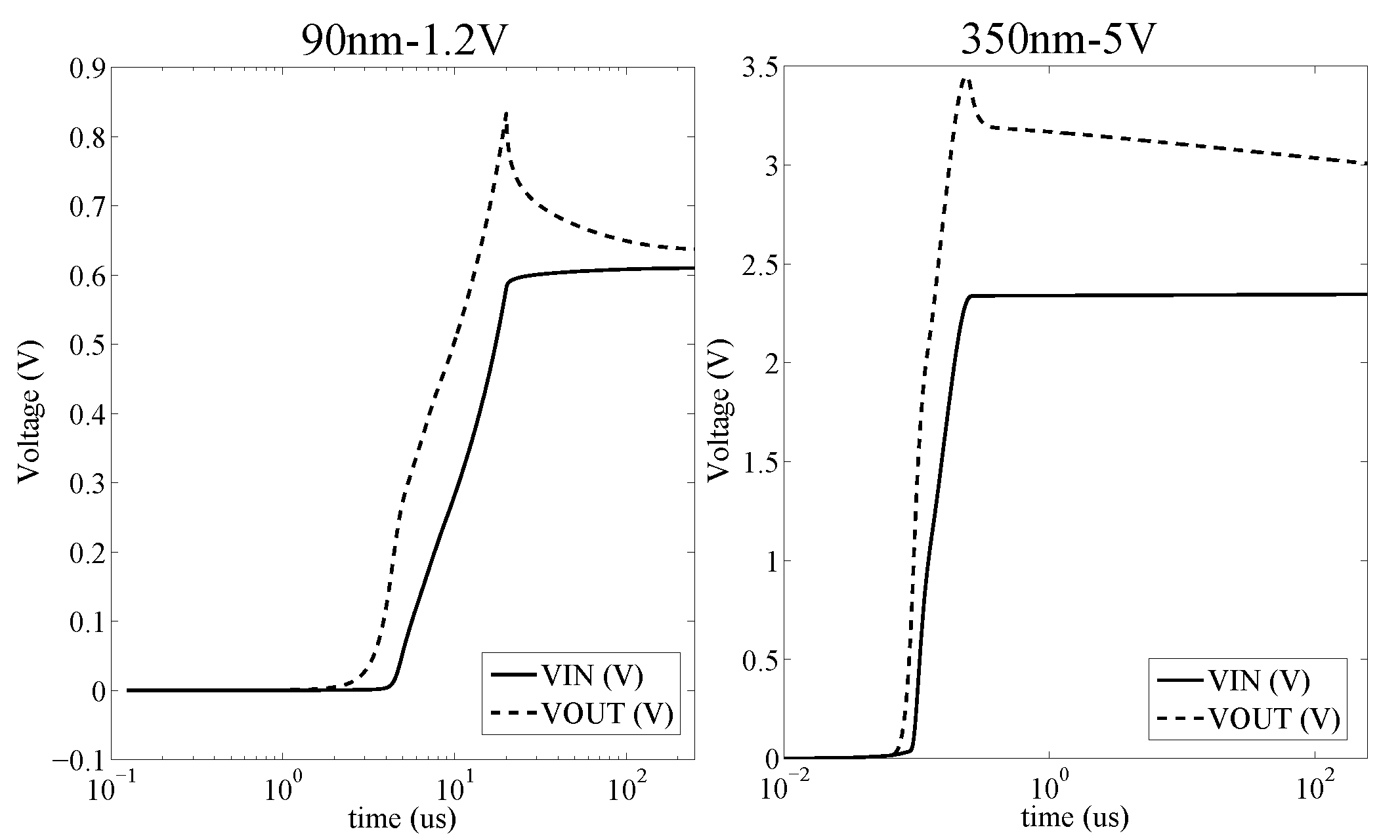A simple representation of this problem is shown in Figure 4.

Figure 4 compares the transient time to reach the equilibrium state of two PFGA, one implemented in high leakage CMOS process Predictive Technology Model (PTM-90nm) and the other one in low leakage CMOS process (Austria Mikro Systeme AMS-350nm). It can be observed that the high leakage PFGA does not take a long time to approach ${\mathrm{V}}_{\mathrm{DD}}/2=0.6$ V, while the low leakage PFGA takes a much longer transient time before it reaches the equilibrium state. This characteristic would be already sufficient to limit the implementation of the bidirectional amplifier to high leakage CMOS processes; however, in this paper, it will be proved that, thanks to the working operation of this front-end, low leakage technologies are also suitable to realize this device.

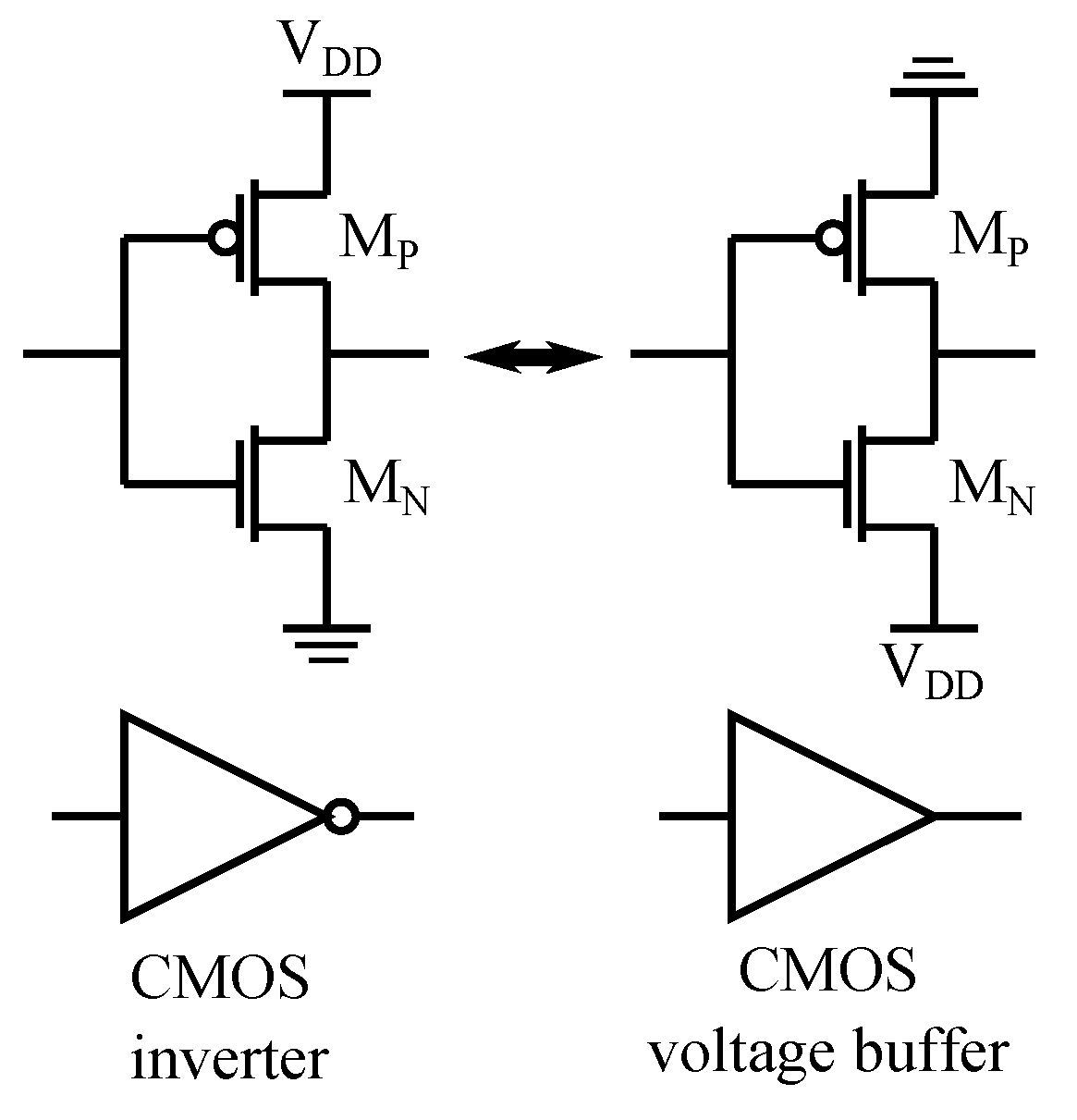
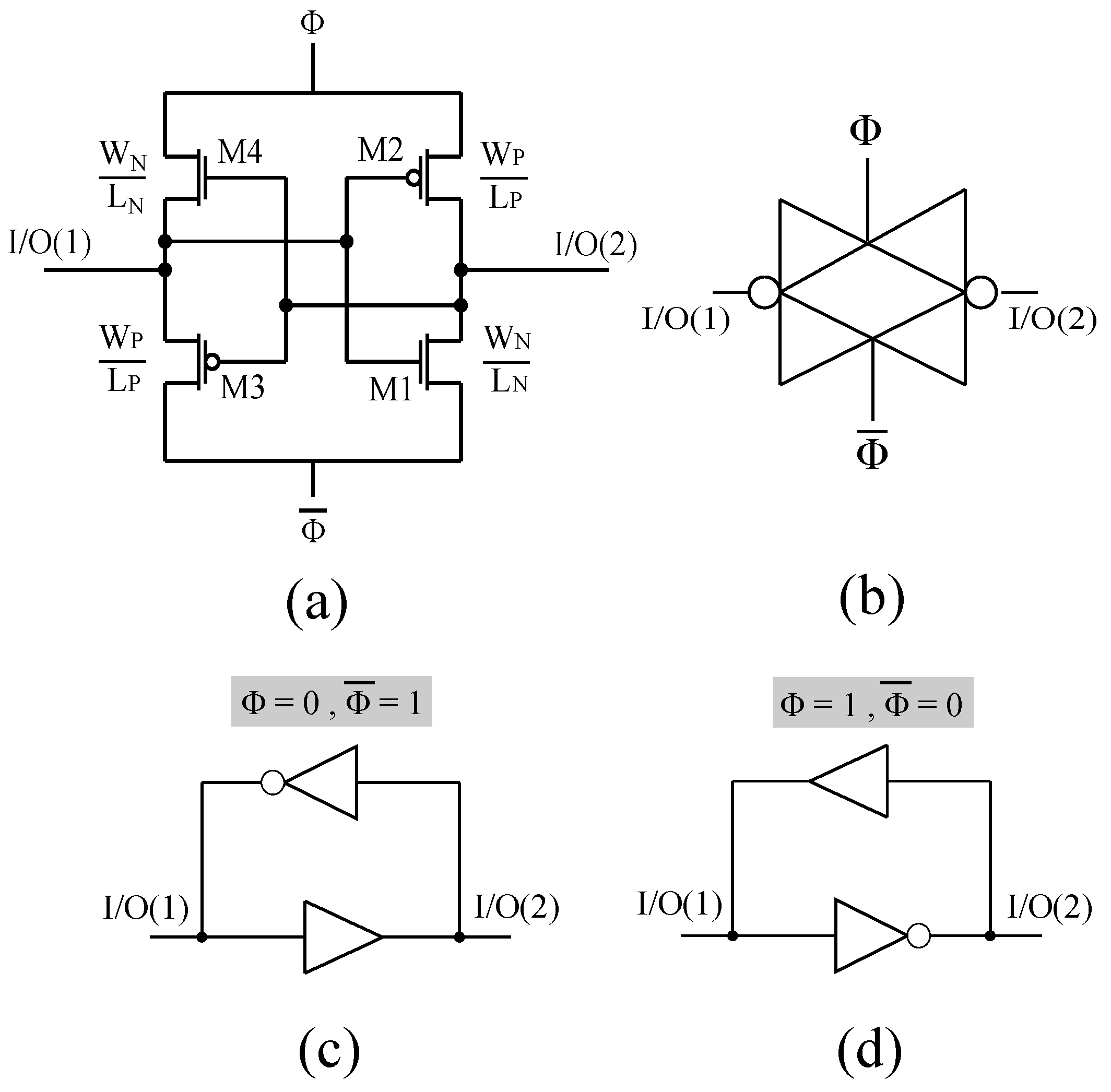
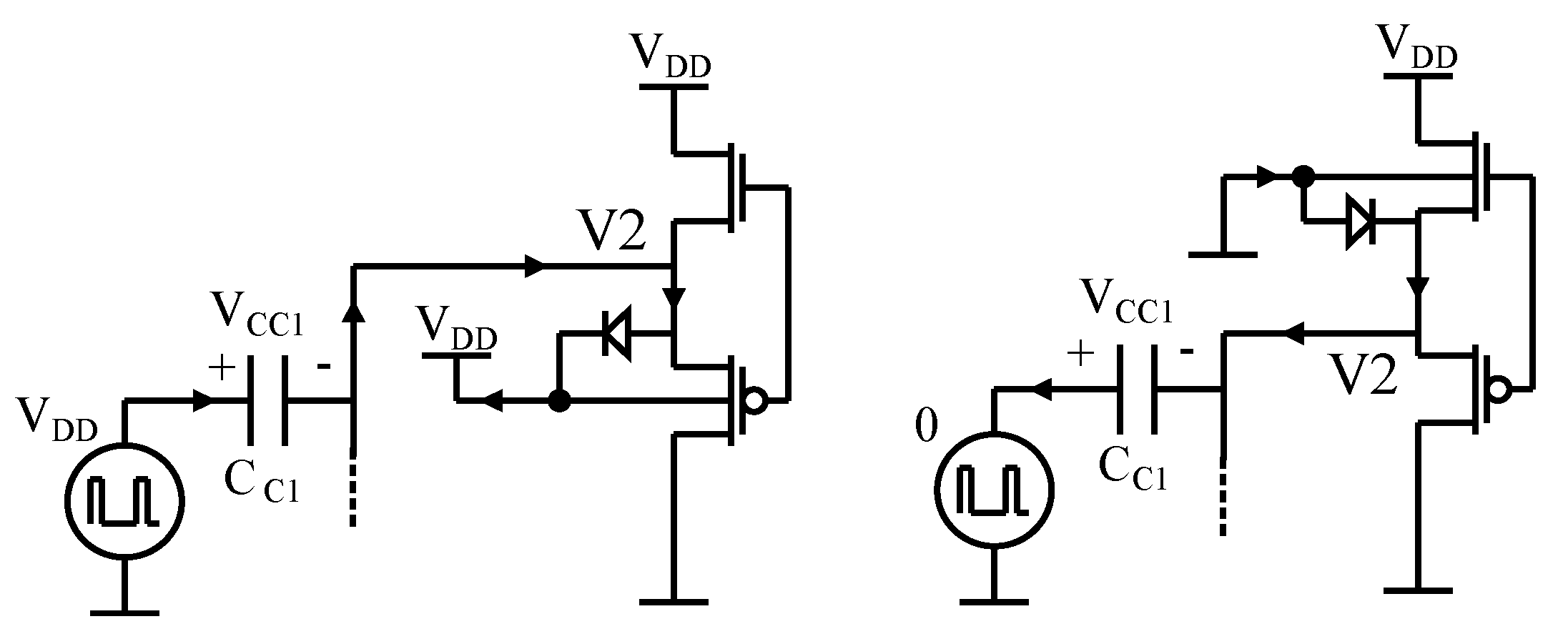
The bidirectionality of the PFGA is achieved by swapping the rails of the power supply. Indeed, the CMOS inverter and the CMOS voltage buffer in the PFGA present a sort of symmetry, which is highlighted in Figure 5.

The working principle of the bidirectional amplifier has been represented in Figure 6 and can be summarized as follows. The power supply of the PFGA is now considered a control signal and indicated with $\mathsf{\Phi }$ and $\overline{\mathsf{\Phi }}$. Signals can flow from I/O(1) to I/O(2) when $\mathsf{\Phi }=$ VDD and $\overline{\mathsf{\Phi }}=$ GND, and vice versa, signals flow from port I/O(2) to port I/O(1) when $\mathsf{\Phi }=$ GND and $\overline{\mathsf{\Phi }}=$ VDD as shown in Figure 6c,d. From an ideal point of view, the bidirectional amplifier can be considered as a normal PFGA, which mirrors or flips when the power supply rails are swapped.

The symbol adopted for this circuit shown in Figure 6b follows by the fact that the amplifier is implemented by a logic inverter, which reverses its direction. At transistor level , it is possible to recognize that if $\mathsf{\Phi }=1$, $\overline{\mathsf{\Phi }}=0$ then M1 and M2 realize the inverter while M3 and M4 the buffer. If $\mathsf{\Phi }=0$, $\overline{\mathsf{\Phi }}=1$, then M1 and M2 realize the buffer while M3 and M4 the inverter. The bidirectional amplifier obtained is compact, made only by four transistors, which implies a small occupation of area on the chip and potentially lower power dissipation.

4. Front-End Modelling

4.1. Working Principle

The proposed front-end is shown in Figure 7 and it is composed of two coupling capacitors ($C_{C1}$, $C_{C2}$), 1 analogue multiplexer/demultiplexer (${\mathrm{S}}_1,{\mathrm{S}}_2$), the bidirectional PFGA and a resonant sensor. The control signals $\mathsf{\Phi },\overline{\mathsf{\Phi }}$ are used to control the switches, which connect opportunely the power supply of the bidirectional amplifier. The effective value of the power supply is represented by the signals ${\mathsf{\Phi }}_0,\overline{{\mathsf{\Phi }}_0}$. The working principle can be divided into two phases: actuation mode (${\mathsf{\Phi }}_0=$ VDD, $\overline{{\mathsf{\Phi }}_0}=$ 0, ${\mathrm{S}}_1$ = close, ${\mathrm{S}}_2$ = open) and read-out mode (${\mathsf{\Phi }}_0=0$, $\overline{{\mathsf{\Phi }}_0}=$ VDD, ${\mathrm{S}}_1$ = open, ${\mathrm{S}}_2$ = close). During the actuation mode, a signal is applied at the input terminal (IN), which passes through the amplifier and actuates the resonant sensor. Then, the sensor reacts generating an electrical oscillation characterized by a frequency that depends on the environmental conditions. This frequency is usually known by the name of resonant frequency. This signal will be read when the front-end changes its state to read-out mode. During this phase, the sensor response is amplified by the bidirectional amplifier and read-out from the output terminal (OUT) of the system. The simplest way to excite the resonant sensor consists in applying a sinusoidal signal at the input terminal during the actuation mode. However, given the narrow band of the load, the frequency of the input signal should be precisely tuned, which makes it difficult to use for this purpose. Furthermore, the resonant frequency is not fixed because it depends on the value of the measurand. An alternative type of input signal, which allows for maximizing the transfer of energy to the transducer during the actuation is obtained by using an amplitude shift keying modulation (ASK). By selecting the frequency of the carrier equal to the resonant frequency of the transducer, it is possible to provide a wide spectrum signal centred in the middle of the narrow bandwidth of the transducer. However, the generation of this signal requires a modulator that increases the complexity of the whole front-end. For all of these reasons, it has been chosen to excite the transducer by using a simple wide bandwidth signal such as an ideal electrical pulse (Dirac Delta function) or a step signal. The electrical pulse or step signal resembles a digital waveform; therefore, it seems reasonable to treat the bidirectional amplifier as a digital circuit during the actuation mode. On the other hand, in read-out mode, the bidirectional amplifier has to be treated as an analogue device since the purpose of this circuit is now to amplify the sensor response. The waveforms expected by an ideal bidirectional front-end are shown in Figure 8.

Figure 8 shows that the duration of the actuation should allow the propagation of the pulse from the input terminal to the sensor. This time interval is usually much shorter than the read-out mode, in which it is necessary to measure multiple periods of the output signal to increase the accuracy of the frequency measurement. The oscillation of the sensor (${\mathrm{V}}_{\mathrm{RLC}}$) is initiated by the input pulse (IN), but the output signal (OUT) can be measured only when the system changes its state in read-out mode. In order not to create ambiguity, the input and the output terminal of the front-end are named IN and OUT, while the input and the output nodes of the bidirectional amplifier are labelled as V2 and V3. Finally, the design of this front-end consists of researching the best value for the coupling capacitors and the parameters of the control signals such as frequency (${\mathrm{f}}_{\mathrm{sw}}$) and duty cycle (D). The following sections will provide the modelling of the bidirectional front-end, which will allow for defining design rules for these parameters.

4.2. Actuation Mode Modelling

First of all, the front-end in actuation mode has been modelled. A simple representation of the system behaviour during this phase is shown in Figure 9.

Figure 9 shows the dynamic of the signals at the input and output node of the bidirectional amplifier. When the state of the system passes in actuation mode $\mathsf{\Phi }:0\to 1$, the input voltage (IN) is initially equal to 0 V and $C_{C1}$ is connected to the input of the bidirectional amplifier (${\mathrm{V}}_2$). After ${\mathrm{S}}_1$ closes, the capacitor $C_{C1}$ is already charged at ${\mathrm{V}}_{\mathrm{DD}}/2$ from the previous actuation mode cycle. Thus, the system is already at the equilibrium point when the transition occurs, implying no variations at ${\mathrm{V}}_2$. This means that this transition doesn’t affect the dynamic of the system, but it just changes the directionality of the amplifier. Next, a rectangular pulse is applied at the input terminal of the front-end and the rising edge of this signal generates a spike at the input and at the output nodes of the bidirectional amplifier as shown in Figure 9b. At this point, the feedback in the PFGA reacts pulling the input and the output of the bidirectional amplifier toward the equilibrium value (${\mathrm{V}}_{\mathrm{DD}}/2$) as shown in Figure 9c. Similar situation occurs when the falling edge of the input pulse generates new spikes as shown in Figure 9d. Once again, the PFGA will react to this event bringing back the equilibrium as shown in Figure 9d. The previous analysis (actuation mode, $\mathsf{\Phi }=1$) reveals the behaviour of the bidirectional amplifier when excited by a pulse. The simulation in Figure 10 has been performed with piece-wise linear models represented in Figure 10a,b, which add further details about the waveforms in the circuit.

Figure 10d shows that the spikes at ${\mathrm{V}}_3$ are squared and they are more similar to rectangular pulses. This is due to the fact that to perform this simulation ${\mathrm{V}}_{\mathrm{IL}},{\mathrm{V}}_{\mathrm{IH}}$ are chosen very close to ${\mathrm{V}}_{\mathrm{DD}}/2$, thus narrowing the linear region of the inverter. Therefore, when ${\mathrm{V}}_{\mathrm{IN}}<{\mathrm{V}}_{\mathrm{IL}}$ or ${\mathrm{V}}_{\mathrm{IN}}>{\mathrm{V}}_{\mathrm{IH}}$, the voltage at ${\mathrm{V}}_3$ is still very close to one of the power supply rails and it reacts to the variations of ${\mathrm{V}}_2$ only when ${\mathrm{V}}_2$ assumes values in the linear region of the inverter VTC curve. The time necessary to bring the system back to the equilibrium state depends on the charge and discharge of the input coupling capacitor $C_{C1}$. Based on the polarity used for ${\mathrm{V}}_{\mathrm{C}\mathrm{C}1}$ in Figure 9, these two times are called ${\mathrm{T}}_{\mathrm{C}\mathrm{C}1-\mathrm{dis}.}$ and ${\mathrm{T}}_{\mathrm{C}\mathrm{C}1-\mathrm{ch}.}$ because they correspond to the discharge and charge of this capacitor respectively. Therefore, by tuning $C_{C1}$, it is possible to set the time during which ${\mathrm{V}}_3$ is fixed at one of the power supply rail. In particular, decreasing the value of $C_{C1}$, it is possible to reduce the time to charge and discharge this capacitor, which, in the limit, can be set to pull ${\mathrm{V}}_3$ toward ${\mathrm{V}}_{\mathrm{DD}}/2$ before it reaches one of the power supply rails. Since the amplitude of the signal ${\mathrm{V}}_3$ is related to the excitation of the transducer, it can be concluded that, by tuning $C_{C1}$, it is possible to vary the magnitude of the energy provided to the transducer and therefore it is possible to control the amplitude of the sensor response during the read-out mode. Other two important parameters are ${\mathrm{T}}_1$ and ${\mathrm{T}}_2$, which are the time intervals that define the relative position of the input pulse inside the actuation mode. The waveform of ${\mathrm{V}}_3$ showed in Figure 10 suggests that the resonant sensor will be excited two times, once for each edge of the input pulse. This is an unwanted phenomenon, which will be analyzed more in detail in the next section performing a simulation.

Figure 11 highlights another secondary effect, which is the turning on of the source-bulk pn junctions inside the PMOS (P-TYPE MOSFET) and the NMOS (N-TYPE MOSFET) of the voltage buffer. Indeed, the simulation with the piecewise linear models in Figure 10d shows that the spikes at the ${\mathrm{V}}_2$ assume values of $\frac{3V_{\mathrm{DD}}}{2}$ and $-\frac{{\mathrm{V}}_{\mathrm{DD}}}{2}$. These values do not belong to the power supply range and they turn on the pn juctions between the source and the body terminal of the MOSFET in the voltage buffer (M3,M4). This phenomenon could increase the power dissipation of the circuit or even worse, and it could start a destructive latch-up phenomenon in the transistors involved. Fortunately, it is possible to prevent the turning on of these pn junctions by using strong NMOS and PMOS in the the voltage buffer or smaller input coupling capacitor $C_{C1}$. This design strategy provides a faster reaction of the feedback when the system becomes imbalanced, so that ${\mathrm{V}}_2$ does not have enough time to reach values outside the power supply range.

Next, the effects of the signal generated by the bidirectional amplifier on the resonating sensor must be analyzed. The model utilized to study this dynamic of the system is shown in Figure 12a.

In order to provide a simple but useful model, a BvD load is used to mimic the behaviour of a resonating sensor. The coupling capacitor $C_{C2}$ has the purpose to separate the DC from the AC signals. Therefore, its value is usually much greater than all the other capacitances in this part of the circuit and it can be considered as a short circuit for most of the AC signals. Figure 12b provides a simple model of the amplifier derived by observing the waveform in Figure 10d. As shown by the piece-wise linear model, the bidirectional amplifier generates two opposite rectangular pulses. The circuit in Figure 12b is linear, so it is possible to evaluate the dynamic of the system by using the superimpose principle. The signal generated by the bidirectional amplifier $V_{OUT}$ is divided into two components as shown in Equation (1):

$$V_{OUT}=V_{OUT1}+V_{OUT2}=(\sum _{n=1}^{\infty }{V}_{OUT}(f_i)-V_{OUT}(f_{res}))+V_{OUT}(f_{res}).$$

(1)

$V_{OUT1}$ is composed of the same spectrum content of the signal $V_{OUT}$ except for the harmonic at the resonant frequency. The second component $V_{OUT2}$ is made of the only harmonic of $V_{OUT}$ at the resonant frequency. The effects of $V_{OUT1}$ can be evaluated considering the total impedance of the RLC elements to be $|Z_{RLC}(f\ne f_{res})|=\infty$. This is the reason why in Figure 12b the RLC has been drawn with dashed lines. Therefore, $V_{RLC1}$ is characterized by a waveform that increases and decreases exponentially since it depends only on the response of a low pass filter made of $R_{out}$ and $C_E$. The waveform obtained is represented in Figure 12d drawn with a dashed line. The effect of $V_{OUT2}$ is to excite the RLC element, which generates an oscillation at the resonant frequency. The RLC elements now behave like an oscillator, which generates a damped sinusoidal signal, so it can be modelled as a current source generator as shown in Figure 12c. This current is divided into two parts, a small part is absorbed by the amplifier, creating a sinusoidal drop voltage on its output resistance, but the greater part will flow through the capacitance $C_E$, because at the resonant frequency it usually shows a very low impedance. The second component of the voltage across the transducer can be calculated as: $V_{RLC2}=\left|Z_{CE}\right|*I_{RLC}$. Finally, the total voltage at this node is equal to $V_{RLC1}+V_{RLC2}$, which means it is a combination of a small sinusoidal oscillation enveloped over an exponential signal as shown in Figure 12e.

In conclusion, the models developed provide a simple way to predict the behaviour of the front-end during the actuation mode. In particular, the possibility to control the feedback rate by choosing the size of the MOSFET in the voltage buffer, the possibility to control the excitation of the transducer by choosing the value of $C_{C1}$, the possibility of latch-up of the source body pn junctions in the MOSFET of the voltage buffer and the effects of the actuation on the voltage across the transducer have all been explored. Furthermore, to minimize the drop voltage across $C_{C2}$, the value of this capacitor must be $\gg C_E+C_S$.

4.3. Modelling of the Transitions between Modes

The bidirectional front-end is characterized by two modes, which work alternatively. Ideally, during the transition between one mode to the other one, only the directionality of the amplifier should change and the electrical quantities in the circuit should not be affected by this event. However, secondary effects take place during these transitions, and this section will try to highlight them in order to have a detailed comprehension of the phenomena involved. First of all, the transition from read-out mode to actuation mode is described.

Variations of the input voltage ${\mathrm{V}}_2$ during this transition can generate variations at the output of the bidirectional amplifier with a consequent excitation of the transducer. This is a very likely situation because the steady state values of ${\mathrm{V}}_2$ and ${\mathrm{V}}_3$ are different, especially if the amplifier is implemented in low leakage technology. A possible scenario is shown in Figure 13.

Figure 13 shows that the steady state value of ${\mathrm{V}}_2$ and ${\mathrm{V}}_3$ changes depending on the directionality of the amplifier. This is due to the input offset intrinsic of the PFGA described in literature. However, if the PFGA is implemented in high leakage CMOS technology, this offset is very small and the effects can be neglected. On the other hand, if the amplifier is realized in low leakage technology, the effects of this transition must be taken into account. Nevertheless, there exists a design strategy to minimize the variations of ${\mathrm{V}}_2$ during this transition. Indeed, during an ideal read-out mode, the steady state value of ${\mathrm{V}}_2$ is ${\mathrm{V}}_{\mathrm{DD}}/2$, but the value of ${\mathrm{V}}_2$ at the beginning of the actuation mode depends on the value stored by the capacitor $C_{C1}$ at the end of the previous actuation mode. Therefore, looking at Figure 10d, it is clear that the condition to minimize the unwanted oscillations at the beginning of the actuation mode is to let $C_{C1}$ to ${\mathrm{V}}_{\mathrm{DD}}/2$ before changing the state of the system into read-out mode. This condition can be quantified as ${\mathrm{T}}_2\ge {\mathrm{T}}_{\mathrm{C}\mathrm{C}1-\mathrm{ch}}$. Next, if the oscillation at the beginning of the actuation mode is negligible, the input pulse can be applied in any moment and there are no constraints in the value of $T_1$. These two conditions will be successively used to define a formal constraint for the duration of the actuation mode.

Next, the transition from actuation mode to read-out mode must be analyzed. This transition doesn’t provide any particular phenomenon if the bidirectional amplifier is implemented in high leakage CMOS technology, but it does if implemented in low leakage process. Therefore, the second case is analyzed here to provide a detailed description of the dynamic of the system. A possible scenario is represented in Figure 14.

At $t=t_0$, the system is in actuation mode (region I). After that, the falling edge of the input pulse occurs and the voltage ${\mathrm{V}}_2$ drops suddenly. Next, the signal ${\mathrm{V}}_3$ rises immediately to respond to the input variation. The feedback reaction tries to bring back the equilibrium pushing these two voltages close to each other until the voltage buffer starts to work in weak inversion at which the dynamic stops (region II). During the dynamic represented in region II, the output waveform could be characterized by a small oscillation that overlaps over the main signal as shown in Figure 14. This is due to current from the transducer, which creates an alternating drop voltage across the output resistance of the inverter. Once the signal $\mathsf{\Phi }$ drops to zero the system passes in read-out mode and the node voltage ${\mathrm{V}}_3$ becomes now the input signal of the bidirectional amplifier, while ${\mathrm{V}}_2$ becomes the output. At the beginning of the read-out mode, ${\mathrm{V}}_3>{\mathrm{V}}_{\mathrm{DD}}/2$ and the inverter brings ${\mathrm{V}}_2$ to 0 V. Then, the PMOS of the voltage buffer (M2) starts to pull down the signal ${\mathrm{V}}_3$ while the PMOS of the inverter (M3) is now pulling up the output signal ${\mathrm{V}}_2$. This process ends when the voltage buffer turns off. For all of the dynamics in region III, both ${\mathrm{V}}_2$ and ${\mathrm{V}}_3$ present an AC component due to the oscillation of the transducer. The dynamics in region II and region III depends on the time constant of the input and the output node; however, it must be observed that the input of the voltage buffer is the signal, which approaches closer to ${\mathrm{V}}_{\mathrm{DD}}/2$, because it is the one that leads the reaction, while the output is just responding to the input variations. The ideal models provided for this transition do not exploit any other particular side effect, except the offset of the amplifier in read-out mode. This is actually not critical because, until the signal ${\mathrm{V}}_3$ is able to cross ${\mathrm{V}}_{\mathrm{DD}}/2$, a relatively wide oscillation can be observed at the output ${\mathrm{V}}_2$ and the frequency of the output waveform can still be measured by using the zero crossing point (${\mathrm{V}}_{\mathrm{DD}}/2$) method. Furthermore, even if the output oscillation is distorted the functionality of the circuit will not be affected because the quantity to measure is the output frequency rather than the amplitude of this signal.

In conclusion, it has been observed that, in order to optimize the transition of the bidirectional amplifier and prepare it for the read-out mode, the main constraint is that the average value of ${\mathrm{V}}_3$ must be very close to ${\mathrm{V}}_{\mathrm{DD}}/2$. Furthermore, an important condition has been provided to avoid oscillations at the beginning of the actuation mode. Finally, it has been emphasized that distortions at the output and at the input of the bidirectional amplifier will not affect the working operation of the whole front-end.

4.4. Read-Out Mode Modelling

During the read-out mode, the bidirectional front-end can be modelled as shown in Figure 15.

It can be observed that the bidirectional amplifier behaves like a PFGA, whose design rules are described in literature. The response of the sensor after being excited is modelled as a current source as shown in Figure 15. Most of this current will flow through CE (parasitic capacitance of the transducer) because even though $C{}_{C2}$ can be considered a short circuit for the oscillation generated by the sensor, the input resistance of the PFGA is still very high. Furthermore, the parasitic gate capacitance of the inverter is relatively low, thus presenting a quite high impedance at the working frequency. The sensor response can be in most of the cases quantified as $V_{RES}=I_{RLC}\left|Z_{CE}\right|$. The only parameter to set is the coupling capacitor $C{}_{C2}$. This capacitor fixes the low cut-off frequency of the amplifier ($f_L=\frac{1}{2\pi R_{OB}{C}_{C2}}$) and controls the distortions in the signals of the circuit. In particular, nonlinearities can be originated when the output signal exceeds the linear region of the inverter, or when it exceeds the off region of the voltage buffer. The total distortion is therefore a combination of these two factors. However, as previously mentioned, the distortion of the signals in the circuit do not play any role and the front-end remains functional. In conclusion, the value of $C{}_{C2}$ must just guarantee that the sensor response falls inside the bandwidth of the circuit.

5. Simulation Results and Design Rules

Simulations by using a low voltage (LV) model nmos4/pmos4 in AMS-350nm technology at $V_{DD}=5$ V has been used to support the modelling previously discussed and to perform a quantitative analysis useful to define design rules for this front-end. It must be noticed that the main results are also valid for high voltage models and high leakage implementations. The dimensions of the MOSFET used in the simulations are listed in

Table 1. MOSFET Parameters for simulations in AMS-350nm.

${\mathit{V}}_{\mathit{DD}}=5$ V
Parameter	MN1	MP1	MN2	MP2
width	1 $\mathsf{\mu }$m	2.3 $\mathsf{\mu }$m	1 $\mathsf{\mu }$m	2.3 $\mathsf{\mu }$m
length	350 nm	350 nm	350 nm	350 nm

.

First of all, the voltage characteristics curves of the PFGA utilized to implement the bidirectional amplifier are shown. These curves are shown in Figure 16.

Figure 16 shows an inverter with a linear region approximately in the range of [1.5 V, 3.5 V] and a voltage buffer characterized by an OFF (output voltage range in which the buffer is turned OFF) region in the range [1.8 V, 3 V]. In literature, it has been proved that this PFGA cannot work if implemented in low leakage CMOS processes because the small magnitude of the leakage currents doesn’t allow the amplifier to reach the equilibrium point. This phenomenon is exploited in the simulation shown in Figure 17.

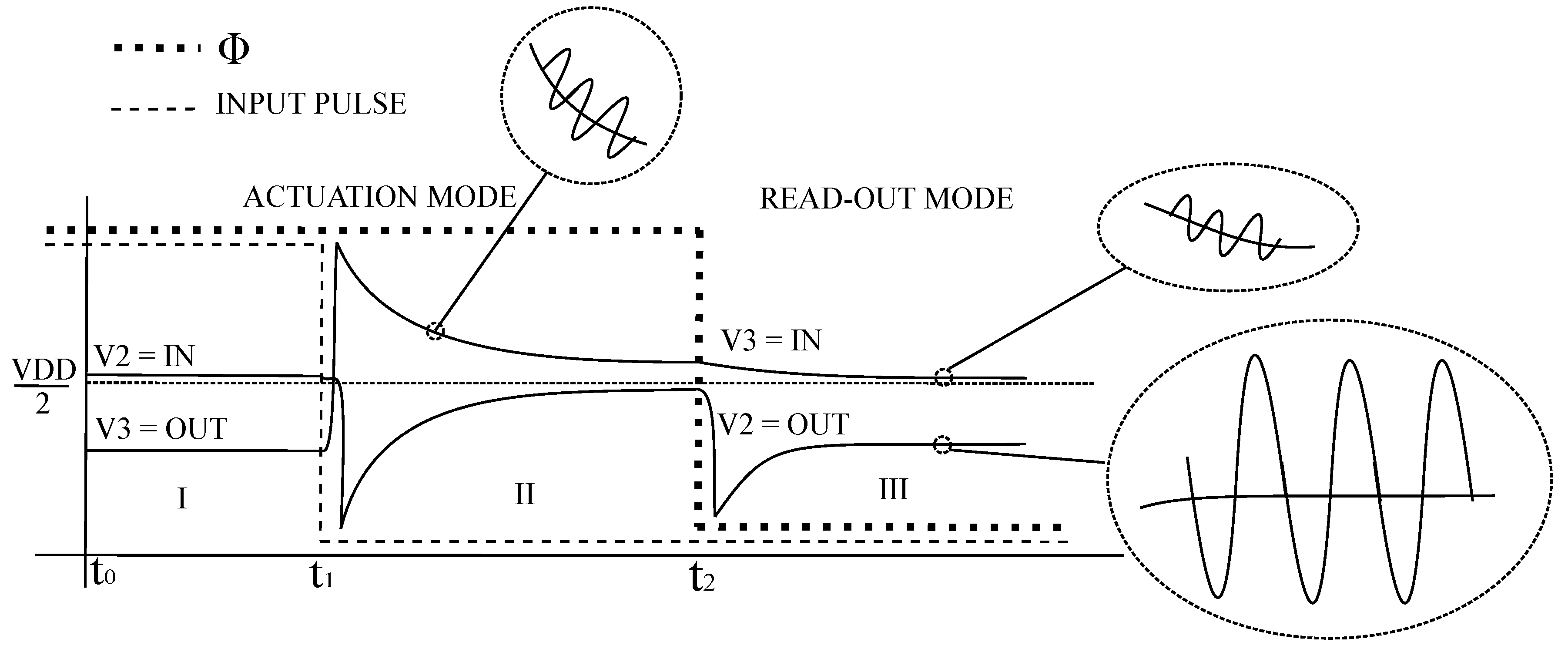
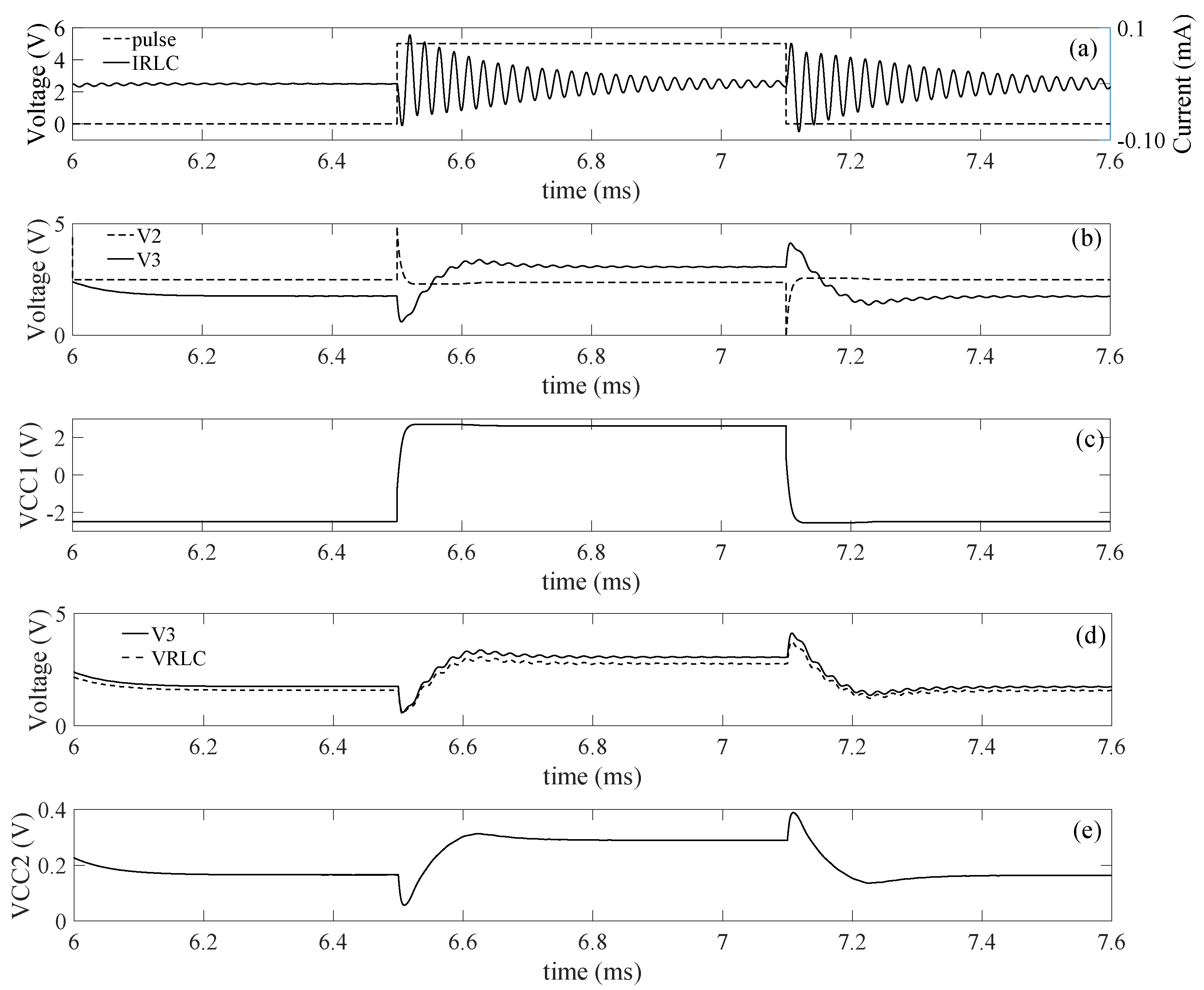
Figure 17 shows the waveforms of the signals in the bidirectional front-end during the actuation mode. In Figure 17b, it can be observed that the steady state value of the input and the output voltage of the bidirectional amplifier are never equal. This is the result of the input offset of the PFGA. The input signal of the bidirectional amplifier assumes the same shape predicted by the theoretical model, while ${\mathrm{V}}_3$ does not reach the power supply rails. This is due to the very fast dynamic of ${\mathrm{V}}_2$, which approaches the steady state value faster than ${\mathrm{V}}_3$. Another expected phenomenon is the double excitation of the resonating sensor as shown in Figure 17a. In this case, ${\mathrm{V}}_2$ always assumes values inside the power supply range, which means that the body diodes shown in Figure 11 are not turned on. This is because the MOSFET (M3, M4) provide a fast feedback reaction, which impede ${\mathrm{V}}_2$ from reaching the power supply rails. Figure 17c shows the voltage across the input coupling capacitor $C_{C1}$ changing between two opposite values. This is due to the fact that the equilibrium in the system is kept by charging and discharging this capacitor. Figure 17d shows that the voltage ${\mathrm{V}}_3$ and $V_{RLC}$ are not equal as expected, but they keep a constant distance between each other. Indeed, $C_{C2}$ is not infinite and therefore the voltage across this capacitor is given by the voltage divider formulas in Equation (2):

$$V_{CC2}=\frac{C_E+C_S}{C_{CC2}+C_E+C_S}{V}_3.$$

(2)

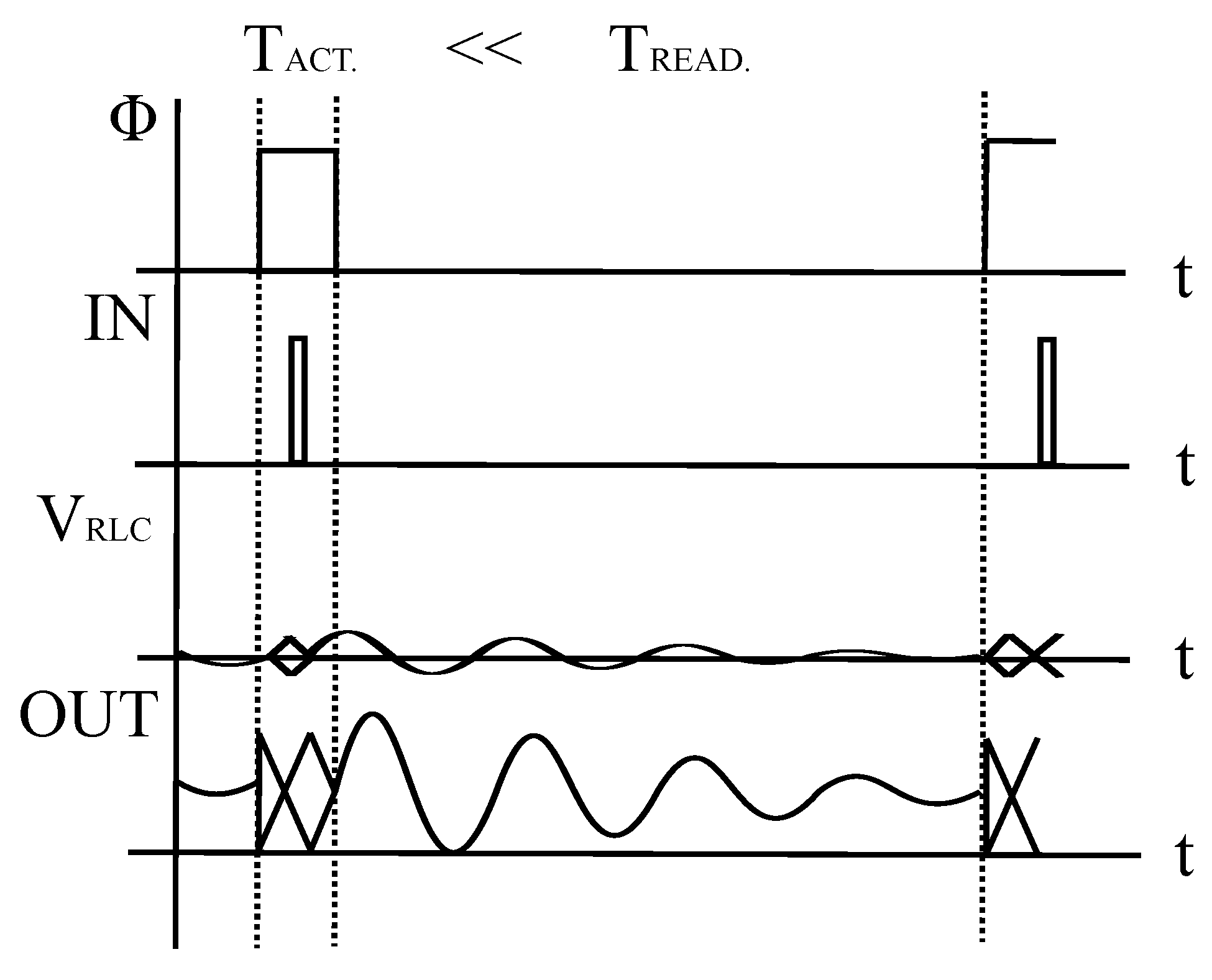
In this particular scenario, $C_{C2}$ = 22 nF, $C_E$ = 2 nF, $C_S$ = 300 pF, which means that $C_{C2}$ is characterized by an average voltage around 1/11 times the steady state value of ${\mathrm{V}}_3$, as proved by the signal shown in Figure 17e. Figure 17a shows a small oscillation at the very beginning of the actuation mode, which is induced by the transition from actuation to read-out mode as described in the previous section. Figure 17b shows that this transition produces a variation in ${\mathrm{V}}_3$, which is probably the cause of the unwanted oscillation. Finally, it can be noted that a small oscillation is overlapping the signal ${\mathrm{V}}_3$ after the rising edge of the input pulse, which is due to the contribution of the RLC series elements to the dynamic of the circuit as described in Figure 12e.

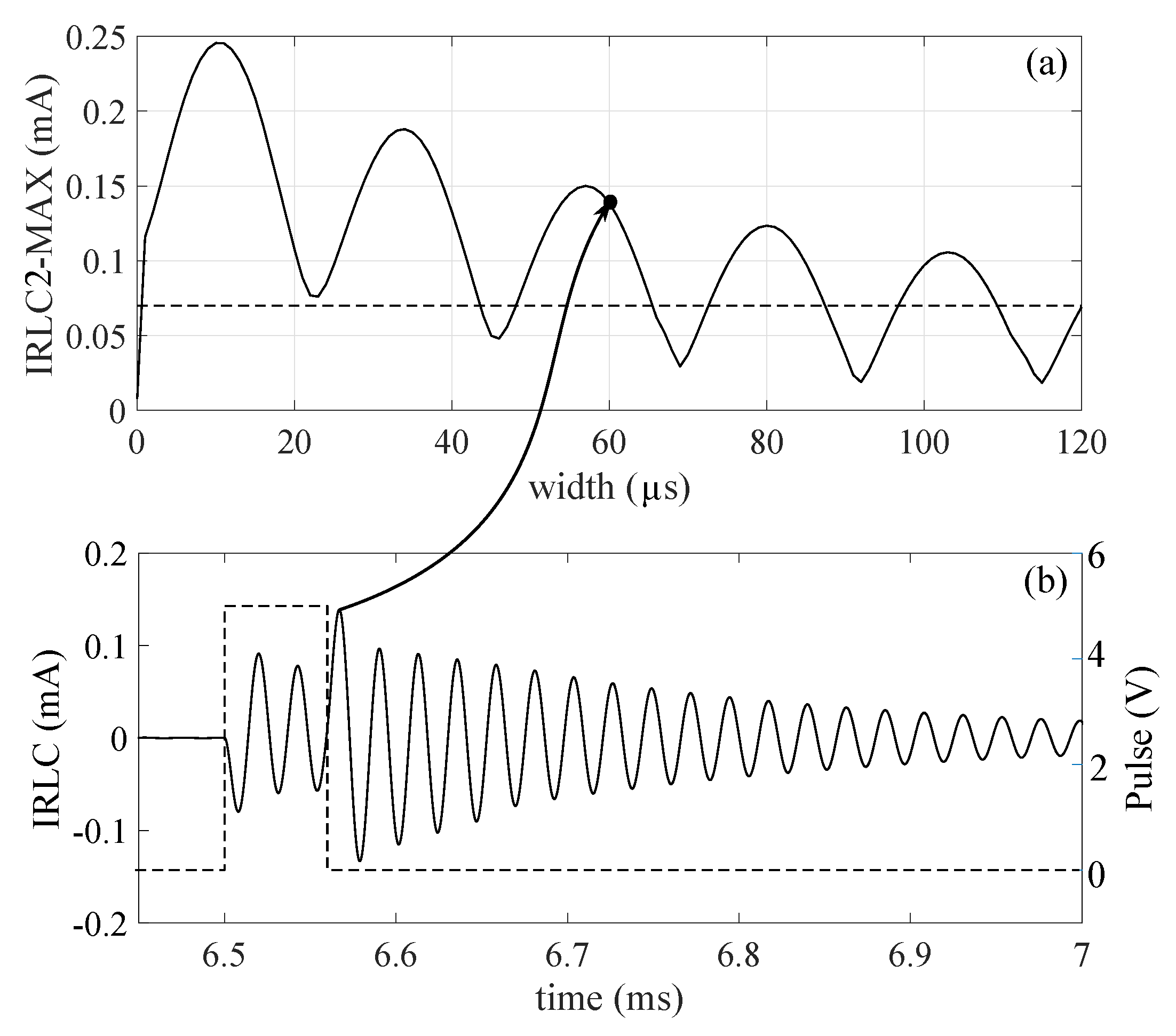
The analysis of these waveforms can be used to extract design rules for this electronic circuit. First of all, the main excitation of the resonating sensor, represented by the current $I_{RLC}$, is the one provided by the falling edge of the input pulse because it is the last one that excites the transducer. However, the amplitude of this oscillation depends on the value of the current $I_{RLC}$ at the occurrence of the falling edge of the input pulse. In particular, it depends on the fact if the oscillation generated by the rising edge of the input pulse is already completely damped or is still going on when the transducer is excited the second time. The possibility to wait the complete damping of the first oscillation to start the second one must be discarded because it limits the performance of the circuit. In this case, the width of the input pulse would be equal to the damping time of the oscillation generated by the sensor, which can be very long, reducing the time available for the read-out mode. Therefore, the interaction between the first and the second oscillation must be accepted, in order to provide reasonable timing for the signals in the circuit. Next, a test has been performed to research the optimum value of the width of the input pulse, which provides the maximum excitation to the transducer. 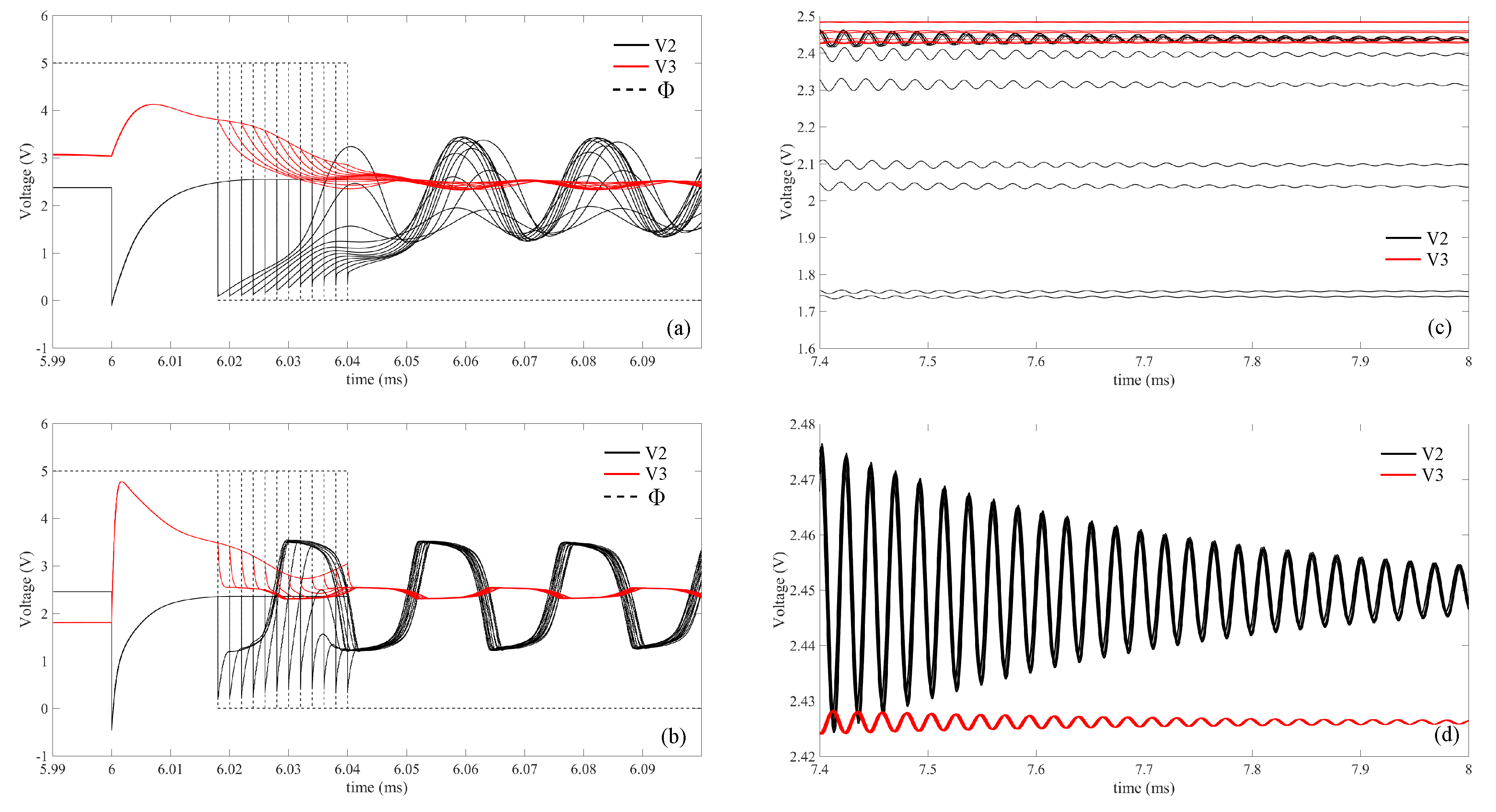The simulation results are shown in Figure 18.

The input pulse width is swept in a range [1 $\mathsf{\mu }$s, 120 $\mathsf{\mu }$s] and, for each test, the first positive peak of the oscillation induced by the falling edge of the input pulse has been recorded as shown in Figure 18b. These values have been collected in a curve called $I_{RLC2-MAX}$ as shown in Figure 18a. Figure 18a shows that the maximum value of this curve is about 3.5 times the value that it would assume if the falling edge is applied after that the first oscillation is completely damped (dashed line). This value is considered as a reference for the minimum $I_{RLC}$ amplitude acceptable. There do exist some values of the input pulse width that reduce the amplitude of the oscillation, with respect to the reference value. On the other hand, there does also exist a range of values in which any value of the width will provide a greater or equal amplitude than the reference value (in this case width ≤ 44 $\mathsf{\mu }$s ). This range will be referred in this paper as the “safe range” for the value of the width of the input pulse. A list of the local maximum of the $I_{RLC2-MAX}$ curve is shown in

Table 2. Local maximum for the curve in Figure 18.

$T_{ON-pulse}$ ($\mathsf{\mu }$s)

10.5

34

57

80

103

.

Table 2 shows that the local maximum occurs with the same period of the resonant oscillation as expected ($T_{res}$ = 23 $\mathsf{\mu }$s, $f_{res}$ = 43.4 kHz). In particular, the absolute maximum is found for a pulse width of 10.5 $\mathsf{\mu }$s, which is almost $T_{res}/2$. In conclusion, the width of the input pulse must be tuned around $T_{res}/2$, in order to obtain the maximum excitation of the sensor, where $T_{res}$ is the period of the oscillation generated by the resonating load. Nevertheless, during the normal operation of this front-end, the resonant frequency can change its value due to variations of the measurand or due to unwanted phenomena, and it can affect the efficiency of this technique. By the way, in both cases, the variation of the resonant frequency is usually just a small percentage of the nominal value, so it doesn’t have a relevant effect on the dynamic of the system.

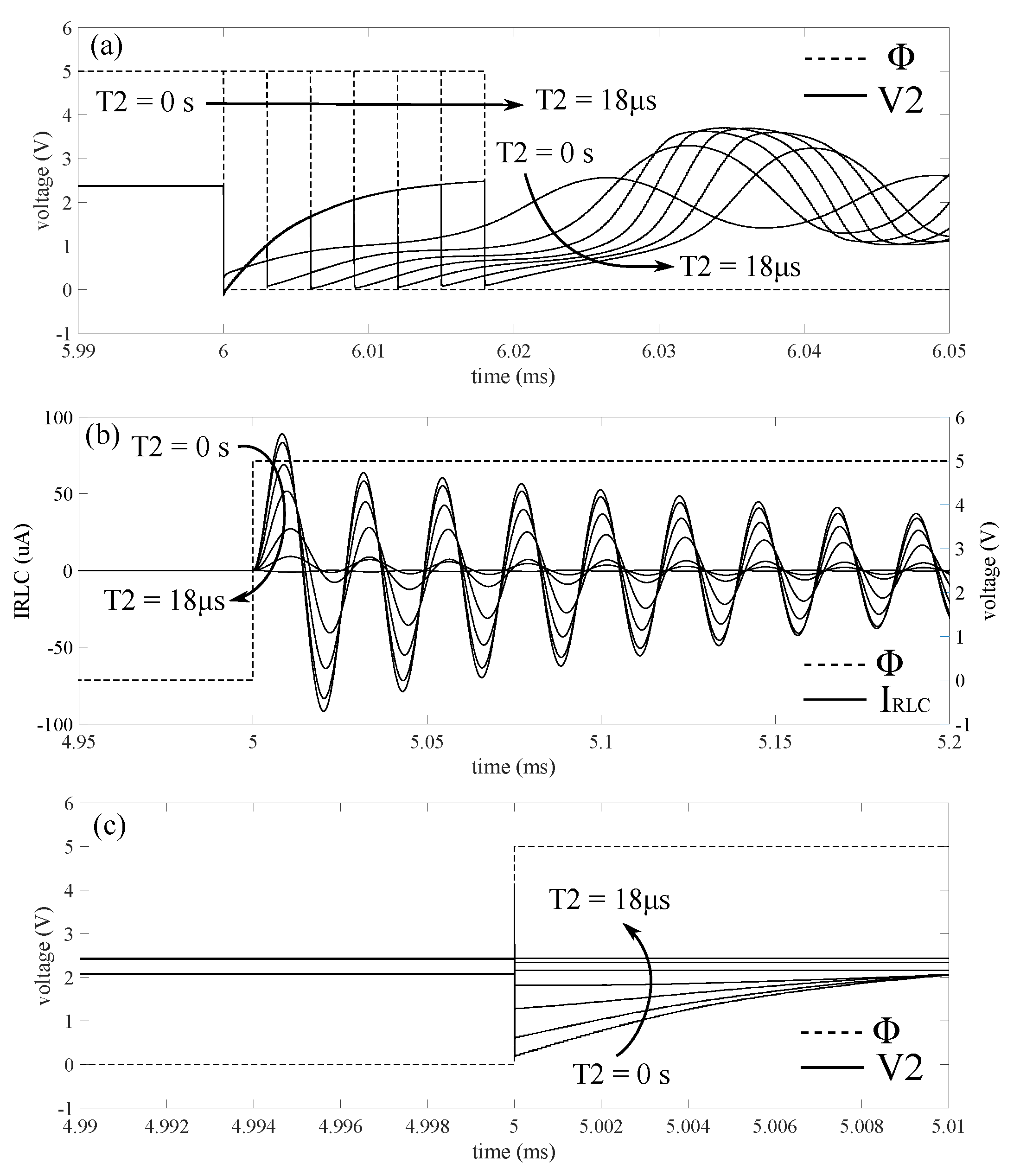
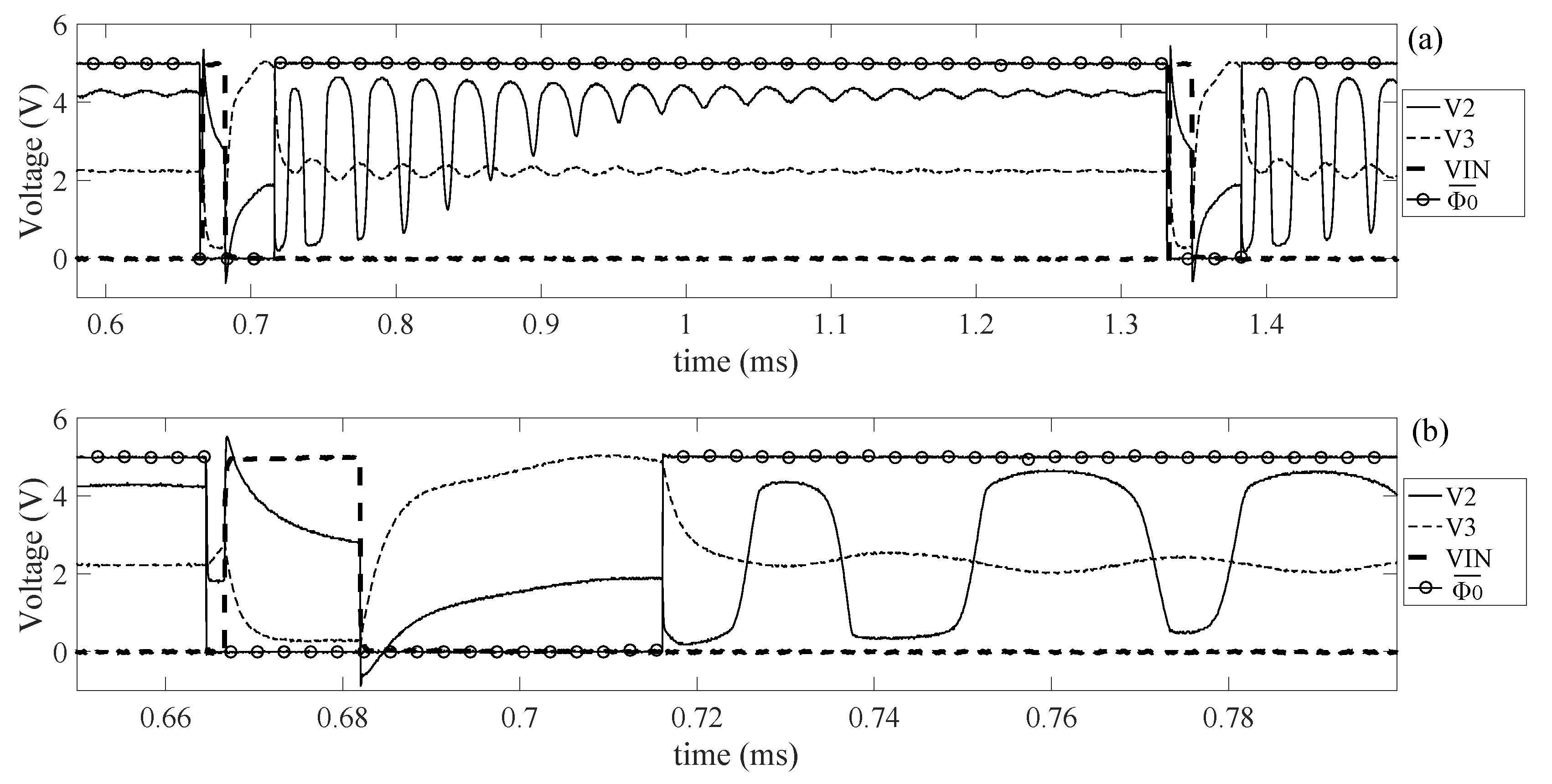
Next, the transition read-out mode to the actuation mode was studied. The simulation results are shown in Figure 19.

Figure 19b shows that this transition brings the transducer to oscillate, as supposed during the modelling. The origin of this oscillation has been investigated by performing a simulation where the transition actuation mode to read-out mode has been delayed of a time interval $T_2$ swept in a range [0 $\mathsf{\mu }$s, 18 $\mathsf{\mu }$s]. As predicted by the modelling provided in the previous section, if the signal ${\mathrm{V}}_2$ approaches ${\mathrm{V}}_{\mathrm{DD}}/2$ before passing to read-out mode, then the oscillation generated at the beginning of the actuation mode reduces its amplitude. This analysis provides the missing parameter for the estimation of $T_{ON-\mathsf{\Phi }}$ or the duration of the actuation mode, which can be expressed as shown in Equation (3):

$$T_{ON-\mathsf{\Phi }}=T1+T_{ON-pulse}+T2\simeq ϵ+\frac{T_{res}}{2}+T_{CC1-ch,}$$

(3)

where $ϵ$ is an arbitrary value. Next, the effects of the transition actuation mode to the read-out mode depend on the duration of the actuation mode duration were analyzed. The simulation results are shown in Figure 20.

A simulation has been performed by sweeping the time interval $T_2$ in the range [18 $\mathsf{\mu }$s, 40 $\mathsf{\mu }$s]. Figure 20a shows the waveforms of ${\mathrm{V}}_2$ and ${\mathrm{V}}_3$ a few instants after the transition from actuation mode to read-out mode, while Figure 20c shows the same waveforms after the oscillations are almost completely damped. The results in Figure 20a,c show dispersive waveforms with different steady state values depending on the value of $T_2$. The main cause of this dependency is supposed to be due to the shape of ${\mathrm{V}}_3$ after the transition. Indeed, ${\mathrm{V}}_3$ approaches the steady state value exponentially and it requires different times. Furthermore, while ${\mathrm{V}}_3$ decreases, the oscillation generated by the transducer overlaps the main signal affecting the shape of ${\mathrm{V}}_3$. The combined effect of these two causes provides different steady state values. The first contribution can be reduced by increasing the rate at which ${\mathrm{V}}_3$ approaches to the steady state value. This can be achieved by increasing the size of M1, M2. Another simulation has been performed by increasing of ten times the size of M1, M2 (${(W/L)}_n$ = 10 $\mathsf{\mu }$m/350 nm, ${(W/L)}_p$ = 23 $\mathsf{\mu }$m/350 nm). The simulation results are shown in Figure 20b,d. As expected, the waveforms provide more regular behaviour, but, most important, they are characterized by the same steady state value. In conclusion, it has been proved that the transition from actuation mode to read-out mode is affected by the duration of the actuation mode. In particular, the position of the bias point is strictly related to the dynamic behaviour of ${\mathrm{V}}_3$. Finally, it has been proved that the stability of the bias point in read-out mode can be improved by using stronger MOSFET M1 and M2.

Another constraint does exist, which can be extracted from this simulation. If the bidirectional front-end is implemented with high threshold voltage transistors (low leakage process), then the threshold voltage of M2 must be: $V_{thp}<V_{DD}/2$. If this condition is not satisfied, the input voltage ${\mathrm{V}}_3$ cannot approach close enough to ${\mathrm{V}}_{\mathrm{DD}}/2$ and the performance of the bidirectional amplifier will degrade.

Finally, the analysis of the read-out mode can be performed by using the results in Figure 20. The oscillation ${\mathrm{V}}_2$ generated by the transducer during the read-out mode presents a sinusoidal shape in Figure 20a, while it is distorted in Figure 20b. The cause of this distortion is the voltage buffer inside the PFGA, which, once turned on, “clamps” the input and consequently the output signal of the amplifier. The voltage buffer turns on only for the case (b,d), because the wider amplitude of the signals $V_2,V_3$ during the read-out mode. This is mainly a consequence of using a strong inverter during the actuation mode for the case (b,c). A strong inverter provides a greater excitation of the transducer for the case represented in Figure 20b than the case in Figure 20a (observe ${\mathrm{V}}_3$(t = 6 ms)). Furthermore, it provides a more stable bias point as shown in Figure 20d than the case shown in Figure 20c, which is due to the lower output resistance of the amplifier. Therefore, the position of the bias point in Figure 20d is closer to the ideal value than the case shown in Figure 20c maximizing the gain of the amplifier. Finally, the combination of these two contributions provides a wider amplitude of the input and the output signals, which turns on the voltage buffer and introduces nonlinearities in the circuit.

The simulation results of the read-out mode has been used to describe the distortion phenomenon presented in the output signal ${\mathrm{V}}_2$, discussing the origin of this phenomenon.

In conclusion, simulation results show that the bidirectional amplifier will work if implemented in both high leakage and low leakage technologies, even though the last one has been proved in literature to not be suitable to implement a standalone PFGA without compensating the offset. An implementation in low leakage technology requires a few more design considerations than the case of a high leakage implementation, but the system is still functional.

5.1. Design Rules

The theoretical modelling and the simulation results provided a deep understanding of the working principle and the secondary phenomena, which take place in the proposed front-end. These results have been collected in this section in order to provide a step-by step procedure to design this device by running a few simulations.

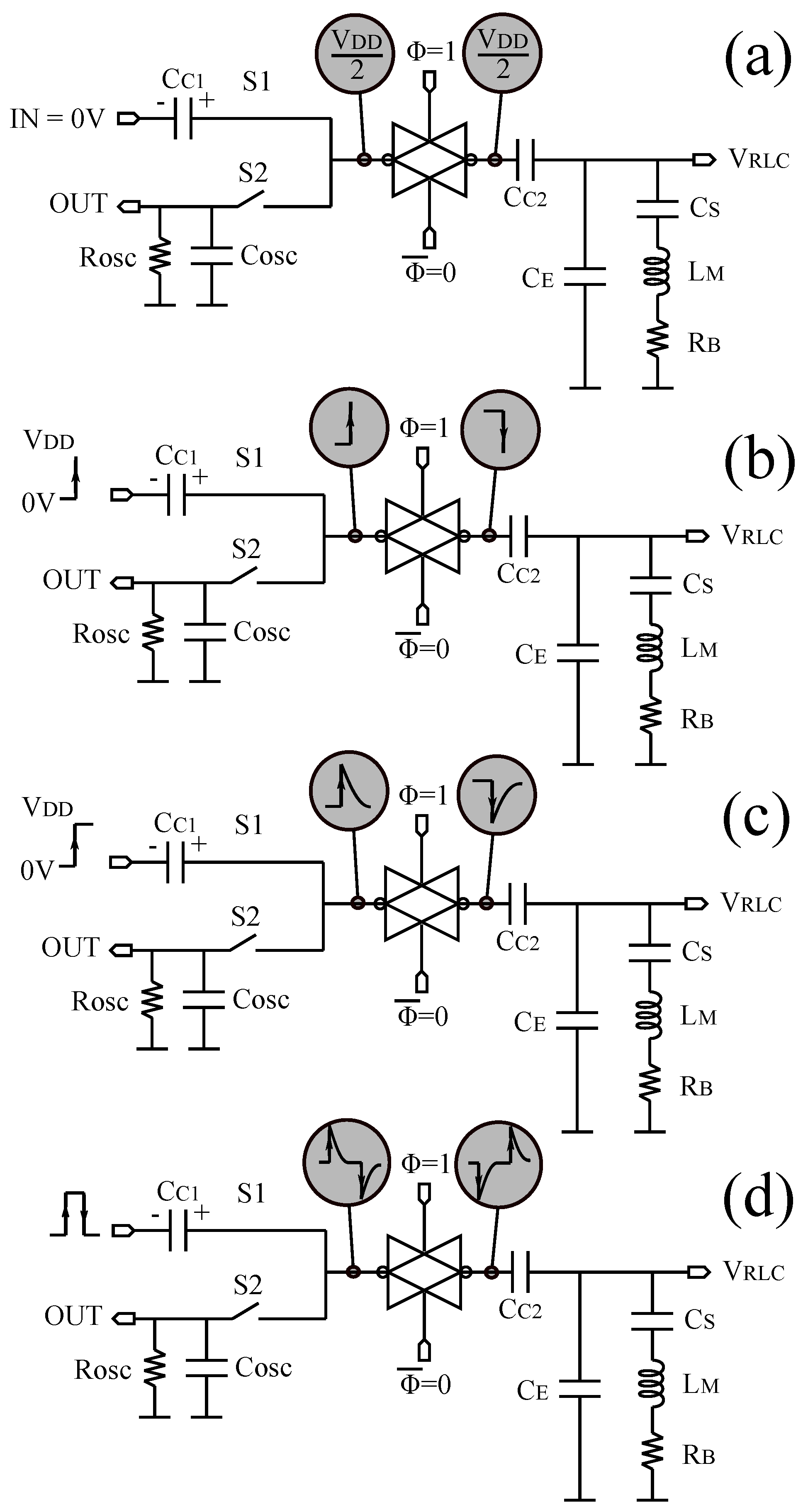
First of all, the following steps will be performed by using a BvD load. Second, the inverter of the bidirectional PFGA must be designed in order to provide the gain, the bandwidth and the output current needed for the application. Once the inverter dimensions are set, the same aspect ratio for the MOSFET of the voltage buffer can be chosen. This will provide the same strength for the feedback and the amplifier. The value of $C_{C2}$ can be set initially to 10 times of $C_E$. This parameter is usually reported in the datasheet or can be extracted by the BvD model of this device. The initial value for $C_{C1}$ is arbitrary because it will be tuned in a next step. A test with very wide input pulse duration and actuation mode must be run as shown in Figure 17. It is now possible to tune $C_{C1}$ to allow the peaks in ${\mathrm{V}}_3$ to reach the rails of the power supply and maximized the excitation provided to the sensor. Then, the time $T_{CC1-ch}$ must be recorded because it will be used to set the duration of the actuation mode. A this point, by measuring the peaks of the signal ${\mathrm{V}}_2$, it is possible to recognize if the source-bulk pn junctions of the MOSFET in the voltage buffer turn on. If these diodes turn on the size of M3, M4 must be increased to reduce the risk of latch up phenomenon. Next, the duration of the input pulse can be set around half of the oscillation period generated by the transducer. Monitoring the current $I_{RLC}$ will help to tune more precisely the duration of the input pulse. Once the excitation of the transducer is maximized, it is possible to fix the duration of the actuation mode by using the value $T_{CC1-ch}$ previously recorded. The duration of the actuation mode can be fixed according the formulas in Equation (3). Finally, a sweep in the duration of the the actuation mode must be performed to check if the bias point of the amplifier is affected by the transition from actuation mode to read-out mode. If the oscillation is influenced by the value of $T_2$, the dimensions of the MOSFET M1, M2 must be increased until the dynamic of ${\mathrm{V}}_3$ becomes independent from the value of $T_2$. This will improve the immunity of the system to the variations of the actuation mode duration. In conclusion, by using these simple steps, it is possible to design the set-up of a bidirectional front-end based on a pseudo floating gate amplifier.

6. Measurement Set-Up

A prototype has been implemented by using discrete components and mounted on a printed circuit board as shown in Figure 21b.

The MOSFETs have been implemented by using a commercial integrated circuit CD4007UB (Texas Instruments). This integrated circuit (IC) contains a set of NMOS and PMOS, which can be connected to implement the proposed bidirectional amplifier as shown in Figure 21d. The multiplexer/demultiplexer have been realized by mean of transmission gates because they allow the output signal to reach the power supply rails and minimize the drop voltage over these switches. The proposed front-end has been tested by using an ultrasound piezoelectric transducer (MURATA MA40S4) and BvD load made by discrete components. The BvD load has been implemented by using a variable capacitor and variable inductor as shown in Figure 21a. The values chosen for these elements are : $R_b$ = 330 $\mathsf{\Omega }$, $C_S$ = 450 pF, $L_m$ = 60 mH, $C_E$ = 2 nF, which are approximately the same values reported in the data-sheet of the ultrasound transducer. The values of the coupling capacitors are $C_{C1}$ = 4.7 nF, $C_{C2}$ = 22 nF.

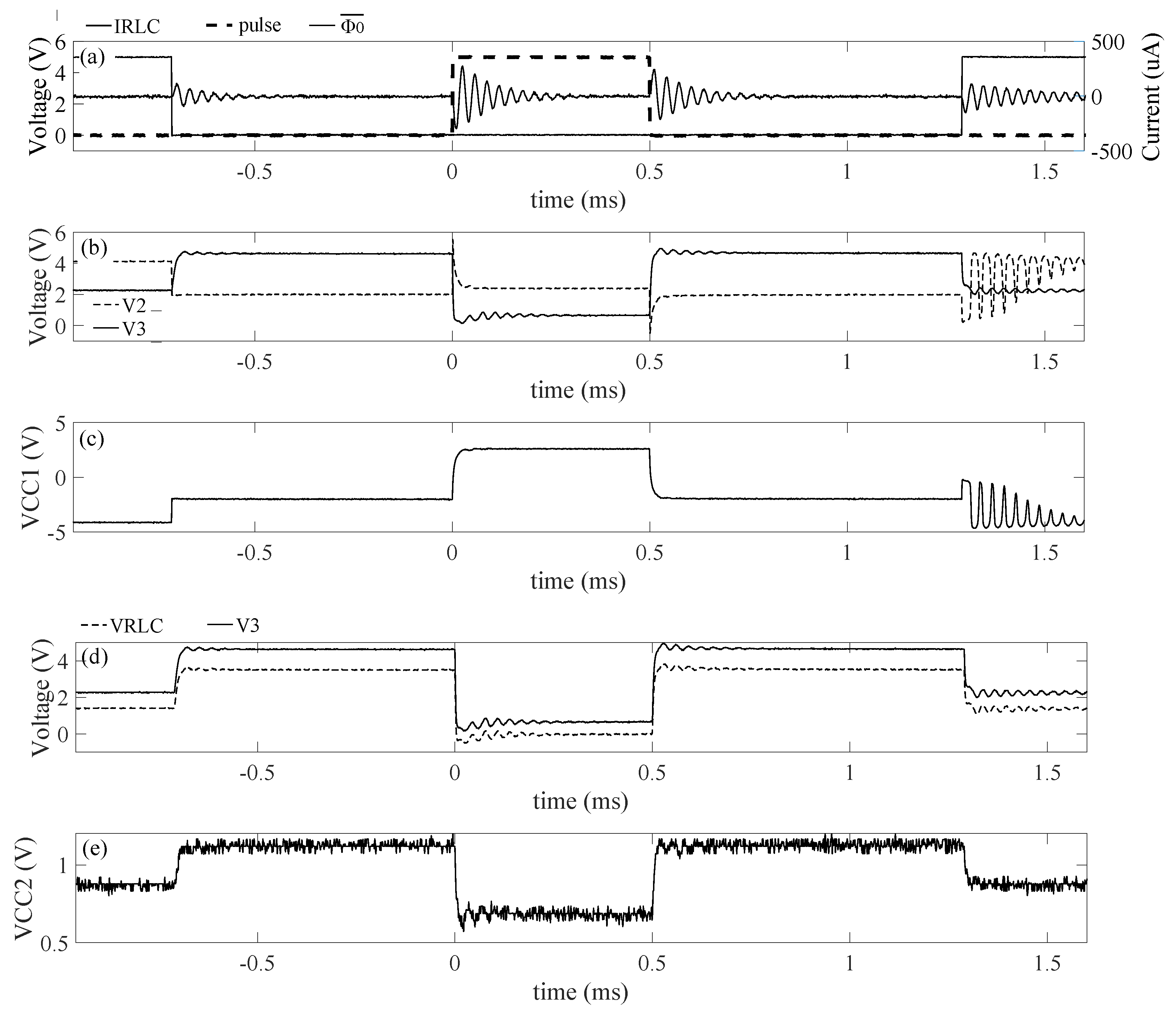
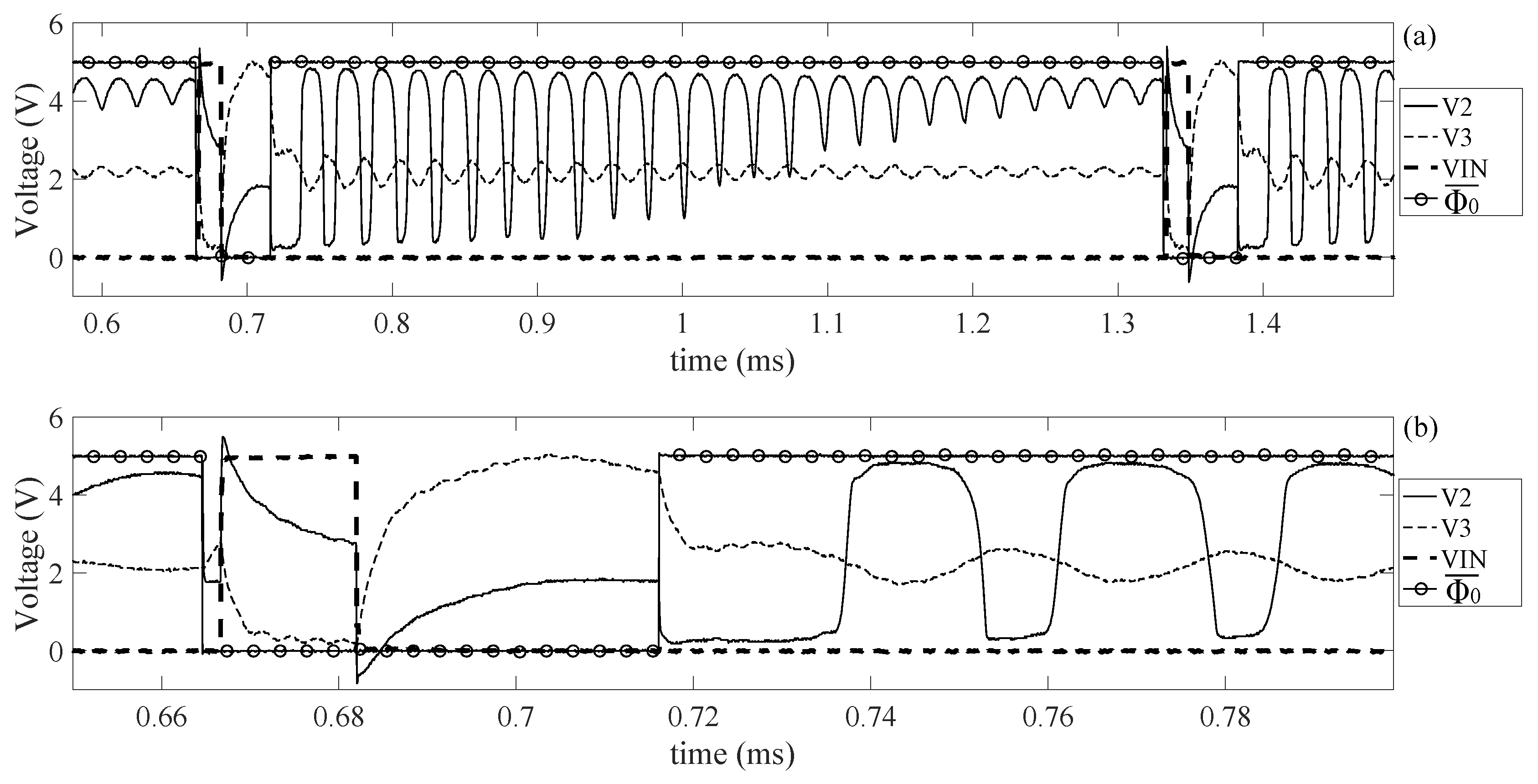
7. Measurement Results

First of all, the signals have been measured during the actuation mode, trying to replicate the simulation results in Figure 17 by using a BvD load. Measurement results are shown in Figure 22.

The waveforms in Figure 22 show good fitting with the simulation results in Figure 17, with a few differences. The first one is that the steady state value of ${\mathrm{V}}_3$ is quite far from the steady state value of ${\mathrm{V}}_2$ because the implemented voltage buffer is characterized by a wide off region. The oscillation generated by the BvD load is characterized by a frequency of 32.4 kHz, which is smaller than the resonant frequency of the real transducer. $V_{CC2}$ is characterized by a greater drop voltage than the value expected ($\simeq {\mathrm{V}}_3/10=0.5$ V). This is probably due to the fact that the parasitic capacitance in the circuit increases the total capacitance at the node $V_{RLC}$, which is greater than the only $C_E$, modifying the voltage divider between $C_{C2}$ and $C_E$. The duration of the read-out mode has been set in order to allow the complete damping of the sensors response. Figure 22a shows the presence of an unwanted oscillation after the transition from read-out mode to actuation mode. In order to neglect any effect of this oscillation, the time $T_1$ has been fixed almost equal to 0. Next, the value for the duty cycle of the input pulse has been set to $0.3\%$ ($freq=200$ Hz) as shown in Figure 23. This value corresponds to 15 $\mathsf{\mu }$s, which is almost half of the oscillating period of the signal generated by the sensor as expected.

The oscillation generated by the falling edge of the input pulse reaches a peak value of 550 $\mathsf{\mu }$A. This value is around 2.5 times the maximum amplitude of the current oscillation $I_{RLC}(t\simeq 5$ ms) = 220 $\mathsf{\mu }$A in Figure 22a. Finally, $T_2$ is fixed to the minimum value, which allows $C_{C1}$ to charge to the steady state value of ${\mathrm{V}}_2$ before to pass in read-out mode. At this point, the duration of the actuation mode has been fixed. The frequency of the signals has been adjusted from 200 Hz to 1.5 kHz to minimize the duration of the read-out mode. Therefore, the optimum duty cycle of the input pulse must be adjusted to $2.3\%$ . 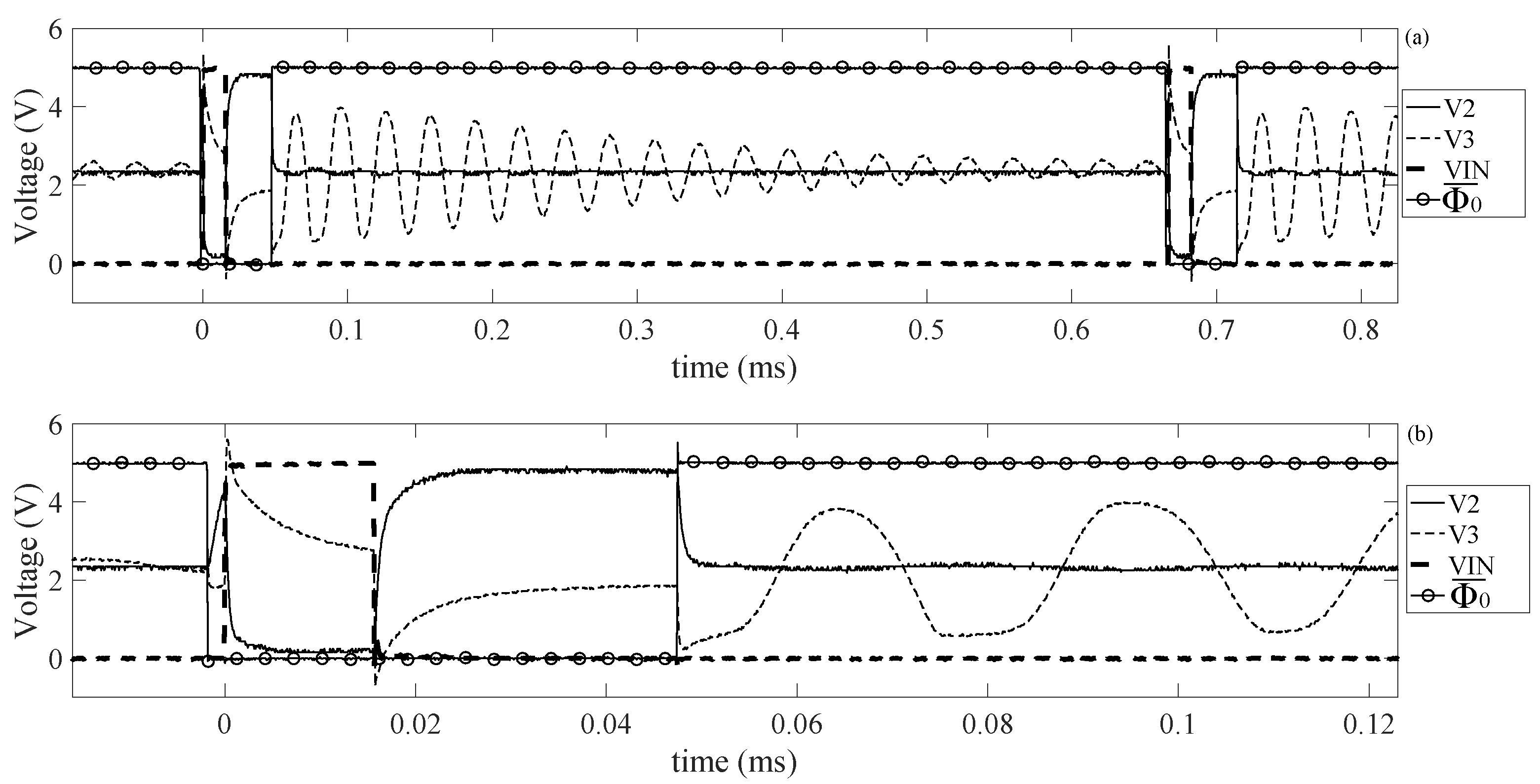The parameters used for the control signals are: $freq=1.5$ kHz, $D_{\overline{{\mathsf{\Phi }}_0}}=92\%, D_{pulse}=2.3\%$. Measurement results of a whole read-out cycle is shown in Figure 24.

Measurement results show signals, which fit the predictions of the simulation results. With two main differences: the first one is the fact that ${\mathrm{V}}_3$ doesn’t show an impulsive waveform, but its shape resembles more the charge and the discharge of a capacitor. The second one is the non ideal positioning of the bias point. This last phenomenon is due to the slow and exponential transient of ${\mathrm{V}}_3$ when it approaches the steady state value in read-out mode. It is interesting to notice that the peaks at ${\mathrm{V}}_2$ exceed the power supply range reaching the values 5.5 V, −0.88 V. These two values indicate that, in this test, the source-bulk pn junctions of the MOSFET M3, M4 are forward biased. Therefore, greater dimensions for these MOSFET must be used to reduce the risk of latch up. Then, a second test has been performed by using the same parameters for the control signals but using a piezoelectric resonator as load. 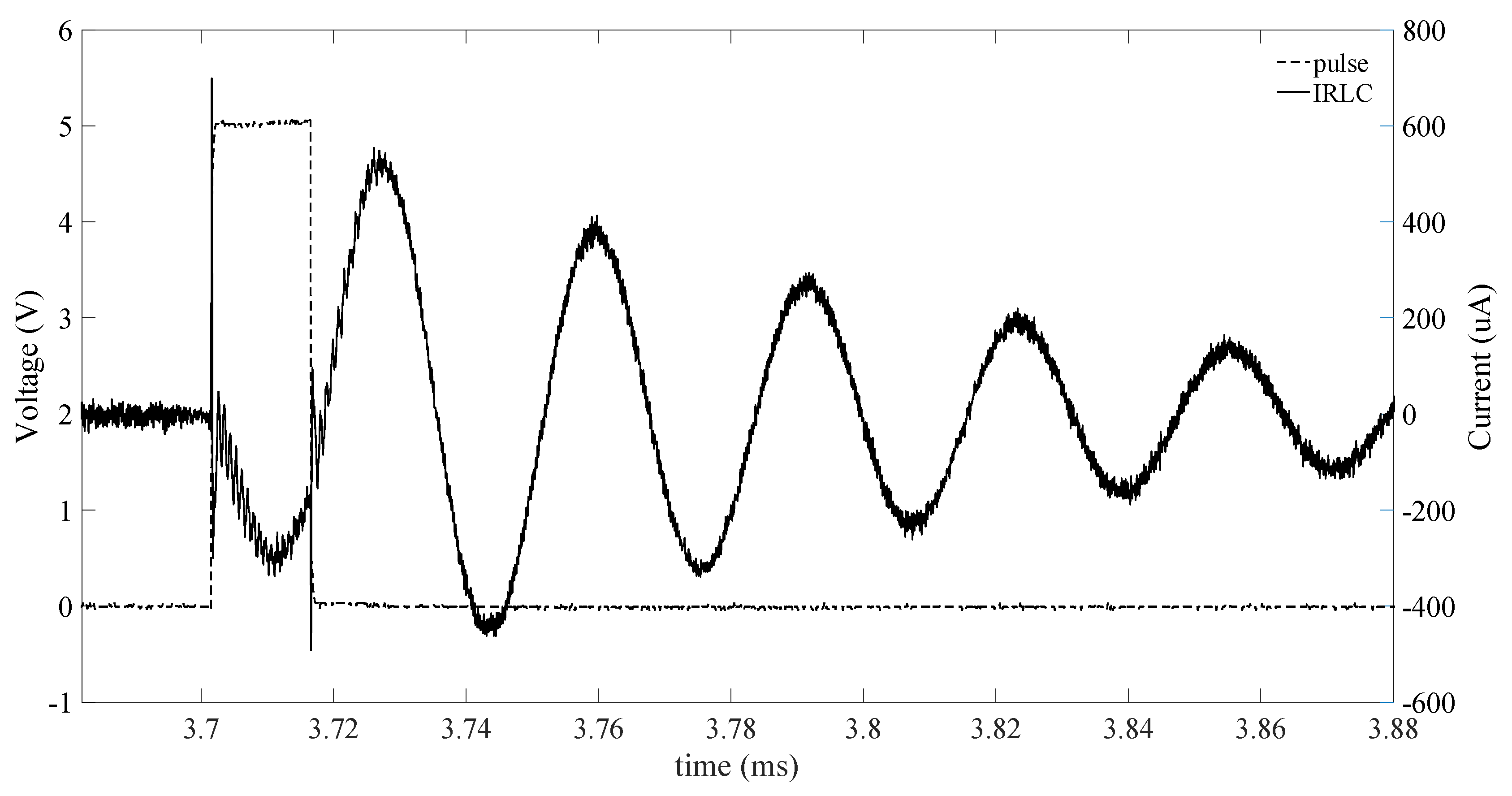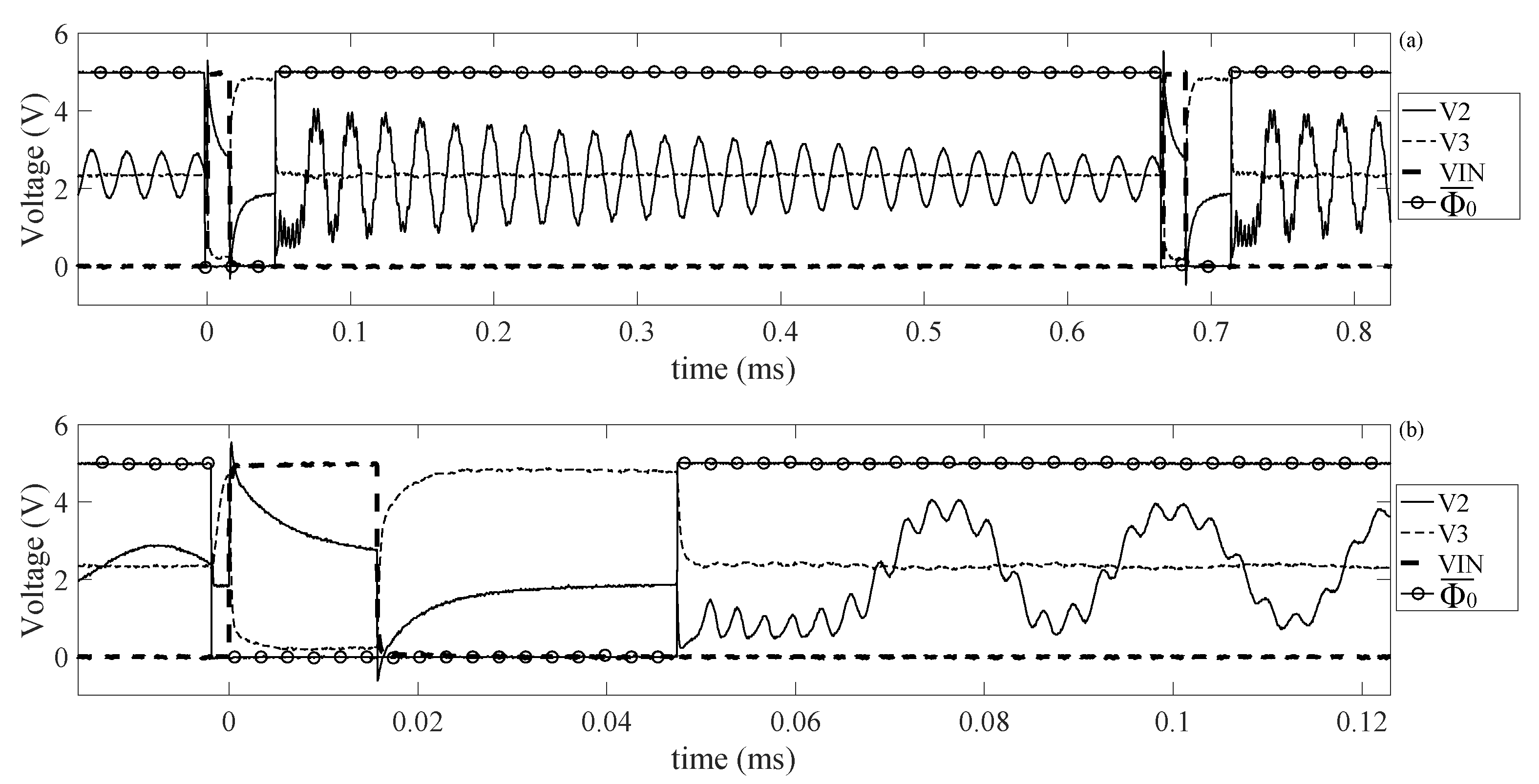Measurement results are shown in Figure 25.

These waveforms are very similar to the one obtained for the BvD load. However, the amplitude of the oscillation of ${\mathrm{V}}_2$ during the read-out mode is larger in this case. This is probably due to the difference in the lumped parameter values of the BvD load utilized and the BvD model of the real sensor. Also in this case, the source-bulk pn junctions of M3, M4 are forward biased. Next, the resonant frequency measured is 40.1 kHz. A careful inspection of ${\mathrm{V}}_3$ shows the presence of high order modes, which damp very fast and do not affect the output signal of the front-end. Both tests present similar waveforms and both cases show that the bias point of the amplifier is not in the optimal position, which is the main problem that affects this front-end. This issue can be addressed by increasing the speed at which the signal ${\mathrm{V}}_3$ approaches ${\mathrm{V}}_{\mathrm{DD}}/2$ after the transition actuation mode to read-out mode. This task can be accomplished easily by designing an ASIC (application specific integrated circuit) and providing greater dimensions for the MOSFET M1, M2. By the way, if this situation is not prevented, the system still works, but the number of the counted oscillations is smaller, reducing the accuracy in the estimation of the resonant frequency. The positioning of the bias point can also be improved reducing the value of $C_{C2}$. In this way, once the system passes in read-out mode, the signal ${\mathrm{V}}_3$ can approach the steady state value faster. A third test is performed with a BvD load using $C_{C2}=560$ pF and keeping the same parameters for the control signals. Measurement results are shown in Figure 26.

Figure 26 shows that the positioning of the bias point has been improved at the cost of a smaller excitation ot the sensor. Indeed, by lowering this capacitor, the drop voltage over $C_{C2}$ increases, reducing the energy given to the load. By applying this technique to a real sensor, another phenomenon shown in Figure 27 can be observed.

Figure 27 shows that, by reducing the value of $C_{C2}$ to 250 pF, it is possible to achieve a good bias point. However, this time higher order oscillations overlap the main signal. This is due to the fact that, even though the amplitude of the oscillations is lower, the gain of the amplifier is maximized by the optimum position of the bias point. The presence of this high order mode at 310 kHz can provide false zero crossing points, and it can affect the measurement of the resonant frequency. This is a situation, where there is a need for a method to tune the bandwidth of the amplifier, in order to remove the high order modes such as the one described in [36].

In conclusion, the cause of the misplaced bias point has been proved to be the slow rate at which ${\mathrm{V}}_3$ approaches the steady state value in read-out mode and lowering the value of $C_{C2}$ presents trade-offs. Therefore, the best solution consists in preventing this problem at the design level by increasing the dimensions of M1, M2.

8. Conclusions

The analysis carried out in this work has shown that a bidirectional front-end based on a pseudo floating gate amplifier is a good candidate to drive and read-out a resonating sensor, even though it has been implemented with commercial components. An optimal front-end could be implemented by designing the system in ASIC. Simulation and measurement results proved the validity of the modelling developed for this device. Furthermore, a simple procedure to design and configure this amplifier has been proposed. Finally, this electronic interface can be utilized in many applications and can be implemented in any CMOS technology such as in low leakage and high leakage CMOS fabrication processes.