An All-Region State-of-Charge Estimator Based on Global Particle Swarm Optimization and Improved Extended Kalman Filter for Lithium-Ion Batteries
Abstract
:1. Introduction
1.1. Review of SOC Estimation Approaches
1.2. Main Contributions
- (1)
- A subregion identification method for model parameter of ECMs in the all-region SOC is proposed to improve the global model accuracy. In this method, the all-region SOC (0–100%) is divided into several subregions, and the parameters in each subregion are identified. Therefore, the model parameter of the all-region is composed of the model parameter of each subregion. Moreover, the optimal number of subregions is investigated to balance the model accuracy and computation time.
- (2)
- An improved EKF-based SOC estimator with varying noise covariance is proposed to improve the accuracy of the SOC estimation in the all SOC range. ECM has a low model accuracy in the low SOC range, resulting in a large SOC estimation error based on the traditional EKF. The effectiveness of the proposed estimator in the all-region SOC is verified by experiments.
- (3)
- Our proposed model parameter identification method and SOC estimator are evaluated by two kinds of batteries under three working cycles.
1.3. Organization of the Paper
2. Experiment
3. Model and Parameter Identification
3.1. Equivalent Circuit Model
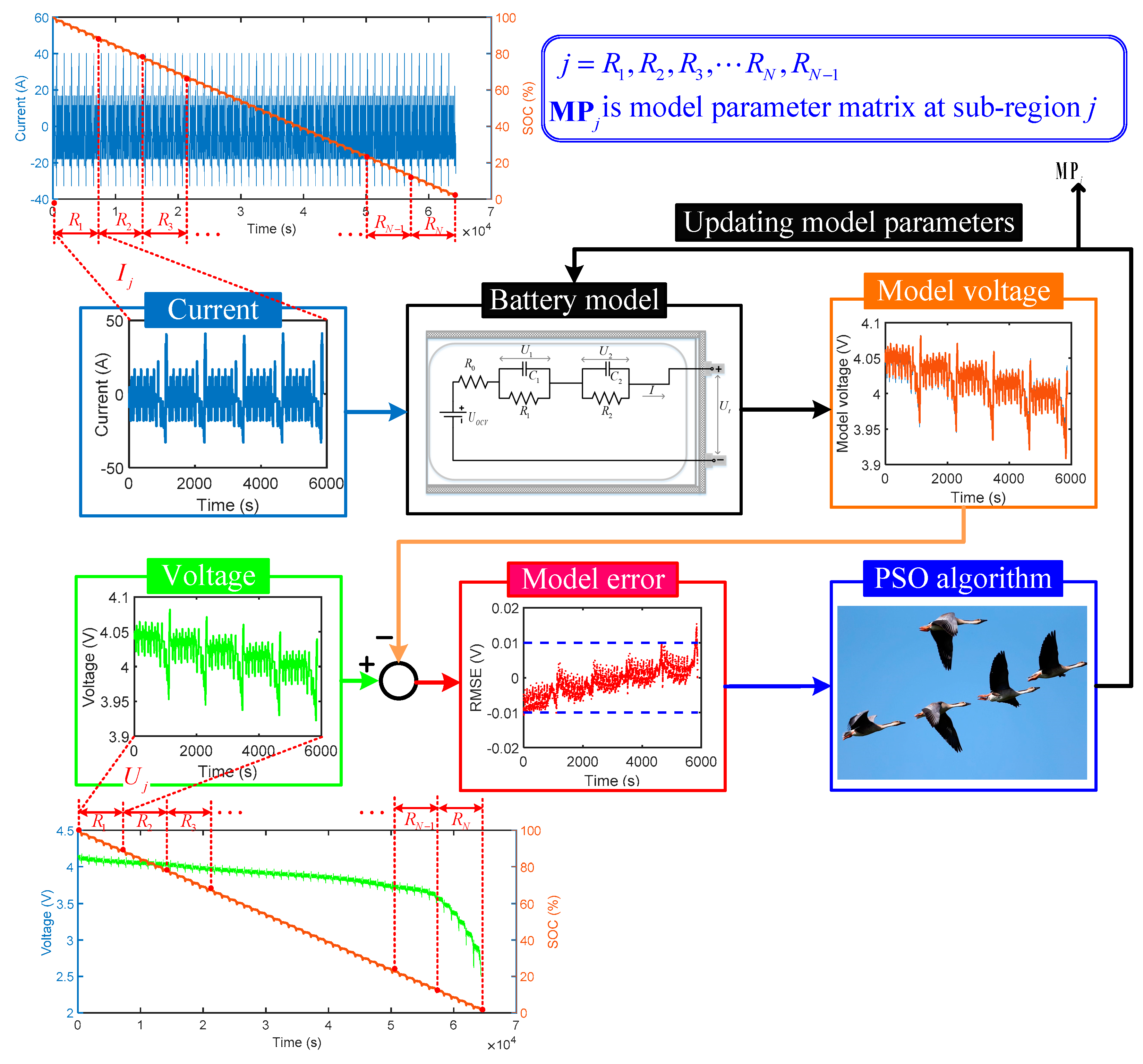
3.2. Model-Parameter Identification Based on Particle Swarm Optimization
| Algorithm 1. Pseudo-code of the PSO algorithm. |
| 1: procedure PSO 2: for each particle i 3: Initialize velocity Vi and position Xi for particle i 4: Evaluate particle i and set Pi = Xi 5: end for 6: gBest = min [21] 7: while not stop 8: for i = 1 to n 9: Update the velocity and position of particle i using Equations (4) and (5) 10: Evaluate particle i 11: if fit (Xi) < fit (Pi) 12: Pi = Xi; 13: if fit(Pg) < fit (gBest) 14: gBest = Pg; 15: end for 16: end while 17: end procedure |
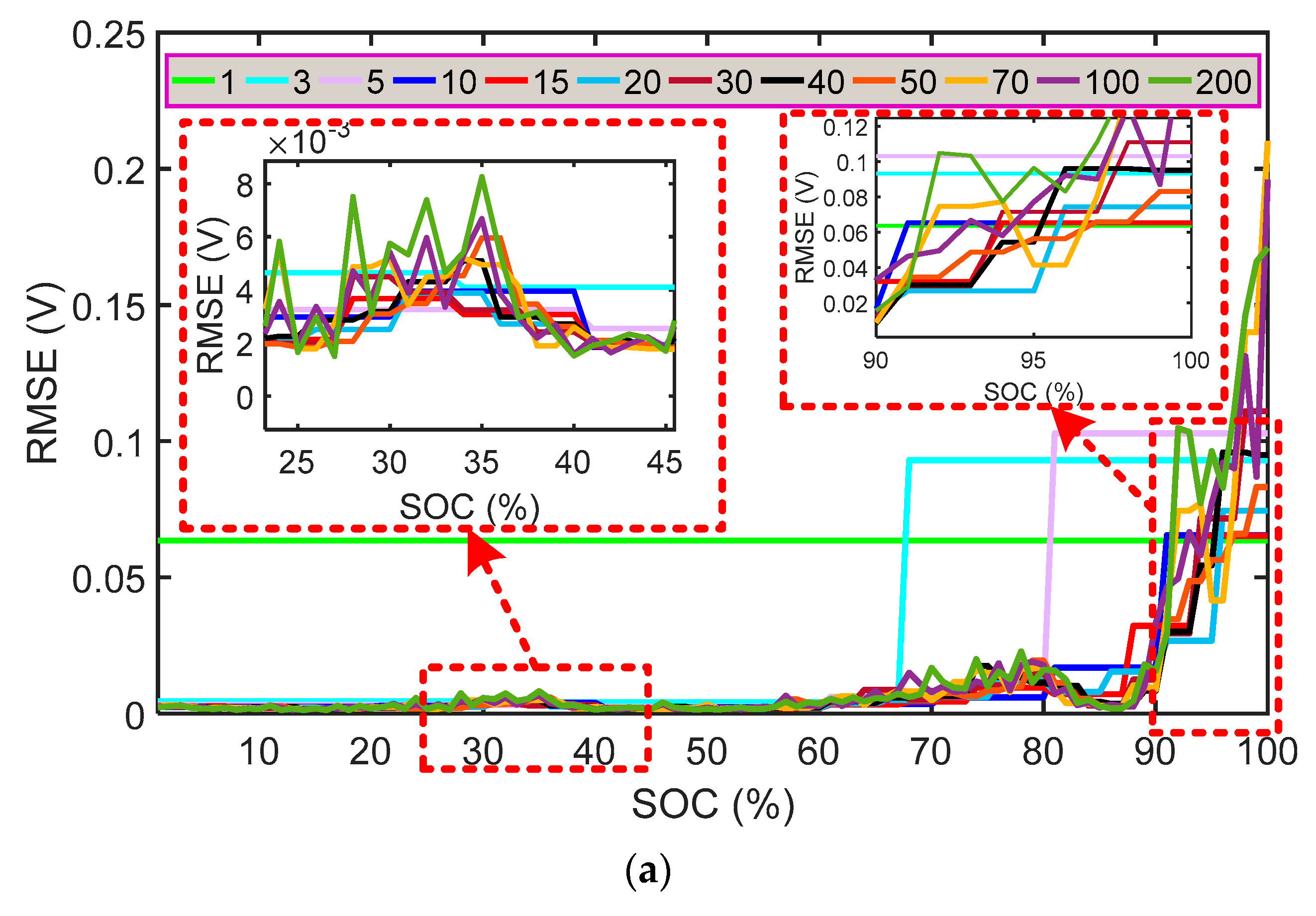
3.3. All-Region Parameter Identification of ECM
4. An Improved EKF-Based SOC Estimator in the All SOC Range
4.1. EKF-Based SOC Estimator
| Algorithm 2. Summary of the extended Kalman filter (EKF)-based state-of-charge (SOC) estimator. |
| 1: Definitions: 2: The nonlinear state-space model:
4: Computation: 5: Time update: 6: ; . 7: Measurement update: 8: Error innovation: . 9: Estimator gain matrix: 10: Measurement update: 11: Error covariance measurement update: where , |
4.2. An Improved EKF-Based SOC Estimator
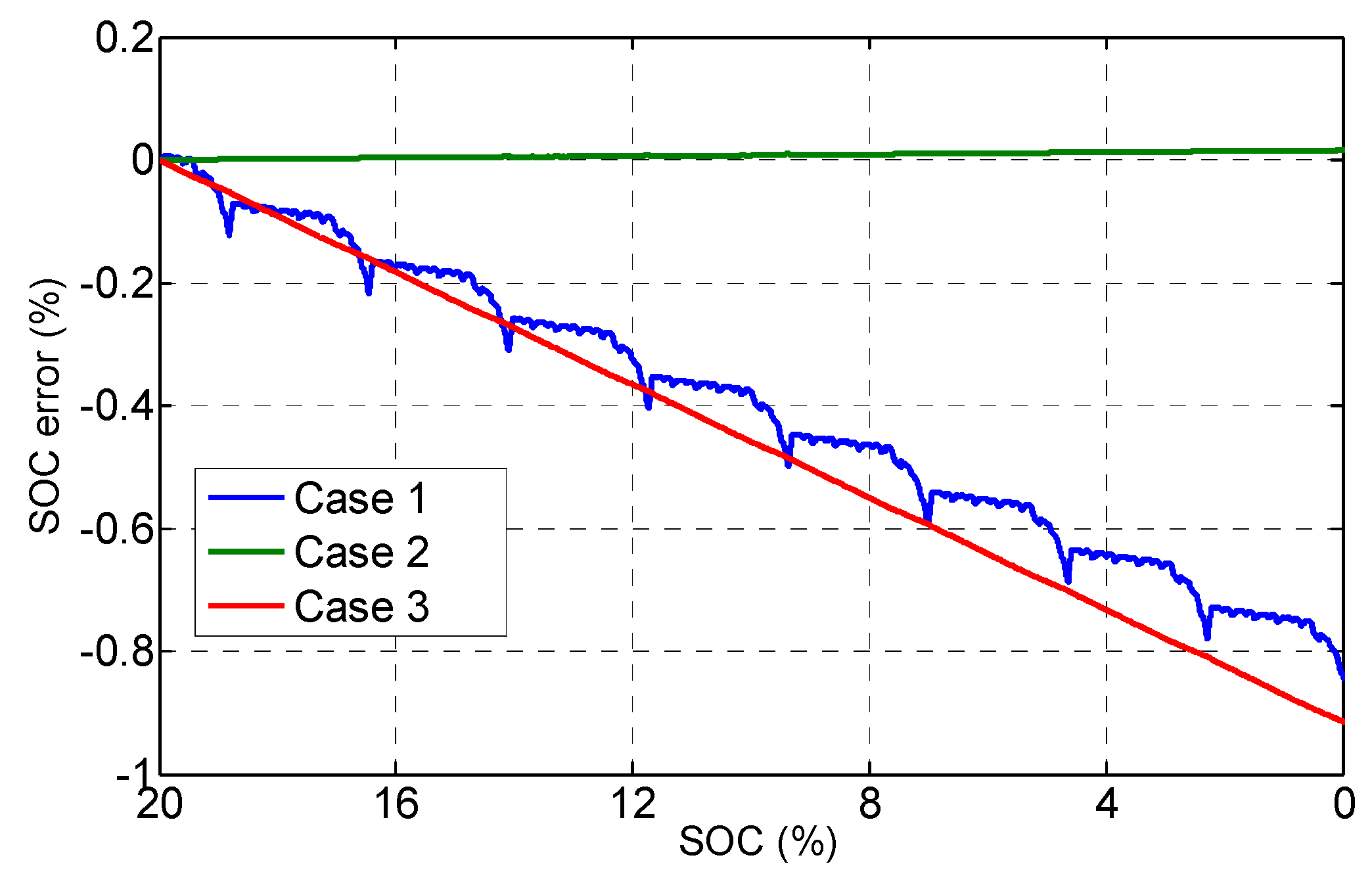
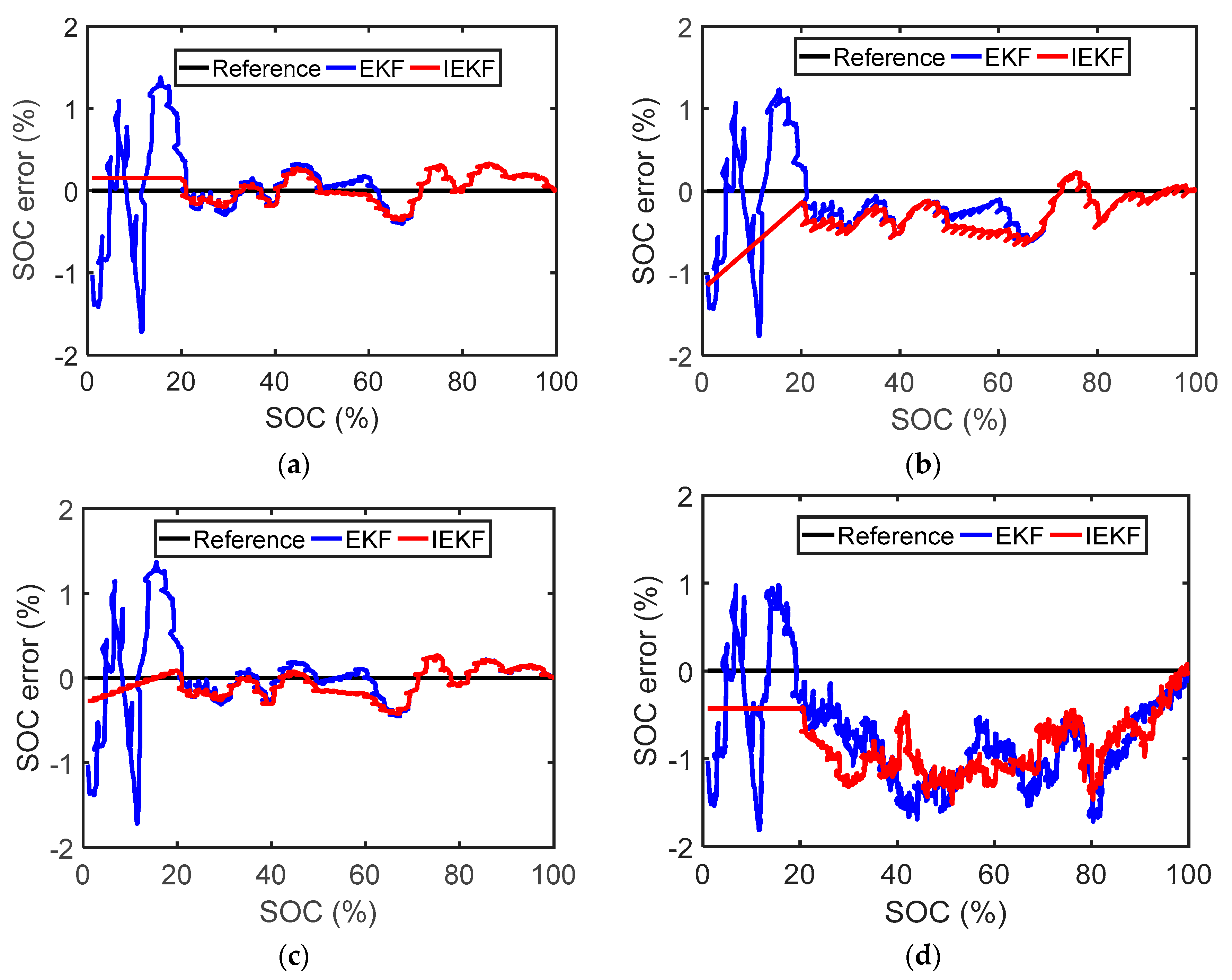
- (a)
- Case 1: the capacity error is 5%. Figure 8 shows that the maximum incremental error of the SOC caused by the AH method in this case is 1% in the low SOC range (0−20%).
- (b)
- Case 2: the coulomb efficiency error is 0.1%. Figure 8 shows that the maximum incremental error caused by the AH method in this case is 0.1% in the low SOC range.
- (c)
- Case 3: the drift of the measured current is 100 mA, and the self-discharge is 1 mA. Figure 8 shows that the maximum incremental error in this case is less than 1%.
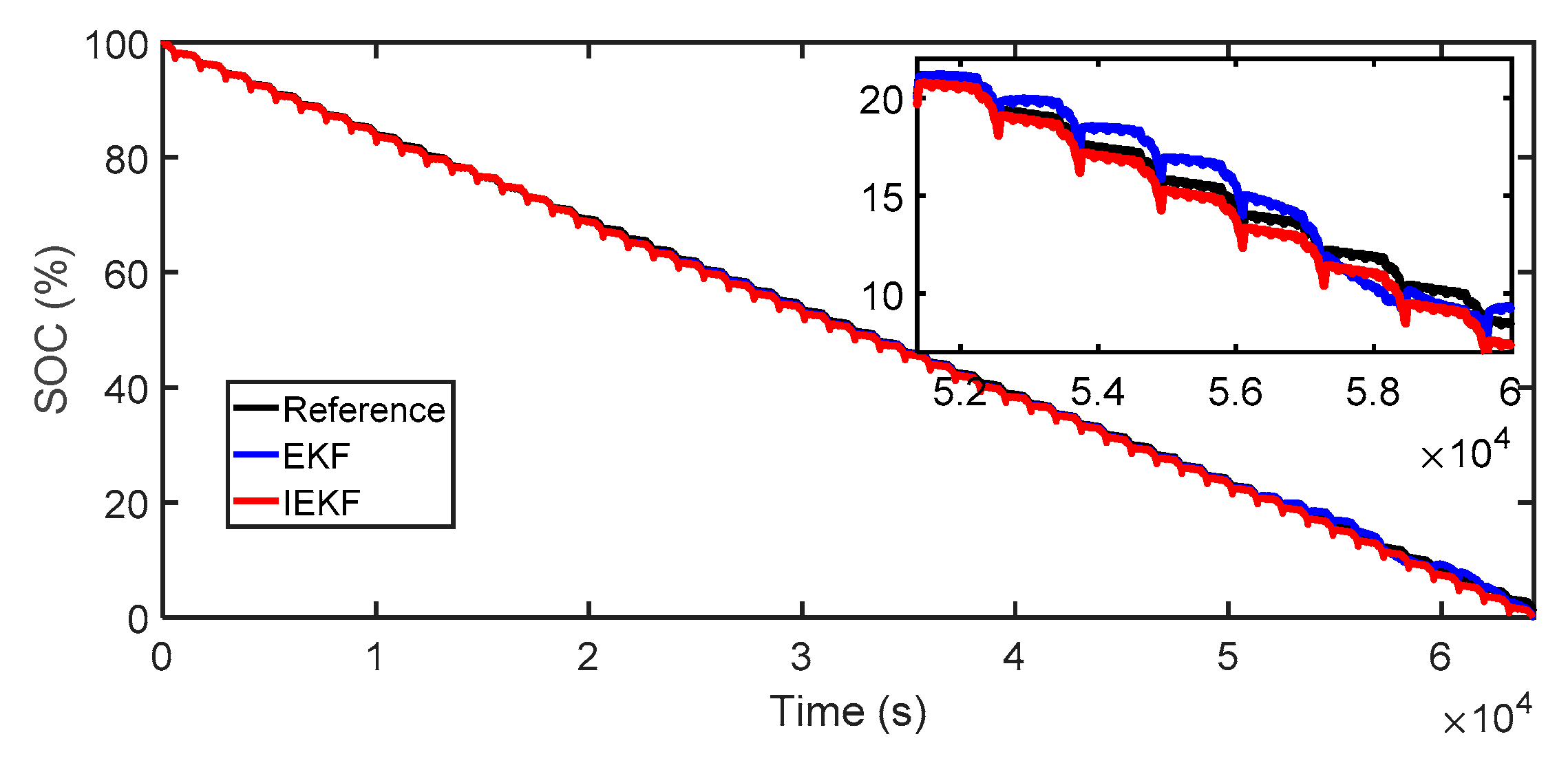
5. Results and Discussion
5.1. Case Studies under NEDC
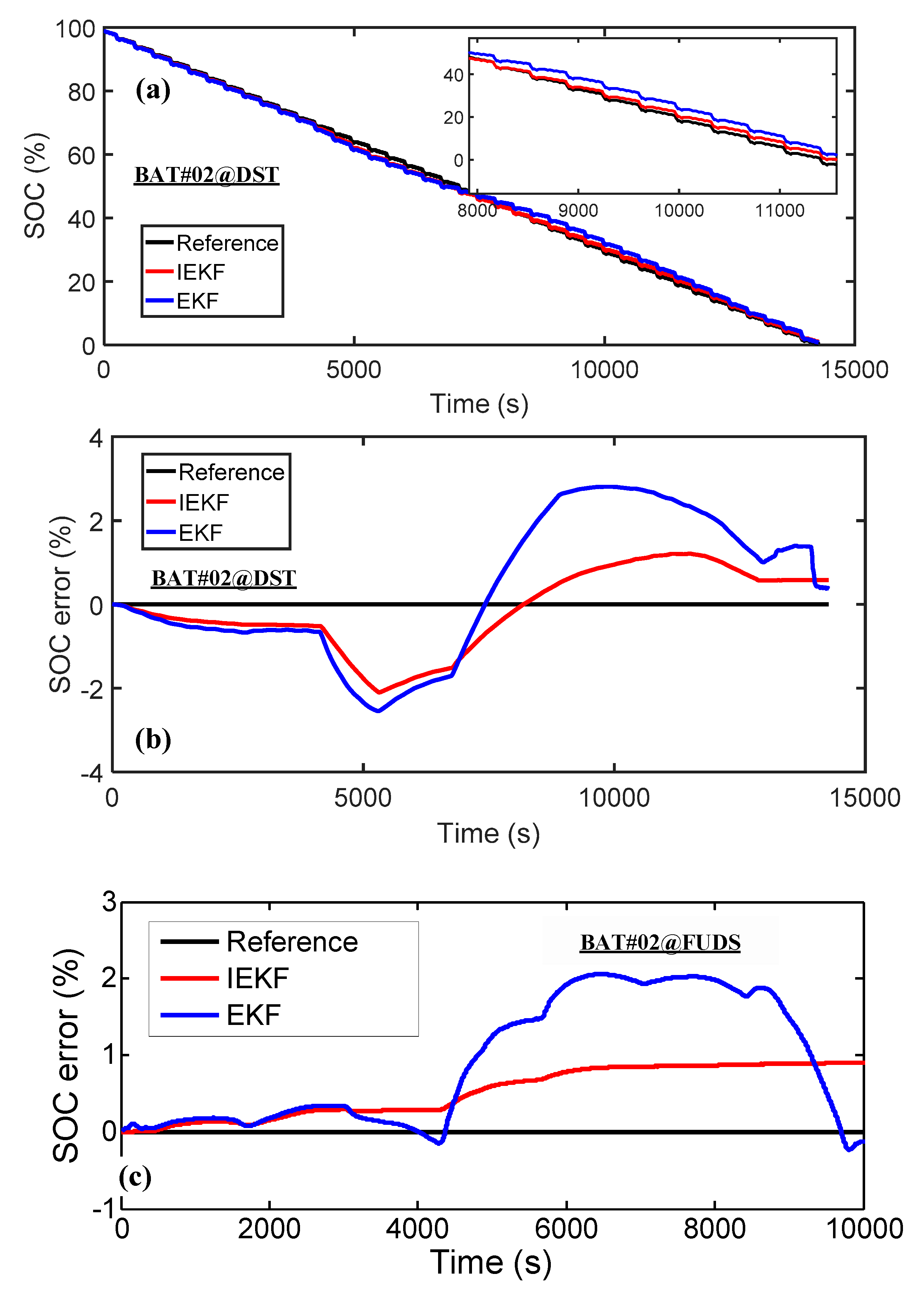
5.2. Additional Validation under the DST and FUDS Working Conditions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.J.; Chen, Z.H. A novel gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.J.; Zhou, L.; Gao, W.K. Electrical behavior of overdischarge-induced internal short circuit in lithium-ion cells. Electrochim. Acta 2018, 278, 245–254. [Google Scholar] [CrossRef]
- Genc, R.; Alas, M.O.; Harputlu, E.; Repp, S.; Kremer, N.; Castellano, M.; Colak, S.G.; Ocakoglu, K.; Erdem, E. High-capacitance hybrid supercapacitor based on multi-colored fluorescent carbon-dots. Sci. Rep. 2017, 7, 11222. [Google Scholar] [CrossRef] [PubMed]
- Garcia, J.; Garcia, P.; Giulii Capponi, F.; De Donato, G. Analysis, modeling, and control of half-bridge current-source converter for energy management of supercapacitor modules in traction applications. Energies 2018, 11, 2239. [Google Scholar] [CrossRef]
- Repp, S.; Harputlu, E.; Gurgen, S.; Castellano, M.; Kremer, N.; Pompe, N.; Worner, J.; Hoffmann, A.; Thomann, R.; Emen, F.M.; et al. Synergetic effects of Fe3+ doped spinel Li4Ti5O12 nanoparticles on reduced graphene oxide for high surface electrode hybrid supercapacitors. Nanoscale 2018, 10, 1877–1884. [Google Scholar] [CrossRef] [PubMed]
- Xia, B.Z.; Cui, D.Y.; Sun, Z.; Lao, Z.Z.; Zhang, R.F.; Wang, W.; Sun, W.; Lai, Y.Z.; Wang, M.W. State of charge estimation of lithium-ion batteries using optimized levenberg-marquardt wavelet neural network. Energy 2018, 153, 694–705. [Google Scholar] [CrossRef]
- Hu, X.S.; Zou, C.F.; Zhang, C.P.; Li, Y. Technological developments in batteries. IEEE Power Energy Mag. 2017, 15, 20–31. [Google Scholar] [CrossRef]
- Lu, L.G.; Han, X.B.; Li, J.Q.; Hua, J.F.; Ouyang, M.G. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.P.; Munoz-Galeano, N.; Sarmiento-Maldonado, H.O. SOC estimation for lithium-ion batteries: Review and future challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.J.; Sun, T. A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries. Electrochim. Acta 2018, 259, 566–577. [Google Scholar] [CrossRef]
- Zheng, L.F.; Zhu, J.G.; Lu, D.D.C.; Wang, G.X.; He, T.T. Incremental capacity analysis and differential voltage analysis based state of charge and capacity estimation for lithium-ion batteries. Energy 2018, 150, 759–769. [Google Scholar] [CrossRef]
- Ungurean, L.; Carstoiu, G.; Micea, M.V.; Groza, V. Battery state of health estimation: A structured review of models, methods and commercial devices. Int. J. Energy Res. 2017, 41, 151–181. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.G.; Lu, L.G.; Li, J.Q.; Feng, X.N. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 92–103. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Ouyang, M.G.; Han, X.B.; Lu, L.G.; Li, J.Q. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.Y.; Yu, Q.Q.; He, H.W.; Sun, F.C. Critical review on the battery state of charge estimation methods for electric vehicles. IEEE Access 2018, 6, 1832–1843. [Google Scholar] [CrossRef]
- Attidekou, P.S.; Lambert, S.; Armstrong, M.; Widmer, J.; Scott, K.; Christensen, P.A. A study of 40 ah lithium ion batteries at zero percent state of charge as a function of temperature. J. Power Sources 2014, 269, 694–703. [Google Scholar] [CrossRef]
- Meng, J.H.; Luo, G.Z.; Ricco, M.; Swierczynski, M.; Stroe, D.I.; Teodorescu, R. Overview of lithium-ion battery modeling methods for state-of-charge estimation in electrical vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Wang, T.P.; Chen, S.Z.; Ren, H.B.; Zhao, Y.Z. Model-based unscented kalman filter observer design for lithium-ion battery state of charge estimation. Int. J. Energy Res. 2018, 42, 1603–1614. [Google Scholar] [CrossRef]
- Xing, Y.J.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Pei, Z.D.; Zhao, X.X.; Yuan, H.M.; Peng, Z.; Wu, L.F. An equivalent circuit model for lithium battery of electric vehicle considering self-healing characteristic. J. Control Sci. Eng. 2018, 2018, 5179758. [Google Scholar] [CrossRef]
- Farmann, A.; Sauer, D.U. Comparative study of reduced order equivalent circuit models for on-board state-of-available-power prediction of lithium-ion batteries in electric vehicles. Appl. Energy 2018, 225, 1102–1122. [Google Scholar] [CrossRef]
- Mesbahi, T.; Khenfri, F.; Rizoug, N.; Chaaban, K.; Bartholomeus, P.; Le Moigne, P. Dynamical modeling of Li-ion batteries for electric vehicle applications based on hybrid particle swarm-nelder-mead (PSO-NM) optimization algorithm. Electr. Power Syst. Res. 2016, 131, 195–204. [Google Scholar] [CrossRef]
- Dai, H.F.; Xu, T.J.; Zhu, L.T.; Wei, X.Z.; Sun, Z.C. Adaptive model parameter identification for large capacity li-ion batteries on separated time scales. Appl. Energy 2016, 184, 119–131. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y. Comparison between two model-based algorithms for li-ion battery soc estimation in electric vehicles. Simul. Model. Pract. Theory 2013, 34, 1–11. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined state of charge and state of health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Wu, X.; Mi, L.; Tan, W.; Qin, J.L.; Zhao, M.N. State of charge (SOC) estimation of Ni-MH battery based on least square support vector machines. Adv. Mater. Res. 2011, 211–212, 1204–1209. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.G.; Deng, J.J.; Chen, Z.; Li, S.Q. The state of charge estimation of lithium-Ion batteries based on a proportional-integral observer. IEEE Trans. Veh. Technol. 2014, 63, 1614–1621. [Google Scholar]
- Li, J.H.; Barillas, J.K.; Guenther, C.; Danzer, M.A. A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles. J. Power Sources 2013, 230, 244–250. [Google Scholar] [CrossRef]
- Chen, X.P.; Shen, W.X.; Cao, Z.W.; Kapoor, A. A novel approach for state of charge estimation based on adaptive switching gain sliding mode observer in electric vehicles. J. Power Sources 2014, 246, 667–678. [Google Scholar] [CrossRef]
- Anton, J.C.A.; Nieto, P.J.G.; Juez, F.J.D.; Lasheras, F.S.; Viejo, C.B.; Gutierrez, N.R. Battery state-of-charge estimator using the mars technique. IEEE Trans. Power Electr. 2013, 28, 3798–3805. [Google Scholar] [CrossRef]
- Wang, L.Y.; Wang, L.F.; Li, Y. A novel state-of-charge estimation algorithm of EV battery based on bilinear interpolation. In Proceedings of the 2013 9th IEEE Vehicle Power and Propulsion Conference (VPPC); IEEE: New York, NY, USA, 2013; pp. 26–29. [Google Scholar]
- Barillas, J.K.; Li, J.H.; Gunther, C.; Danzer, M.A. A comparative study and validation of state estimation algorithms for Li-ion batteries in battery management systems. Appl. Energy 2015, 155, 455–462. [Google Scholar] [CrossRef]
- Ouyang, M.G.; Liu, G.M.; Lu, L.G.; Li, J.Q.; Han, X.B. Enhancing the estimation accuracy in low state-of-charge area: A novel onboard battery model through surface state of charge determination. J. Power Sources 2014, 270, 221–237. [Google Scholar] [CrossRef]
- Lai, X.; Qiao, D.; Zheng, Y.; Zhou, L. A fuzzy state-of-charge estimation algorithm combining ampere-hour and an extended kalman filter for Li-ion batteries based on multi-model global identification. Appl. Sci. 2018, 8, 2028. [Google Scholar] [CrossRef]
- Xin Lai, C.Q.; Gao, W.; Zheng, Y.; Yi, W. A state of charge estimator based extended kalman filter using an electrochemistry-based equivalent circuit model for lithium-ion batteries. Appl. Sci. 2018, 8, 1592. [Google Scholar]
- Wang, S.C.; Liu, Y.H. A pso-based fuzzy-controlled searching for the optimal charge pattern of Li-ion batteries. IEEE Trans. Ind. Electron. 2015, 62, 2983–2993. [Google Scholar] [CrossRef]
- Anton, J.C.A.; Nieto, P.J.G.; Gonzalo, E.G.; Perez, J.C.V.; Vega, M.G.; Viejo, C.B. A new predictive model for the state-of-charge of a high-power lithium-ion cell based on a PSO-optimized multivariate adaptive regression spline approach. IEEE Trans. Veh. Technol. 2016, 65, 4197–4208. [Google Scholar] [CrossRef]
- Kermadi, M.; Berkouk, E. A maximum power point tracker based on particle swarm optimization for pv-battery energy system under partial shading conditions. In Proceedings of the 3rd International Conference on Control, Engineering & Information Technology (Ceit 2015), Tlemcen, Algeria, 25–27 May 2015. [Google Scholar]
- Wei, J.; Dong, G.; Chen, Z.; Kang, Y. System state estimation and optimal energy control framework for multicell lithium-ion battery system. Appl. Energy 2017, 187, 37–49. [Google Scholar] [CrossRef]
- Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Lai, X.; Hu, X. Micro-short circuit diagnosis for series-connected lithium-ion battery packs using mean-difference model. IEEE Trans. Ind. Electron. 2019, 66, 2132–2142. [Google Scholar] [CrossRef]
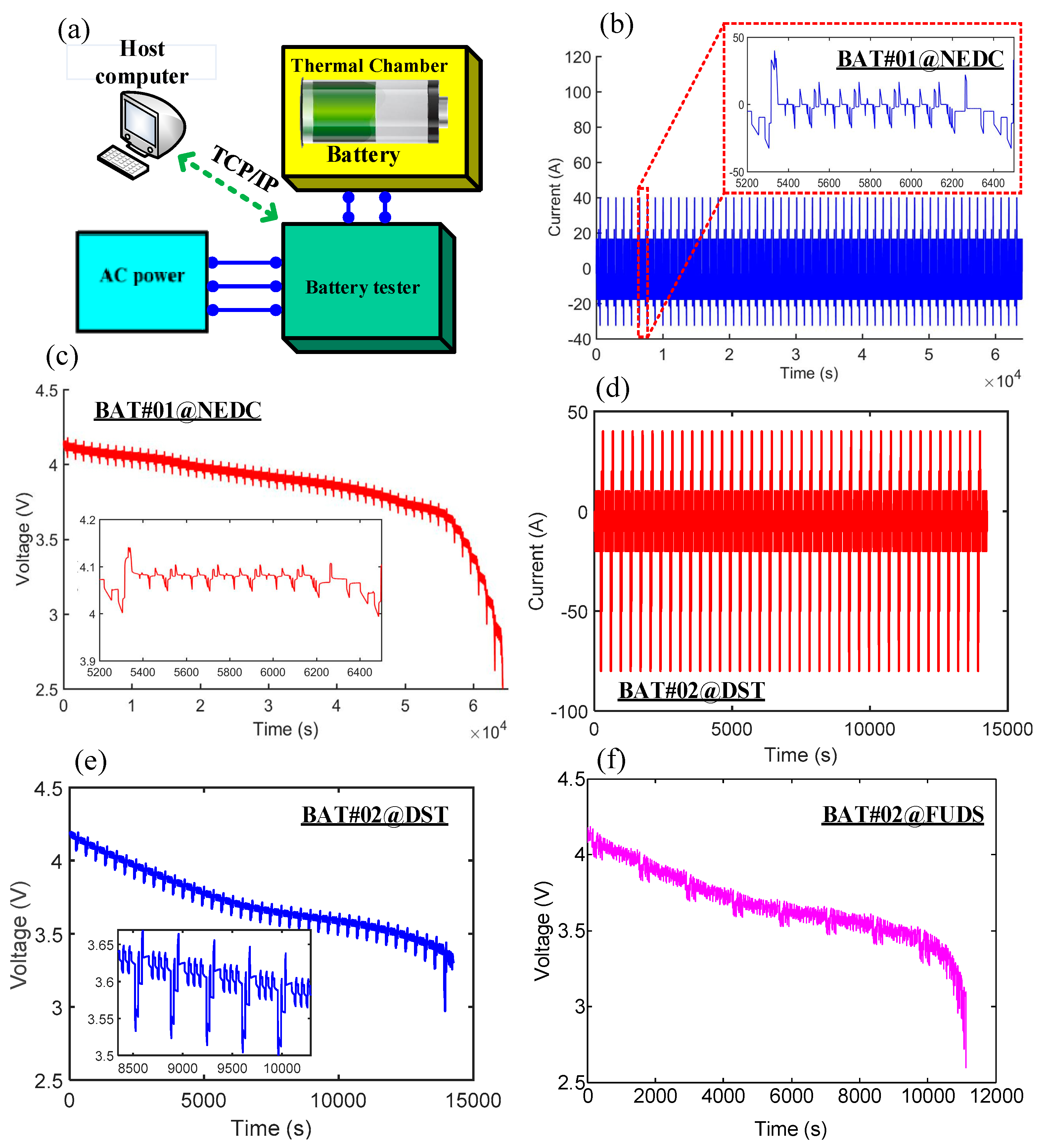





| Nominal Capacity (Ah) | Lower Cut-Off Voltage (V) | Upper Cut-Off Voltage (V) | Maximum Charge Current (A) | |
|---|---|---|---|---|
| BAT#01 | 32.5 | 2.5 | 4.15 | 65 |
| BAT#02 | 40 | 2.8 | 4.2 | 100 |
| SOC Range (%) | ||||||
|---|---|---|---|---|---|---|
| 0–5 | 0.00151 | 0.00150 | 0.000802 | 25.96175 | 5.35 × 10−11 | 910.1351 |
| 5–10 | 0.00142 | 0.00149 | 0.000144 | 4.291183 | 0.00089 | 36.14319 |
| 10–15 | 0.00128 | 0.00155 | 0.000428 | 7.268605 | 0.001204 | 76.50539 |
| 15–20 | 0.00142 | 0.00162 | 0.001829 | 292.5856 | 0.000979 | 26.74074 |
| 20–25 | 0.00130 | 0.00153 | 0.000559 | 11.88647 | 0.002403 | 149.2718 |
| 25–30 | 0.00136 | 0.00165 | 0.000891 | 29.3174 | 0.004348 | 725.8318 |
| 30–35 | 0.00137 | 0.00167 | 0.003932 | 493.7445 | 0.00058 | 18.99163 |
| 35–40 | 0.00139 | 0.00163 | 0.000674 | 23.38255 | 0.001858 | 363.3004 |
| 40–45 | 0.00130 | 0.00155 | 0.000478 | 12.50162 | 0.001385 | 152.1977 |
| 45–50 | 0.00118 | 0.00161 | 0.001177 | 172.2351 | 0.000491 | 11.14567 |
| 50–55 | 0.00139 | 0.00157 | 0.000675 | 23.54001 | 0.001762 | 262.7994 |
| 55–60 | 0.00143 | 0.00162 | 0.003075 | 609.9358 | 0.000921 | 37.09781 |
| 60–65 | 0.00132 | 0.00174 | 0.000826 | 34.21432 | 0.005307 | 862.0298 |
| 65–70 | 0.00130 | 0.00177 | 0.008134 | 766.7005 | 0.00057 | 18.45616 |
| 70–75 | 0.00144 | 0.00171 | 0.011066 | 934.3178 | 0.000646 | 23.98743 |
| 75–80 | 0.00130 | 0.00177 | 0.000409 | 8.049046 | 0.012025 | 788.1887 |
| 80–85 | 0.00133 | 0.00184 | 0.003062 | 377.0807 | 0.000918 | 32.84381 |
| 85–90 | 0.00169 | 0.00176 | 1.93 × 10−11 | 307.087 | 0.016334 | 1000 |
| 90–95 | 0.00200 | 0.00168 | 0.067043 | 1000 | 0.003688 | 999.9995 |
| 95–100 | 0.00200 | 0.00200 | 0.082935 | 1000 | 0.064369 | 999.9998 |
| Case | EKF | IEKF |
|---|---|---|
| Case A | 0.43% | 0.17% |
| Case B | 0.44% | 0.41% |
| Case C | 0.57% | 0.44% |
| Case D | 1.47 | 1.25% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, X.; Yi, W.; Zheng, Y.; Zhou, L. An All-Region State-of-Charge Estimator Based on Global Particle Swarm Optimization and Improved Extended Kalman Filter for Lithium-Ion Batteries. Electronics 2018, 7, 321. https://doi.org/10.3390/electronics7110321
Lai X, Yi W, Zheng Y, Zhou L. An All-Region State-of-Charge Estimator Based on Global Particle Swarm Optimization and Improved Extended Kalman Filter for Lithium-Ion Batteries. Electronics. 2018; 7(11):321. https://doi.org/10.3390/electronics7110321
Chicago/Turabian StyleLai, Xin, Wei Yi, Yuejiu Zheng, and Long Zhou. 2018. "An All-Region State-of-Charge Estimator Based on Global Particle Swarm Optimization and Improved Extended Kalman Filter for Lithium-Ion Batteries" Electronics 7, no. 11: 321. https://doi.org/10.3390/electronics7110321
APA StyleLai, X., Yi, W., Zheng, Y., & Zhou, L. (2018). An All-Region State-of-Charge Estimator Based on Global Particle Swarm Optimization and Improved Extended Kalman Filter for Lithium-Ion Batteries. Electronics, 7(11), 321. https://doi.org/10.3390/electronics7110321






