Spectrum Values in Suburban/Urban Environments above 1.5 GHz
Abstract
:1. Introduction
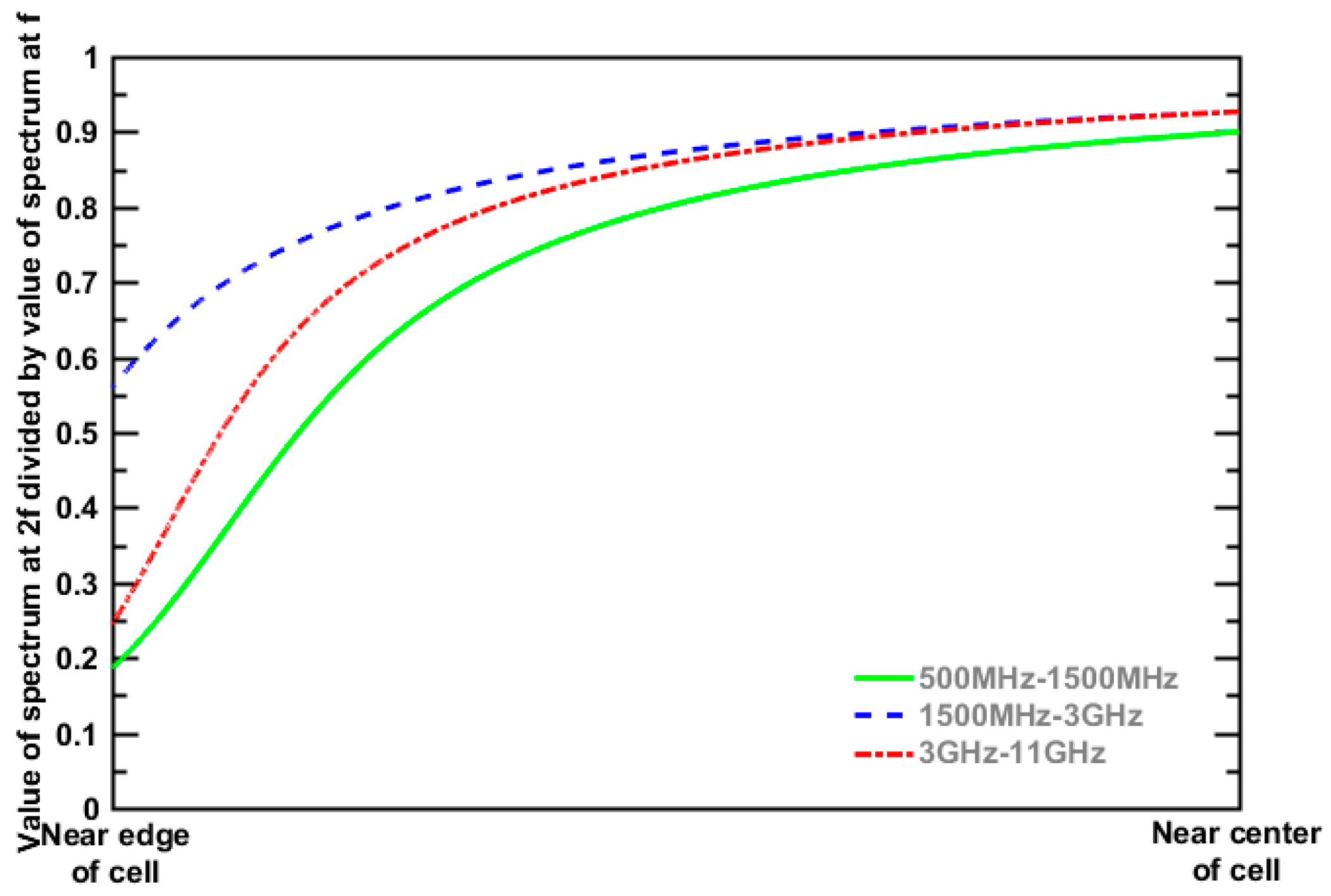
- Much wider frequency bands ranging from 500 MHz to 40 GHz are investigated. In suburban environments, 500 MHz to 1.5 GHz, 1.5 GHz to 3 GHz, and 3 GHz to 11 GHz using Hata and SUI models are investigated. For urban environments, 500 MHz to 40 GHz using the 3D propagation model by 3GPP is evaluated.
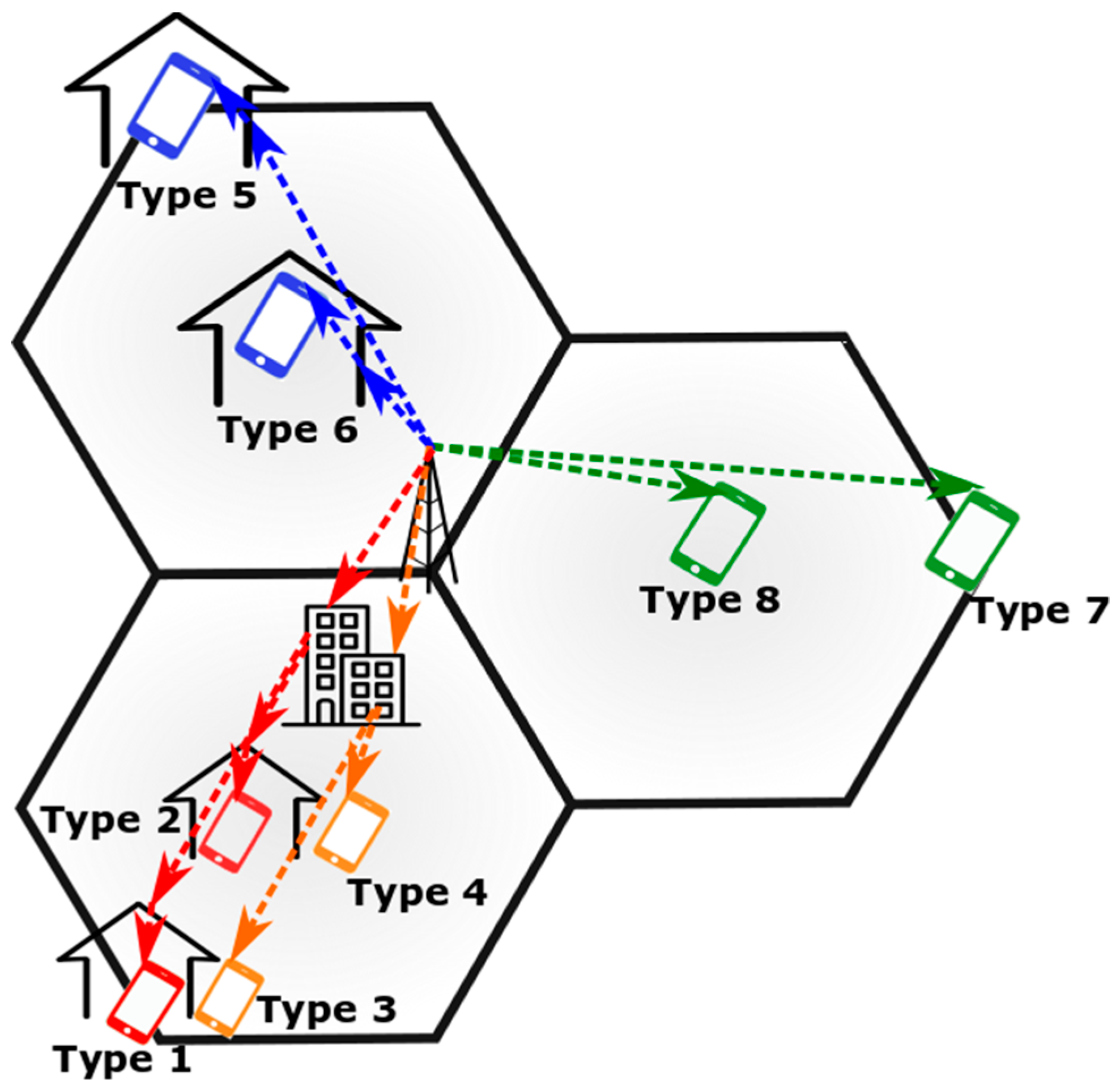
- For urban environments, eight types of users are considered under conditions of non-line-of-sight (NLoS) or line-of-sight (LoS), indoor or outdoor, and user location in the cell. The variation of signal propagation due to various factors is one of the main technological challenges in the spectrum management field [10]. It is also important to consider diverse user conditions, especially for indoor environments, where most data traffic is generated but users experience poor quality of service [11].
- For urban environments, various simulation parameters in the 3D model by 3GPP are taken into consideration to reflect a more practical environment. The 3D model includes such parameters as different shadow fading for LoS and NLoS, different base station (BS) antenna heights for outdoor and indoor environments, parameters used in penetration loss calculation, and effective environment heights. Furthermore, the urban environment is categorized into UMa and UMi-street canyon scenarios. In the UMa scenario, base station antennas are mounted above the rooftop levels of surrounding buildings. In contrast, in the UMi-street canyon scenario, the antennas are below the building rooftops. Another difference between UMa and UMi-street canyon is that the Inter-site Distance (ISD) for UMa is bigger than that for the UMi-street canyon.
- To reveal the complicated urban city environment for spectrum value analysis, a novel method of classifying users is designed depending on their specific propagation conditions. Different user types can also stand for different application scenarios in smart city;
- To the best of our knowledge, there is no literature which includes the similar investigations on spectrum values in suburban/urban environment above 1.5 GHz by means of novel analysis model and state-of-art propagation model;
- To provide general guidelines for frequency selection and deployment in different network environment and scenarios wide range of spectrum covering both the conventional frequency bands and novel 5G spectrum bands are investigated.
2. Analysis of Spectrum Values
2.1. Suburban Environment
2.2. Urban Environment
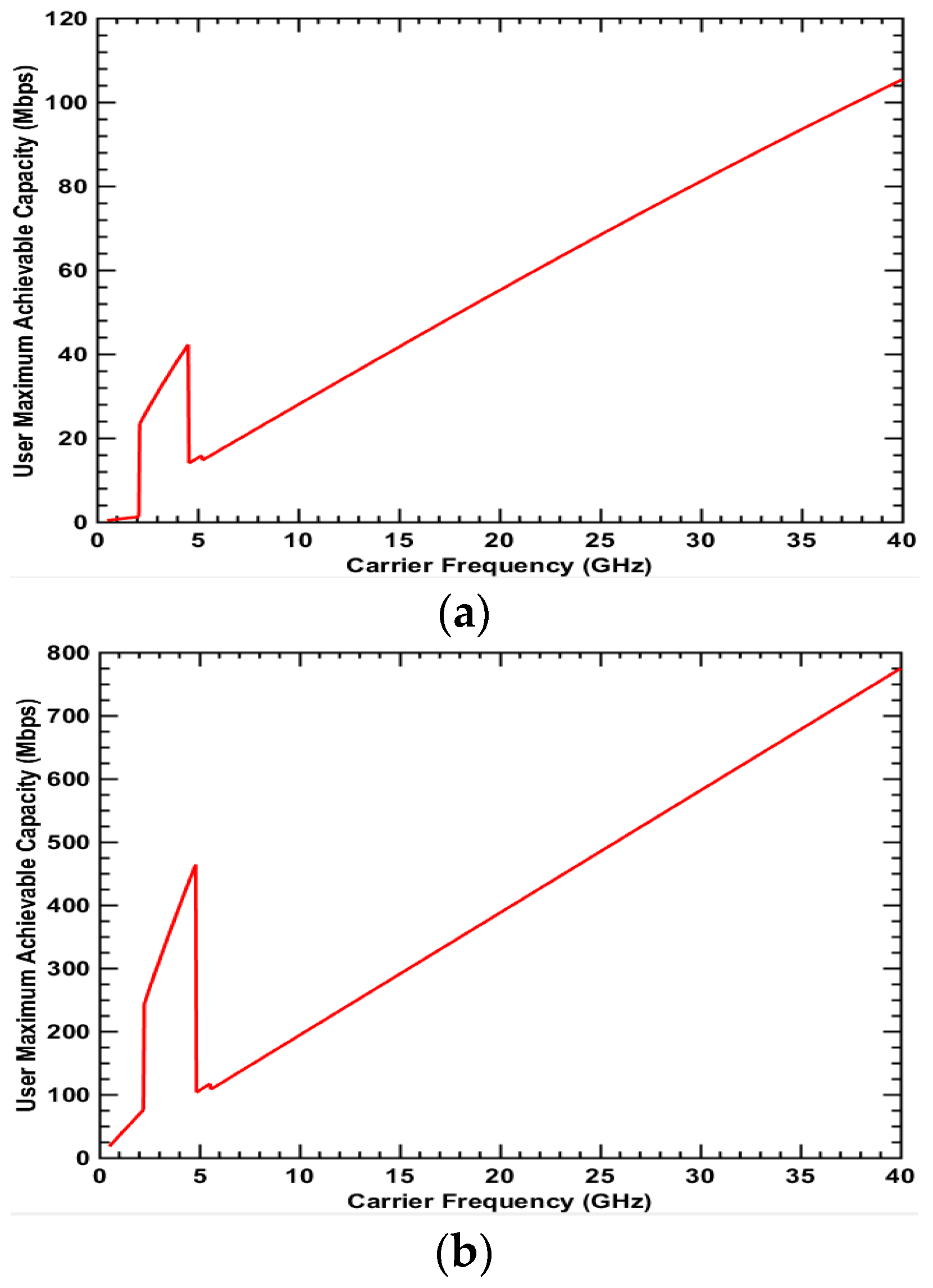
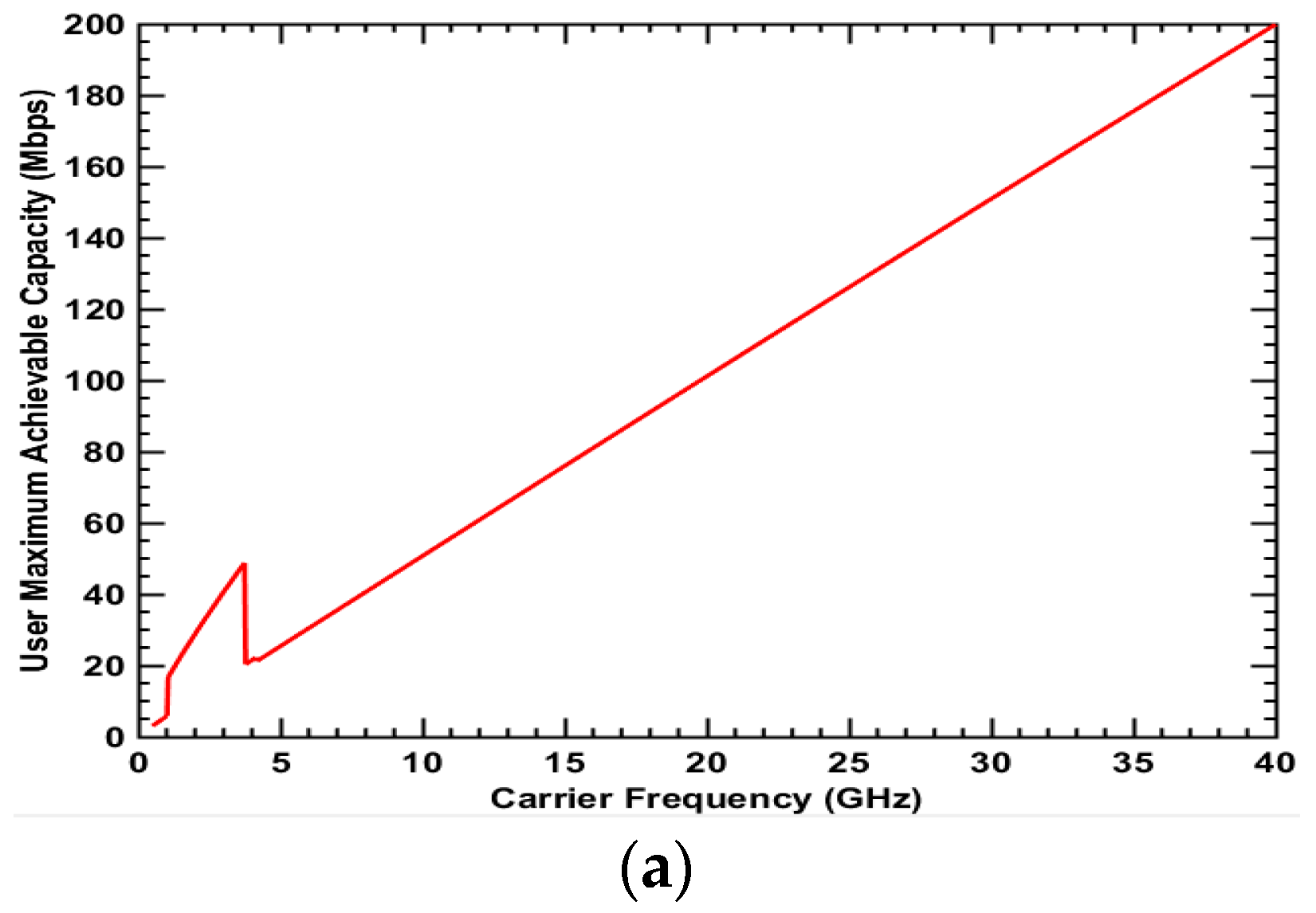
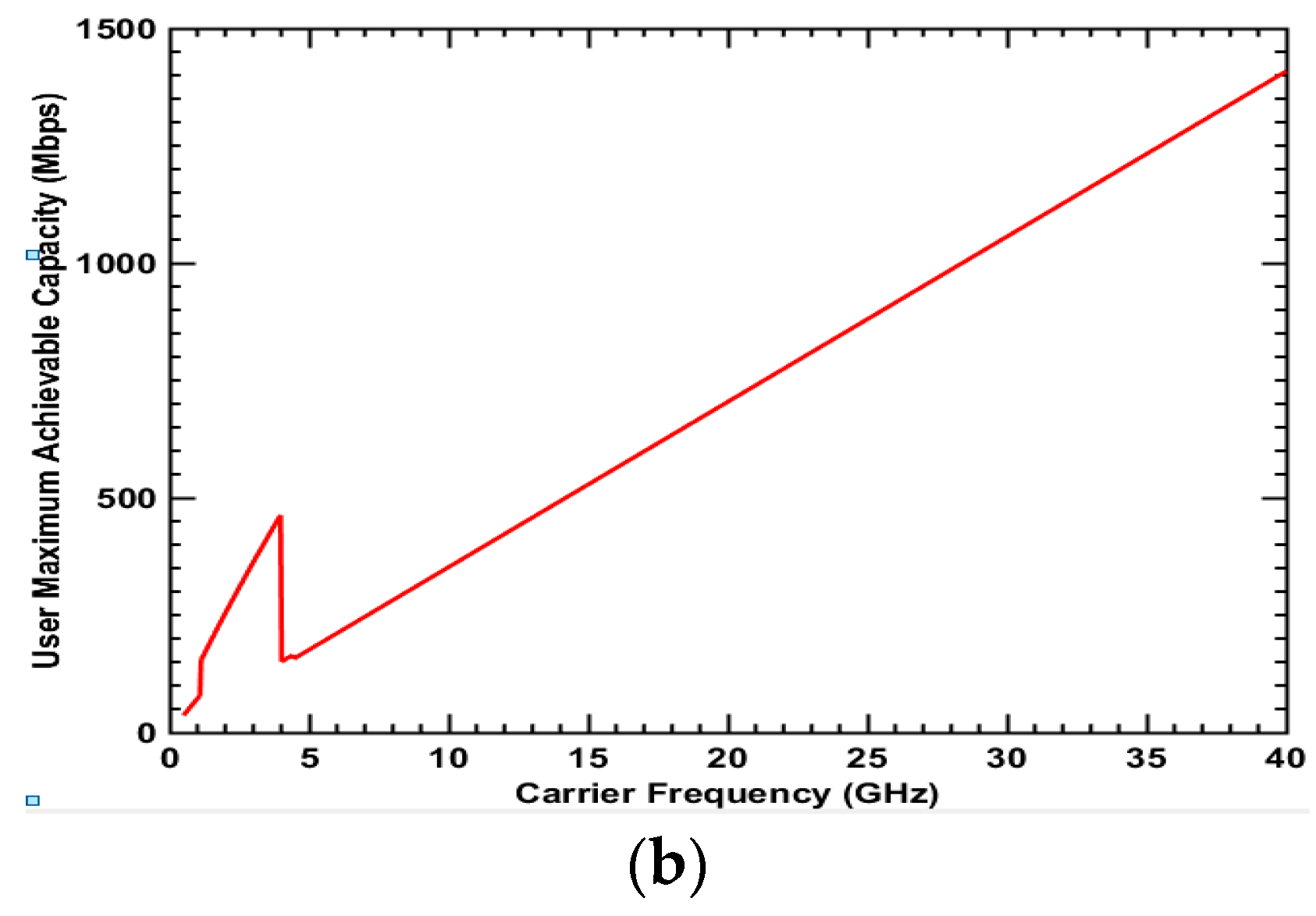
3. Numerical Results
3.1. Suburban Environment
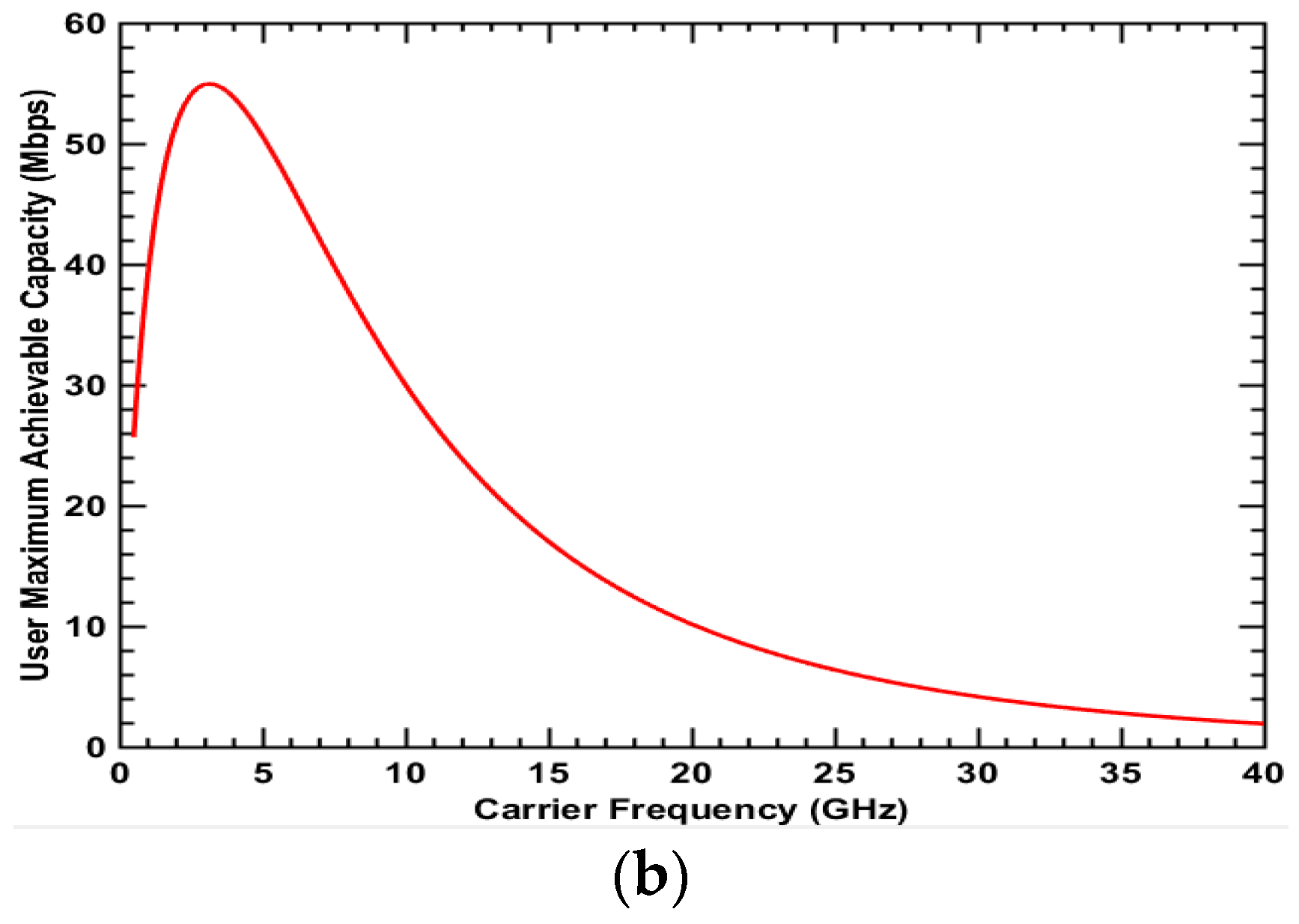
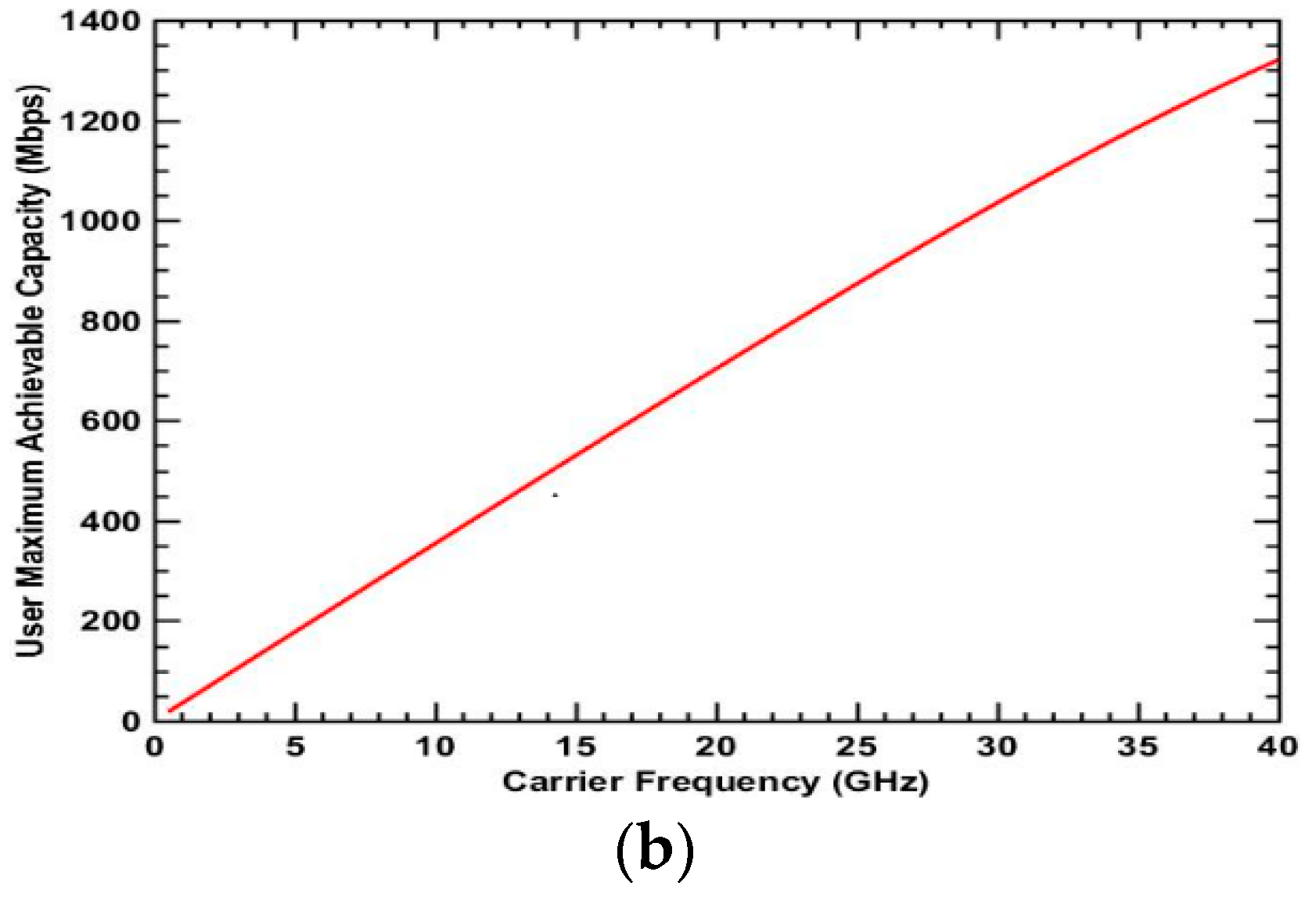
3.2. Urban Environment
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lutilsky, D.; Mazor, K. Theoretical approaches for spectrum pricing. In Proceedings of the 2015 57th International Symposium ELMAR, Zadar, Croatia, 28–30 September 2015; pp. 57–60. [Google Scholar]
- Malisuwan, S.; Kaewphanuekrungsi, W.; Milindavanij, D. Mobile spectrum value and reserve price by using benchmarking approaches. Int. J. Sci. Eng. Technol. 2016, 5, 81–84. [Google Scholar]
- Peha, J.M. Cellular Competition and the Weighted Spectrum Screen. In Proceedings of the TPRC 41: The 41st Research Conference on Communication, Information and Internet Policy, Arlington, VA, USA, 27–29 September 2013. [Google Scholar]
- Bazelon, C.; McHenry, G. Spectrum value. Telecommun. Policy 2013, 37, 737–747. [Google Scholar] [CrossRef]
- Li, Q.C.; Niu, H.; Papathanassiou, A.T.; Wu, G. 5G network capacity: Key elements and technologies. IEEE Veh. Technol. Mag. 2014, 9, 71–78. [Google Scholar] [CrossRef]
- Abhayawardhana, V.; Wassell, I.; Crosby, D.; Sellars, M.; Brown, M. Comparison of empirical propagation path loss models for fixed wireless access systems. In Proceedings of the 2005 IEEE 61st Vehicular Technology Conference, Stockholm, Sweden, 30 May–1 June 2005; Volume 1, pp. 73–77. [Google Scholar]
- Hata, M. Empirical formula for propagation loss in land mobile radio services. IEEE Trans. Veh. Technol. 1980, 29, 317–325. [Google Scholar] [CrossRef]
- 3GPP. Study on Channel Model for Frequencies from 0.5 to 100 GHz (Release 14); 3GPP: Valbonne, France, 2017. [Google Scholar]
- Wei, Y.; Hwang, S. Investigation of spectrum values in rural environments. ICT Express 2018, in press. [Google Scholar] [CrossRef]
- Matheson, R.; Morris, A.C. The technical basis for spectrum rights: Policies to enhance market efficiency. Telecommun. Policy 2012, 36, 783–792. [Google Scholar] [CrossRef]
- Lamas, S.R.; Gonzalez, D.; Hamalainen, J. Indoor planning optimization of ultra-dense cellular networks at high carrier frequencies. In Proceedings of the Wireless Communications and Networking Conference Workshops (WCNCW), New Orleans, LA, USA, 9–12 March 2015; pp. 23–28. [Google Scholar]
- Osseiran, A.; Monserrat, J.F.; Marsch, P. (Eds.) 5G Mobile and Wireless Communications Technology; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Afrić, W.; Pilinsky, S.Z. UMTS LTE downlink cell size calculation. In Proceedings of the ELMAR-2012, Zadar, Croatia, 12–14 September 2012; pp. 105–108. [Google Scholar]
- López-Pérez, D.; Ding, M.; Claussen, H.; Jafari, A.H. Towards 1 Gbps/UE in cellular systems: Understanding ultra-dense small cell deployments. IEEE Commun. Surv. Tutor. 2015, 17, 2078–2101. [Google Scholar] [CrossRef]
- 3GPP. Evolved Universal Terrestrial Radio Access (E-UTRA); Radio Frequency (RF) Requirements for LTE Pico Node B (Release 14); 3GPP: Valbonne, France, 2017. [Google Scholar]
- Holma, H.; Toskala, A. WCDMA for UMTS: HSPA Evolution and LTE; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Jing, S.; Tse, D.N.; Soriaga, J.B.; Hou, J.; Smee, J.E.; Padovani, R. Multicell downlink capacity with coordinated processing. EURASIP J. Wirel. Commun. Netw. 2008, 2008, 18. [Google Scholar] [CrossRef]
- 3GPP. Evolved Universal Terrestrial Radio Access (E-UTRA); Radio Frequency (RF) System Scenarios (Release 14); 3GPP: Valbonne, France, 2017. [Google Scholar]








| Parameters | Hata/SUI Model |
|---|---|
| TX Antenna Height (m) | 50 |
| RX Antenna Height (m) | 1.5 |
| TX Antenna Gain, GT (dBi) | 15 |
| RX Antenna Gain, GR (dBi) | 0 |
| BS TX Power, PT (dBm) | 46 |
| Thermal noise density (dBm/Hz) | −174 |
| Interference margin (dB) | 5 |
| Cell radius (km) | 5 |
| User Type | User Condition | Smart City Application Scenario |
|---|---|---|
| Type 1 | NLoS + Indoor + Cell Edge | Smart home, Smart office, Shopping mall |
| Type 2 | NLoS + Indoor + Cell center | |
| Type 3 | NLoS + Outdoor + Cell Edge | Intelligent vehicle in dense urban, Stadium |
| Type 4 | NLoS + Outdoor + Cell center | |
| Type 5 | LoS + Indoor + Cell Edge | Skyscraper |
| Type 6 | LoS + Indoor + Cell center | |
| Type 7 | LoS + Outdoor + Cell Edge | Innovative highway transportation |
| Type 8 | LoS + Outdoor + Cell center |
| Parameters | UMa | UMi—Street Canyon |
|---|---|---|
| TX Antenna Height (m) | 25 | 10 |
| Outdoor user RX antenna height (m) | 1.5 | 1.5 |
| Indoor user RX antenna height (m) | 9 | 9 |
| Inter-site Distance ISD (m) | 500 | 200 |
| TX antenna gain, GT (dBi) | 15 | 15 |
| RX antenna gain, GR (dBi) | 0 | 0 |
| BS TX power, PT (dBm) | 46 | 46 |
| Thermal noise density (dBm/Hz) | −174 | −174 |
| Effective environment height (m) | 1 | 1 |
| Active user number (users/km2) | 300 | 300 |
| Minimum coupling loss, MCL (dB) | 70 | 70 |
| Shadow fading in LOS (dB) | 4 | 4 |
| Shadow fading in NLOS (dB) | 6 | 7.82 |
| Environment | Frequency Ranges | Propagation Model |
|---|---|---|
| Suburban | 500 MHz~1500 MHz | Hata Model |
| 1500 MHz~3000 MHz | SUI Model | |
| 3000 MHz~11,000 MHz | SUI Model | |
| Urban | 500 MHz~40,000 MHz | 3D Model (3GPP) |
| UMa | Umi—Street Canyon | |||||||
|---|---|---|---|---|---|---|---|---|
| User Type | C at 3.5 GHz (Mbps) | C at 28 GHz (Mbps) | fC for Max C(GHz) | Remark* | C at 3.5 GHz (Mbps) | C at 28 GHz (Mbps) | fC for Max C (GHz) | Remark* |
| Type 1 | 0.000 | 0.000 | 0.5 | Lower band | 1.24 | 0.04 | 0.5 | Lower band |
| Type 2 | 0.01 | 0.000 | 0.5 | Lower band | 54.70 | 4.898 | 3.2 | 3 GHz |
| Type 3 | 0.001 | 0.000 | 0.5 | Lower band | 23.91 | 3.62 | 2.0 | 2 GHz |
| Type 4 | 0.28 | 0.04 | 0.5 | Lower band | 193.60 | 257.25 | 19.0 | 19 GHz |
| Type 5 | 9.59 | 17.14 | 15.1 | 15 GHz | 68.05 | 501.50 | 40.0 | Higher band |
| Type 6 | 27.76 | 83.65 | 28.2 | 28 GHz | 124.30 | 972.00 | 40.0 | Higher band |
| Type 7 | 34.65 | 76.10 | 40.0 | Higher band | 355.75 | 542.50 | 40.0 | Higher band |
| Type 8 | 46.17 | 141.10 | 40.0 | Higher band | 414.75 | 986.50 | 40.0 | Higher band |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Hwang, S.-H. Spectrum Values in Suburban/Urban Environments above 1.5 GHz. Electronics 2018, 7, 401. https://doi.org/10.3390/electronics7120401
Wei Y, Hwang S-H. Spectrum Values in Suburban/Urban Environments above 1.5 GHz. Electronics. 2018; 7(12):401. https://doi.org/10.3390/electronics7120401
Chicago/Turabian StyleWei, Yiqiao, and Seung-Hoon Hwang. 2018. "Spectrum Values in Suburban/Urban Environments above 1.5 GHz" Electronics 7, no. 12: 401. https://doi.org/10.3390/electronics7120401
APA StyleWei, Y., & Hwang, S.-H. (2018). Spectrum Values in Suburban/Urban Environments above 1.5 GHz. Electronics, 7(12), 401. https://doi.org/10.3390/electronics7120401






