Model for the Prediction of Rain Attenuation Affecting Free Space Optical Links
Abstract
:1. Introduction
2. Predicting Rain Attenuation Impairing FSO Links
2.1. MultiEXCELL
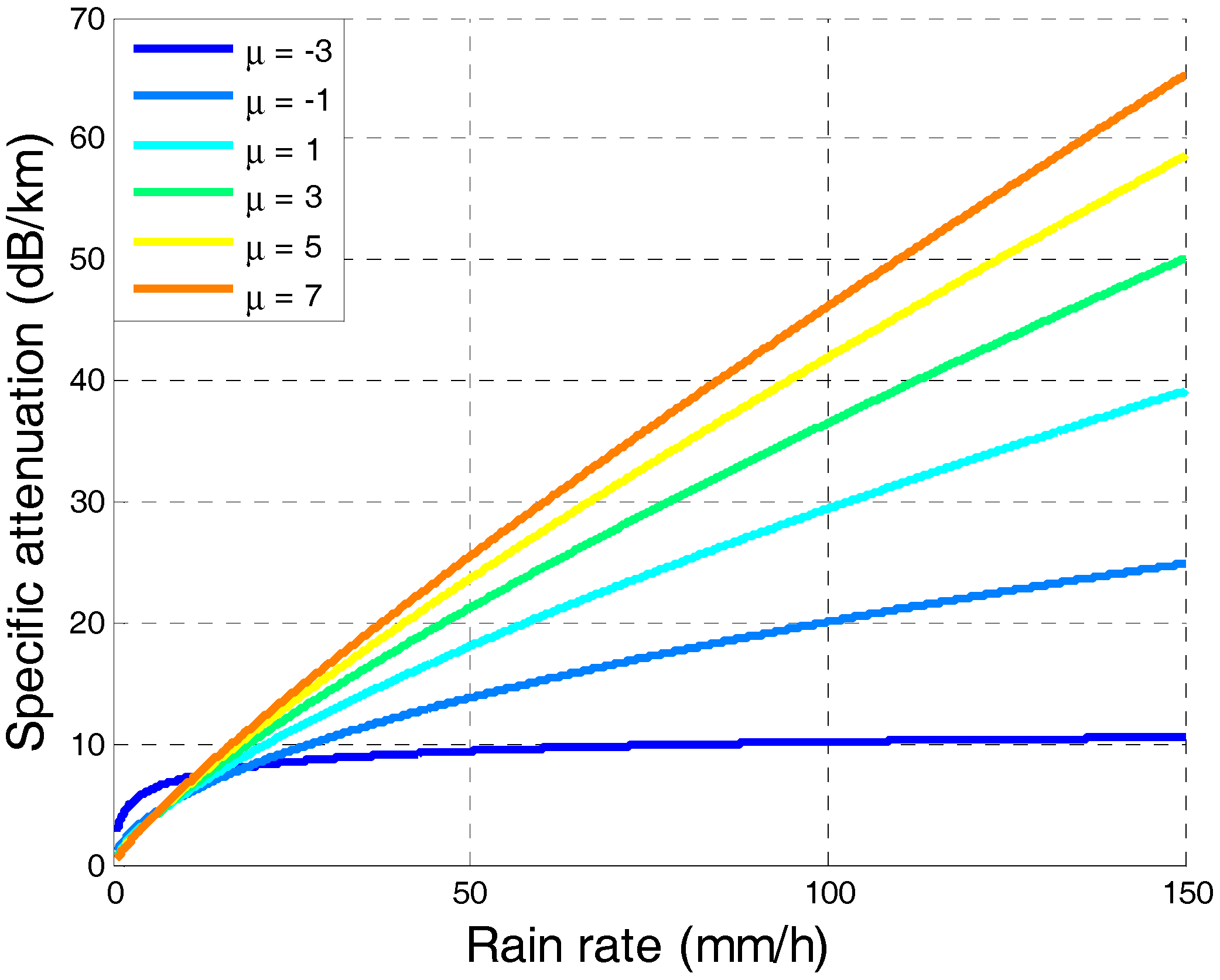
2.2. Specific Attenuation
2.3. Path Attenuation
3. Comparison with Analytical Methods
3.1. Rain Attenuation Models for Terrestrial Radio Links
3.1.1. ITU-R P.530-16 Model
- Compute the effective path length of the link, deff, by multiplying the actual path length L (km) by the path reduction factor r, which can be expressed as:where f is the frequency in GHz; L is the path length; α is extracted from Table 1; and R0.01 is the rain rate exceeded for 0.01% of the time in a year, to be extracted from the local P(R). According to [10], if r > 2.5, its value is bounded to 2.5.
- The path attenuation exceeded for 0.01% of the yearly time is calculated as:
- The prediction of the full P(A), for 0.001% ≤ P ≤ 1%, is given by:with C1, C2, and C3 being empirical coefficients depending on frequency f [10].
3.1.2. Lin Model
3.1.3. Moupfouma Model
3.1.4. Brazilian Model
3.2. Performance Assessment
4. Multiple Scattering Effects
4.1. Multiple Scattering Gain
4.2. Monte-Carlo Simulation Results
- Beam type: collimated (i.e., zero divergence), transmitted beam width = 2.5 cm
- Receiver aperture: 10 cm radius (circular)
- Receiver field of view: 90° (open detector)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Khalighi, M.A.; Uysal, M. Survey on Free Space Optical Communication: A Communication Theory Perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter Wave Mobile Communications for 5G Cellular: It Will Work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef] [Green Version]
- Bloom, S.; Korevaar, E.; Schuster, J.; Willebrand, H. Understanding the Performance of Free-Space Optics. J. Opt. Commun. Netw. 2003, 2, 178–200. [Google Scholar]
- Ijaz, M.; Ghassemlooy, Z.; Perez, J.; Brazda, V.; Fiser, O. Enhancing the Atmospheric Visibility and Fog Attenuation Using a Controlled FSO Channel. IEEE Photonics Technol. Lett. 2013, 25, 1262–1265. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE: Bellingham, WA, USA, 2005. [Google Scholar]
- Clay, M.R.; Lenham, A.P. Transmission of Electromagnetic Radiation in Fogs in the 0.53–10.1 µm Wavelength Range. Appl. Opt. 1981, 20, 3831–3832. [Google Scholar] [CrossRef]
- Chimelis, V. Extinction of CO2 Laser Radiation by Fog and Rain. Appl. Opt. 1982, 21, 3367–3372. [Google Scholar] [CrossRef]
- Strickland, B.R.; Lavan, M.J.; Woodbridge, E.; Chan, V. Effects of Fog on the Bit-Error Rate of a Free-Space Laser Communication System. Appl. Opt. 1999, 38, 424–431. [Google Scholar] [CrossRef] [PubMed]
- Nebuloni, R.; Capsoni, C. Effect of Adverse Weather on Free-Space Optics. In Optical Wireless Communications: An Emerging Technology; Uysal, M., Capsoni, C., Ghassemlooy, Z., Boucouvalas, A., Udvary, E., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 47–68. [Google Scholar] [CrossRef]
- ITU-R Recommendation P.530-16. Propagation Data and Prediction Methods Required for the Design of Terrestrial Line-of-Sight Systems; ITU: Geneva, Switzerland, 2015. [Google Scholar]
- Da Silva Mello, L.A.R.; Pontes, M.S.; Souza, R.M.D.; Garcia, N.A.P. Prediction of Rain Attenuation in Terrestrial Links Using Full Rainfall Rate Distribution. IEEE Electron. Lett. 2007, 43, 1442–1443. [Google Scholar] [CrossRef]
- Lin, S.H. National Long Term Rain Statistics and Empirical Calculation of 11 GHz Microwave Rain Attenuation. Bell Syst. Tech. J. 1977, 56, 1581–1604. [Google Scholar] [CrossRef]
- Moupfouma, F. Electromagnetic Waves Attenuation due to Rain: A Prediction Model for Terrestrial or L.O.S SHF and EHF Radio Communication Links. J. Infrared Millim. Terahertz Waves 2009, 30, 622–632. [Google Scholar] [CrossRef]
- Vasseur, H.; Gibbins, C.J. Prediction of apparent extinction for optical transmission through rain. Appl. Opt. 1996, 35, 7144–7150. [Google Scholar] [CrossRef]
- Carbonneau, T.H.; Wisely, D.R. Opportunities and challenges for optical wireless; the competitive advantage of free space telecommunications links in today’s crowded market place. Proc. SPIE 1998, 3232. [Google Scholar] [CrossRef]
- Capsoni, C.; Nebuloni, R. Effect of Rain on Free Space Optics. In Proceedings of the Eleventh URSI Commission F Open Symposium on Radio Wave Propagation and Remote Sensing PUC-RIO, Rio de Janeiro, Brazil, 30 October–2 November 2007; pp. 277–280. [Google Scholar]
- Kvicera, V.; Grabner, M.; Fiser, O. Propagation Characteristics Obtained on Parallel Terrestrial FSO Links at 860 nm and 1550 nm. In Proceedings of the 2nd International Workshop on Optical Wireless Communications (IWOW), Newcastle Upon Tyne, UK, 21 October 2013. [Google Scholar] [CrossRef]
- Abele, J.; Raidt, H.; Höhn, D.H. Studies on the Influence of Meteorological Parameters on Atmospheric Laser Transmission. Opt. Acta Int. J. Opt. 1980, 27, 1445–1464. [Google Scholar] [CrossRef]
- Luini, L.; Capsoni, C. MultiEXCELL: A New Rain Field Model for Propagation Applications. IEEE Trans. Antennas Propag. 2011, 59, 4286–4300. [Google Scholar] [CrossRef]
- Uppala, S.M.; Kållberg, P.W.; Simmons, A.J.; Andrae, U.; Da Costa Bechtold, V.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez, A.; Kelly, G.A.; et al. The ERA-40 Re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Capsoni, C.; Luini, L.; D’Amico, M. The MultiEXCELL Model for the Prediction of the Radio Interference due to Hydrometeor Scattering. In Proceedings of the Forth European Conference on Antennas and Propagation, Barcelona, Spain, 12–16 April 2010; pp. 1–5. [Google Scholar]
- Luini, L.; Emiliani, L.; Capsoni, C. Planning of Advanced SatCom Systems Using ACM Techniques: The Impact of Rain Fade. In Proceedings of the Fifth European Conference on Antennas and Propagation, Rome, Italy, 11–15 April 2011; pp. 3965–3969. [Google Scholar]
- Luini, L.; Capsoni, C. A Rain Cell Model for the Simulation and Performance Evaluation of Site Diversity Schemes. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 1327–1330. [Google Scholar] [CrossRef]
- Luini, L.; Capsoni, C. A Physically Based Methodology for the Evaluation of the Rain Attenuation on Terrestrial Radio Links. In Proceedings of the Forth European Conference on Antennas and Propagation, Barcelona, Spain, 12–16 April 2010; pp. 1–5. [Google Scholar]
- Ghiani, R.; Luini, L.; Fanti, A. A Physically-Based Rain Attenuation Model for Terrestrial Links. Radio Sci. 2017, 52, 972–980. [Google Scholar] [CrossRef]
- Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler Radar Characteristics of Precipitation at Vertical Incidence. Rev. Geophys. Space Phys. 1973, 2, 1–35. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural Variations in the Analytical form of the Raindrop Size Distribution. J. Clim. Appl. Meteor. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- ITU-R Recommendation P.837-6. Characteristics of Precipitation for Propagation Modelling; ITU: Geneva, Switzerland, 2012. [Google Scholar]
- Wiscombe, W.J. Improved Mie scattering algorithms. Appl. Opt. 1980, 19, 1505–1509. [Google Scholar] [CrossRef]
- ITU-R Recommendation P.311-15. Acquisition, Presentation and Analysis of Data in Studies of Tropospheric Propagation; ITU: Geneva, Switzerland, 2015. [Google Scholar]
- Grabner, M.; Kvicera, V. Multiple Scattering in Rain and Fog on Free-Space Optical Links. J. Lightwave Technol. 2014, 32, 513–520. [Google Scholar] [CrossRef]









| Shape Parameter (μ) | k | α |
|---|---|---|
| −3 | 4.0684 | 0.2077 |
| −2 | 2.2838 | 0.4050 |
| −1 | 1.5921 | 0.5506 |
| 0 | 1.2924 | 0.6436 |
| 1 | 1.1394 | 0.7057 |
| 2 | 1.0505 | 0.7497 |
| 3 | 0.9938 | 0.7823 |
| 4 | 0.9551 | 0.8074 |
| 5 | 0.9273 | 0.8273 |
| 6 | 0.9065 | 0.8435 |
| 7 | 0.8905 | 0.8569 |
| 8 | 0.8779 | 0.8682 |
| Rain Rate (mm/h) | μ = 1 | μ = 2 | μ = 3 | |||
|---|---|---|---|---|---|---|
| a | b | a | b | a | b | |
| 1 | 0.011 | 0.484 | 0.010 | 0.522 | 0.008 | 0.553 |
| 2 | 0.016 | 0.521 | 0.015 | 0.547 | 0.013 | 0.576 |
| 5 | 0.026 | 0.562 | 0.024 | 0.592 | 0.021 | 0.622 |
| 10 | 0.036 | 0.601 | 0.033 | 0.636 | 0.031 | 0.657 |
| 20 | 0.046 | 0.651 | 0.044 | 0.685 | 0.042 | 0.709 |
| 50 | 0.063 | 0.723 | 0.062 | 0.757 | 0.062 | 0.773 |
| 100 | 0.080 | 0.777 | 0.082 | 0.804 | 0.086 | 0.817 |
| μ = 1 | μ = 2 | μ = 3 | ||||
|---|---|---|---|---|---|---|
| a | b | a | b | a | b | |
| p0 | 0.0112 | 0.4965 | 0.0103 | 0.5194 | 0.0092 | 0.5504 |
| p1 | 0.0060 | 0.0390 | 0.0040 | 0.0389 | 0.0019 | 0.0372 |
| p2 | 0.0019 | 0.0053 | 0.0025 | 0.0052 | 0.0031 | 0.0047 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korai, U.A.; Luini, L.; Nebuloni, R. Model for the Prediction of Rain Attenuation Affecting Free Space Optical Links. Electronics 2018, 7, 407. https://doi.org/10.3390/electronics7120407
Korai UA, Luini L, Nebuloni R. Model for the Prediction of Rain Attenuation Affecting Free Space Optical Links. Electronics. 2018; 7(12):407. https://doi.org/10.3390/electronics7120407
Chicago/Turabian StyleKorai, Umair Ahmed, Lorenzo Luini, and Roberto Nebuloni. 2018. "Model for the Prediction of Rain Attenuation Affecting Free Space Optical Links" Electronics 7, no. 12: 407. https://doi.org/10.3390/electronics7120407
APA StyleKorai, U. A., Luini, L., & Nebuloni, R. (2018). Model for the Prediction of Rain Attenuation Affecting Free Space Optical Links. Electronics, 7(12), 407. https://doi.org/10.3390/electronics7120407






