1. Introduction
Low Probability of Intercept (LPI) radar waveforms possess many characteristics. They are widely used in many fields, such as air defense radar, airborne fire control radar and beyond visual range radar and so forth. However, the detection of them is a difficult thing. Therefore, it is important to study LPI radar waveform recognition.
Many recognition methods have been put forward to recognize radar waveforms. For instance, extracting the bispectrum cascade feature to identify six kinds of waveforms (CW, LFM, NLFM, BPSK, QPSK and FSK) in [
1]. Atomic Decomposition (AD) and Expectation Maximization (EM) algorithms are used to detect radar waveforms [
2]. But only LFM and BPSK can be identified in this method. In [
3], power spectrum accumulation and similarity theory are utilized to detect the noise frequency modulation signal. When SNR is −3 dB and the duration is 1 ms, the recognition rate is 100%. The method based on the statistics of energy for detecting noise frequency modulation signal is proposed [
4]. But it has good performance only for the signals of long time. The paper [
5] presents Bispestra Diagonal Slice (BDS) to distinguish four types of waveforms (including FMCW, Frank code, Costas codes and FSK/PSK). The ratio of successful recognition (RSR) is more than 93.4% when signal-to-noise ratio (SNR) ≥8 dB. In [
6], random projections and sparse classification are adopted to recognize LFM, FSK and PSK. The RSR is about 90% when SNR is 0 dB. Lunden explored the system based on Choi-Williams distribution (CWD) and Wigner-Ville distribution (WVD) to distinguish eight kinds of waveforms [
7]. However, the algorithm requires prior information and the RSR is 98% at SNR of 6 dB. In [
8], Zhang proposes the system to recognize eight radar waveforms. The RSR is 94.7% at SNR of −2 dB and the number of features is 23. Therefore, it is a challenge for the existing methods to distinguish more radar waveforms with fewer features under high noise environment.
The system for recognizing eight LPI waveforms is proposed in this paper. The recognizable radar waveforms contain BPSK, Costas codes, LFM, P1-P4 and Frank codes. The classifier is the support vector machine (SVM) of artificial bee colony (ABC) algorithm. The features what we use are roughly divided into two types. Some features are calculated by time-domain signals and we call them time features. The other features are from time-frequency analysis and we call them time-frequency (T-F) features. Time features are extracted from the power spectral density (PSD), second order moments and cumulants and instantaneous properties. T-F features are related to WVD and CWD. Simulation results indicate that recognition rate can reach up to 92% when SNR is −4 dB.
The contributions of this paper are mainly in four aspects: (1) the recognition system is proposed and getting better results than other methods; (2) proposing three new features, that is, the ratio of peak values of WVD (), the number of extreme points () and the oscillation amplitude of the sidelobe (); (3) the number of features of this article is less than other methods; (4) and prior information is not needed in the system.
The framework of this article is shown below.
Section 2 mainly presents the structure of system. The classifier is explained in
Section 3. All the features and the principle of each feature are introduced in
Section 4.
Section 5 conveys the simulation results and the conclusions are drawn in
Section 6.
2. Recognition System Structure
Recognition system is employed to classify the intercepted waveforms and we can obtain the category of them. Recognition System can be divided into two parts, that is, features and classifier. First of all, the features of the intercepted radar waveforms are extracted, that is, time features and T-F features. Then, to select part of the data as the training set and get the model through training. Finally, to take the rest of data as the test set and put the test set and model into the classifier to get the classified results. For more details, see
Figure 1.
The intercepted signal in system can be given by
where
is the radar waveform.
is the noise and we assume it is additive white Gaussian noise (AWGN).
and
are the amplitude and phase sequence, respectively. The phase
of BPSK, Costas, LFM and polyphase codes is listed in
Table 1.
In
Table 1,
is the carrier frequency. For BPSK,
is the initial phase and its value is 0 or
. For Costas,
is the frequency sequence and it is given by
where
. For LFM,
is the slope of instantaneous frequency and it equals to the ratio of bandwidth
to pulse width
. For polyphase codes,
is the number of symbols,
,
and
. In addition,
must be the even for P2 codes.
The classifier in the system is composed of network1 and network2. It can classify eight waveforms. BPSK, Costas and LFM can be directly classified by network1 and network2 does not work at this time. When the signal is deemed to be polyphase codes (P1-P4 and Frank codes) by network1, then network2 is used to classify polyphase codes in detail. The purpose of adopting two classification networks is to reduce input features and improve the classification accuracy. For more details, see
Figure 2.
3. Classifier
The classifier of the system is ABC-SVM and it is applied in two networks. In SVM, parameter selection has a significant impact on the classification accuracy of model. Therefore, ABC algorithm is adopted to find the optimal parameters of SVM.
In SVM [
9], the hyperplane is used to separate different types of data because the symbols on both sides of the hyperplane are different. When the interval between hyplane and data is greater, the confidence of classification is greater. Therefore, the key question for SVM is to find the hyperplane that can separate the training data without mistakes and make the geometric interval (margin) is the largest, that is optimal separating hyperplane. The SVM about two classes and linear separable problems is shown in
Figure 3. We assume that the number of samples is
, the training vectors
,
, an indicator vector
and
. The hyperplane is
. Therefore, the problem of solving the optimal hyperplane is turned into an optimization problem [
10]:
where
is the normal vector of hyperplane,
and
mean the slack variable and threshold, respectively.
is the error penalty factor and it need to be designed.
is the result of non-linear transformation of
in the new space. Then the optimization problem is converted to its dual problem by the method of Lagrange [
10]:
where
is the Lagrange multiplier,
is a vector of all ones and
is an positive semidefinite matrix, that is,
.
is the kernel function and it is influenced by the kernel function parameter
. It can be given by
When the Formula (3) is calculated, the solution
can be obtained and the vector
is also be confirmed, that is,
is estimated by
and the classified decision function is [
10]
Thus, the choice of
and
has an important impact on the classification results of SVM [
11,
12].
ABC algorithm proposed by Karaboga [
13] is utilized to evaluate the parameters of SVM in this paper. ABC is a global optimization algorithm and its purpose is to search the optimum solution of problems by imitating the behavior of honey bee swarm in nature. ABC algorithm is composed of scouts, onlookers and employed bees. The quantity of employed bees is one half of the populations and the amount of food sources (solutions) is equal to the employed bees. The specific process is described as below [
14]: the first step is to initialize the food sources. Then, employed bees search around the food sources in some way to find new sources and choose the better ones according to the nectar amount (fitness). Next, onlookers pick good food sources further on the basis of the message of employed bees and confirm the quantity. If nectar amount of that food source is not improved within given steps, the employed bee will turn into the scouts. The task of scouts is to find new food sources. When the cycle reaches the terminating condition, the optimal food source will be received. For more details, see
Table 2.
In initialize stage, we assume the number of solutions is
and the solutions are randomly generated. The quantity of employed bees is
, as well. Initial solutions are given by
where
is a D-dimensional vector,
represents the amount of optimized parameters and
.
is the
th parameter of
.
In employed bees stage, employed bees calculate the fitness and search around the initial values to find new solutions. If new fitness is more than the original, employed bees will remember the new solutions and forget the original ones. When employed bees finish seeking and return to the beehives, they share information with onlookers. The formula of searching new solutions is given by
where
,
and
.
is a random number of
.
In the onlooker bees stage, onlookers select solutions according to the received message with a certain probability. Then, onlookers search the solutions in the same way of employed bees to produce new solutions. If new fitness is better, we will replace the previous. The probability of onlookers to choose the solutions is given by
where
is the fitness of the
th solution.
In the scout bees stage, if the solution is not improved within , it will be abandoned. The employed bees of that position will turn into the scouts and a new solution is produced by Formula (8). When the number of cycles reaches the maximum cycle number (MCN), the best solution will be obtained.
6. Conclusions
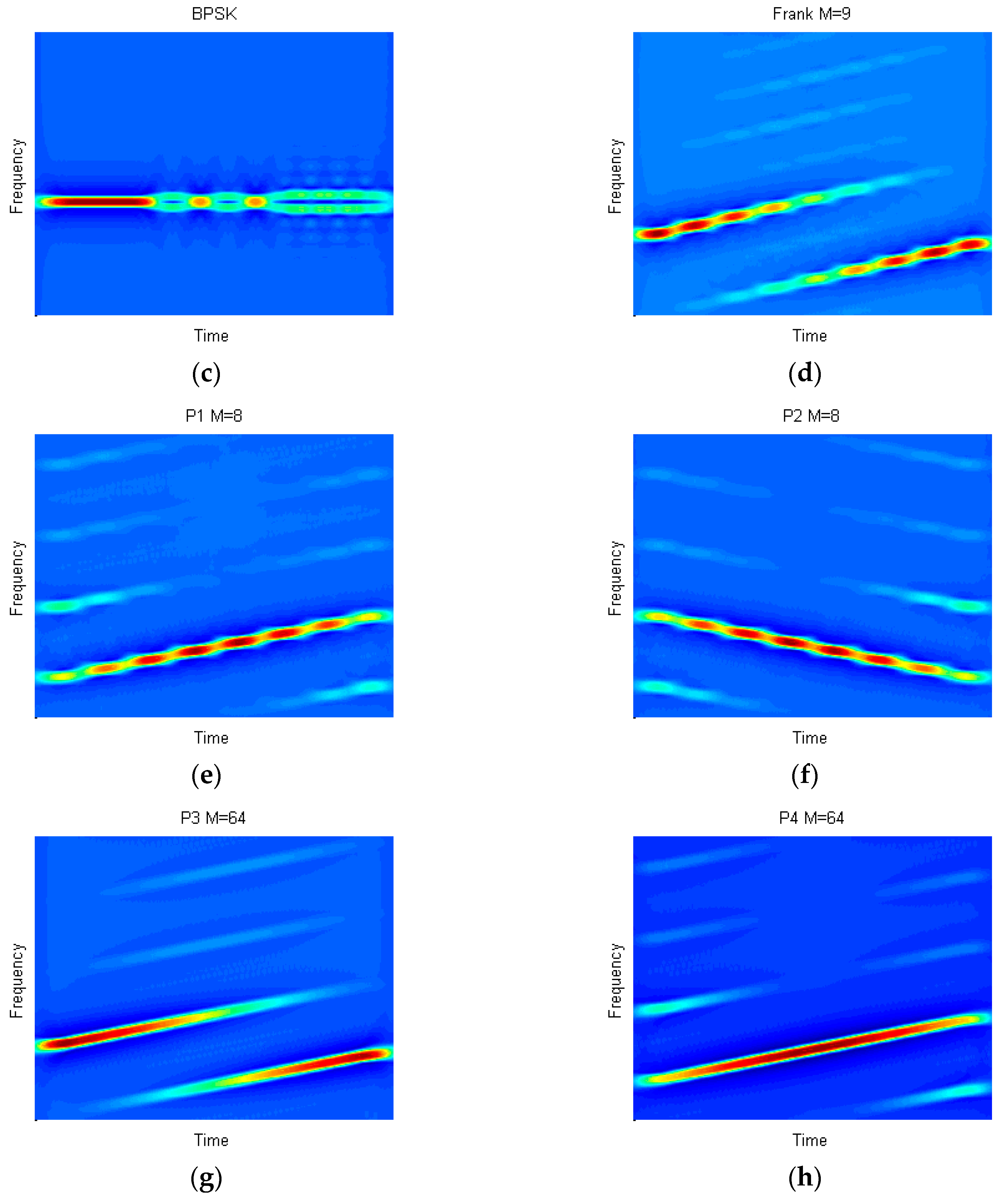
In this paper, the system for recognizing 8 LPI radar waveforms is explored. The identifiable waveforms are BPSK, Costas codes, LFM, P1–P4 and Frank codes. There are only 14 features in the system and they are divided into time features and T-F features. Time features are obtained from the time domain signals. T-F features are related to the WVD and CWD and 3 new T-F features are proposed. The classifier of the system is SVM based on ABC algorithm. ABC is adopted to optimize the parameters of SVM and it can avoid the problem of local optimal solution to some extent.
The system has good performance and the details are as follows: Firstly, it has high recognition rate. When SNR at −4 dB, the overall RSR is 92% and the RSR of each waveform is all over 84%. Especially for LFM and P2 code, the RSR is about 97% which is far better than other systems. Secondly, it shows well robustness. When the training data is reduced to 100, the recognition rate is only dropped by 0.7% at SNR of −2 dB. Lastly, it possesses excellent computational complexity. The runtime of this paper is far less than other methods.