A Variation-Aware Design Methodology for Distributed Arithmetic
Abstract
:1. Introduction
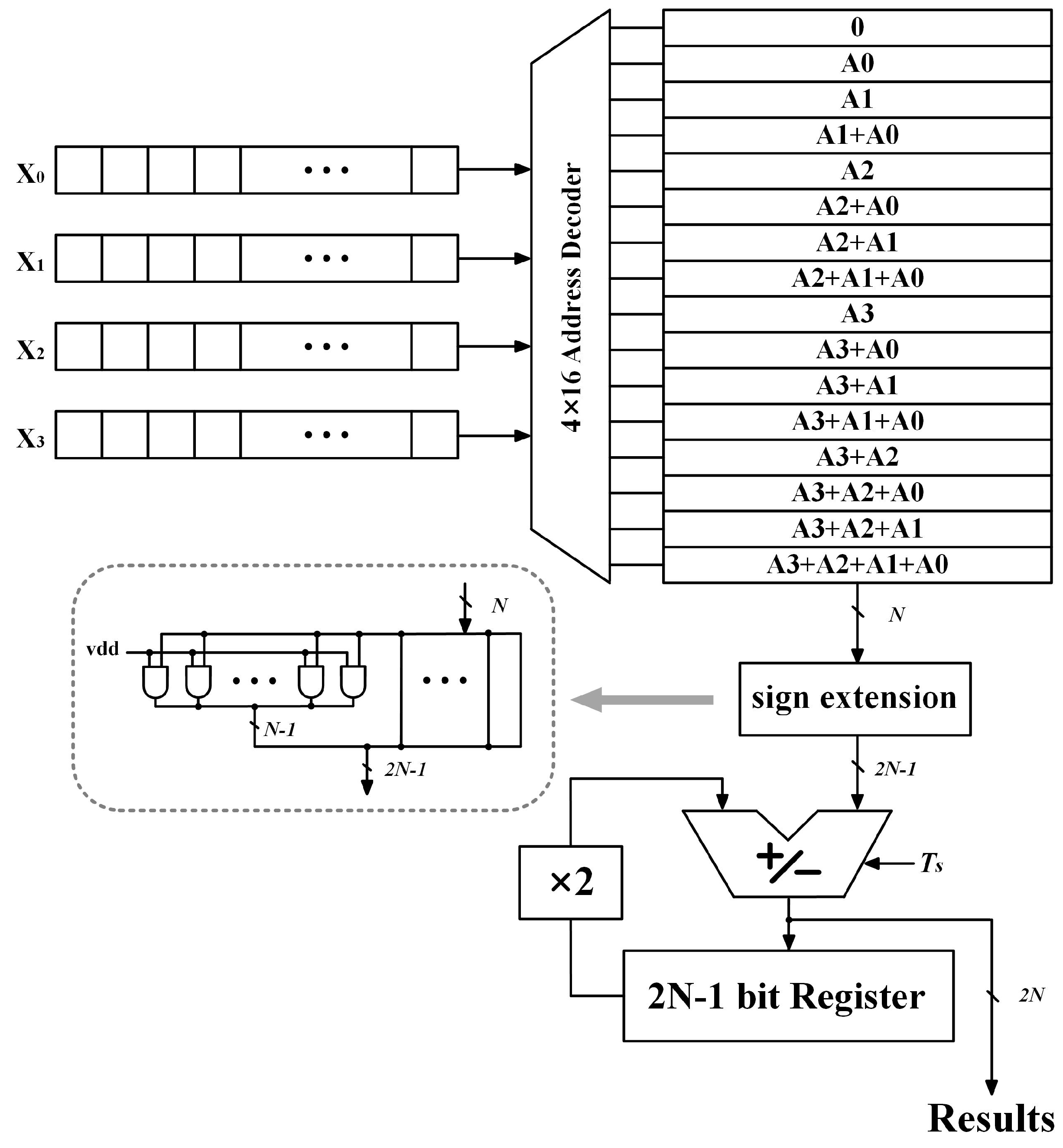
2. MSB-First Distributed Arithmetic (DA) Computation
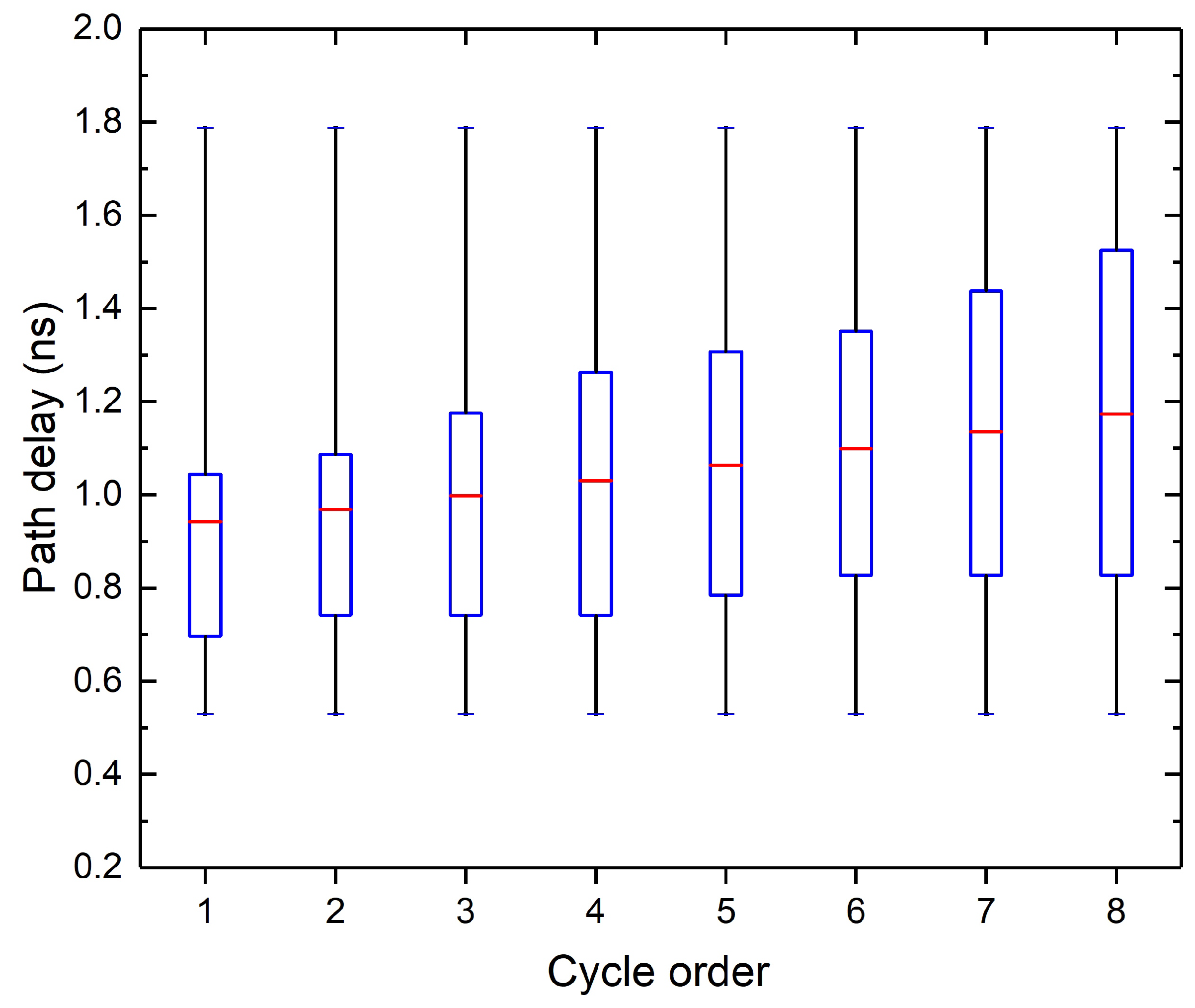
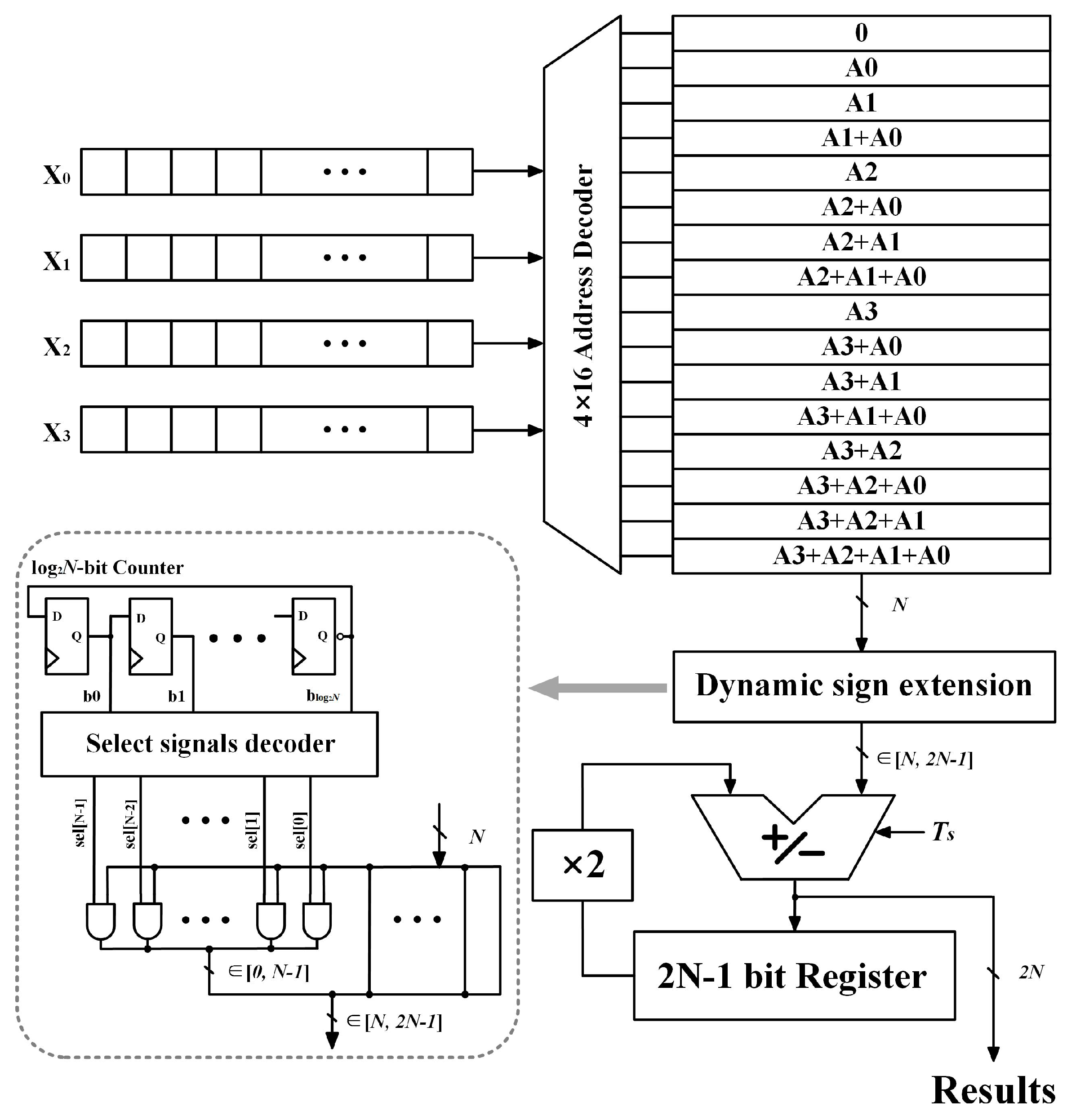
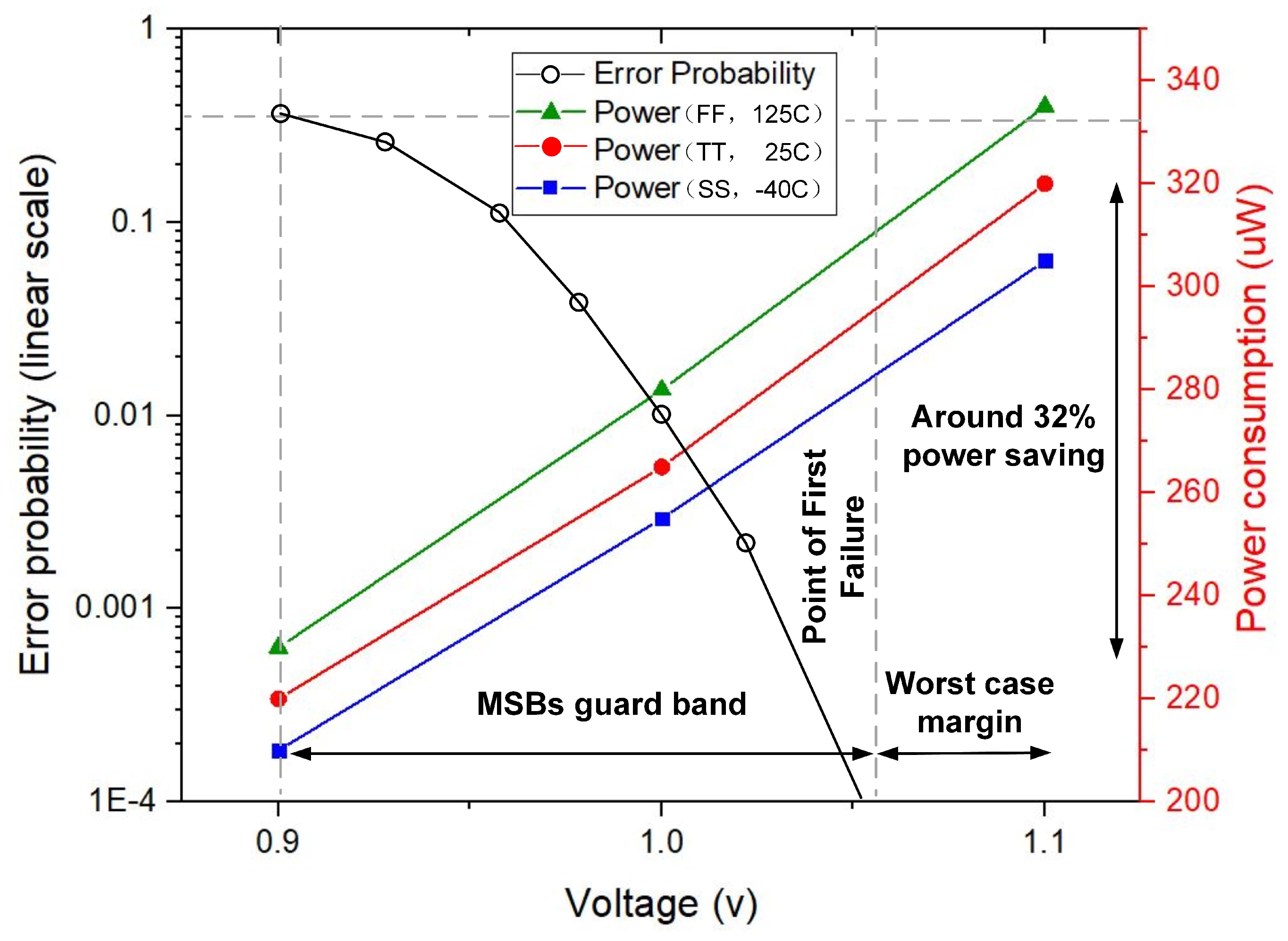
3. Proposed Variation-Aware DA Computation
3.1. Dynamic Sign Extension
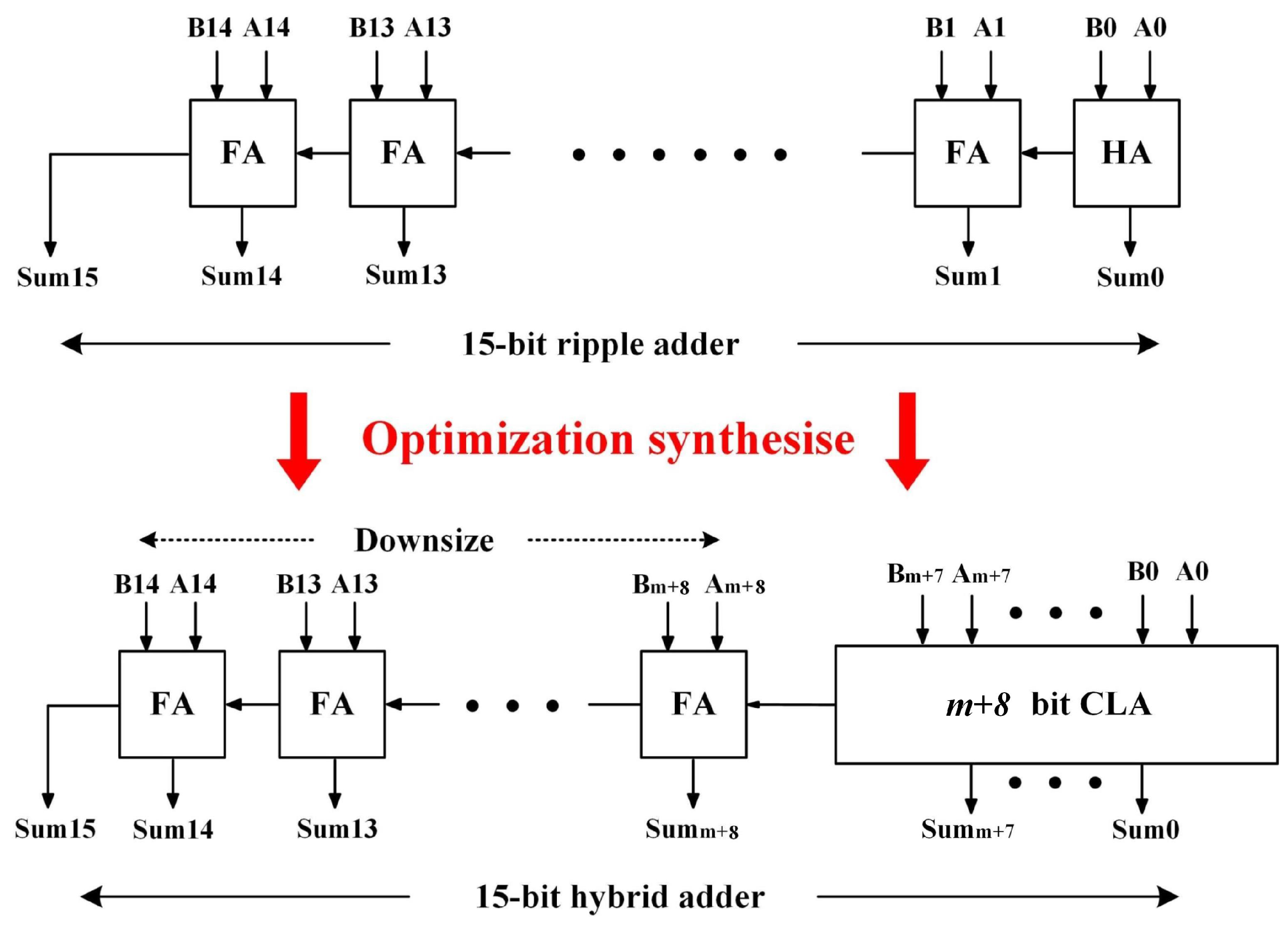
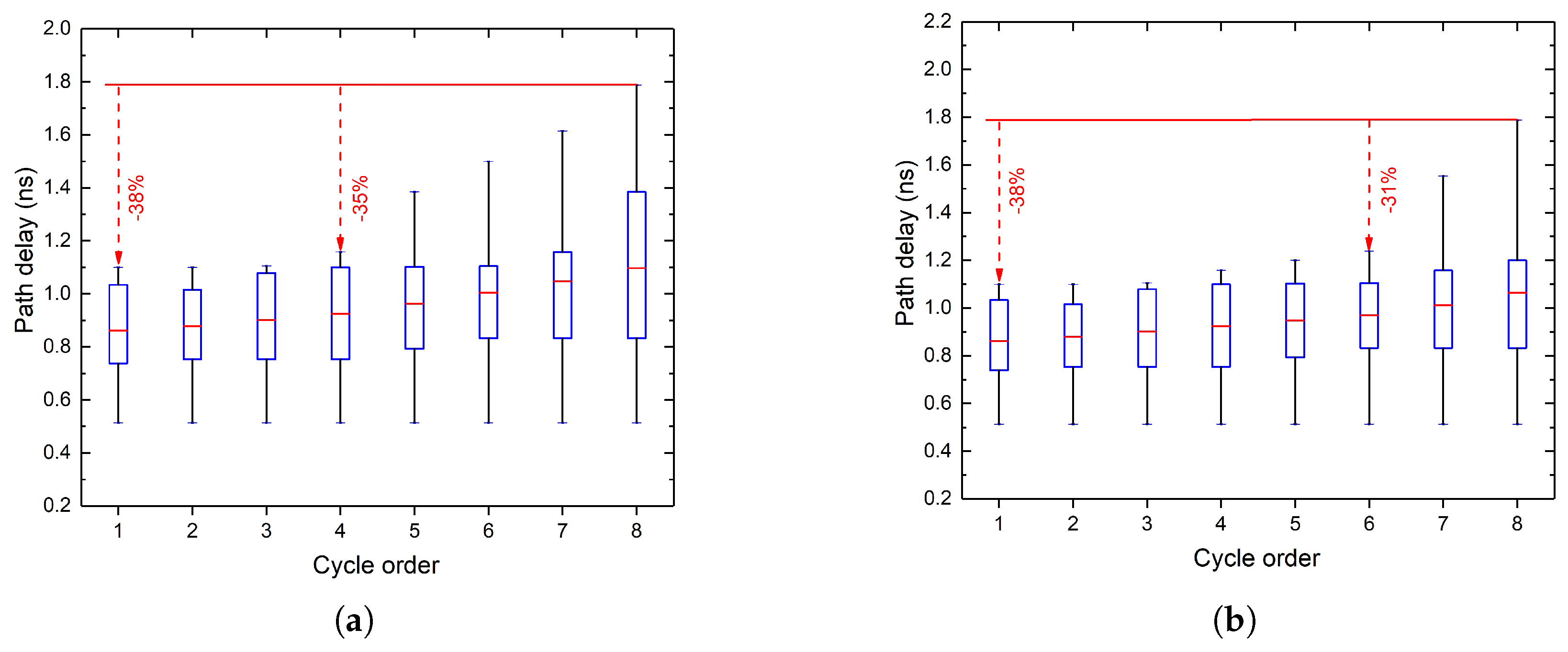
3.2. Synthesis for Further Altering Path Delay Distribution
| Algorithm 1 Synthesis for accuracy specification |
| Require: the arrival times of MSB have more than n% timing margin; procedure syn() max delay/(1+n%); signal arrival time of MSB; // Adder replacement if then all ripple adders on the critical path ending at MSB; 2; ▹ the number of 1-bit adders that can be replaced by a CLA repeat Replace i 1-bit adders of by a CLA i increases; until ; // Gate downsizing all gates that are irrelevant to MSB; Downsize . |
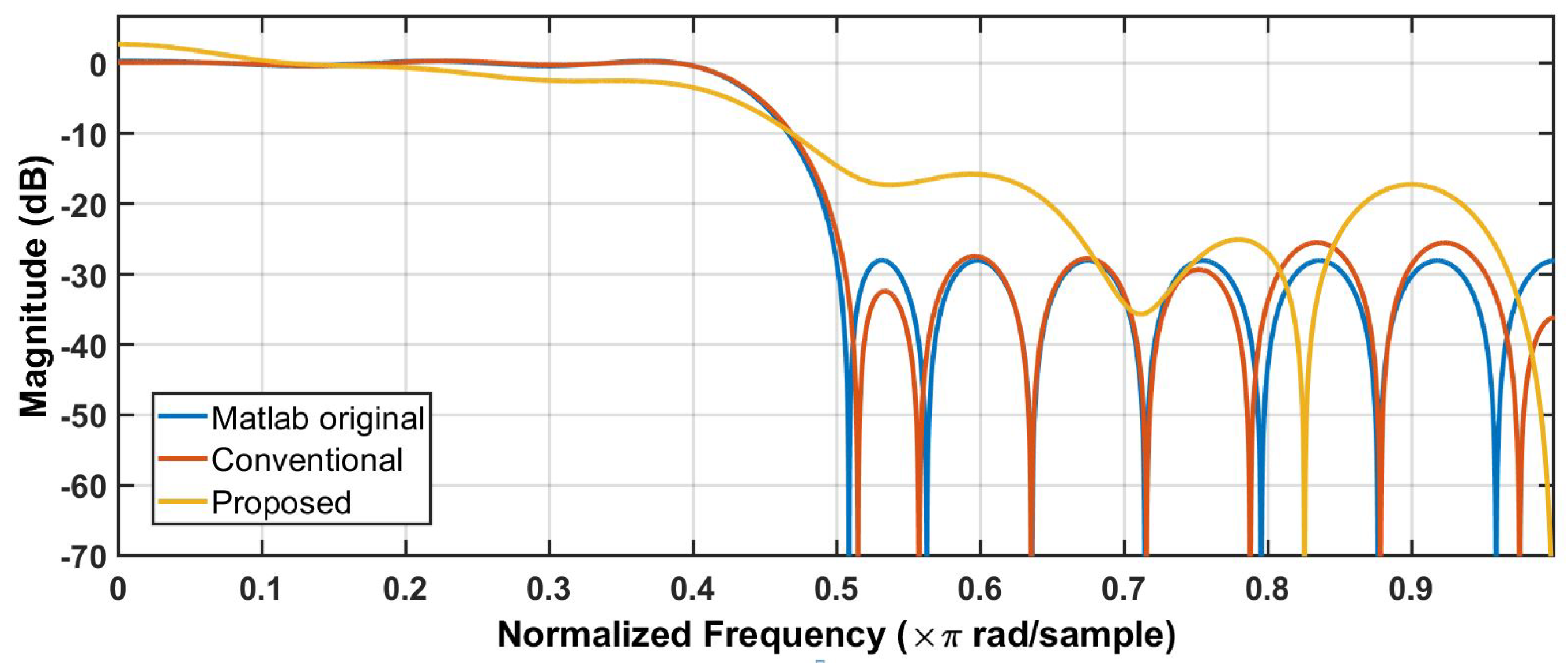
4. Case Study: FIR Filter VLSI Implementation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Muhic, I.; Hodzic, M. Internet of Things: Current Technological Review and New Low Power Wireless Sensor Network Protocol Proposal. Southeast Eur. J. Soft Comput. 2014, 3. [Google Scholar] [CrossRef] [Green Version]
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. Internet of Things (IoT): A vision, architectural elements, and future directions. Future Gener. Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef] [Green Version]
- Golanbari, M.S.; Tahoori, M.B. Runtime adjustment of IoT system-on-chips for minimum energy operation. In Proceedings of the 55th Annual Design Automation Conference, San Francisco, CA, USA, 24–28 June 2018; p. 145. [Google Scholar]
- Kiamehr, S.; Ebrahimi, M.; Golanbari, M.S.; Tahoori, M.B. Temperature-aware dynamic voltage scaling to improve energy efficiency of near-threshold computing. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 2017–2026. [Google Scholar] [CrossRef]
- Licciardo, G.D.; Cappetta, C.; Di Benedetto, L.; Vigliar, M. Weighted Partitioning for Fast Multiplierless Multiple-Constant Convolution Circuit. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 66–70. [Google Scholar] [CrossRef]
- Panwar, M.; Padmini, J.; Acharyya, A.; Biswas, D. Modified distributed arithmetic based low complexity CNN architecture design methodology. In Proceedings of the 2017 European Conference on Circuit Theory and Design (ECCTD), Catania, Italy, 4–6 September 2017; pp. 1–4. [Google Scholar]
- Xie, J.; Meher, P.K.; He, J. Hardware-efficient realization of prime-length DCT based on distributed arithmetic. IEEE Trans. Comput. 2013, 62, 1170–1178. [Google Scholar] [CrossRef]
- Martina, M.; Masera, G.; Roch, M.R.; Piccinini, G. Result-biased Distributed-Arithmetic-based filter architectures for approximately computing the DWT. IEEE Trans. Circuits Syst. I Reg. Pap. 2015, 62, 2103–2113. [Google Scholar] [CrossRef]
- Singhal, S.K.; Mohanty, B.K. Efficient Parallel Architecture for Fixed-Coefficient and Variable-Coefficient FIR Filters Using Distributed Arithmetic. J. Circuits Syst. Comput. 2016, 25, 1650073. [Google Scholar] [CrossRef]
- Park, S.Y.; Meher, P.K. Low-power, high-throughput, and low-area adaptive FIR filter based on distributed arithmetic. IEEE Trans. Circuits Syst. II Express Briefs 2013, 60, 346–350. [Google Scholar] [CrossRef]
- Venkatachalam, S.; Ko, S.B. Approximate Sum-of-Products Designs Based on Distributed Arithmetic. IEEE Trans. Very Large Scale Integr. Syst. 2018, 26, 1604–1608. [Google Scholar] [CrossRef]
- Mittal, S. A survey of techniques for approximate computing. ACM Comput. Surv. 2016, 48, 62. [Google Scholar] [CrossRef]
- Radfar, M.; Singh, J. A yield improvement technique in severe process, voltage, and temperature variations and extreme voltage scaling. Microelectron. Reliab. 2014, 54, 2813–2823. [Google Scholar] [CrossRef]
- Islam, A.; Hasan, M. A technique to mitigate impact of process, voltage and temperature variations on design metrics of SRAM Cell. Microelectron. Reliab. 2012, 52, 405–411. [Google Scholar] [CrossRef]
- Golanbari, M.S.; Gebregiorgis, A.; Moradi, E.; Kiamehr, S.; Tahoori, M.B. Balancing resiliency and energy efficiency of functional units in ultra-low power systems. In Proceedings of the 23rd Asia and South Pacific Design Automation Conference, Jeju, Korea, 22–25 January 2018; pp. 637–644. [Google Scholar]
- Khairy, M.S.; Gholamipour, A.; Kurdahi, F.J.; Eltawil, A.M. Reliable low power Distributed Arithmetic filters via N-Modular Redundancy. In Proceedings of the 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 4–7 November 2012; pp. 621–625. [Google Scholar]
- Ting, Y.H.; Lin, T.J.; Chang, C.C.; Hu, C.C.; Yeh, C.; Wang, J.S. Approximate Distributed Arithmetic for Variable-Latency Table Lookup. In Proceedings of the 2017 New Generation of CAS (NGCAS), Genova, Genoa, 6–9 September 2017; pp. 137–140. [Google Scholar] [CrossRef]
- Alam, M. Reliability-and process-variation aware design of integrated circuits. Microelectron. Reliab. 2008, 48, 1114–1122. [Google Scholar] [CrossRef]
- Zhang, S.; Shanbhag, N.R. Embedded algorithmic noise-tolerance for signal processing and machine learning systems via Data Path Decomposition. IEEE Trans. Signal Process. 2016, 64, 3338–3350. [Google Scholar] [CrossRef]
- Vaseghi, S.V. Advanced Digital Signal Processing and Noise Reduction; John Wiley & Sons: Chichester, West Sussex, UK; 2008; ISBN 978-0-470-75406-1. [Google Scholar]
- Ernst, D.; Kim, N.S.; Das, S.; Pant, S.; Rao, R.; Pham, T.; Ziesler, C.; Blaauw, D.; Austin, T.; Flautner, K.; et al. Razor: A low-power pipeline based on circuit-level timing speculation. In Proceedings of the 36th Annual IEEE/ACM International Symposium on Microarchitecture, Washington, DC, USA, 3–5 December 2003; p. 7. [Google Scholar]
- Choi, J.H.; Banerjee, N.; Roy, K. Variation-aware low-power synthesis methodology for fixed-point FIR filters. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2009, 28, 87–97. [Google Scholar] [CrossRef]
- Whatmough, P.N.; Das, S.; Bull, D.M.; Darwazeh, I. Circuit-level timing error tolerance for low-power DSP filters and transforms. IEEE Trans. Very Large Scale Integr. Syst. 2013, 21, 989–999. [Google Scholar] [CrossRef]
- Tiwari, A.; Sarangi, S.R.; Torrellas, J. ReCycle: Pipeline Adaptation to Tolerate Process Variation; ACM SIGARCH Computer Architecture News; ACM: New York, NY, USA, 2007; Volume 35, pp. 323–334. [Google Scholar]
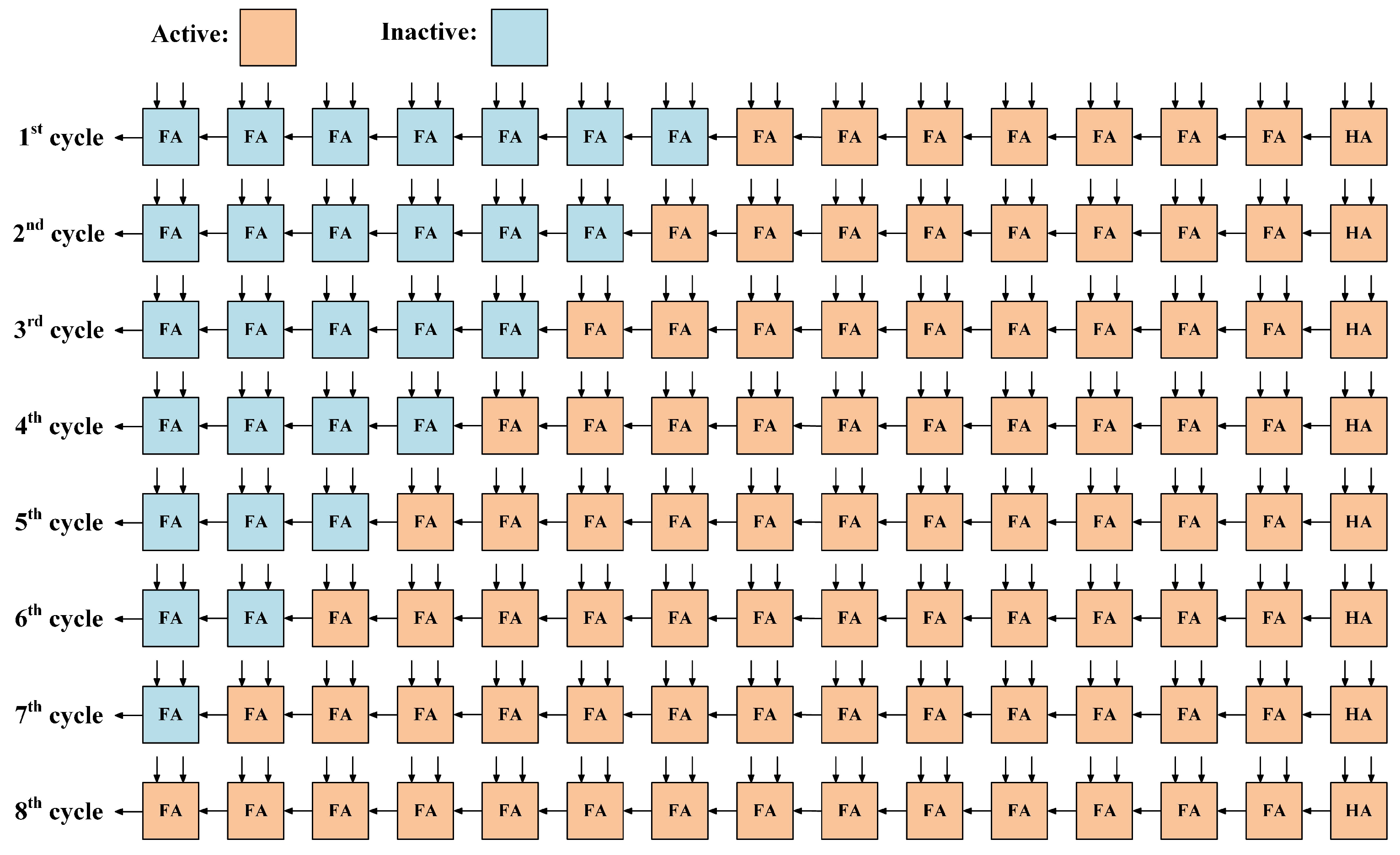


| Cycle Order | Counter () | Signal Select [6:0] | Select [Cycle Order − 1] |
|---|---|---|---|
| 1 | 000 | 0000000 | |
| 2 | 001 | 0000001 | |
| 3 | 010 | 0000011 | |
| 4 | 011 | 0000111 | |
| 5 | 100 | 0001111 | |
| 6 | 101 | 0011111 | |
| 7 | 110 | 0111111 | |
| 8 | 111 | 1111111 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Duan, S.; Halak, B.; Kazmierski, T. A Variation-Aware Design Methodology for Distributed Arithmetic. Electronics 2019, 8, 108. https://doi.org/10.3390/electronics8010108
Lu Y, Duan S, Halak B, Kazmierski T. A Variation-Aware Design Methodology for Distributed Arithmetic. Electronics. 2019; 8(1):108. https://doi.org/10.3390/electronics8010108
Chicago/Turabian StyleLu, Yue, Shengyu Duan, Basel Halak, and Tom Kazmierski. 2019. "A Variation-Aware Design Methodology for Distributed Arithmetic" Electronics 8, no. 1: 108. https://doi.org/10.3390/electronics8010108
APA StyleLu, Y., Duan, S., Halak, B., & Kazmierski, T. (2019). A Variation-Aware Design Methodology for Distributed Arithmetic. Electronics, 8(1), 108. https://doi.org/10.3390/electronics8010108






