Lyapunov Based Reference Model of Tension Control in a Continuous Strip Processing Line with Multi-Motor Drive
Abstract
:1. Introduction
- Autonomous (decoupled) control of controlled variables of CL (tension and speed values).
- Invariance against additive disturbances.
- Robustness against changes of important line parameters (change of the processed material and its dimensions which cause change of damping constant and constant of elasticity and change of the moment of inertia of the drive).
- Required dynamics of the controlled variable (time courses of tensions in line sections without any overshoots).
- Stability of the controlled system.
2. Continuous Line Model
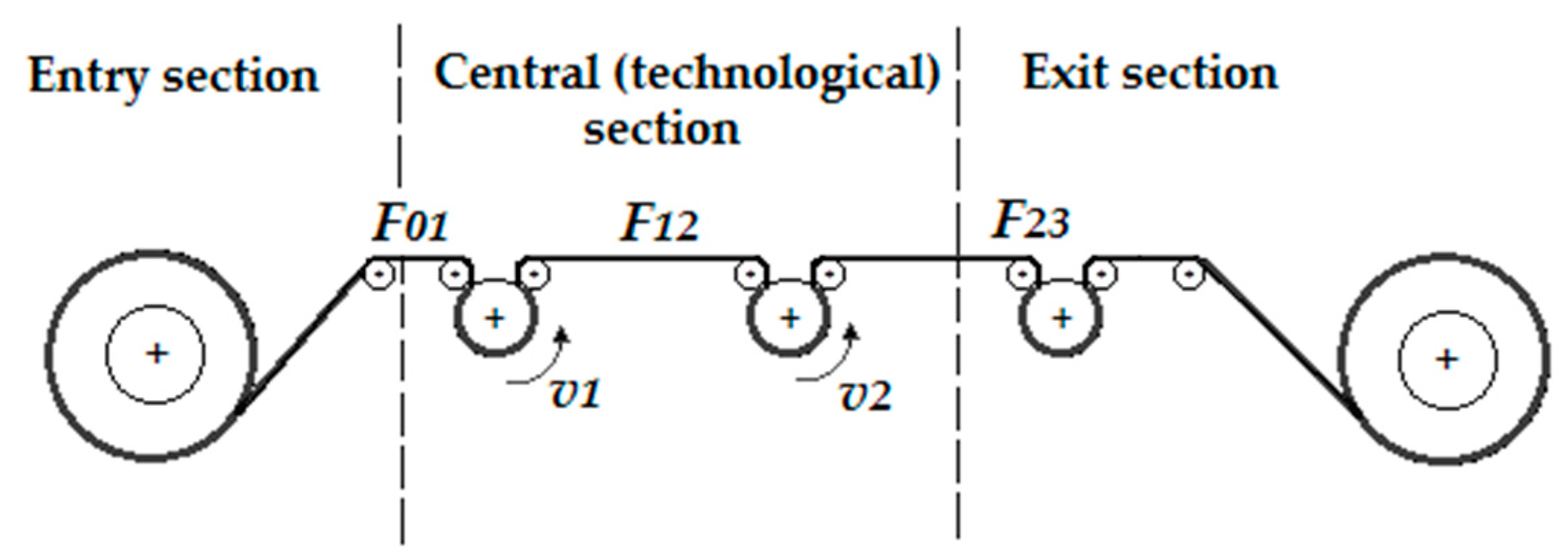
2.1. Continuous Line Description
- The entry section consisting of un-coiler, strip linking machine and entry accumulator serving for accumulation of a stock of material for the technological section and sometimes also for reduction of tension in the strip (between the uncoiler and the following part of the line).
- The central (technological section), where technological operations are carried out according to the technological prescription for the particular material.
- The exit section consisting of coiler for coiling of the strip materials (including also exit accumulator and strip divider).
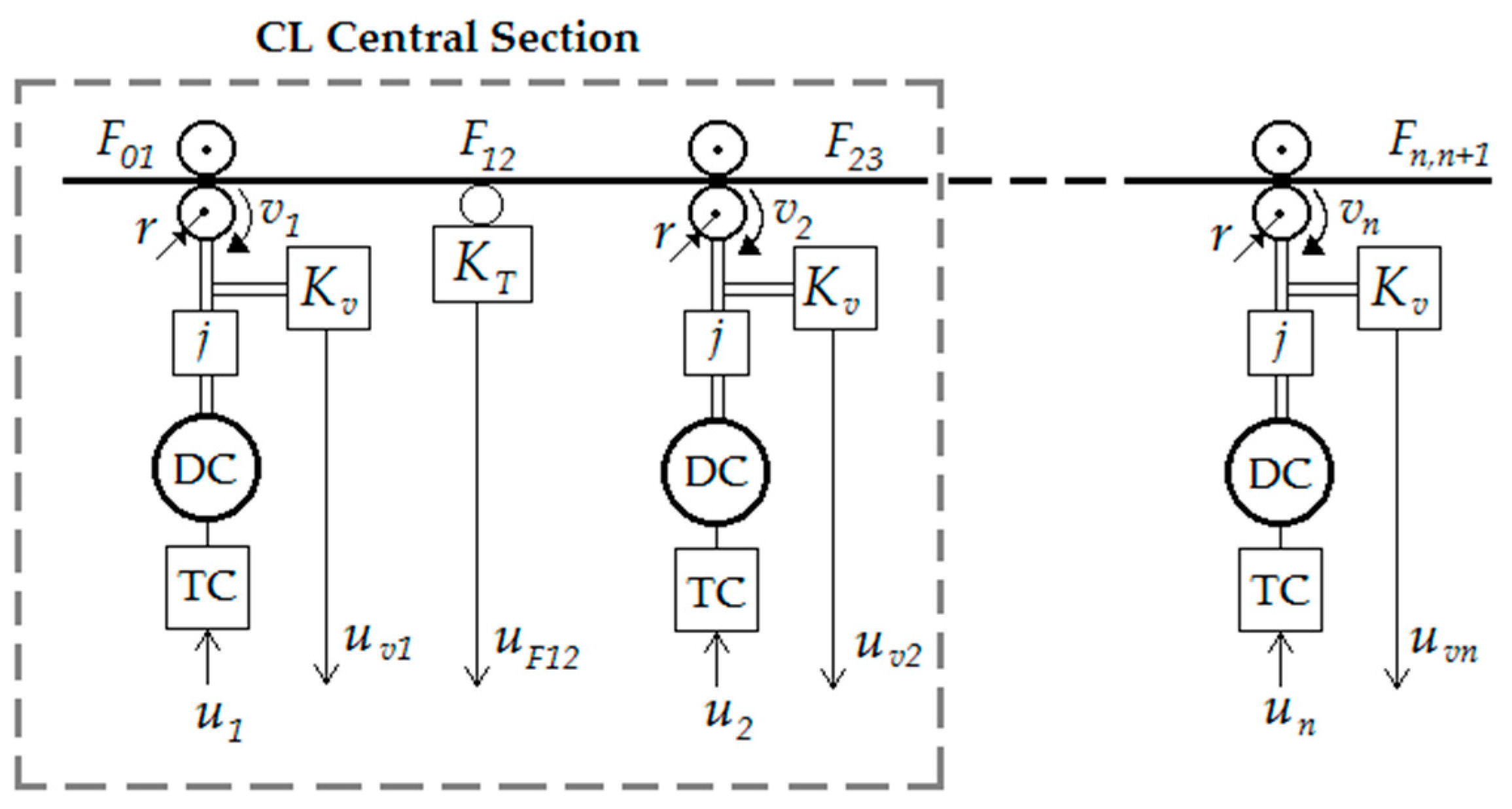
2.2. Mathematical Model of a Part of a Continuous Line with Two Machines
2.3. Analysis of Properties of the Central Section of the Continuous Line
3. Design of a Control Structure with Reference Model for the Central Section of a Continuous Line
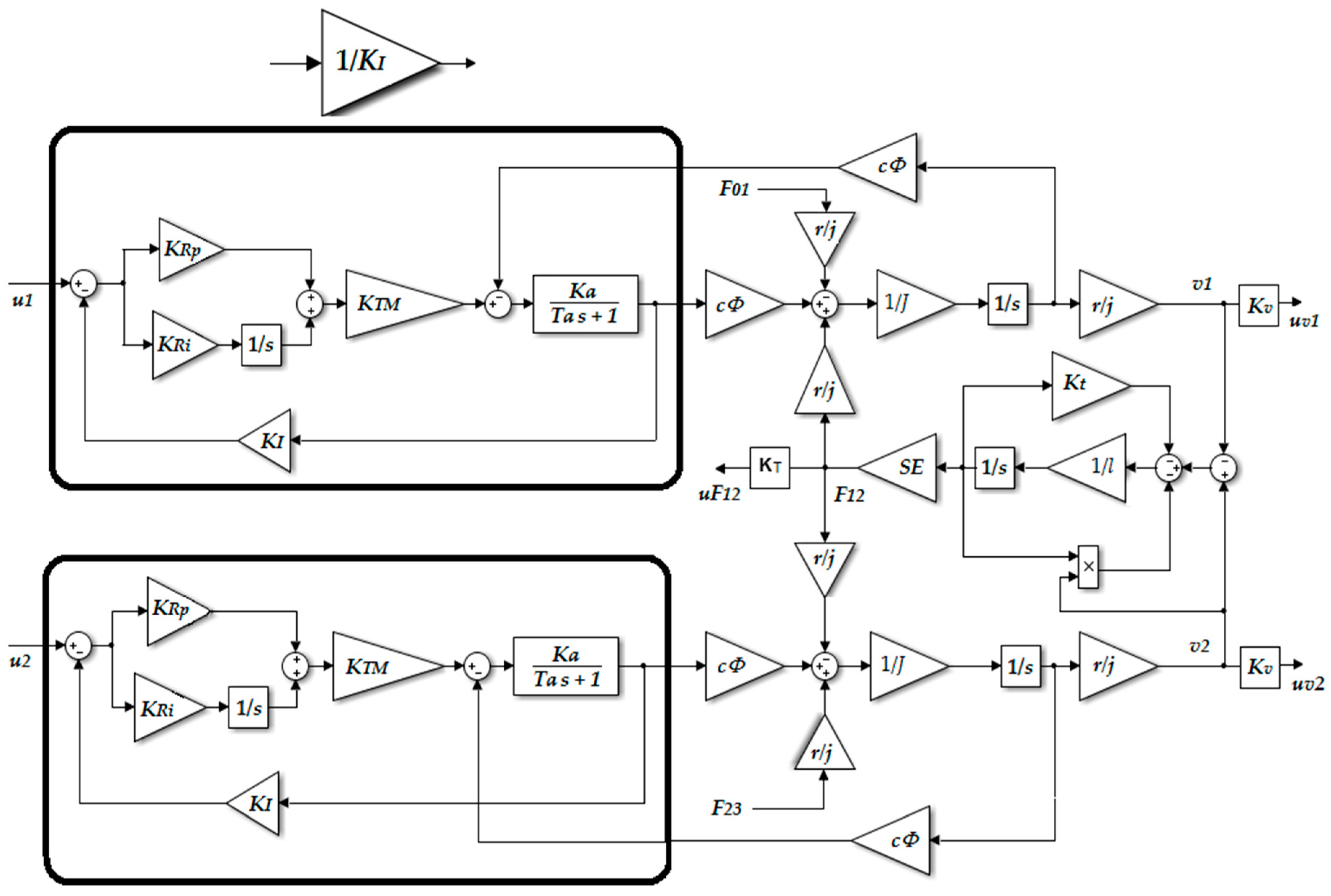
3.1. Mathematical Model of the Tension Subsystem
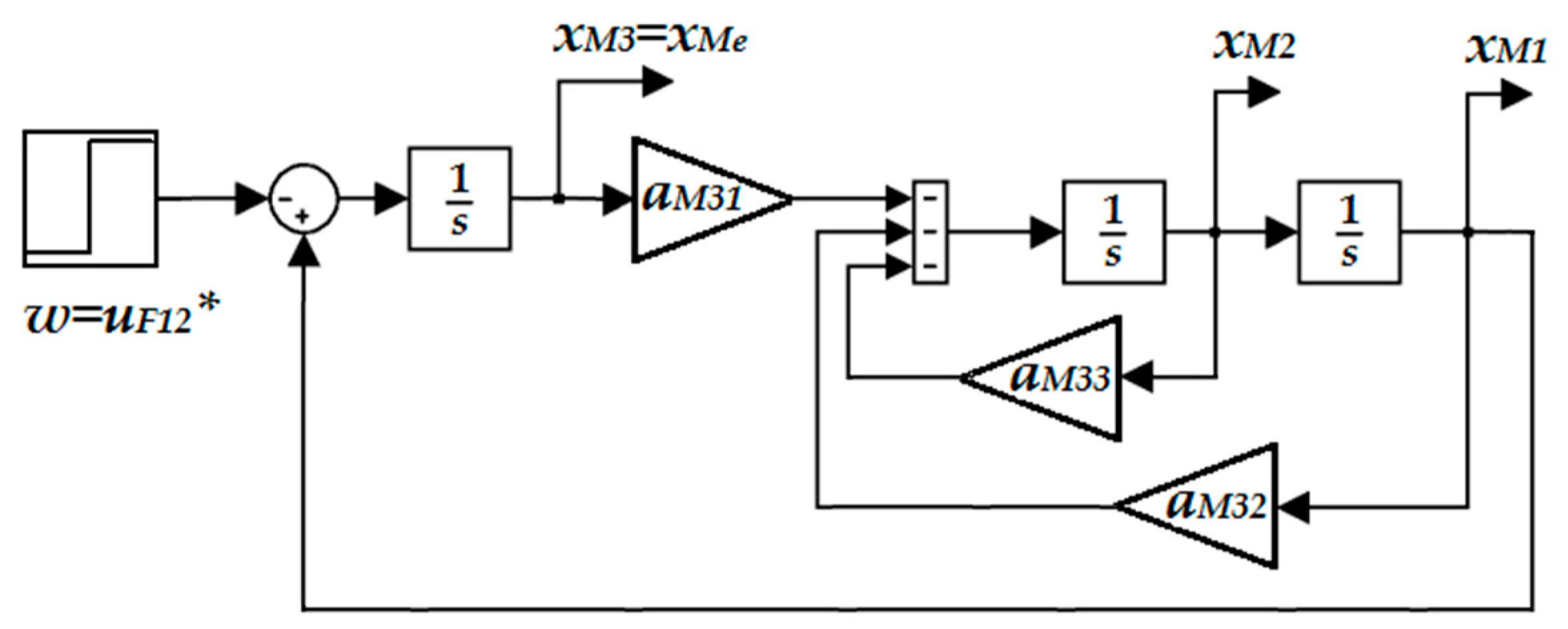
3.2. Reference Model Design
3.3. Extended Tension Subsystem
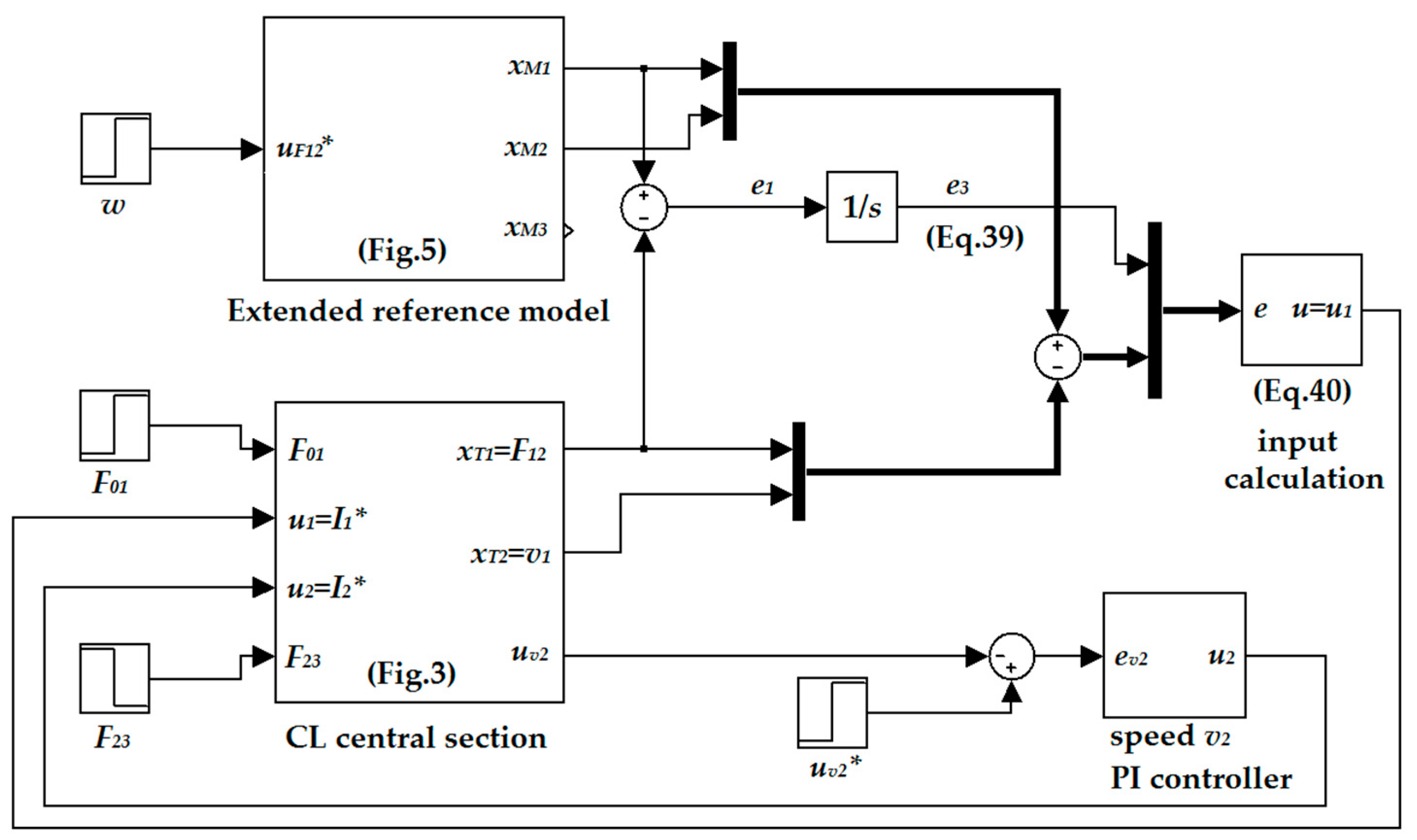
3.4. Principle of the Tension Controller Design by the Second Lyapunov Method
4. Verification of the Designed Control Structure
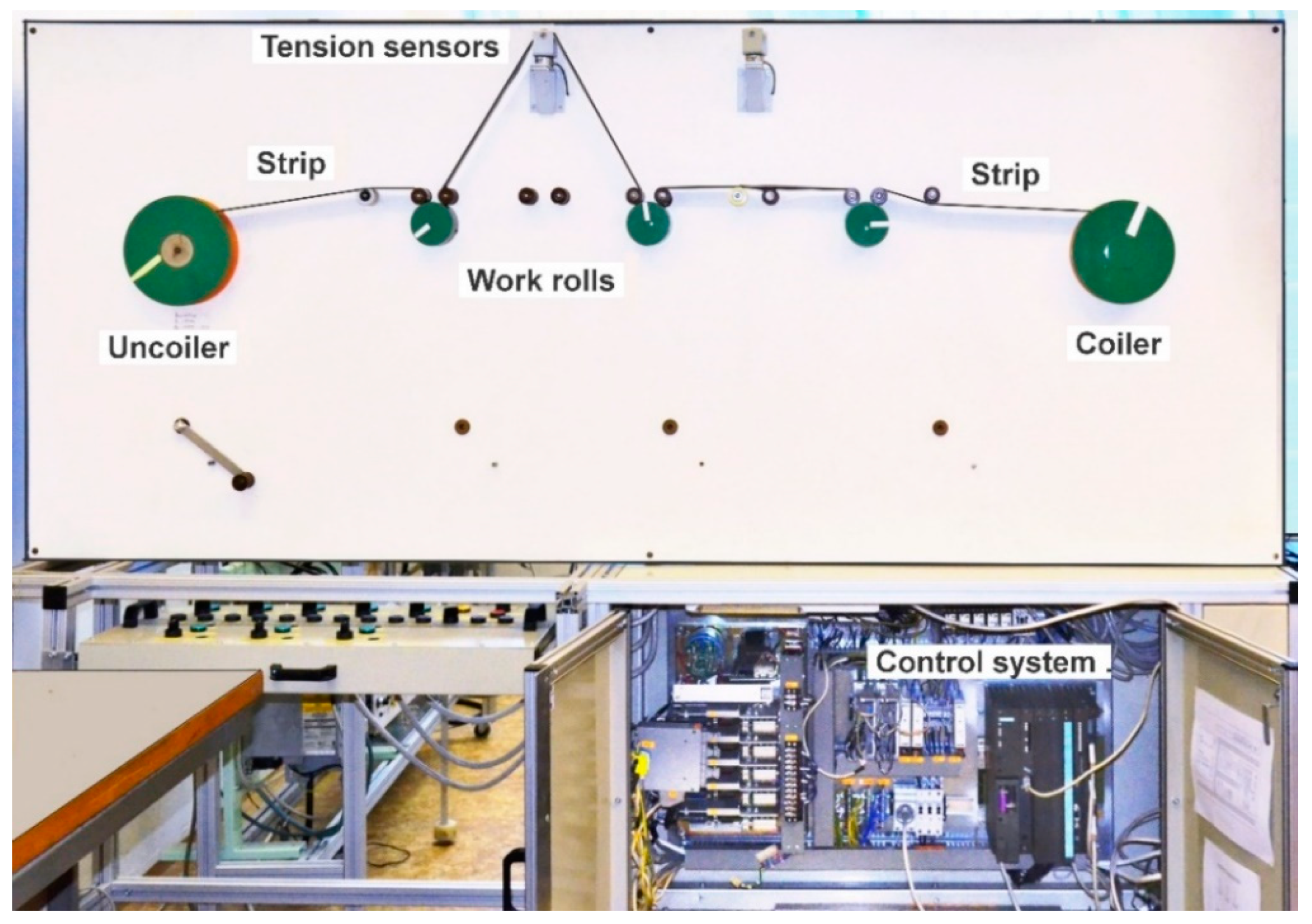
4.1. Experimental Setup
4.2. Experimental Results
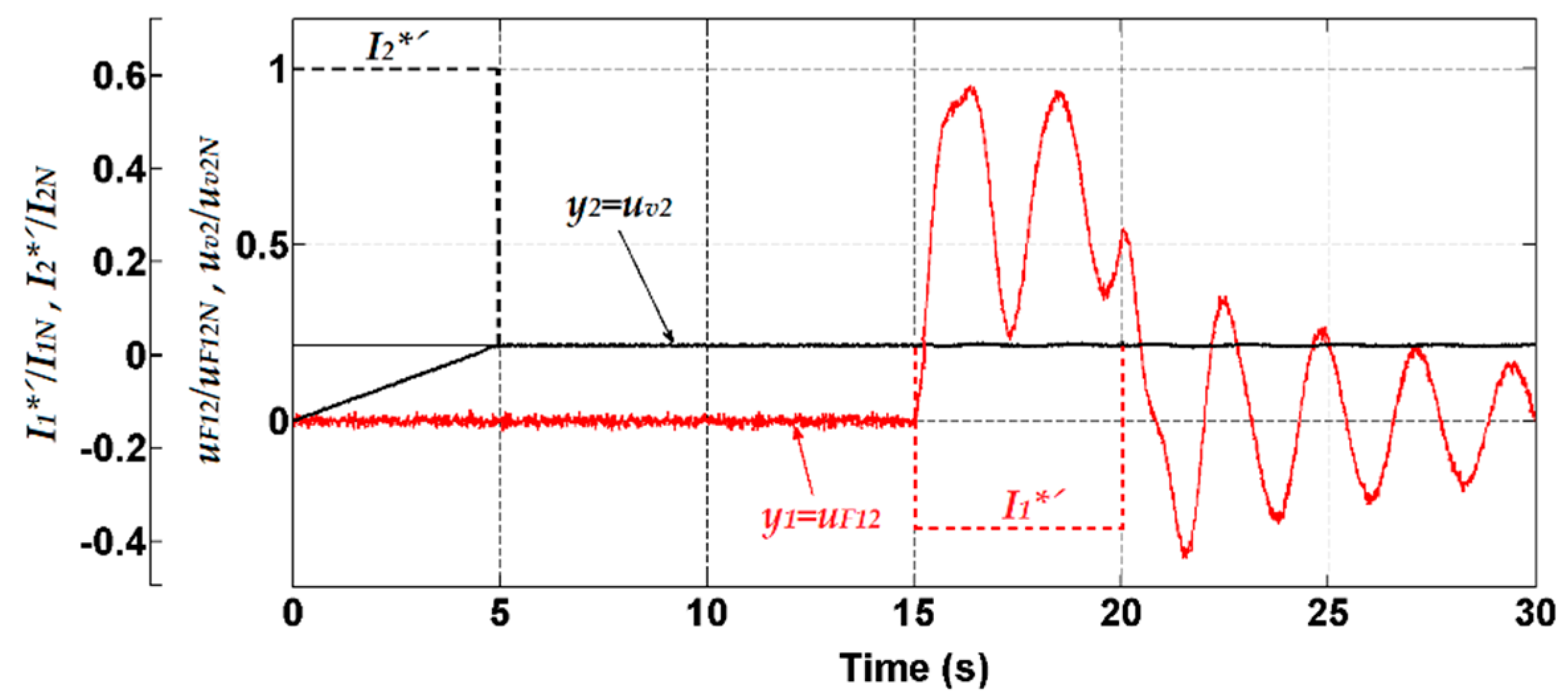
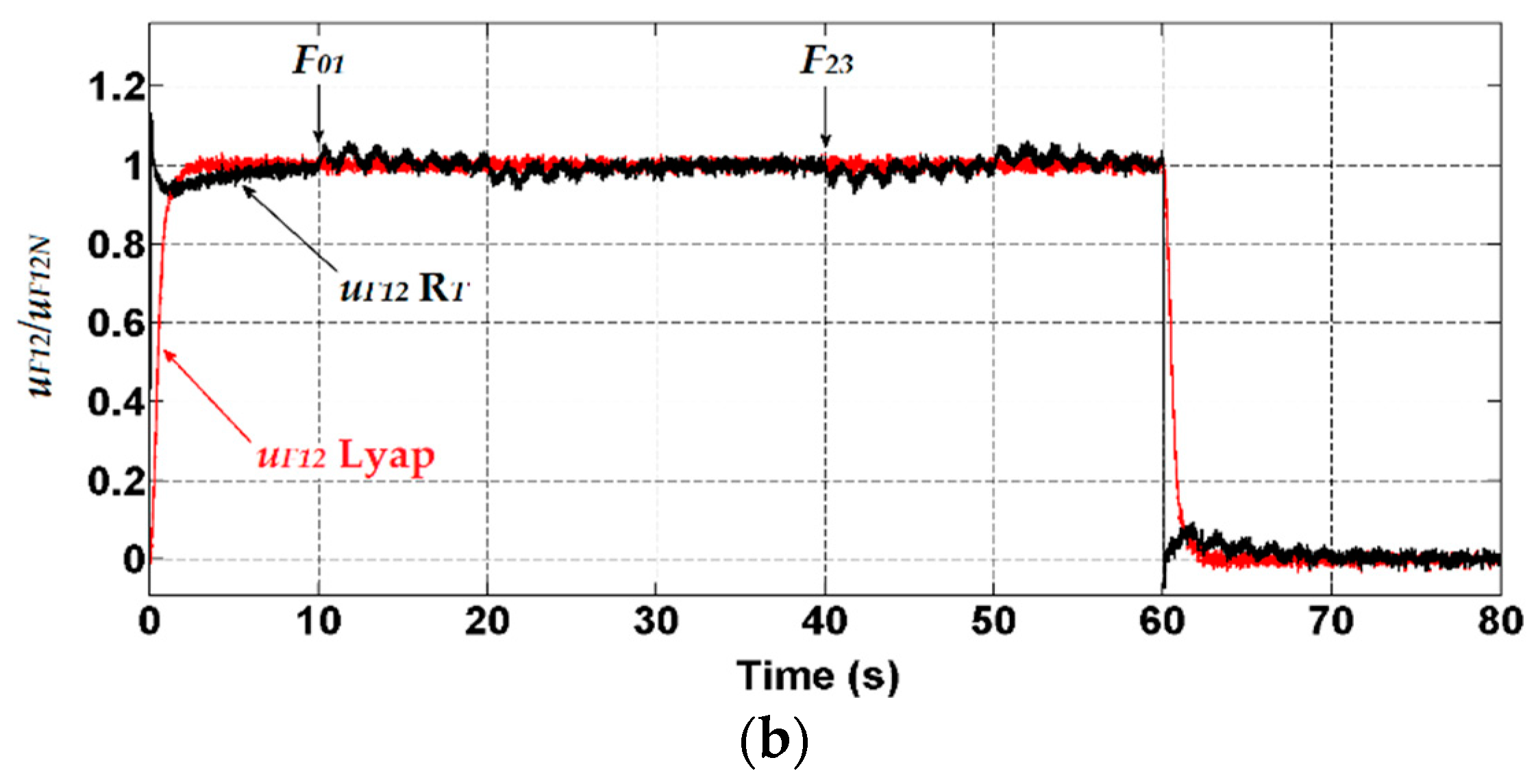
- Step changes of the tension before (F01) and after (F23) the considered line section with the amplitude of nominal tension at time t = 10 s and t = 40 s (Figure 9). In real line these disturbances are caused by sudden short changing the thickness in the material strip—when end of one strip is joined by welding to begin of other one.
- Slowly changing line speed v2, which is controlled by a standard PI controller. The time course of the strip speed v2 for the desired value equal to the nominal speed, i.e., for v2 = 0.6 ms−1, is shown in Figure 9 at simultaneous occurrence of the disturbances F01 and F23.
4.2.1. Experimental Results for the Designed Controller based on the Second Lyapunov Method
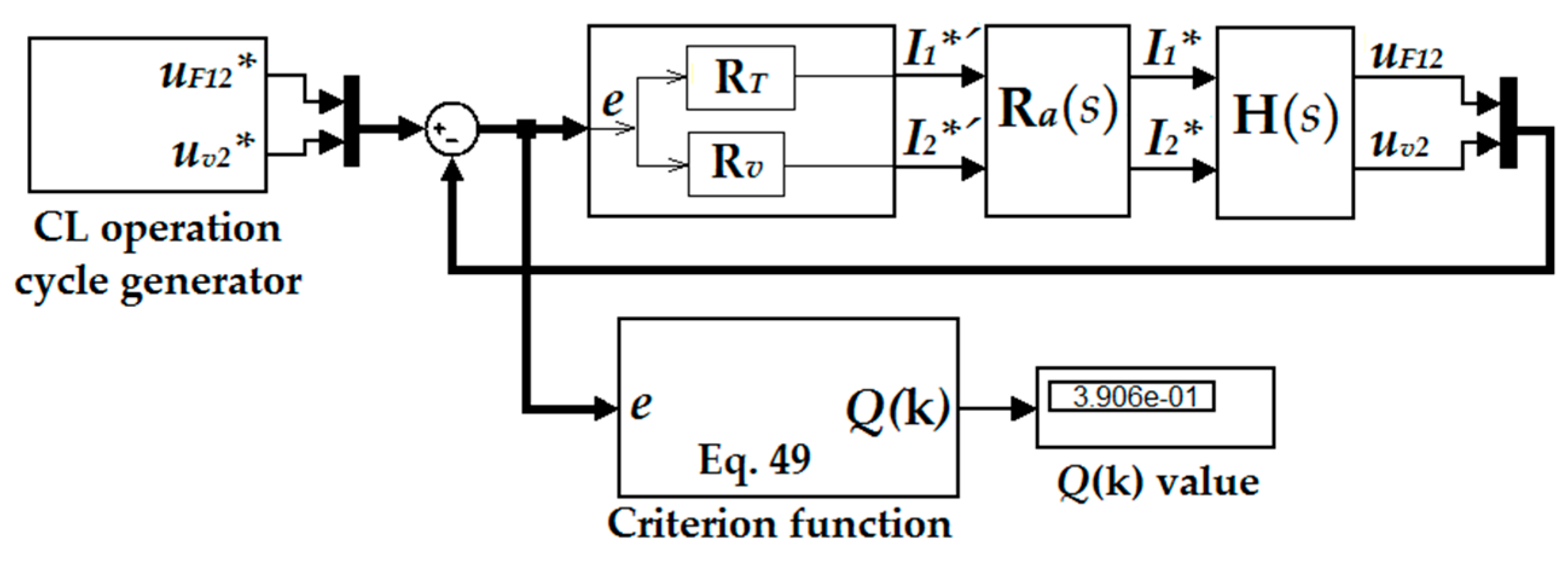
4.2.2. Design of a CSCL Controller by MIMO System Design Method in Frequency Domain
4.2.3. Comparison of Results Obtained by Both Types of Controllers
- The structure with the reference model structure and tension controller designed by the second Lyapunov method (having notation “Lyap” in time responses below).
- The structure with the speed and tension controllers designed in the frequency domain (notation and ) for the decoupled system, were compared for the reference values equal to the nominal tension and speed values, i.e., uF12 = 100% uF12N, uv2 = 100% uv2N, and with external additive disturbances, as shown in Figure 16.
5. Discussion of the Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Parameters of the Continuous Line Laboratory Model
- PI speed controller gains for a stable structure with a reference model: KP = 20, KI = 2
- PID tension controller gains designed for standard control: P = 9, I = 20, D = 18
- PI speed controller gains for standard control: P = 7, I = 80
References
- Li, J.; Liu, S.H.; Cai, L.J. Coupling model and controller design for four-layer register system. In Proceedings of the International Conference on Mechatronics, Manufacturing and Materials Engineering (MMME 2016), Wuhan, China, 15–16 October 2016; Volume 63. [Google Scholar]
- Norris, R.N. Sectional electric drive for paper machines. Trans. Am. Inst. Electr. Eng. 2009, 45, 496–511. [Google Scholar]
- Valenzuela, M.A.; Bentley, J.M.; Lorenz, R.D. Evaluation of torsional oscillations in paper machine sections. IEEE Trans. Ind. Appl. 2005, 41, 493–501. [Google Scholar] [CrossRef]
- Jeftenič, B.; Bebič, M.; Štatkič, S. Controlled multi-motor drives. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion—SPEEDAM 2006, Taormina, Italy, 23–26 May 2006. [Google Scholar]
- Wolfermann, W. Tension control of webs, a review of the problems and solutions in the present and future. In Proceedings of the Third International Conference on strip Handling, Stillwater, OK, USA, 18–21 June 1995; pp. 198–229. [Google Scholar]
- Allaoua, B.; Laoufi, A.; Gasbaoui, B. Multi-drive paper system control based on multi-input multi-output PID controller. Leonardo J. Sci. 2010, 16, 59–70. [Google Scholar]
- Bouchiba, B.; Hazzab, A.; Glaoui, H.; Med-Karim, F.; Bousserhane, I.K.; Sicard, P. Decentralized PI controller for multi-motors strip winding system. J. Autom. Mob. Robot. Intell. Syst. 2012, 6, 32–36. [Google Scholar]
- Lin, P.; Lan, M.S. Effects of PID gains for controller with dancer mechanism on strip tension. In Proceedings of the Second International Conference on strip Handling, Stillwater, OK, USA, 6–9 June 1993; pp. 66–76. [Google Scholar]
- Pagilla, P.R.; Siraskar, N.B.; Dwivedula, R.V. Decentralized control of strip processing lines. IEEE Trans. Control Syst. Technol. 2007, 15, 106–117. [Google Scholar] [CrossRef]
- Thiffault, C.; Sicard, P.; Bouscayrol, A. Tension control loop using a linear actuator based on the energetic macroscopic representation. In Proceedings of the Canadian Conference on Electrical and Computer Engineering—CCECE, Niagara Falls, ON, Canada, 2–5 May 2004. [Google Scholar]
- Priya, N.H.; Kavitha, P.; Srinivasan, N.M.S.; Ramkumar, K. Design of PSO-based PI controller for tension control in strip transport systems. In Proceedings of the International Conference Soft Computing Systems; Springer: New Delhi, India, 2015; pp. 509–516. [Google Scholar]
- Noura, H.; Bastogne, T. Tension optimal control of a multivariable winding process. In Proceedings of the American Control Conference, Albuquerque, NM, USA, 6 June 1997; pp. 2499–2503. [Google Scholar]
- Perduková, D.; Fedor, P.; Timko, J. Modern methods of complex drives control. Acta Tech. CSAV 2004, 49, 31–45. [Google Scholar]
- Fang, S.; Franitza, D.; Torlo, M.; Bekes, F.; Hiller, M. Motion control of a tendon-based parallel manipulator using optimal tension distribution. IEEE/ASME Trans. Mechatron. 2004, 9, 561–568. [Google Scholar] [CrossRef]
- Zhao, W.; Ren, X. Adaptive robust control for four-motor driving servo system with uncertain nonlinearities. Control Theory Technol. 2017, 15, 45–57. [Google Scholar] [CrossRef]
- Tan, S.; Wang, L.; Liu, J. Research on decoupling method of thickness and tension control in rolling process. In Proceedings of the 11th IEEE World Congress on Intelligent Control and Automation (WCICA 2014), Shenyang, China, 29 June–4 July 2014; pp. 4715–4717. [Google Scholar]
- Pin, G.; Francesconi, V.; Cuzzola, F.A.; Parisini, T. Adaptive task-space metal strip-flatness control in cold multi-roll mill stands. J. Process Control 2013, 23, 108–119. [Google Scholar] [CrossRef]
- Baumgart, M.D.; Pao, L.Y. Robust Lyapunov-based feedback control of nonlinear web-winding systems. In Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003. [Google Scholar]
- Koc, H.; Knittel, D.; Mathelin, M.D.; Abba, G. Robust gain-scheduled control of winding systems. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, NSW, Australia, 12–15 December 2000. [Google Scholar]
- Pagilla, P.R.; King, E.O.; Dreinhoefer, L.H.; Garimella, S.S. Robust observer-based control of an aluminium strip processing line. IEEE Trans. Ind. Appl. 2000, 36, 865–870. [Google Scholar] [CrossRef]
- Benlatreche, A.; Knittel, D.; Ostertag, E. Robust decentralised control strategies for large-scale strip handling systems. Control Eng. Pract. 2008, 16, 736–750. [Google Scholar] [CrossRef]
- Lee, G.T.; Shin, J.M.; Kim, H.M.; Kim, J.S. A strip tension control strategy for multi-span strip transport systems in annealing furnace. ISIJ Int. 2010, 50, 854–863. [Google Scholar] [CrossRef]
- Shafiei, B.; Ekramian, M.; Shojaei, K. Robust tension control of strip for 5-stand tandem cold mills. J. Eng. 2014, 2014, 409014. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Q. Robust control of strip tension for tandem cold rolling mill. In Proceedings of the 30th Chinese Control Conference (CCC 2011), Yantai, China, 22–24 July 2011; pp. 2390–2393. [Google Scholar]
- Koofigar, H.R.; Sheikholeslam, F.; Hosseinnia, S. Unified gauge-tension control in cold rolling mills: A robust control technique. Int. J. Precis. Eng. Manuf. 2011, 12, 393–403. [Google Scholar] [CrossRef]
- Hoshino, I.; Okamura, Y.; Kimura, H. Observer based multivariable tension control of aluminium hot rolling mills. In Proceedings of the 35th IEEE Conference on Decision Control, Kobe, Japan, 13 December 1996. [Google Scholar]
- Lin, K.C. Observer-based tension feedback control with friction and inertia compensation. IEEE Trans. Control Syst. Technol. 2003, 11, 109–118. [Google Scholar]
- Song, S.H.; Sul, S.K. A new tension controller for continuous strip processing line. IEEE Trans. Ind. Appl. 2000, 36, 633–639. [Google Scholar]
- Angermann, A.; Aicher, M.; Schroder, D. Time optimal tension control for processing plants with continuous moving webs. In Proceedings of the 35th Annual Meeting-IEEE Industry Applications Conference, Rome, Italy, 8–12 October 2000. [Google Scholar]
- Knittel, D.; Laroche, E.; Giran, D.; Koc, H. Tension control for winding systems with two-degrees-of-freedom H/sub /spl infin// controllers. IEEE Trans. Ind. Appl. 2003, 39, 113–120. [Google Scholar] [CrossRef]
- Giannoccaro, N.; Nishida, T.; Sakamoto, T. Decentralized H∞ based control of a strip transport system. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011; pp. 8651–8656. [Google Scholar]
- He, F.; Wang, Q. Compensation and fuzzy control of tension in strip winding control system. In Proceedings of the 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012. [Google Scholar]
- Okada, K.; Sakamoto, T. An adaptive fuzzy control for strip tension control system. In Proceedings of the 24th Annual Conference of the IEEE Industrial Electronics Society (IECON ’98), Aachen, Germany, 31 August–4 September 1998; pp. 1762–1768. [Google Scholar]
- Perduková, D.; Fedor, P. APPLICATION OF FUZZY LOGIC IN MOTION CONTROL. Int. Sci. J. Mach. Technol. Mater. 2007, 28–31. [Google Scholar]
- Wang, S.Y.; Tseng, C.L.; Lin, S.C.; Chiu, C.J.; Chou, J.H. An adaptive supervisory sliding fuzzy cerebellar model articulation controller for sensorless vector-controlled induction motor drive systems. Sensors 2015, 15, 7323–7348. [Google Scholar] [CrossRef]
- Saghafinia, A.; Ping, H.W.; Uddin, M.N. Sensored field oriented control of a robust induction motor drive using a novel boundary layer fuzzy controller. Sensors 2013, 13, 17025–17056. [Google Scholar] [CrossRef]
- Perduková, D.; Fedor, P.; Bačík, J.; Herčko, J.; Rofár, J. Multi-motor drive optimal control using a fuzzy model based approach. J. Ambient Intell. Smart Environ. 2017, 9, 329–344. [Google Scholar]
- Butler, H. Model Reference Adaptive Control: From Theory to Practice; Prentice Hall: Upper Saddle River, NJ, USA, 1992; pp. 80–113. [Google Scholar]
- Landau, I. Adaptive Control; Springer: London, UK, 2011; pp. 523–541. [Google Scholar]
- Orsag, M.; Korpela, C.; Bogdan, S.; Oh, P. Lyapunov based model reference adaptive control for aerial manipulation. In Proceedings of the International Conference Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; pp. 966–973. [Google Scholar]
- Tang, M.; Cao, J.; Yang, X.; Wang, X.; Gu, B. Model reference adaptive control based on Lyapunov stability theory. In Proceedings of the 26th Chinese Control and Decision Conf. (CCDC 2014), Changsha, China, 31 May–2 June 2014; pp. 1828–1833. [Google Scholar]
- Sassano, M.; Astolfi, A. Dynamic Lyapunov functions. Automatica 2013, 49, 1056–1067. [Google Scholar] [CrossRef]
- Lakshmikantham, V. Advances in stability theory of Lyapunov: Old and new. Syst. Anal. Model. Simul. 2000, 37, 407–416. [Google Scholar]
- He, W.; Sun, C.; Ge, S.S. Top tension control of a flexible marine riser by using integral-barrier Lyapunov function. IEEE/ASME Trans. Mechatron. 2015, 20, 497–505. [Google Scholar] [CrossRef]
- Narendra, K.S.; Valavani, L.S. A comparison of Lyapunov and hyperstability approaches to adaptive control of continuous systems. IEEE Trans. Autom. Control 1980, 25, 243–247. [Google Scholar] [CrossRef]
- Lyapunov, A.M. Stability of Motion; Academic Press: New York, NY, USA; London, UK, 1966. [Google Scholar]
- Furasov, V.D. Ustojcivosť Dvizenija, Ocenki i Stabilizacija; Nauka: Moskva, Russia, 1977; pp. 213–220. (In Russian) [Google Scholar]
- Brandenburg, G. Ein mathematisches Modell fuer eine durchlaufende elastische Stoffbahn in einem System angetriebener umschlungener Walzen, Teil 1. Regelungstechnik und Prozessdatenverarbeitung 1973, 21, 69–77. [Google Scholar]
- Brandenburg, G. Ein mathematisches Modell fuer eine durchlaufende elastische Stoffbahn in einem System angetriebener umschlungener Walzen, Teil 2. Regelungstechnik und Prozessdatenverarbeitung 1973, 21, 125–129. [Google Scholar]
- Brandenburg, G. Ein mathematisches Modell fuer eine durchlaufende elastische Stoffbahn in einem System angetriebener umschlungener Walzen, Teil 3. Regelungstechnik und Prozessdatenverarbeitung 1973, 21, 157–162. [Google Scholar]










© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perduková, D.; Fedor, P.; Fedák, V.; Padmanaban, S. Lyapunov Based Reference Model of Tension Control in a Continuous Strip Processing Line with Multi-Motor Drive. Electronics 2019, 8, 60. https://doi.org/10.3390/electronics8010060
Perduková D, Fedor P, Fedák V, Padmanaban S. Lyapunov Based Reference Model of Tension Control in a Continuous Strip Processing Line with Multi-Motor Drive. Electronics. 2019; 8(1):60. https://doi.org/10.3390/electronics8010060
Chicago/Turabian StylePerduková, Daniela, Pavol Fedor, Viliam Fedák, and Sanjeevikumar Padmanaban. 2019. "Lyapunov Based Reference Model of Tension Control in a Continuous Strip Processing Line with Multi-Motor Drive" Electronics 8, no. 1: 60. https://doi.org/10.3390/electronics8010060
APA StylePerduková, D., Fedor, P., Fedák, V., & Padmanaban, S. (2019). Lyapunov Based Reference Model of Tension Control in a Continuous Strip Processing Line with Multi-Motor Drive. Electronics, 8(1), 60. https://doi.org/10.3390/electronics8010060






