Neoteric Fuzzy Control Stratagem and Design of Chopper fed Multilevel Inverter for Enhanced Voltage Output Involving Plug-In Electric Vehicle (PEV) Applications
Abstract
1. Introduction
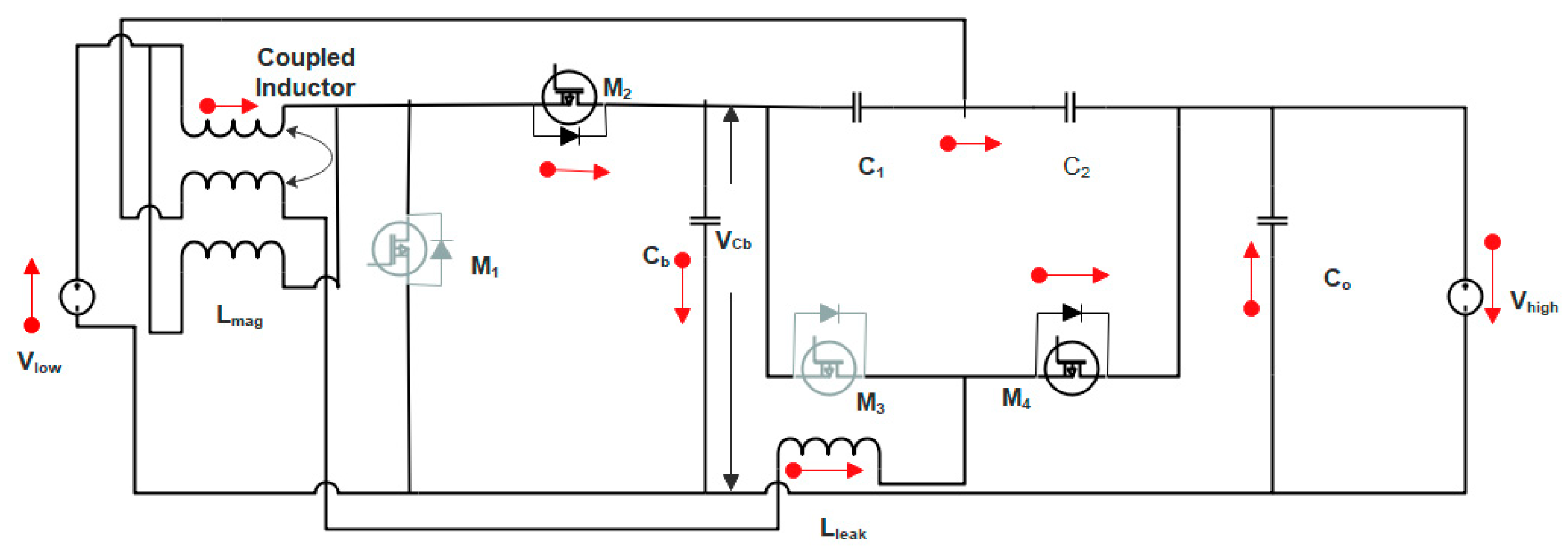
2. Chopper Configuration
- Since, the voltage on the two segments of the converter are matched with that of the turns ratio of coupled inductor, the current circulating across the switches are reduced and soft switching is also accomplished.
- High voltage conversion is achieved with the transformer less configuration.
- High power density is attained due to the winding of inductors on the same core.
2.1. Operating Modes
2.1.1. Mode I (t0 < t < t1)
2.1.2. Mode II (t1 < t < t2)
2.1.3. Mode III (t2 < t < t3)
2.1.4. Mode IV (t3 < t < t4)
2.1.5. Mode V (t4 < t < t5)
2.1.6. Mode VI (t5 < t < t6)
2.1.7. Mode VII (t6 < t < t7)
2.1.8. Mode VIII (t7 < t < t8)
2.2. Voltage Equations
2.2.1. Voltage Conversion Ratio
2.2.2. Voltage across Capacitance
3. Multilevel Inverter
- To acquire the voltage level of +2Vdc the switches S1, S4 of the H-bridge circuit and the switches S5, S6, and S7 of the DSCC circuit is held High.
- To acquire the voltage level of +3Vdc/2 the switches S1, S4 of the H-bridge circuit and the switches S5, S6, and S9 of the DSCC circuit is held High.
- The voltage level of +Vdc is achieved by holding the switches S1 and S4 of the H-bridge circuit and the switches S5 and S8 of the DSCC circuit at High position.
- To obtain the next level of multilevel output i.e., +Vdc/2, the switches S1 and S4 of the H-bridge circuit and the switches S8 and S9 of the DSCC circuit is held High.
- The zero level voltage is obtained by holding the switches S2 and S4 of the H-bridge circuit and the switches S8 and S9 of the DSCC circuit at High position.
- To achieve the voltage level of –Vdc/2, the switches S2 and S3 of the H-bridge circuit and the switches S8 and S9 of the DSCC circuit is held High.
- The negative cycle of Vdc (i.e., –Vdc) is achieved by holding the switches S2 and S3 of the H-bridge circuit and the switches S5 and S8 of the DSCC circuit is held High.
- To obtain the voltage level of –3Vdc/2, the switches S2 and S3 of the H-bridge circuit and the switches S5, S6, and S9 of the DSCC circuit is held High.
- To acquire the voltage level of –2Vdc the switches S2 and S3 of the H-bridge circuit and the switches S5, S6, and S7 of the DSCC circuit is held High.
4. Controller Circuit
4.1. PI Controller
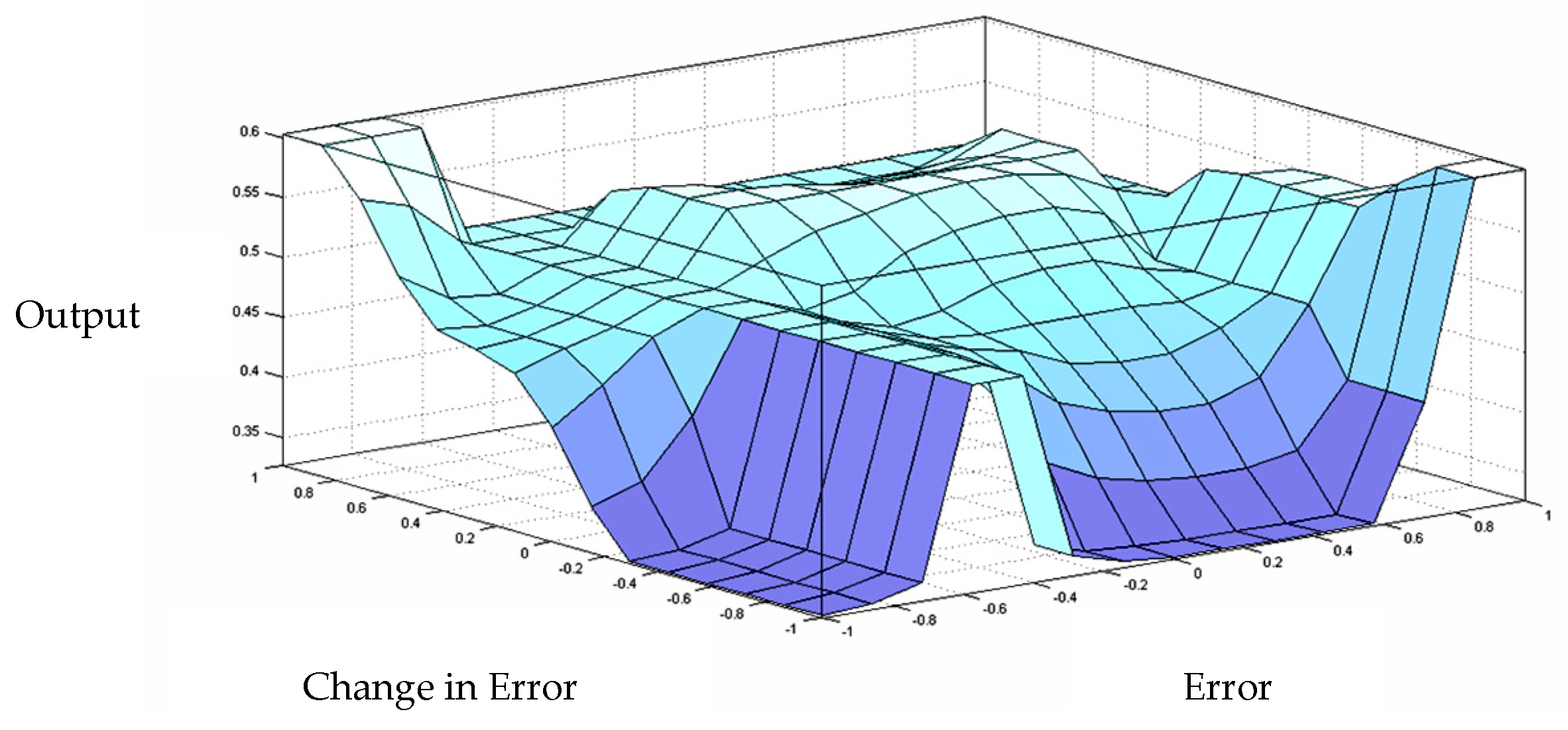
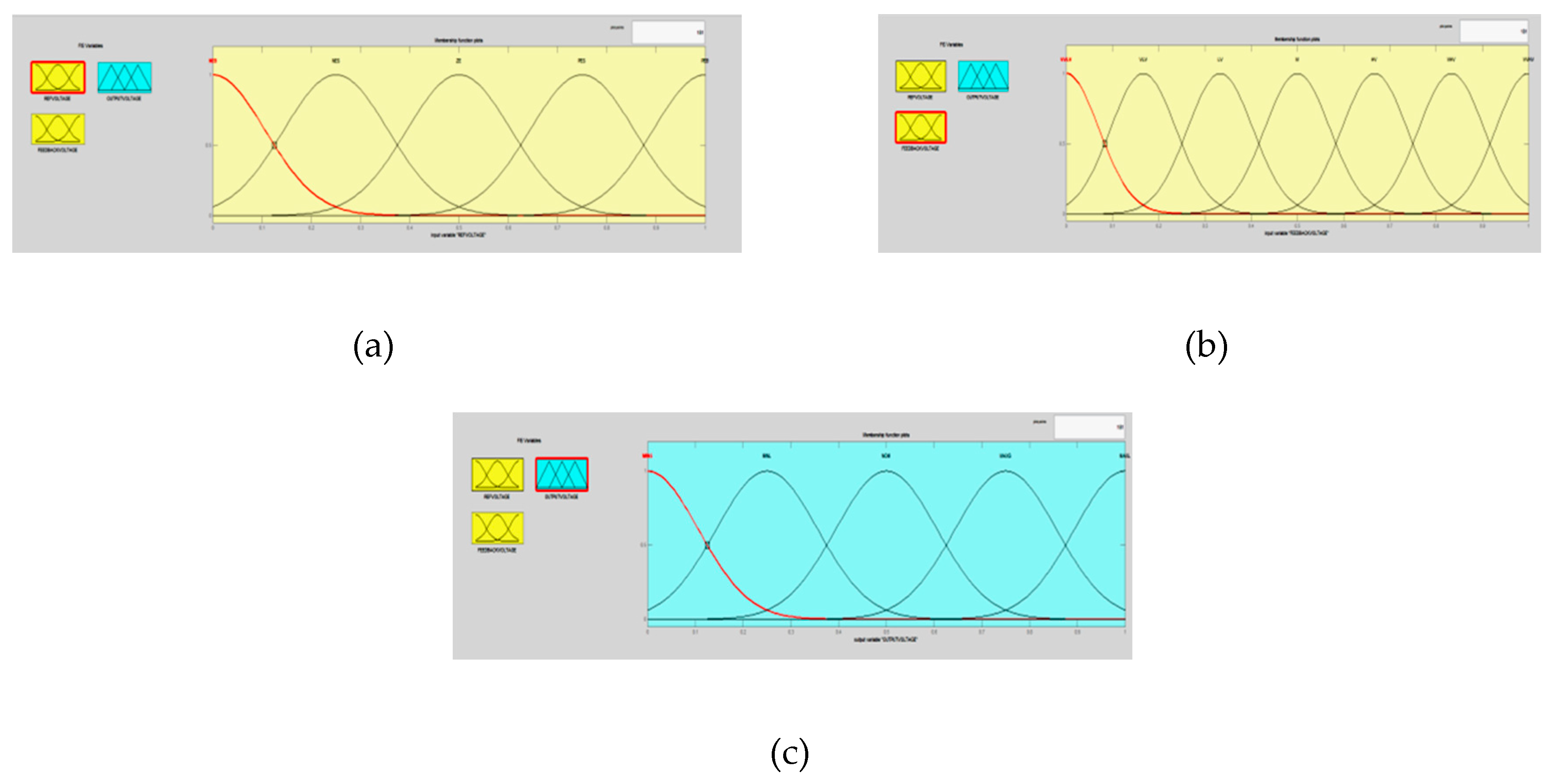
4.2. Proposed Fuzzy Logic Based Controller
4.2.1. Rule 1
4.2.2. Rule 2
4.2.3. Rule 3
4.2.4. Rule 4
4.3. Novel Hybrid Controller
4.3.1. Proposed Hybrid Controller-1
4.3.2. Proposed Hybrid Controller-2
4.3.3. Proposed Hybrid Controller-3
4.3.4. Proposed Hybrid Controller-4
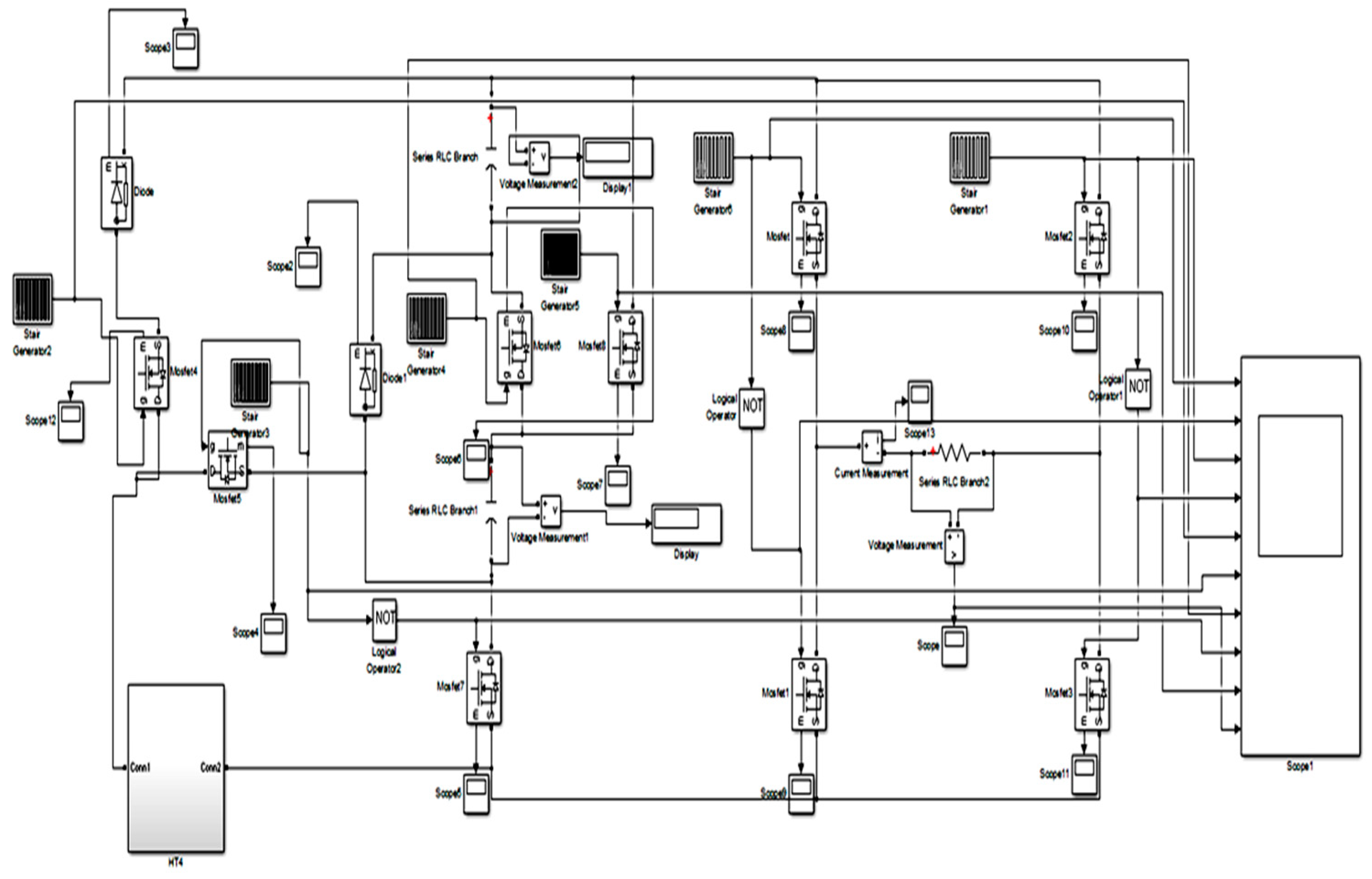
5. Simulation Result
5.1. Bidirectional Converter and Multilevel Inverter with PI Controller
5.2. Bidirectional Converter and Multilevel Inverter with Fuzzy Controller
5.3. Bidirectional Converter and Multilevel Inverter with Hybrid Controller-1
5.4. Bidirectional Converter and Multilevel Inverter with Hybrid Controller-2
5.5. Bidirectional Converter and Multilevel Inverter with Hybrid Controller-3
5.6. Bidirectional Converter and Multilevel Inverter with Hybrid Controller-4
6. Discussion
7. Conclusions
8. Future Scope
Author Contributions
Conflicts of Interest
References
- Vasiladiotis, M.; Rufer, A. Transformer with Integrated Split Battery Energy Storage for Versatile Ultrafast EV Charging Stations. IEEE Trans. Ind. Electron. 2015, 62, 3213–3222. [Google Scholar] [CrossRef]
- Rathore, A.K.; Prasanna, U.R. Analysis, Design, and Experimental Results of Novel Snubberless Bidirectional Naturally Clamped Converter for Fuel Cell Vehicles. IEEE Trans. Ind. Electron. 2013, 60, 4482–4491. [Google Scholar] [CrossRef]
- Rangarajan, S.S.; Collins, E.R.; Fox, J.C. Efficacy of a Smart Photovoltaic inverter as a virtual detuner for mitigating Network Harmonic Resonance in Distribution Systems. Electr. Power Syst. Res. 2019, 171, 175–184. [Google Scholar] [CrossRef]
- Rangarajan, S.S.; Collins, E.R.; Fox, J.C. Smart PV and Smart Park inverters as suppressors of TOV phenomenon in distribution systems. IET Gener. Transm. Distrib. 2018, 12, 5909–5917. [Google Scholar] [CrossRef]
- Rangarajan, S.S.; Collins, E.R.; Fox, J.C. Harmonic Resonance Repercussions of PV and Associated Distributed Generators on Distribution Systems. In Proceedings of the North American Power Symposium NAPS, Morgantown, WV, USA, 17–19 September 2017. [Google Scholar]
- Basso, T.R.D. IEEE Smart Grid Series of Standards IEEE 2030 (Interoperability) and IEEE 1547 (Interconnection) Status; Preprint Thomas Basso and Richard De Blasio; National Renewable Energy Laboratory, NREL: Golden, CO, USA, 2016.
- Pan, X.; Rathore, A.K.S. Novel Bidirectional Snubberless Naturally Isolated DC/DC Converter for Fuel Cell Vehicles. IEEE Trans. Ind. Electron. 2014, 61, 2307–2315. [Google Scholar] [CrossRef]
- Das, P.S.; Mousavi, S.A.; Moschopoulos, G.S. Analysis and Design of a Nonisolated Bidirectional ZVS-PWMDC—DC Converter with Coupled Inductors. IEEE Trans. Power Electron. 2010, 25, 2630–2641. [Google Scholar] [CrossRef]
- Singh, B.L.; Dubey, S.P.; Singh, S.P. Design and analysis of coupled inductor bidirectional DC—DC converter for high-voltage diversity applications. IET Power Electron. 2012, 5, 998–1007. [Google Scholar]
- Rodr, A.; Aitor, V.; Lamar, D.G.; Hernando, M.M.; Sebasti, J. Different Purpose Design Strategies and Techniques to Improve the Performance of a Dual Active Bridge with Phase-Shift Control. IEEE Trans. Power Electron. 2015, 30, 790–804. [Google Scholar]
- Khawla, E.M.; Chariag, D.E. A Control Strategy for a Three-Phase Grid Connected PV System under Grid Faults. Electronics 2019, 8, 906. [Google Scholar] [CrossRef]
- Estévez-Bén, A.A.; Carlos López Tapia, H.J.; Carrillo-Serrano, R.V.; Rodríguez-Reséndiz, J.; Vázquez Nava, N. A New Predictive Control Strategy for Multilevel Current-Source Inverter Grid-Connected. Electronics 2019, 8, 902. [Google Scholar]
- Rodríguez, J.; Lai, J. Multilevel Inverters: A Survey of Topologies, Controls, and Applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef]
- Hiltunen, J.; Vesa, V. Variable- Frequency Phase Shift Modulation of a Dual Active Bridge Converter. IEEE Trans. Power Electron. 2015, 30, 7138–7148. [Google Scholar] [CrossRef]
- Liu, J.; Wu, J.; Zeng, J.; Guo, H. A Novel Nine-Level Inverter Employing One Voltage Source and Reduced Components as High Frequency AC Power Source. IEEE Trans. Power Electron. 2016, 8993, 1–9. [Google Scholar] [CrossRef]
- Babaei, E.; Gowgani, S.S. Hybrid multilevel inverter using switched capacitor units. IEEE Trans. Ind. Electron. 2014, 61, 4614–4621. [Google Scholar] [CrossRef]
- Hemachandu, P.; Reddy, V.C.V.; Reddy, V.C.J.M.; Reddy, V.U. A PV/FC Co-Generation Based Micro-Grid System Using Compact Integrated 7-Level Inverter. In Proceedings of the Conference on Power, Control, Communication and Computational Technologies for Sustainable Growth (PCCCTSG), Kurnool, India, 11–12 December 2015; pp. 252–258. [Google Scholar]
- Davis, R. Unit control systems engineering. In Proceedings of the Western Computer Conference: Trends in Computers: Automatic Control and Data Processing (AIEE-IRE), Philadelphia, PA, USA, 11–12 February 1954; pp. 89–95. [Google Scholar]
- Kickert, W.J.M.; Mamdani, E.H. Analysis of a fuzzy logic controller. Fuzzy Sets Syst. 1978, 1, 29–44. [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy Systems as Universal Approximators. IEEE Trans. Comput. 1994, 43, 1329–1333. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic=computingwithwords. IEEE Trans. Fuzzy Syst. 1996, 4, 103–111. [Google Scholar] [CrossRef]
- Bhandari, K.S. A Resource Oriented Route Selection Framework Using Contextual Information Based on Fuzzy Logic. Electronics 2019, 8, 1023. [Google Scholar] [CrossRef]


















































| Vo | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 |
|---|---|---|---|---|---|---|---|---|---|
| 2Vdc | High | Low | High | High | High | High | High | Low | Low |
| 3Vdc/2 | High | Low | Low | High | High | High | Low | Low | High |
| Vdc | High | Low | Low | High | High | Low | Low | High | Low |
| Vdc/2 | High | Low | Low | High | Low | Low | Low | High | High |
| 0 | Low | High | Low | High | Low | Low | Low | High | High |
| –Vdc/2 | Low | High | High | Low | Low | Low | Low | High | High |
| –Vdc | Low | High | High | Low | High | Low | Low | High | Low |
| –3Vdc/2 | Low | High | High | Low | High | High | Low | Low | High |
| 2Vdc | Low | High | High | Low | High | High | High | Low | Low |
| Parameter | Kp | Ki |
| Range | 1.5 | 1 |
| e | N | Z | P | |
|---|---|---|---|---|
| ce | ||||
| N | L | L | M | |
| Z | L | M | H | |
| P | M | H | H | |
| e | NB | NS | Z | PS | PB | |
|---|---|---|---|---|---|---|
| ce | ||||||
| NB | VL | VL | L | M | M | |
| NS | VL | VL | L | M | M | |
| Z | L | L | M | M | VH | |
| PS | M | M | H | VH | VH | |
| PB | M | M | H | VH | VH | |
| R.V | NE-B | NE-S | ZE | PE-S | PE-B | |
|---|---|---|---|---|---|---|
| F.V | ||||||
| VVLV | MINL | MINL | MINL | MINS | MINS | |
| VLV | MINL | MINL | MINS | MINS | NOM | |
| LV | MINL | MINL | MINS | NOM | MINS | |
| M | MINS | MINS | NOM | MAXS | MAXS | |
| HV | MINS | NOM | MAXS | MAXS | MAXL | |
| VHV | NOM | MAXS | MAXS | MAXL | MAXL | |
| VVHV | MAXS | MAXS | MAXL | MAXL | MAXL | |
| RC | −2.5 | −1.5 | 0 | 1.5 | 2.5 | |
|---|---|---|---|---|---|---|
| FC | ||||||
| −2.5 | −1.01 | −1.01 | −1.01 | −0.31 | −0.01 | |
| −1.5 | −1.01 | −1.01 | −0.31 | −0.01 | 0.29 | |
| 0 | −1.01 | −0.31 | −0.01 | 0.29 | 0.99 | |
| 1.5 | −0.31 | −0.01 | 0.29 | 0.99 | 0.99 | |
| 2.5 | −0.01 | 0.29 | 0.99 | 0.99 | 0.99 | |
| Specifications | |
|---|---|
| Input Voltage (Vb) | 40 V |
| Output Voltage (Vh) | 300 V |
| Duty ratio (D) | 0.4–0.6 |
| Turns Ratio (n) | 3 |
| Leakage Inductance (Lleak) | 25 µH |
| Magnetising Inductance (Lmag) | 20 µH |
| Ca1,Ca2 | 10 µF |
| Ch | 470 µF |
| Cb | 2.5 µF |
| PARAMETERS | PI Based BDC with MLI | Fuzzy Based BDC with MLI | Hybrid Controller for BDC interfaced with MLI | |||
|---|---|---|---|---|---|---|
| Type I | Type II | Type III | Type IV | |||
| Output Voltage (BDC) (in Volts) | 279.9 | 282.6 | 297.7 | 300.3 | 303.4 | 301.9 |
| Ripple Voltage(BDC) (in Volts) | 4 | 3.5 | 3.3 | 2.9 | 2.5 | 2.8 |
| Output voltage for MLI (in Volts) | 551.2 | 556.4 | 589.17 | 574.5 | 592.8 | 578.4 |
| Parameter | PI Based Converter | Fuzzy Based Converter |
|---|---|---|
| Rise Time | 0.01 s | 0.001 s |
| Settling Time | 0.6 s | 0.3 s |
| Peak Time | 0.06 s | 0.04 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poyyamani Sunddararaj, S.; S. Rangarajan, S.; Gopalan, S. Neoteric Fuzzy Control Stratagem and Design of Chopper fed Multilevel Inverter for Enhanced Voltage Output Involving Plug-In Electric Vehicle (PEV) Applications. Electronics 2019, 8, 1092. https://doi.org/10.3390/electronics8101092
Poyyamani Sunddararaj S, S. Rangarajan S, Gopalan S. Neoteric Fuzzy Control Stratagem and Design of Chopper fed Multilevel Inverter for Enhanced Voltage Output Involving Plug-In Electric Vehicle (PEV) Applications. Electronics. 2019; 8(10):1092. https://doi.org/10.3390/electronics8101092
Chicago/Turabian StylePoyyamani Sunddararaj, Suvetha, Shriram S. Rangarajan, and Swaminathan Gopalan. 2019. "Neoteric Fuzzy Control Stratagem and Design of Chopper fed Multilevel Inverter for Enhanced Voltage Output Involving Plug-In Electric Vehicle (PEV) Applications" Electronics 8, no. 10: 1092. https://doi.org/10.3390/electronics8101092
APA StylePoyyamani Sunddararaj, S., S. Rangarajan, S., & Gopalan, S. (2019). Neoteric Fuzzy Control Stratagem and Design of Chopper fed Multilevel Inverter for Enhanced Voltage Output Involving Plug-In Electric Vehicle (PEV) Applications. Electronics, 8(10), 1092. https://doi.org/10.3390/electronics8101092






