An Ultra-Wide Band Polarization-Independent Random Coding Metasurface for RCS Reduction

Abstract

In this paper, a novel ultra-wide band (UWB) random 3-bit coding metasurface with polarization independence has been designed to realize radar cross-section (RCS) reduction. The proposed structure consists of polarization conversion metasurfaces (PCMs), which possess the capability of rotating linear polarization waves to their orthogonal ones in an UWB. The polarization-independent property can be attributed to the random rotation angle of each constituting unit. Due to the randomness of 3-bit coding and rotation angle of each element, the divergence of the reflected beam is greatly improved. In addition, the effect of RCS reduction with respect to the unit period length and the unit position are also discussed. Finally, a prototype is fabricated and measured to validate the simulation. The experimental results demonstrate that an ultra-wide band RCS reduction over 10 dB, ranging from 18.3–42.2 GHz, can be attained by the proposed coding metasurface and the maximum reduction is 28.7 dB.

1. Introduction

Metamaterials are usually composed of periodically or non-periodically arranged units. By changing the size and arrangement of the metamaterial structure, the dielectric constant and permeability can be controlled to effectively manipulate electromagnetic waves [1,2,3]. Metasurface is a new kind of two-dimensional planar metamaterial, which is realized by designing special artificial metal unit structures on the interface of two mediums [4,5]. Then, the phase discontinuity of the incident electromagnetic wave on the interface can be generated to achieve the abnormal refraction and reflection, satisfying the request of regulating and controlling the incoming electromagnetic waves [6,7,8,9,10]. Based on metasurfaces, many interesting works have been presented in the optical field, such as negative refractions, negative reflections and polarized rotations, where ordinary electromagnetic surfaces would be insufficient [11,12,13].

Radar cross-section (RCS) is the key concept in radar stealth technology. It represents a physical quantity of echo intensity produced by a target irradiated by radar wave. One of the important applications of metasurface is electromagnetic cloaking, which reduces the detectability of a target radar by decreasing the scattering cross-section [14]. Electromagnetic cloaking is of great significance in modern warfare, which can greatly improve the survivability of weapon platforms. RCS can also be reduced by radar-absorbing metasurfaces, which can convert electromagnetic energy into heat energy, although the operating frequency band is usually limited [15]. In addition, phase gradient metasurfaces can couple incident electromagnetic waves to surface waves or cause abnormal reflection of incident electromagnetic waves, so that they also can reduce backward RCS by careful design [16,17]. But, at present, there are still some problems such as narrow frequency band, large size and high structure requirement for better application of phase gradient metasurfaces in RCS reduction. Moreover, artificial magnetic conductors (AMCs) have also been utilized to reduce RCS reflection [18]. However, realization of a broadband AMC structure is usually difficult to be implemented. Therefore, it still remains a huge challenge to obtain UWB RCS reduction with metasurface structure.

In 2014, professor Cui Tiejun et al. of Southeast University put forward the theory of coding metasurface [19]. By adjusting the phase of each unit, it can produce a stable phase difference. The energy of electromagnetic wave can be scattered to all directions by coding metasurface [20,21,22]. On the other hand, random surface is based on design method of microstrip reflective array antenna. When the metasurface units are randomly arranged, the incident wave is irregularly reflected back to the free space, so the scattering energy of each direction beam is very small, resulting in RCS reduction. [22,23].

In this paper, combining the concepts of random surface and coding metasurface, one unit structure with broadband polarization conversion characteristic is used to design a new coding metasurface, by which not only the electromagnetic wave can be scattered in all directions, but also the incident electromagnetic wave can be converted into another linear polarized emitted wave with cross polarization. The simulation and experimental results show that it can significantly reduce the radar cross-section of the target, and has a good broadband stealth effect. This metasurface consists of eight elements, whose phase difference is close to 45° in an ultra-wide frequency band. The phase and amplitude of cross-polarized reflection can be controlled by changing the certain geometric parameters and rotation angle of the unit, respectively. By encoding and designing the spatial arrangement of these eight basic units, the diffuse reflection of incident electromagnetic waves can be achieved, and thus the RCS can be reduced.

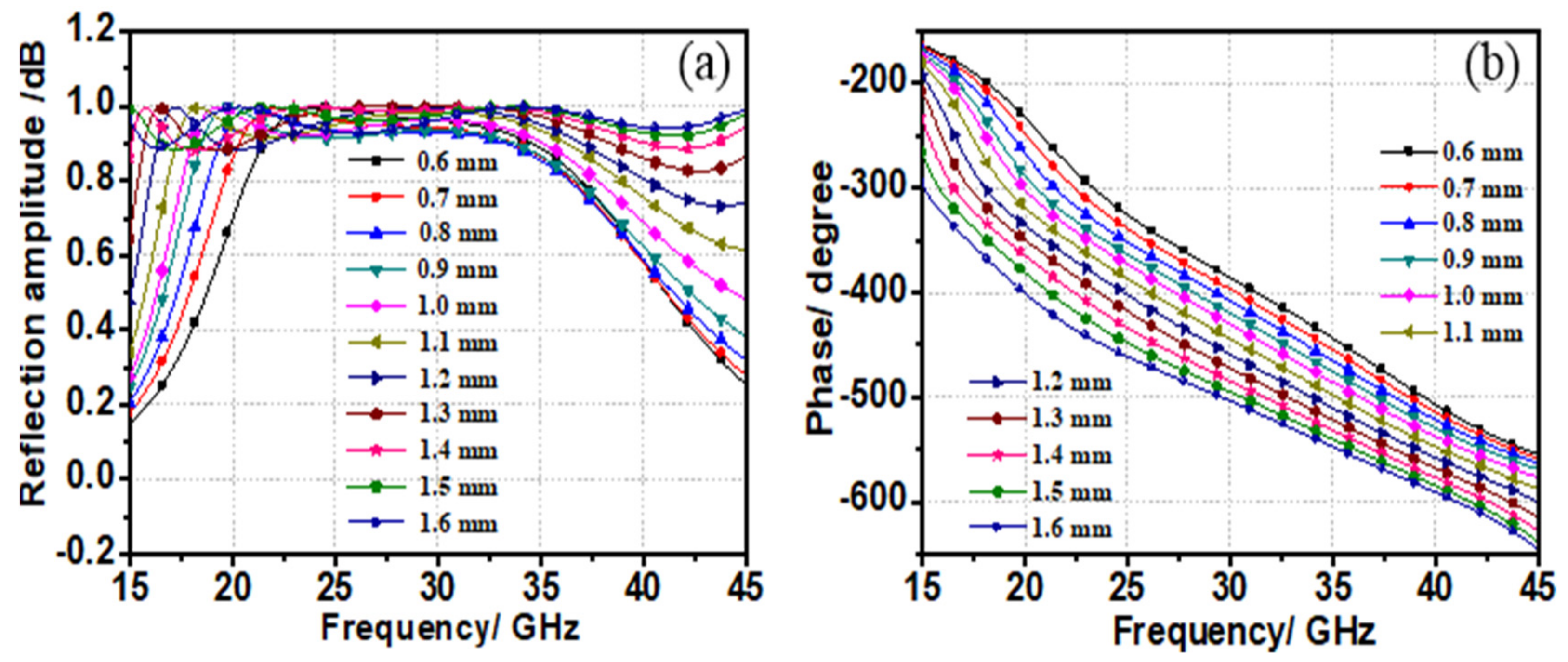
2. Design of the Unit and Theoretical Analysis

The unit of the designed PCM is sketched in Figure 1, and detailed geometric parameters are as follow: p = 4 mm, b = 2.6 mm, c = 0.2 mm, a = 1.5 mm, d = 1.6 mm and α = 80°. The double arrow structure and the ground plane that separated by the substrate are designed by copper, whose conductivity and thickness are σ =5.8 × 10⁷ S/m and s = 0.035 mm, respectively. F4B is chosen as dielectric substrate, and the dielectric constant and loss tangent are tan δ = 0.001 and ɛ_r = 2.2, respectively. The rotation angle at the center of the unit is β, which is equal to 45° in Figure 1b.

The PCM is homogeneous and anisotropic, with dispersive relative permeability and permittivity. When a plane wave impinges on this PCM with a specified polarization, both x- and y-polarized plane waves can be generated by transmission and reflection due to the anisotropic characteristics of the metasurface. The waves undergo multiple reflections between the PCM and the metallic sheet layer, and the final reflected waves are a result of the mutual interference of waves. Therefore, the thickness of the dielectric layer can be utilized to control the phase and amplitude of the final reflected waves.

To better understand the response of the PCM, we consider that the incident plane wave is polarized along the y-axis. Thus, the electric field can be decomposed into two perpendicular components u and v, as seen in Figure 2. Hence, the electric field of the incident plane wave can be expressed as

$${\overrightarrow{E}}_r={\tilde{r}}_u\overrightarrow{u}{E}_{iu}{e}^{j\phi }+{\tilde{r}}_v\overrightarrow{v}{E}_{iv}{e}^{j\phi }$$

(1)

and the electric field of the reflected wave can be written as

$${\overrightarrow{E}}_r={\tilde{r}}_u\overrightarrow{u}{E}_{iu}{e}^{j\phi }+{\tilde{r}}_v\overrightarrow{v}{E}_{iv}{e}^{j\phi }$$

(2)

In which ${\tilde{r}}_u$ and ${\tilde{r}}_v$ are the reflection coefficients along the u-and v-axes, respectively. Owing to the anisotropic characteristic of the PCM, a phase difference Δφ can be generated between ${\tilde{r}}_u$ and ${\tilde{r}}_v$. when Δφ ≈ π and the modulus satisfy r_u ≈ r_v, the synthetic field for E_ru and E_rv will be along with the x-direction, as shown in Figure 2, and the incident polarization is rotated by 90°. In fact, the double-V-shaped structure supports symmetric and anti-symmetric modes, which are excited by electric field components along the v- and u-axes, and the cut-wire structure supports multi-order dipolar resonances which are excited by electric field components along the v-axis. We predict the presence of multiple resonances for the composited structure. To numerically inverstigate the performance of our design, the reflection amplitude and phase of the unit have been simulated in CST Microwave Studio, see in Figure 3.

To investigate the polarization conversion of the designed double arrow-shaped metasurface in more detail, we first define r_yy = E_yr/E_yi and r_xy = E_xr/E_yi to denote the reflection coefficients for different polarization conversions. Here, E denotes the electric field; the subscripts i and r indicate the incidence and reflection of electromagnetic wave (EM) waves, respectively; and the subscripts x and y denote the polarization directions of EM waves, respectively. By using the commercial software CST Microwave Studio, we can investigate the polarization conversion ability of the proposed polarization converter by simulating the reflection coefficients r_yy and r_xy. In the simulation, a single unit cell with periodic boundary conditions along the x- and y-directions are used to simulate r_yy and r_xy. The EM wave impinging on the unit is in the xy-plane, with a transverse electric polarization (i.e., E is along the y-axis, as shown in Figure 2).

The cross-polarization r_xy (r_yx) and co-polarization r_xx (r_yy) of the unit under normal incident wave are shown in Figure 3. The cross-polarization reflection coefficients r_xy (r_yx) are close to 1 (0 dB) in UWB, which indicates that the polarization conversion can be realized under the normal incidence for both x- and y-polarization [24]. The UWB polarization conversion is resulted from its four resonant frequencies at 14.4 GHz, 20.1 GHz, 34.1 GHz and 45.5 GHz, and the polarization conversion efficiency is roughly 100% (see in Figure 3).

Figure 4 illustrates the amplitude and phase responses of the proposed structure with different lengths of a while β is fixed. As shown in Figure 4a, the amplitudes of cross-polarized reflections are greater than 0.9, as a increases, the linearity of phase is not affected and only the constant phase shifts can be observed from 15 GHz to 45 GHz. And as illustrated in Figure 4b, the range of phase shift covers over 180° in an UWB. In addition, when the value of a remains unchanged, the cross-polarized reflection coefficients with respect to different rotation angle β are shown in Figure 5. Obviously, by adjusting the rotation angle β, the amplitude of cross-polarization reflection coefficients can be continuously adjusted in a broadband (Figure 5a), while only a phase shift of 180° exists (Figure 5b).

Schematic of x-to-y polarization conversion for the PCM unit and the mirrored one are shown in the Figure 6. Owing to the symmetry, the mirror structure shown in Figure 6b can produce the same cross-polarized reflection, although a phase shift of 180° is generated. In this way, the phase and amplitude of cross-polarized reflection can be continuously controlled in a broadband by adjusting certain geometric parameter a and the rotation angle β, respectively. Thus, the electromagnetic wave propagation and RCS reduction can be completely manipulated by the proposed structure, which satisfies the design requirement given in [25].

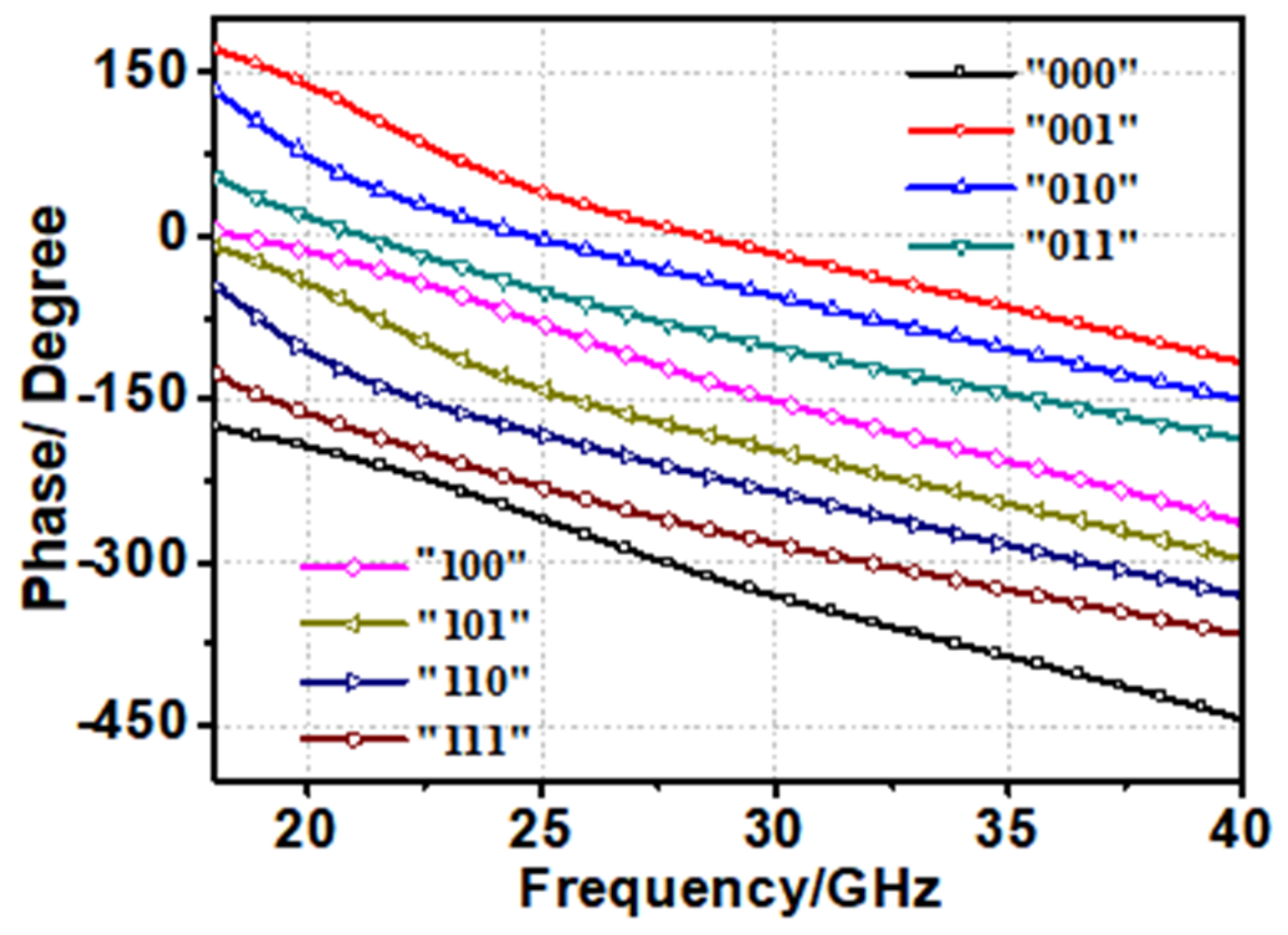
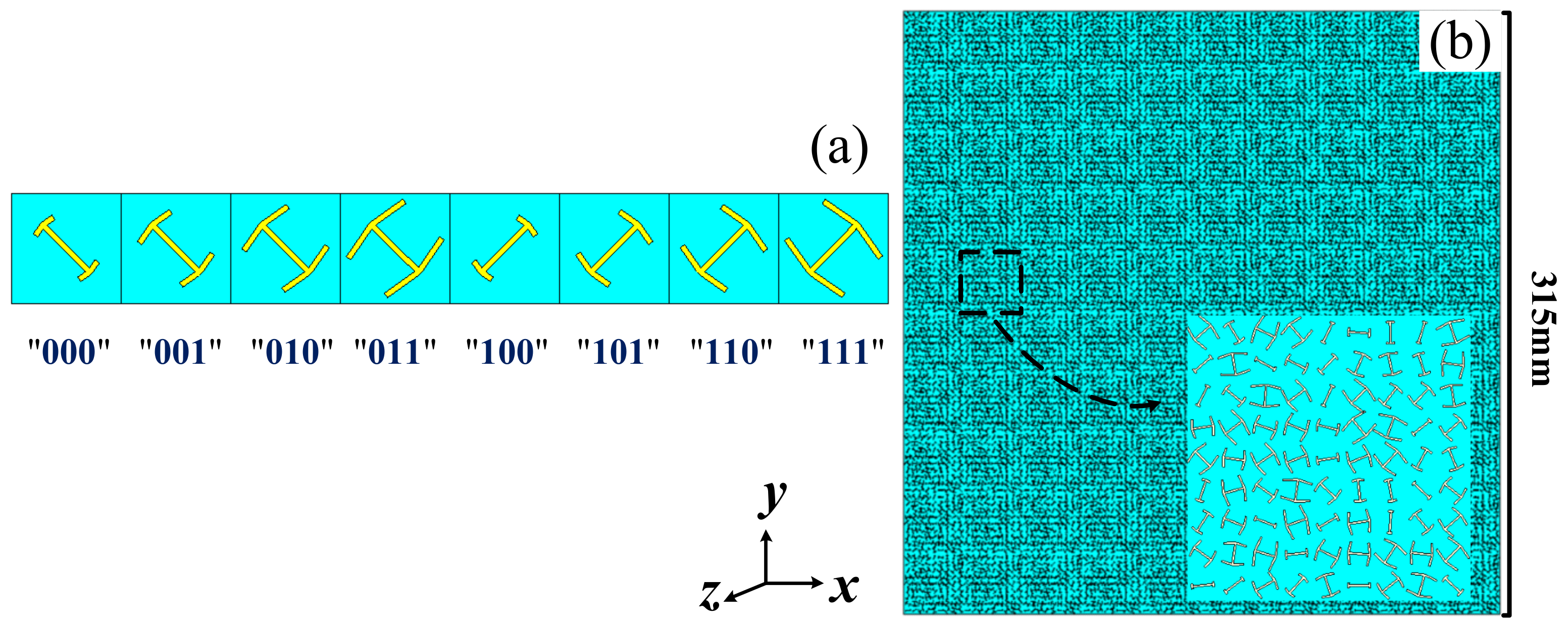
3. Design of the PCM Metasurface and Simulations

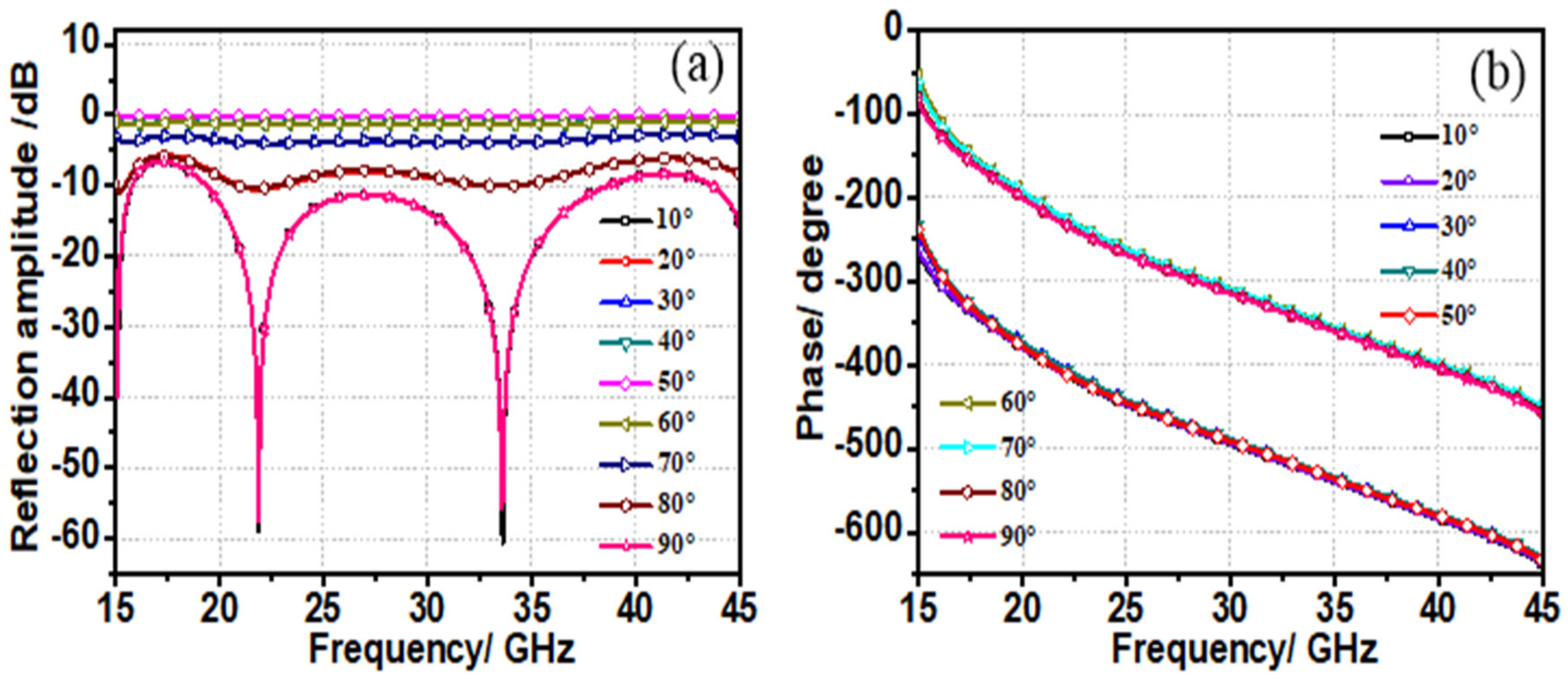
3.1. Theoretical Analysis of the Designed PCM Metasurface

The design concept of this random coding metasurface is as follows: firstly, the PCM unit is proposed through optimum design and simulation. Secondly, the cross-polarization reflection phases at the center frequency (30 GHz) are selected as the design reference. Then, according to Cubic Spline Interpolation, the curves of cross-polarization reflection phase following the change of the length a are fitted by MATLAB [26]. Finally, the cross-polarized reflection phases are selected as 0, 1/4ᴨ, 2/8ᴨ, 3/8ᴨ, 2ᴨ, 5/8ᴨ, 3/4ᴨ and 7/8ᴨ, corresponding to the codes “000”, “001”, “010”, “011”, “100”, “101”, “110” and “111”, respectively.

The phase of the eight basic elements are shown in Figure 7. According to the function relation of phase shift curve, the basic structure dimensions of these eight elements can be obtained. The length a and the rotation angle β of the eight elements are (a, β) = (0.4 mm, 0°), (0.73 mm, 0°), (1.06 mm, 0°), (1.39 mm, 0°), (0.4 mm, 90°), (0.73 mm, 90°), (1.06 mm, 90°) and (1.39 mm, 90°), and the other structural dimensions are α = 80°, b = 2.6 mm, c = 0.2 mm and d =1.6 mm. Finally, the 6 × 6 random matrices which determine the random rotation angle β of the eight codes are generated by MATLAB. The designed eight basic units and 3-bit random coding metasurface is presented in Figure 8a,b, respectively.

Figure 9 depicts the comparison of the monostatic RCS results between the proposed coding metasurface and a bare metal plane of the same sizes. It can be observed that, an UWB RCS reduction above 10 dB, ranging from 18.3–42.2 GHz, can be attained by the proposed coding PCM.

As shown in Figure 10, scattering patterns of the designed PCM (Figure 10a–d) and a bare metal plane of the same size (Figure 10e–h) in XOZ-plane are compared at four frequencies of 18 GHz, 25 GHz, 32 GHz and 40 GHz. According to the conservation law of energy, it is necessary to suppress the main lobe and strengthen side lobes for the metasurface to achieve RCS reduction [27]. It can be observed that a strong main lobe exists in the reverse direction of the metal surface in the entire working frequency band (as shown in Figure 10e–h), while the main lobes are reduced to some extent with the side lobes significantly increased in Figure 10a–d. Compared with the bare metal plane of the same size, the metasurface suppresses the main lobe energy and scatters the side lobes energy at 25 GHz and 40 GHz, which near the resonance points, as shown in Figure 9 and Figure 10b,d,f,h. While at 18 GHz and 32 GHz, the main lobe suppression are not obvious, which are consistent with the results in Figure 8.

Figure 11a–d show the simulated far-field scattering patterns of random coding metasurfaces with different coding sequences at 20 GHz. In Figure 11d, it can be clearly observed that the main lobe reduces significantly and many side lobes are produced. Therefore, the proposed 3-bit metasurface with random coding and random rotation angle are more conducive to realizing RCS reduction, compared with the cases in Figure 11a–c, which are 1-bit 00/00 or 11/11 PCM structure, 1-bit chessboard structure, and 3-bit random coding metasurface without random rotation angle, respectively.

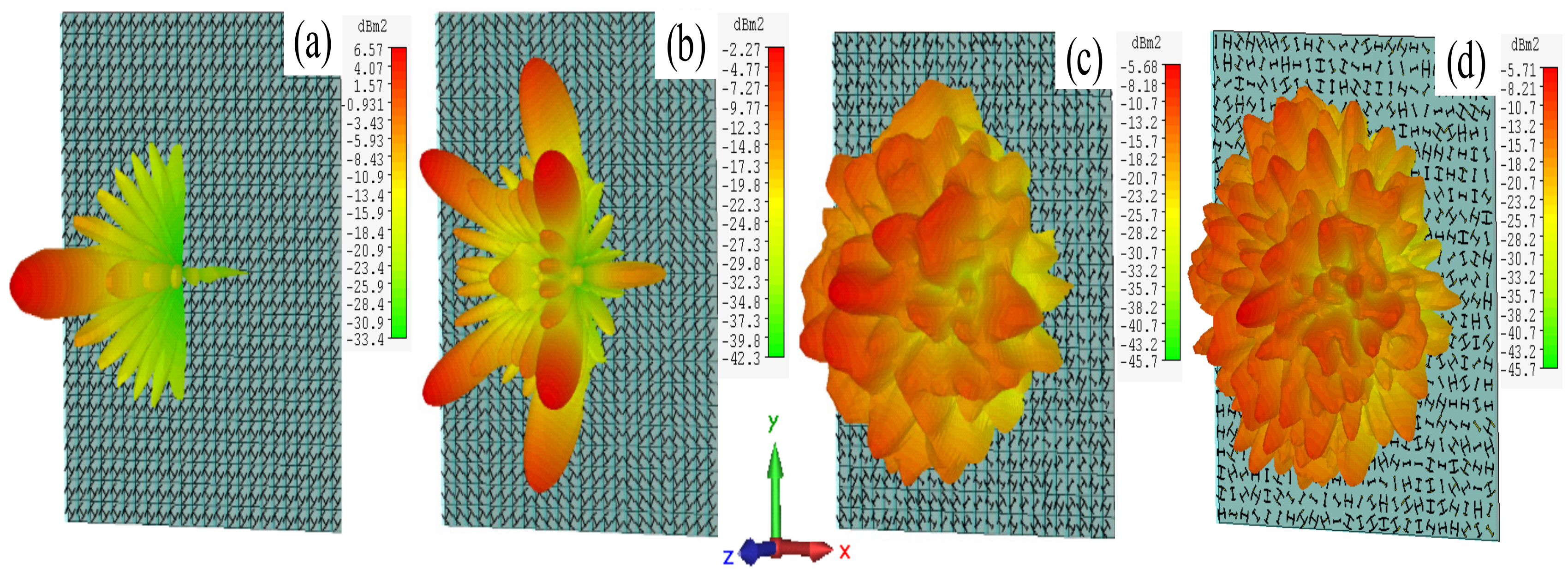
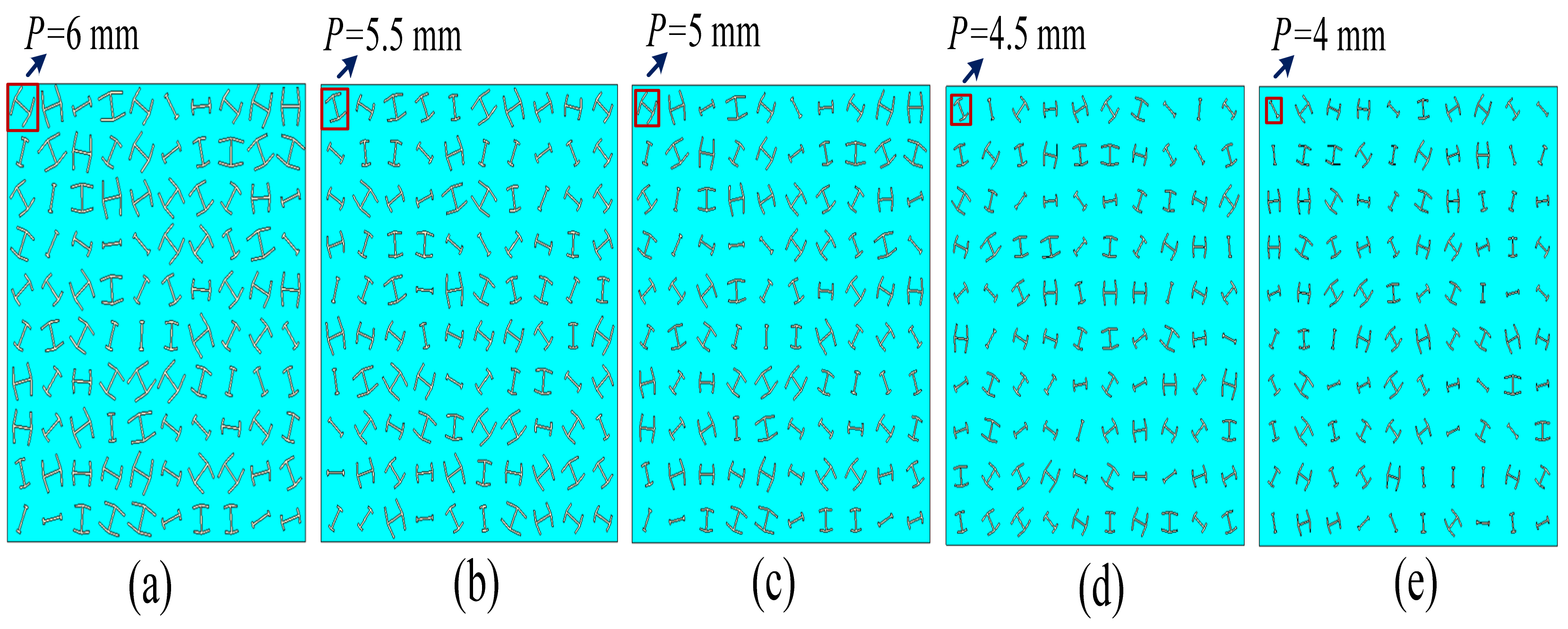
3.2. RCS Reduction Comparisons with Different Period Length

As shown in Figure 12, the RCS reduction changes when the length of period p varies from 4 mm to 6 mm, (see in Figure 13a–e) a wider bandwidth of RCS reduction can be achieved with a smaller period value. In a few words, when the unit size is the same, in a certain range, the shorter the period length is, that is, the denser the units are, the better RCS reduction effect of the metasurface basically can be realized.

3.3. RCS Reduction Comparisons with Random Coding and Random Position of Each Unit

All the cases discussed above are analyzed with random coding order and random rotation angle with the fixed position of the units. In the following, the position of each unit is also randomized. As shown in Figure 14, four different random position distributions are given. Figure 14a indicates that each unit position is fixed and unchanged, while the randomness of the distance to the center for each unit is increased from Figure 14b to Figure 14d. The RCS reduction of the metasurfaces with four different random codings and random positions are shown in Figure 15, and it can be seen that the RCS reduction result is not the best when the location of each element is fixed (metasurface 1). Metasurface 2 and metasurface 4 both have wider RCS random bandwidths over 10 dB. While metasurface 3 is not better than metasurface 2 for improving RCS reduction effect. Therefore, it can be concluded that the RCS reduction can be also optimized by the appropriate randomness element position.

4. Experimental Results and Discussion

A fabricated prototype of 3-bit coding metasurface with the total size is 264 mm × 264 mm, containing 66 × 66 units, is shown in Figure 16a. The arrangement orders and rotation angles of the eight basic units are all random. The experiment is carried out in a microwave anechoic chamber. As shown in the experimental setup in Figure 16b, two identical horn antennas, one for transmitter and the other one for receiver, are used in measurement. The antennas and the sample are put in the same horizontal position, and enough distance is ensured to avoid the near field effect. A slight angle (less than 5°) between the two antennas is maintained to guarantee the normal transmitting and receiving. Besides, two pairs of horn antennas, whose frequency band are 18–26.5 GHz and 26.5–40 GHz, are used to cover the wide frequency band in the experiment. The antennas are connected with a vector network analyzer Agilent N5245A, and the function of time-domain gating is employed to remove delayed reflected waves. When rotated by 90°, the horn antennas can be reconfigured between transverse-magnetic (TM) and transverse-electric (TE) modes, so that both the co- and cross-polarized reflection coefficients r_xx and r_xy can be measured. In the case of normal incidence, the transmitting and receiving horn antennas are placed adjacently. Both the transmitting and receiving horn antennas can move along the circumference trace to obtain the scattering at different incident angles.

Comparisons of RCS between the proposed metasurface and a bare metal plate of the same sizes are shown in Figure 17. Compared with the bare metal plate of the same size, the proposed random 3-bit coding PCM can realize RCS reduction over 10 dB in an UWB ranging from 18.3–42.2 GHz. The comparison of RCS reduction measured by simulation and experiment are shown in Figure 18. The experimental results are in basically agreement with the simulation results, and a slight disparity between them can be explained by the uncertainty in the measure environment. In addition, the fluctuations which maybe attributed to: (1) an ideal plane wave is used in simulation while the plane wave used in the experiment is generated by the far-field radiation of the horn antennas; (2) the limited dynamic range of the vector network analyzer (VNA) at high frequencies and others.

A comparison between the proposed converter and other polarization converters reported in References [23], [28] and [29] is shown in

Table 1. Comparison with the present state-of-the-art for polarization conversion metasurface (PCM).

	OB (GHz)	RB (%)	d (mm)	p (mm)
Ref. [29]	10.6–17	49	3	10
Ref. [28]	12.4–27.96	77	1.6	6.4
Ref. [26]	6.3–20.1	95.7	1.5	10
Present study	14.4–48.5	108.4	1.5	4

p: unit periodicity of the polarization converter; t: dielectric substrate thickness of the polarization converter; OB: operating bandwidth (PCR > 90%); RB: relative bandwidth (PCR > 90%).

. The comparison shows that the proposed converter is ultra-thin and has an ultra-wide frequency band in which PCR is greater than 90%, implying good performance. Therefore, the reduction of UWB RCS is more advantageous.

5. Conclusions

In this paper, a 3-bit random coding PCM with the capability of reducing RCS in UWB has been designed, fabricated and measured. The proposed structure consists of eight basic elements with different geometric parameters and rotation angles. The UWB RCS reduction performance of the proposed metasurface is attributed to the UWB linear polarization conversion characteristics and the flexible phase modulation capability of the designed unit. Moreover, the features of polarization independence and beam divergence are achieved by the random coding and random rotation angle. Both simulation and experiment results demonstrate that the designed metasurface can achieve RCS reduction in an UWB. In addition, the effect of RCS reduction with respect to the unit period length and the unit position are also discussed. Compared with the previous studies, the proposed 3-bit random coding PCM has the advantages of ultra-wide bandwidth, polarization independence, and simple element structure, which makes it a good candidate for electromagnetic cloaking.