An Improved UAV-PHD Filter-Based Trajectory Tracking Algorithm for Multi-UAVs in Future 5G IoT Scenarios
Abstract
:1. Introduction
2. System Model
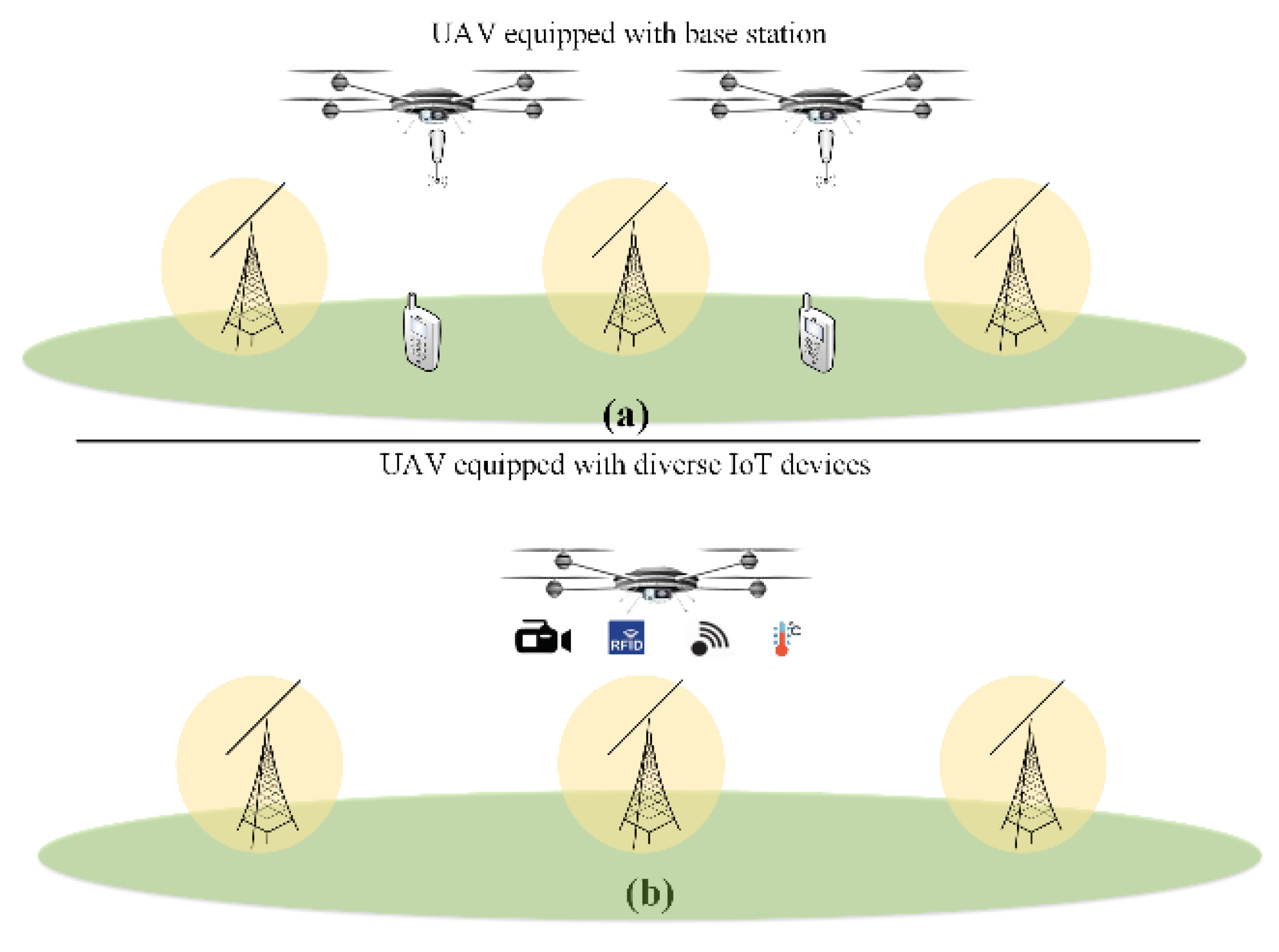
2.1. UAVs in a 5G-IoT Scenario
2.2. Target Tracking
2.2.1. Target Tracking Background
2.2.2. Traditional GM-PHD filter
3. Multitarget Tracking Algorithm for UAVs Based on Improved GM-PHD Filter
3.1. Proposed UAV-PHD Filter
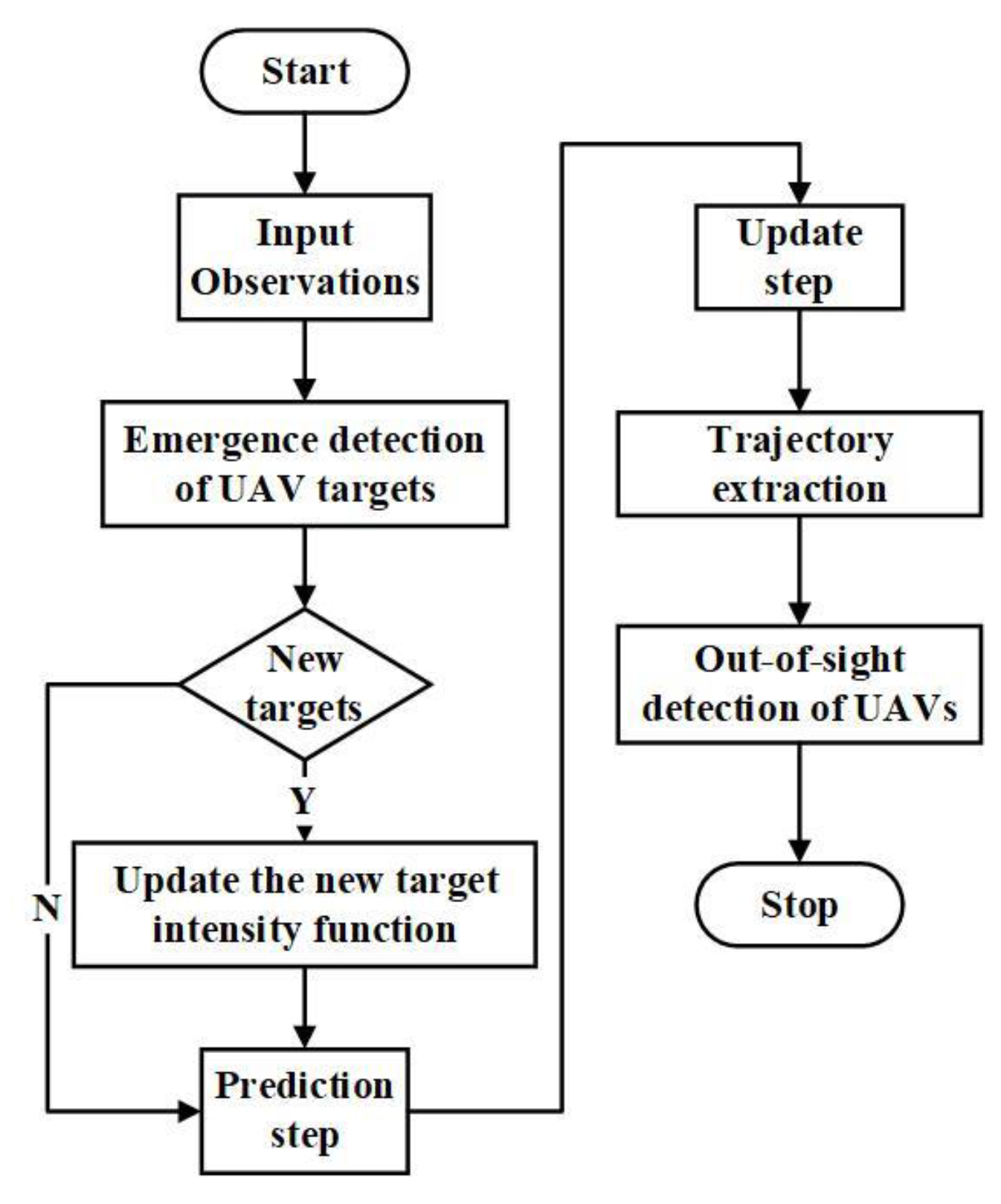
3.2. Steps for Trajectory Tracking of Multiple UAV Targets
3.2.1. Emergence Detection of UAV Targets
- It is assumed that the observation sets at times k, k − 1, and k − 2 are Mk, Mk−1, and Mk−2, respectively, and represent the i-th observation generated at time k, with N observations at this time. In the two-dimensional scene, the observed value r = (x, y) represents the two-dimensional coordinates of a certain position.
- The nearest point pairs are located if the following conditions are met:In this work, is considered as a set of candidate occurrence and is taken as the location of the target. Subscript T is the radar scan period and are the minimum speed, maximum speed, and maximum acceleration of the UAV targets, respectively, which can be obtained from prior knowledge.
- The new target intensity function is calculated and updated.
3.2.2. Trajectory Extraction of UAV Targets
- Input the existing trajectory set at time k-1 and the k time filter result set , where , .
- Cluster centers are set and the k time track set is initialized.
- The Euclidean distance of the filtered values and , are determined respectively, and recorded as . The nearest value of the distance is obtained and recorded as .
- The sample is divided into the corresponding cluster: .
- The above steps are repeated until all the values in have been iterated.
- Steps 2–5 are repeated until the algorithm results converge.
- If , the current target has no observations, and the algorithm calculates the estimated value based on the first two frames of data.
- If , the unclassified value is used as the starting point for the new track.
- Output: The updated tracks set
3.2.3. Out-of-Sight Detection of UAV
- Using the algorithm proposed in the previous section, the track set is input at time k, and the matrix is used to represent the state of N targets. The initial state of S is entirely 0 matrix.
- If , the estimated value is calculated based on the first two frames of data: , and is set to record the disappearance of the target at this time frame.
- The above steps are repeated to iterate through all the data.
- If , it indicates that the i-th target has been missed three times in a row, and the target can be judged as out of sight.
- Set . The targets in the trajectory that are far away from the radar monitoring range are thus eliminated, and the updated trajectory set E is output.
4. Simulation Results
4.1. Model and Parameter Settings
4.1.1. Proposed UAV Dynamic System Model
4.1.2. Tracking Performance Evaluation Indicators
4.2. Experiment Results
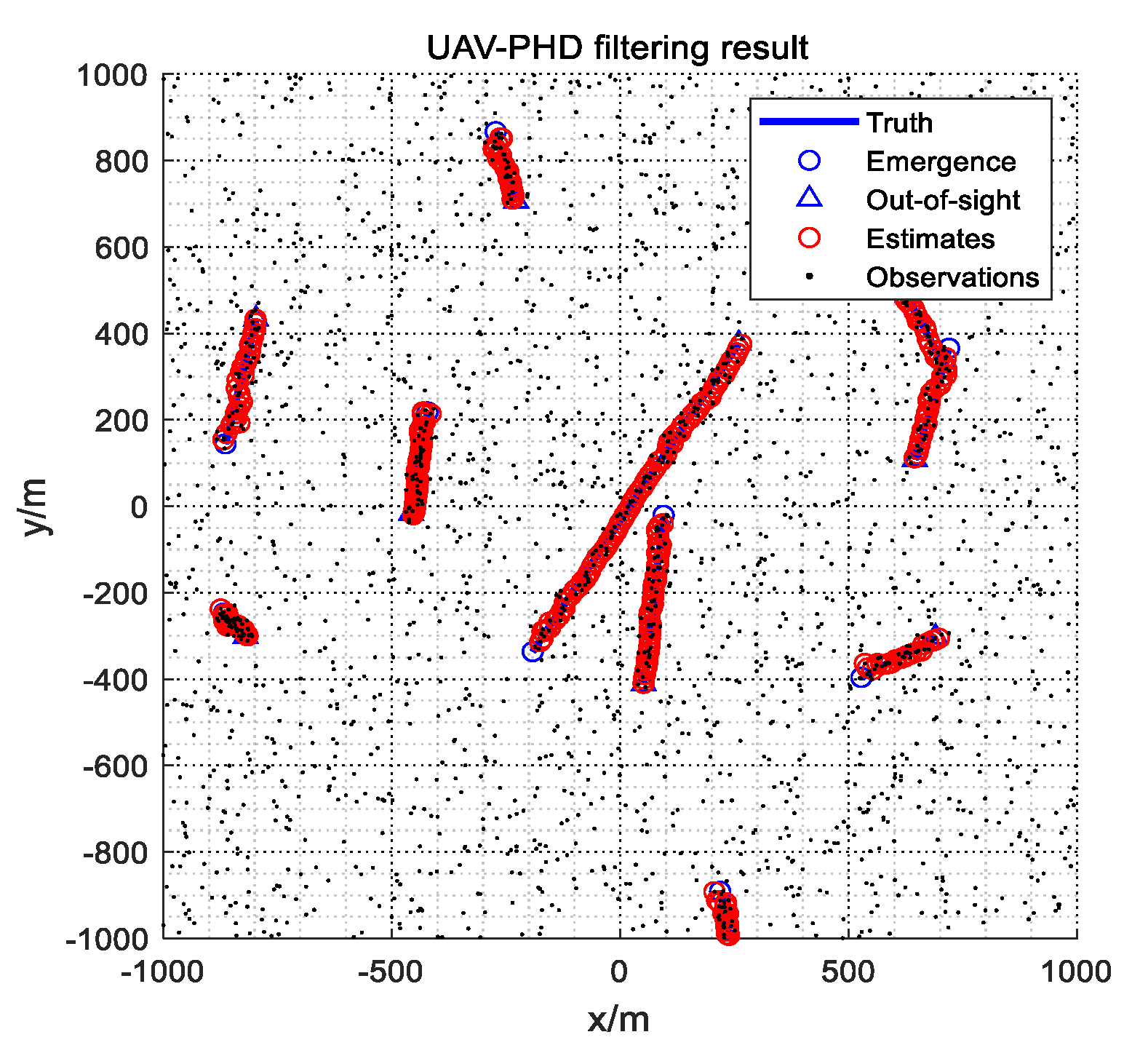
4.2.1. UAV-PHD Filter Simulation
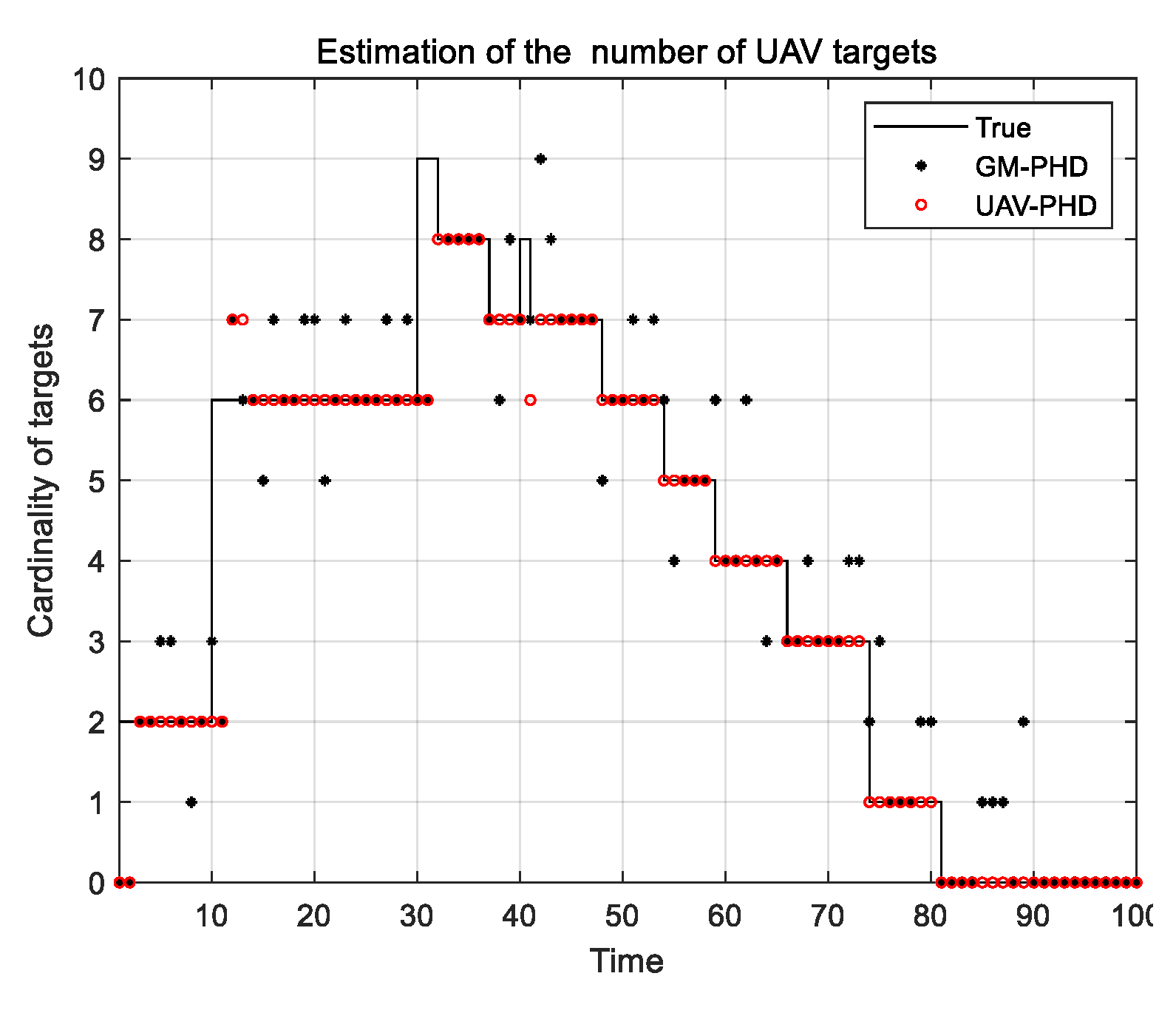
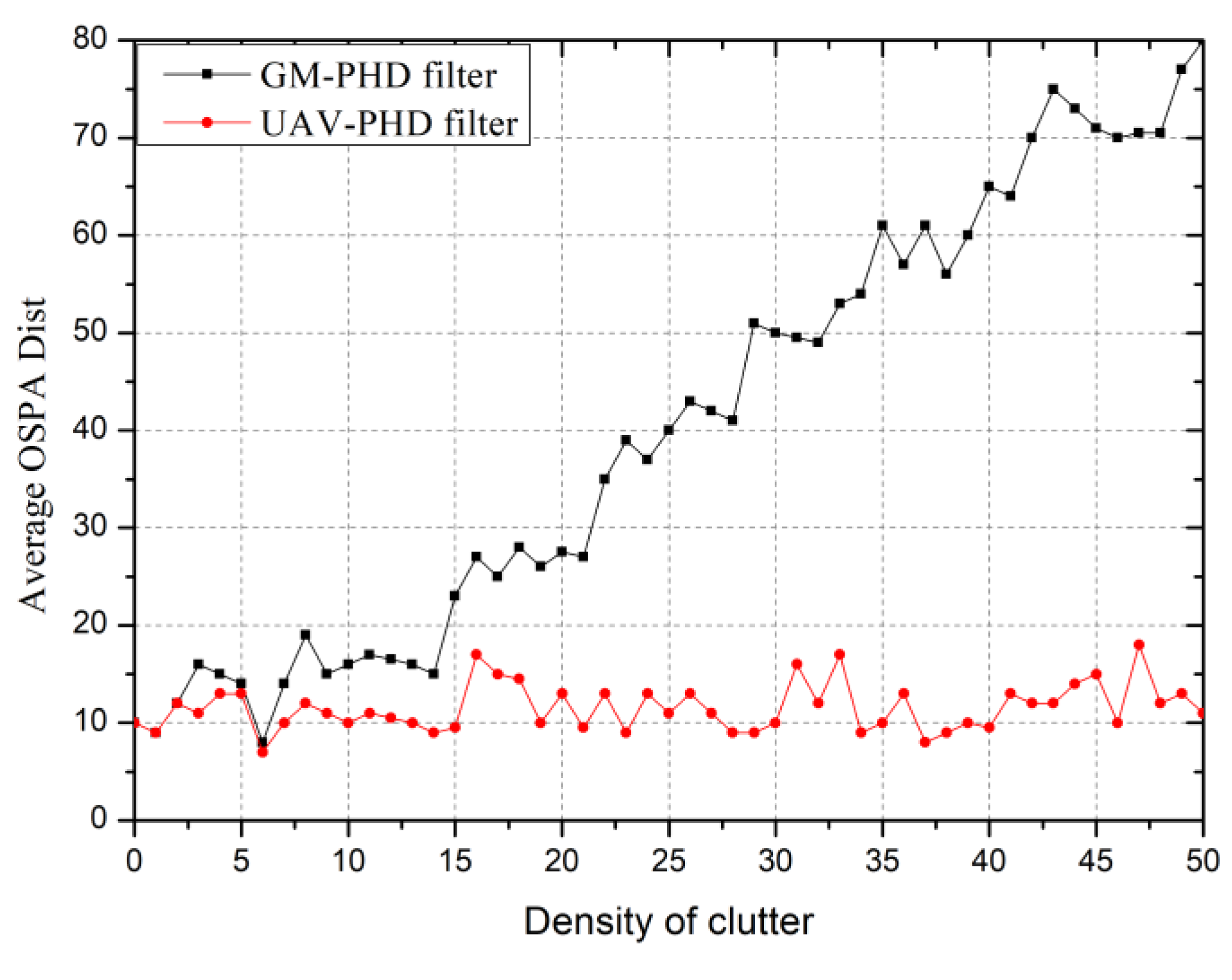
4.2.2. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wollschlaeger, M.; Sauter, T.; Jasperneite, J. The future of industrial communication: Automation networks in the Era of the internet of things and industry 4.0. IEEE Ind. Electron. Mag. 2017, 11, 17–27. [Google Scholar] [CrossRef]
- Al-Falahy, N.; Alani, O.Y. Technologies for 5G networks: Challenges and opportunities. IT Prof. 2017, 19, 12–20. [Google Scholar] [CrossRef]
- Dhillon, H.S.; Huang, H.; Viswanathan, H. Wide-area wireless communication challenges for the internet of things. IEEE Commun. Mag. 2017, 55, 168–174. [Google Scholar] [CrossRef]
- Ni, J.; Lin, X.; Shen, X.S. Efficient and secure service-oriented authentication supporting network slicing for 5G-enabled IoT. IEEE J. Sel. Areas Commun. 2018, 36, 644–657. [Google Scholar] [CrossRef]
- Wang, D.; Chen, D.; Song, B.; Guizani, N.; Yu, X.; Du, X. From IoT to 5G I-IoT: The next generation IoT-based intelligent algorithms and 5G technologies. IEEE Commun. Mag. 2018, 56, 114–120. [Google Scholar] [CrossRef]
- Khurpade, J.M.; Rao, D.; Sanghavi, P.D. A survey on IOT and 5G network. In Proceedings of the 2018 International Conference on Smart City and Emerging Technology (ICSCET 2018), Mumbai, India, 5 January 2018; pp. 1–3. [Google Scholar]
- Moongilan, D. 5G Internet of Things (IOT) near and far-fields and regulatory compliance intricacies. In Proceedings of the 2019 IEEE 5th World Forum on Internet of Things (WF-IoT), Limerick, Ireland, 15–18 April 2019; pp. 894–898. [Google Scholar]
- Balevi, E.; Gitlin, R.D. A random access scheme for large scale 5G/IoT applications. In Proceedings of the 2018 IEEE 5G World Forum (5GWF), Silicon Valley, CA, USA, 9–11 July 2018; pp. 452–456. [Google Scholar]
- Dutkiewicz, E.; Jayawickrama, B.A.; He, Y. Radio spectrum maps for emerging IoT and 5G networks: Applications to smart buildings. In Proceedings of the 2017 International Conference on Electrical Engineering and Computer Science (ICECOS), Palembang, Indonesia, 22–23 August 2017; pp. 7–9. [Google Scholar]
- Hwang, Y.; Shin, J. A study on management of access in industry IoT based 5G new radio standalone system. In Proceedings of the 2018 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Korea, 17–19 October 2018; pp. 883–885. [Google Scholar]
- Rahimi, H.; Zibaeenejad, A.; Safavi, A.A. A novel IoT architecture based on 5G-IoT and next generation technologies. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 Novmber 2018; pp. 81–88. [Google Scholar]
- Hellaoui, H.; Bekkouche, O.; Bagaa, M.; Taleb, T. Aerial control system for spectrum efficiency in UAV-to-cellular communications. IEEE Commun. Mag. 2018, 56, 108–113. [Google Scholar] [CrossRef]
- Motlagh, N.H.; Bagaa, M.; Taleb, T. UAV-based IoT platform: A crowd surveillance use case. IEEE Commun. Mag. 2017, 55, 128–134. [Google Scholar] [CrossRef]
- Yuan, Z.; Jin, J.; Sun, L.; Chin, K.; Muntean, G. Ultra-reliable IoT communications with UAVs: A swarm use case. IEEE Commun. Mag. 2018, 56, 90–96. [Google Scholar] [CrossRef]
- Beard, M.; Reuter, S.; Granström, K.; Vo, B.T.; Vo, B.N.; Scheel, A. Multiple extended target tracking with labeled random finite sets. IEEE Trans. Signal Process. 2016, 64, 1638–1653. [Google Scholar] [CrossRef]
- Kamal, A.T.; Bappy, J.H.; Farrell, J.A.; Roy-Chowdhury, A.K. Distributed multitarget tracking and data association in vision networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1397–1410. [Google Scholar] [CrossRef] [PubMed]
- Mahler, R.P.S. Multitarget bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electr. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Vo, B.; Ma, W. The gaussian mixture probability hypothesis density filter. IEEE Trans. Signal Process. 2006, 54, 4091–4104. [Google Scholar] [CrossRef]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electr. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Mahler, R. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007. [Google Scholar]
- Yazdian-Dehkordi, M.; Azimifar, Z. An improvement on GM-PHD filter for target tracking in presence of subsequent miss-detection. In Proceedings of the Iranian Conference on Electrical Engineering, Tehran, Iran, 10–14 May 2015; pp. 765–769. [Google Scholar]
- Fu, Z.; Naqvi, S.M.; Chambers, J. Enhanced GM-PHD filter using cnn-based weight penalization for multitarget tracking. In Proceedings of the Sensor Signal Processing for Defence Conference (SSPD 2017), London, UK, 6–7 December 2017; pp. 1–5. [Google Scholar]
- Santana, G.M.D.; Cristo, R.S.; Dezan, C.; Diguet, J.; Osorio, D.P.M.; Branco, K.R.L.J.C. Cognitive Radio for UAV communications: Opportunities and future challenges. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 760–768. [Google Scholar]
- Motlagh, N.H.; Bagaa, M.; Taleb, T. UAV Selection for a UAV-Based Integrative IoT Platform. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Ebrahimi, D.; Sharafeddine, S.; Ho, P.; Assi, C. UAV-aided projection-based compressive data gathering in wireless sensor networks. IEEE Internet Things J. 2019, 6, 1893–1905. [Google Scholar] [CrossRef]
- Motlagh, N.H.; Taleb, T.; Arouk, O. Low-altitude unmanned aerial vehicles-based internet of things services: Comprehensive survey and future perspectives. IEEE Internet Things J. 2016, 3, 899–922. [Google Scholar] [CrossRef]
- Zhao, J.; Fu, X.; Yang, Z.; Xu, F. Radar-assisted uav detection and identification based on 5g in the internet of things. Wirel. Commun. Mob. Comput. 2019, 2019, 12. [Google Scholar] [CrossRef]
- Oriuchi, M. Multitarget tracking based on features of sensing results and wireless parameters for physical wireless parameter conversion sensor networks. In Proceedings of the 2016 IEEE Radio and Wireless Symposium (RWS), Austin, TX, USA, 24–27 January 2016; pp. 230–233. [Google Scholar]
- Baser, E.; Kirubarajan, T.; Efe, M.; Balaji, B. Improved multitarget multi—Bernoulli filter with modelling of spurious targets. IET Radar Sonar Navig. 2016, 10, 285–298. [Google Scholar] [CrossRef]
- Li, G.; Yi, W.; Jiang, M.; Kong, L. Distributed fusion with PHD filter for multitarget tracking in asynchronous radar system. In Proceedings of the 2017 IEEE Radar Conference (RC), Seattle, WA, USA, 8–12 May 2017; pp. 1434–1439. [Google Scholar]
- Khalil, M. An improved approach for multitarget detection and tracking in automotive radar systems. In Proceedings of the 2016 International Conference on Electromagnetics in Advanced Applications (ICEAA), Cairns, Australian, 19–23 September 2016; pp. 480–483. [Google Scholar]
- Fu, Z.; Angelini, F.; Chambers, J.; Naqvi, S.M. Multi-level cooperative fusion of gm-phd filters for online multiple human tracking. IEEE Trans. Multimed. 2019, 21, 2277–2291. [Google Scholar] [CrossRef]
- Song, Y.; Jeon, M. Online multiple object tracking with the hierarchically adopted GM-PHD filter using motion and appearance. In Proceedings of the 2016 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia), Seoul, Korea, 26–28 October 2016; pp. 1–4. [Google Scholar]
- Qu, C.; Feng, Q.; Li, T.; Zhou, Q. Passive multitarget tracking with the marginalized Kalman GM-PHD filter. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 December 2017; pp. 167–172. [Google Scholar]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, T.; Hong, T.; Hong, H.; Ji, S.; Mumtaz, S.; Cheriet, M. An Improved UAV-PHD Filter-Based Trajectory Tracking Algorithm for Multi-UAVs in Future 5G IoT Scenarios. Electronics 2019, 8, 1188. https://doi.org/10.3390/electronics8101188
Tang T, Hong T, Hong H, Ji S, Mumtaz S, Cheriet M. An Improved UAV-PHD Filter-Based Trajectory Tracking Algorithm for Multi-UAVs in Future 5G IoT Scenarios. Electronics. 2019; 8(10):1188. https://doi.org/10.3390/electronics8101188
Chicago/Turabian StyleTang, Tao, Tao Hong, Haohui Hong, Senyuan Ji, Shahid Mumtaz, and Mohamed Cheriet. 2019. "An Improved UAV-PHD Filter-Based Trajectory Tracking Algorithm for Multi-UAVs in Future 5G IoT Scenarios" Electronics 8, no. 10: 1188. https://doi.org/10.3390/electronics8101188
APA StyleTang, T., Hong, T., Hong, H., Ji, S., Mumtaz, S., & Cheriet, M. (2019). An Improved UAV-PHD Filter-Based Trajectory Tracking Algorithm for Multi-UAVs in Future 5G IoT Scenarios. Electronics, 8(10), 1188. https://doi.org/10.3390/electronics8101188





