A Smart Overvoltage Monitoring and Hierarchical Pattern Recognizing System for Power Grid with HTS Cables
Abstract
:1. Introduction
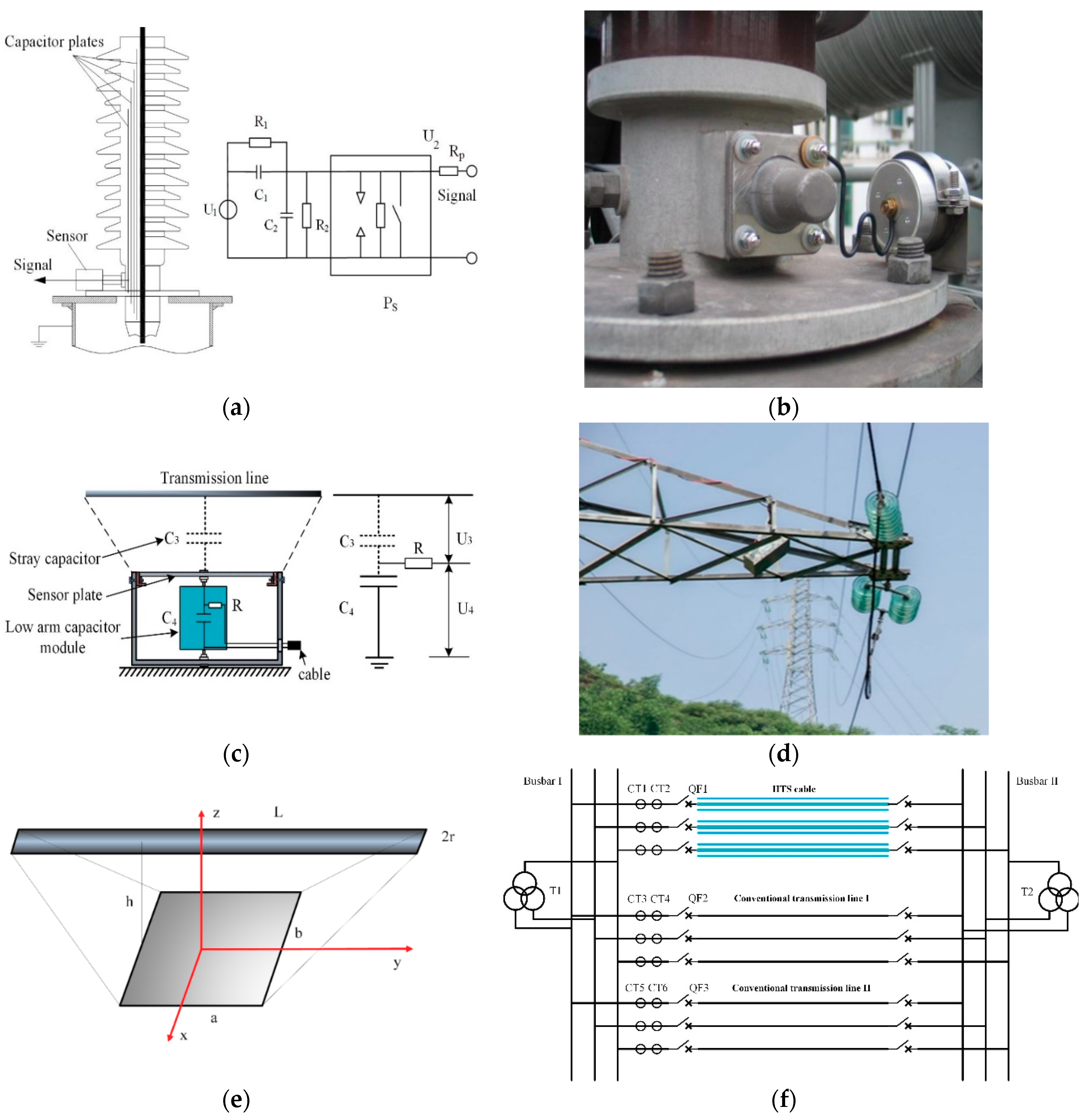
2. Non-Contact Overvoltage Monitoring System
2.1. Overvoltage Sensor
2.1.1. Non-Contact Transformer Bushing Tap Sensor
2.1.2. Non-Contact Transmission Line Sensor
2.2. The Online Variable Sampling Frequency Monitoring System
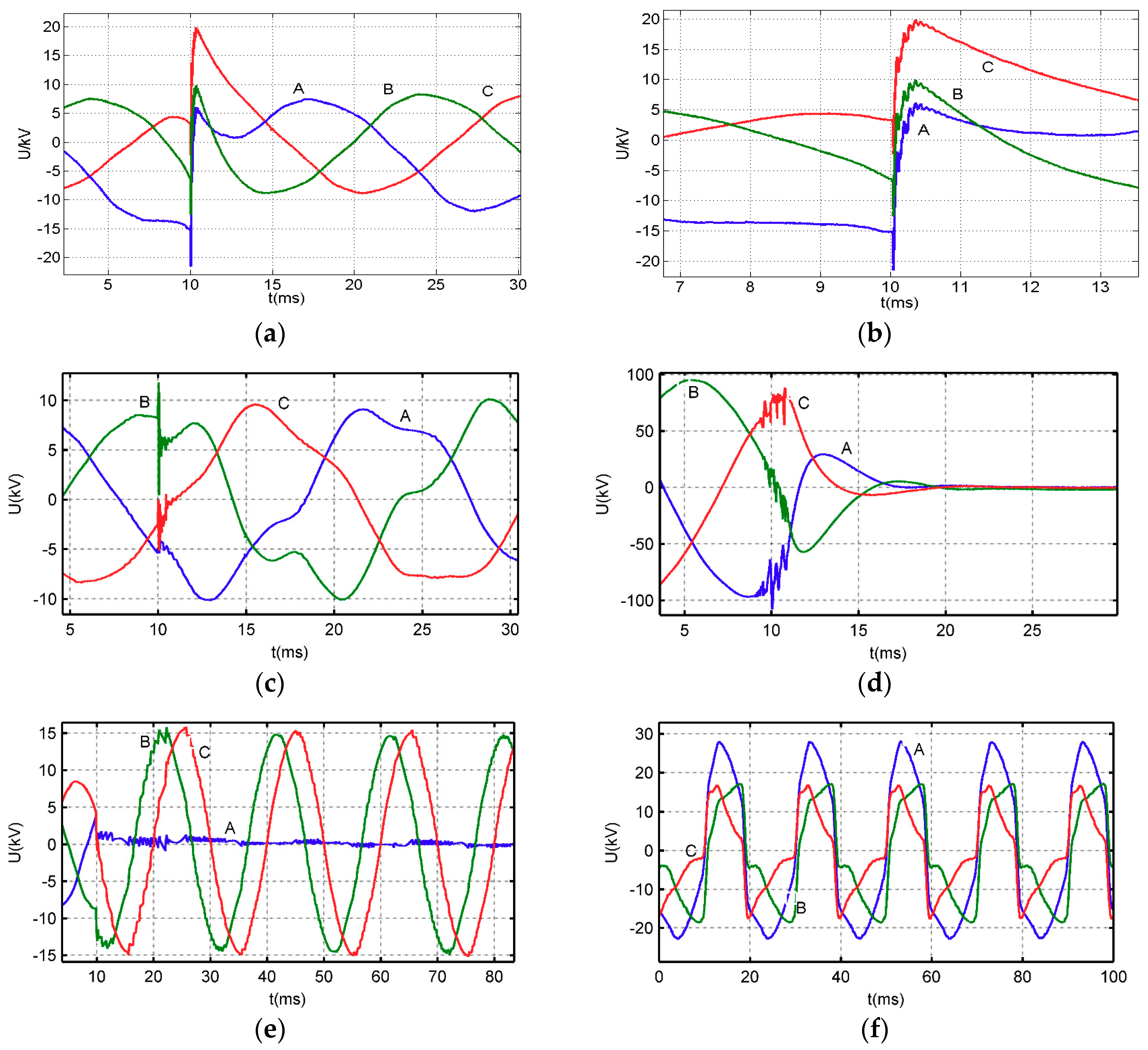
2.3. Typical Field-Captured Overvoltage Waveform
3. Feature Extraction for Overvoltage Records
3.1. Wavelet Feature Extraction
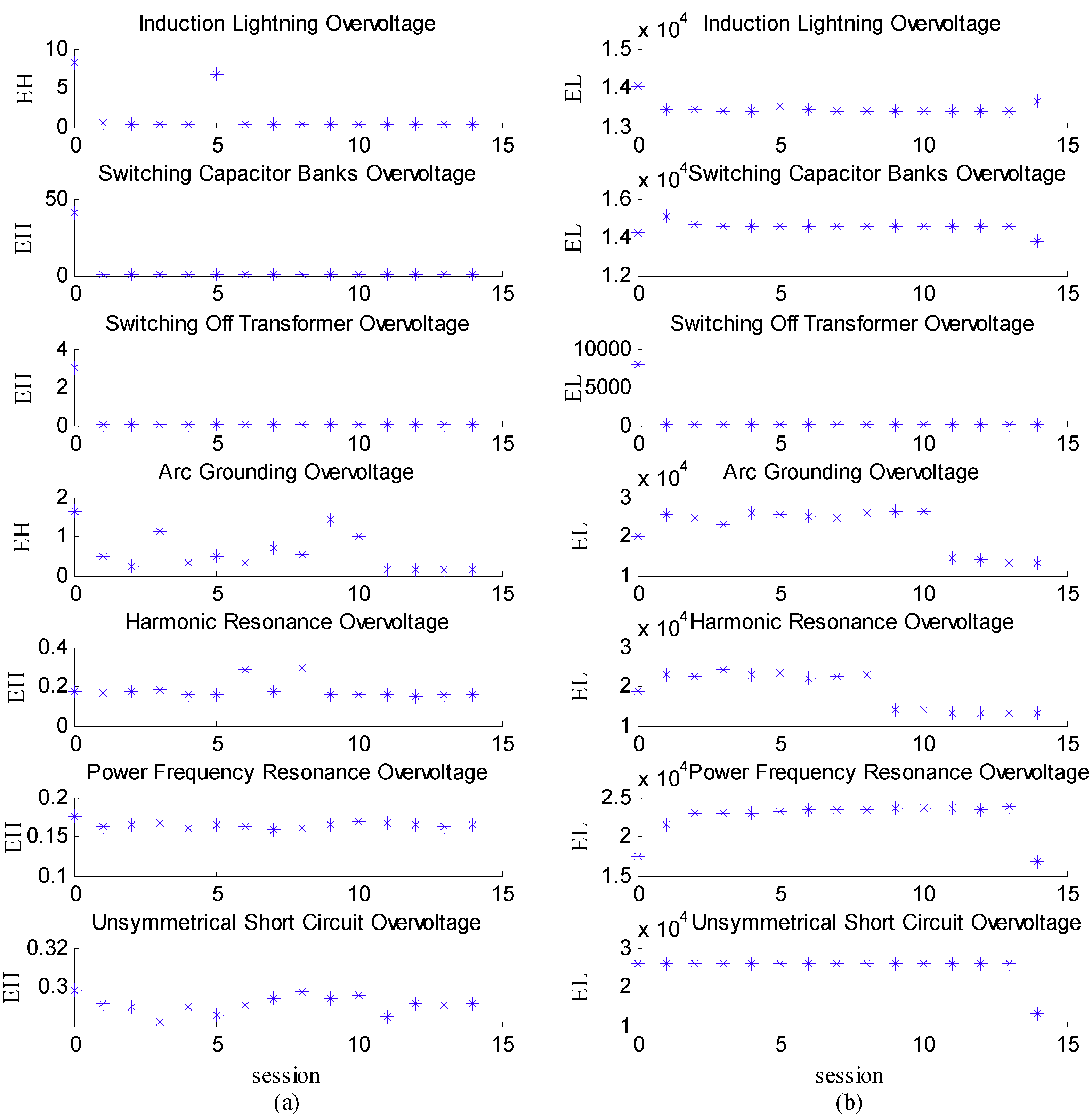
3.2. S-Transform SVD Feature Extraction
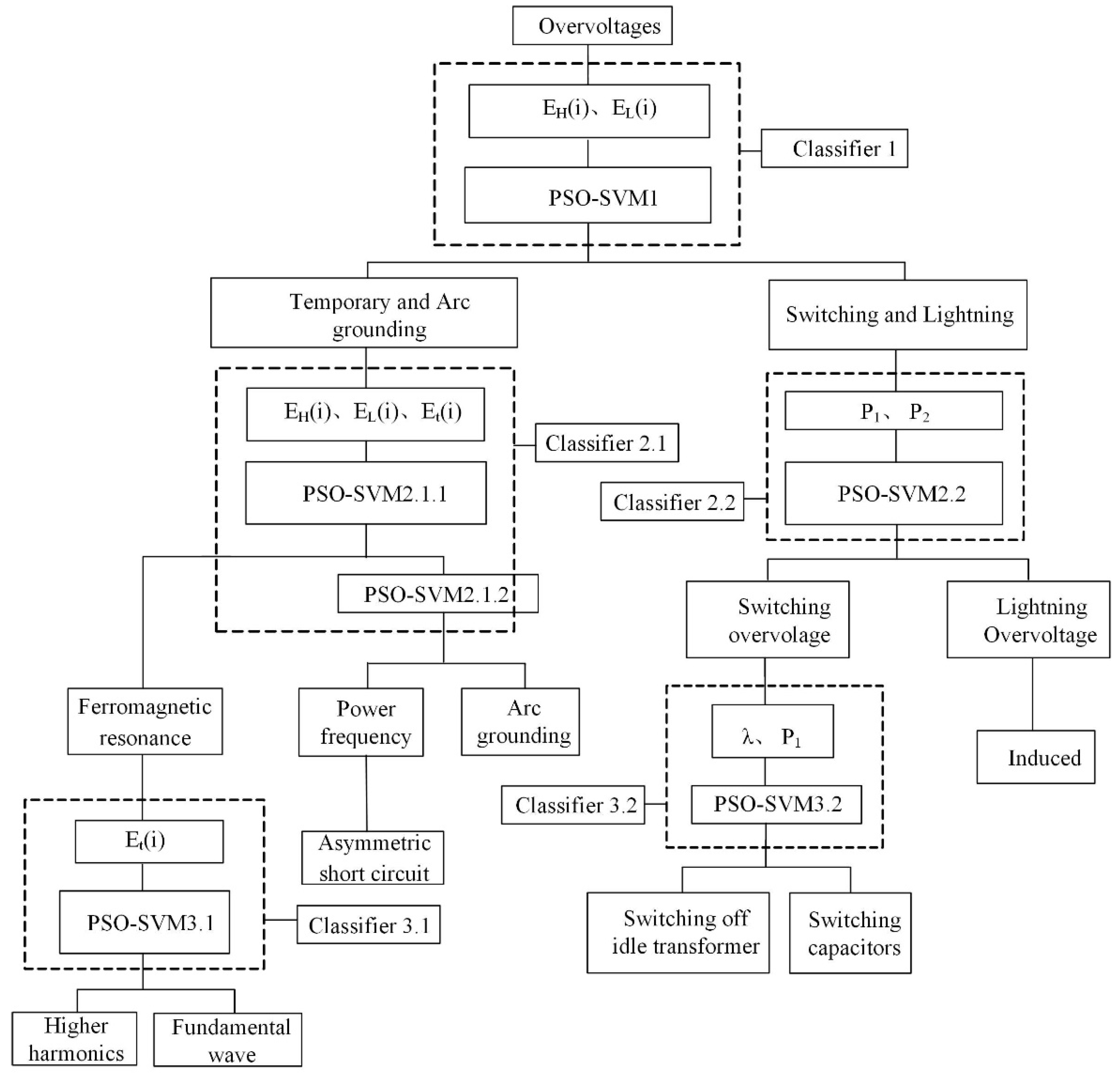
4. PSO-SVM Overvoltage Recognition Algorithm
4.1. Particle Swarm Optimization
4.2. PSO-SVM Classifier
- (1)
- The initial value of the PSO algorithm is set, and a random set of particles is produced {,}.
- (2)
- The training samples are divided into different training groups mi.
- (3)
- is used as the training sample, and other samples are used as testing sets. Then, the recognition rate of the sample set is calculated.
- (4)
- The suitable value f of the SVM parameters is calculated by using the following equation:
- (5)
- The values of velocity and the particles are renewed iteratively according to the suitable value f.
- (6)
- Whether the current values of the particles are the best values for the SVM parameters is determined. If not, Step (3) is repeated, or the final value set of SVM is output.
4.3. Recognition Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weiss, J.D.; Mulder, T.; ten Kate, H.J.; van der Laan, D.C. Introduction of CORC (R) wires: Highly flexible, round high-temperature superconducting wires for magnet and power transmission applications. Supercond. Sci. Technol. 2017, 30, 1. [Google Scholar] [CrossRef]
- Laan, D.C.v.d.; Weiss, J.D.; Kim, C.H.; Graber, L.; Pamidi, S. Development of CORC ® cables for helium gas cooled power transmission and fault current limiting applications. Supercond. Sci. Technol. 2018, 31, 085011. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, M.; Grilli, F.; Zhu, Z.; Yuan, W. Study of the magnetization loss of CORC ® cables using a 3D T-A formulation. Supercond. Sci. Technol. 2019, 32, 025003. [Google Scholar] [CrossRef]
- Laan, D.C.v.d.; Lu, X.F.; Goodrich, L.F. Compact GdBa2Cu3O7–δ coated conductor cables for electric power transmission and magnet applications. Supercond. Sci. Technol. 2011, 24, 042001. [Google Scholar] [CrossRef]
- van der Laan, D.C.; McRae, D.M.; Weiss, J.D. Effect of monotonic and cyclic axial tensile stress on the performance of superconducting CORC® wires. Supercond. Sci. Technol. 2019, 32, 054004. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, J.; Zhu, Z.; Zhang, M.; Yuan, W. Quench behavior of high-temperature superconductor (RE)Ba2Cu3Ox CORC cable. J. Phys. D: Appl. Phys. 2019, 52, 345303. [Google Scholar] [CrossRef]
- Malewski, R.; Douville, J.; Lavallee, L. Measurement of switching transients in 735 kV substations and assessment of their severity for transformer insulation. IEEE Trans. Power Deliv. 1988, 3, 1380–1390. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, J.; Chen, L.; Sima, W.X.; Xie, B. Identification Method of Back Flash Overvoltage and Shielding Failure of Transmission Lines Considering the Effect of Impulse Corona. High Volt. Eng. 2011, 37, 1149–1157. [Google Scholar]
- Sima, W.X.; Xie, B.; Yang, Q.; Wang, J. Identification of Lightning Over-voltage about UHV Transmission Line. High Volt. Eng. 2010, 36, 306–312. [Google Scholar]
- Mokryani, G.; Haghifam, M.R.; Esmaeilpoor, J. Identification of ferroresonance based on wavelet transform and artificial neural network. Eur. Trans. Electr. Power 2009, 19, 474–486. [Google Scholar] [CrossRef]
- Mokryani, G.; Siano, P.; Piccolo, A. Identification of ferroresonance based on S-transform and support vector machine. Simul. Model. Pract. Theory 2010, 18, 1412–1424. [Google Scholar] [CrossRef]
- Long, Y.; Yao, C.; Mi, Y.; Hu, D.; Yang, N.; Liao, Y. Identification of direct lightning strike faults based on mahalanobis distance and S-transform. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2019–2030. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Q.; Sima, W.; Yuan, T.; Zahn, M. A Smart Online Over-Voltage Monitoring and Identification System. Energies 2011, 4, 599–615. [Google Scholar] [CrossRef] [Green Version]
- Jiang, K.; Du, L.; Chen, H.; Yang, F.; Wang, Y. Non-Contact Measurement and Polarity Discrimination-Based Identification Method for Direct Lightning Strokes. Energies 2019, 12, 263. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Du, L.; Li, J. Research on Characteristics of Noncontact Capacitive Voltage Divider Monitoring System Under AC and Lightning Overvoltages. IEEE Trans. Appl. Supercond. 2014, 24, 1203–1205. [Google Scholar]
- Chen, S.; Wang, H.; Du, L.; Li, J. Research on a New Type of Overvoltages Monitoring Sensor and Decoupling Technology. IEEE Trans. Appl. Supercond. 2014, 24, 1304–1307. [Google Scholar]
- Guo, M.; Wu, Z. Noise Reduction for High-Accuracy Automatic Calibration of Resolver Signals via DWT-SVD Based Filter. Electronics 2019, 8, 316. [Google Scholar] [CrossRef]
- Yin, Z.; Wang, L.; Zhang, Y.; Gao, Y. A Novel Arc Fault Detection Method Integrated Random Forest, Improved Multi-scale Permutation Entropy and Wavelet Packet Transform. Electronics 2019, 8, 396. [Google Scholar] [CrossRef]
- Chilukuri, M.V.; Dash, P.K. Multiresolution S-Transform-Based Fuzzy Recognition System for Power Quality Events. IEEE Trans. Power Deliv.. 2004, 19, 323–330. [Google Scholar] [CrossRef]
- Rodríguez, A.; Aguado, J.A.; Martín, F.; López, J.J.; Muñoz, F.; Ruiz, J.E. Rule-based classification of power quality disturbances using S-transform. Electr. Power Syst. Res. 2012, 86, 113–121. [Google Scholar] [CrossRef]
- Zang, B.; Zhu, M.; Zhou, X.; Zhong, L. Application of S-Transform in ISAR Imaging. Electronics 2019, 8, 676. [Google Scholar] [CrossRef]
- Biswal, M.; Dash, P.K. Estimation of time-varying power quality indices with an adaptive window-based fast generalised S-transform. IET Sci. Meas. Technol. 2012, 6, 189–197. [Google Scholar] [CrossRef]
- Jiang, J.; Wu, Y.; Wang, H.; Lv, Y.; Qiu, L.; Yu, D. Optimization Algorithm for Multiple Phases Sectionalized Modulation Jamming Based on Particle Swarm Optimization. Electronics 2019, 8, 160. [Google Scholar] [CrossRef]
- Huang, J.; Hu, X.; Geng, X. An intelligent fault diagnosis method of high voltage circuit breaker based on improved EMD energy entropy and multi-class support vector machine. Electr. Power Syst. Res. 2011, 81, 400–407. [Google Scholar] [CrossRef]
- Liu, L.; Wang, S.; Zhao, Z. Radar Waveform Recognition Based on Time-Frequency Analysis and Artificial Bee Colony-Support Vector Machine. Electronics 2018, 7, 59. [Google Scholar] [CrossRef]
- Ozgonenel, O.; Yalcin, T.; Guney, I.; Kurt, U. A new classification for power quality events in distribution systems. Electr. Power Syst. Res. 2013, 95, 192–199. [Google Scholar] [CrossRef]
- Chothani, N.G.; Parikh, U.B.; Bhalja, B.R. New support vector machine-based digital relaying scheme for discrimination between power swing and fault. IET Gener. Transm. Distrib. 2014, 8, 17–25. [Google Scholar] [CrossRef]






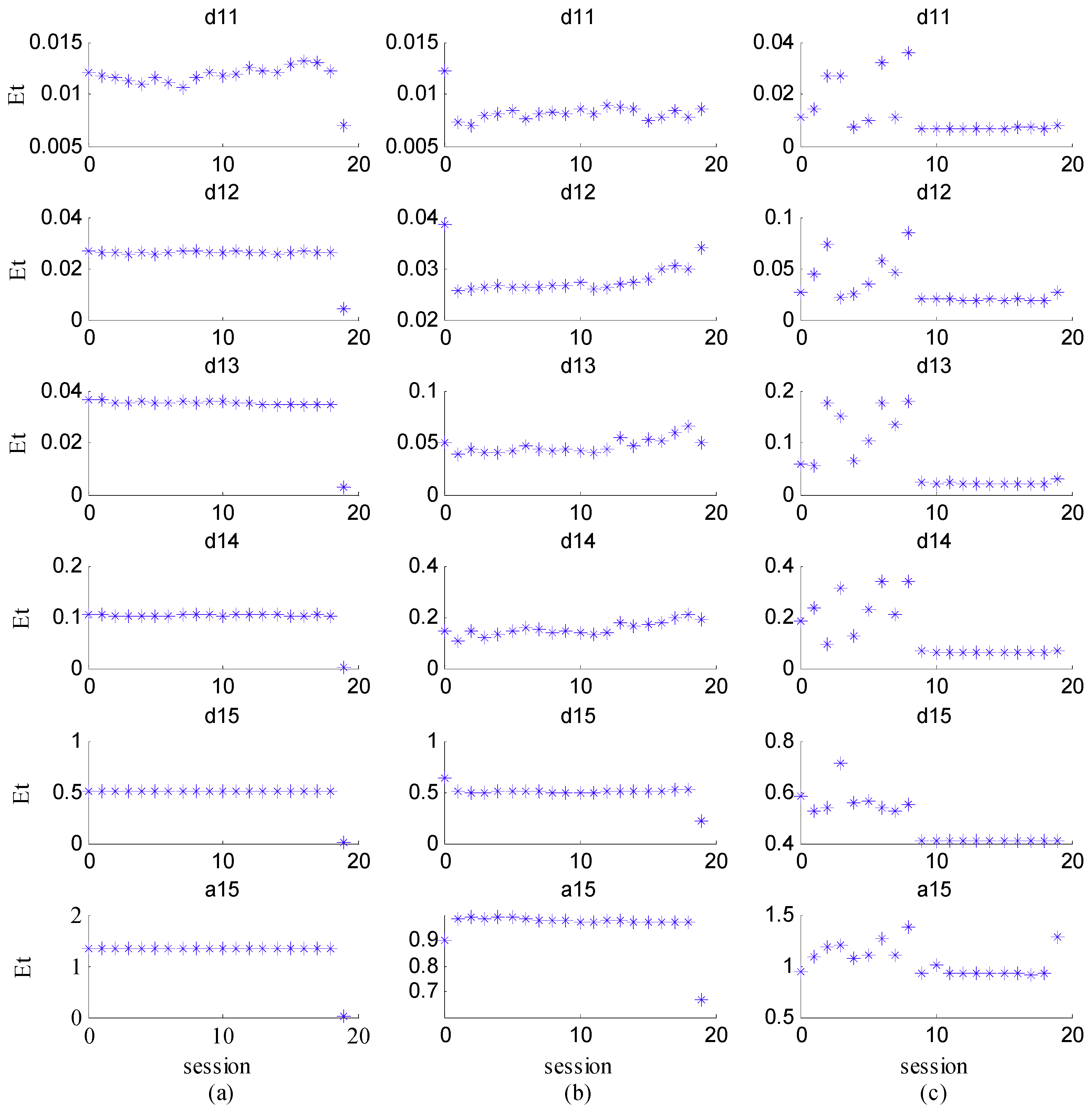
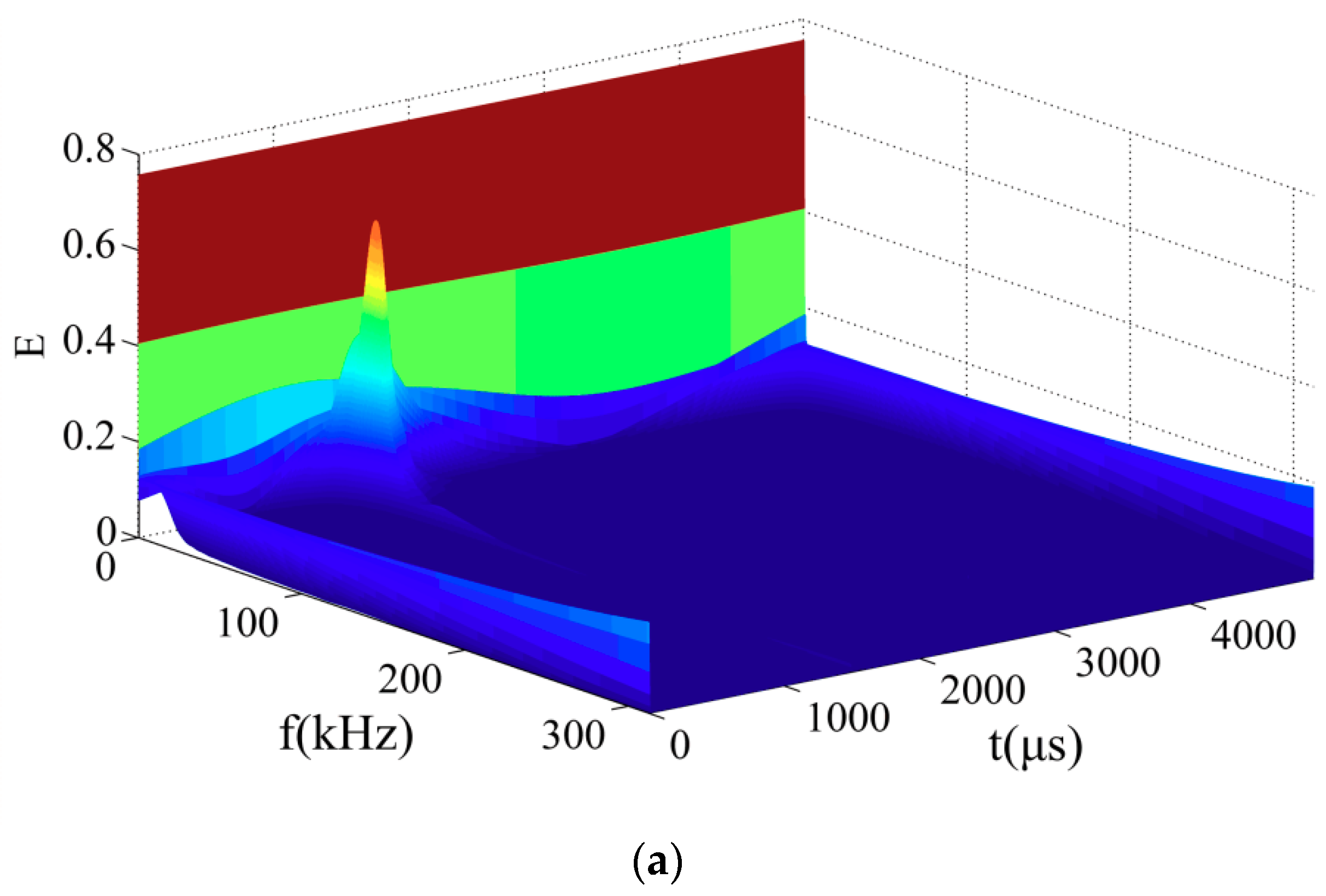
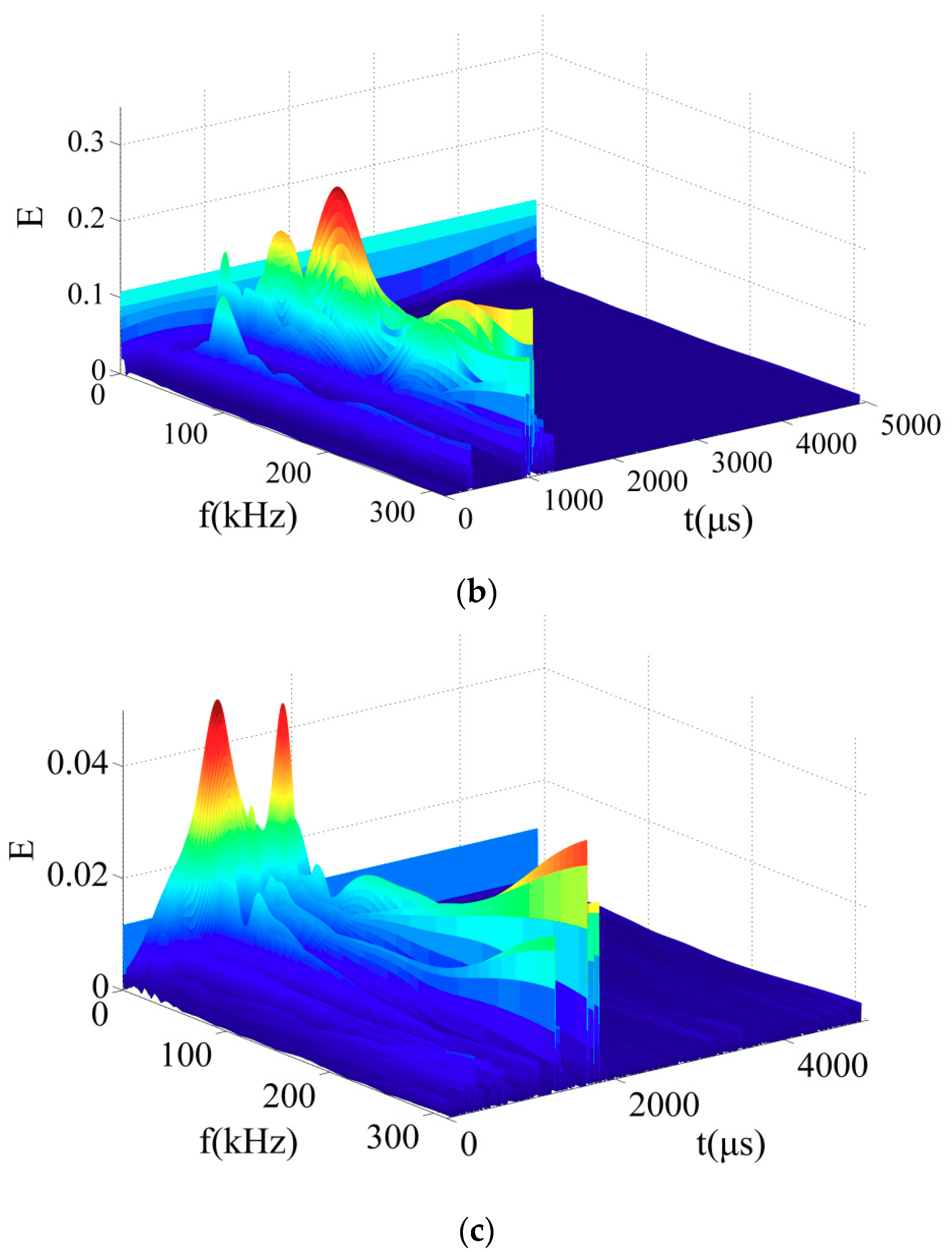
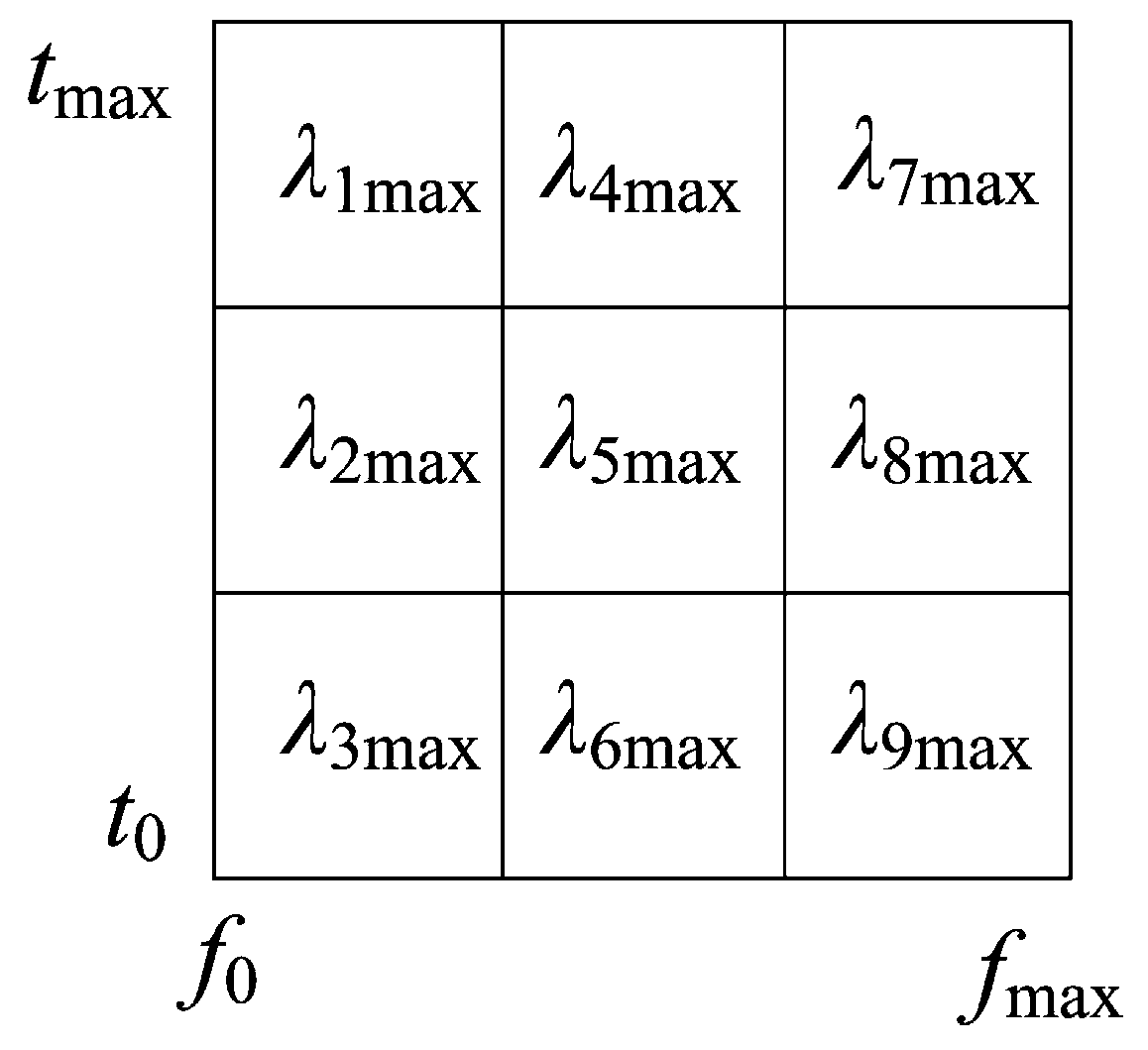

| Level | d1 | d2 | d3 | d4 |
| Frequency Band (kHz) | 1.25–2.5k | 625–1.25k | 312–625 | 156–312 |
| Level | d5 | d6 | d7 | d8 |
| Frequency Band (kHz) | 78–156 | 39–78 | 19.5–39 | 9.75–19.5 |
| Level | d9 | d10 | d11 | d12 |
| Frequency Band (kHz) | 4.875–9.75 | 2.44–4.875 | 1.22–2.44 | 0.61–1.22 |
| Level | d13 | d14 | d15 | a15 |
| Frequency Band (kHz) | 0.305–0.61 | 0.1525–0.305 | 0.07625–0.1525 | 0–0.07625 |
| Classifier | Feature Parameters |
|---|---|
| Classifier 1 | EH(i), EL(i) |
| Classifier 2.1 | EH(i), EL(i), Et(i) |
| Classifier 2.2 | P1, P2 |
| Classifier 3.1 | Et(i) |
| Classifier 3.2 | λ, P1 |
| Classifier | 1 | 2.1.1 | 2.1.2 | 2.2 | 3.1 | 3.2 |
|---|---|---|---|---|---|---|
| SVM | 95.6% | 90.1% | 92.8% | 89.4% | 87.6% | 85.7% |
| PSO-SVM | 97.4% | 92.6% | 96.3% | 93.8% | 91.5% | 94.2% |
| Overvoltage | PSO-SVM | SVM | BPAN |
|---|---|---|---|
| Switching-off idle transformer | 96.60% | 90.30% | 84.50% |
| Switching capacitors | 94.70% | 89.60% | 83.60% |
| Arc grounding | 92.80% | 88.50% | 82.80% |
| Asymmetric short circuit | 90.40% | 87.20% | 70.70% |
| High-frequency ferromagnetic resonance | 96.20% | 90.80% | 84.30% |
| Fundamental ferromagnetic resonance | 95.30% | 91.40% | 76.60% |
| Induced lightning | 100% | 92.70% | 82.50% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, K.; Du, L.; Wang, Y.; Li, J. A Smart Overvoltage Monitoring and Hierarchical Pattern Recognizing System for Power Grid with HTS Cables. Electronics 2019, 8, 1194. https://doi.org/10.3390/electronics8101194
Jiang K, Du L, Wang Y, Li J. A Smart Overvoltage Monitoring and Hierarchical Pattern Recognizing System for Power Grid with HTS Cables. Electronics. 2019; 8(10):1194. https://doi.org/10.3390/electronics8101194
Chicago/Turabian StyleJiang, Kaihua, Lin Du, Yubo Wang, and Jianwei Li. 2019. "A Smart Overvoltage Monitoring and Hierarchical Pattern Recognizing System for Power Grid with HTS Cables" Electronics 8, no. 10: 1194. https://doi.org/10.3390/electronics8101194
APA StyleJiang, K., Du, L., Wang, Y., & Li, J. (2019). A Smart Overvoltage Monitoring and Hierarchical Pattern Recognizing System for Power Grid with HTS Cables. Electronics, 8(10), 1194. https://doi.org/10.3390/electronics8101194





