Polynomial Cancellation Coded DFT-s-OFDM for Low-PAPR Uplink Signaling
Abstract
:1. Introduction
- Time-domain transform and the SS function of PCC-DFT-s-OFDM are proposed for the PAPR reduction. By using the designed parameter to perform different orders of PCC, a wide range of trade-offs between spectral efficiency and energy efficiency performance can be achieved.
- The computational complexity of PCC-mapped DFT precoding matrix is analyzed. Comparing most of significant PAPR reduction techniques, e.g., selected mapping (SLM) [24] and partial transmit sequence (PTS) [25], the PCC increases complexity negligibly (add a simple subtractor circuit only) based on DFT-s-OFDM, which has been widely used in the uplink for existing LTE/NR systems.
- A comprehensive numerical simulation of the PCC-DFT-s-OFDM transceiver for a single user and multiple users in terms of PAPR, power spectral density (PSD) and bit error rate (BER) performances are provided. It shows that the PAPR of DFT-s-OFDM signals can be significantly reduced using the proposed method, thereby enhancing the PSD and BER, particularly when PA nonlinearity and inter-user interference are considered.
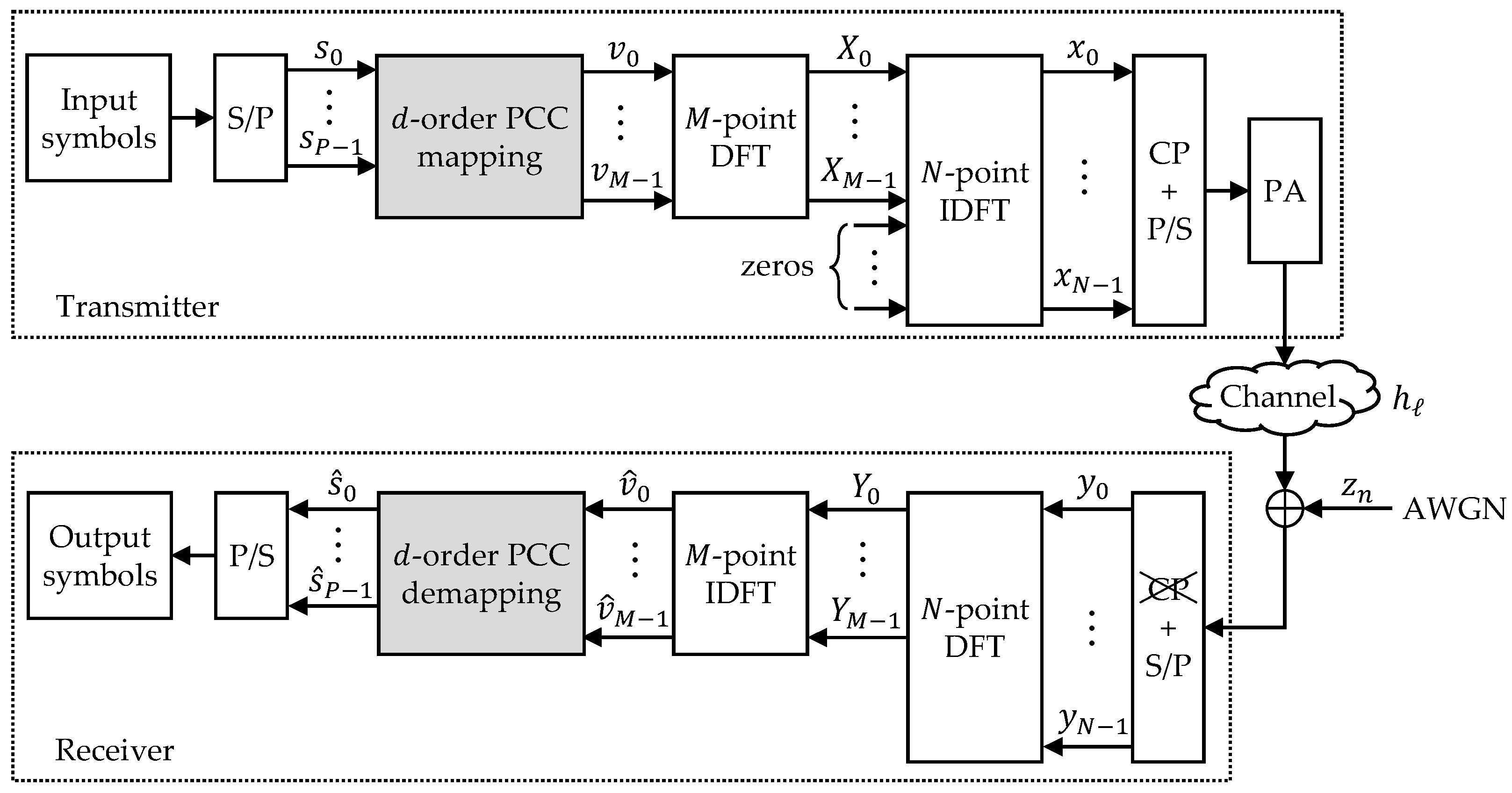
2. System Model
3. Analysis of PCC-DFT-s-OFDM
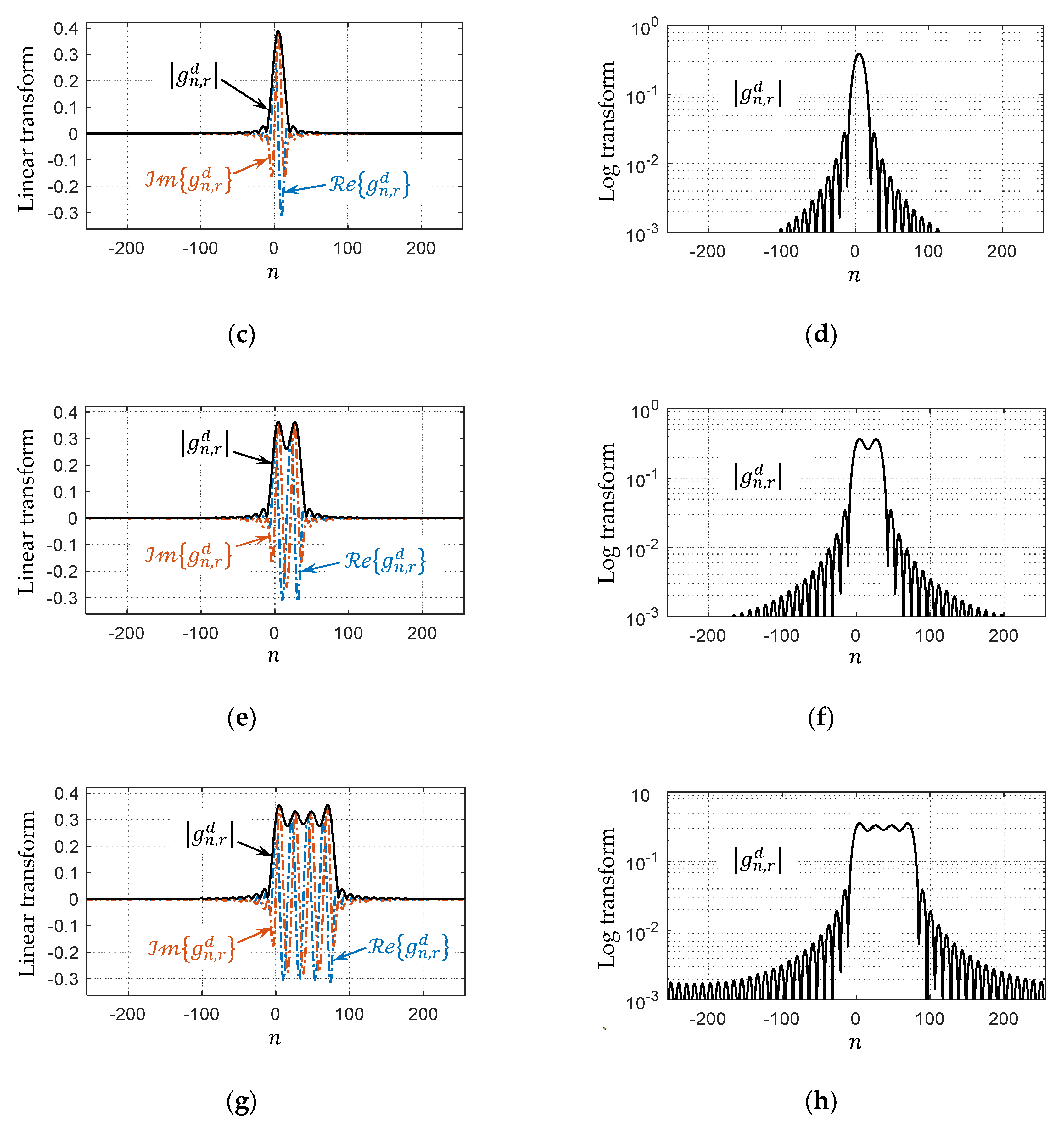
3.1. Time-Domain Aspect
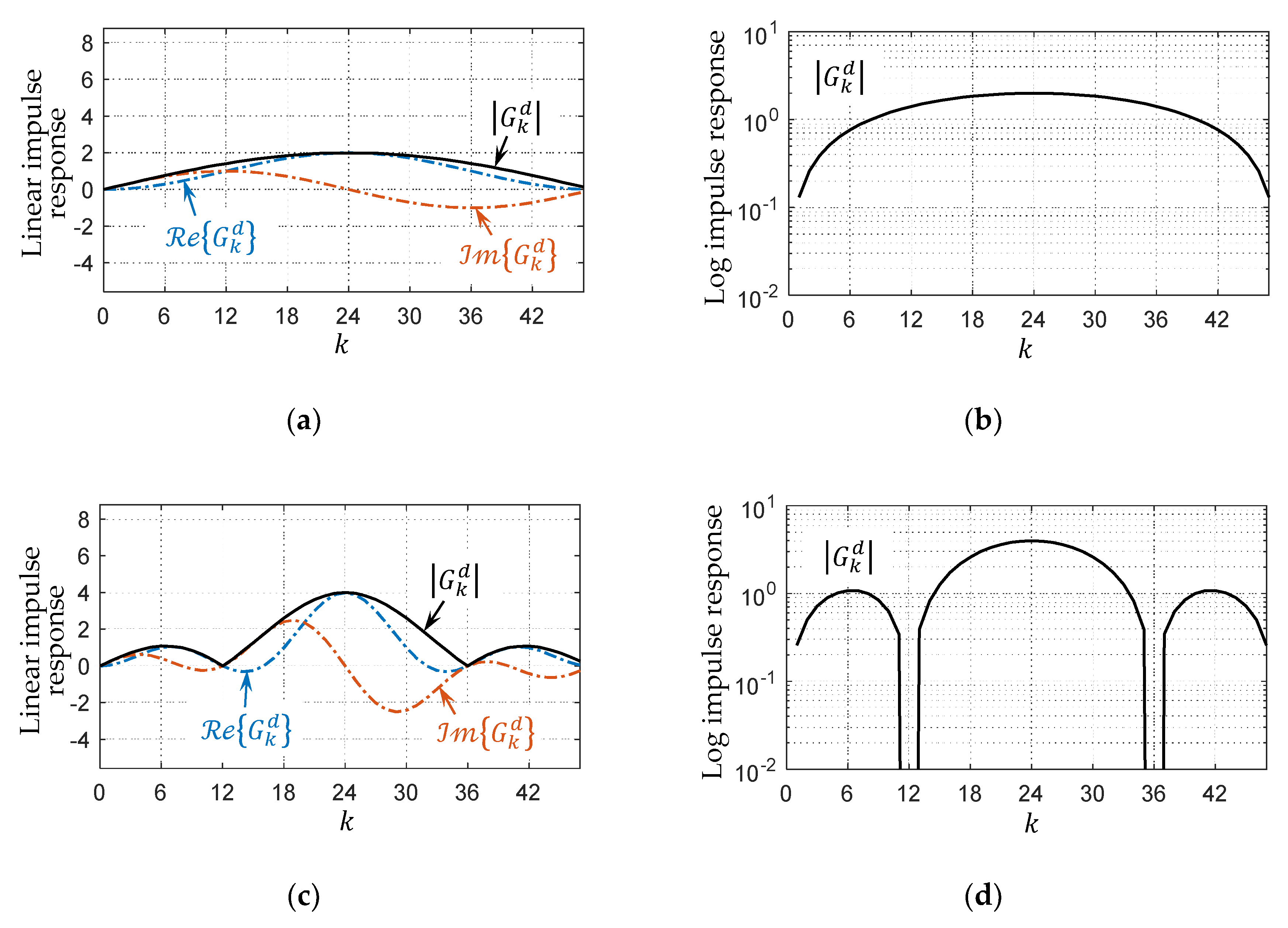
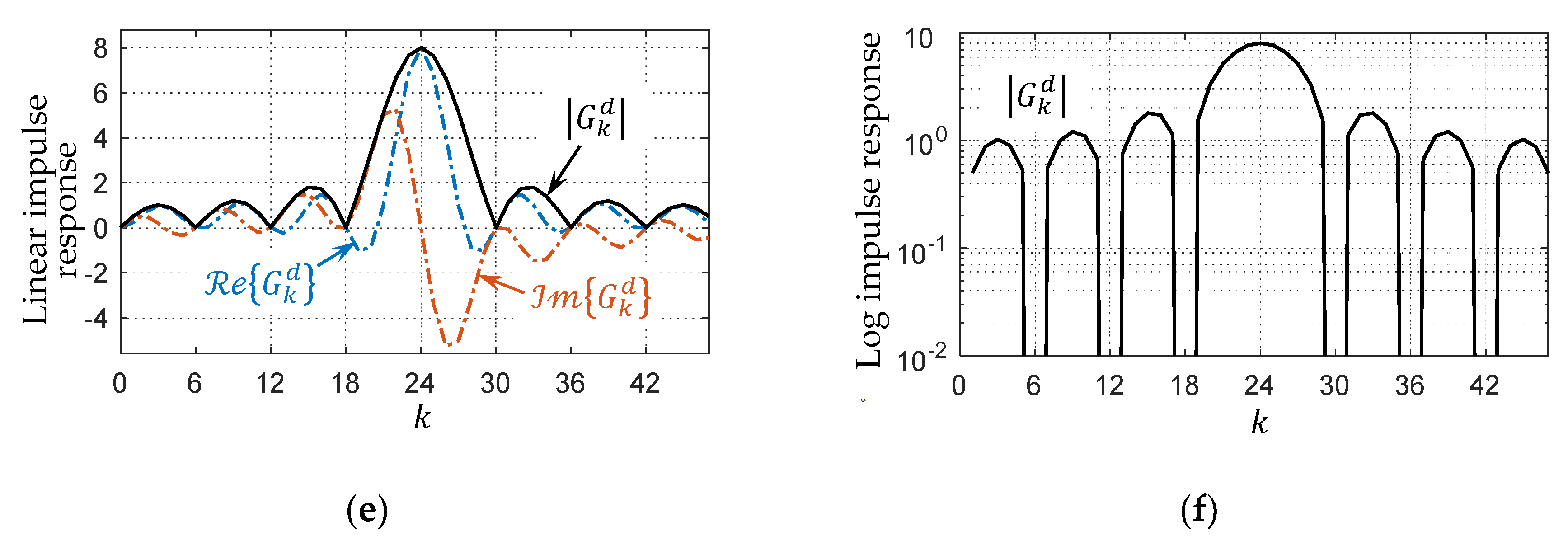
3.2. Frequency-Domain Aspect
3.3. Computational Complexity
4. Simulation and Discussion
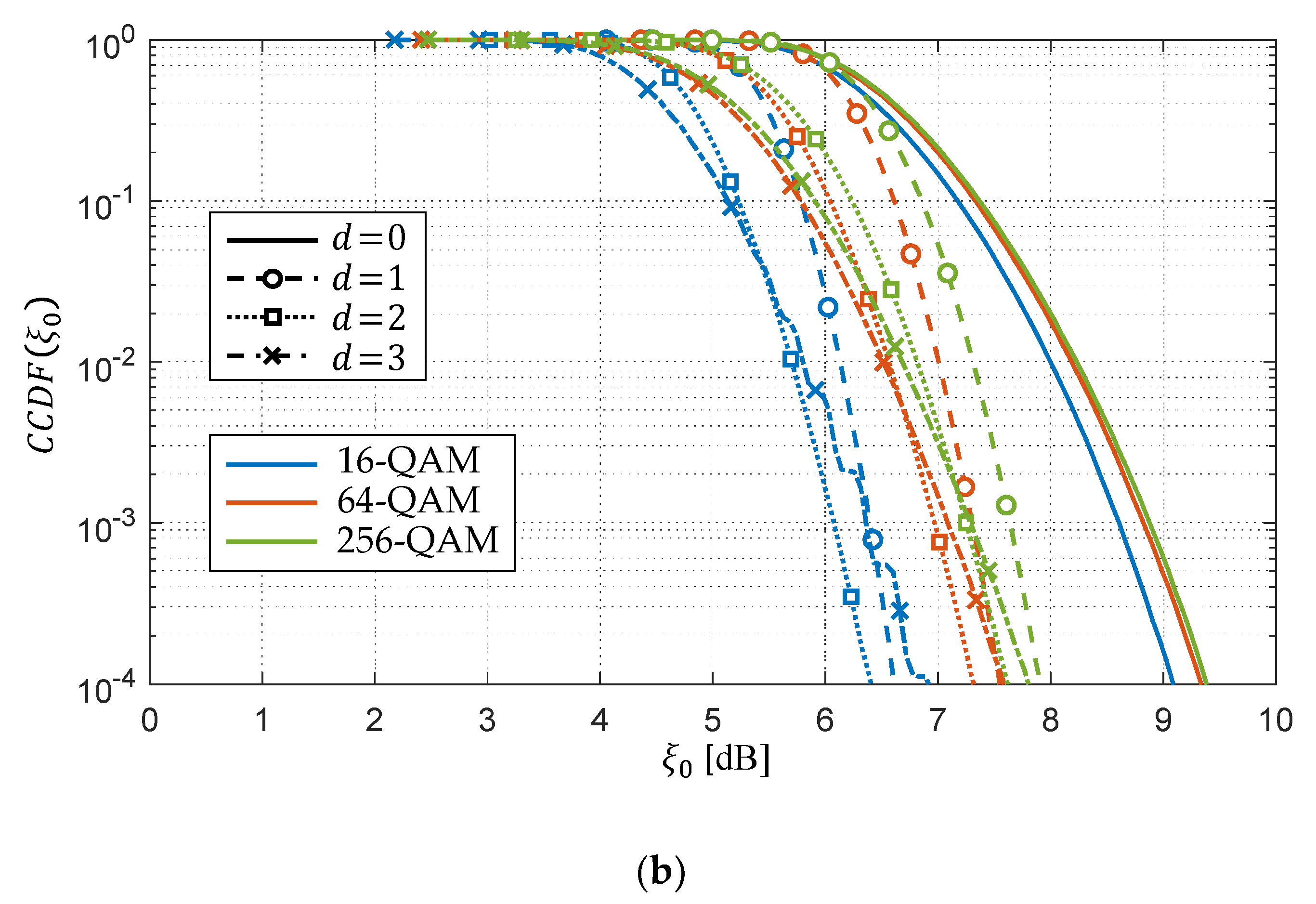
4.1. Peak-to-Average Power Ratio
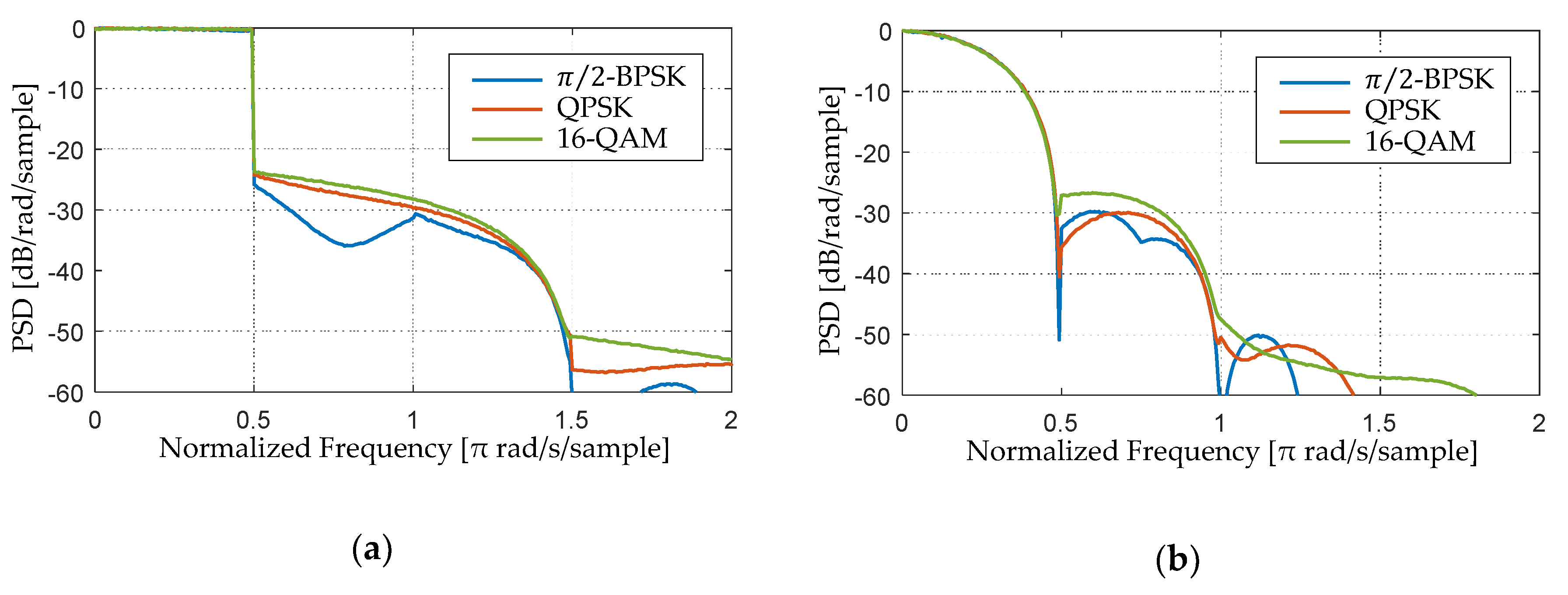
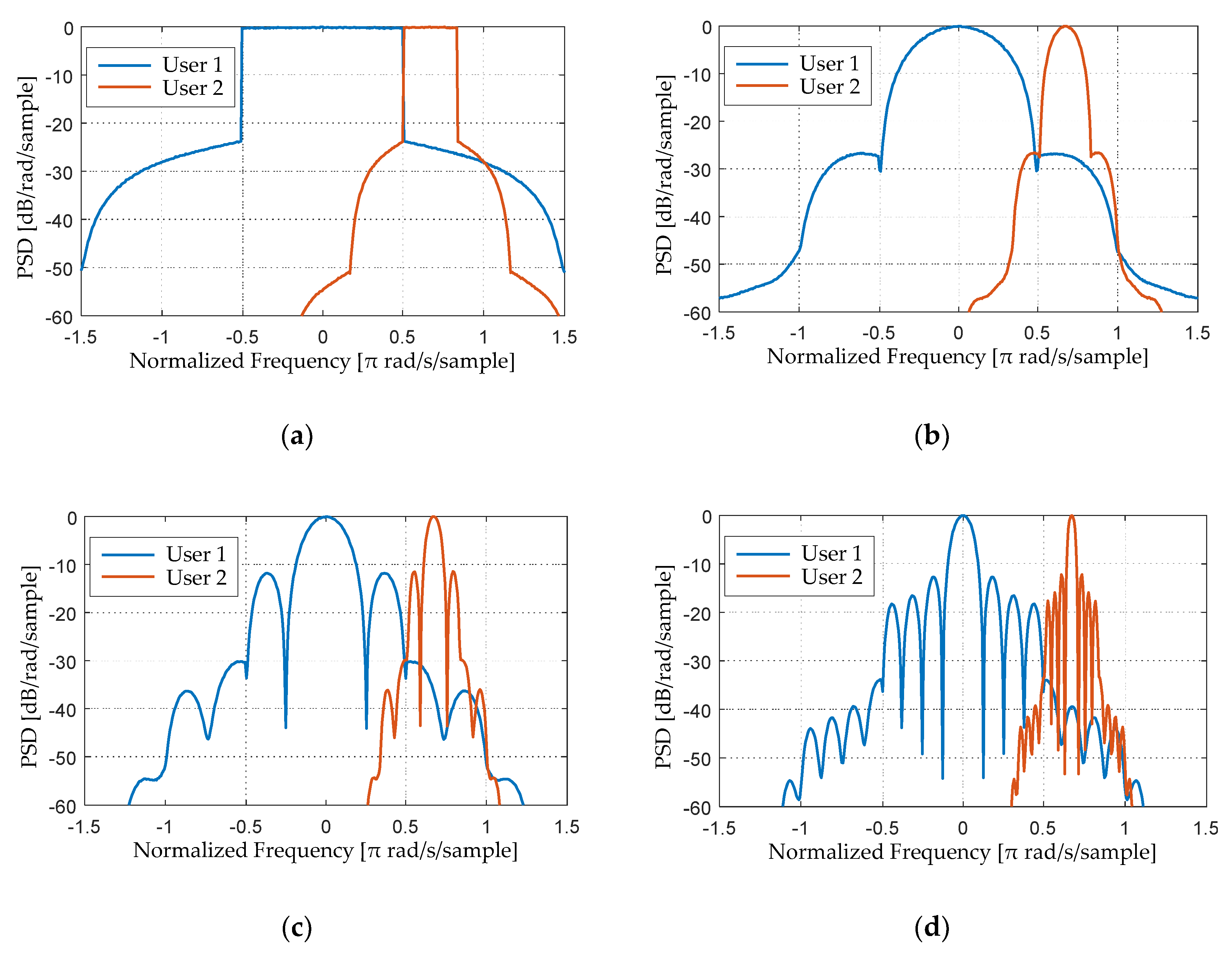
4.2. Power Spectral Density
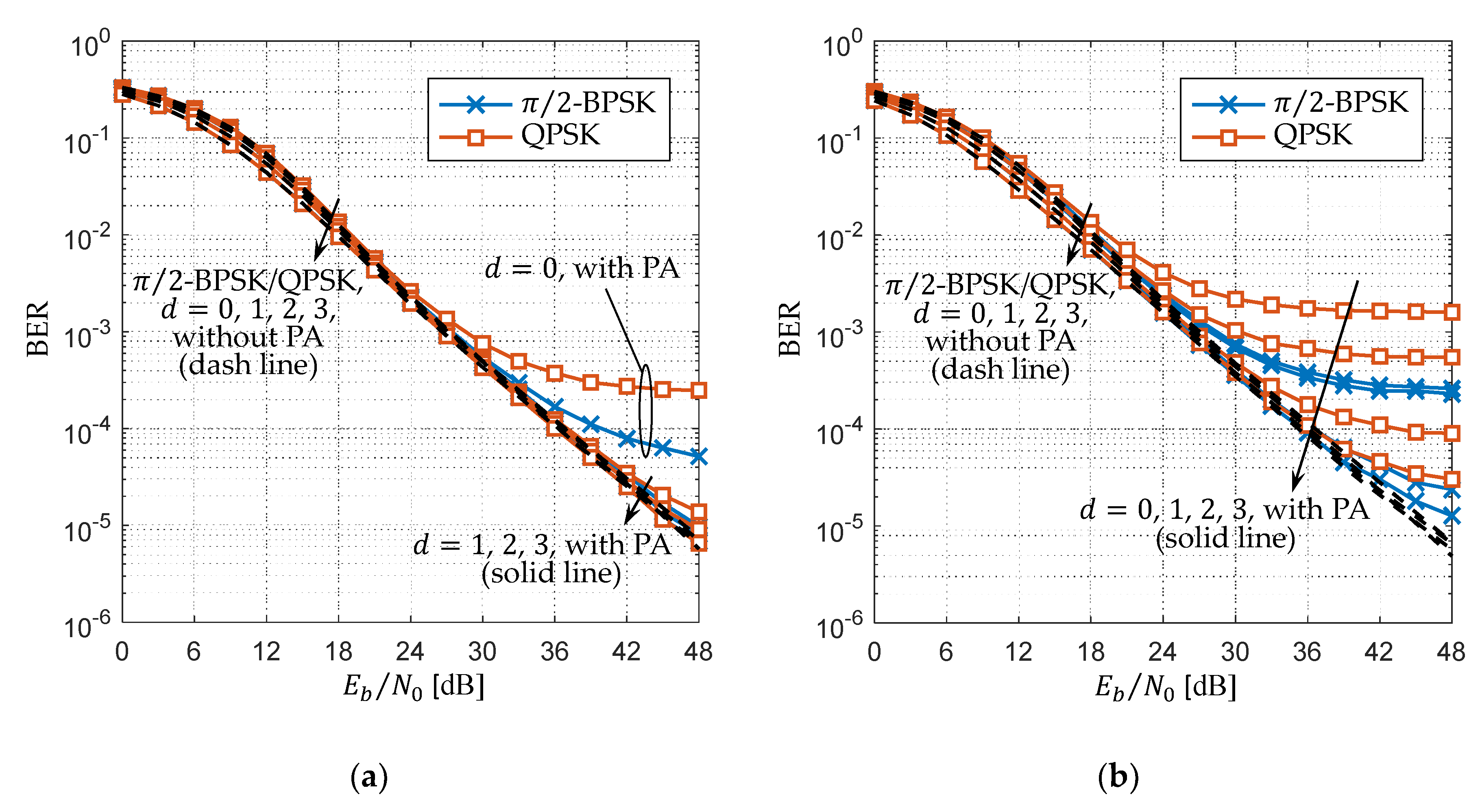
4.3. Bit Error Rate
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Spectral Shaping Function of PCC-DFT-s-OFDM
References
- Hwang, T.; Yang, C.; Wu, G.; Li, S.; Li, G.Y. OFDM and Its Wireless Applications: A Survey. IEEE Trans. Veh. Technol. 2009, 58, 1673–1694. [Google Scholar] [CrossRef]
- 3GPP. TS 36.211 V15.7.0. In Technical Specification Group Radio Access Network; Physical Channels and Modulation (Release 15); 3rd Generation Partnership Project: Newport Beach, CA, USA, 2019. [Google Scholar]
- 3GPP. TS 38.211 V15.7.0. In Technical Specification Group Radio Access Network; Physical Channels and Modulation (Release 15); 3rd Generation Partnership Project: Newport Beach, CA, USA, 2019. [Google Scholar]
- Wunder, G.; Fischer, R.F.H.; Boche, H.; Litsyn, S.; No, J.-S. The PAPR Problem in OFDM Transmission: New Directions for a Long-Lasting Problem. IEEE Signal Process. Mag. 2013, 30, 130–144. [Google Scholar] [CrossRef]
- Han, S.H.; Lee, J.H. An overview of peak-to-average power ratio reduction techniques for multicarrier transmission. IEEE Wirel. Commun. 2005, 12, 56–65. [Google Scholar] [CrossRef]
- Jiang, T.; Wu, Y. An Overview: Peak-to-Average Power Ratio Reduction Techniques for OFDM Signals. IEEE Trans. Broadcast. 2008, 54, 257–268. [Google Scholar] [CrossRef]
- Rahmatallah, Y.; Mohan, S. Peak-To-Average Power Ratio Reduction in OFDM Systems: A Survey And Taxonomy. IEEE Commun. Surv. Tutor. 2013, 15, 1567–1592. [Google Scholar] [CrossRef]
- Sandoval, F.; Poitau, G.; Gagnon, F. Hybrid Peak-to-Average Power Ratio Reduction Techniques: Review and Performance Comparison. IEEE Access 2017, 5, 27145–27161. [Google Scholar] [CrossRef]
- Nokia, Alcatel-Lucent Shanghai Bell. Potential for System Level Gains with Low PAPR Waveforms, R1-167795. 2016. Available online: https://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_86/Docs/R1-167795.zip (accessed on 31 October 2019).
- Zaidi, A.A.; Baldemair, R.; Tullberg, H.; Bjorkegren, H.; Sundstrom, L.; Medbo, J.; Kilinc, C.; Da Silva, I. Waveform and Numerology to Support 5G Services and Requirements. IEEE Commun. Mag. 2016, 54, 90–98. [Google Scholar] [CrossRef]
- Ankarali, Z.E.; Pekoz, B.; Arslan, H. Flexible Radio Access Beyond 5G: A Future Projection on Waveform, Numerology, and Frame Design Principles. IEEE Access 2017, 5, 18295–18309. [Google Scholar] [CrossRef]
- Demir, A.F.; Elkourdi, M.; Ibrahim, M.; Arslan, H. Waveform Design for 5G and Beyond. In 5G Networks: Fundamental Requirements, Enabling Technologies, and Operations Management; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018; pp. 51–76. [Google Scholar]
- Farhang-Boroujeny, B.; Moradi, H. OFDM Inspired Waveforms for 5G. IEEE Commun. Surv. Tutor. 2016, 18, 2474–2492. [Google Scholar] [CrossRef]
- Myung, H.; Lim, J.; Goodman, D. Single carrier FDMA for uplink wireless transmission. IEEE Veh. Technol. Mag. 2006, 1, 30–38. [Google Scholar] [CrossRef]
- 3GPP. TS 36.211 V13.3.0. In Technical Specification Group Radio Access Network; Physical Channels and Modulation (Release 13); 3rd Generation Partnership Project: New Orleans, LA, USA, 2016. [Google Scholar]
- Cho, L.; Liao, H.-C.; Hsu, C.-Y. Adjustable PAPR reduction for DFT-s-OFDM via improved general precoding scheme. Electron. Lett. 2018, 54, 903–905. [Google Scholar] [CrossRef]
- International Telecommunication Union (ITU). IMT Vision—Framework and Overall Objectives of the Future Development of IMT for 2020 and Beyond; ITU-R: Geneva, Switzerland, 2015; p. 21. [Google Scholar]
- 3GPP. TS 23.303 V15.1.0. In Technical Specification Group Services and System Aspects; Technical Specification Group Services and System Aspects; Proximity-Based Services (ProSe); Stage 2 (Release 15); 3rd Generation Partnership Project: La Jolla, CA, USA, 2018. [Google Scholar]
- Hori, Y.; Ochiai, H. A New Uplink Multiple Access Based on OFDM With Low PAPR, Low Latency, and High Reliability. IEEE Trans. Commun. 2018, 66, 1996–2008. [Google Scholar] [CrossRef]
- Mauritz, O.; Popovic, B. Optimum Family of Spectrum-Shaping Functions for PAPR Reduction of DFT-Spread OFDM Signals. In Proceedings of the IEEE Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 25–28 September 2006; pp. 1–5. [Google Scholar]
- Hsu, C.-Y.; Liao, H.-C. Generalised precoding method for PAPR reduction with low complexity in OFDM systems. IET Commun. 2018, 12, 796–808. [Google Scholar] [CrossRef]
- Armstrong, J.; Grant, P.M.; Povey, G. Polynomial cancellation coding of OFDM to reduce intercarrier interference due to Doppler spread. In Proceedings of the IEEE Global Telecommun. Conf. (GLOBECOM), Sydney, Australia, 8–12 November 1998; pp. 2771–2776. [Google Scholar]
- Kongara, G.; Yang, L.; He, C.; Armstrong, J. A Comparison of CP-OFDM, PCC-OFDM and UFMC for 5G Uplink Communications. IEEE Access 2019, 7, 157574–157594. [Google Scholar] [CrossRef]
- Bäuml, R.W.; Fischer, R.F.H.; Huber, J.B. Reducing the peak-to-average power ratio of multicarrier modulation by selected mapping. Electron. Lett. 1996, 32, 2056–2057. [Google Scholar] [CrossRef]
- Müller, S.H.; Huber, J.B. OFDM with reduced peak-to-average power ratio by optimum combination of partial transmit sequences. Electron. Lett. 1997, 33, 368–369. [Google Scholar] [CrossRef]
- Ochiai, H. On Instantaneous Power Distributions of Single-Carrier FDMA Signals. IEEE Wirel. Commun. Lett. 2012, 1, 73–76. [Google Scholar] [CrossRef]
- Ali, H.; Yaqub, R. A Low Complexity Linear Moving Average Filtering Technique for PAR Reduction in OFDM Systems. Int. J. Commun. Netw. Syst. Sci. 2018, 11, 199–215. [Google Scholar] [CrossRef]
- Samsung. Frequency Domain Spectrum Shaping for DFT-s-OFDM, R1-1703016. 2017. Available online: https://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_88/Docs/R1-1703016.zip (accessed on 31 October 2019).
- Rapp, C. Effect of HPA-nonlinearity on 4-DPSK/OFDM-signal for a digital sound broadcasting system. In Proceedings of the 2nd European Conf. Satellite Commun. (ECSC), Liege, Belgium, 22–24 October 1991; pp. 179–184. [Google Scholar]
- Ryu, H.-G.; Li, Y.; Park, J.-S. An Improved ICI Reduction Method in OFDM Communication System. IEEE Trans. Broadcast. 2005, 51, 395–400. [Google Scholar] [CrossRef]
- Tang, T.; Zhang, Y.; Jiang, J.; Zhang, P. A MIMO-PCC-OFDM System for Multipath Fading Channels with Carrier Frequency Offset. In Proceedings of the Int. Symp. Commun. and Inform. Technol. (ISCIT), Bangkok, Thailand, 18–20 October 2006; pp. 511–515. [Google Scholar]
- Li, X.; Armstrong, J. An Improved MIMO PCC OFDM System with Reduced Sensitivity to Imperfect CSI. In Proceedings of the IEEE Wirel. Commun. and Netw. Conf. (WCNC), Sydney, Australia, 18–21 April 2010; pp. 1–6. [Google Scholar]
- Wang, S.; Armstrong, J.; Thompson, J.S. Waveform performance for asynchronous wireless 5G uplink communications. In Proceedings of the IEEE 27th Annu. Int. Symp. Personal, Indoor, and Mobile Radio Commun. (PIMRC), Valencia, Spain, 4–8 September 2016; pp. 1–6. [Google Scholar]
- Wang, S.; Thompson, J.S.; Grant, P.M. Closed-Form Expressions for ICI/ISI in Filtered OFDM Systems for Asynchronous 5G Uplink. IEEE Trans. Commun. 2017, 65, 4886–4898. [Google Scholar] [CrossRef]






| Computational Complexity | Conventional DFT Precoding | PCC-Based DFT Precoding | |||
|---|---|---|---|---|---|
| Function | Big-O 1 | Function | Big-O 1 | ||
| Number of complex multiplications | Tx | ||||
| Rx | |||||
| Number of complex additions | Tx | ||||
| Rx | |||||
| Parameter | Value |
|---|---|
| Carrier Bandwidth | 10 MHz |
| Subcarrier Spacing | 15 kHz |
| Fast Fourier Transform (FFT) Size () | 1024 |
| Number of allocated subcarriers for User 1 (medium bandwidth) | 144 (12 PRBs) |
| Number of allocated subcarriers for User 2 (narrow bandwidth) | 48 (4 PRBs) |
| Cyclic prefix (CP) length 1 | 72 |
| Modulation | -BPSK, QPSK, 16-QAM |
| Without PA Nonlinearity | With PA Nonlinearity | |||||||
|---|---|---|---|---|---|---|---|---|
| 12 | ||||||||
| 21 | ||||||||
| 30 | ||||||||
| 39 | ||||||||
| Without PA Nonlinearity | With PA Nonlinearity | |||||||
|---|---|---|---|---|---|---|---|---|
| 12 | ||||||||
| 21 | ||||||||
| 30 | ||||||||
| 39 | ||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, L.; Kuo, Y.-M.; Wu, Y.-S.; Hsu, C.-Y. Polynomial Cancellation Coded DFT-s-OFDM for Low-PAPR Uplink Signaling. Electronics 2019, 8, 1349. https://doi.org/10.3390/electronics8111349
Cho L, Kuo Y-M, Wu Y-S, Hsu C-Y. Polynomial Cancellation Coded DFT-s-OFDM for Low-PAPR Uplink Signaling. Electronics. 2019; 8(11):1349. https://doi.org/10.3390/electronics8111349
Chicago/Turabian StyleCho, Li, Yu-Ming Kuo, Yi-Shin Wu, and Chau-Yun Hsu. 2019. "Polynomial Cancellation Coded DFT-s-OFDM for Low-PAPR Uplink Signaling" Electronics 8, no. 11: 1349. https://doi.org/10.3390/electronics8111349
APA StyleCho, L., Kuo, Y.-M., Wu, Y.-S., & Hsu, C.-Y. (2019). Polynomial Cancellation Coded DFT-s-OFDM for Low-PAPR Uplink Signaling. Electronics, 8(11), 1349. https://doi.org/10.3390/electronics8111349





