A Compromising Approach to Switching Losses and Waveform Quality in Three-phase Voltage Source Converters with Double-vector based Predictive Control Method
Abstract
:1. Introduction
2. Conventional Finite Predictive Current Control Method Using Two-Vector For Three-Phase Rectifier
3. Proposed Switching Loss Reduction Strategy for Three-Phase Rectifier Using Two-Vector Based on Offset Voltage Injection
4. Simulation and Experimental Results
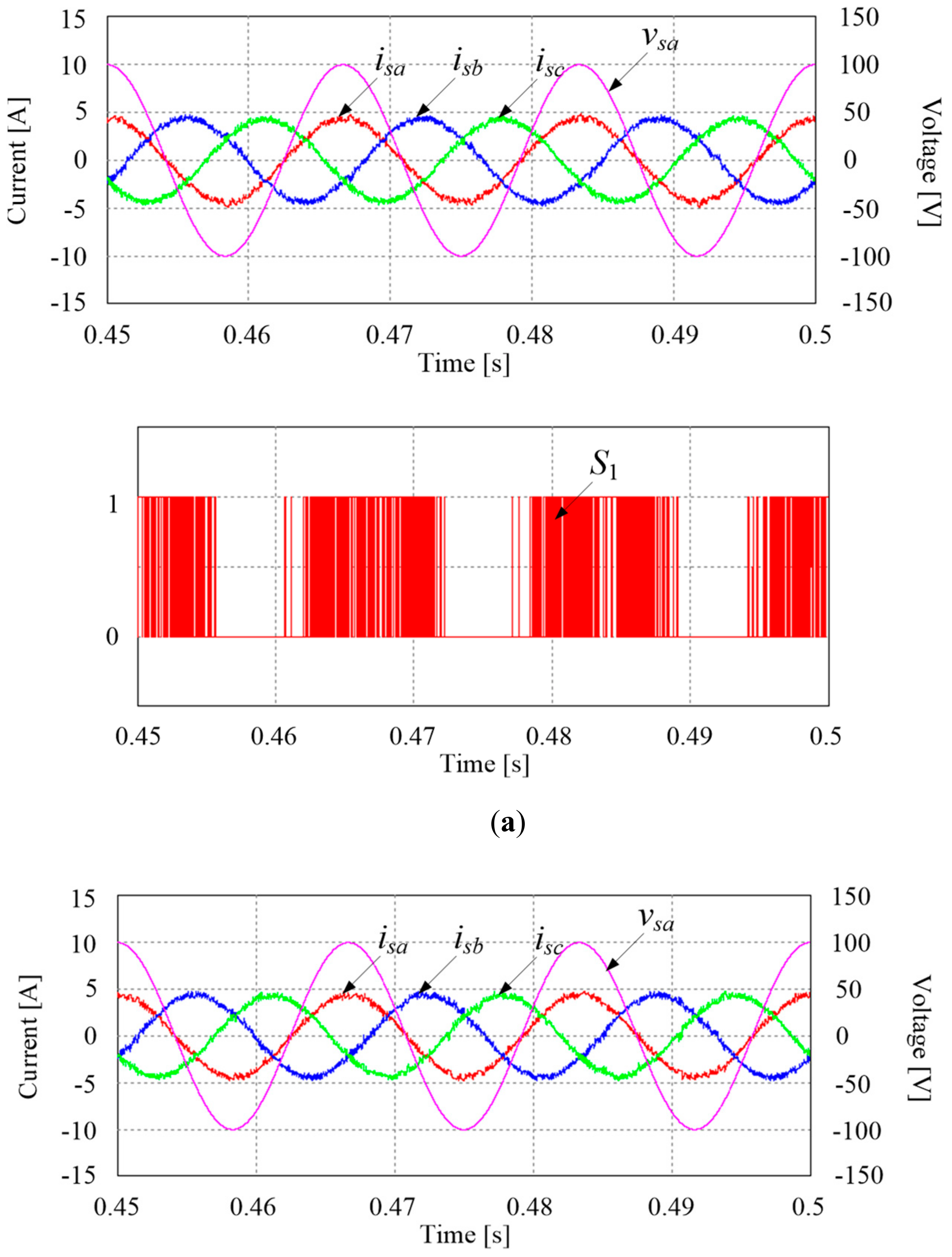
4.1. Simulation Results
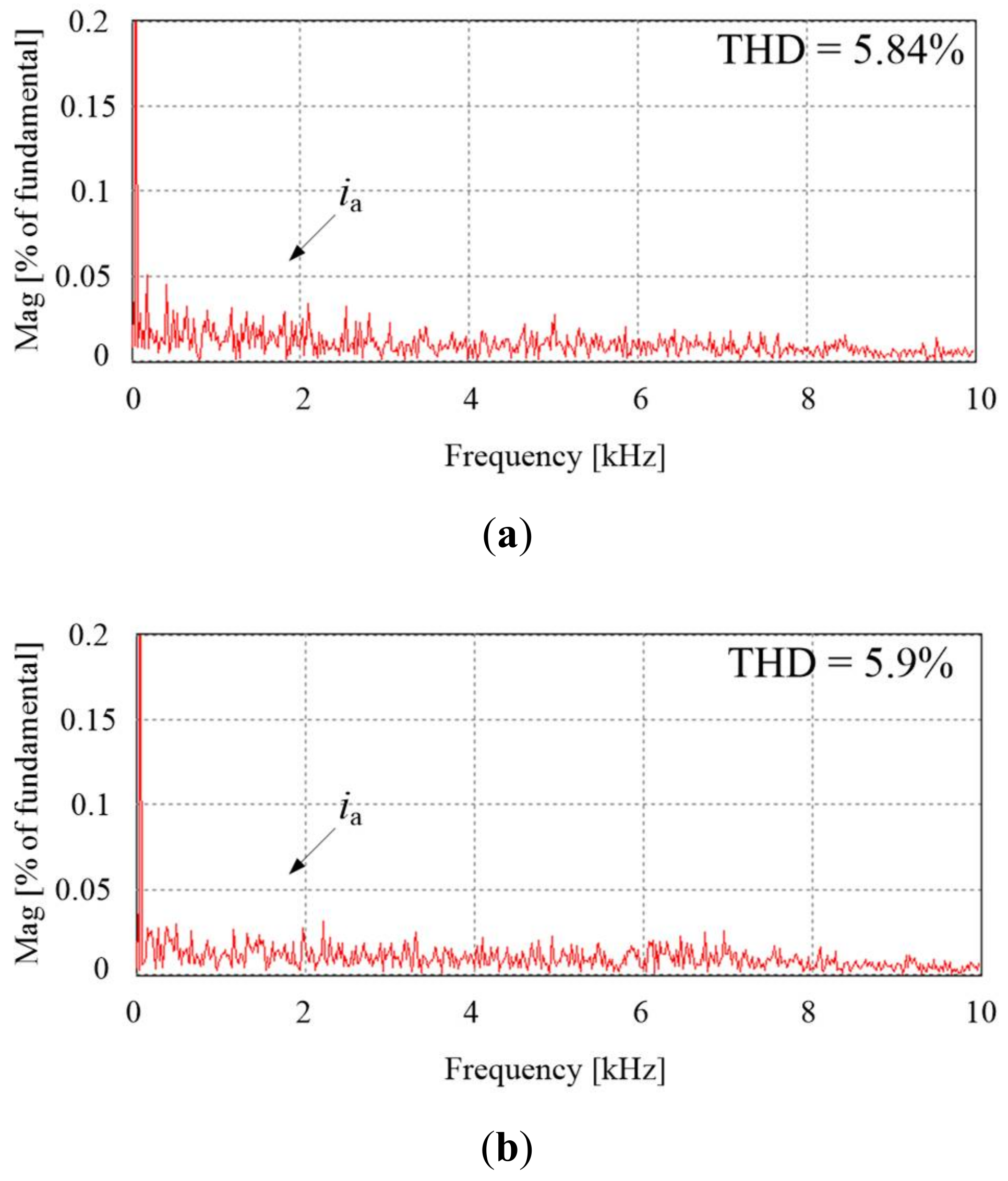
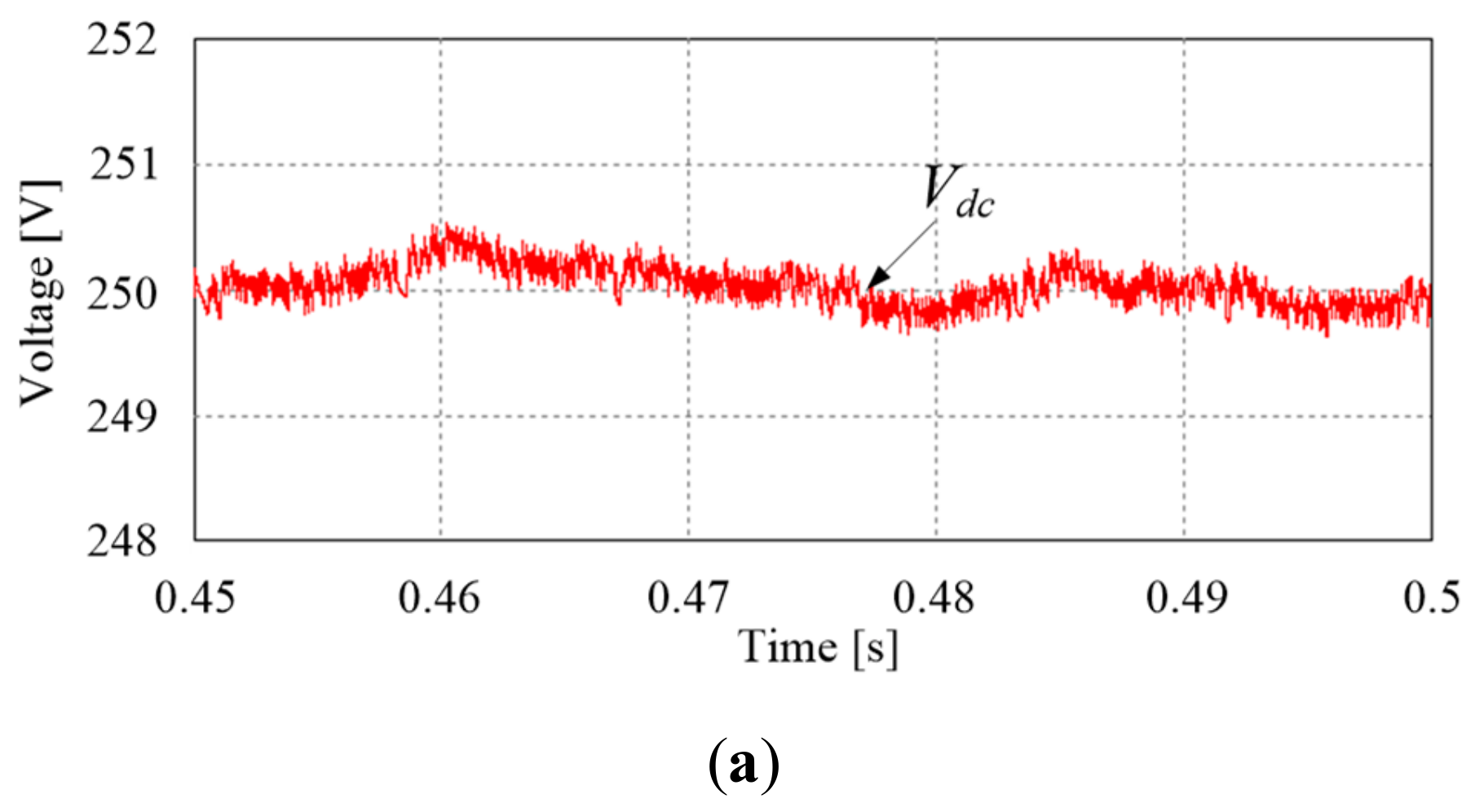
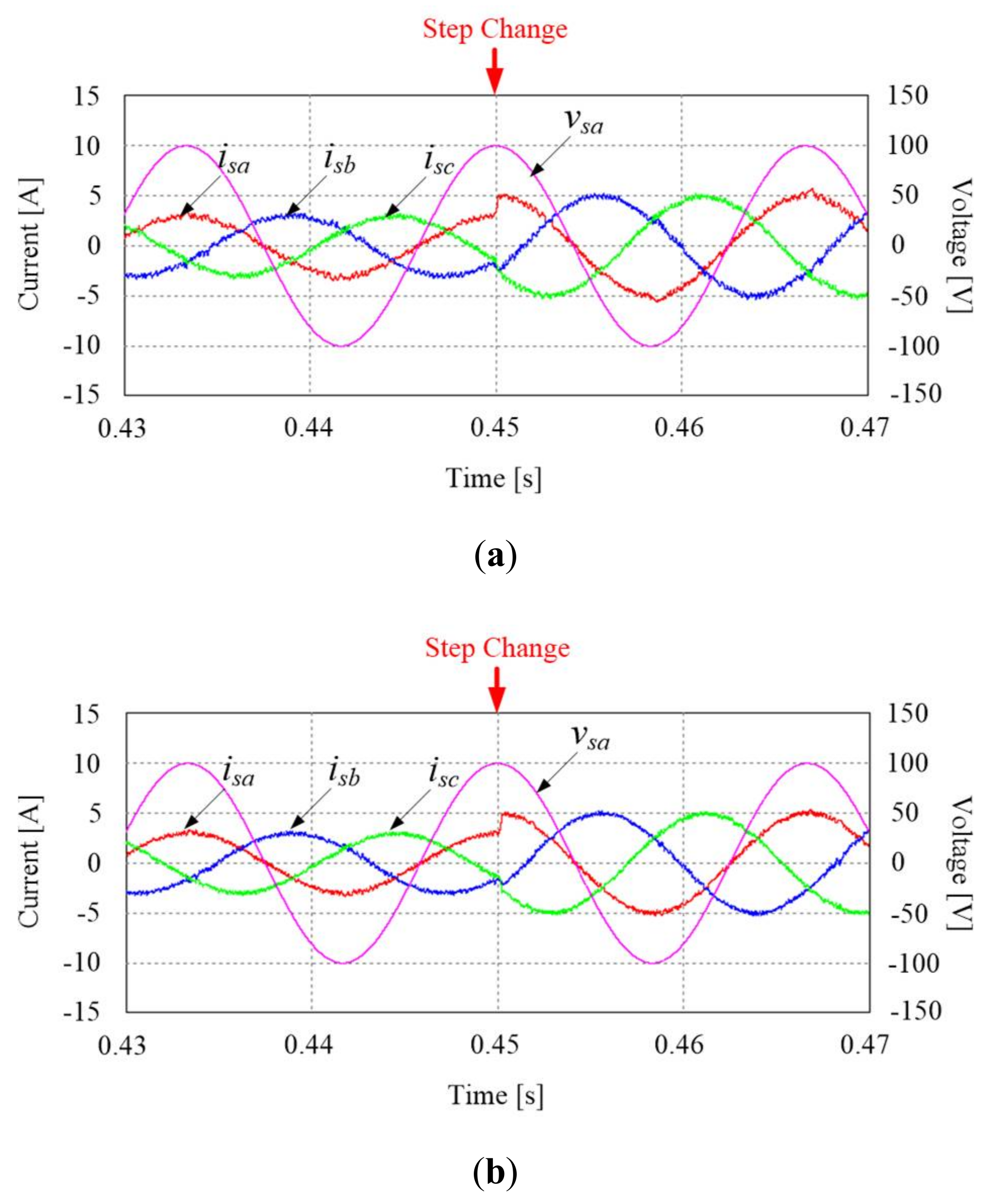
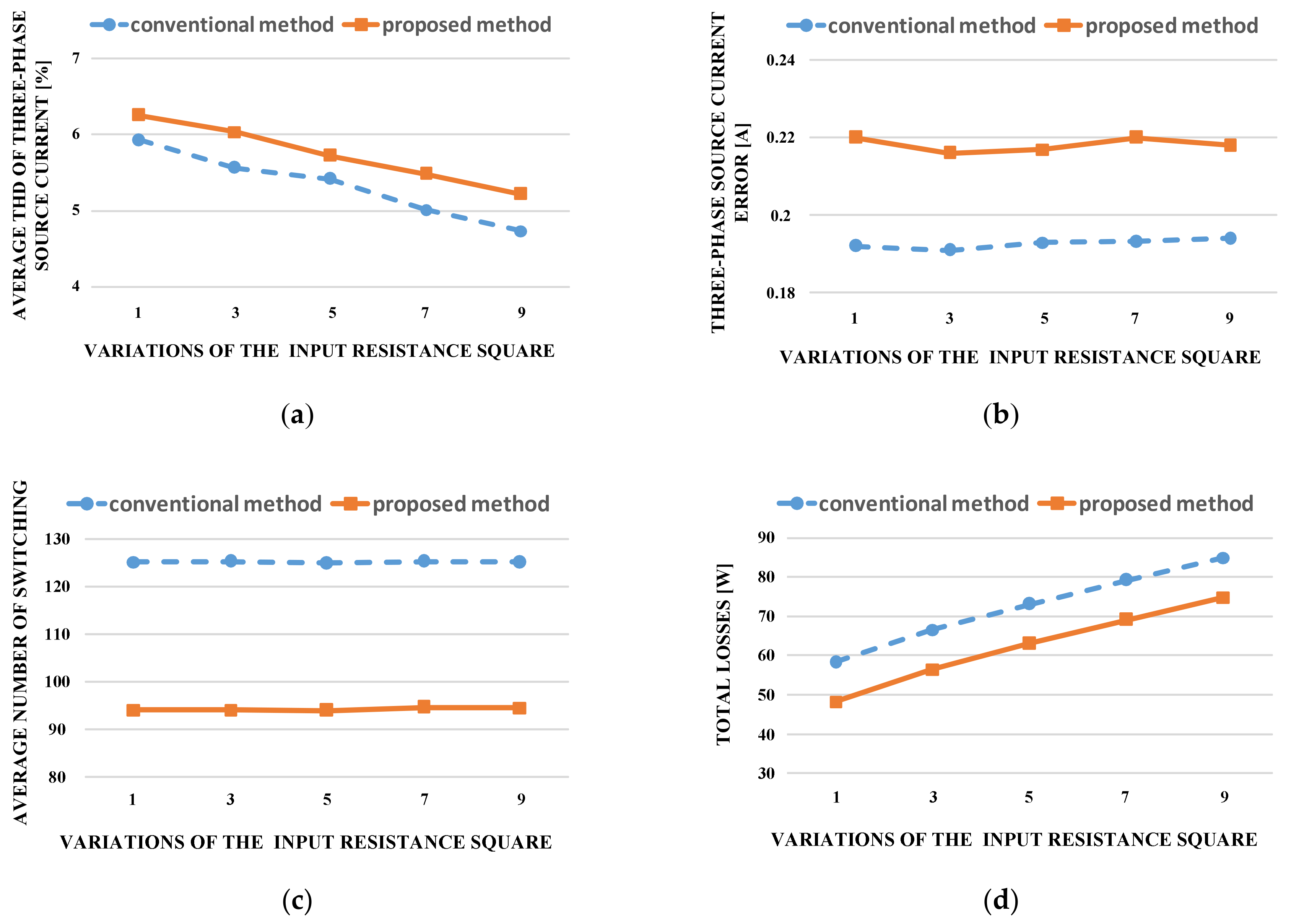
4.2. Experimental Results
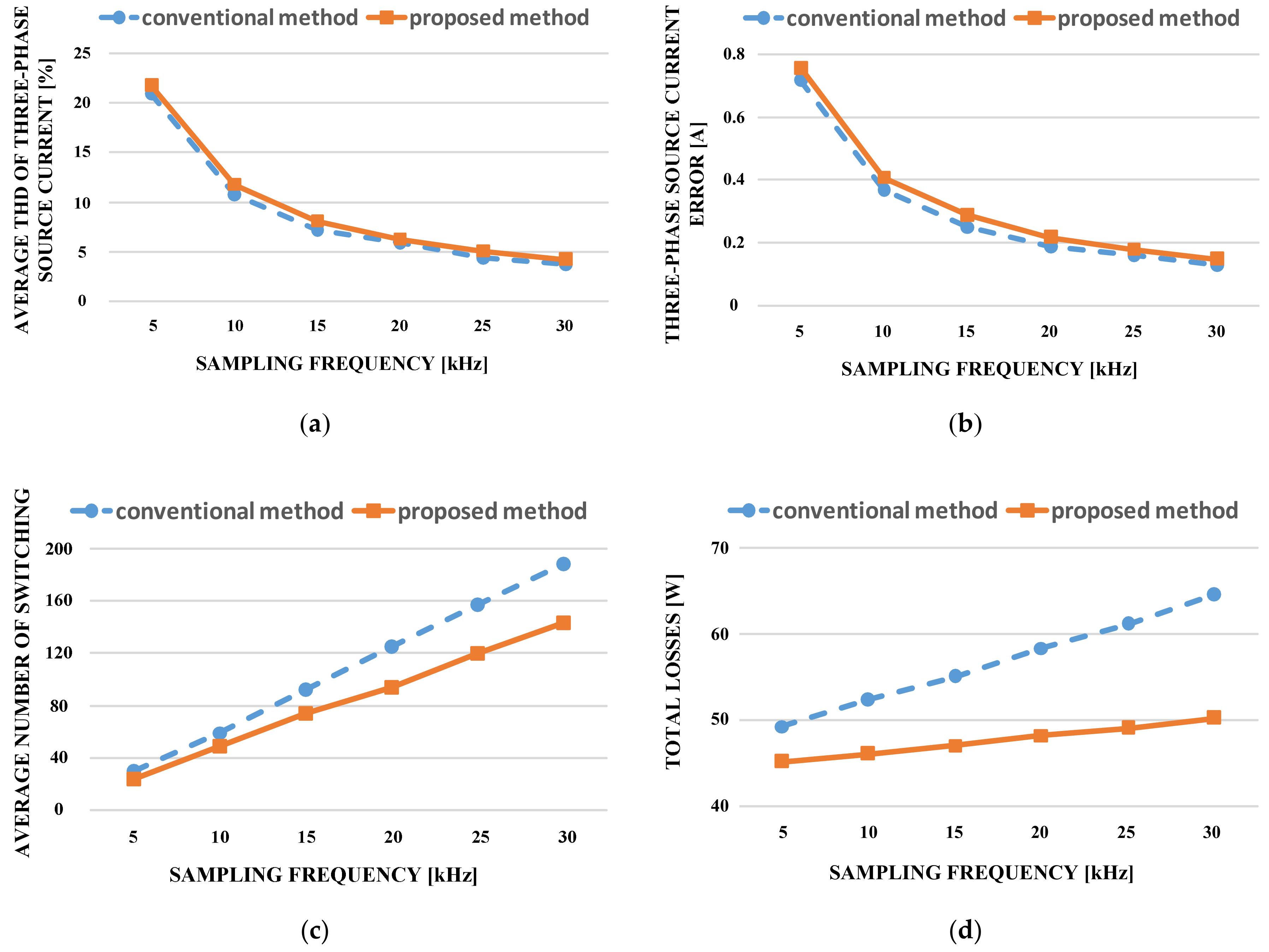
5. Performance Comparison
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nene, H.; Zaitsu, T. Bi-Directional PSFB DC-DC Converter with Unique PWM Control Schemes and Seamless Mode Transitions Using Enhanced Digital Control. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 3229–3233. [Google Scholar]
- Fuchs, S.; Beck, S.; Biela, J. Analysis and Reduction of the Output Voltage Error of PWM for Modular Multilevel Converters. IEEE Trans. Ind. Electron. 2019, 66, 2291–2301. [Google Scholar] [CrossRef]
- Padhee, V.; Sahoo, A.K.; Mohan, N. Modulation Techniques for Enhanced Reduction in Common-Mode Voltage and Output Voltage Distortion in Indirect Matrix Converters. IEEE Trans. Power Electron. 2017, 32, 8655–8670. [Google Scholar] [CrossRef]
- Foti, S.; Testa, A.; Scelba, G.; Sabatini, V.; Lidozzi, A.; Solero, L. A Low THD Three-Level Rectifier For Gen-Set Applications. IEEE Trans. Ind. Appl. 2019, 55, 6150–6160. [Google Scholar] [CrossRef]
- Kwak, S.; Toliyat, H.A. Design and rating comparisons of PWM voltage source rectifiers and active power filters for AC drives with unity power factor. IEEE Trans. Power Electron. 2005, 20, 1133–1142. [Google Scholar] [CrossRef]
- Kwak, S.; Toliyat, H.A. Design and performance comparisons of two multi-drive systems with unity power factor. IEEE Trans. Power Deliv. 2005, 20, 417–426. [Google Scholar]
- Wai, R.; Yang, Y. Design of Backstepping Direct Power Control for Three-Phase PWM Rectifier. IEEE Trans. Ind. Appl. 2019, 55, 3160–3173. [Google Scholar] [CrossRef]
- Habetler, T.G. A space vector based rectifier regulator for AC/DC/AC converters. IEEE Trans. Power Electron. 1993, 8, 3–36. [Google Scholar] [CrossRef]
- Restrepo, J.; Aller, J.; Viola, J.; Bueno, A.; Habetler, T. Optimum space vector computation technique for direct power control. IEEE Trans. Power Electron. 2009, 24, 1637–1645. [Google Scholar] [CrossRef]
- Liu, J.; Gong, C.; Han, Z.; Yu, H. IPMSM Model Predictive Control in Flux-Weakening Operation Using an Improved Algorithm. IEEE Trans. Ind. Electron. 2018, 65, 9378–9387. [Google Scholar] [CrossRef]
- Kubasiak, N. Model Predictive Control of Transistor Pulse Converter for Feeding Electromagnetic Valve Actuator with Energy Storage. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 6794–6799. [Google Scholar]
- Mercorelli, P.; Kubasiak, N.; Liu, S. Multilevel Bridge Governor by Using Model Predictive Control in Wavelet Packets for Tracking Trajectories. In Proceedings of the IEEE 2004 International Conference on Robotics and Automation, (ICRA ’04), New Orleans, LA, USA, 26 April–1 May 2004; Volume 4, pp. 4079–4084. [Google Scholar]
- Mercorelli, P. A Multilevel Inverter Bridge Control Structure with Energy Storage Using Model Predictive Control for Flat Systems. J. Eng. 2013, 2013, 750190. [Google Scholar] [CrossRef]
- Gardezi, M.S.M.; Hasan, A. Machine Learning Based Adaptive Prediction Horizon in Finite Control Set Model Predictive Control. IEEE Access 2018, 6, 32392–32400. [Google Scholar] [CrossRef]
- Kabzan, J.; Lukas, H.; Liniger, A.; Zeilinger, M.N. Learning-Based Model Predictive Control for Autonomous Racing. IEEE Robot. Autom. Lett. 2019, 4, 3363–3370. [Google Scholar] [CrossRef]
- Ma, J.; Song, W.; Wang, S.; Feng, X. Model Predictive Direct Power Control for Single Phase Three-Level Rectifier at Low Switching Frequency. IEEE Trans. Power Electron. 2018, 33, 1050–1062. [Google Scholar] [CrossRef]
- Wang, X.; Sun, D. Three-Vector-Based Low-Complexity Model Predictive Direct Power Control Strategy for Doubly Fed Induction Generators. IEEE Trans. Power Electron. 2017, 32, 773–782. [Google Scholar] [CrossRef]
- Cortes, P.; Rodriguez, J.; Antoniewicz, P.; Kazmierkowski, M. Direct power control of an AFE using predictive control. IEEE Trans. Power Electron. 2008, 23, 2516–2523. [Google Scholar] [CrossRef]
- Kim, J.; Park, J.; Kwak, S. Predictive Direct Power Control Technique for Voltage Source Converter with High Efficiency. IEEE Access 2018, 6, 23540–23550. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Rodriguez, P.; Blaabjerg, F.; Malinowski, M. Reduction of switching losses in active power filters with a new generalized discontinuous-PWM strategy. IEEE Trans. Ind. Electon. 2008, 55, 467–471. [Google Scholar] [CrossRef]
- Chung, D.; Sul, S. Minimum-loss strategy for three-phase PWM rectifier. IEEE Trans. Ind. Electron. 1999, 46, 517–526. [Google Scholar] [CrossRef]
- Jiang, W.; Li, L.; Ma, M.; Zhai, F.; Li, J. A Novel Discontinuous PWM Strategy to Control Neutral Point Voltage for Neutral Point Clamped Three-Level Inverter With Improved PWM Sequence. IEEE Trans. Power Electron. 2019, 34, 9329–9341. [Google Scholar] [CrossRef]
- Cortes, P.; Rodriguez, J.; Silva, C.; Flores, A. Delay compensation in model predictive current control of a three-phase inverter. IEEE Trans. Ind. Electron. 2012, 59, 1323–1325. [Google Scholar] [CrossRef]
- Park, S.; Kwak, S. Comparative Study of Three Model Predictive Current Control Methods with Two Vectors for Three-Phase DC/AC VSIs. IET Electr. Power Appl. 2017, 11, 1284–1297. [Google Scholar] [CrossRef]
- Jun, E.; Park, S.; Kwak, S. A Comprehensive Double-Vector Approach to Alleviate Common-Mode Voltage in Three-Phase Voltage-Source Inverters with a Predictive Control Algorithm. Electronics 2019, 8, 872. [Google Scholar] [CrossRef]
- Kwak, S.; Park, J. Predictive Control Method with Future Zero-Sequence Voltage to Reduce Switching Losses in Three-Phase Voltage Source Inverters. IEEE Trans. Power Electron. 2015, 30, 1558–1566. [Google Scholar] [CrossRef]
- Jun, E.; Park, S.; Kwak, S. Model Predictive Current Control Method with Improved Performances for Three-phase Voltage Source Inverters. Electronics 2019, 8, 625. [Google Scholar] [CrossRef] [Green Version]

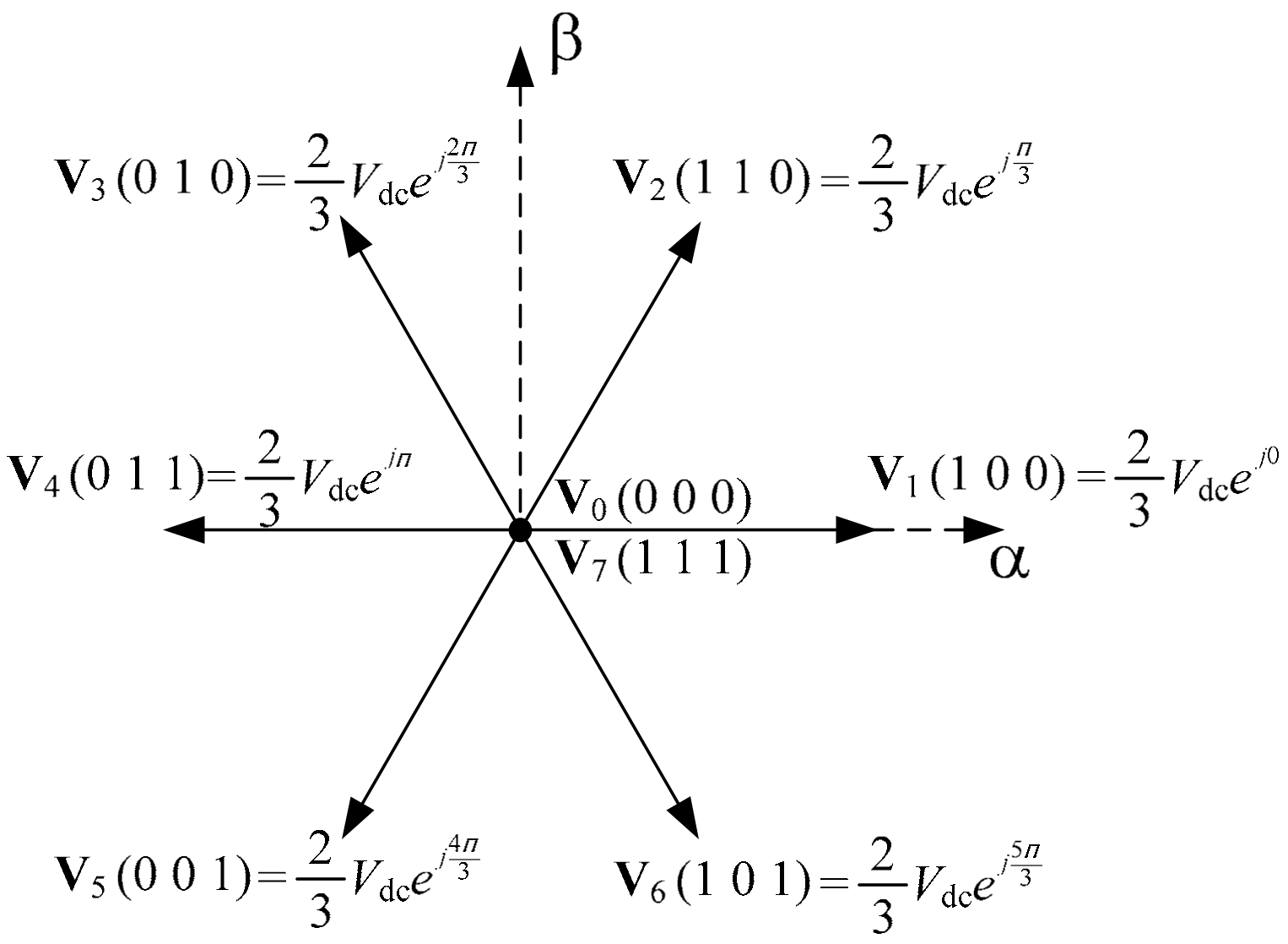
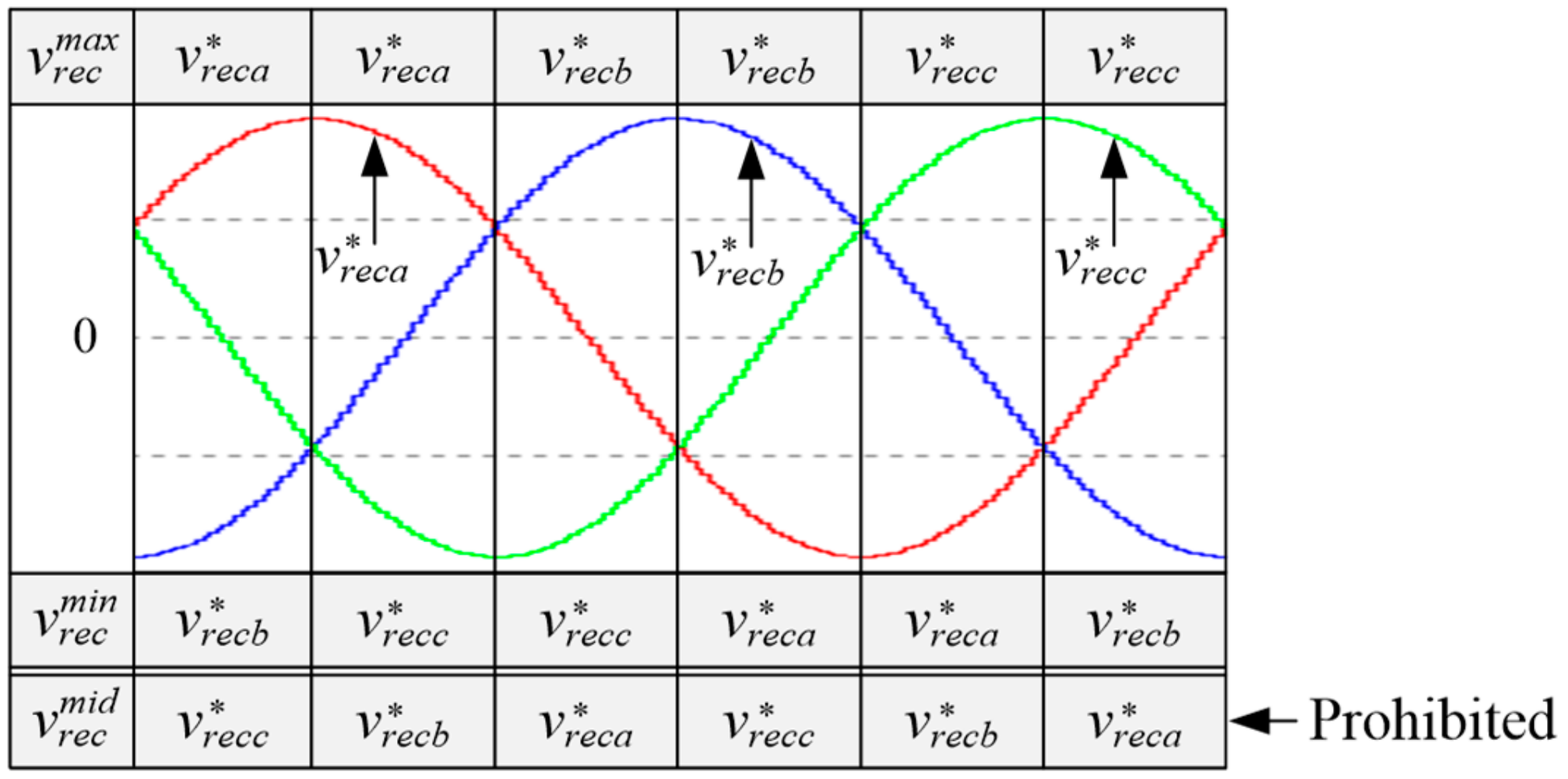
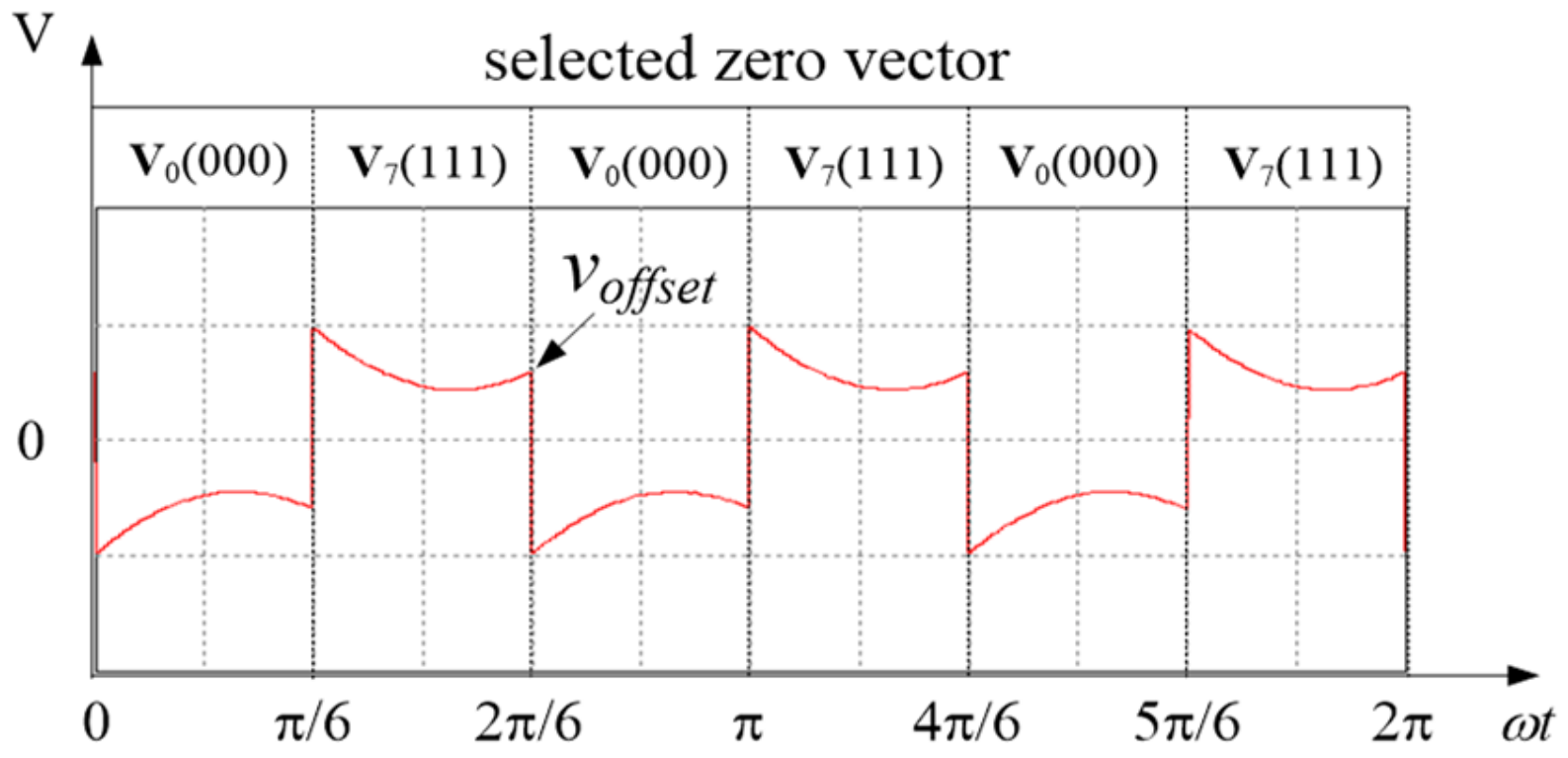











| Voltage Vector | |||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | |||
| 1 | 1 | 0 | |||
| 0 | 1 | 0 | |||
| 0 | 1 | 1 | |||
| 0 | 0 | 1 | |||
| 1 | 0 | 1 | |||
| 1 | 1 | 1 | 0 | 0 |
| Control Method | THD [%] | Current Error [A] | # of Switching | Total Losses [W] |
|---|---|---|---|---|
| Conventional Method | 5.84 | 0.19 | 125.28 | 58.4 |
| Proposed Method | 5.9 | 0.22 | 94.17 | 48.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jun, E.-S.; Kwak, S. A Compromising Approach to Switching Losses and Waveform Quality in Three-phase Voltage Source Converters with Double-vector based Predictive Control Method. Electronics 2019, 8, 1372. https://doi.org/10.3390/electronics8111372
Jun E-S, Kwak S. A Compromising Approach to Switching Losses and Waveform Quality in Three-phase Voltage Source Converters with Double-vector based Predictive Control Method. Electronics. 2019; 8(11):1372. https://doi.org/10.3390/electronics8111372
Chicago/Turabian StyleJun, Eun-Su, and Sangshin Kwak. 2019. "A Compromising Approach to Switching Losses and Waveform Quality in Three-phase Voltage Source Converters with Double-vector based Predictive Control Method" Electronics 8, no. 11: 1372. https://doi.org/10.3390/electronics8111372
APA StyleJun, E. -S., & Kwak, S. (2019). A Compromising Approach to Switching Losses and Waveform Quality in Three-phase Voltage Source Converters with Double-vector based Predictive Control Method. Electronics, 8(11), 1372. https://doi.org/10.3390/electronics8111372




