Modeling, Design Procedure and Control of a Low-Cost High-Gain Multi-Input Step-Up Converter
Abstract
1. Introduction
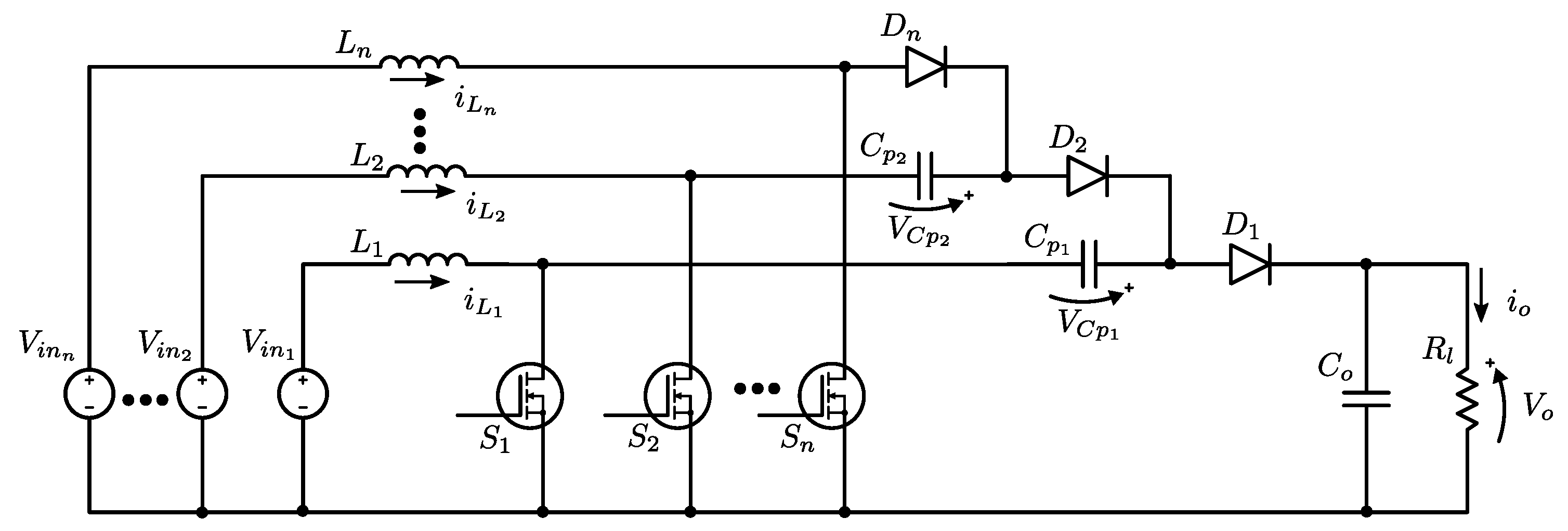
2. A Multi-Input High Gain Step-Up Converter
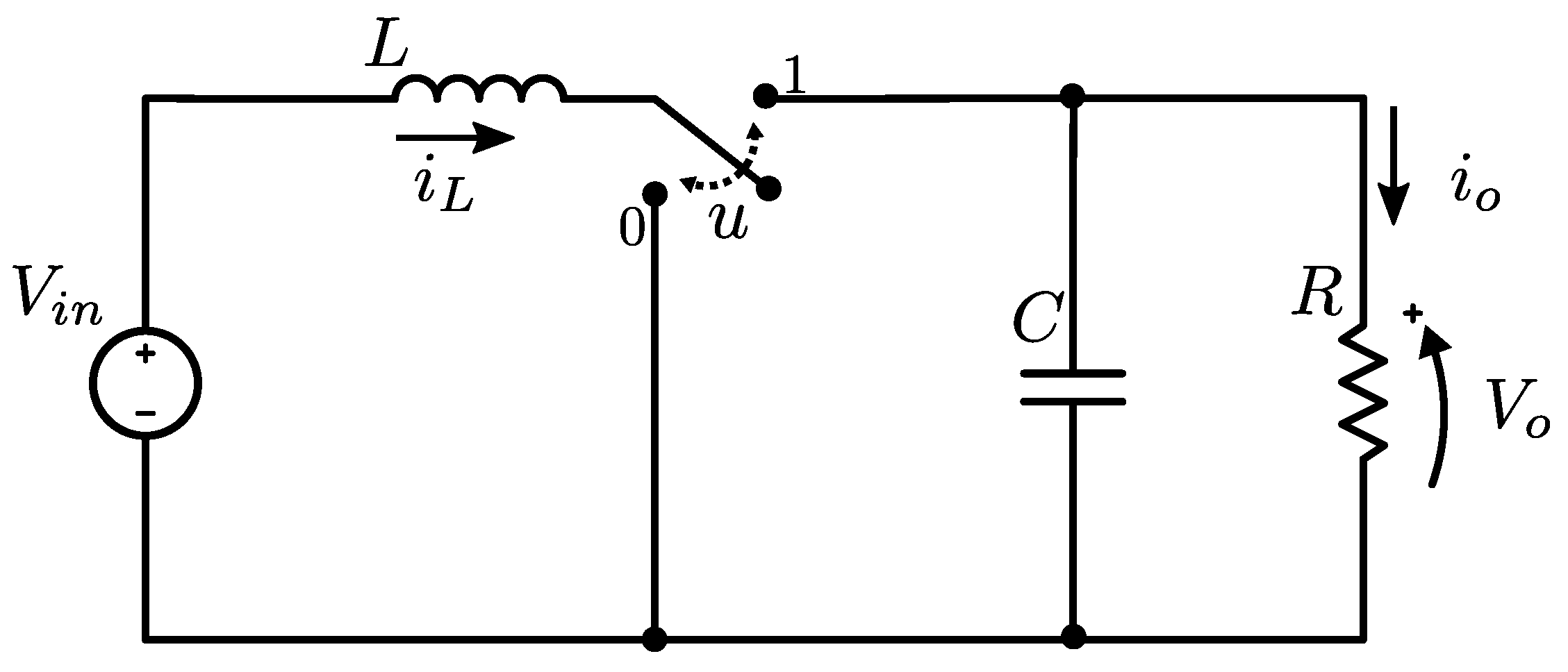
3. A Nonlinear Model for the Converter
- Mode 1 and Mode 3: , on:
- Mode 2: on, off:
- Mode 4: off, on:
4. The Design Procedure
4.1. Analysis of Ripple Signals in the Stationary State
4.2. General Expressions for Calculating Components’ Values
4.3. Design Example
5. Experimental Validation of the Design Procedure
6. Proposed Control Strategy
6.1. Indirect Control in Multi-Input Converters
6.2. Control Simulation Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Symbols
| Input Voltage 1 | |
| Input Voltage 2 | |
| Inductor 1 | |
| Inductor 2 | |
| capacitor | |
| Output capacitor | |
| Load | |
| Switch 1 | |
| Switch 2 | |
| Diode 1 | |
| Diode 2 | |
| , | Current on Inductor 1 |
| , | Current on Inductor 2 |
| , | Voltage on capacitor |
| , , | Voltage on capacitor , output voltage |
| Output current | |
| Switching frequency | |
| Switching period | |
| Duty cycle of Switch 1 | |
| Duty cycle of Switch 2 | |
| if Switch 1 is off (on) | |
| if Switch 2 is off (on) | |
| Gain of Source 1 | |
| Gain of Source 2 | |
| Power contributed by Source 1 | |
| Power contributed by Source 2 | |
| Output power | |
| Efficiency | |
| Output voltage reference | |
| e | Output voltage error |
| Contribution of Source 1 to the total power | |
| Contribution of Source 2 to the total power | |
| Current contribution of Source 1 | |
| Current contribution of Source 2 | |
| Ripple of signal x | |
| Average of signal x | |
| Steady state of signal x | |
| Time derivative of signal x |
References
- Gupta, A.K.; Saxena, R. Review on widely-used MPPT techniques for PV applications. In Proceedings of the 2016 International Conference on Innovation and Challenges in Cyber Security (ICICCS-INBUSH), Noida, India, 3–5 February 2016; pp. 270–273. [Google Scholar] [CrossRef]
- Khan, O.; Xiao, W. An Efficient Modeling Technique to Simulate and Control Submodule-Integrated PV System for Single-Phase Grid Connection. IEEE Trans. Sustain. Energy 2016, 7, 96–107. [Google Scholar] [CrossRef]
- Prasanth Ram, J.; Rajasekar, N. A Novel Flower Pollination Based Global Maximum Power Point Method for Solar Maximum Power Point Tracking. IEEE Trans. Power Electron. 2017, 32, 8486–8499. [Google Scholar] [CrossRef]
- Furusho, Y.; Noto, Y.; Fujii, K. 1MW Power Conditioning System with Multiple DC Inputs for PVs and Batteries. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018—ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 3711–3716. [Google Scholar] [CrossRef]
- Malinowski, M.; Milczarek, A.; Kot, R.; Goryca, Z.; Szuster, J.T. Optimized Energy-Conversion Systems for Small Wind Turbines: Renewable energy sources in modern distributed power generation systems. IEEE Power Electron. Mag. 2015, 2, 16–30. [Google Scholar] [CrossRef]
- Ssekulima, E.B.; Anwar, M.B.; Al Hinai, A.; El Moursi, M.S. Wind speed and solar irradiance forecasting techniques for enhanced renewable energy integration with the grid: A review. IET Renew. Power Gener. 2016, 10, 885–989. [Google Scholar] [CrossRef]
- Yaramasu, V.; Dekka, A.; Durán, M.J.; Kouro, S.; Wu, B. PMSG-based wind energy conversion systems: Survey on power converters and controls. IET Electr. Power Appl. 2017, 11, 956–968. [Google Scholar] [CrossRef]
- Yamashita, D.; Nakao, H.; Yonezawa, Y.; Nakashima, Y.; Ota, Y.; Nishioka, K.; Sugiyama, M. A new solar to hydrogen conversion system with high efficiency and flexibility. In Proceedings of the 2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017; pp. 441–446. [Google Scholar] [CrossRef]
- Neuhaus, K.; Alonso, C.; Gladysz, L.; Delamarre, A.; Watanabe, K.; Sugiyama, M. Solar to Hydrogen Conversion using Concentrated Multi-junction Photovoltaics and Distributed Micro-Converter Architecture. In Proceedings of the 2018 7th International Conference on Renewable Energy Research and Applications (ICRERA), Paris, France, 14–17 October 2018; pp. 744–747. [Google Scholar] [CrossRef]
- Teng, Y.; Wang, Z.; Li, Y.; Ma, Q.; Hui, Q.; Li, S. Multi-energy storage system model based on electricity heat and hydrogen coordinated optimization for power grid flexibility. CSEE J. Power Energy Syst. 2019, 5, 266–274. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y. A Systematic Approach to Synthesizing Multi-Input DC/DC Converters. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2626–2632. [Google Scholar] [CrossRef]
- Akhtar, F.; Rehmani, M.H. Energy Harvesting for Self-Sustainable Wireless Body Area Networks. IT Prof. 2017, 19, 32–40. [Google Scholar] [CrossRef]
- Lee, W.; Schubert, M.J.W.; Ooi, B.; Ho, S.J. Multi-Source Energy Harvesting and Storage for Floating Wireless Sensor Network Nodes With Long Range Communication Capability. IEEE Trans. Ind. Appl. 2018, 54, 2606–2615. [Google Scholar] [CrossRef]
- Chew, Z.J.; Ruan, T.; Zhu, M. Power Management Circuit for Wireless Sensor Nodes Powered by Energy Harvesting: On the Synergy of Harvester and Load. IEEE Trans. Power Electron. 2019, 34, 8671–8681. [Google Scholar] [CrossRef]
- Kumar, N.; Vasilakos, A.V.; Rodrigues, J.J.P.C. A Multi-Tenant Cloud-Based DC Nano Grid for Self-Sustained Smart Buildings in Smart Cities. IEEE Commun. Mag. 2017, 55, 14–21. [Google Scholar] [CrossRef]
- Pooranian, Z.; Abawajy, J.H.; P, V.; Conti, M. Scheduling Distributed Energy Resource Operation and Daily Power Consumption for a Smart Building to Optimize Economic and Environmental Parameters. Energies 2018, 11, 1348. [Google Scholar] [CrossRef]
- Asa, E.; Colak, K.; Czarkowski, D. Analysis of cascaded multi-output-port converter for wireless plug-in Hybrid/On-Board EV chargers. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 1323–1328. [Google Scholar] [CrossRef]
- Harighi, T.; Bayindir, R.; Padmanaban, S.; Mihet-Popa, L.; Hossain, E. An Overview of Energy Scenarios, Storage Systems and the Infrastructure for Vehicle-to-Grid Technology. Energies 2018, 11, 2174. [Google Scholar] [CrossRef]
- Kamel, M.; Ur Rehman, M.M.; Zhang, F.; Zane, R.; Maksimovic, D. Control of Independent-Input, Parallel-Output DC/DC Converters for Modular Battery Building Blocks. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 234–240. [Google Scholar] [CrossRef]
- Zhang, Y.; He, J.; Ionel, D.M. Modeling and Control of a Multiport Converter based EV Charging Station with PV and Battery. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Wei, Z.; Meng, S.; Xiong, B.; Ji, D.; Tseng, K.J. Enhanced online model identification and state of charge estimation for lithium-ion battery with a FBCRLS based observer. Appl. Energy 2016, 181, 332–341. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; Ji, D.; Tseng, K.J. A multi-timescale estimator for battery state of charge and capacity dual estimation based on an online identified model. Appl. Energy 2017, 204, 1264–1274. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; Xiong, R.; Dong, G.; Pou, J.; Tseng, K.J. Online Estimation of Power Capacity With Noise Effect Attenuation for Lithium-Ion Battery. IEEE Trans. Ind. Electron. 2019, 66, 5724–5735. [Google Scholar] [CrossRef]
- Schumacher, D.; Beik, O.; Emadi, A. Standalone Integrated Power Electronics System: Applications for Off-Grid Rural Locations. IEEE Electrif. Mag. 2018, 6, 73–82. [Google Scholar] [CrossRef]
- Eshetu Abaye, A.; Dengesu Haro, R. Assessment of Resource Potential and Feasibility Study of Standalone PV-Wind-Biogas Hybrid System for Rural Electrification. In Proceedings of the 2018 2nd International Conference on Electronics, Materials Engineering Nano-Technology (IEMENTech), Kolkata, India, 4–5 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Aswat, M.; Dangor, M.R.E.; Cronje, W. A Standalone Personal Consumer Grid for Rural Household Electrification. In Proceedings of the 2019 Southern African Universities Power Engineering Conference/ Robotics and Mechatronics/Pattern Recognition Association of South Africa (SAUPEC/RobMech/PRASA), Bloemfontein, South Africa, 28–30 January 2019; pp. 487–492. [Google Scholar] [CrossRef]
- Lavanya, A.; Navamani, J.D.; Vijayakumar, K.; Rakesh, R. Multi-input DC-DC converter topologies—A review. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 2230–2233. [Google Scholar] [CrossRef]
- Nguyen, B.L.; Cha, H.; Nguyen, T.; Kim, H. Family of Integrated Multi-Input Multi-Output DC-DC Power Converters. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018—ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 3134–3139. [Google Scholar] [CrossRef]
- Smith, N.; McCann, R. Analysis and simulation of a multiple input interleaved boost converter for renewable energy applications. In Proceedings of the 2014 IEEE 36th International Telecommunications Energy Conference (INTELEC), Vancouver, BC, Canada, 28 September–2 October 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Tang, C.Y.; Lin, J.T. Bidirectional Power Flow Control of a Multi Input Converter for Energy Storage System. Energies 2019, 12, 3756. [Google Scholar] [CrossRef]
- Fong, Y.C.; Cheng, K.W.E.; Raman, S.R.; Wang, X. Multi-Port Zero-Current Switching Switched-Capacitor Converters for Battery Management Applications. Energies 2018, 11, 1934. [Google Scholar] [CrossRef]
- Mohammadi, S.; Dezhbord, M.; Babalou, M.; Eskandarpour Azizkandi, M.; Hosseini, S.H. A New Non-Isolated Multi-Input DC-DC Converter with High Voltage gain and Low Average of Normalized Peak Inverse Voltage. In Proceedings of the 2019 10th International Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Shiraz, Iran, 12–14 February 2019; pp. 515–520. [Google Scholar] [CrossRef]
- Peterchev, A.V.; Xiao, J.; Sanders, S.R. Architecture and IC implementation of a digital VRM controller. IEEE Trans. Power Electron. 2003, 18, 356–364. [Google Scholar] [CrossRef]
- GarcÍa, O.; Zumel, P.; de Castro, A.; Alou, P.; Cobos, J.A. Current Self-Balance Mechanism in Multiphase Buck Converter. IEEE Trans. Power Electron. 2009, 24, 1600–1606. [Google Scholar] [CrossRef]
- Luo, Y.; Su, Y.; Huang, Y.; Lee, Y.; Chen, K.; Hsu, W. Time-Multiplexing Current Balance Interleaved Current-Mode Boost DC-DC Converter for Alleviating the Effects of Right-half-plane Zero. IEEE Trans. Power Electron. 2012, 27, 4098–4112. [Google Scholar] [CrossRef]
- Moradisizkoohi, H.; Elsayad, N.; Mohammed, O.A. An Integrated Interleaved Ultra High Step-Up DC-DC Converter Using Dual Cross-Coupled Inductors With Built-in Input Current Balancing for Electric Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2019. [Google Scholar] [CrossRef]
- Colalongo, L.; Dotti, D.; Richelli, A.; Kovács-Vajna, Z.M. Non-isolated multiple-input boost converter for energy harvesting. Electron. Lett. 2017, 53, 1132–1134. [Google Scholar] [CrossRef]
- Lara-Salazar, G.; Vázquez, N.; Hernández, C.; López, H.; Arau, J. Multi-input DC/DC converter with battery backup for renewable applications. In Proceedings of the 2016 13th International Conference on Power Electronics (CIEP), Guanajuato, Mexico, 20–23 June 2016; pp. 47–51. [Google Scholar] [CrossRef]
- Varesi, K.; Hosseini, S.H.; Sabahi, M.; Babaei, E.; Vosoughi, N. An improved Non-Isolated Multiple-Input buck dc-dc converter. In Proceedings of the 2017 8th Power Electronics, Drive Systems Technologies Conference (PEDSTC), Mashhad, Iran, 14–16 February 2017; pp. 119–124. [Google Scholar] [CrossRef]
- Babaei, E.; Abbasi, O. Structure for multi-input multi-output dc–dc boost converter. IET Power Electron. 2016, 9, 9–19. [Google Scholar] [CrossRef]
- Sun, Z.; Bae, S. Multiple-input Soft-switching Ćuk Converter. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 2272–2276. [Google Scholar] [CrossRef]
- Balaji, C.; Dash, S.S.; Hari, N.; Babu, P.C. A four port non-isolated multi input single output DC-DC converter fed induction motor. In Proceedings of the 2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017; pp. 631–637. [Google Scholar] [CrossRef]
- Seyed Mahmoodieh, M.E.; Deihimi, A. Battery-integrated multi-input step-up converter for sustainable hybrid energy supply. IET Power Electron. 2019, 12, 777–789. [Google Scholar] [CrossRef]
- Sahu, L.K.; Allamsetty, H.C.; Ghosh, S. Performance analysis of multiple input converter for standalone photovoltaic system. IET Power Electron. 2019, 12, 1295–1306. [Google Scholar] [CrossRef]
- Mishra, S.K.; Nayak, K.K.; Rana, M.S.; Dharmarajan, V. Switched-Boost Action Based Multiport Converter. IEEE Trans. Ind. Appl. 2019, 55, 964–975. [Google Scholar] [CrossRef]
- Akar, F.; Tavlasoglu, Y.; Ugur, E.; Vural, B.; Aksoy, I. A Bidirectional Nonisolated Multi-Input DC–DC Converter for Hybrid Energy Storage Systems in Electric Vehicles. IEEE Trans. Veh. Technol. 2016, 65, 7944–7955. [Google Scholar] [CrossRef]
- Macias, I.; Navarro, D.; Cortes, D. Controlling multi-input converters to act as electric energy router. In Studies in Informatics and Control; ICI Bucharest: Bucharest, Romania, 2015; pp. 23–32. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, B.; Luo, Q. High step-up converter with capacity of multiple input. IET Power Electron. 2012, 5, 524–531. [Google Scholar] [CrossRef]
- Lavanya, A.; Jayaseelan, N.; Navamani, J.D.; Kumar, K.V. Dual input DC-DC converter for renewable energy systems. In Proceedings of the 2017 International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 19–20 January 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Utkin, V. Sliding Modes in Control and Optimization; Communications and Control Egineering; Springer: New York, NY, USA, 1991; ISBN 3540535160. [Google Scholar]
- Kassakian, J.; Schlecht, M.; Verghese, G. Principles of Power Electronics; Adison Wesley: Boston, MA, USA, 1991; ISBN 0-201-09689-7. [Google Scholar]
- Fairchild. Switch Node Ring Control in Synchronous Buck Regulators; Technical Report AN-4162; Fairchild Semiconductor Corporation: Sunnyvale, CA, USA, 2013. [Google Scholar]
- Falin, J. Minimizing Ringing at the Switch Node of a Boost Converter; Technical Report; Texas Instruments Incorporated: Dallas, TX, USA, 2006. [Google Scholar]
- Kazimierczuk, M.K. Pulse-Width Modulated DC-DC Power Converters; John Wiley & Sons, Ltd.: New York, NY, USA, 2016. [Google Scholar]
- Sira-Ramirez, H. Nonlinear P-I controller design for switchmode DC-to-DC power converters. IEEE Trans. Circuits Syst. 1991, 38, 410–417. [Google Scholar] [CrossRef]
- Cortes, D.; Alvarez, J.; Alvarez, J. Robust sliding mode control for the boost converter. In Proceedings of the VIII IEEE International Power Electronics Congress, Technical Proceedings, CIEP 2002, Guadalajara, Mexico, 24 October 2002; pp. 208–212. [Google Scholar] [CrossRef]
- Middlebrook, R.D. Modeling current-programmed buck and boost regulators. IEEE Trans. Power Electron. 1989, 4, 36–52. [Google Scholar] [CrossRef]
- El Fadil, H.; Girt, F. Backstepping based control of PWM DC-DC boost power converters. Int. J. Electr. Power Eng. 2007, 1, 395–400. [Google Scholar] [CrossRef]
- Salimi, M.; Soltani, J.; Arab Markadeh, G.R.; Abjadi, N. Indirect output voltage regulation of DC-DC buck/boost converter operating in continuous and discontinuous conduction modes using adaptive backstepping approach. IET Power Electron. 2013, 6, 732–741. [Google Scholar] [CrossRef]
- Valenciaga, F.; Puleston, P.F.; Battaiotto, P.E. Power control of a photovoltaic array in a hybrid electric generation system using sliding mode techniques. IEE Proc. Control Theory Appl. 2001, 148, 448–455. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Power management of an isolated hybrid AC/DC micro-grid with fuzzy control of battery banks. IET Renew. Power Gener. 2015, 9, 484–493. [Google Scholar] [CrossRef]
- Mercorelli, P.; Kubasiak, N.; Liu, S. Multilevel bridge governor by using model predictive control in wavelet packets for tracking trajectories. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Volume 2004, pp. 4079–4084. [Google Scholar]
- Mercorelli, P.; Kubasiak, N.; Liu, S. Model predictive control of an electromagnetic actuator fed by multilevel PWM inverter. In Proceedings of the 2004 IEEE International Symposium on Industrial Electronics, Ajaccio, France, 4–7 May 2004; Volume 1, pp. 531–535. [Google Scholar]

















| Parameter | Value |
|---|---|
| Input voltages (, ) | 24 V, 24 V |
| Output voltage () | V |
| Output power () | 500 W |
| Sources power contribution (, ) | , |
| Switching Frequency () | 100 kHz |
| Max current ripple on () | of |
| Max current ripple on () | of |
| Max voltage ripple on () | of |
| Max voltage ripple on () | of |
| Results When V, V | Results When V, V | |
|---|---|---|
| Conduction loss of | W | W |
| Conduction loss of | W | W |
| Conduction loss of | W | W |
| Conduction loss of | W | W |
| Conduction loss of | W | W |
| Conduction loss of | W | W |
| Conduction loss of | W | W |
| Conduction loss of | W | W |
| Total power losses | W | W |
| Parameter | Results When V, V, | Results When V, V, | Results When V, V, |
|---|---|---|---|
| Input current | 12 A | A | A |
| Input current | 12 A | A | A |
| Input power | 280 W | 322 W | W |
| Input power | 280 W | 212 W | W |
| Output voltage | V | V | V |
| Gain | |||
| Gain | |||
| Output current | A | A | A |
| Output power | 521 W | 510 W | W |
| Efficiency | 90% | % |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Netzahuatl, E.; Cortes, D.; Ramirez-Salinas, M.A.; Resa, J.; Hernandez, L.; Hernandez, F.-D. Modeling, Design Procedure and Control of a Low-Cost High-Gain Multi-Input Step-Up Converter. Electronics 2019, 8, 1424. https://doi.org/10.3390/electronics8121424
Netzahuatl E, Cortes D, Ramirez-Salinas MA, Resa J, Hernandez L, Hernandez F-D. Modeling, Design Procedure and Control of a Low-Cost High-Gain Multi-Input Step-Up Converter. Electronics. 2019; 8(12):1424. https://doi.org/10.3390/electronics8121424
Chicago/Turabian StyleNetzahuatl, Edgardo, Domingo Cortes, Marco A. Ramirez-Salinas, Jorge Resa, Leobardo Hernandez, and Francisco-David Hernandez. 2019. "Modeling, Design Procedure and Control of a Low-Cost High-Gain Multi-Input Step-Up Converter" Electronics 8, no. 12: 1424. https://doi.org/10.3390/electronics8121424
APA StyleNetzahuatl, E., Cortes, D., Ramirez-Salinas, M. A., Resa, J., Hernandez, L., & Hernandez, F.-D. (2019). Modeling, Design Procedure and Control of a Low-Cost High-Gain Multi-Input Step-Up Converter. Electronics, 8(12), 1424. https://doi.org/10.3390/electronics8121424





