Salp Swarm Optimization Algorithm-Based Fractional Order PID Controller for Dynamic Response and Stability Enhancement of an Automatic Voltage Regulator System
Abstract
:1. Introduction
2. Mathematical Modelling of AVR System
3. Salp Swarm Optimization Algorithm and Its Implementation in the Current Study
- The algorithm keeps the best-obtained solution after each iteration and assigns it to the global optimum (food source) variable. Hence, it can never be wiped out even if the whole population deteriorates;
- The SSA updates the position of the leading salp with respect to the food source only which is the best solution obtained so far; therefore, the leader salp always explores and exploits the space around it for a better solution;
- The SSA updates the position of follower salps with respect to each other in order to let them move towards the leading salp gradually;
- Gradual movements of follower salps prevent the SSA from easily stagnating into local optima;
- Parameter c1 is decreased adaptively over the course of iterations which helps the algorithm to explore the search space at starting and exploits it at the ending phase;
- The SSA has only one main controlling parameter (c1) which reduces the complexity and makes it easy to implement.
4. Fitness Function Formulation and Implementation
5. Results and Discussion
5.1. SSA Convergence Behavior
5.2. Transient Response Analysis
5.3. Stability Analysis
5.4. Robustness Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Karimi-Ghartemani, M.; Zamani, M.; Sadati, N.; Parniani, M. An optimal fractional order controller for an AVR system using particle swarm optimization algorithm. In Proceedings of the 2007 Large Engineering Systems Conference on Power Engineering, Montreal, QC, Canada, 10–12 October 2007; pp. 244–249. [Google Scholar]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.; HosseinNia, S.H.; Petlenkov, E. FOPID controllers and their industrial applications: A survey of recent results. IFAC PapersOnLine 2018, 51, 25–30. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PI/sup/spl lambda//D/sup/spl mu//-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Li, N.; Han, M.; Tang, Y.; Liu, F. Optimal fractional order PID controller design for automatic voltage regulator system based on reference model using particle swarm optimization. Int. J. Mach. Learn. Cybern. 2017, 8, 1595–1605. [Google Scholar] [CrossRef]
- Zamani, M.; Karimi-Ghartemani, M.; Sadati, N.; Parniani, M. Design of a fractional order PID controller for an AVR using particle swarm optimization. Control Eng. Pract. 2009, 17, 1380–1387. [Google Scholar] [CrossRef]
- Ramezanian, H.; Balochian, S.; Zare, A. Design of optimal fractional-order PID controllers using particle swarm optimization algorithm for automatic voltage regulator (AVR) system. J. Control Autom. Electr. Syst. 2013, 24, 601–611. [Google Scholar] [CrossRef]
- Lahcene, R.; Abdeldjalil, S.; Aissa, K. Optimal tuning of fractional order PID controller for AVR system using simulated annealing optimization algorithm. In Proceedings of the 2017 5th International Conference on Electrical Engineering-Boumerdes, Boumerdes, Algeria, 29–31 October 2017; pp. 1–6. [Google Scholar]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A. Fractional adaptive control for an automatic voltage regulator. ISA Trans. 2013, 52, 807–815. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Chaotic multi-objective optimization based design of fractional order PIλDμ controller in AVR system. Int. J. Electr. Power Energy Syst. 2012, 43, 393–407. [Google Scholar] [CrossRef] [Green Version]
- Jumani, T.A.; Mustafa, M.W.; Rasid, M.M.; Mirjat, N.H.; Baloch, M.H.; Salisu, S. Optimal Power Flow Controller for Grid-Connected Microgrids using Grasshopper Optimization Algorithm. Electronics 2019, 8, 111. [Google Scholar] [CrossRef] [Green Version]
- Jumani, T.A.; Mustafa, M.W.; Rasid, M.M.; Mirjat, N.H.; Leghari, Z.H.; Saeed, M.S. Optimal Voltage and Frequency Control of an Islanded Microgrid using Grasshopper Optimization Algorithm. Energies 2018, 11, 3191. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Du, W.; Nian, F. An adaptive particle swarm optimization algorithm based on directed weighted complex network. Math. Probl. Eng. 2014, 2014, 7. [Google Scholar] [CrossRef] [Green Version]
- Gozde, H.; Taplamacioglu, M.C. Comparative performance analysis of artificial bee colony algorithm for automatic voltage regulator (AVR) system. J. Frankl. Inst. 2011, 348, 1927–1946. [Google Scholar] [CrossRef]
- Sahib, M.A. A novel optimal PID plus second order derivative controller for AVR system. Eng. Sci. Technol. Int. J. 2015, 18, 194–206. [Google Scholar] [CrossRef] [Green Version]
- Hekimoğlu, B.; Ekinci, S. Grasshopper optimization algorithm for automatic voltage regulator system. In Proceedings of the 2018 5th International Conference on Electrical and Electronic Engineering (ICEEE), Istanbul, Turkey, 3–5 May 2018; pp. 152–156. [Google Scholar]
- Güvenç, U.; Işik, A.H.; Yiğit, T.; Akkaya, I. Performance analysis of biogeography-based optimization for automatic voltage regulator system. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 1150–1162. [Google Scholar] [CrossRef]
- Sahu, B.K.; Panda, S.; Mohanty, P.K.; Mishra, N. Robust analysis and design of PID controlled AVR system using Pattern Search algorithm. In Proceedings of the 2012 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bengaluru, India, 16–19 December 2012; pp. 1–6. [Google Scholar]
- Mukherjee, V.; Ghoshal, S. Intelligent particle swarm optimized fuzzy PID controller for AVR system. Electr. Power Syst. Res. 2007, 77, 1689–1698. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Robust optimal power management system for a hybrid AC/DC micro-grid. IEEE Trans. Sustain. Energy 2015, 6, 675–687. [Google Scholar] [CrossRef]
- Schonberger, J.; Duke, R.; Round, S.D. DC-bus signaling: A distributed control strategy for a hybrid renewable nanogrid. IEEE Trans. Ind. Electron. 2006, 53, 1453–1460. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Tolba, M.; Rezk, H.; Diab, A.; Al-Dhaifallah, M. A novel robust methodology based Salp swarm algorithm for allocation and capacity of renewable distributed generators on distribution grids. Energies 2018, 11, 2556. [Google Scholar] [CrossRef] [Green Version]
- El-Fergany, A.A. Extracting optimal parameters of PEM fuel cells using Salp Swarm Optimizer. Renew. Energy 2018, 119, 641–648. [Google Scholar] [CrossRef]
- Abusnaina, A.A.; Ahmad, S.; Jarrar, R.; Mafarja, M. Training neural networks using salp swarm algorithm for pattern classification. In Proceedings of the 2nd International Conference on Future Networks and Distributed Systems, Amman, Jordan, 26–27 June 2018; p. 17. [Google Scholar]
- Kumari, S.; Shankar, G. A Novel Application of Salp Swarm Algorithm in Load Frequency Control of Multi-Area Power System. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Madras, India, 18–21 December 2018; pp. 1–5. [Google Scholar]
- Seborg, D.E.; Mellichamp, D.A.; Edgar, T.F.; Doyle, F.J., III. Process Dynamics and Control, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Killingsworth, N.; Krstic, M. Auto-tuning of PID controllers via extremum seeking. In Proceedings of the American Control Conference 2005, Portland, OR, USA, 8–10 June 2005; pp. 2251–2256. [Google Scholar]
- Jumani, T.A.; Mustafa, M.; Rasid, M.M.; Anjum, W.; Ayub, S. Salp Swarm Optimization Algorithm-Based Controller for Dynamic Response and Power Quality Enhancement of an Islanded Microgrid. Processes 2019, 7, 840. [Google Scholar] [CrossRef] [Green Version]

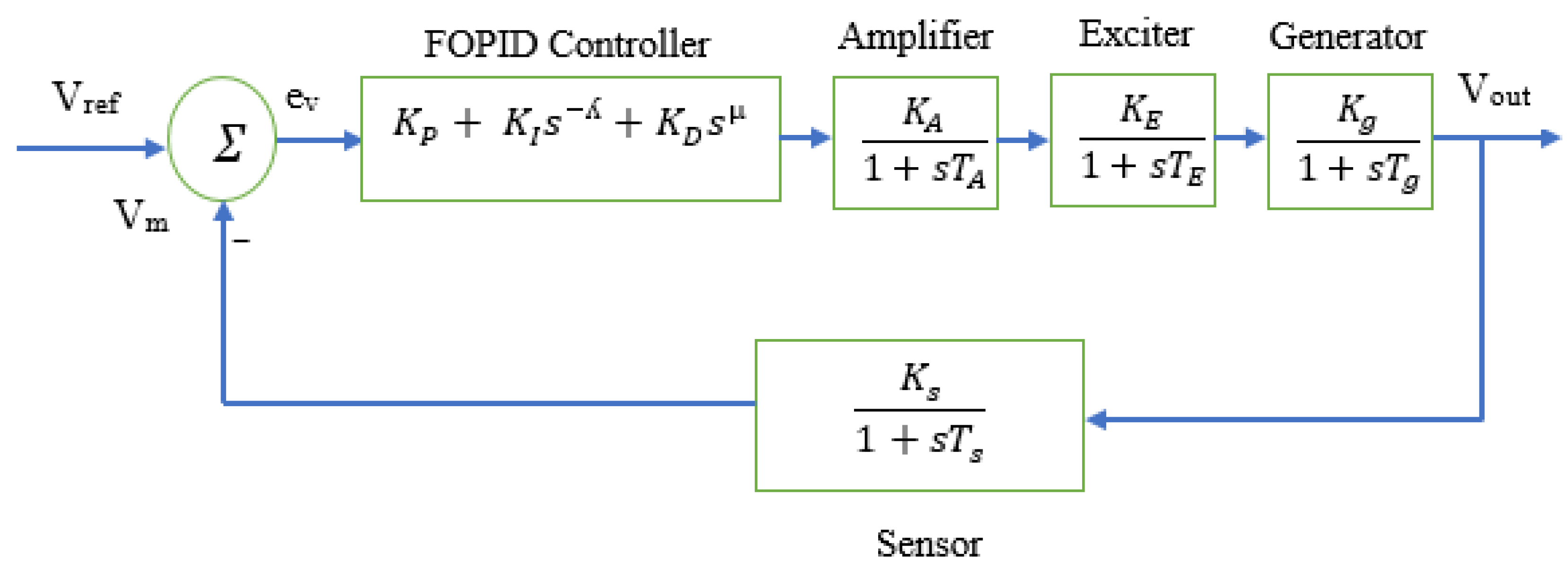








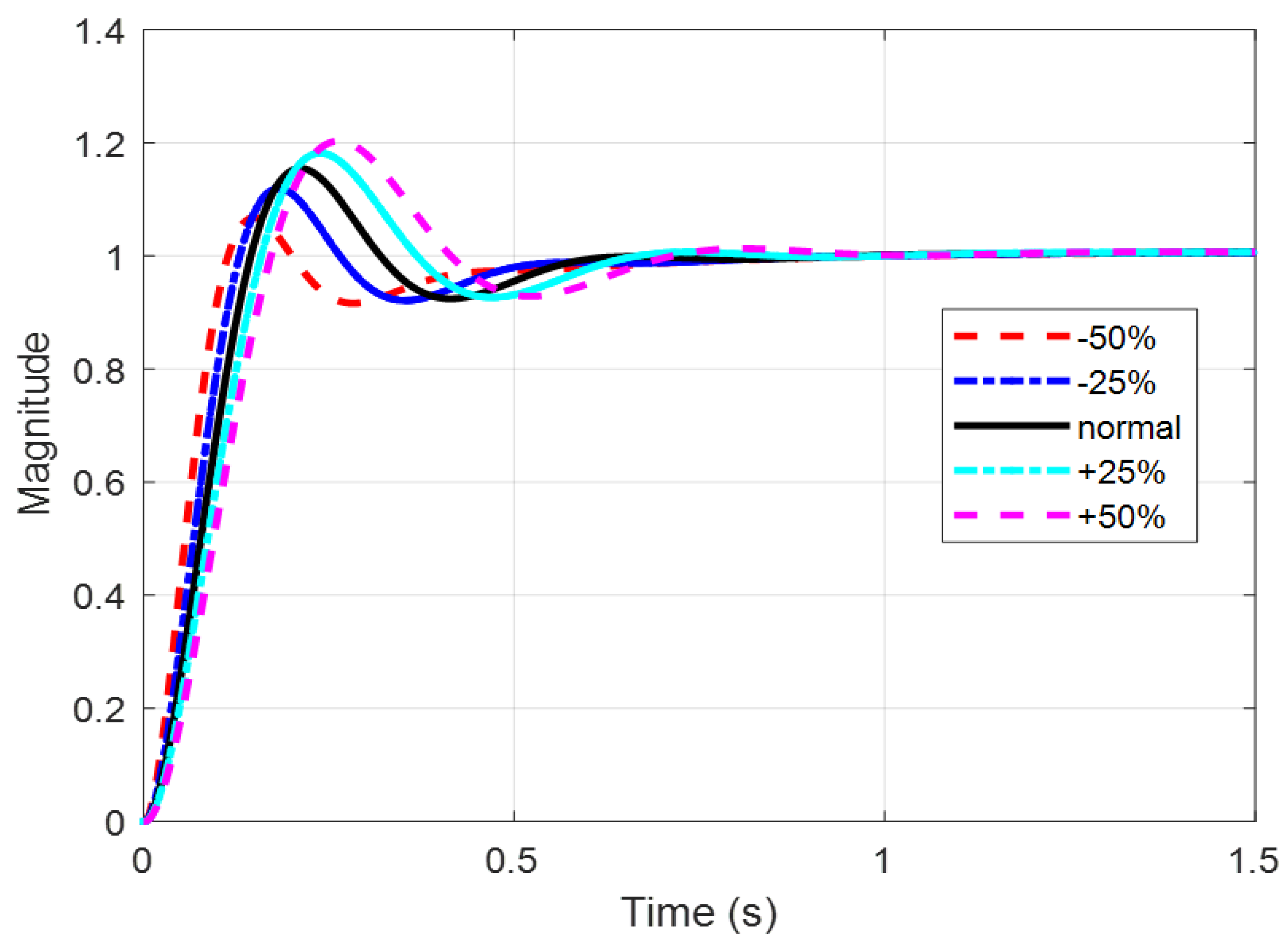
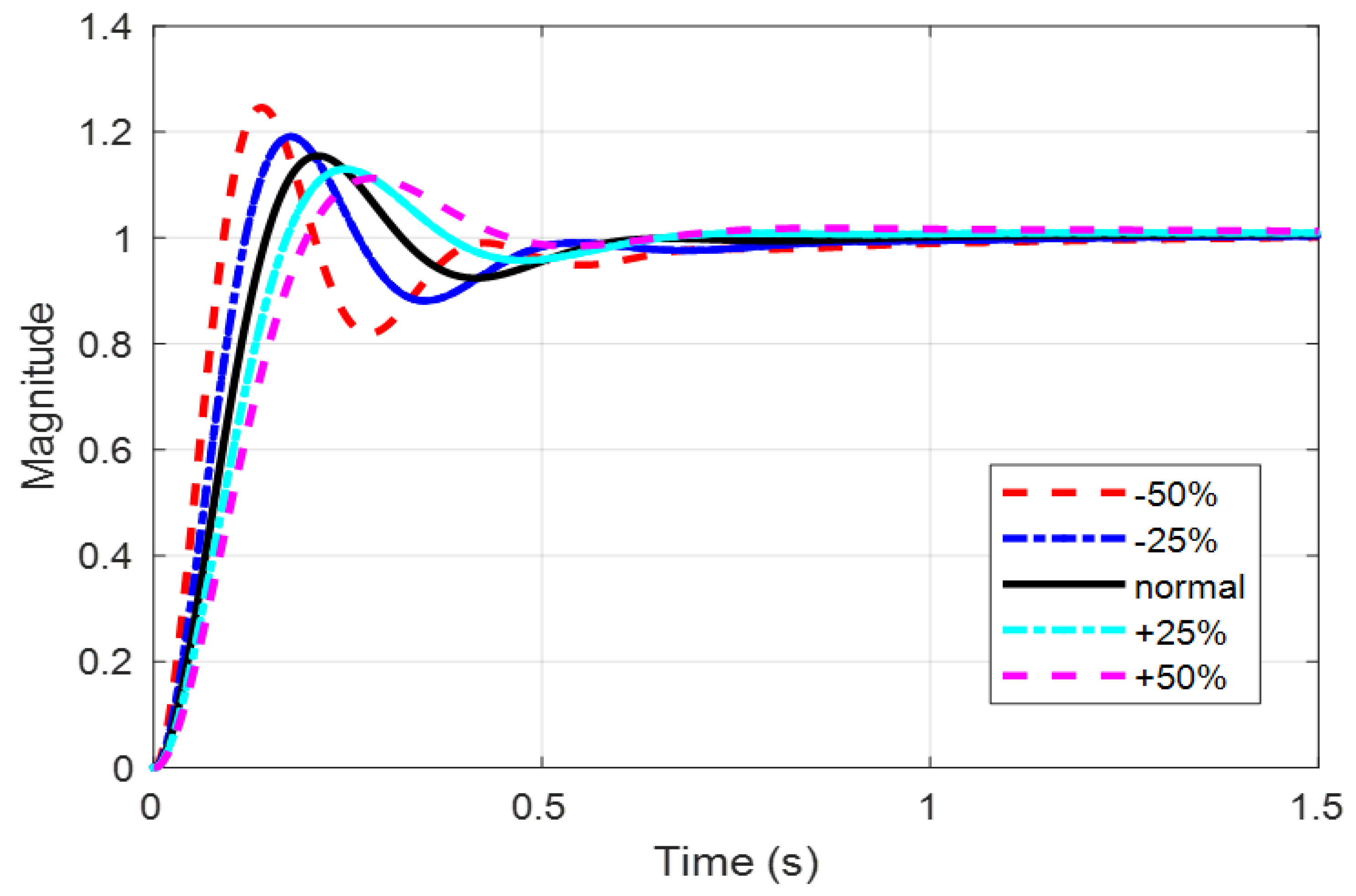


| PID/FOPID Tuning Method | Dynamic Response Comparison | ||||
|---|---|---|---|---|---|
| Peak Value | %Mp | tr | tp | ts | |
| SSA-FOPID (proposed) | 1.15 | 15.5 | 0.0981 | 0.209 | 0.551 |
| WOA-FOPID | 1.23 | 22.5 | 0.111 | 0.256 | 0.931 |
| DE-PID [14] | 1.3285 | 32.8537 | 0.1516 | 0.3655 | 2.6495 |
| PSO-PIDD 2 [15] | 1.1882 | 18.8183 | 0.1493 | 0.3372 | 0.8145 |
| ABC-PID [14] | 1.2501 | 25.0071 | 0.1557 | 0.3676 | 3.0939 |
| GOA-PID [16] | 1.2053 | 20.5306 | 0.1300 | 0.2862 | 0.9706 |
| BBO-PID [17] | 1.1552 | 15.5187 | 0.1485 | 0.3165 | 1.4457 |
| PSA-PID [18] | 1.1684 | 16.8449 | 0.1445 | 0.3060 | 0.8039 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, I.A.; Alghamdi, A.S.; Jumani, T.A.; Alamgir, A.; Awan, A.B.; Khidrani, A. Salp Swarm Optimization Algorithm-Based Fractional Order PID Controller for Dynamic Response and Stability Enhancement of an Automatic Voltage Regulator System. Electronics 2019, 8, 1472. https://doi.org/10.3390/electronics8121472
Khan IA, Alghamdi AS, Jumani TA, Alamgir A, Awan AB, Khidrani A. Salp Swarm Optimization Algorithm-Based Fractional Order PID Controller for Dynamic Response and Stability Enhancement of an Automatic Voltage Regulator System. Electronics. 2019; 8(12):1472. https://doi.org/10.3390/electronics8121472
Chicago/Turabian StyleKhan, Ismail Akbar, Ali S. Alghamdi, Touqeer Ahmed Jumani, Arbab Alamgir, Ahmed Bilal Awan, and Attaullah Khidrani. 2019. "Salp Swarm Optimization Algorithm-Based Fractional Order PID Controller for Dynamic Response and Stability Enhancement of an Automatic Voltage Regulator System" Electronics 8, no. 12: 1472. https://doi.org/10.3390/electronics8121472
APA StyleKhan, I. A., Alghamdi, A. S., Jumani, T. A., Alamgir, A., Awan, A. B., & Khidrani, A. (2019). Salp Swarm Optimization Algorithm-Based Fractional Order PID Controller for Dynamic Response and Stability Enhancement of an Automatic Voltage Regulator System. Electronics, 8(12), 1472. https://doi.org/10.3390/electronics8121472






