A Two-Degree-of-Freedom Cantilever-Based Vibration Triboelectric Nanogenerator for Low-Frequency and Broadband Operation
Abstract
1. Introduction
2. Design and Analysis
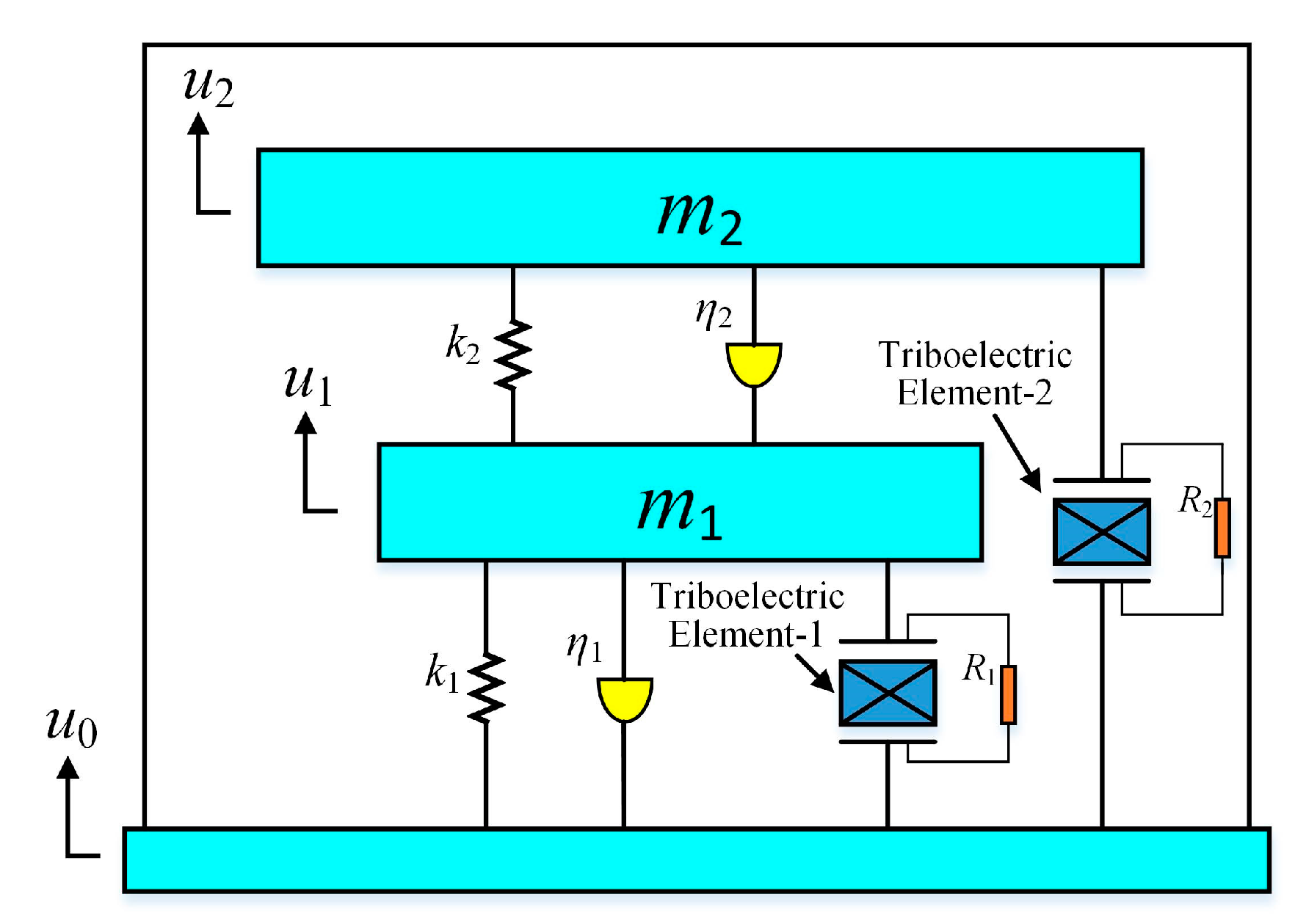
2.1. Device Configuration
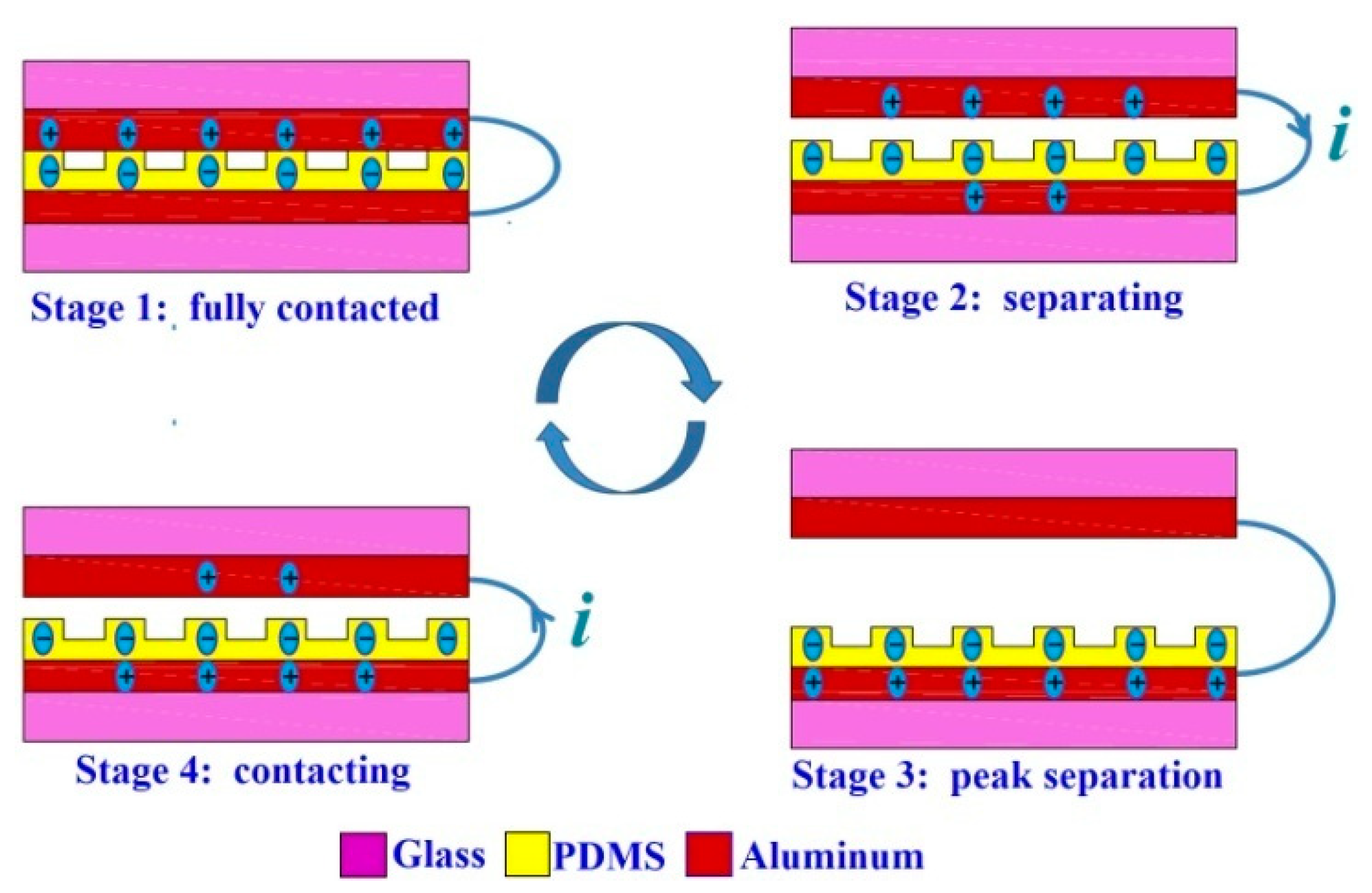
2.2. Principle of Operation
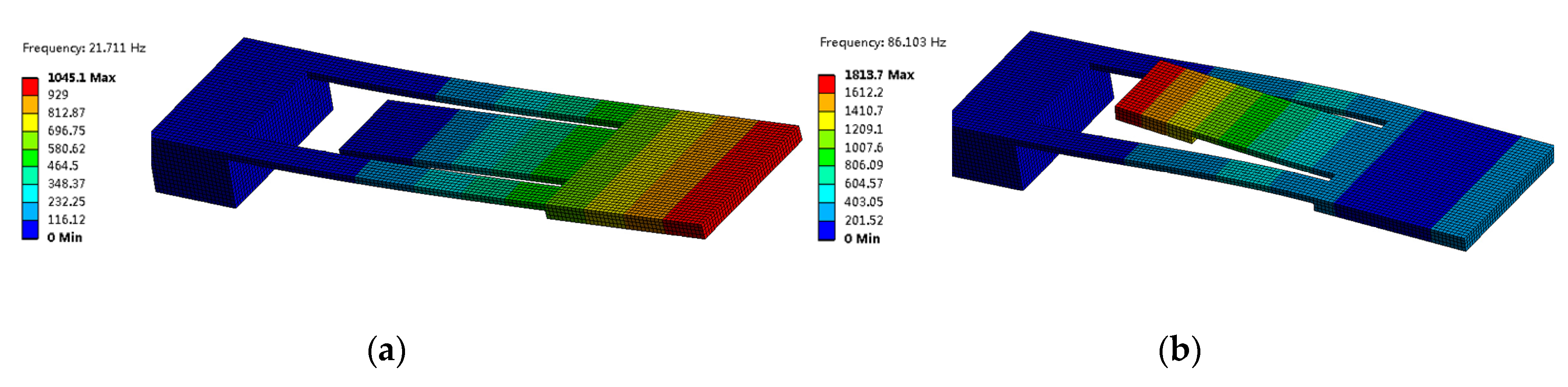
2.3. Theoretical Analysis
2.4. Fabrication Process
3. Testing and Discussion
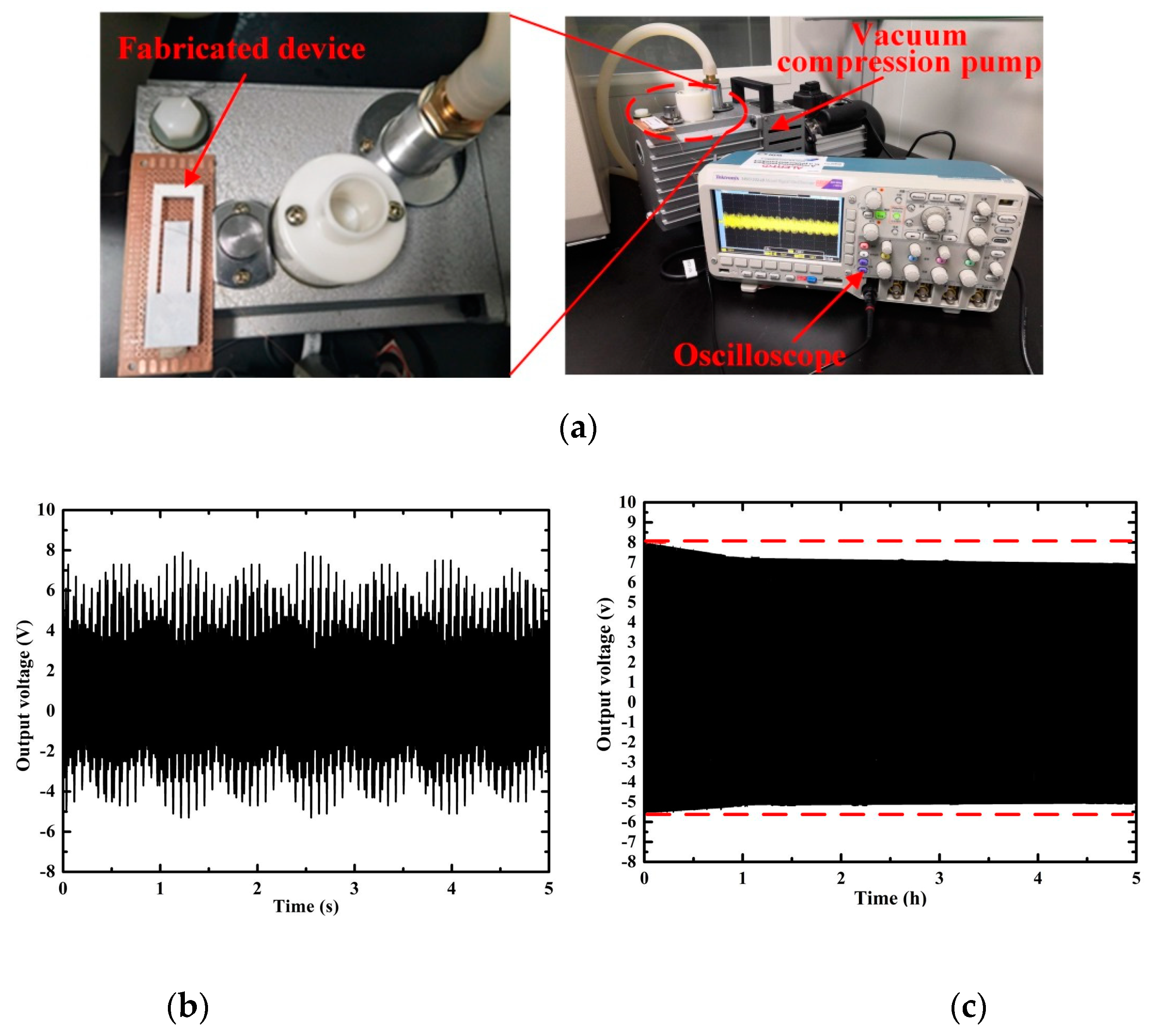
3.1. Testing Setup
3.2. Tip Amplitudes of the VTENG without Bottom Parts Assembly
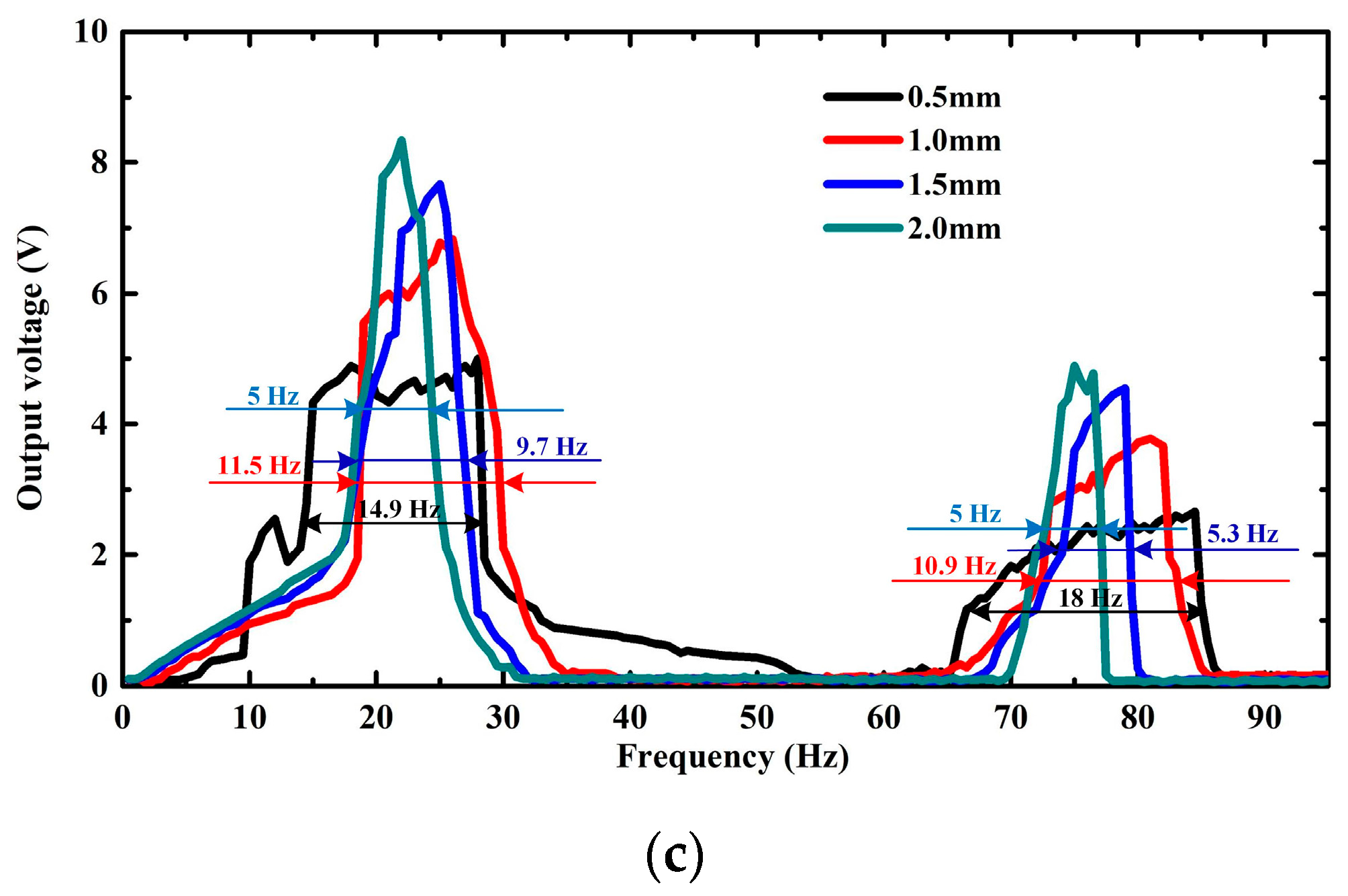
3.3. Effect of Different PDMS Microstructures Configuration
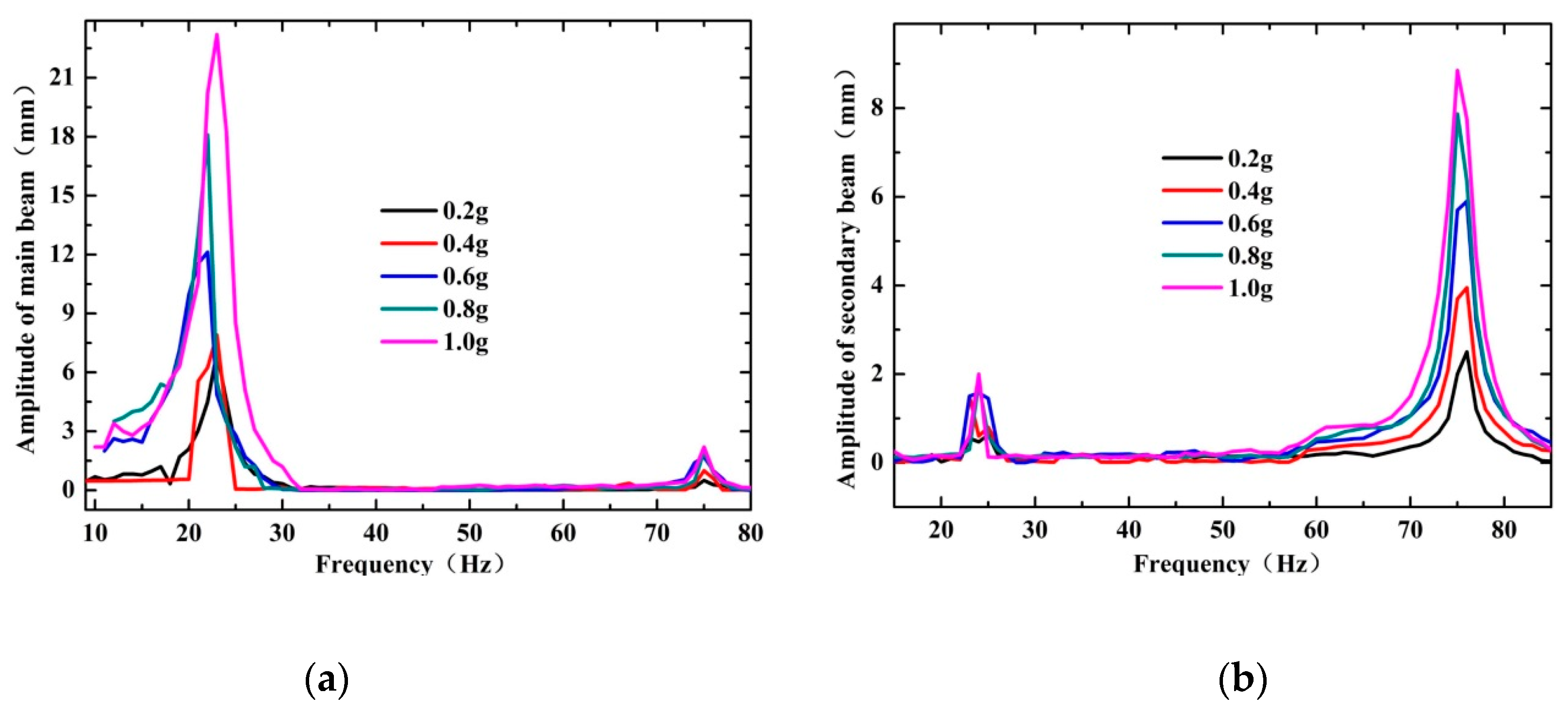
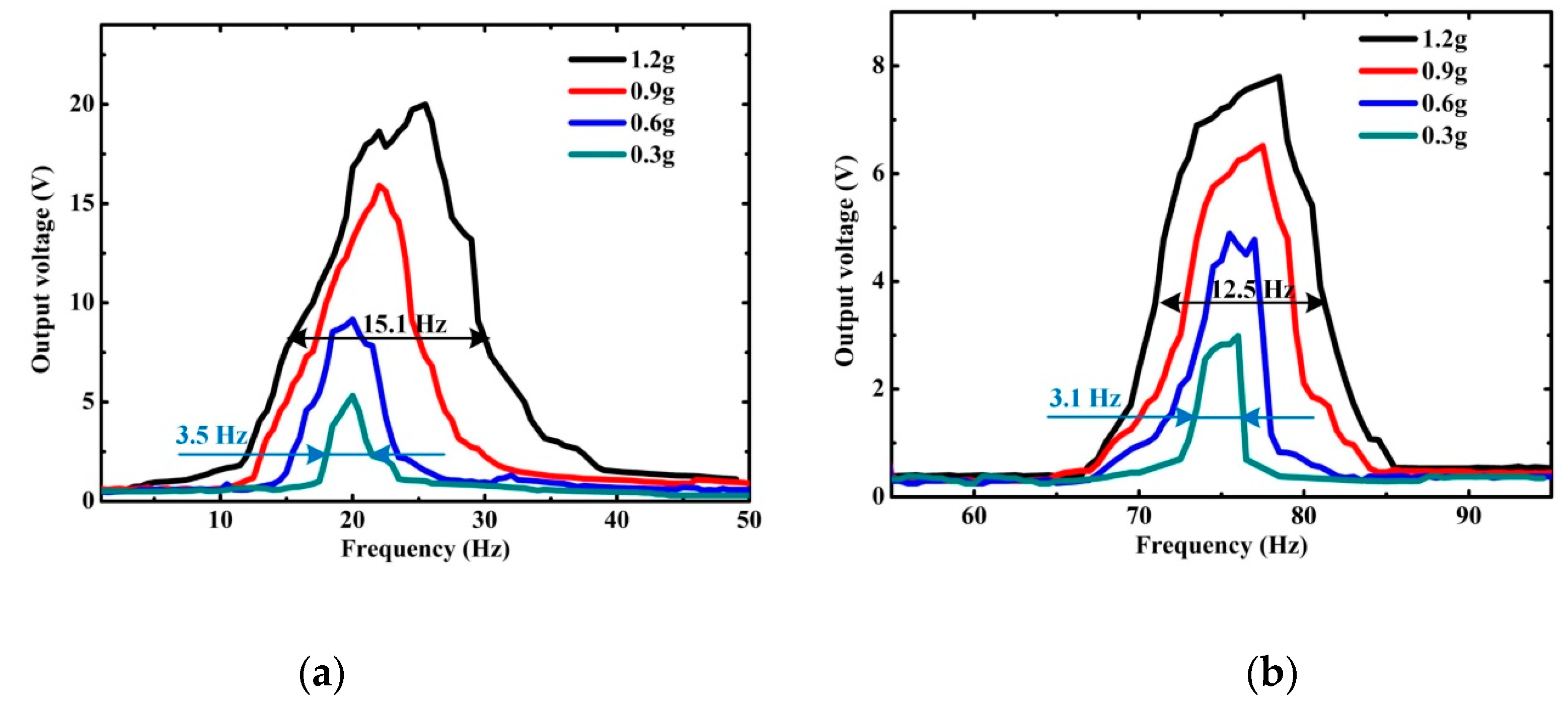
3.4. Broadband Behavior of VTENG
3.5. Voltage and Power Characteristics
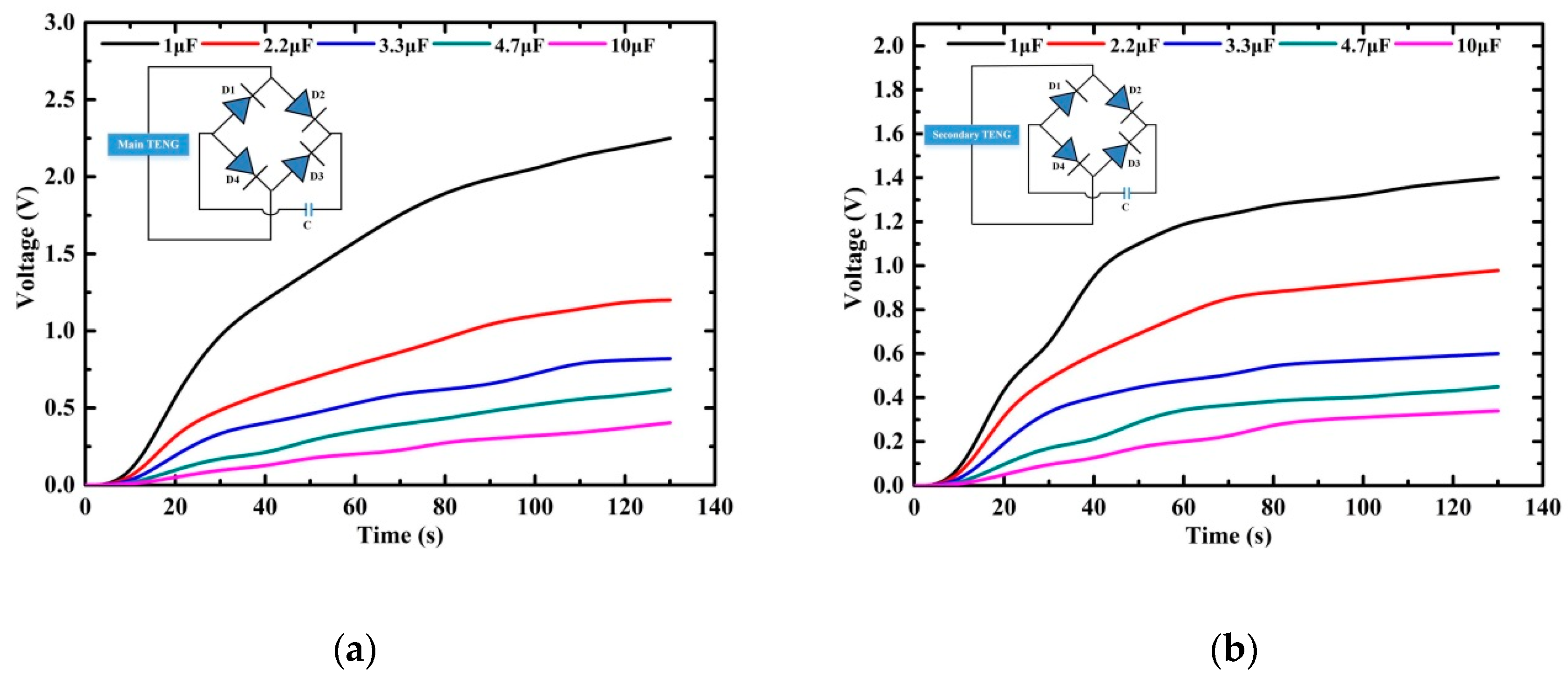
3.6. Capacitor Charging Characteristics
3.7. The Application of Fabricated VTENG
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, P.; Pan, L.; Wang, J.; Xu, M.; Dai, G.; Zou, H.; Dong, K.; Wang, Z.L. An ultra-low-friction triboelectric-electromagnetic hybrid nanogenerator for rotation energy harvesting and self-powered wind speed sensor. ACS Nano 2018, 12, 9433–9440. [Google Scholar] [CrossRef] [PubMed]
- Ud Din, A.; Kamran, M.; Mahmood, W.; Aurangzeb, K.; Saud Altamrah, A.; Lee, J. An efficient CMOS dual switch rectifier for piezoelectric energy-harvesting circuits. Electronics 2019, 8, 66. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, B.; Liu, J.; Wang, X.; Wang, L.; Chen, X.; Yang, C. A flexible and biocompatible triboelectric nanogenerator with tunable internal resistance for powering wearable devices. Sci. Rep. 2016, 6, 22233. [Google Scholar] [CrossRef] [PubMed]
- Khalili, M.; Biten, A.B.; Vishwakarma, G.; Ahmed, S.; Papagiannakis, A.T. Electromechanical characterization of a piezoelectric energy harvester. Appl. Energy 2019, 8, 113585. [Google Scholar] [CrossRef]
- Tang, G.; Liu, J.; Yang, B.; Luo, J.; Liu, H.; Li, Y.; Yang, C.; He, D.; Dao, V.D.; Tanaka, K.; et al. Fabrication and analysis of high-performance piezoelectric MEMS generators. J. Micromech. Microeng. 2012, 22, 065017. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, Z.; Shu, C.; Zhang, J.; Zhang, Q.; Li, C. A rotational piezoelectric energy harvester for efficient wind energy harvesting. Sens. Actuators. A 2017, 262, 123–129. [Google Scholar] [CrossRef]
- Ju, S.; Ji, C. Impact-based piezoelectric vibration energy harvester. Appl. Energy 2018, 214, 139–151. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Wang, F.; Luo, A.; Hu, Y.; Li, X. Micro electrostatic energy harvester with both broad bandwidth and high normalized power density. Appl. Energy 2018, 212, 362–371. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Zhang, A.; Peng, Z.; Luo, D.; Chen, R.; Wang, F. Electrostatic energy harvesting device with dual resonant structure for wideband random vibration sources at low frequency. Rev. Sci. Instrum. 2016, 87, 125001. [Google Scholar] [CrossRef]
- Pan, Y.; Lin, T.; Qian, F.; Liu, C.; Yu, J.; Zuo, L.; Zuo, J. Modeling and field-test of a compact electromagnetic energy harvester for railroad transportation. Appl. Energy 2019, 247, 309–321. [Google Scholar] [CrossRef]
- Fan, K.; Cai, M.; Liu, H.; Zhang, Y. Capturing energy from ultra-low frequency vibrations and human motion through a monostable electromagnetic energy harvester. Energy 2019, 169, 356–368. [Google Scholar] [CrossRef]
- Ravichandran, A.N.; Calmes, C.; Serres, J.R.; Ramuz, M.; Blayac, S. Compact and high performance wind actuated venturi triboelectric energy harvester. Nano Energy 2019, 62, 449–457. [Google Scholar] [CrossRef]
- Lee, B.; Kim, D.H.; Park, J.; Park, K.; Lee, K.J.; Jeong, C.K. Modulation of surface physics and chemistry in triboelectric energy harvesting technologies. Sci. Technol. Adv. Mater. 2019, 20, 758–773. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Ouyang, H.; Davis, R.B. Triboelectric energy harvesting from the vibro-impact of three cantilevered beams. Mech. Syst. Sig. Process. 2019, 121, 509–531. [Google Scholar] [CrossRef]
- Cheng, T.; Li, Y.; Wang, Z.L.; Wang, Y.; Gao, Q.; Ma, T. Triboelectric nanogenerator by integrating a cam and a movable frame for ambient mechanical energy harvesting. Nano Energy 2019, 60, 137–143. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, X.; Wang, S.; Ouyang, H.; Chen, P.; Song, L.; Wang, Z.L. Honeycomb structure inspired triboelectric nanogenerator for highly effective vibration energy harvesting and self-powered engine condition monitoring. Adv. Energy Mater. 2019, 9, 1902460. [Google Scholar] [CrossRef]
- Sari, I.; Balkan, T.; Kulah, H. An electromagnetic micro power generator for wideband environmental vibrations. Sens. Actuators A 2008, 145–146, 405–413. [Google Scholar] [CrossRef]
- Liu, J.; Fang, H.; Xu, Z.; Mao, X.; Shen, X.; Chen, D.; Cai, B. A MEMS-based piezoelectric power generator array for vibration energy harvesting. Microelectron. J. 2008, 39, 802–806. [Google Scholar] [CrossRef]
- Qi, S.; Shuttleworth, R.; Olutunde Oyadiji, S.; Wright, J. Design of a multiresonant beam for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2010, 19, 094009. [Google Scholar] [CrossRef]
- Ou, Q.; Chen, X.; Gutschmidt, S.; Wood, A.; Leigh, N. A two-mass cantilever beam model for vibration energy harvesting applications. In Proceedings of the 2010 IEEE International Conference on Automation Science and Engineering (CASE), Toronto, ON, Canada, 21–24 August 2010. [Google Scholar]
- Arafa, M.; Akl, W.; Aladwani, A.; Aldraihem, O.; Baz, A. Experimental implementation of a cantilevered piezoelectric energy harvester with a dynamic magnifier. Proc. SPIE 2011, 7977, 79770Q-1–79770Q-9. [Google Scholar] [CrossRef]
- Wu, H.; Tang, L.; Yang, Y.; Soh, C.K. A novel two-degrees-of-freedom piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2012, 24, 357–368. [Google Scholar] [CrossRef]
- Kim, J.E.; Kim, Y.Y. Power enhancing by reversing mode sequence in tuned mass-spring unit attached vibration energy harvester. AIP Adv. 2013, 3, 72103. [Google Scholar] [CrossRef]
- Soliman, M.S.M.; Abdel-Rahman, E.M.; El-Saadany, E.F.; Mansour, R.R. A wideband vibration-based energy harvester. J. Micromech. Microeng. 2008, 18, 115021. [Google Scholar] [CrossRef]
- Liu, H.; Lee, C.; Kobayashi, T.; Tay, C.J.; Quan, C. Investigation of a MEMS piezoelectric energy harvester system with a frequency-widened-bandwidth mechanism introduced by mechanical stoppers. Smart Mater. Struct. 2012, 21, 035005. [Google Scholar] [CrossRef]
- Liu, H.; Tay, C.J.; Quan, C.; Kobayashi, T.; Lee, C. Piezoelectric MEMS energy harvester for low-frequency vibrations with wideband operation range and steadily increased output power. J. Microelectromech. Syst. 2011, 20, 1131–1142. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, A.; Hu, H.; Zhu, H. Hybrid electromagnetic and triboelectric nanogenerators with multi-impact for wideband frequency energy harvesting. Energies 2017, 10, 2024. [Google Scholar] [CrossRef]
- Ibrahim, A.; Ramini, A.; Towfighian, S. Modeling an impact vibration harvester with triboelectric transduction. In Proceedings of the International Design Engineering Technical Conferences & Computers and Information in Engineering Conference IDETC/CIE, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Bhatia, D.; Kim, S.W.; Kim, W.; Lee, S.; Choi, D. Tandem triboelectric nanogenerators for optimally scavenging mechanical energy with broadband vibration frequencies. Nano Energy 2017, 33, 515–521. [Google Scholar] [CrossRef]
- Yang, J.; Chen, J.; Yang, Y.; Zhang, H.; Yang, W.; Bai, P.; Wang, Z.L. Broadband vibrational energy harvesting based on a triboelectric nanogenerator. Adv. Energy Mater. 2014, 4, 1301322. [Google Scholar] [CrossRef]
- Ibrahim, A.; Ramini, A.; Towfighian, S. Experimental and theoretical investigation of an impact vibration harvester with triboelectric transduction. J. Sound Vib. 2018, 416, 111–124. [Google Scholar] [CrossRef]
- Nelson, D.; Ibrahim, A.; Towfighian, S. A tunable triboelectric wideband energy harvester. J. Intell. Mater. Syst. Struct. 2019, 30, 1745–1756. [Google Scholar] [CrossRef]
- Dhakar, L.; Tay, F.E.H.; Lee, C. Investigation of contact electrification based broadband energy harvesting mechanism using elastic PDMS microstructures. J. Micromech. Microeng. 2014, 24, 104002. [Google Scholar] [CrossRef]
- Dhakar, L.; Tay, F.E.H.; Lee, C. Development of a broadband triboelectric energy harvester with SU-8 micropillars. J. Microelectromech. Syst. 2014, 24, 91–99. [Google Scholar] [CrossRef]
- Nafari, A.; Sodano, H.A. Surface morphology effects in a vibration based triboelectric energy harvester. Smart Mater. Struct. 2017, 27, 015029. [Google Scholar] [CrossRef]
- Niu, S.; Wang, S.; Lin, L.; Liu, Y.; Zhou, Y.S.; Hu, Y.; Wang, Z.L. Theoretical study of contact-mode triboelectric nanogenerators as an effective power source. Energy Environ. Sci. 2013, 6, 3576–3583. [Google Scholar] [CrossRef]
- Xu, G.; Li, X.; Xia, X.; Fu, J.; Ding, W.; Zi, Y. On the force and energy conversion in triboelectric nanogenerators. Nano Energy 2019, 59, 154–161. [Google Scholar] [CrossRef]
- Zayed, A.A.A.; Assal, S.F.M.; Nakano, k.; Kaizuka, T.; EI-Bab, A.M.R.F. Design procedure and experimental verification of a broadband quad-stable 2-DOF vibration energy harvester. Sensors 2019, 19, 2893. [Google Scholar] [CrossRef]
- Wu, H.; Tang, L.; Yang, Y.; Soh, C.K. Development of a broadband nonlinear two-degree-of-freedom piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2014, 25, 1875–1889. [Google Scholar] [CrossRef]
- Fan, F.; Lin, L.; Zhu, G.; Wu, W.; Zhang, R.; Wang, Z.L. Transparent triboelectric nanogenerators and self-powered pressure sensors based on micropatterned plastic films. Nano Lett. 2012, 12, 3109–3114. [Google Scholar] [CrossRef]
- Jeon, S.; Kim, D.; Seol, M.; Park, S.; Choi, Y. 3-Dimensional broadband energy harvester based on internal hydrodynamic oscillation with a package structure. Nano Energy 2015, 17, 82–90. [Google Scholar] [CrossRef]
- Quan, T.; Yang, Y. Fully enclosed hybrid electromagnetic–triboelectric nanogenerator to scavenge vibrational energy. Nano Res. 2016, 9, 2226–2233. [Google Scholar] [CrossRef]
- Yang, W.; Chen, J.; Zhu, G.; Wen, X.; Bai, P.; Su, Y.; Wang, Z.L. Harvesting vibration energy by a triple-cantilever based triboelectric nanogenerator. Nano Res. 2013, 6, 880–886. [Google Scholar] [CrossRef]






| Component | Design Parameter | Value |
|---|---|---|
| Main beam | Length (L1) | 60 mm |
| Width (W1) | 4.85 mm | |
| Thickness (T1) | 0.8 mm | |
| Secondary beam | Length (L2) | 30 mm |
| Width (W2) | 10 mm | |
| Thickness (T2) | 0.8 mm | |
| Top part-1 | Length * width | 20 mm * 20 mm |
| Glass/aluminum thickness | 1 mm/0.2 μm | |
| Top part-2 | Length * width | 10 mm * 10 mm |
| Glass/aluminum thickness | 1 mm/0.2 μm | |
| Bottom part-1 | Length * width | 20 mm * 20 mm |
| PDMS/aluminum/glass thickness | 0.3 mm/0.2 μm/1 mm | |
| Bottom part-2 | Length * width | 10 mm * 10 mm |
| PDMS/aluminum/glass thickness | 0.3 mm/0.2 μm/1 mm |
| Author | Approaches to Improve Bandwidth | Acceleration (g) | Resonant Frequency (Hz) | Operating Bandwidth (Hz) |
|---|---|---|---|---|
| Ibrahim et al. [28] | Nonlinear stiffening | 1.0 g | 20 Hz | 18 Hz |
| Bhatia et al. [29] | Tandem + nonlinear stiffening | 0.2 g | 20 Hz, 27 Hz, 34 Hz, 40 Hz | 25 Hz |
| Dhakar et al. [33] | Nonlinear stiffening | 1.0 g | 31.5 Hz | 11.9 Hz |
| Dhakar et al. [34] | Nonlinear stiffening | 1.4 g | 24.5 Hz | 22.05 Hz |
| Jeon et al. [41] | Nonlinear stiffening | 17.5 g | 5 Hz | 22 Hz |
| Tang et al. (this work) | Multimodal + nonlinear stiffening | 0.6 g | 23 Hz, 75 Hz | 32.9 Hz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, G.; Cheng, F.; Hu, X.; Huang, B.; Xu, B.; Li, Z.; Yan, X.; Yuan, D.; Wu, W.; Shi, Q. A Two-Degree-of-Freedom Cantilever-Based Vibration Triboelectric Nanogenerator for Low-Frequency and Broadband Operation. Electronics 2019, 8, 1526. https://doi.org/10.3390/electronics8121526
Tang G, Cheng F, Hu X, Huang B, Xu B, Li Z, Yan X, Yuan D, Wu W, Shi Q. A Two-Degree-of-Freedom Cantilever-Based Vibration Triboelectric Nanogenerator for Low-Frequency and Broadband Operation. Electronics. 2019; 8(12):1526. https://doi.org/10.3390/electronics8121526
Chicago/Turabian StyleTang, Gang, Fang Cheng, Xin Hu, Bo Huang, Bin Xu, Zhibiao Li, Xiaoxiao Yan, Dandan Yuan, Wenjing Wu, and Qiongfeng Shi. 2019. "A Two-Degree-of-Freedom Cantilever-Based Vibration Triboelectric Nanogenerator for Low-Frequency and Broadband Operation" Electronics 8, no. 12: 1526. https://doi.org/10.3390/electronics8121526
APA StyleTang, G., Cheng, F., Hu, X., Huang, B., Xu, B., Li, Z., Yan, X., Yuan, D., Wu, W., & Shi, Q. (2019). A Two-Degree-of-Freedom Cantilever-Based Vibration Triboelectric Nanogenerator for Low-Frequency and Broadband Operation. Electronics, 8(12), 1526. https://doi.org/10.3390/electronics8121526






