Two-Bit Terahertz Encoder Realized by Graphene-Based Metamaterials
Abstract
:1. Introduction
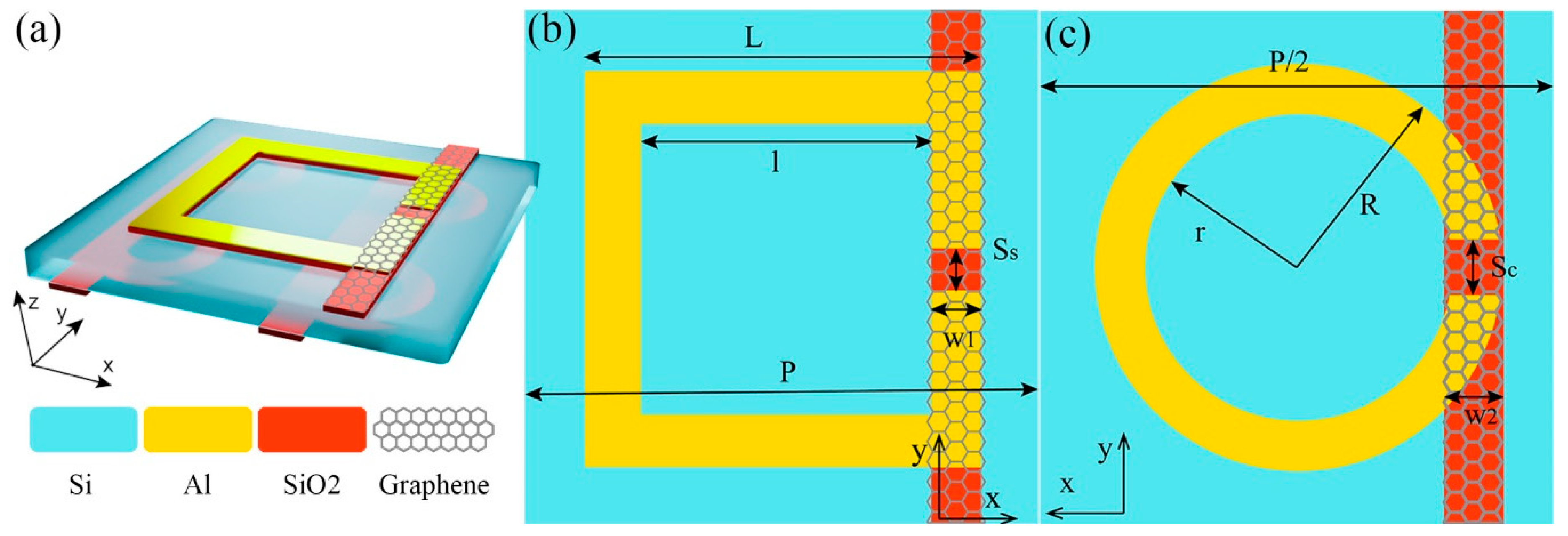
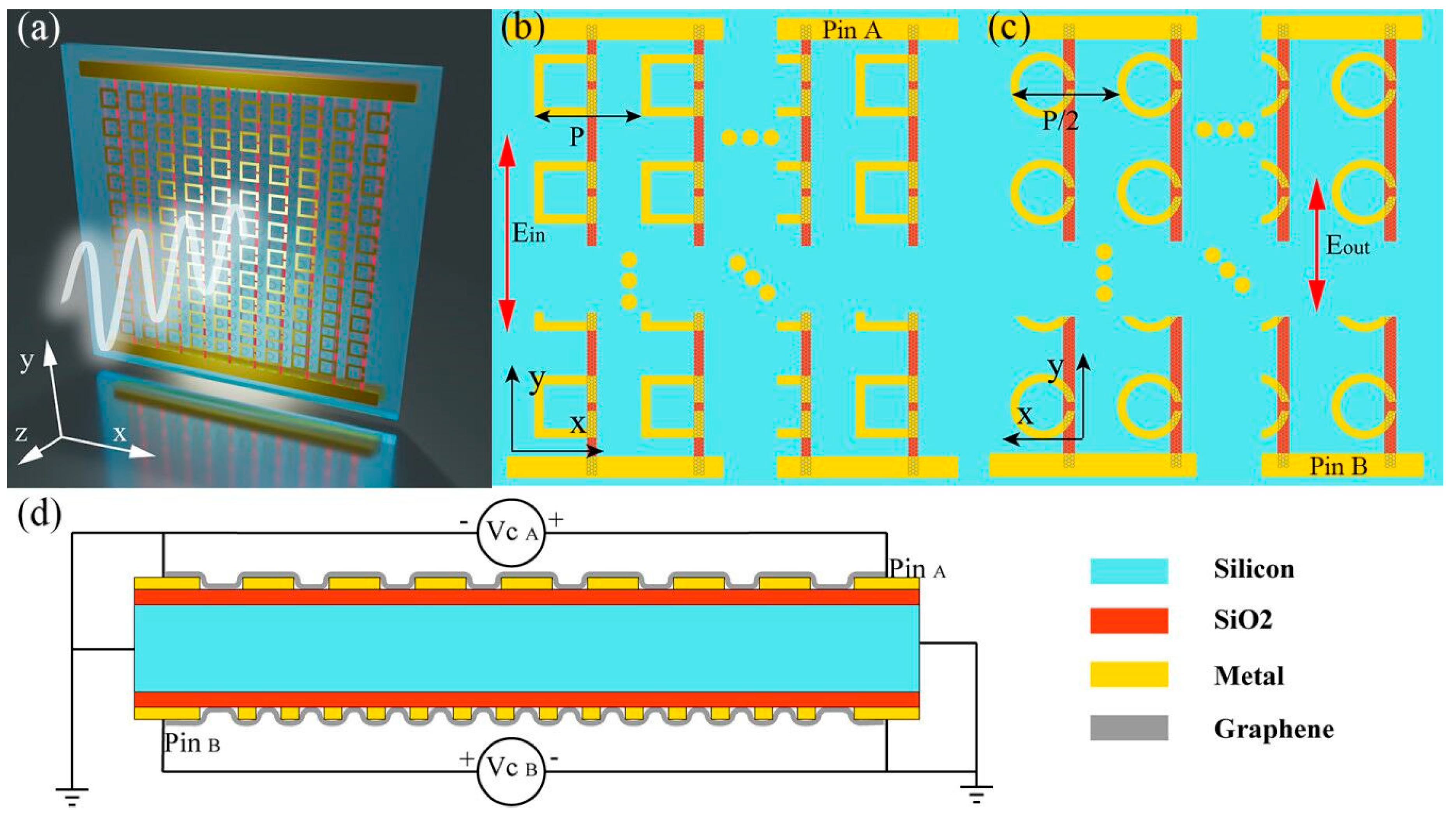
2. Device Design and Simulation
3. Results and Discussion
3.1. Equivalent Circuit for the Resonators
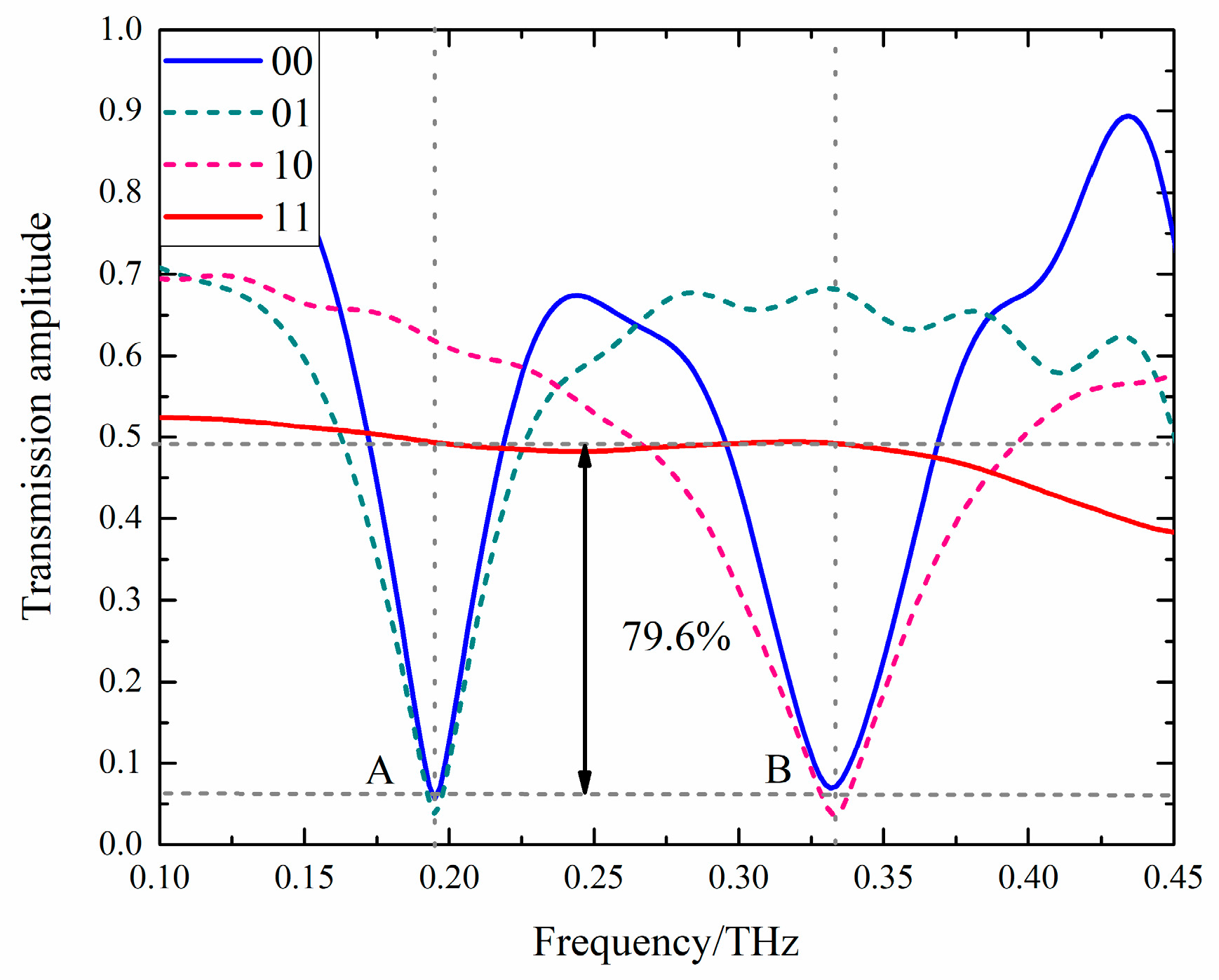
3.2. Performance of the Encoder
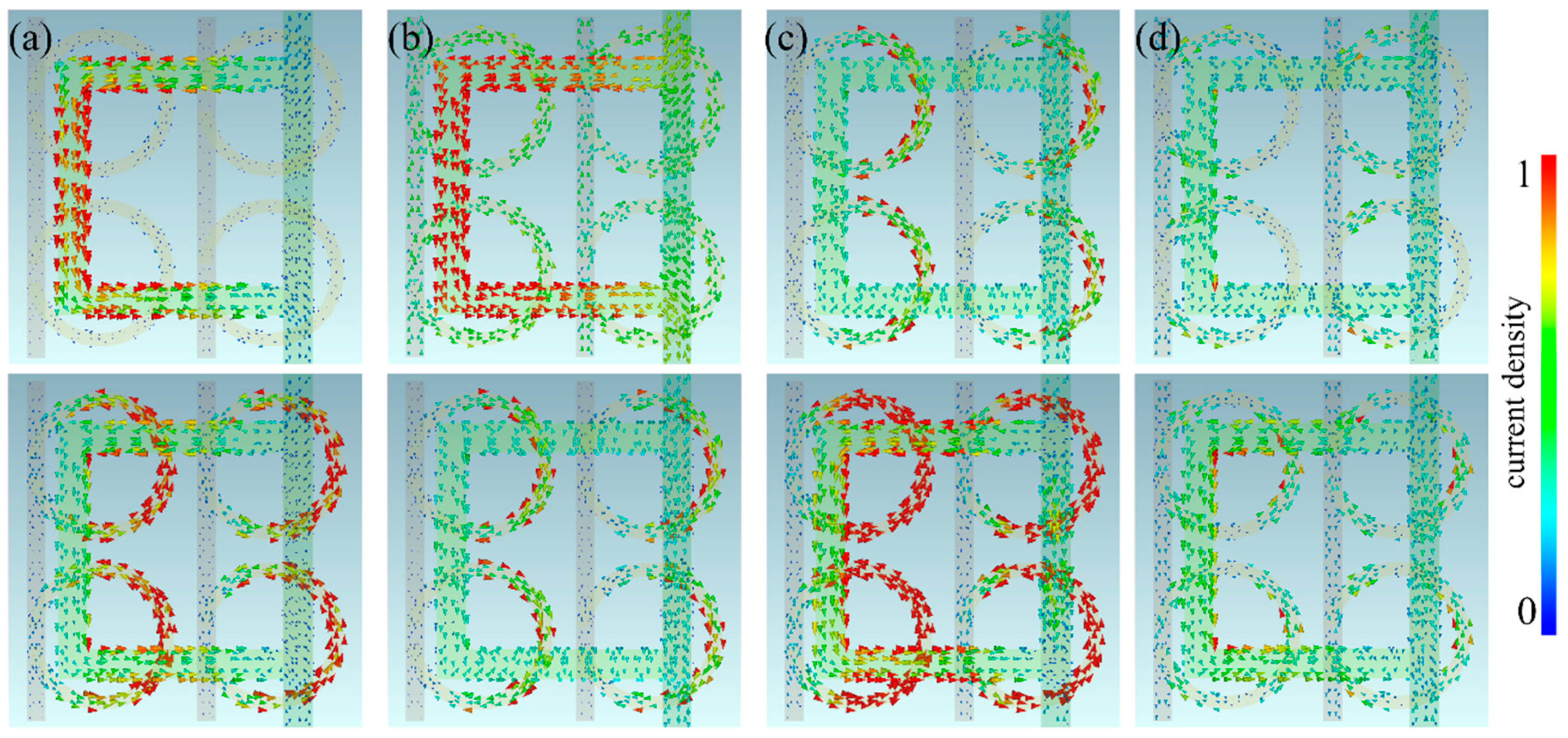
3.3. Further Discussion
4. Conclusions
5. Patents
Author Contributions
Funding
Conflicts of Interest
References
- Ferguson, B.; Zhang, X.C. Materials for terahertz science and technology. Nat. Mater. 2002, 1, 26. [Google Scholar] [CrossRef] [PubMed]
- Dhillon, S.S.; Vitiello, M.S.; Linfield, E.H.; Davies, A.G.; Hoffmann, M.C.; Booske, J.; Paoloni, C.; Gensch, M.; Weightman, P.; Williams, G.P.; et al. The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2017, 50, 043001. [Google Scholar] [CrossRef]
- Chen, H.-T.; O’Hara, J.F.; Azad, A.K.; Taylor, A.J.; Averitt, R.D.; Shrekenhamer, D.B.; Padilla, W.J. Experimental demonstration of frequency-agile terahertz metamaterials. Nat. Photonics 2008, 2, 295–298. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Chang, C.C.; Zhou, Q.; Zhang, C.; Chen, H.T. Resonance coupling and polarization conversion in terahertz metasurfaces with twisted split-ring resonator pairs. Opt. Express 2017, 25, 25842–25852. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Hu, F.; Chen, X.; Han, J.; Chen, T.; Xiong, X.; Zhang, W. Ruler equation for precisely tailoring the resonance frequency of terahertz U-shaped metamaterials. J. Opt. 2019, 21, 025101. [Google Scholar] [CrossRef]
- Hu, F.; Guo, E.; Xu, X.; Li, P.; Xu, X.; Yin, S.; Wang, Y.; Chen, T.; Yin, X.; Zhang, W. Real-timely monitoring the interaction between bovine serum albumin and drugs in aqueous with terahertz metamaterial biosensor. Opt. Commun. 2017, 388, 62–67. [Google Scholar] [CrossRef]
- Huang, W.; Rangelov, A.A.; Kyoseva, E. Complete achromatic optical switching between two waveguides with a sign flip of the phase mismatch. Phys. Rev. A 2014, 90, 053837. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Ghosh, S.; Xu, Q.; Ouyang, C.; Li, Y.; Zhang, X.; Tian, Z.; Gu, J.; Liu, L.; Azad, A.K.; et al. Active control of polarization-dependent near-field coupling in hybrid metasurfaces. Appl. Phys. Lett. 2018, 113, 061111. [Google Scholar] [CrossRef]
- Chen, H.-T.; Padilla, W.J.; Cich, M.J.; Azad, A.K.; Averitt, R.D.; Taylor, A.J. A metamaterial solid-state terahertz phase modulator. Nat. Photonics 2009, 3, 148–151. [Google Scholar] [CrossRef]
- Li, H.; Cao, Q.; Liu, L.; Wang, Y. An Improved Multifunctional Active Frequency Selective Surface. IEEE Trans. Antennas Propag. 2018, 66, 1854–1862. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Guo, X.; Chen, T.; Liang, H.; Hao, X.; Hou, X.; Kou, W.; Zhao, Y.; Zhou, T.; et al. A Review of THz Modulators with Dynamic Tunable Metasurfaces. Nanomaterials 2019, 9, 965. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jnawali, G.; Rao, Y.; Yan, H.; Heinz, T.F. Observation of a transient decrease in terahertz conductivity of single-layer graphene induced by ultrafast optical excitation. Nano Lett. 2013, 13, 524–530. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Cheng, Z.; Wang, L.; Jin, K.; Wang, W. Graphene, a material for high temperature devices--intrinsic carrier density, carrier drift velocity, and lattice energy. Sci. Rep. 2014, 4, 5758. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, W.; Liang, S.-J.; Kyoseva, E.; Ang, L.K. Adiabatic control of surface plasmon-polaritons in a 3-layers graphene curved configuration. Carbon 2018, 127, 187–192. [Google Scholar] [CrossRef] [Green Version]
- Dabidian, N.; Kholmanov, I.; Khanikaev, A.B.; Tatar, K.; Trendafilov, S.; Mousavi, S.H.; Magnuson, C.; Ruoff, R.S.; Shvets, G. Electrical Switching of Infrared Light Using Graphene Integration with Plasmonic Fano Resonant Metasurfaces. ACS Photonics 2015, 2, 216–227. [Google Scholar] [CrossRef]
- Farmer, D.B.; Avouris, P.; Li, Y.; Heinz, T.F.; Han, S.J. Ultrasensitive Plasmonic Detection of Molecules with Graphene. ACS Photonics 2016, 3, 553–557. [Google Scholar] [CrossRef]
- Li, Q.; Tian, Z.; Zhang, X.; Singh, R.; Du, L.; Gu, J.; Han, J.; Zhang, W. Active graphene-silicon hybrid diode for terahertz waves. Nat. Commun. 2015, 6, 7082. [Google Scholar] [CrossRef]
- Kindness, S.J.; Almond, N.W.; Wei, B.; Wallis, R.; Michailow, W.; Kamboj, V.S.; Braeuninger-Weimer, P.; Hofmann, S.; Beere, H.E.; Ritchie, D.A.; et al. Active Control of Electromagnetically Induced Transparency in a Terahertz Metamaterial Array with Graphene for Continuous Resonance Frequency Tuning. Adv. Opt. Mater. 2018, 6, 1800570. [Google Scholar] [CrossRef] [Green Version]
- Kleine-Ostmann, T.; Nagatsuma, T. A Review on Terahertz Communications Research. J. Infrared Millim. Terahertz Waves 2011, 32, 143–171. [Google Scholar] [CrossRef]
- Naeem, N.; Parveen, S.; Ismail, A. Terahertz Communications for 5G and Beyond. In Antenna Fundamentals for Legacy Mobile Applications and Beyond; Elfergani, I., Hussaini, A.S., Rodriguez, J., Abd-Alhameed, R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 305–322. [Google Scholar]
- Gao, W.; Shu, J.; Reichel, K.; Nickel, D.V.; He, X.; Shi, G.; Vajtai, R.; Ajayan, P.M.; Kono, J.; Mittleman, D.M.; et al. High-Contrast Terahertz Wave Modulation by Gated Graphene Enhanced by Extraordinary Transmission through Ring Apertures. Nano Lett. 2014, 14, 1242–1248. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Qian, Y.; Yin, S.; Li, D.; Jiang, M.; Lin, X.; Hu, F. Multi-band tunable terahertz bandpass filter based on vanadium dioxide hybrid metamaterial. Mater. Res. Express 2019, 6, 055809. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Liu, T.; Yan, X.; Li, Z.; Xu, C. Active modulation of electromagnetically induced transparency analogue in terahertz hybrid metal-graphene metamaterials. Carbon 2018, 126, 271–278. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, Y.K.; Manjappa, M.; Cong, L.; Cao, W.; Al-Naib, I.; Zhang, W.; Singh, R. Ultrahigh-Q Fano Resonances in Terahertz Metasurfaces: Strong Influence of Metallic Conductivity at Extremely Low Asymmetry. Adv. Opt. Mater. 2015, 4, 457–463. [Google Scholar] [CrossRef]
- Ordal, M.A.; Long, L.L.; Bell, R.J.; Bell, S.E.; Bell, R.R.; Alexander, R.W.; Ward, C.A. Optical properties of the metals Al, Co, Cu, Au, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W in the infrared and far infrared. Appl. Opt. 1983, 22, 1099–1120. [Google Scholar] [CrossRef]
- Liu, T.; Zhou, C.; Cheng, L.; Jiang, X.; Wang, G.; Xu, C.; Xiao, S. Actively tunable slow light in a terahertz hybrid metal-graphene metamaterial. J. Opt. 2019, 21, 035101. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Meng, H.; Deng, S.; Lao, C.; Wei, Z.; Wang, F.; Tan, C.; Huang, X. Hybrid Metal Graphene-Based Tunable Plasmon-Induced Transparency in Terahertz Metasurface. Nanomaterials 2019, 9, 385. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Diaz, J.S.; Moldovan, C.; Capdevila, S.; Romeu, J.; Bernard, L.S.; Magrez, A.; Ionescu, A.M.; Perruisseau-Carrier, J. Self-biased reconfigurable graphene stacks for terahertz plasmonics. Nat. Commun. 2015, 6, 6334. [Google Scholar] [CrossRef]
- Gaboriau, F.; Cartry, G.; Peignon, M.C.; Cardinaud, C. Selective and deep plasma etching of SiO2: Comparison between different fluorocarbon gases (CF4, C2F6, CHF3) mixed with CH4 or H2 and influence of the residence time. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. 2002, 20, 1514. [Google Scholar] [CrossRef]
- Shamonin, M.; Shamonina, E.; Kalinin, V.; Solymar, L. Properties of a metamaterial element: Analytical solutions and numerical simulations for a singly split double ring. J. Appl. Phys. 2004, 95, 3778–3784. [Google Scholar] [CrossRef]
- Shelton, D.J.; Brener, I.; Ginn, J.C.; Sinclair, M.B.; Peters, D.W.; Coffey, K.R.; Boreman, G.D. Strong coupling between nanoscale metamaterials and phonons. Nano Lett. 2011, 11, 2104–2108. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qun, W.; Ming-Feng, W.; Fan-Yi, M.; Jian, W.; Le-Wei, L. Modeling the effects of an individual SRR by equivalent circuit method. In Proceedings of the 2005 IEEE Antennas and Propagation Society International Symposium, Washington, DC, USA, 3–8 July 2005; pp. 631–634. [Google Scholar]

| Code | Voltage of Controller | Transmission Amplitude | ||
|---|---|---|---|---|
| Pin_A | Pin_B | Band A | Band B | |
| 00 | Off 1 | Off | Low | Low |
| 01 | Off | On | Low | High |
| 10 | On 2 | Off | High | Low |
| 11 | On | On | High | High |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, S.; Shi, X.; Huang, W.; Zhang, W.; Hu, F.; Qin, Z.; Xiong, X. Two-Bit Terahertz Encoder Realized by Graphene-Based Metamaterials. Electronics 2019, 8, 1528. https://doi.org/10.3390/electronics8121528
Yin S, Shi X, Huang W, Zhang W, Hu F, Qin Z, Xiong X. Two-Bit Terahertz Encoder Realized by Graphene-Based Metamaterials. Electronics. 2019; 8(12):1528. https://doi.org/10.3390/electronics8121528
Chicago/Turabian StyleYin, Shan, Xintong Shi, Wei Huang, Wentao Zhang, Fangrong Hu, Zujun Qin, and Xianming Xiong. 2019. "Two-Bit Terahertz Encoder Realized by Graphene-Based Metamaterials" Electronics 8, no. 12: 1528. https://doi.org/10.3390/electronics8121528
APA StyleYin, S., Shi, X., Huang, W., Zhang, W., Hu, F., Qin, Z., & Xiong, X. (2019). Two-Bit Terahertz Encoder Realized by Graphene-Based Metamaterials. Electronics, 8(12), 1528. https://doi.org/10.3390/electronics8121528





