Unified Power Flow Controller Based on Autotransformer Structure

Abstract

This paper proposes a new unified power flow controller (UPFC) topology. A single phase of them system with the proposed topology consists of an N:2 transformer with a center tap at the low-voltage side and a power converter module comprising full- and half-bridge converters. A three-phase system can be implemented with three devices. While the conventional UPFC topology uses two three-phase transformers, which are called series and parallel transformers, the proposed topology utilizes three single-phase transformers to implement a three-phase UPFC system. By using an autotransformer structure, the power rating of the transformers and the voltage rating of switches in the power converter module can be significantly decreased. As a result, it is possible to reduce the installation spaces and costs compared with the conventional UPFC topology. In addition, by adopting a full- and half-bridge converter structure, the proposed topology can be easily implemented with conventional power devices and control techniques. The techniques used to control the proposed topology are described in this paper. The results obtained from simulations and experiments verify the effectiveness of the proposed UPFC topology.

1. Introduction

In a modern, civilized society, electricity is essential. The demand for electricity is increasing annually with industrial and economic development [1]. Fundamental solutions to meet the electricity demand include the expansion of generating plants and electric power transmission systems of the power grids. However, social and environmental factors restrict the scope for such expansion.

In addition, concerns about global warming, environmental pollution due to the use of fossil fuels, and the exhaustion of fossil fuels are increasing [2]. Therefore, new and renewable energy systems, such as wind and solar power, are being added to conventional power grid systems [3,4]. However, the power generation of new and renewable energy systems varies significantly depending on the weather. In addition, the erratic power supplies of new and renewable energy systems have adverse effects on the power grid systems, including voltage, frequency, and transient state instabilities. Consequently, the increase in the amount of electricity that can be generated by these systems is limited.

Conventional power grid systems are characterized by the following problems, which reduce their efficiencies: (1) low utilization of transmission lines [5] and (2) load imbalance due to limited control capabilities [6,7,8].

One solution to these problems is to use a flexible alternating current transmission system (FACTS), which is a power electronic-based system, along with other static equipment to manage one or more AC transmission system parameters to enhance the controllability and increase the power transfer capability [9]. By improving the utilization of the transmission lines, FACTS devices have the same effect as the installation of a new transmission line. In addition, FACTS devices ensure stable operation of the power grid system. To change the power flow simply, a phase-shifting transformer [10] can be used. A phase-shifting transformer changes power flow by adjusting the phase angle of the transmission line by changing taps. However, while FACTS devices actively enable real-time power flow control, the phase-shifting transformer requires passive operation and shows step changes of the power flow.

Since the late 1980s, various FACTS devices have been developed in several countries around the world, and research regarding their commercialization has been conducted. As a result, FACTS devices, such as thyristor-controlled series capacitors (TCSCs) [11], static var compensators (SVCs) [12], static synchronous compensators (STATCOMs) [13], static series synchronous compensators (SSSCs) [14], and unified power flow controllers (UPFCs) [15,16] have been developed and tested or used in actual applications [17,18,19,20,21,22]. The UPFCs, which can control the power flow of the transmission system, are the most capable FACTS devices.

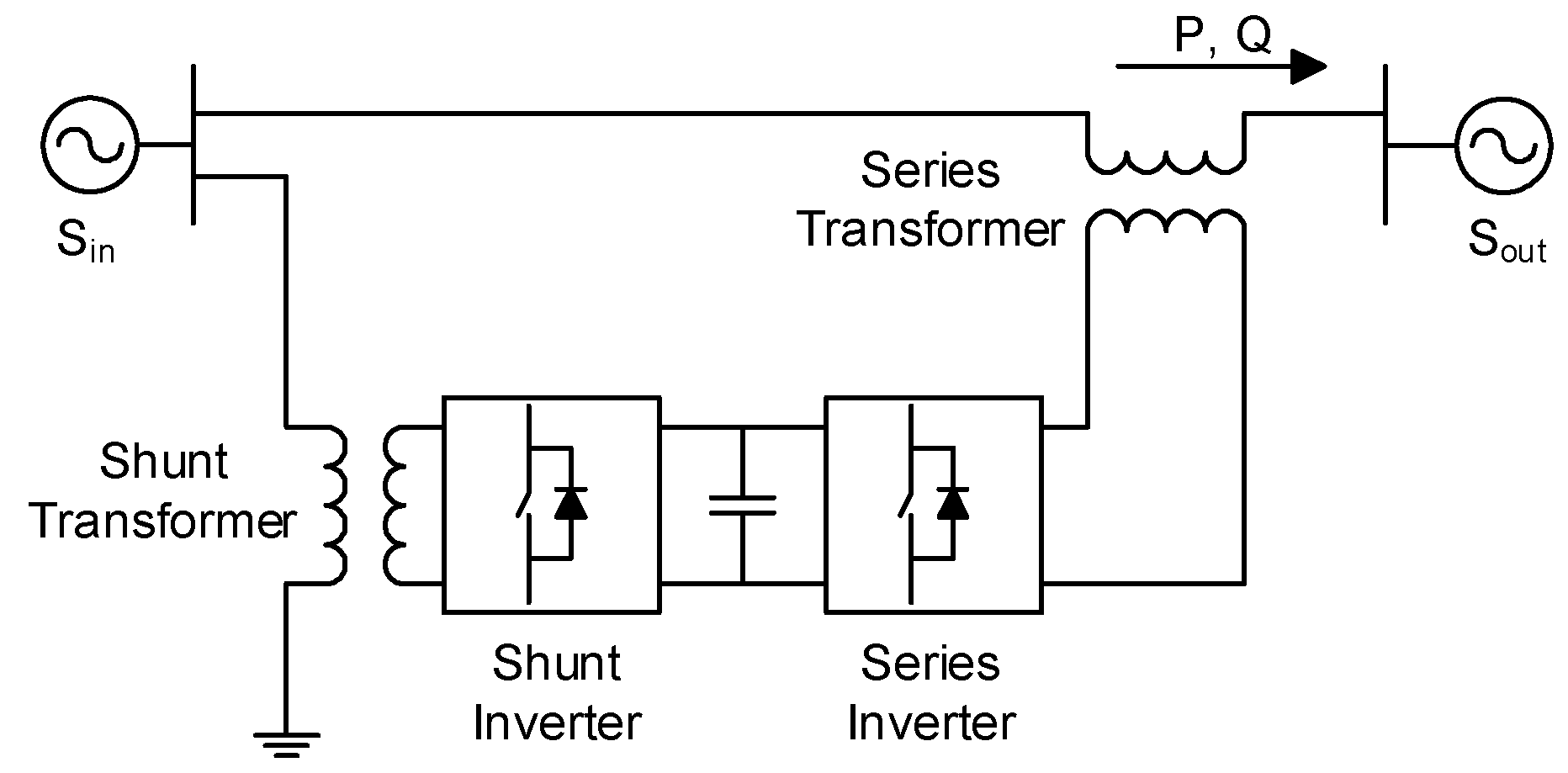
A conventional UPFC is a combination of a STATCOM and SSSC, which share a DC link capacitor. Figure 1 shows the configuration of the conventional UPFC system, which comprises two transformers and two power converters. Among the power converters, the series inverter controls the power flow and improves the dynamic stability in the transient state by controlling the voltages in the steady state. In contrast, the parallel inverter compensates the reactive power and supplies the power required for the series inverter. However, the series transformer and inverter are bulky and expensive because a large amount of transmission-line current flows through them [23]. Therefore, the use of conventional UPFCs has been limited, although their performance is outstanding. Consequently, the demand for a smaller, lower-cost topology has increased.

To mitigate the disadvantages and exploit the merits of UPFCs, various topologies have been proposed, such as a distributed power flow controller (DPFC) [24], UPFC based on a matrix converter (MC-UPFC) [25], and transformerless UPFC based on a multilevel inverter [6]. However, because of the low-rating converters, the volume of the DPFC may be larger than that of the conventional UPFC. In addition, if the MC-UPFC system is defective, the power grid system might be unstable because of the short circuit current and surge voltage. Transformerless UPFCs based on a multilevel inverter require several switches and connection lines, which make the system complex. As a result, a smaller, lower-cost, and simpler UPFC topology is required.

This paper proposes a new UPFC topology. The single phase of the system consists of a single-phase transformer, interface filter, and power converter module. An N:2 transformer with a center tap is used as single-phase transformer and is connected using an autotransformer structure. The power converter module includes full- and half-bridge converters. A three-phase UPFC system can be simply implemented using three devices.

Using the proposed topology, the number of transformers decreases from two to one compared with the conventional topology. Owing to the merits of having an autotransformer structure, the power rating of the transformer can be significantly reduced. By using a transformer with a high turns ratio, the voltage rating of the switches, and thus the manufacturing costs, can be reduced. In addition, the power converter module requires only three legs. One leg is used for an output half-bridge inverter and the others are utilized for an input full-bridge converter. Established inverter techniques can be applied to control the proposed topology. In general, for a large capacity system, a three-phase system consists of three single-phase systems for convenience of manufacturing. With the proposed system, because each phase of the power converter module is manufactured separately, the insulation between modules is easy.

On the other hand, since the voltage of the power converter module is floated from the ground, insulations should be carefully considered. However, by applying the insulation method used for power converters in HVDC or FACTS, the proposed topology could be insulated in a similar manner. In those applications, the power converters are installed away from the ground and walls of buildings, and they are hung on the ceiling of the building and fixed.

This paper was previously presented at the 10th International Conference on Power Electronics (ICPE 2019) and ECCE Asia; in the present publication, more details and a discussion of the results are provided [26].

2. Proposed UPFC Topology and Control

2.1. Configuration of the Proposed UPFC Topology

Figure 2 shows the configuration of the proposed UPFC topology. Figure 2a shows three-phase system and Figure 2b shows single-phase system. Single-phase system consists of a single-phase transformer, interface filter, and power converter module, and a three-phase system can be implemented with three devices.

An N:2 transformer with a center tap was used as the single-phase transformer. The center tap at the low-voltage side is connected to bus 1 at the transformer’s high-voltage side (Figure 2). Thus, the transformer is connected using an autotransformer structure.

The power converter module consists of two parts: (1) an input full-bridge converter and (2) output half-bridge inverter. The input currents of the power converter module, that is, i_a and i_b in Figure 2, consist of two current components, i_com and i_dif. The first one flows in the same direction and is related to the power delivery from bus 1 to bus 2. Therefore, it is known as the common mode current, i_com. The second one flows in the opposite direction through DC link capacitors. Therefore, it is related to the voltage control of the DC link of the power converter module and is known as the differential mode current, i_dif. Based on these definitions, the input currents of each leg can be described as

$$i_a=i_{com}+i_{dif},i_b=i_{com}-i_{dif}.$$

(1)

By using Equation (1), the differential mode current can be calculated. To calculate this current, it is necessary to measure the input currents of each leg, i_a and i_b, in Figure 2:

$$i_{dif}=\frac{i_a-i_b}{2}.$$

(2)

The input full-bridge converter is connected to the low side of the transformer via an interface filter. By controlling the differential mode current, the input full-bridge converter controls the DC link voltage of the power converter module. In contrast, the output half-bridge inverter is connected to the transmission line and synthesizes the injection voltage to control the power flow of the power grid.

An interface filter is used to reduce the effects of the switching from the power converter module. In the proposed topology, the common mode inductance should be sufficiently low because it can be considered as a burden in the transmission line for the power delivery. However, the differential mode inductance is considered to be an inductor load that is used to control the differential mode current, and thus the DC link voltage. Therefore, an appropriate differential mode inductance is necessary. To implement the common and differential mode inductances, a coupled inductor was used as the interface filter [27].

When the UPFC is defective or not used, a bypass circuit can be activated. In this situation, the UPFC is bypassed.

2.2. Full-Bridge Converter Control

The input full-bridge converter controls the DC link voltage by controlling the differential mode current among the input currents. Figure 3 shows the control block diagram of the input full-bridge converter. A notch filter is used as a feedback filter for the voltage feedback to remove the second harmonic component of the DC link voltage.

The DC link voltage control can be implemented using a conventional voltage control scheme [28]. To prevent DC link voltage overshoot, the controller is designed as an integral proportional (IP) controller. The output signal of the DC link voltage controller is the magnitude of the differential mode current reference, which has a DC value. This means that the phase angle of the grid voltage is required to establish the differential mode current reference.

The grid voltage of the phase-locked loop (PLL) can be measured at the low-voltage side of the transformer. The second-order generalized integrator PLL (SOGI-PLL) [29] is used as an angle estimator. As a result, the differential mode current reference can be obtained using the magnitude of the differential mode current reference and the phase of the grid voltage, as shown in Figure 3.

To track the differential mode AC reference, a proportional resonant (PR) controller [30] is adopted for the differential mode current controller. The output signal of the PR controller is used to generate switching signals for each leg of the input full-bridge converter. As a pulse width modulation (PWM) scheme, a sinusoidal pulse width modulation (SPWM) was used to keep the voltages at bus 1 and bus n in Figure 2 equal.

2.3. Half-Bridge Inverter Control

Figure 4 shows the phasor diagram of the UPFC operation. The complex power transfer between bus 1 and 2 can be controlled by adding an injection voltage, V_in, at the endpoint of V₁. The half-bridge inverter synthesizes an appropriate injection voltage to control the power flow of the transmission line. The parameter V_in is the injection voltage between bus n and bus o in Figure 2. Because the full-bridge converter keeps the voltages at bus 1 and bus n equal, the voltage of bus o can be calculated as V₁ + V_in. The magnitude of the controllable complex power depends on the size of the injection voltage; that is, the radius of the circle of V_in in Figure 4 and the line impedance, Z, between bus 1 and bus 2. Z can be described using Equation (3) and can be obtained from the transmission line data or estimated using UPFC operations.

$$Z=R+jX$$

(3)

Figure 5 shows the single-line diagram of the UPFC and grid. Here, δ means the phase angle of each voltage. Considering that the UPFC system is installed at bus 1, the phase angle of V₁, which is δ₁ in Figure 5, can be measured and set to zero, as shown in Figure 4. The injection voltage, V_in, can be added between bus 1 and bus 2 to adjust the complex power flow. The line current, I, can be expressed as

$$I=\frac{V_1+V_{in}\cos {\delta }_{in}-V_2\cos {\delta }_2}{R+jX}+j\frac{V_{in}\sin {\delta }_{in}-V_2\sin {\delta }_2}{R+jX}.$$

(4)

The complex power at the bus between the UPFC system and the line impedance can be described as

$$S_0+S_{\mathrm{ref}}=(V_{\mathrm{in}}+V_1)\cdot I^{*}$$

(5)

The complex power is the sum of S₀ and S_ref, where S₀ is the initial complex power without UPFC operation when V_in is zero, and S_ref is the complex power added by the UPFC operation. The parameter S₀ can be described using Equation (6), where I₀ is the line current without the UPFC. Therefore, I₀ can be described using Equation (7).

$$S_0=V_1\cdot I_0^{*}$$

(6)

$$I_0=\frac{(V_1-V_2\cos {\delta }_2)-j{V}_2\sin {\delta }_2}{R+jX}.$$

(7)

Based on the use of Equations (4) and (5), the active and reactive powers can be calculated using Equations (8) and (9), respectively.

$$P_0+P_{ref}=\frac{V_1}{|Z{|}^2}\left\{R(V_1+V_{in}\cos {\delta }_{in}-V_2\cos {\delta }_2)\right\}+\frac{V_1}{|Z{|}^2}\left\{X(V_{in}\sin {\delta }_{in}-V_2\sin {\delta }_2)\right\}.$$

(8)

$$Q_0+Q_{ref}=-\frac{V_1}{|Z{|}^2}\left\{R(V_{in}\sin {\delta }_{in}-V_2\sin {\delta }_2)\right\}+\frac{V_1}{|Z{|}^2}\left\{X(V_1+V_{in}\cos {\delta }_{in}-V_2\cos {\delta }_2)\right\}.$$

(9)

The parameters P₀ and Q₀ are the active and reactive powers of S₀, respectively, and P_ref and Q_ref are the active and reactive powers of S_ref, respectively. By using Equations (6)–(9) and the active and reactive power references of the UPFC, the injection voltage can be calculated as

$$V_{in}\cos {\delta }_{in}=\frac{R{P}_{ref}+X{Q}_{ref}}{V_1}$$

(10)

$$V_{in}\sin {\delta }_{in}=\frac{X{P}_{ref}-R{Q}_{ref}}{V_1}$$

(11)

By synthesizing the injection voltage, the complex power can be controlled similarly to the conventional one.

3. Verification Results

To verify the proposed system, simulations and experiments were performed. The verification results in this section were intended to demonstrate that the proposed system is as capable of power flow control as the conventional one.

3.1. Simulations

The proposed UPFC topology, as shown in Figure 2, was simulated using the parameters listed in

Table 1. Nominal simulation parameters.

Parameter	Value
Grid voltage	345 kV
Length of the transmission line	50 km
Line impedance	3 + j9.5 Ω
Turns ratio of the transformer	78:2
Switching frequency	5 kHz
DC link voltage reference	10 kV
Capacitance of the DC link capacitor	2.8 mF
Common mode inductance	0.2 mH
Differential mode inductance	1.5 mH

. Figure 6 shows the simulation model. MATLAB and PLECS were the software used for simulations. Although only the proposed single-phase system was simulated, a three-phase system can be implemented using three single-phase systems.

In the simulation, the grid voltage was assumed to be 345 kV. The transmission line was assumed to be 50 km, such that the line impedance was modeled as 3 + j9.5 Ω, considering the impedance per length of the transmission line [31]. The turns ratio of the transformer was designed to be 78:2.

As the power converter module, a two-level topology was used for simplicity and its switching frequency was set to 5 kHz. However, various types of well-developed topologies can be adopted, such as multilevel inverters and modular multilevel converters. The nominal DC link voltage was set to 10 kV, which is much smaller than the grid voltage. A coupled inductor structure was used as an interface filter. The common and differential modes were set to 0.2 and 1.5 mH, respectively.

Figure 7 shows the simulation results from 0 to 12 s. The switching of the power converter module was started after 1 s, and the differential mode current was set to zero. After 1.5 s, the DC link voltage was controlled at a nominal value. After 3 and 4 s, the active and reactive power references of three-phase system were increased to 50 MW and 40 MVar, respectively. After 5 and 6 s, respectively, they were both reduced to zero. After 7 and 8 s, they were changed to −50 MW and −40 MVar, respectively. After 9 and 10 s, respectively, they were changed to zero. In the simulations, the references ware changed using a slope of 500 MVA/s.

Figure 7a shows the performance of the DC link voltage control. Because the regulator was designed as an IP controller, an overshoot phenomenon was not observed, and the voltage could be controlled well. Figure 7b shows the active and reactive powers of the transmission line and their references. The active and reactive power were controlled as references at steady states. The transient response was stable because the references were changed as a ramp function, using a slope of 500 MVA/s. There were minimal coupling phenomena, and, in reality, coupling can be mitigated because the references are changed using appropriate slopes. The active and reactive powers were controlled well according to their references. Figure 7c,d shows the magnitude and phase of the injection voltage, respectively, which were used to control the power flow. By synthesizing an appropriate injection voltage, the performance of the power flow control could be verified.

Figure 8 shows the transient waveforms of V₁, V_in, and I after the change of the power reference. The signals of V_in and I are magnified for clarity. Figure 8a shows the waveforms of V₁, V_in, and I after the power reference was changed from 0 to 50 + j0 MVA. Because the phases of V₁ and I were the same, it is possible to confirm that only active power was delivered as the power reference.

Figure 8b–d shows the same waveforms as Figure 8a. Figure 8b shows the waveforms of V₁, V_in, and I after the power reference was changed from 50 MW to 50 + j40 MVA. Before 4 s, because the phases of V₁ and I were the same, it is possible to confirm that only active power was delivered. However, after 4 s, the magnitude of I was increased and the phase of I was changed. At the steady state, the phase difference between V₁ and I was about 38 degrees. Therefore, it is possible to confirm that active power and reactive power were delivered as references.

Figure 8c shows the same waveform after the power reference was changed from 50+j40 MVA to 40 Mvar. Before 4 s, the phase difference between V₁ and I was about 38 degrees. However, after 5 s, the magnitude of I was decreased and the phase difference between V₁ and I was about 90 degrees at steady state. So, it is possible to confirm that only reactive power was delivered as the power reference.

Figure 8d shows the same waveform after the power reference was changed from 40 Mvar to 0 VA. Before 6 s, the phase difference between V₁ and I was about 90 degrees; however, after 6 s, at steady state, the magnitude of I was decreased to zero. So, the proposed system delivered no power as a reference.

With the proposed UPFC topology, the complex powers could be regulated according to the references, which verifies the proposed system.

3.2. Experiments

Laboratory-scale experiments on the proposed topology were performed using the parameters listed in

Table 2. Nominal experiment parameters.

Parameters	Value
Grid voltage, rms	220 V
Line impedance	0.04 + j1.5 Ω
Turns ratio of the transformer	5:2
Switching frequency	5 kHz
DC link voltage reference	150 V
Capacitance of DC link capacitor	2.8 mF
Common mode inductance	0.5 mH
Differential mode inductance	6 mH

. Figure 9a,b shows the configuration of the experimental setup and equivalent circuit, respectively. Two three-phase Δ-Y transformers were used to emulate the grid voltages V₁ and V₂. These voltages were set to 220 V in the experiments.

The turns ratio of the transformer in the laboratory-scale UPFC system was 5:2. Two single-phase 5:1 transformers, which were held in the laboratory, were used to implement a 5:2 transformer with a center tap. They were connected using an autotransformer structure. Because the turn ratio of the transformers was lower than that of the simulations, the nominal DC link voltage was set to 150 V, which is a relatively large value.

A coupled inductor was used for the interface filter of the proposed system. The common and differential mode inductances were 0.5 and 6 mH, respectively. To emulate the line impedance, a 4 mH inductor was used.

A two-level topology was used as a power converter module for simplicity; its switching frequency was set to 5 kHz. The capacitance of the DC link capacitor was 2.8 mF.

Figure 10 shows the experimental results. Figure 10a shows the performance of the DC link voltage control. The voltage of the DC link was controlled well according to the reference of 150 V. Figure 10b shows the performances of the DC link voltage and differential mode current controls after the DC link voltage control was started. The differential mode current was regulated well using the PR controller. In addition, by controlling the differential mode current, the DC link voltage could be controlled well.

Figure 11 shows the experimental results. The waveforms of V₁, V_in*, V₁ + V_in, and I are shown. In this study, V₁ represents the grid voltage measured by a differential probe, as shown in Figure 2, and V₁ + V_in is the output voltage of the power converter module measured by a differential probe. In addition, V_in* is the injection voltage reference according to the complex power references, which was scattered by a digital to analog converter (DAC). Owing to the switching of the power converter module to the actual voltage, V_in shows PWM waveforms, whose magnitude is the same as that of the DC link voltage. Therefore, the voltage of V₁ + V_in is the sum of V₁ and the PWM waveform of V_in. The parameter I represents the line current measured by the current sensor. Therefore, switching ripples were only included in V₁ + V_in.

Figure 11a shows the transient waveforms of V₁, V_in, and I after the single-phase complex power reference was changed from 0 to 1 + j0 kVA. In the experiments, the reference was changed using a slope of 20 kVA/s. Because of the appropriate slope, the experimental results show no coupling phenomenon, which leads to overshoot and distortions. Because the phases of V₁ and I are the same and the magnitude of the line current is ~6.5 A, it can be confirmed that the UPFC only delivers active power according to the complex power reference.

Figure 11b–d shows the same waveform as Figure 11a. Figure 11b shows the transient waveforms of V₁, V_in, and I after the single-phase complex power reference was changed from 1 + j0 kVA to 1 + j1 kVA. Because the phase difference between of V₁ and I was the same at almost 45 degrees in steady state, it is possible to confirm that the complex power was delivered as a reference.

Figure 11c shows the transient waveforms of V₁, V_in, and I after the single-phase complex power reference was changed from 1+j1 kVA to 1 kvar. Because the phase difference between V₁ and I was the same at almost 90 degrees in steady state, it is possible to confirm that only reactive power was delivered as the reference. At steady state, the magnitude of I was decreased to zero. So, the proposed system delivered no power as reference.

Figure 11d shows the transient waveforms of V₁, V_in, and I after the single-phase complex power reference was changed from 1 kvar to 0 kVA. All figures in Figure 11 show that the complex power could be controlled well according to its reference, similar to the simulation results. These experimental results confirm the validity of the proposed UPFC topology.

With the simulations and experiments, it is hard to verify the cost savings and smaller installation spaces, however, the advantages of the proposed system can be inferred due to the fact that the proposed system can increase the turn ratio of the transformer.

4. Conclusions

Conventional power grid systems have the following problems that reduce their efficiencies: (1) low utilization of transmission lines and (2) load imbalance due to limited control capabilities. One solution to solve these problems is to use FACTS devices. Among them, UPFC, which can control the power flow of the transmission system, is the most capable FACTS device. A conventional UPFC system is a combination of a STATCOM and SSSC, which share a DC link capacitor, and comprises two transformers and two power converters, which are bulky and expensive. Consequently, although their performance is outstanding, the use of conventional UPFCs has been limited because of these shortcomings.

To mitigate the disadvantages and exploit the merits of UPFCs, this paper proposes a new UPFC topology based on an autotransformer structure. A single phase of the proposed UPFC system consists of an N:2 transformer with a center tap at the low-voltage side, a power converter module, and an interface filter. A three-phase of UPFC system can be simply implemented using three devices. A power converter module consists of two parts: (1) an input full-bridge converter and (2) output half-bridge inverter. By controlling the differential current among input currents, the input full-bridge converter controls the DC link voltage for the output half-bridge inverter. By synthesizing an appropriate injection voltage, the half-bridge inverter controls the power flow of the transmission line. The effectiveness of the proposed topology has been verified through simulations and experiments.

Based on the proposed system, only one single-phase transformer is required per phase, which means the number of the single-phase transformer is halved compared to the conventional one. With the proposed system, because each phase of the power converter module is manufactured separately, the insulation between power converter modules is easier. In addition, by using a transformer with a high turn ratio, the voltage rating of the power converter module can be significantly reduced. Consequently, the manufacturing costs and installation space required can be reduced compared with those of the conventional UPFC topology. Based on these advantages, the utilization of the UPFC with the proposed topology can be increased, which could be useful for the implementation of smart grids.