Towards Human Motion Tracking: Multi-Sensory IMU/TOA Fusion Method and Fundamental Limits

Abstract

Human motion tracking could be viewed as a multi-target tracking problem towards numerous body joints. Inertial-measurement-unit-based human motion tracking technique stands out and has been widely used in body are network applications. However, it has been facing the tough problem of accumulative errors and drift. In this paper, we propose a multi-sensor hybrid method to solve this problem. Firstly, an inertial-measurement-unit and time-of-arrival fusion-based method is proposed to compensate the drift and accumulative errors caused by inertial sensors. Secondly, Cramér–Rao lower bound is derived in detail with consideration of both spatial and temporal related factors. Simulation results show that the proposed method in this paper has both spatial and temporal advantages, compared with traditional sole inertial or time-of-arrival-based tracking methods. Furthermore, proposed method is verified in 3D practical application scenarios. Compared with state-of-the-art algorithms, proposed fusion method shows better consistency and higher tracking accuracy, especially when moving direction changes. The proposed fusion method and comprehensive fundamental limits analysis conducted in this paper can provide a theoretical basis for further system design and algorithm analysis. Without the requirements of external anchors, the proposed method has good stability and high tracking accuracy, thus it is more suitable for wearable motion tracking applications.

1. Introduction

Human Motion Tracking (HMT) [1,2] has been a hot topic in the area of body area network (BAN) [3,4] during the last decade. It aims to obtain human body movement information via quantitative methods to capture and analyze human motion. The information obtained by HMT are mainly relative positions in 2D/3D space of various joints and limbs. With the booming of BAN [5,6,7], human-centric applications have been raising in both academic and industrial areas, such as interactive games, computer cinematography, animation, etc. [1]. Many entrepreneurial firms have been formed in these areas [8,9]. Besides, HMT also plays a big role in medical field [5], and military and security applications [6].

HMT systems could be classified into two categories: computer vision (CV)-based [10] and wearable sensor (WS)-based [6]. CV-based technology takes advantages of deployed web-depth cameras to monitor human activities, and has been applied in practical applications, such as film shooting [11], security monitoring [6] and so on. Many technology companies have also been working on the research and development of professional human motion tracking systems, such as Vicon [12] and Optotrak [13]. They perform with high accuracy when operated in controlled scenario, however they rely heavily on environment factors, such as shooting angle and lights [10]. These inevitable defects make it only suitable for smaller and controllable situations. WS-based HMT systems, by contrast, do not need to deploy devices in scenarios and are less sensitive to the environment. Thus, they are more suitable for large-scale and dynamic applications [14].

In the present stage, WS-based HMT systems are mainly composed of inertial measurement units (IMUs), such as accelerometers and gyroscopes. The basic principle is to measure the triaxial acceleration and angular velocity of the motion by these sensors, and obtain the trajectory of monitoring points through integral operations [15,16,17,18]. However, inertial sensors may inevitably throw off errors that accumulate over time [19,20,21]. The accumulative and drift error is the biggest challenge faced by WS-based HMT systems.

For better solving the drift error problem and improving HMT accuracy, the most common methods are as follows:

• The hardware aspect uses inertial sensors with high precision, such as XSens [15] and Invensense [16] tracking units.
• The algorithm aspect enhances the system by using multi-sensor data fusion means [1,19,22,23].

However, the above-mentioned methods cannot fundamentally solve the drift problem. High precision hardware used by wearable tracking systems is usually very expensive, and the cost of a single suit could be hundreds of thousands or even millions of dollars [15,16,17,18]. In the aspect of algorithms, filtering methods, such as Kalman and particle filter [24], can somehow slow down the accumulation process, but cannot eliminate it completely. Thus, the inevitable drift problem of inertial sensors has become a crucial constraint for wearable HMT systems, which limits its use in long term or large space applications.

In essence, human motion tracking can be viewed as a local multi-target real-time high-precision three-dimensional positioning problem [23]. Ultra-Wideband (UWB)-based time-of-arrival (TOA) ranging is the most commonly used high-precision localization technology, its measurement accuracy can reach the centimeter level, and it does not have the drawback of accumulative errors, compared with inertial-sensor-based HMT systems [23,25]. The size of TOA chip is small enough to be integrated into wearable devices. Thereinto, IMU/TOA fusion is an effective way to overcome the accumulative errors of drifting problem faced by solo IMU method [26].

Some achievements on IMU/TOA fusion have been reported in many studies (e.g., [20,21,23,25]) However, state-of-the-art studies, (e.g., [23,27]), mainly face the following two drawbacks:

• Requirements of fixed external anchors: They need to be deployed in certain scenarios; for example, Zihajehzadeh et al. [23] introduced a magnetometer-free algorithm for human lower-body motion tracking by fusing inertial sensors with an UWB localization system. However, it is hard to realize wearable systems, and is not suitable for BAN applications.
• State-of-the-art studies seldom concentrate on the fundamental limits of IMU/TOA fusion methods, and the error correction effects are not satisfying. For example, Nilsson et al. [27] proposed a cooperative localization method by fusion of dual foot-mounted inertial sensors and inter-agent UWB ranging, but the experiment results show that, compared with the performance lower bounds [22], there is still a lot of room for improvement.

Based on these considerations, we propose an external-anchor-free IMU/TOA fusion method, and analyze its fundamental limits to lay a theoretical foundation for realizing low cost and high precision motion tracking system that is suitable for medium and long term use in large space.

The rest of the paper is organized as follows: Section 2 briefly introduces the related works about human motion tracking techniques and Cramér–Rao lower bound (CRLB). Section 3 describes the problem definition, IMU/TOA fusion-based model and its error sources. Section 4 introduces our external-anchor-free IMU/TOA fusion method, and analyzes its fundamental limits. Section 5 and Section 6, respectively, verify the spatial and temporal performance of proposed fusion-method. Section 7 presents a practical use case to verify the feasibility of proposed method when compared with state-of-the-art methods. Finally, Section 8 presents the conclusion.

2. Related Work

The development of HMT has been rising with the booming of Internet of Things (IoTs) and the rapid progress of human-centric applications [28,29,30,31] in the last decades. Particularly, HMT has become an essential task within the fields, such as clinical, military and security applications. In this section, we present a brief literature review on the following aspects: human motion tracking systems and applications, multi-sensory fusion methods and CRLB.

2.1. HMT Systems and Applications

HMT has shown a tremendous potential in the areas of industrial applications. Benefiting from the development of various systems, HMT has permeated into every aspect of social life, including clinical areas, emergency and rescue areas, security and entertainment, to name a few [5,6,7,8,9]. The most widely used HMT systems could be mainly classified into two categories: CV-based [10] and WS-based [6]. Next, we give a brief introduction and discussion about their merits and demerits.

Computer-vision-based systems, such as Vicon [12] or Optotrak [13], have a high accuracy when operating in controlled environments, e.g., several fixed cameras calibrated and correlated in a specific place and capturing configuration. Famous TV shows and movies, such as The Walking Dead, Game of Thrones and Guardians of the Galaxy, are all powered by human motion animators [15]. CV-based systems can provide a large amount of redundant data. Ambulatory systems, such as those using a Kinect [32] to capture human motion, are set in relatively uncontrolled environments and have a restricted field of view. These systems have a restricted margin of maneuverability and are more suitable for indoor use.

In contrast, a very promising frontier for reliable human motion tracking is WS-based [6] system, especially using IMUs. Iyengar et al. [33] defined a framework that managed common tasks for healthcare monitoring applications to aid development of BAN. Anwary et al. [34] utilized a pressure sensor array and IMU for gait analysis. Ghasemzadeh et al. [35] introduced a novel classification model that identified physical movements from body-worn inertial sensors while considering the collaborative nature and limited resources of the system. Inertial sensors are integrated with UWB localization system in [23] for simultaneous 3-D trajectory tracking and lower body motion capture (MoCap) under various dynamic activities such as walking and jumping.

WS-based HMT systems do not need to deploy devices in scenarios and are less sensitive to the environment. Thus, they are more suitable for large-scale and dynamic applications [2,6]. Currently, WS-based HMT systems [6] are mainly composed of inertial sensors, such as accelerometers and gyroscopes. However, inertial sensors may inevitably throw off errors that accumulate over time [8,15,25]. The accumulative and drift error is the biggest challenge faced by WS-based HMT systems.

2.2. Sensor Fusion and Filtering

Despite the advantages mentioned above, there still exist challenges when wearable sensors are applied to human motion tracking. As human motion tracking could be viewed as a multiple-target localization issue of human body joints, tracking accuracy is the most important consideration. However, sensor drift errors and distortion (especially in long time monitoring) are the main problems [8,15,25].

Kalman filter and calibration algorithms are the most widely adopted method to overcome drift errors. They are both used to overcome the instantaneous error problem and multiple sensor fusion problem. Yun et al. [36] realized a method to measure the orientation of human body segments using Kalman filter that takes into account the spectra of the signals, as well as a fluctuating gyroscope offset, and thereby improves the estimation accuracy. Zhao et al. [37] proposed a Kalman/UFIR filtering method for state estimation with uncertain parameters and noise statistics. Briese et al. [38] presented an adapting covariance Kalman filter based on the fusion of Ultra-Wideband (UWB) and inertial measurements. Since both sensor results are separately used in the Kalman filter, no registration between the implemented sensors is needed. Kim et al. [39] proposed a fusion algorithm based on a particle filter using vertical and road intensity information for robust vehicle localization in a large-scale urban area. However, filtering methods lack in terms of dynamic behavior and the algorithm performance varies with the change of state matrixes [38,39]. They can somewhat slow down the error accumulation process, but not eliminate it completely [40,41]. With the booming of artificial intelligence, deep neural networks [42] have been applied in the fusion of multi-sensors, while the requirement of a large scale of data still remains a big challenge in practical applications.

2.3. Cramér–Rao Lower Bound

The location of a target node is uncertain due to the influence of random factors, such as noise, fading, multi-path, and non-line-of-sight propagation, which ultimately affects the positioning accuracy [1,8]. Cramér–Rao lower bound (CRLB) defines the theoretical lower bound of the unbiased estimator variance and is used as a general criterion and benchmark for evaluating the performance of a positioning system [8].

Tichavsky et al. [43] provided the formulation of recursive posterior CRLB for nonlinear filters based on the Bayesian framework. For range-based wireless localization system, many research studies have provided CRLB results for different scenarios. Qi et al. [44] proposed a generalized CRLB (G-CRLB) of the wireless system for non-line-of-sight (NLOS) environment. Other similar works also give CRLB for different ranging techniques [45]. Although some other methods can be used for performance analysis [14], CRLB is still popular for wireless localization research due to its simplicity and general expression.

However, CRLB only focuses on the influence of the relationship between relative positions in spatial state on the accuracy of the positioning target, neglecting the time information, thus cannot meet the requirements of the time evaluation in the positioning system. The posterior Cramér–Rao lower bound (PCRLB) considers the time domain information [46] and can be used as another criterion for the performance evaluation of the positioning system. PCRLB has recently been used as the basis for determining optimal observer trajectories in bearings-only tracking (e.g., [47]). Recent interest in the PCRLB is primarily a result of an excellent paper [43] in which a computationally efficient (and general) formulation of the bound is derived. This has led to a number of further developments, including derivations of the bound and associated information reduction factors in cluttered environments [14] and the establishment of PCRLBs in multi-target tracking with either preprocessed [1,5] or raw sensor data [8,15].

To better comprehend HMT problems and provide a theoretical basis for the system verification and algorithm design, in this paper, we conduct a comprehensive analysis on performance evaluation of HMT system based on IMU/TOA fusion. By the derivation of CRLB and PCRLB, we present a feasible assessment means to evaluate IMU/TOA fusion system in both temporal and spatial aspects.

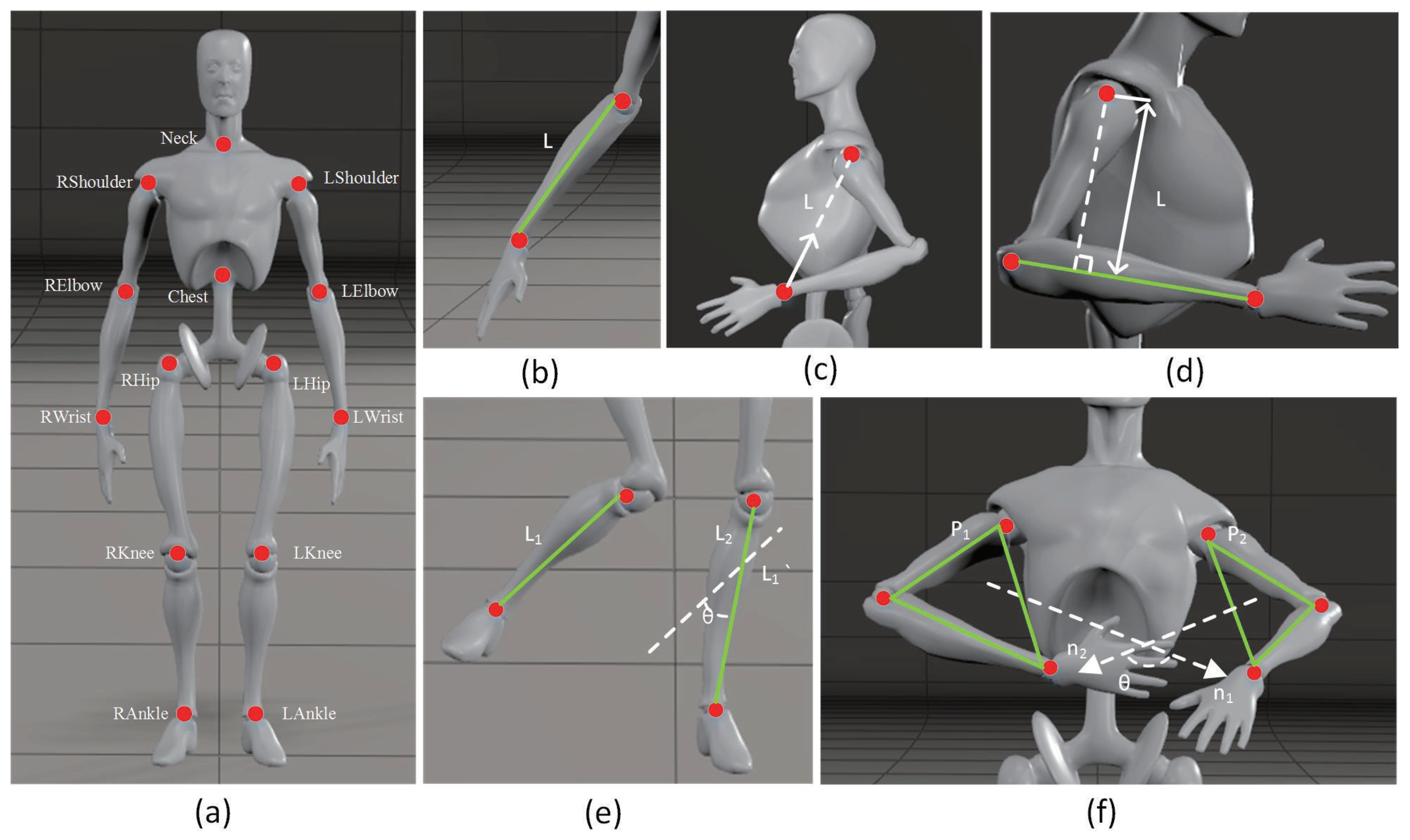
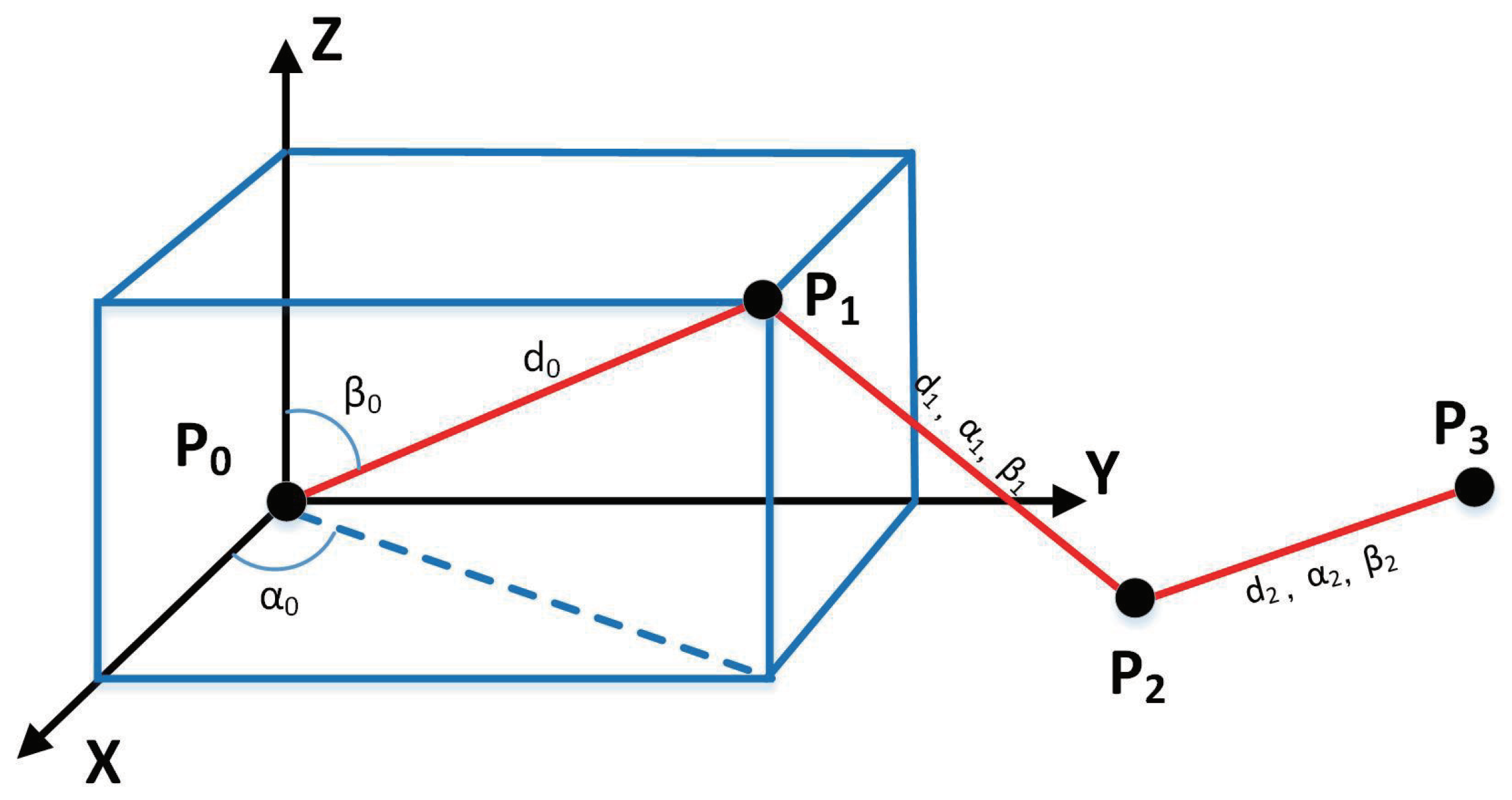
3. Problem Definition

The body can be viewed as an interconnected whole, and each movement is done in collaboration with a number of body parts. The part of body that is connected to each other is called the joint. We call this chain of rigid limbs and joints the “chain of motion”. Therefore, HMT can be considered as a collaborative tracking process of the motion chain composed of multiple human joints.

3.1. Model Description

Generally speaking, a 3D human motion is considered as a set of multiple joints and limbs movement, which can be described using mathematical expressions of coordinates and direction. As shown in Figure 1, the whole body is divided into five connected parts, namely left upper limb, right upper limb, trunk, left lower limb and right lower limb. We use dots to represent joints and lines for limbs. The whole human body acts as a unity of these limbs and joints.

As shown in Figure 1, the human body consists of 15 joints and 14 limbs. To better describe the complicated human body movements, Denavit–Hartenbe (D-H) equation [22,25] is generally used in the description of HMT features and parameters. Its measurement parameters mainly include the distances between joints (Figure 1b,c) joint and limbs (Figure 1d) and the relative angles between limbs (Figure 1e,f). To simplify the above tracking problem, we abstract the HMT serialization process as shown in Figure 1, representing the target’s coordinate and measurement parameters in time sequence $T=\{t_0,t_1,\cdots ,t_n\}$.

On the basis of random motion model [25], we assume a Gauss–Markov process to describe the movement of the joints of the body, as shown in Figure 2. Thanks to Inertial Measurement Unit (IMU), acceleration and angular data can be obtained and, furthermore, the rotation angle of the target position within the history frames can be calculated by means of Attitude and Heading Reference System (AHRS) [20]. In addition, distance-related information can be obtained using the TOA technique [19], after a few simple calculations. Compared with IMU-based dead reckoning method [25], TOA-based tracking method does not have to face the problem of drifting.

3.2. Error Sources

As mentioned above, the measurement parameters of the system are derived from IMU and TOA. The measurement error sources can be divided into two aspects: distance measurement error and angle measurement error. Thereinto, target node’s distance parameter ${\widehat{d}}_t$ at time t is defined as:

$${\widehat{\mathit{d}}}_t={\mathit{d}}_t+n_d$$

(1)

where ${\mathit{d}}_t$ is the actual distance value and $n_d$ is Gauss distributed measurement noise whose variance is ${\sigma }_d^2$, namely $n_d\sim \mathcal{N}(0,{\sigma }_d^2)$. Vector ${\widehat{\mathit{d}}}_t={[{\widehat{d}}_1,{\widehat{d}}_2,\cdots ,{\widehat{d}}_{n+m-1}]}^T$ is introduced to collect distance information, namely the distance between target node and reference nodes, respectively, standing for one body joint.

Horizontal heading estimates from inertial-sensor-based approach $\alpha$ reads:

$${\widehat{\alpha }}_t={\alpha }_t+u_t,u_t\sim N(0,{ϵ}_t^2)$$

(2)

where ${\alpha }_t$ is the true value of actual horizontal heading. $u_t$ is uncorrelated zero-mean Gaussian random variable with variance ${ϵ}_t^2$, which is independent from z direction and is also uncorrelated with $\widehat{d}$. The horizontal heading is an instantaneous measurement parameters, which may introduce cumulative error by the characteristics of IMU. Namely, ${\widehat{\alpha }}_t$ is a time-dependent parameter. Vector ${\alpha }_t={[{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_{N_{\alpha }}]}^T$ is introduced to collect ${\alpha }_t$, i.e., the angular cumulative information in the past $N_{\alpha }$ frames.

Vertical elevation estimates from inertial-sensor-based approach $\beta$ reads:

$${\widehat{\beta }}_t={\beta }_t+v_t,v_t\sim N(0,{\xi }_t^2)$$

(3)

where ${\beta }_k$ is the actual vertical elevation. $v_t$ is uncorrelated zero-mean Gaussian random variable with variances ${\xi }_t^2$, which is independent from z direction and is also uncorrelated with both $\widehat{\alpha }$ and $\widehat{d}$. ${\widehat{\beta }}_t$ is also a time-independent parameter. Vector ${\beta }_t={[{\beta }_1,{\beta }_2,\cdots ,{\beta }_{N_{\beta }}]}^T$ is introduced to collect ${\beta }_k$, i.e., the angular cumulative information in the past $N_{\beta }$ frames. As above mentioned angles $\alpha$ and $\beta$ are all measured from IMU, thus, for ease of expression, we take ${\sigma }_{IMU}$ as the variance of both these two parameters.

3.3. Model Presentation

In continuous human motion tracking process, some body parts remain relatively steady in comparison to the end joints or limbs of the human body, such as the trunk. Thus, these positions may be set as reference nodes, defined as ${\mathcal{P}}_a=\{1,\dots ,m\}$, in which the kth reference node’s coordinate is defined as ${\mathit{a}}_{\mathit{k}}$. m indicates the number of reference nodes. In addition, the position state of the target is denoted by ${\mathit{p}}_t={[p_t^X{p}_t^Y{p}_t^Z]}^T$, where $p_t^X$, $p_t^Y$ and $p_t^Z$ are the coordinates in the 3-D positioning system, and T is the transpose operator. The target nodes set is represented as ${\mathcal{P}}_x=\{1,2,\dots ,n\}$, and the ith target node’s coordinate is defined as ${\mathit{p}}_{\mathit{i}}$. n indicates the number of target nodes.

According to the Bayesian theorem [22,25], at time t, the state estimation ${\mathit{x}}_{t-1}$ could be represented as:

$${\mathit{p}}_t={\mathbf{f}}_t({\mathit{p}}_{t-1})+{\mathbf{q}}_t$$

(4)

where Equation (4) is the prediction equation, and ${\mathbf{f}}_t(·)$ is the transition equation, and the noise of ${\mathit{x}}_t$ follows standard normal distribution with variance $Q_t$, namely ${\mathbf{q}}_t\sim \mathcal{N}(0,Q_t)$.

To describe the measurement parameters of human motion in a more general way, we define the measurement parameters of the system as:

$${\mathbf{z}}_t={\mathbf{h}}_t\left(\mathbf{d}({\mathit{p}}_t,\mathit{k}),\mathbf{\phi }\right)+{\mathbf{r}}_t$$

(5)

where the measurement vector ${\mathbf{z}}_t$, whose noise follows normal distribution, i.e., ${\mathbf{r}}_t\sim \mathcal{N}(0,R_t)$, contains two parts, namely TOA measurement parameter (distance) and IMU measurement parameter (acceleration, angular velocity, etc.). ${\mathbf{h}}_{\mathbf{t}}(·)$ is nonlinear observation equation, which is related with actual measurement values of target ${\mathbf{p}}_{\mathbf{t}}$, including $\mathbf{d}({\mathbf{p}}_{\mathbf{t}},\mathbf{k})$ (the distance vector at time t), and $\mathbf{\phi }$ (the angle vector at time t). $\mathbf{k}=[k_1,\cdots ,k_j,\cdots ,k_{m+n-1}]$ is distance measurement indicator, such as line-of-sight (LOS)/non-line-of-sight (NLOS), the reference node accuracy indicator, etc. $m+n-1$ is the total number of both reference and target nodes. $\mathbf{\phi }=[{\phi }_1,\cdots ,k_i,\cdots ,{\phi }_s]$ is the vector of angle measurement values, whose amount is s. $\mathit{k}$ and $\mathbf{\phi }$ are auxiliary parameters that are not essential but may help increase the localization accuracy and could be calculated in real time. The effects of these parameters can be verified in subsequent simulation experiments.

4. IMU/TOA Fusion Based HMT Method

Our analysis considers the possible unknown random factors that may influence the human motion tracking. Considering the characteristics of sequential human motion tracking, we define the measuring variable at time slot t as ${\mathbf{\theta }}_t$ (for simplicity, it is abbreviated as $\mathbf{\theta }$), namely

$$\mathbf{\theta }\triangleq {\left[\begin{array}{cccc}{\mathit{p}}_t^T& {\mathit{p}}_{t-1}^T& {\mathit{k}}^T& {\mathbf{\phi }}^T\end{array}\right]}^T$$

(6)

where ${\mathit{p}}_t$ is the target position vector at the moment, and ${\mathit{p}}_{t-1}$ is historical target location information at the former time slot.

Cramér–Rao lower bound (CRLB) [22] is defined as the inverse of Fisher Information Matrix (FIM) and represents the theoretical lower bound of the observed variance of unbiased estimators [22,25]. Suppose that $p(\mathbf{\theta },{\mathit{z}}_{\mathit{t}})$ represents the joint probability density function of observation vectors ${\mathit{z}}_{\mathit{t}}$ and $\mathbf{\theta }$, then FIM could be derived as the variance of its log likelihood function gradient, namely

$$\mathbf{J}(\mathbf{\theta })\triangleq \mathbb{E}[{\Delta }_{\theta }^{\theta }\ln p(\mathbf{\theta },{\mathit{z}}_{\mathbf{t}})]$$

(7)

where $\mathbb{E}\{·\}$ represent the expectation of parameters. ${\nabla }_{\mathbf{\theta }}=[\frac{\partial }{\partial {\theta }_1},\cdots ,\frac{\partial }{\partial {\theta }_n}]$, ${\Delta }_{\alpha }^{\beta }={\nabla }_{\beta }{\nabla }_{\alpha }^T$. Thus,

$${\mathbf{Cov}}_{\mathbf{\theta }}(\tilde{\mathbf{\theta }})⪰{\left\{\mathbf{J}(\mathbf{\theta })\right\}}^{-1}$$

(8)

where $A\ge B$ for the sake of simplicity, represents that matrix $A-B$ is non-negatively defined.

According to the Bayesian theorem, $p(\mathbf{\theta },{\mathit{z}}_{\mathit{t}})=p({\mathit{z}}_{\mathit{t}}|\mathbf{\theta })p(\mathbf{\theta })$, then $\mathbf{J}(\mathbf{\theta })$ could be divided into two parts, namely

$$\mathbf{J}(\mathbf{\theta })={\mathbf{J}}_{\mathbf{D}}(\mathbf{\theta })+{\mathbf{J}}_{\mathbf{P}}(\mathbf{\theta })$$

(9)

where ${\mathbf{J}}_{\mathbf{D}}$ is the information matrix obtained by measuring parameters. ${\mathbf{J}}_{\mathbf{P}}$ is the information matrix obtained by prior information. We describe the representation of these two variables separately in the following section.

4.1. Measurement Parameter Information Matrix

Due to the measurement equation, we get $\mathbf{h}={\mathbf{h}}_t\left(\mathbf{d}({\mathit{p}}_t,\mathit{k}),\mathbf{\phi }\right)$, and then, based on the chain rules [48], ${\mathbf{J}}_{\mathbf{D}}$ could be represented as:

$${\mathbf{J}}_{\mathbf{D}}=\mathbf{H}·{\mathbf{J}}_{\mathbf{h}}·{\mathbf{H}}^T$$

(10)

where $\mathbf{H}=[{\nabla }_{\mathbf{\theta }}h]$, $J_h$ is the FIM of h, namely

$${\mathbf{J}}_{\mathbf{h}}=\mathbb{E}\left\{{\nabla }_{\mathbf{h}}\ln p({\mathbf{z}}_t|\mathbf{\theta }){\left[{\nabla }_{\mathbf{h}}\ln p({\mathbf{z}}_t|\mathbf{\theta })\right]}^T\right\}$$

(11)

where transition matrix $\mathbf{H}$ could be further decomposed into four components

$$\mathbf{H}={\left[\begin{array}{cccc}{\mathbf{H}}_t& {\mathbf{H}}_{t-1}& \mathbf{K}& \Phi \end{array}\right]}^T$$

(12)

where ${\mathbf{H}}_t=[{\nabla }_{p_t}\mathit{h}]$, ${\mathbf{H}}_{t-1}=[{\nabla }_{p_{t-1}}\mathit{h}]$, $\mathbf{K}=[{\nabla }_k\mathit{h}]$, $\Phi =[{\nabla }_{\phi }\mathit{h}]$. Because the distance is a instantaneous measurement parameter, it has no error accumulation problems. Thus, $\mathbf{d}$ has no relationship with prior information ${\mathit{p}}_{\mathit{t}-\mathbf{1}}$, namely ${\mathbf{H}}_{t-1}=0$. Then,

$$\mathbf{H}={\left[\begin{array}{cccc}{\mathbf{H}}_t& \mathbf{0}& \mathbf{K}& \Phi \end{array}\right]}^T$$

(13)

For ${\mathbf{J}}_h$, we can use diagonal matrices of order n to represent it,

$${\mathbf{J}}_{\mathbf{h}}=\mathbf{\Lambda }=\mathbf{diag}({\lambda }_1,\dots ,{\lambda }_j,\dots ,{\lambda }_n)$$

(14)

where ${\lambda }_j$ stands for the jth measurement value. Then, ${\mathbf{J}}_{\mathbf{D}}$ is represented as a $(4+m+n+s)\times (4+m+n+s)$ matrix,

$$\begin{array}{cc}\hfill {\mathbf{J}}_{\mathbf{D}}& =\mathbf{H}·\mathbf{\Lambda }·{\mathbf{H}}^T\hfill \\ & =\left[\begin{array}{cccc}{\mathbf{D}}_{11}& \mathbf{0}& {\mathbf{D}}_{13}& {\mathbf{D}}_{14}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ {\mathbf{D}}_{13}^T& \mathbf{0}& {\mathbf{D}}_{33}& {\mathbf{D}}_{34}\\ {\mathbf{D}}_{14}^T& \mathbf{0}& {\mathbf{D}}_{34}^T& {\mathbf{D}}_{44}\end{array}\right]\hfill \end{array}$$

(15)

where

$$\begin{array}{cccc}\hfill {\mathbf{D}}_{11}& ={\mathbf{H}}_t\Lambda {\mathbf{H}}_t^T\hfill & \hfill {\mathbf{D}}_{13}& ={\mathbf{H}}_t\Lambda {\mathbf{K}}^T\hfill \\ \hfill {\mathbf{D}}_{14}& ={\mathbf{H}}_t\Lambda {\Phi }^T\hfill & \hfill {\mathbf{D}}_{33}& =\mathbf{K}\Lambda {\mathbf{K}}^T\hfill \\ \hfill {\mathbf{D}}_{34}& =\mathbf{K}\Lambda {\Phi }^T\hfill & \hfill {\mathbf{D}}_{44}& =\Phi \Lambda {\Phi }^T\hfill \end{array}$$

(16)

4.2. State Parameter Information Matrix

It could be known by the whole probability formula, for the variable $\mathbf{\theta }$, the probability $p(\mathbf{\theta })=p({\mathit{p}}_{\mathit{t}}|{\mathit{p}}_{\mathit{t}-\mathbf{1}})p(\mathit{k})p(\mathbf{\phi })$. Then, log-likelihood function could be represented as:

$$\ln p(\mathbf{\theta })=\left[\ln p({\mathit{p}}_t|{\mathit{p}}_{t-1})\right]+\ln p(\mathit{k})+\ln p(\mathbf{\phi })$$

(17)

where $p(\mathit{k})$ and $p(\mathbf{\phi })$ are corresponding independent information of ${\mathit{p}}_t$ and ${\mathit{p}}_{t-1}$. We decompose the vector $\mathbf{\theta }$ into two components, namely state vector ${[{\mathit{p}}_{\mathit{t}}{\mathit{p}}_{\mathit{t}-\mathbf{1}}]}^T$ and observation vector ${[\mathit{k}\mathbf{\phi }]}^T$. Thus, ${\mathit{J}}_{\mathit{P}}$ could be represented as:

$$\begin{array}{cc}\hfill {\mathbf{J}}_{\mathbf{P}}& =\mathbb{E}[{\Delta }_{\mathbf{\theta }}^{\mathbf{\theta }}\ln p(\mathbf{\theta })]\hfill \\ & =\left[\begin{array}{cc}{\mathbf{J}}_{{\mathbf{P}}_{11}}& {\mathbf{J}}_{{\mathbf{P}}_{12}}\\ {\mathbf{J}}_{{\mathbf{P}}_{12}}^T& {\mathbf{J}}_{{\mathbf{P}}_{22}}\end{array}\right]\hfill \end{array}$$

(18)

where ${\mathit{J}}_{{\mathit{P}}_{\mathbf{11}}}$ could be obtained with the recursion of vectors ${\mathit{p}}_{\mathit{t}}$ and ${\mathit{p}}_{\mathit{t}-\mathbf{1}}$, which, according to Tichavsky et al. [43], could be described as:

$${\mathbf{J}}_{{\mathbf{P}}_{11}}=\left[\begin{array}{cc}{\mathbf{M}}_{11}& {\mathbf{M}}_{12}\\ {\mathbf{M}}_{12}^T& {\mathbf{M}}_{22}+\mathbf{J}({\mathit{p}}_{t-1})\end{array}\right]$$

(19)

where

$$\begin{array}{cc}\hfill {\mathbf{M}}_{11}& ={\mathbf{Q}}_t^{-1}\hfill \\ \hfill {\mathbf{M}}_{12}& ={\nabla }_{{\mathit{p}}_{t-1}}{\mathbf{f}}_t({\mathit{p}}_{t-1}){\mathbf{Q}}_t^{-1}\hfill \\ \hfill {\mathbf{M}}_{22}& ={\nabla }_{{\mathit{p}}_{t-1}}{\mathbf{f}}_t({\mathit{p}}_{t-1}){\mathbf{Q}}_t^{-1}{\left[{\nabla }_{{\mathit{p}}_{t-1}}{\mathbf{f}}_t({\mathit{p}}_{t-1})\right]}^T\hfill \end{array}$$

(20)

$\mathbf{J}({\mathit{p}}_{t-1})$ is the FIM of ${\mathit{p}}_{t-1}$. As $p(\mathit{k})$ and $p(\mathbf{\phi })$ are independent from ${\mathit{p}}_t$ and ${\mathit{p}}_{t-1}$, ${\mathit{J}}_{{\mathit{P}}_{\mathbf{12}}}$ is $\mathbf{0}$, namely

$${\mathbf{J}}_{{\mathbf{P}}_{12}}=\left[\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]$$

(21)

Similarly, the prior probability $p({\mathit{p}}_t|{\mathit{p}}_{t-1})$ are independent from $\mathit{k}$ and $\mathbf{\phi }$. Thus, ${\mathit{J}}_{{\mathit{P}}_{\mathbf{12}}}=$${\mathit{J}}_{{\mathit{P}}_{\mathbf{21}}}^{\mathit{T}}=\mathbf{0}$. Finally,

$${\mathbf{J}}_{{\mathbf{P}}_{22}}=\left[\begin{array}{cc}{\mathbf{J}}_{\mathbf{K}}& \mathbf{0}\\ \mathbf{0}& {\mathbf{J}}_{\Phi }\end{array}\right]$$

(22)

where ${\mathbf{J}}_{\mathbf{K}}$ and ${\mathbf{J}}_{\Phi }$ are, respectively, the FIM of vectors $\mathit{k}$ and $\mathbf{\phi }$:

$$\begin{array}{cc}\hfill {\mathbf{J}}_{\mathbf{K}}& =\mathbb{E}[{\Delta }_{\mathit{k}}^{\mathit{k}}\ln p(\mathit{k})]\hfill \\ \hfill {\mathbf{J}}_{\Phi }& =\mathbb{E}[{\Delta }_{\mathbf{\phi }}^{\mathbf{\phi }}\ln p(\mathbf{\phi })]\hfill \end{array}$$

(23)

4.3. Integral Information Matrix

Due to the analysis above, substituting Equations (15) and (18) into Equation (9), the FIM of variable $\mathbf{\theta }$ could be represented as:

$$\mathbf{J}(\mathbf{\theta })=\left[\begin{array}{cccc}{\mathbf{M}}_{11}+{\mathbf{D}}_{11}& {\mathbf{M}}_{12}& {\mathbf{D}}_{13}& {\mathbf{D}}_{14}\\ {\mathbf{M}}_{12}^T& {\mathbf{M}}_{22}+\mathbf{J}(x_{t-1})& \mathbf{0}& \mathbf{0}\\ {\mathbf{D}}_{13}^T& \mathbf{0}& {\mathbf{D}}_{33}+{\mathbf{J}}_{\mathbf{K}}& {\mathbf{D}}_{34}\\ {\mathbf{D}}_{14}^T& \mathbf{0}& {\mathbf{D}}_{34}^T& {\mathbf{D}}_{44}+{\mathbf{J}}_{\Phi }\end{array}\right].$$

(24)

However, only the lower bound of ${\mathit{p}}_{\mathit{t}}$ is of interest, namely a small submatrix of $\mathbf{J}(\mathbf{\theta })$, ${\mathbf{J}}^{-1}({\mathit{p}}_{\mathit{t}})={[{\mathbf{J}}^{-1}(\mathbf{\theta })]}_{2\times 2}$.

Furthermore, due to the Schur complement theorem [49], $\mathbf{J}({\mathit{p}}_t)$ could be divided into two components, namely state matrix ${\mathit{J}}_{\mathit{S}}$ and measurement matrix ${\mathit{J}}_{\mathit{C}}$, then

$$\mathbf{J}({\mathit{p}}_t)={\mathbf{J}}_S-{\mathbf{J}}_C$$

(25)

where

$$\begin{array}{cc}\hfill {\mathbf{J}}_{\mathbf{S}}& ={\mathbf{M}}_{11}+{\mathbf{D}}_{11}-{\mathbf{M}}_{12}{\left({\mathbf{M}}_{22}+\mathbf{J}({\mathit{p}}_{t-1})\right)}^{-1}{\mathbf{M}}_{12}^T\hfill \\ \hfill {\mathbf{J}}_{\mathbf{A}}& =\left[\begin{array}{cc}{\mathbf{D}}_{13}& {\mathbf{D}}_{14}\end{array}\right]{\left[\begin{array}{cc}{\mathbf{D}}_{33}+{\mathbf{J}}_{\mathbf{K}}& {\mathbf{D}}_{34}\\ {\mathbf{D}}_{34}^T& {\mathbf{D}}_{44}+{\mathbf{J}}_{\mathbf{C}}\end{array}\right]}^{-1}{\left[\begin{array}{cc}{\mathbf{D}}_{13}& {\mathbf{D}}_{14}\end{array}\right]}^T\hfill \end{array}$$

(26)

As mentioned above, we demonstrate a comprehensive analysis of how distance and angle measurements are related with human motion tracking accuracy in IMU/TOA fusion systems. The detailed calculation process is shown in Algorithm 1. In the next two sections, we further evaluate the overall performance of the fusion system from two aspects, namely spatial and temporal performance, in theory.

Algorithm 1 Proposed IMU/TOA fusion-based human motion tracking method.

0: Initialization:  1: Define measuring variable at time slot t as ${\mathbf{\theta }}_t\triangleq {\left[\begin{array}{cccc}{\mathit{p}}_t^T& {\mathit{p}}_{t-1}^T& {\mathit{k}}^T& {\mathbf{\phi }}^T\end{array}\right]}^T$. Set the time slot index $t=0$. Choose an initial value for ${\mathit{p}}_{t-1}$ of variable ${\mathbf{\theta }}_t$, generally as 0. Part 1: measurement parameter information  2: Calculate parameter matrix ${\mathbf{H}}_t$, $\mathbf{K}$, $\Phi$.  3: Update the matrix parameters $\mathbf{H}={\left[\begin{array}{cccc}{\mathbf{H}}_t& {\mathbf{H}}_{t-1}& \mathbf{K}& \Phi \end{array}\right]}^T$.  4: Calculate parameter matrix ${\mathbf{D}}_{11}$, ${\mathbf{D}}_{13}$, ${\mathbf{D}}_{14}$, ${\mathbf{D}}_{33}$, ${\mathbf{D}}_{34}$ and ${\mathbf{D}}_{44}$.  5: Update the matrix parameter ${\mathbf{J}}_{\mathbf{h}}$.  6: Update the information matrix obtained by measuring parameters, i.e., ${\mathbf{J}}_{\mathbf{D}}(\mathbf{\theta })=\mathbf{H}·{\mathbf{J}}_{\mathbf{h}}·{\mathbf{H}}^T$ Part 2: state parameter information  7: Calculate parameter matrix ${\mathbf{M}}_{11}$, ${\mathbf{M}}_{12}$, ${\mathbf{M}}_{22}$, ${\mathbf{J}}_{\mathbf{K}}$ and ${\mathbf{J}}_{\Phi }$.  8: Update the matrix parameters ${\mathbf{J}}_{{\mathbf{P}}_{11}}$, ${\mathbf{J}}_{{\mathbf{P}}_{12}}$ and ${\mathbf{J}}_{{\mathbf{P}}_{12}}$.  9: Update the information matrix obtained by prior information, i.e., ${\mathbf{J}}_{\mathbf{P}}=\left[\begin{array}{cc}{\mathbf{J}}_{{\mathbf{P}}_{11}}& {\mathbf{J}}_{{\mathbf{P}}_{12}}\\ {\mathbf{J}}_{{\mathbf{P}}_{12}}^T& {\mathbf{J}}_{{\mathbf{P}}_{22}}\end{array}\right]$. Part 3: integral information 10: Update the FIM matrix by $\mathbf{J}(\mathbf{\theta })={\mathbf{J}}_{\mathbf{D}}(\mathbf{\theta })+{\mathbf{J}}_{\mathbf{P}}(\mathbf{\theta })$ 11: Update Schur complement parameters of $\mathbf{J}(\mathbf{\theta })$, namely state matrix ${\mathit{J}}_{\mathit{S}}$ and measurement matrix ${\mathit{J}}_{\mathit{C}}$ 12: Update the estimation result ${\mathit{p}}_t=\mathbf{J}({\mathit{p}}_t)={\mathbf{J}}_S-{\mathbf{J}}_C$ Part 4: recursive computation 13: $t+1\to t$, go to step 2.

5. Spatial Performance Analysis

When it comes to spatial performance, we suppose that the tracking system has time independence, namely $\mathit{J}({\mathit{p}}_{\mathit{t}})$ and $\mathit{J}({\mathit{p}}_{\mathit{t}-\mathbf{1}})$ are independent from each other. Thus, ${\mathit{M}}_{\mathbf{12}}$, ${\mathit{M}}_{\mathbf{22}}$, ${\mathit{J}}_{{\mathit{p}}_{\mathit{t}-\mathbf{1}}}$, ${\mathit{J}}_{\mathit{K}}$, ${\mathit{D}}_{\mathbf{13}}$, ${\mathit{D}}_{\mathbf{33}}$ and ${\mathit{D}}_{\mathbf{34}}$ are all $\mathbf{0}$, namely

$$\mathbf{J}({\mathit{p}}_t)={\mathbf{M}}_{11}+{\mathbf{D}}_{11}-{\mathbf{D}}_{14}{[{\mathbf{D}}_{44}+{\mathbf{J}}_{\Phi }]}^{-1}{\mathbf{D}}_{14}^T$$

(27)

Movement characteristics of each body part should be taken into consideration. Because of the spatial features of human motion sensing, it could be classified into two categories: 2-D and 3-D conditions. 2D motions refer to the body movements that can be captured by a plane, such as raising one’s arms into Y pose or T pose. 3D motions refer to stereoscopic movements such as walking, running or swing hands. The different relative positions may contribute to various capture accuracy. Therefore, both the CRLB of human body in 2D and 3D scenarios are taken into consideration. CRLB of each location is derived as following demonstration and performance of proposed fusion method is verified. See Appendix A for the detailed derivation process of CRLB for spatial performance analysis.

5.1. Scenario Setup

As mentioned above, the trunk remains relatively steady in comparison to the end joints or limbs of the human body. In consideration of end-effector problem, we set the joints of neck, chest, left and right hip as reference nodes for error bounds estimation. A constrained scenario of 2 m × 2 m is set up for further experiments. The entire human body is supposed to located in the center of this region. In contrast, two sequences of reference nodes combination are considered, namely $Case1=\{Neck,Chest,LHip,RHip\}$ and $Case2=\{Neck,LShoulder,RShoulder,Chest,LHip,RHip\}$. The body is allowed to move freely in this space.

5.2. Performance Analysis

To demonstrate the typical calculation results, CRLB, when the variance of distance measurement ${\sigma }_d$ is 0.2 and ${\sigma }_{IMU}$ is 0.1, is selected upon common commercial motion sensing systems, such as Xsens. From the experiment results, as shown in Figure 3, the following conclusions could be obtained:

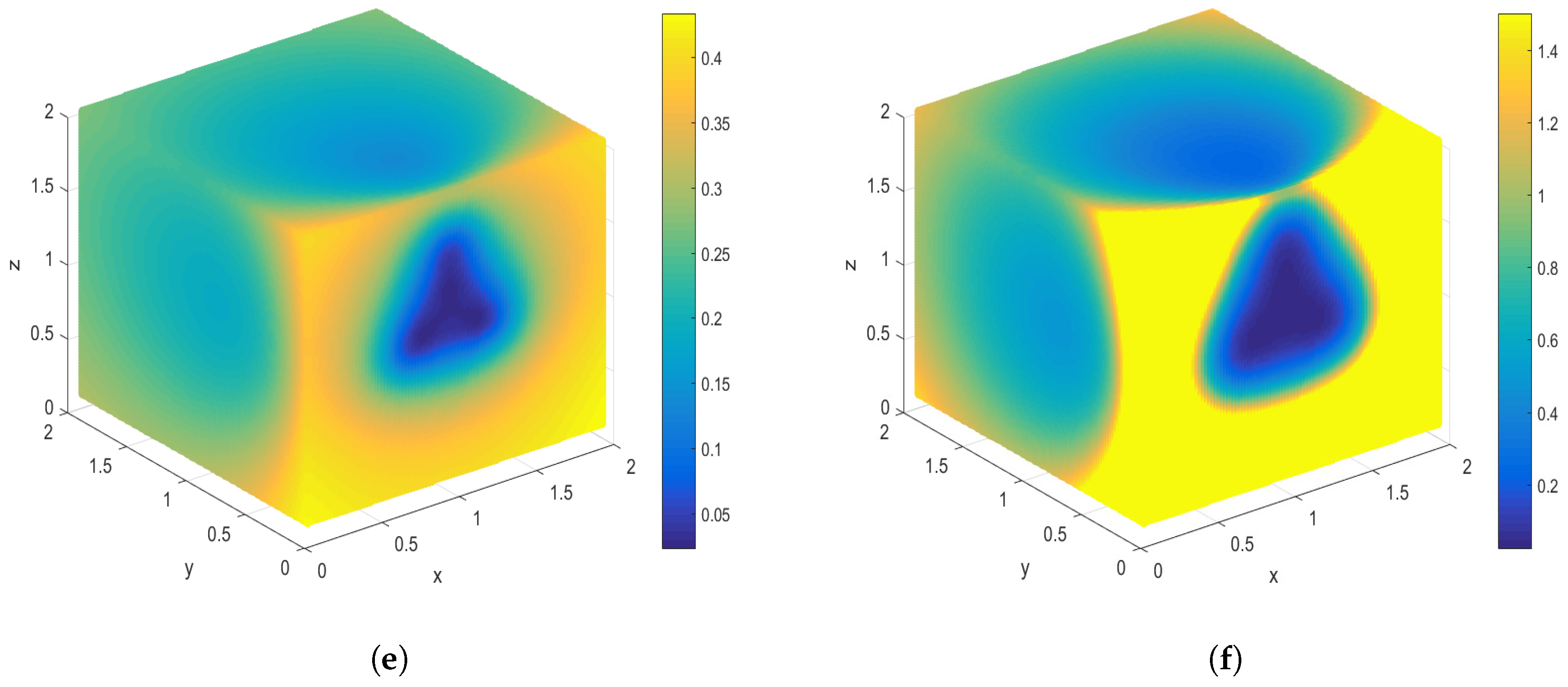
• In the aspect of two-dimensional condition, shown in Figure 3a,b, lower CRLB is shown when the position is closer to the trunk. It is also lower in the lower limb than the upper, which is possibly due to the selection of reference nodes. To verify this, a comparison experiment was conducted when the reference nodes were chosen differently. Results shown in Figure 3a,b indicate that the relative position of the reference nodes cause different CRLB of human motion and the more uniform the nodes distribute, the relative lower CRLB it achieves. The same result can also be seen in Figure 3c,d when only distance measurement is applied in the human motion sensing process.
• Since human motion is a three-dimensional process, stereoscopic presentation is shown in Figure 3e,f. The human is assumed to be placed in the XOZ plane when the y is set as zero. The 3D version of CRLB is likely to be a 2D one that stretches along the Z-axis. Similar results could be seen in 3D condition that, the closer to the trunk, the lower the CRLB that could be achieved.
• For comparison, the CRLB under two measurement method were calculated, respectively, independent distance measurement and the fusion of IMU and distance measurement. Comparison results are shown in Figure 3a,c (also in pair of Figure 3b,d).

To clearly show the different capture capability of distance measurement and IMU, Figure 4 is presented. As shown, under different ${\sigma }_d^2$, CRLB increases along with the increase of ${\sigma }_{IMU}^2$. When ${\sigma }_{IMU}^2$ is fixed, CRLB also increases along with the increase of ${\sigma }_d^2$. However, the change is more apparent when ${\sigma }_d^2$ is fixed. It means that the accuracy of IMU measurement matters more in the fusion process, but the distance measurement helps restrain the bounds of CRLB. It is worth mentioning that, for a given ${\sigma }_{IMU}^2$, CRLB shows little variation with the increase of ${\sigma }_d^2$ if it is larger than 0.2. It indicates that the distance measurement may be not the main limiting factor of CRLB, but ${\sigma }_{IMU}^2$ is.

6. Temporal Performance Analysis

We suppose that the tracking system has cumulative recursion characteristics, namely $\mathit{J}({\mathit{p}}_{\mathit{t}})$ and $\mathit{J}({\mathit{p}}_{\mathit{t}-\mathbf{1}})$ are not independent from each other. Based on [22], Equation (26) could be simplified into a recursive form, namely Posterior Cramér–Rao Lower Bound (PCRLB) [22,25].

$$\mathbf{J}({\mathit{x}}_t)={\mathbf{M}}_{11}+{\mathbf{D}}_{11}-{\mathbf{M}}_{12}{\left[{\mathbf{M}}_{22}+\mathbf{J}({\mathit{x}}_{t-1})\right]}^{-1}{\mathbf{M}}_{12}^T$$

(28)

See Appendix B for the detailed derivation process of PCRLB for temporal performance analysis.

6.1. Scenario Setup

Even though there are elegant expressions to recursively calculate the FIM, Equation (27) usually does not have analytical close-form solution. To deal with that, we employ the Monte Carlo approach [50] to convert those continuous integrals into discrete summations, and finally work out the PCRLB. The root-mean-square of PCRLB is given by $\frac{1}{L}{\sum }_{i=1}^L{P}_k^i$, where $P_k^i$ is the PCRLB on the Root-Mean-Square Error (RMSE) of joint at step k in the ith Monte Carlo trial. L is the total Monte Carlo trial number ($L=1000$ was used in this study). Note that, for each Monte Carlo trial, we randomly selected the initial location for PCRLB calculation to get a fair average of the entire human body moving process.

6.2. Performance Analysis

We mainly analyzed the influence of different factors on PCRLB from the following two perspectives: fusion method factor and topology factor.

(1) Fusion method factor: Considering different $Q_t$ and $R_t$ in IMU/TOA fusion methods, as well as using sole TOA or IMU method, may lead to different results of human motion tracking accuracy.

Figure 5 shows in IMU/TOA fusion methods, the lower bounds under different $Q_t$ and $R_t$ as well as in the use of sole TOA or IMU method. As shown in the figure:

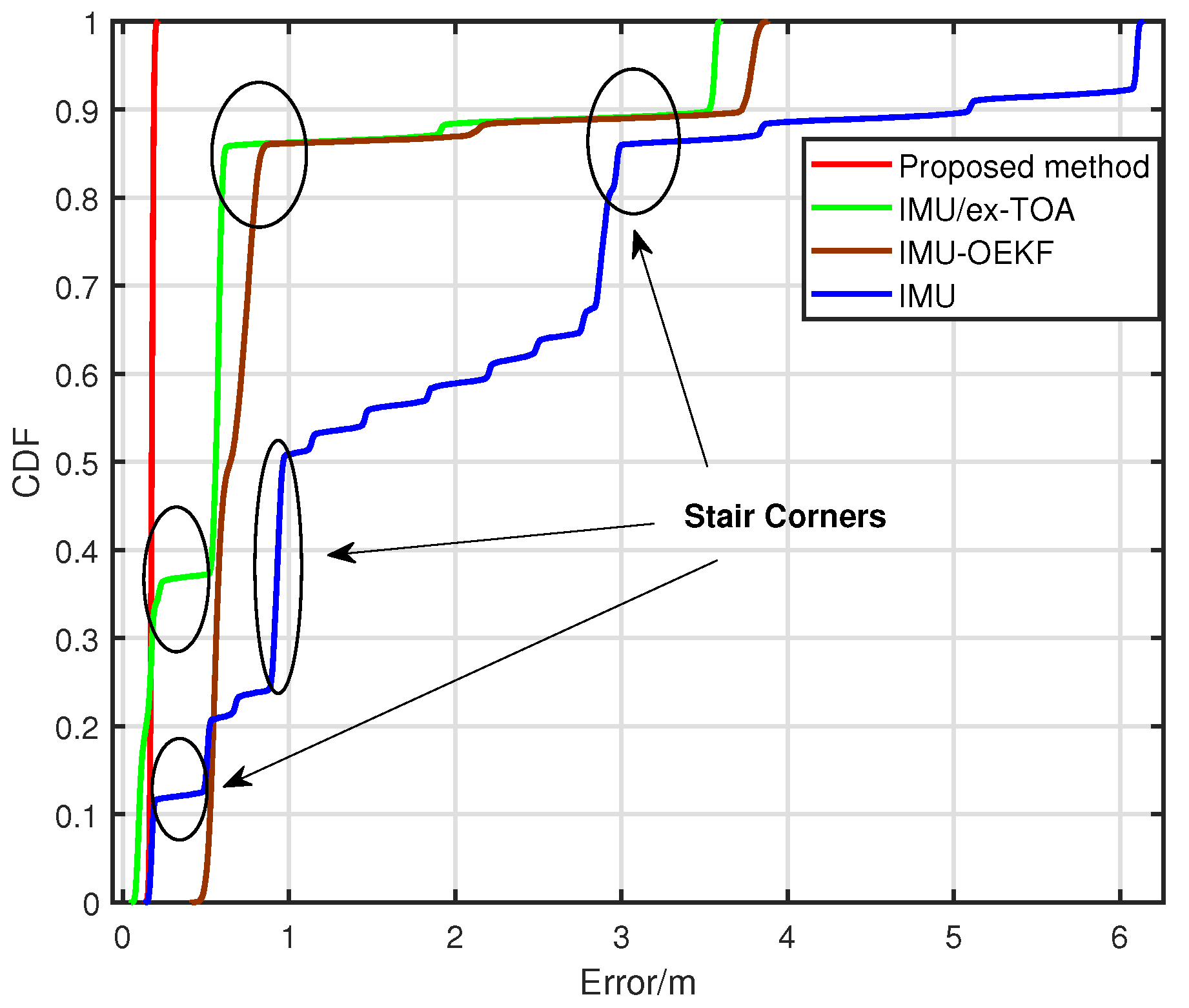
• When only inertial sensors are adopted in the tracking system, as indicated by the black solid line in Figure 5, the accumulative errors may tend to be diverging. Theoretically, this confirms that IMU based HMT system faces the problem of accumulative errors. However, IMU/TOA fusion method can avoid this divergence. The performance curves of proposed approaches achieve stability after certain steps, i.e., their errors converge.
• Compared with sole TOA tracking method, IMU/TOA fusion-based method can significantly increase the accuracy of human body motion tracking. The lower bound of proposed fusion method could drop below 8 cm.
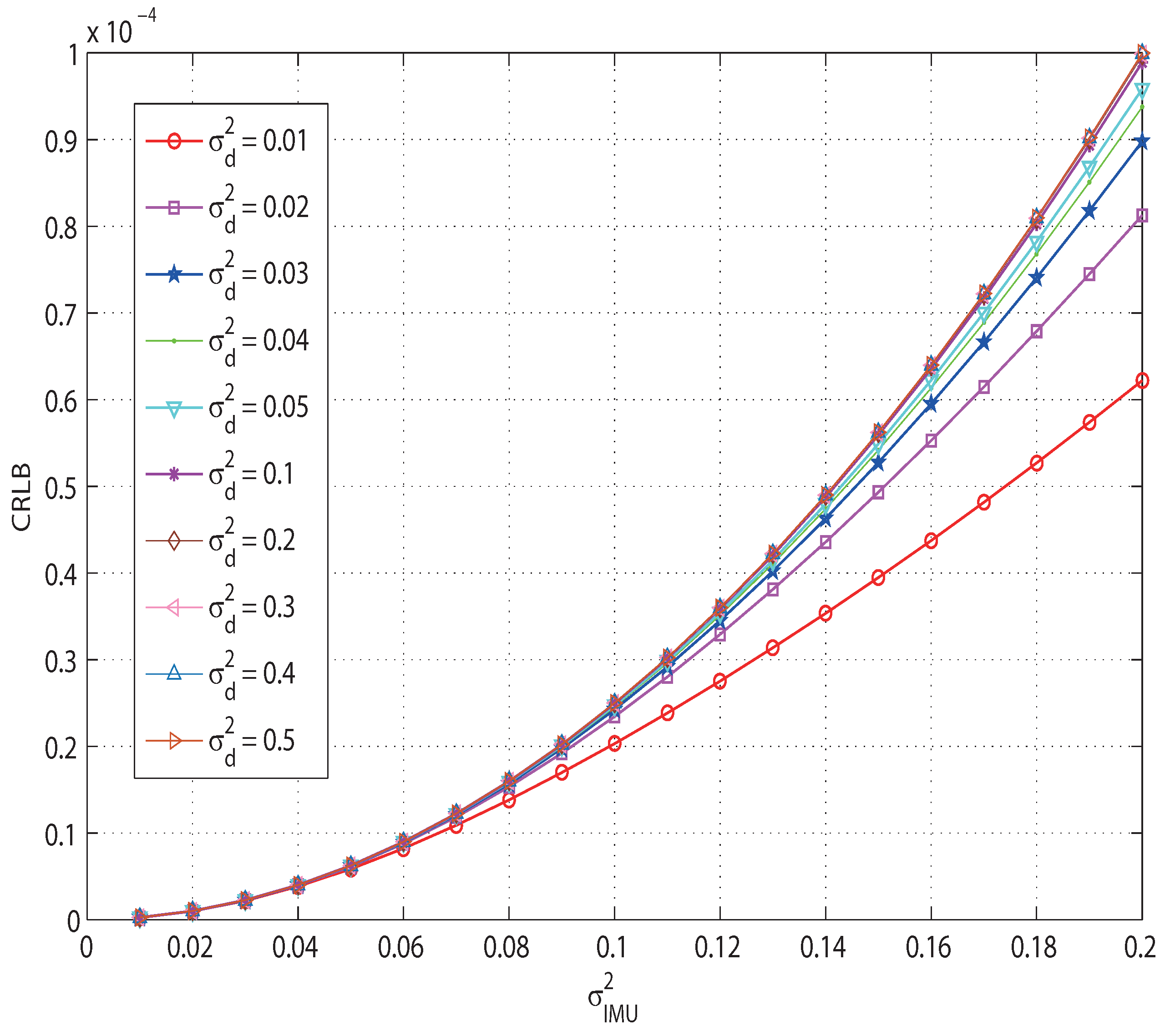
• With increase of $Q_t$ and $R_t$, PCRLB also increases, which means that the accuracy is inversely proportional to these two parameters.

(2) Topology factor: As already indicated in Section IV-B, topologies have much influence on the performance of certain tracking systems. We work out the PCRLB of different topologies shown in Figure 6, where $Q_t$ is 0.1 and $R_t$ is 0.05. As shown in Figure 7, we could draw the following conclusions:

• Under different topologies, the theoretical accuracy lower bounds of the tracking system are different.
• The different topological conditions tend to be stable after the same iteration number (around 15), which means the convergence rate is roughly the same under various topologies.
• Topology 3 suffers the largest RMSE, which may be due to the dense reference nodes. The minimum RMSE is less than 8 cm, as shown in Topology 4, which makes it a better choice for practice applications.
• The proposed fusion HMT systems with TOA integrated share identical trend results with that of solely TOA ranging.

7. Practical Use Case

In above sections, the theoretical effectiveness of our proposed human motion tracking method is verified in terms of both spatial and temporal performances. The introduced IMU/TOA fusion method utilizes both distance and IMU information to lower the expected error bounds in theory. In this section, we take advantage of this method in 3D practical application scenarios to verify its performance.

7.1. Platform Overview and Experiment Setup

A minimized wearable sensing platform was specially designed for the tracking of human motion in 3D scenario. It aimed to collect spatial and temporal information during the human motion process. Sensing nodes were designed and intended to be put on joints to capture the movement conditions. Target data included accelerated velocity, angular velocity and the distances between joints and body parts. Among these, distance information was especially different when compared with other platforms, such as Xsens and Invensense. We sampled data using above-mentioned platform at 10 Hz. All processing work were performed online in Matlab with PC (Intel Core i7-6700M CPU, 16GB RAM). The communication between wearable nodes and the PC was via Bluetooth.

Our integrated wearable sensor system was composed of two parts: one control unit and several data acquisition units. The control unit worked as a gateway to control the whole operation process via Bluetooth communication. Data acquisition unit was mainly responsible for data sensing. Each data acquisition unit had a six-axis sensor (MPU6050, which integrated a triaxial accelerometer and a triaxial gyroscope), a barometer sensor (MS5611) and a UWB-TOA ranging module (DWM1000) [19]. The MEMS sensors were connected to a micro-controller (STM32F103) for the sake of sampling efficiency at a rate of 10 Hz. Data were transferred to the control unit in real-time and also written into its SD card as backups for other offline analysis and applications. Three sensing nodes were mounted onto the ankle, knee and hip joint. Distance measurements were conducted between these nodes. The whole system architecture is demonstrated in Figure 8.

We proposed an IMU/TOA fusion method for human motion tracking applications, introducing distance information into inertial systems. However, one of the most obvious difference between the proposed method and that in [23] is: the algorithm in [23] needs to take advantage of external UWB stations as reference nodes, namely anchors. However, in our method, we simply utilized internal tags (mounted onto body joints) to range and conduct the fusion process, which can significantly reduce the complexity of tracking systems.

Based on above considerations, human lower limb movement analysis in 3D scenario was chosen as a typical verification experiment, for better demonstrate the performance of proposed method when it is applied to human motion tracking.

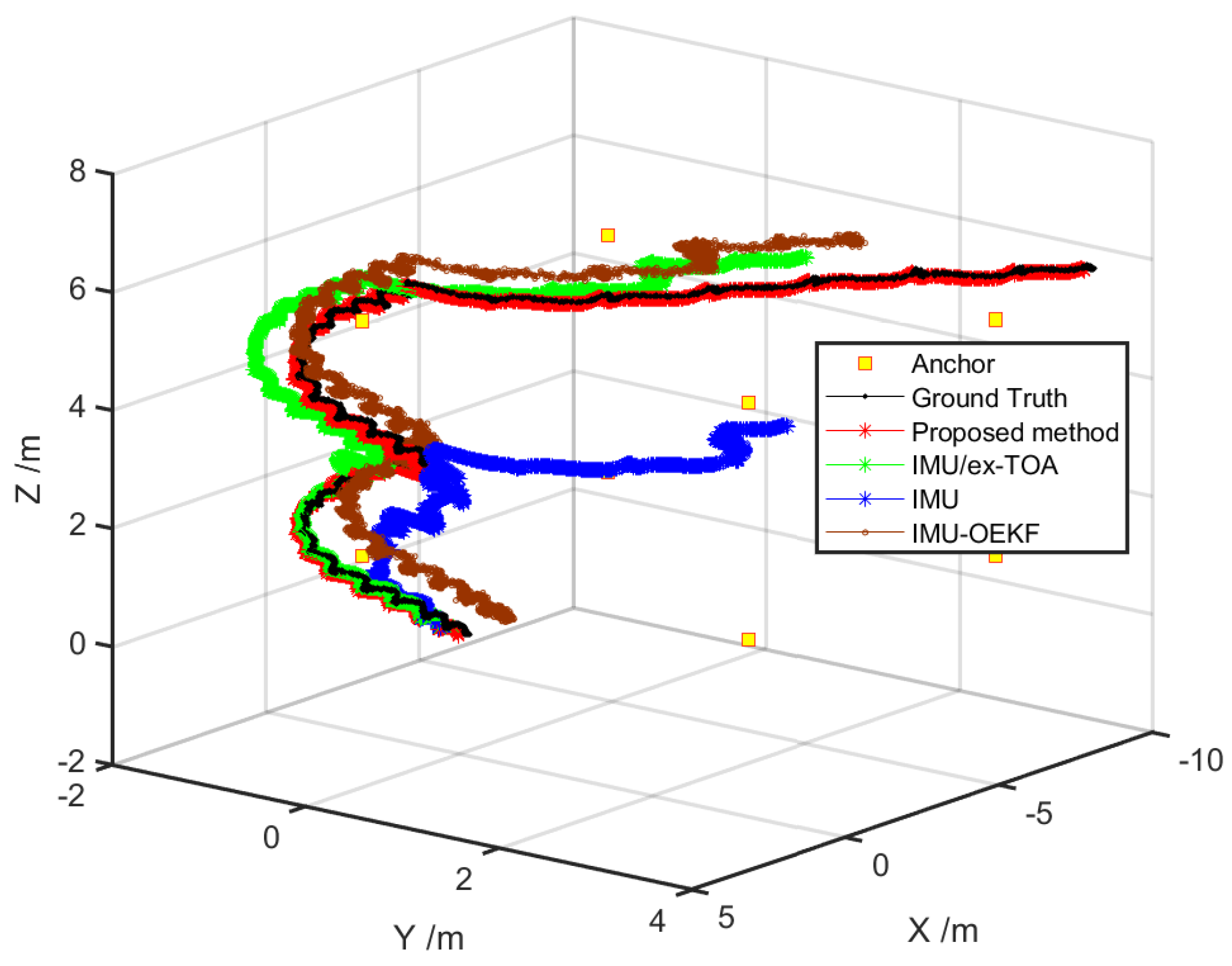
7.2. Practical Use Case in 3D Scenario

A spiral-stairs (between two floors) scenario Was selected as a 3D use case and four UWB anchors were located at each floor (totally eight anchors were used), as shown in Figure 9. The location of anchors in each floor are referred to those in [23] and only used in comparative experiments. Three comparative algorithms were also tested:

(1)

Only IMU was used for human lower limb tracking. Zero velocity update (ZUPT) algorithm [51] was applied. For simplicity, we denoted it as “IMU” method.

(2)

IMU and TOA fusion method in [23] was applied. UWB based TOA tag nodes were mounted to the right lower limb and communicated with external anchor nodes, implementing TOA localization algorithm. For simplicity, and to separate it from our proposed method, we denoted it as “IMU/ex-TOA” method.

(3)

Optimal Enhanced Kalman Filter (OEKF)-based method in [52] was applied. The cumulative errors in attitude and velocity were corrected using the attitude fusion filtering algorithm and ZUPT, respectively. For simplicity, and to separate it from our proposed method, we denoted it as “IMU-OEKF” method.

Experiment results are shown in Figure 9 and Figure 10.

For better comparison, ground truth and tracking trajectories applying all mentioned methods (the proposed method and three comparative ones) are drawn in Figure 9. It is clearly seen that, when applying the proposed method, the experiment results were far closer to the ground truth, while the results when applying methods of IMU [51], IMU/ex-TOA [23] and IMU-OEKF [52] were drifting away as time accumulates. The result remained similar at the very beginning; however, the gap became larger over time.

Detailed accumulated errors are shown in Figure 10. IMU, IMU/ex-TOA and IMU-OEKF faced the problem of drift error, especially when the experimenter turned around at stair corners. Time accumulated errors were more likely to be caused when moving direction changes. With IMU/ex-TOA and IMU-OEKF methods applied into the algorithm, localization errors to some extent could be fixed, but still existed and were critical at turns. On the contrary, our proposed human motion tracking method showed a good stability and no clear drift errors were observed in our experiment. This is because, with the use of proposed method, body connections are considered and temporal transitions are estimated. Especially at turns, body constraints could to some extent fix time accumulated errors. The results suggest that our proposed method performed well while applied in human lower limb analysis. This also confirmed the conclusion obtained in theoretical simulation (Section 4 and Section 5). Methods with only inertial sensors faced the problem of drift errors, but our proposed model could fix time accumulative errors.

From above analysis, our proposed method had significantly higher accuracy, as well as little drift problem. Besides, compared with IMU/ex-TOA method [23] and IMU-OEKF method [52], our method did not need external anchors and had higher tracking accuracy, thus is more suitable for wearable motion tracking applications.

8. Conclusions

A IMU/TOA fusion-based human motion tracking method is proposed in this paper. IMU based HMT technique faces the tough problem of accumulative errors and drift. Time of Arrival (TOA) is considered to compensate the drift and accumulation caused by IMU. On this basis, Cramér–Rao lower bound (CRLB) is derived in detail with consideration of both temporal and spatial related factors. Simulation results show that the IMU/TOA fusion-based HMT method proposed in this paper has significantly higher accuracy, as well as little drift problem, compared with the traditional independent IMU or TOA tracking methods. The comprehensive fundamental limits analysis conducted in this paper can provide a theoretical basis for further system design and algorithm analysis. In the practical use case, proposed IMU/TOA fusion method also shows obvious performance advantages when compared with state-of-the-art methods. Besides, it does not need external anchors, thus it is more suitable for wearable motion tracking applications.