Optimization Algorithm for Multiple Phases Sectionalized Modulation Jamming Based on Particle Swarm Optimization
Abstract
:1. Introduction
2. Principle of MPSM Jamming
2.1. MPSM Jamming Modeling
2.2. Pulse Compression Result of MPSM Jamming
3. Analysis of Influence Factors in MPSM Jamming
3.1. Section Situation
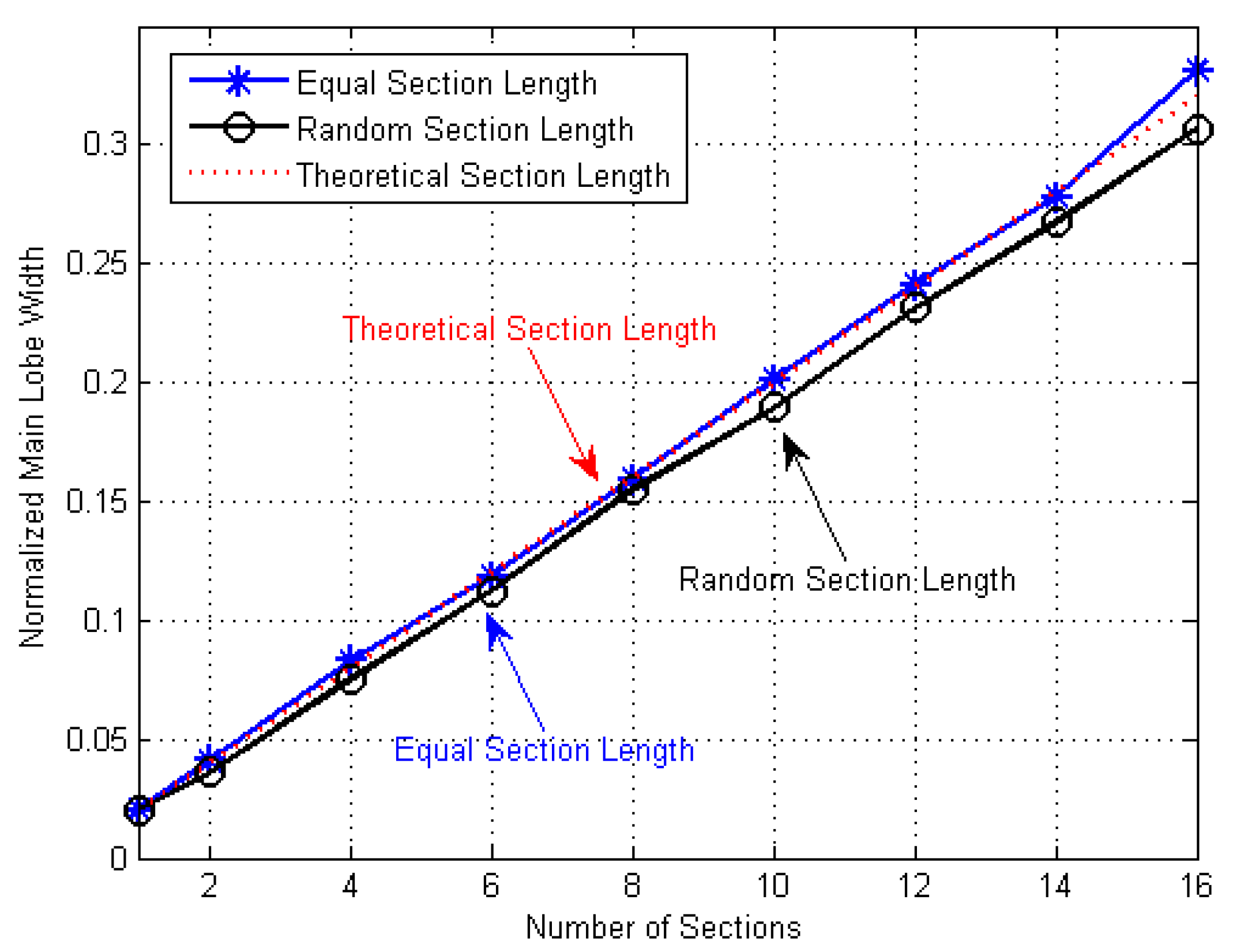
3.1.1. Equal Section Length
3.1.2. Random Section Length
3.2. Phase Situation
4. Optimization Algorithm for MPSM Jamming
4.1. Principle of PSO Algorithm
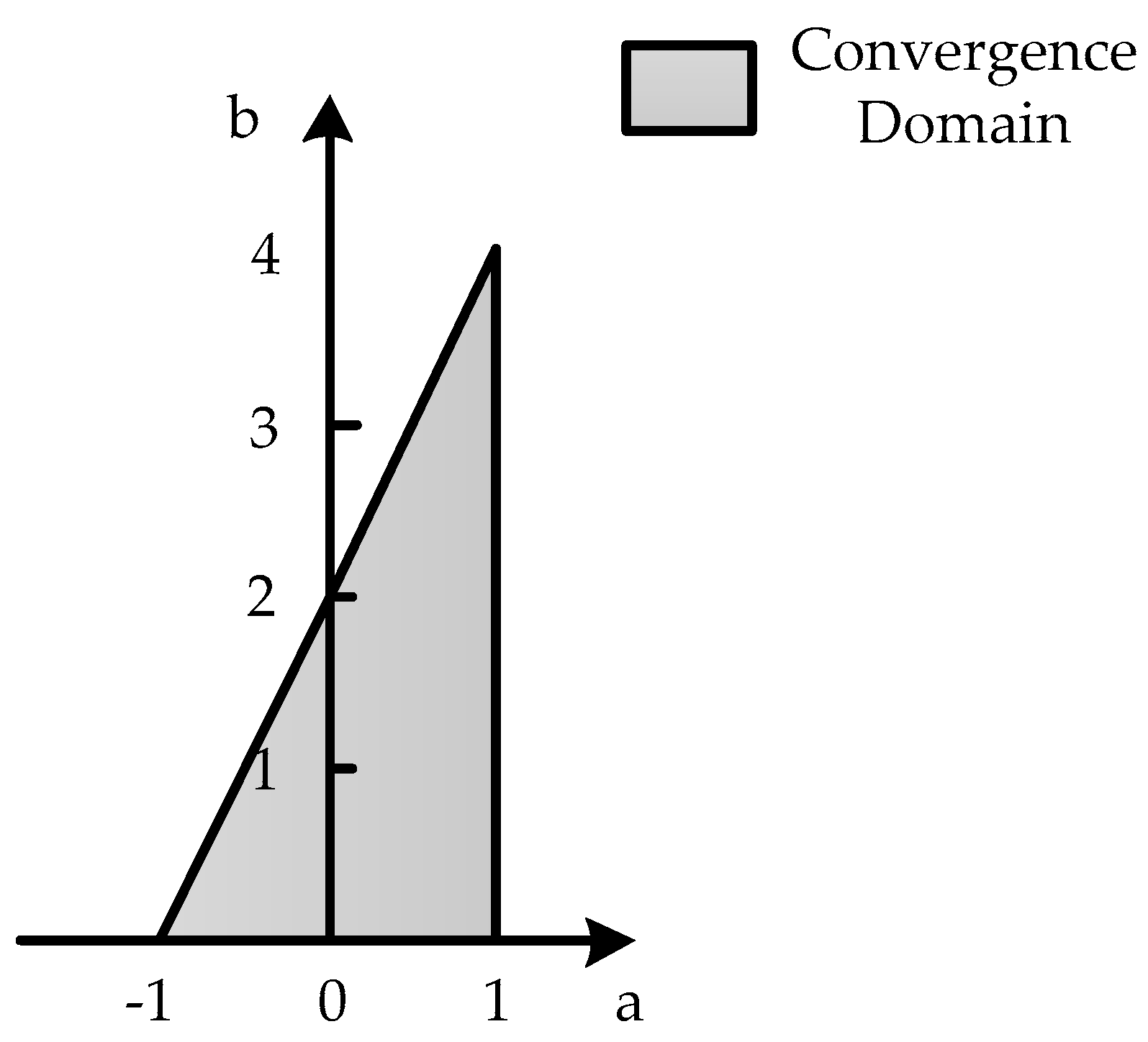
4.2. Analysis of Parameters in PSO
4.2.1. Inertia Weight
4.2.2. Acceleration Coefficient
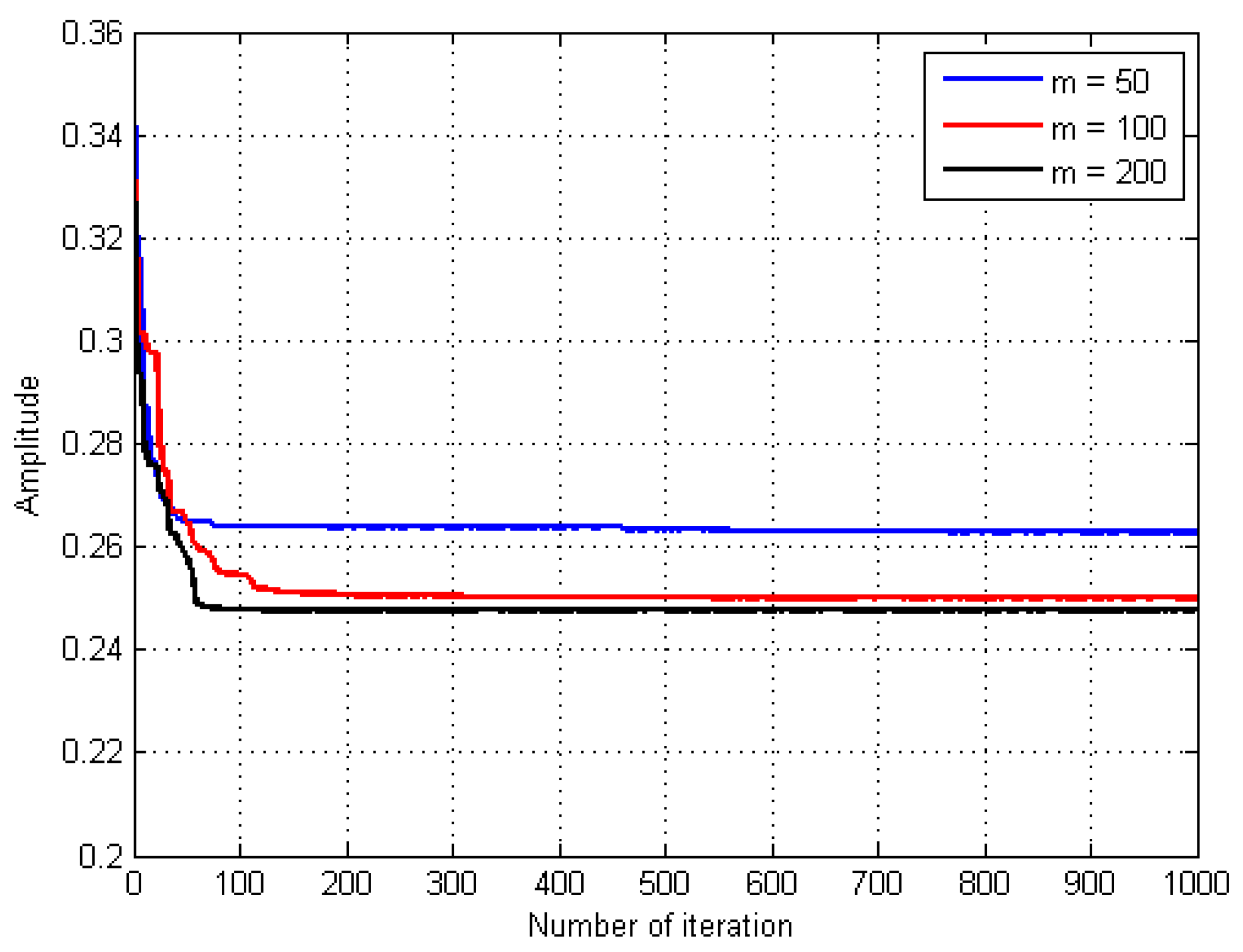
4.2.3. Population Size
4.3. Analysis of Fitness Function and Fitness Value
4.4. Steps of Optimization Algorithm for MPSM Jamming Based on PSO
5. Experiments and Results
5.1. Parameter Settings
5.2. Comparison of Convergence and Computation Time with Different PSO Parameters
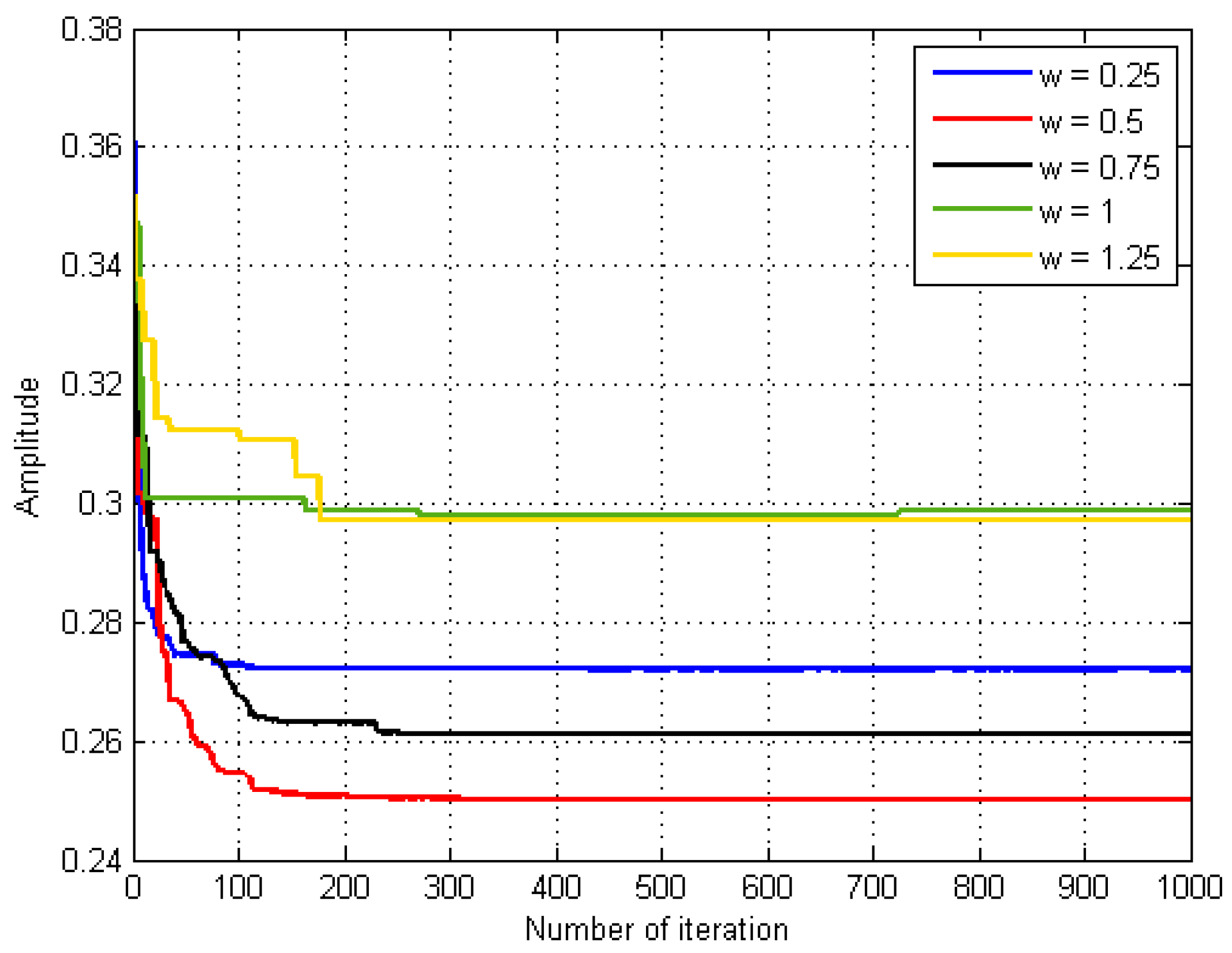
5.2.1. Inertia Weight
5.2.2. Acceleration Coefficient
5.2.3. Population Size
5.3. Comparison of Convergence and Computation Time of PSO and GA
5.4. Relationship Between Number of Sections and Main Lobe Width
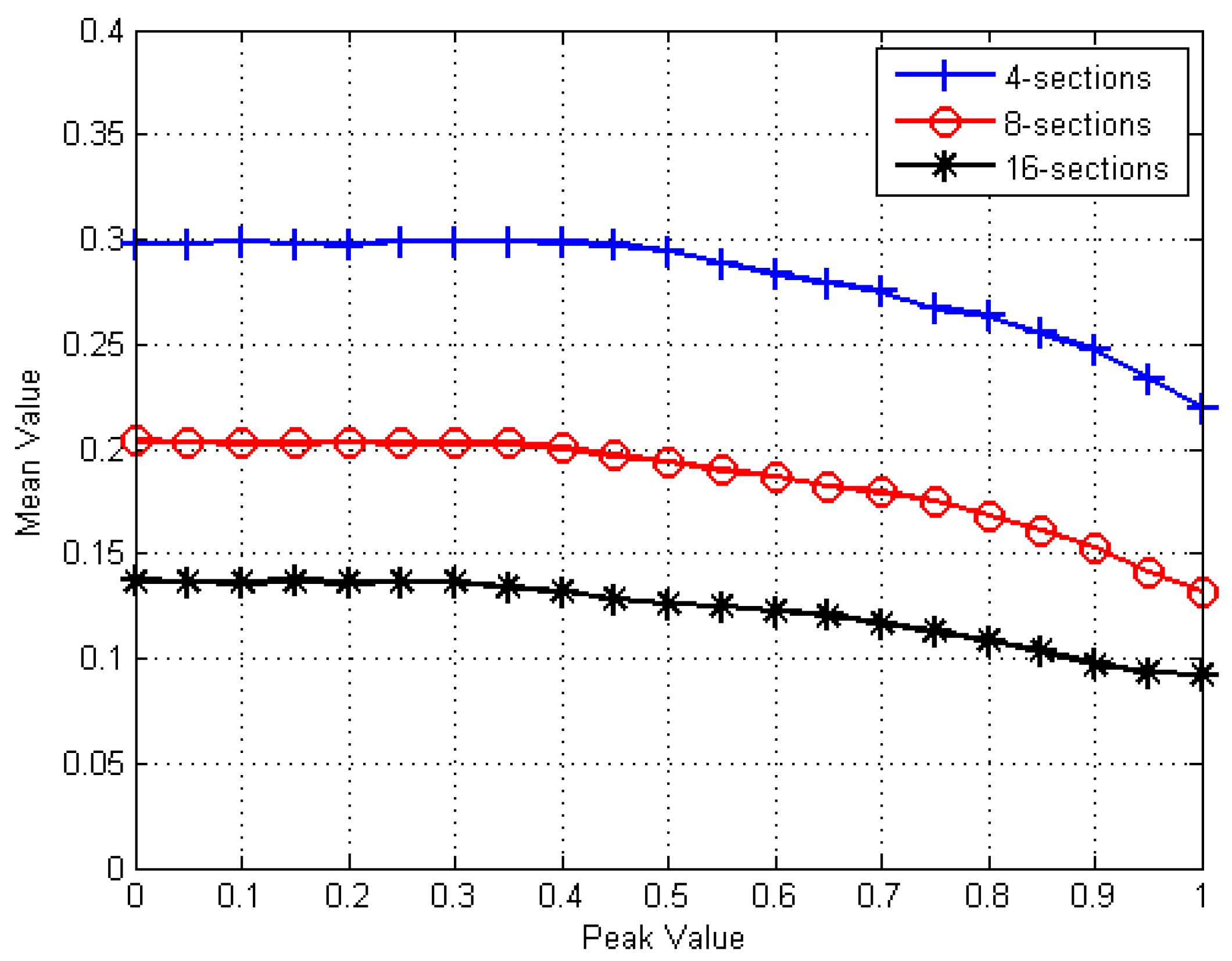
5.5. Relationship Between Peak Value and Mean Value of Main Lobe
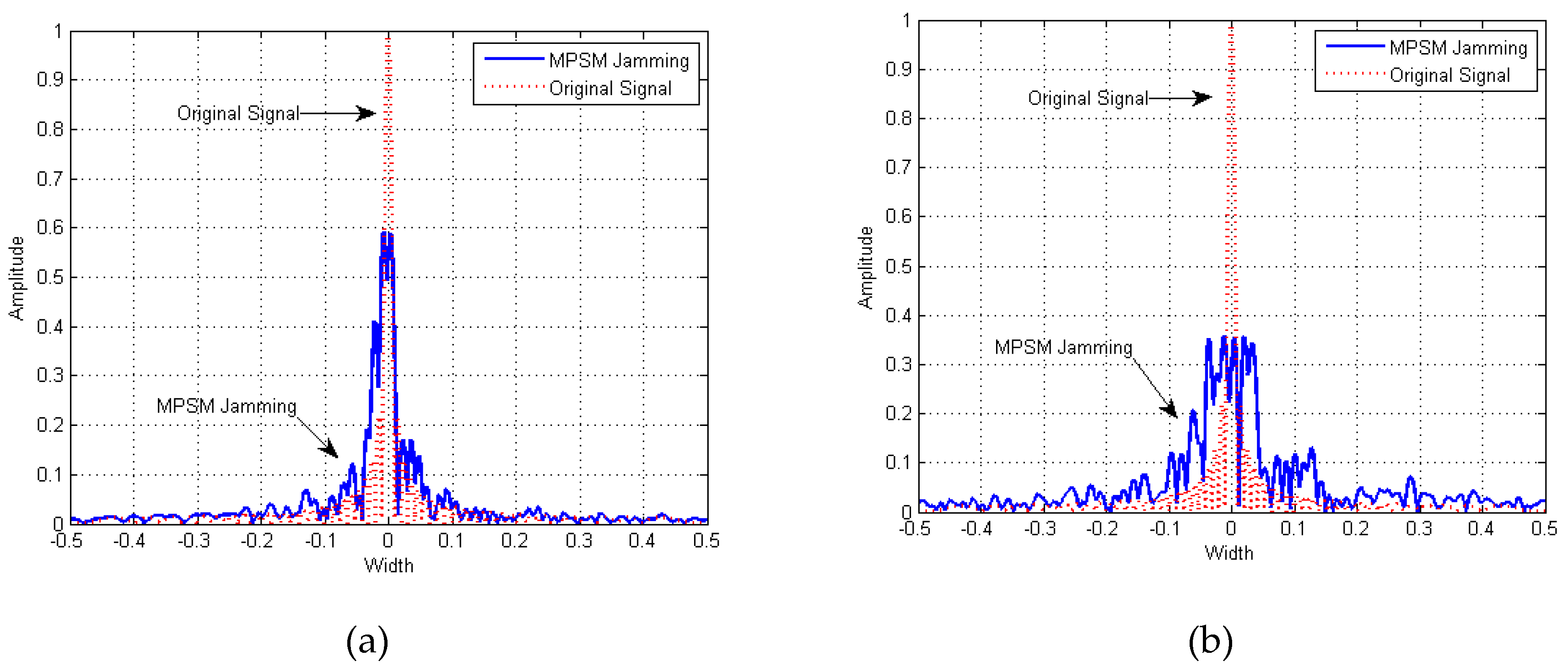
5.6. Random MPSM Jamming and Optimized MPSM Jamming
5.6.1. Random Section Situation and Phase Situation
5.6.2. Optimized Section Situation
5.6.3. Optimized Phase Situation
5.6.4. Optimized Section Situation and Phase Situation
5.6.5. Summary
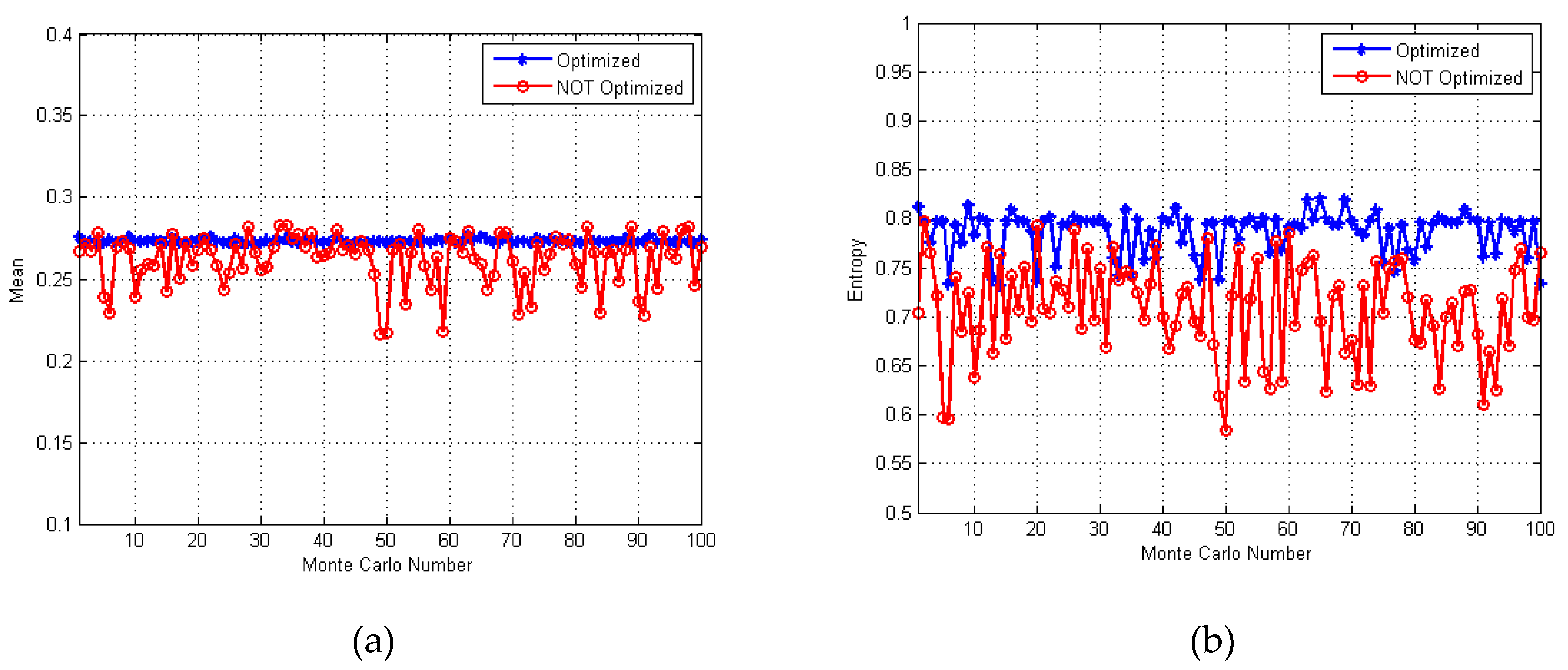
5.7. Statistical Results of Different Optimized MPSM Jamming
5.7.1. Optimized Section Situation
5.7.2. Optimized Phase Situation
5.7.3. Optimized Section Situation and Phase Situation
5.7.4. Summary
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Spezio, A.E. Electronic warfare systems. IEEE Trans. Microw. Theory Tech. 2002, 50, 633–644. [Google Scholar] [CrossRef]
- Adamy, D. EW 101: A First Course in Electronic Warfare; Artech House: London, UK, 2001. [Google Scholar]
- Sun, Q.; Shu, T.; Yu, K.B. Efficient Deceptive Jamming Method of Static and Moving Targets against SAR. IEEE Sens. J. 2018, 18, 3610–3618. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Pan, X. A frequency-domain three-stage algorithm for active deception jamming against synthetic aperture radar. IET Radar Sonar Navig. 2014, 8, 639–646. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Pan, X. Influence of Estimate Error of Radar Kinematic Parameter on Deceptive Jamming Against SAR. IEEE Sens. J. 2016, 16, 5904–5911. [Google Scholar] [CrossRef]
- Wang, G.X.; Peng, S.R.; Sun, J.J. Effect evaluation for SAR suppression jamming based on edge strength image. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015. [Google Scholar]
- Jiang, J.; Wu, Y.; Wang, H. Analysis of active noise jamming against synthetic aperture radar ground moving target indication. In Proceedings of the International Congress on Image & Signal Processing, Shenyang, China, 14–16 October 2015. [Google Scholar]
- He, J.; Peng, F.; Liu, Z. The Analysis of Noise Frequency Modulation Jamming Signal Based on Stochastic Differential. In Proceedings of the International Conference on Computer Application and System Modeling, Taiyuan, China, 7 July 2012. [Google Scholar]
- Guo, J.; Wang, X.; Xing, W. New smart noise jamming of radar signal frequency modulation. J. Xidian Univ. 2013, 40, 155–160. [Google Scholar] [CrossRef]
- Zhu, N.L.; Liu, H.L. Research into the Influence of Frequency Shift on Smart Noise Jamming with Convolution Modulation. Shipboard Electron. Countermeasure 2016, 39, 17–20. [Google Scholar] [CrossRef]
- Zhao, J.-y.; Liu, X.-w.; Yang, G. Research into Modeling and Jamming Methods of High Precision Phased Array Early Warning Radar Signal. Shipboard Electron. Countermeasure 2018, 37–41. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Wang, M.; Zhang, L.; Ma, L.Z. A smart interference method based on trapezoidal wave convolution modulation. J. Airf. Early Warn. Acad. 2018, 48–54. [Google Scholar]
- Yuan, T.; Tao, J.F.; Li, X.C. Research on Convolution Jamming Technique Based on Triangle Wave Modulation. Meas. Control Technol. 2017, 36, 42–46. [Google Scholar] [CrossRef]
- Dong, H.L.; Xie, L.; Ren, G.H. Concluding and Analysis of Dense False Targets Producing Method by Using Convolution-Modulated Jamming. Fire Control Radar Technol. 2016, 45, 31–34. [Google Scholar] [CrossRef]
- Jiang, J.-w.; Wu, Y.-h.; Wang, H.-y.; Chen, J.-b. A Dense False Target Jamming Technique against SAR-GMTI. Shipboard Electron. Countermeasure 2016, 39, 9–14. [Google Scholar] [CrossRef]
- Hao, H.; Zeng, D.; Ge, P. Research on the Method of Smart Noise Jamming on Pulse Radar. In Proceedings of the Fifth International Conference on Instrumentation and Measurement, Computer, Communication and Control, Qinhuangdao, China, 18–20 September 2016. [Google Scholar]
- Tang, L.; Li, S. Application research on scatter-wave jamming for spaceborne SAR. Aerosp. Electron. Warfare 2016, 32, 34–36. [Google Scholar] [CrossRef]
- Hu, H.; Jia, X.; Wu, Y.; Wu, J. Research on the Theory of 2-D Interrupted Sampling Repeater Scatter-wave Jamming to SAR. J. Acad. Equip. Command Technol. 2012, 23, 94–97. [Google Scholar] [CrossRef]
- Wang, D.; Qu, F.; Jiao, J. Generation of scatter-wave jamming signal to SAR and jamming effects analysis. Aerosp. Electron. Warfare 2013, 29, 27–30. [Google Scholar] [CrossRef]
- Hu, D.; Wu, Y. The Scatter-Wave Jamming to SAR. Acta Electron. Sin. 2002, 30, 1882–1884. [Google Scholar] [CrossRef]
- Li, T.; Chen, W.; Lu, G.; Wang, D.J. A Study on Scatter-Wave Jamming for Countering SAR. In Proceedings of the International Conference on Microwave and Millimeter Wave Technology, Guilin, China, 18–21 April 2007. [Google Scholar]
- Wang, C.; Zhu, H.; Pan, Y.J.; Yuan, N.C. Novel noise jamming method against ISAR. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015. [Google Scholar]
- Daobin, Y.; Yanhong, W.; Wang, H.; Xin, J. Research on Multiple Phase Sectionalized Modulation Jamming Method for Inverse Synthetic Aperture Radar. J. Electron. Inf. Technol. 2017, 39, 423–429. [Google Scholar] [CrossRef]
- Yu, D.B.; Wu, Y.H.; Jia, X.; Wang, H.Y. Research on Multiple Phase Sectionalized Modulation Jamming Method for Pulse Compression Radar. J. Signal Process. 2016, 32, 1178–1186. [Google Scholar] [CrossRef]
- Sun, Y.X.; Qi, G.Y.; Wang, Z.H.; Barend, J. Chaotic particle swarm optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, Shanghai, China, 28–30 March 2010. [Google Scholar]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Li, X.P.; Chen, Q.; Zou, X.H. Kalman filtering decoupling algorithm based on particle swarm optimization. Syst. Eng. Electron. 2018, 751–755. [Google Scholar] [CrossRef]
- Yang, Q.; Sun, S. Radar emitter recognition based on particle swarm optimization algorithm. Laser J. 2018, 118–121. [Google Scholar] [CrossRef]
- Buonamici, F.; Carfagni, M.; Furferi, R.; Governi, L.; Lapini, A.; Volpe, Y. Reverse Engineering of Mechanical Parts: A Template-Based Approach. J. Comput. Des. Eng. 2017, 5, 145–159. [Google Scholar] [CrossRef]
- Ines, A.V.M.; Honda, K.; Gupta, A.D.; Droogers, P.; Celemente, R.S. Combining remote sensing-simulation modeling and genetic algorithm optimization to explore water management options in irrigated agriculture. Agric. Water Manag. 2006, 83, 221–232. [Google Scholar] [CrossRef]
- Monteiro, R.P.; Lima, G.A.; Oliveira, J.P.G.; Cunha, D.S.C.; Bastos-Filho, C.J.A. Accelerating the convergence of adaptive filters for active noise control using particle swarm optimization. In Proceedings of the 2017 IEEE Latin American Conference on Computational Intelligence, Arequipa, Peru, 8–10 November 2017. [Google Scholar]
- Luo, H.; Jia, P.; Qiao, S.; Duan, S. Enhancing electronic nose performance based on a novel QPSO-RBM technique. Sens. Actuators, B 2018, 259, 241–249. [Google Scholar] [CrossRef]
- Bashir, Z.A.; El-Hawary, M.E. Applying Wavelets to Short-Term Load Forecasting Using PSO-Based Neural Networks. IEEE Trans. Power Syst. 2009, 24, 20–27. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Amjad, M.; Mekhilef, S. An Improved Particle Swarm Optimization (PSO)–Based MPPT for PV With Reduced Steady-State Oscillation. IEEE Trans. Power Electron. 2012, 27, 3627–3638. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Parameter Selection in Particle Swarm Optimization. In Proceedings of the International Conference on Evolutionary Programming VII, San Diego, USA, 25–27 March 1998. [Google Scholar]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]














| Parameter | Value | Unit |
|---|---|---|
| bandwidth | 100 | Hz |
| pulse width | 1 | s |
| frequency rate | 100 | Hz/s |
| sampling rate | 2000 | Hz |
| sampling points | 2000 | |
| Jamming-signal power ratio (JSR) | 0 | dB |
| Inertia Weight | Computation Time (s) |
|---|---|
| 0.25 | 123 |
| 0.5 | 109 |
| 0.75 | 107 |
| 1 | 130 |
| 1.25 | 132 |
| Acceleration Coefficient | Computation Time (s) |
|---|---|
| 1 | 116 |
| 2 | 109 |
| 3 | 133 |
| Population Size | Computation Time (s) |
|---|---|
| 50 | 81 |
| 100 | 109 |
| 200 | 324 |
| Algorithm | Computation Time (s) |
|---|---|
| PSO | 109 |
| GA | 354 |
| Figure 15 | Section Situation | Phase Situation |
|---|---|---|
| (a) | 0.250, 0.315, 0.410, 0.025 | 0.095π, 0.685π, 1.472π, 1.589π |
| (b) | 0.025, 0.082, 0.057, 0.112, 0.042, 0.041, 0.061, 0.061, 0.055, 0.124, 0.058, 0.039, 0.080, 0.001, 0.092, 0.070 | 1.107π, 1.454π, 1.970π, 0.525π, 0.315π, 0.723π, 0.227π, 0.360π, 1.127π, 0.677π, 0.379π, 1.506π, 0.205π, 1.588π, 0.021π, 0.020π |
| Figure 15 | Peak | Mean | Entropy |
|---|---|---|---|
| (a) | 0.810 | 0.264 | 0.726 |
| (b) | 0.487 | 0.137 | 0.905 |
| Figure 16 | Section Situation | Phase Situation |
|---|---|---|
| (a) | 0.114, 0.184, 0.079, 0.623 | 0.095π, 0.685π, 1.472π, 1.589π |
| (b) | 0.083, 0.085, 0.046, 0.060, 0.068, 0.124, 0.045, 0.070, 0.116, 0.096, 0.097, 0.060, 0.017, 0.017, 0.008, 0.008 | 1.107π, 1.454π, 1.970π, 0.525π, 0.315π, 0.723π, 0.227π, 0.360π, 1.127π, 0.677π, 0.379π, 1.506π, 0.205π, 1.588π, 0.021π, 0.020π |
| Figure 16 | Peak | Mean | Entropy |
|---|---|---|---|
| (a) | 0.591 | 0.282 | 0.727 |
| (b) | 0.357 | 0.138 | 0.923 |
| Figure 17 | Section Situation | Phase Situation |
|---|---|---|
| (a) | 0.114, 0.184, 0.079, 0.623 | 0.325π, 1.067π, 0.468π, 1.567π |
| (b) | 0.083, 0.085, 0.046, 0.060, 0.068, 0.124, 0.045, 0.070, 0.116, 0.096, 0.097, 0.060, 0.017, 0.017, 0.008, 0.008 | 0.341π, 1.465π, 1.146π, 0.073π, 0.758π, 1.608π, 0.159π, 0.109π, 0.836π, 0.478π, 1.706π, 0.620π, 1.841π, 1.504π, 0.398π, 1.430π |
| Figure 17 | Peak | Mean | Entropy |
|---|---|---|---|
| (a) | 0.549 | 0.275 | 0.805 |
| (b) | 0.281 | 0.141 | 0.939 |
| Figure 18 | Section Situation | Phase Situation |
|---|---|---|
| (a) | 0.154,0.242,0.151,0.453 | 0.751π,1.786π,0.794π,1.727π |
| (b) | 0.106, 0.043, 0.058, 0.076, 0.069, 0.005, 0.018, 0.036, 0.138, 0.002, 0.095, 0.117, 0.071, 0.064, 0.049, 0.053 | 0.740π, 1.601π, 0.453π, 1.593π, 0.467π, 1.173π, 1.804π, 0.035π, 1.543π, 0.158π, 0.899π, 1.653π, 0.272π, 1.459π, 0.443π, 0.908π |
| Figure 18 | Peak | Mean | Entropy |
|---|---|---|---|
| (a) | 0.429 | 0.300 | 0.798 |
| (b) | 0.290 | 0.133 | 1.028 |
| Figure 19 | Mean | Variance | ||
|---|---|---|---|---|
| Random | Optimized | Random | Optimized | |
| (a) | 0.268 | 0.288 | 0.011 | 0.008 |
| (b) | 0.714 | 0.741 | 0.034 | 0.028 |
| Figure 20 | Mean | Variance | ||
|---|---|---|---|---|
| Random | Optimized | Random | Optimized | |
| (a) | 0.262 | 0.273 | 0.016 | 0.001 |
| (b) | 0.708 | 0.786 | 0.050 | 0.022 |
| Figure 21 | Mean | Variance | ||
|---|---|---|---|---|
| Random | Optimized | Random | Optimized | |
| (a) | 0.263 | 0.299 | 0.017 | 0.007 |
| (b) | 0.709 | 0.832 | 0.059 | 0.029 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Wu, Y.; Wang, H.; Lv, Y.; Qiu, L.; Yu, D. Optimization Algorithm for Multiple Phases Sectionalized Modulation Jamming Based on Particle Swarm Optimization. Electronics 2019, 8, 160. https://doi.org/10.3390/electronics8020160
Jiang J, Wu Y, Wang H, Lv Y, Qiu L, Yu D. Optimization Algorithm for Multiple Phases Sectionalized Modulation Jamming Based on Particle Swarm Optimization. Electronics. 2019; 8(2):160. https://doi.org/10.3390/electronics8020160
Chicago/Turabian StyleJiang, Jiawei, Yanhong Wu, Hongyan Wang, Yakun Lv, Lei Qiu, and Daobin Yu. 2019. "Optimization Algorithm for Multiple Phases Sectionalized Modulation Jamming Based on Particle Swarm Optimization" Electronics 8, no. 2: 160. https://doi.org/10.3390/electronics8020160
APA StyleJiang, J., Wu, Y., Wang, H., Lv, Y., Qiu, L., & Yu, D. (2019). Optimization Algorithm for Multiple Phases Sectionalized Modulation Jamming Based on Particle Swarm Optimization. Electronics, 8(2), 160. https://doi.org/10.3390/electronics8020160





