Multi-Points Cooperative Relay in NOMA System with N-1 DF Relaying Nodes in HD/FD Mode for N User Equipments with Energy Harvesting
Abstract
:1. Introduction
- The first, this article proposes a down-link side NOMA network with random N UEs.
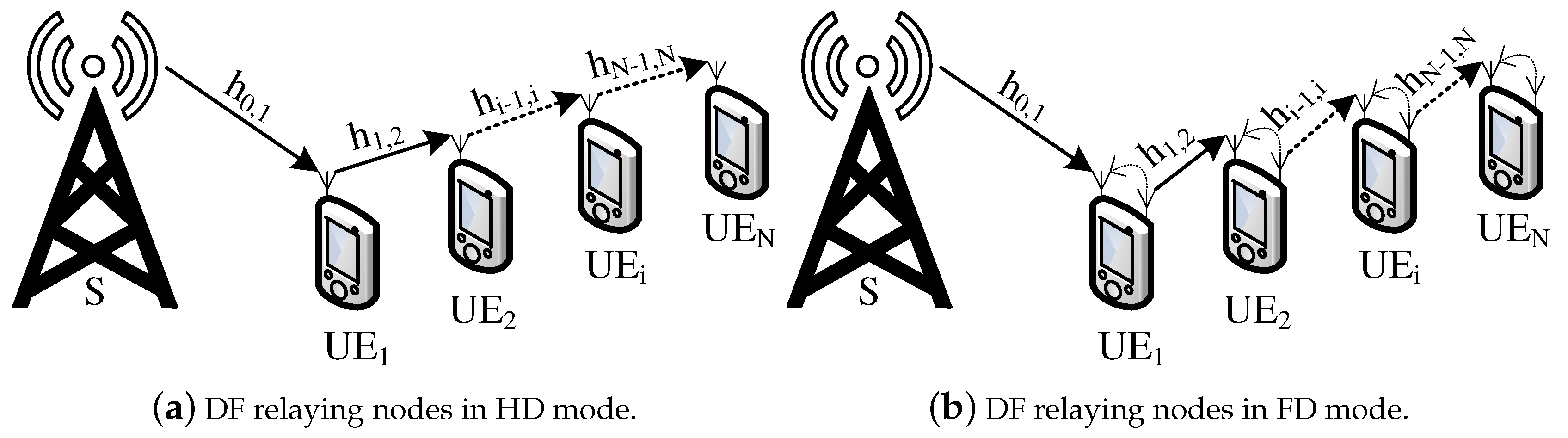
- The next, the MPCR model is proposed to improve QoS for the Nth UE with farthest distance from BS among the others users by using UEs as DF relaying nodes in HD/FD mode. Each · relaying node receives and forwards a superposed signal to next hop, namely , which is nearest from . This work will loop until the superposed signal is sent to last UE, namely .
- A algorithm for selecting relay nodes in MPCR is also presented clearly in next section.
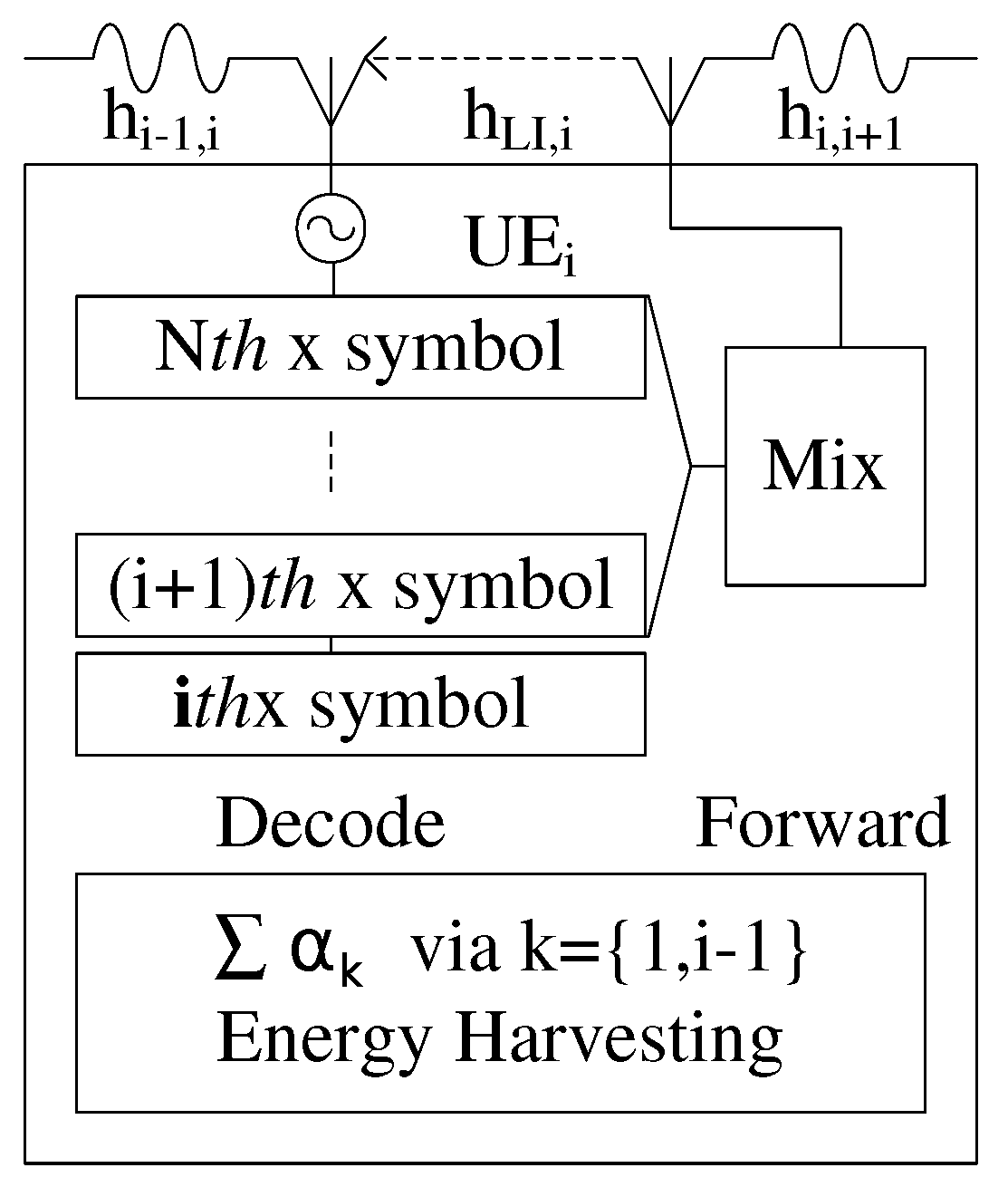
- At with , the received signal has an excess power that is used for EH to charge the battery with assuming unlimited capacity of the battery.
- In additional, this study investigates and finds an outage probability and system throughput for each UE, which are written in closed-form expressions.
- Further, The analysis and simulation results are presented in a clear way by the Monte Carlo simulation ( samples of channels) from the Matlab software to prove our propositions.
- is a channel from source a to destination b.
- is an allocation power coefficient for the i-th UE.
- is the received signal at the i-th UE with protocol where .
- is a signal-to-interference-plus-noise-ratios (SINRs) at i-th UE while the i-th UE decodes symbol.
- is a probability.
- or is an outage probability of the i-th UE with protocol over Rayleigh or Nakagami-m fading channels, respectively.
- is a bit rate threshold of the i-th UE.
2. Experimental Models
2.1. Direct Link Scenario
2.2. DF Relaying Nodes Scenario
3. The System Performance Analysis
3.1. Outage Probability
3.2. System Throughput
3.3. A Proposal for Energy Harvesting
3.4. A Proposed Algorithm for Relaying Nodes
- 1.
- Generate a random N UEs in the network with N channels from BS to UEs.
- 2.
- Creating a list of channels in descending order with the element at the top of the list is the best channel. Upon completion of the arrangement, BS will know which user is best chosen to use for first hop relaying node.
- 3.
- Through the results of the analysis [30], the authors have found that the performance of the NOMA system depends on the efficiency of the power allocation and the selection of the bit rate threshold, accordingly. Lack of CSI may affect the performance of the NOMA system. We have assumed that at BS and at each UE, there is full CSI of the UEs. Based on ordering of SCI as shown in (3), allocate the power coefficients and select the bit rate threshold for the UEs as, respectivelyandwhere in ordering and paring and . After the BS allocates the transmit power factor to the UEs, logically, a superposed signal will be sent to the nearest UE which is selected as the first hop relaying node, namely .
- 4.
- The receives and decodes symbol with by (20a)–(21b), and excess power is collected by the UE for recharging. The will select a next relay node by (23) and send a superposed signal as (18) or (19) to next hop relaying node after detects its own symbol, namely , successfully. This work (step 4) will be repeated until the superposed signal will be transmitted to the last UE, namely in model. The outage probability will occur when , where , cannot be detected successfully at with .
4. Numerical Results and Discussion
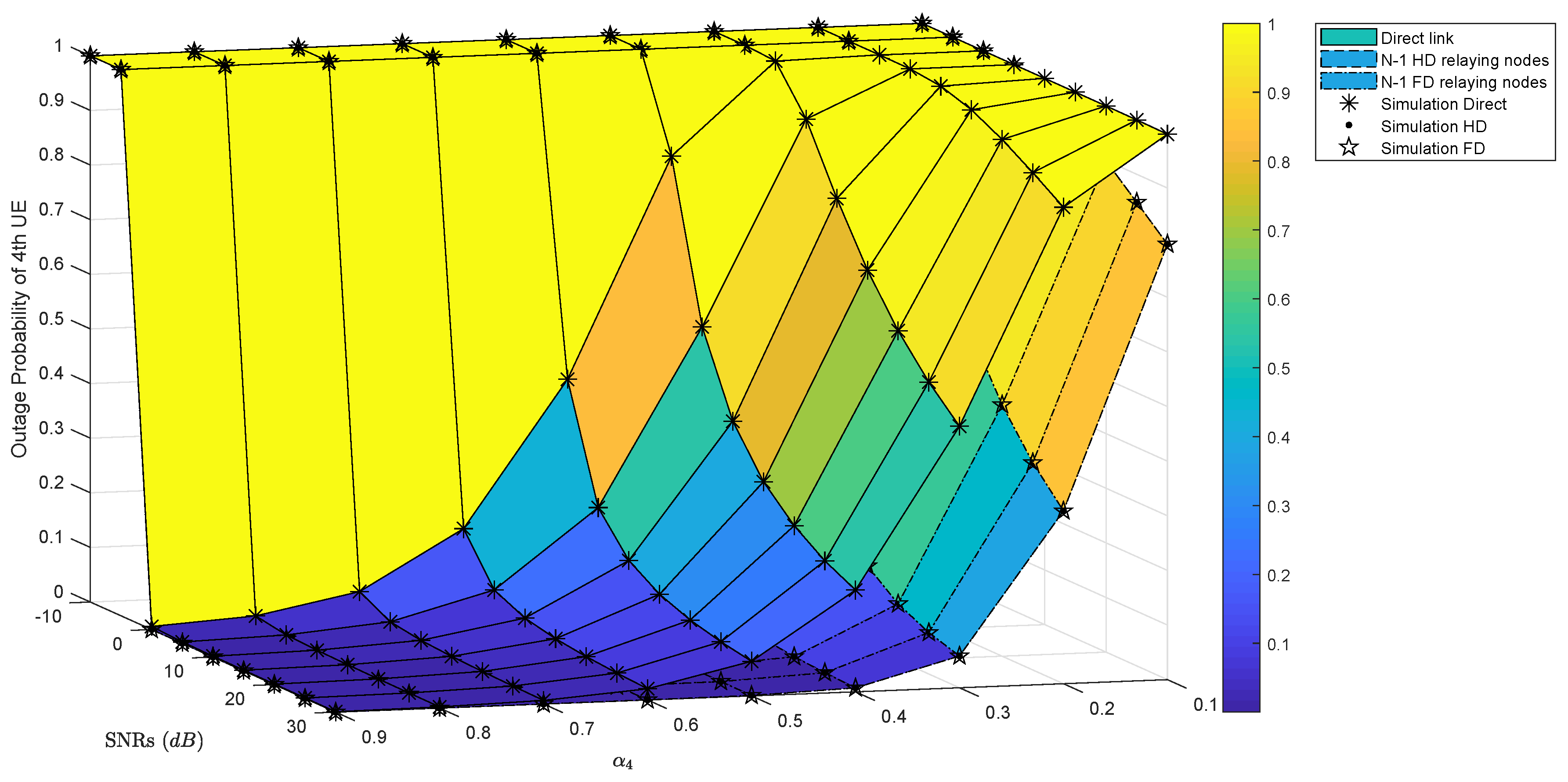
4.1. Numerical Results and Discussion for Outage Probability
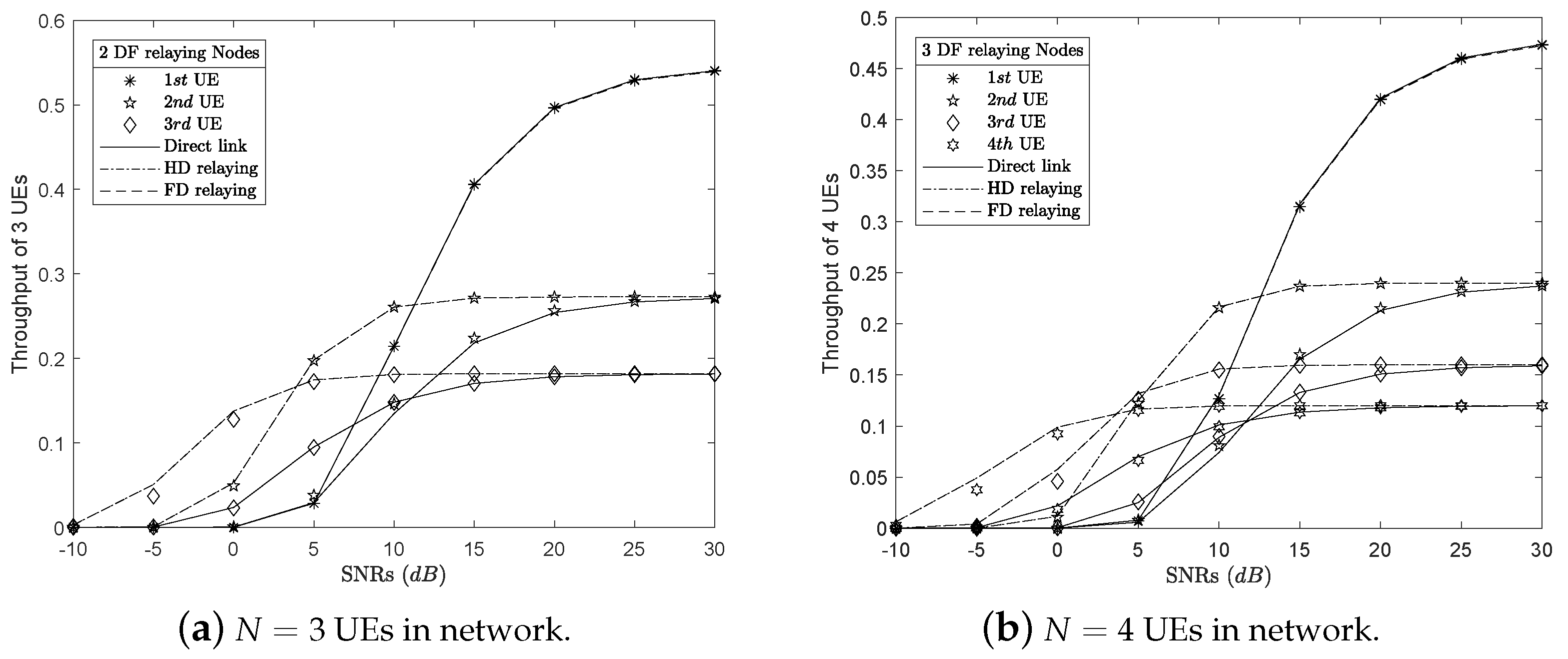
4.2. Numerical Results and Discussion for System Throughput
4.3. N UEs with HD/FD Relaying Nodes
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| No. | Abbreviations | Full description |
| 1 | AWGNs | Additive white Gaussian noises |
| 2 | BS | Base station |
| 3 | CDF | Cummuative distribution function |
| 4 | CSI | Channel state information |
| 5 | FD | Full-duplex |
| 6 | Fig. | Figure |
| 7 | HD | Half-duplex |
| 8 | MPCR | Multi-Point Cooperative Relay |
| 9 | NOMA | non-orthogonal multiple access |
| 10 | Probability density function | |
| 11 | QoS | Quality of service |
| 12 | S | Source |
| 13 | SIC | Successive interference cancellation |
| 14 | SINR | Signal-to-interference-plus-noise ratio |
| 15 | SNR | Signal-to-noise ratio |
| 16 | UEs | User Equipments |
Appendix A
References
- Saito, Y.; Benjebbour, A.; Kishiyama, Y.; Nakamura, T. System-level performance evaluation of downlink non-orthogonal multiple access (NOMA). In Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013. [Google Scholar]
- Ding, Z.; Yang, Z.; Fan, P.; Poor, H. On the Performance of Non-Orthogonal Multiple Access in 5G Systems with Randomly Deployed Users. IEEE Signal Process. Lett. 2014, 21, 1501–1505. [Google Scholar]
- Higuchi, K.; Benjebbour, A. Non-orthogonal Multiple Access (NOMA) with Successive Interference Cancellation for Future Radio Access. IEICE Trans. Commun. 2015, 98, 403–414. [Google Scholar]
- Men, J.; Ge, J.; Zhang, C. Performance Analysis for Downlink Relaying Aided Non-Orthogonal Multiple Access Networks with Imperfect CSI Over Nakagami-m Fading. IEEE Access 2017, 5, 998–1004. [Google Scholar] [CrossRef]
- Ding, Z.; Peng, M.; Poor, H. Cooperative Non-Orthogonal Multiple Access in 5G Systems. IEEE Commun. Lett. 2015, 19, 1462–1465. [Google Scholar]
- Xiao, Y.; Hao, L.; Ma, Z.; Ding, Z.; Zhang, Z.; Fan, P. Forwarding Strategy Selection in Dual-Hop NOMA Relaying Systems. IEEE Commun. Lett. 2018, 22, 1644–1647. [Google Scholar]
- Davoodi, A.; Emadi, M.; Aref, M. Analytical power allocation for a full duplex decode-and-forward relay channel. In Proceedings of the 2013 Iran Workshop on Communication and Information Theory, Tehran, Iran, 8–9 May 2013. [Google Scholar]
- Ding, Z.; Dai, H.; Poor, H. Relay Selection for Cooperative NOMA. IEEE Wirel. Commun. Lett. 2016, 5, 416–419. [Google Scholar]
- Gao, H.; Ejaz, W.; Jo, M. Cooperative Wireless Energy Harvesting and Spectrum Sharing in 5G Networks. IEEE Access 2016, 4, 3647–3658. [Google Scholar]
- Tonello, A.; Versolatto, F.; D’Alessandro, S. Opportunistic Relaying in In-Home PLC Networks. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM 2010, Miami, FL, USA, 6–10 December 2010. [Google Scholar]
- Lampe, L.; Vinck, A. Cooperative multihop power line communications. In Proceedings of the 2012 IEEE International Symposium on Power Line Communications and Its Applications, Beijing, China, 27–30 March 2012; pp. 1–6. [Google Scholar]
- Cheng, X.; Cao, R.; Yang, L. Relay-aided amplify-and-forward powerline communications. IEEE Trans. Smart Grid 2013, 4, 265–272. [Google Scholar]
- Rabie, K.; Adebisi, B.; Gacanin, H.; Nauryzbayev, G.; Ikpehai, A. Performance evaluation of multi-hop relaying over non-gaussian PLC channels. J. Commun. Netw. 2017, 19, 531–538. [Google Scholar]
- Dubey, A.; Mallik, R.K.; Schober, R. Performance analysis of a multi-hop power line communication system over log-normal fading in presence of impulsive noise. IET Commun. 2015, 9, 1–9. [Google Scholar]
- Dubey, A.; Mallik, R.K. PLC system performance with AF relaying. IEEE Trans. Commun. 2015, 63, 2337–2345. [Google Scholar]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless networks with RF energy harvesting: A contemporary survey. IEEE Commun. Surv. Tutor. 2015, 17, 757–789. [Google Scholar]
- Nasir, A.A.; Tuan, H.D.; Ngo, D.T.; Durrani, S.; Kim, D.I. Path-following algorithms for beamforming and signal splitting in RF energy harvesting networks. IEEE Commun. Lett. 2016, 20, 1687–1690. [Google Scholar]
- Nguyen, V.D.; Duong, T.Q.; Tuan, H.D.; Shin, O.S.; Poor, H.V. Spectral and energy efficiencies in full-duplex wireless information and power transfer. IEEE Trans. Commun. 2017, 65, 2220–2233. [Google Scholar]
- Tam, H.H.M.; Tuan, H.D.; Nasir, A.A.; Duong, T.Q.; Poor, H.V. MIMO energy harvesting in full-duplex multi-user networks. IEEE Trans. Wirel. Commun. 2017, 16, 3282–3297. [Google Scholar]
- Nasir, A.A.; Tuan, H.D.; Duong, T.Q.; Poor, H.V. Secrecy rate beamforming for multicell networks with information and energy harvesting. IEEE Trans. Signal Process. 2017, 65, 677–689. [Google Scholar]
- Dai, L.; Wang, B.; Ding, Z.; Wang, Z.; Chen, S.; Hanzo, L. A Survey of Non-Orthogonal Multiple Access for 5G. IEEE Commun. Surv. Tutor. 2018, 20, 2294–2323. [Google Scholar]
- Islam, S.; Avazov, N.; Dobre, O.; Kwak, K. Power-Domain Non-Orthogonal Multiple Access (NOMA) in 5G Systems: Potentials and Challenges. IEEE Commun. Surv. Tutor. 2017, 19, 721–742. [Google Scholar]
- Islam, S.; Zeng, M.; Dobre, O.; Kwak, K. Resource Allocation for Downlink NOMA Systems: Key Techniques and Open Issues. IEEE Wirel. Commun. 2018, 25, 40–47. [Google Scholar]
- Shi, S.; Yang, L.; Zhu, H. Outage Balancing in Downlink Non-Orthogonal Multiple Access with Statistical Channel State Information. IEEE Trans. Wirel. Commun. 2016, 15, 4718–4731. [Google Scholar]
- Di, B.; Song, L.; Li, Y. Sub-Channel Assignment, Power Allocation, and User Scheduling for Non-Orthogonal Multiple Access Networks. IEEE Trans. Wirel. Commun. 2016, 15, 7686–7698. [Google Scholar]
- Lei, L.; Yuan, D.; Ho, C.; Sun, S. Power and Channel Allocation for Non-Orthogonal Multiple Access in 5G Systems: Tractability and Computation. IEEE Trans. Wirel. Commun. 2016, 15, 8580–8594. [Google Scholar]
- Fang, F.; Zhang, H.; Cheng, J.; Leung, V. Energy-Efficient Resource Allocation for Downlink Non-Orthogonal Multiple Access Network. IEEE Trans. Commun. 2016, 64, 3722–3732. [Google Scholar]
- Hanif, M.; Ding, Z.; Ratnarajah, T.; Karagiannidis, G. A Minorization-Maximization Method for Optimizing Sum Rate in the Downlink of Non-Orthogonal Multiple Access Systems. IEEE Trans. Signal Process. 2016, 64, 76–88. [Google Scholar]
- Ding, Z.; Adachi, F.; Poor, H. The Application of MIMO to Non-Orthogonal Multiple Access. IEEE Trans. Wirel. Commun. 2016, 15, 537–552. [Google Scholar]
- Wan, D.; Wen, M.; Ji, F.; Liu, Y.; Huang, Y. Cooperative NOMA Systems with Partial Channel State Information Over Nakagami-m Fading Channels. IEEE Trans. Commun. 2018, 66, 947–958. [Google Scholar]
- Timotheou, S.; Krikidis, I. Fairness for Non-Orthogonal Multiple Access in 5G Systems. IEEE Signal Process. Lett. 2015, 22, 1647–1651. [Google Scholar]
- Liu, H.; Ding, Z.; Kim, K.; Kwak, K.; Poor, H. Decode-and-Forward Relaying for Cooperative NOMA Systems with Direct Links. IEEE Trans. Wirel. Commun. 2018, 17, 8077–8093. [Google Scholar]
- Sadek, A.K.; Han, Z.; Liu, K.J.R. A distributed relay-assignment algorithm for cooperative communications in wireless networks. In Proceedings of the 2006 IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006. [Google Scholar]
- Sreng, V.; Yanikomeroglu, H.; Falconer, D.D. Relay selection strategies in cellular networks with peer-to-peer relaying. In Proceedings of the 2003 IEEE 58th Vehicular Technology Conference, VTC 2003-Fall (IEEE Cat. No.03CH37484), Orlando, FL, USA, 6–9 October 2003. [Google Scholar]
- Jing, Y.; Jafarkhani, H. Single and multiple relay selection schemes and their achievable diversity orders. IEEE Trans. Wirel. Commun. 2009, 8, 1414–1423. [Google Scholar]
- Kim, J.B.; Lee, I.H. Capacity Analysis of Cooperative Relaying Systems Using Non-Orthogonal Multiple Access. IEEE Commun. Lett. 2015, 19, 1949–1952. [Google Scholar]
- Thanh-Nam, T.; Dinh-Thuan, D.; Voznak, M. Full-duplex Cognitive Radio NOMA Networks: Outage and Throughput Performance Analysis. Int. J. Electron. Telecommun. 2019. in processing. [Google Scholar]
- Thanh-Nam, T.; Dinh-Thuan, D.; Voznak, M. On Outage Probability and Throughput Performance of Cognitive Radio Inspired NOMA Relay System. Adv. Electr. Electron. Eng. 2018, 16, 501–512. [Google Scholar]





| UEs | Channels | Allocation Power Coefficients | Bit Rate Thresholds |
|---|---|---|---|
| UEs | Channels | Allocation Power Coefficents | Bit Rate Thresholds |
|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, T.-N.; Voznak, M. Multi-Points Cooperative Relay in NOMA System with N-1 DF Relaying Nodes in HD/FD Mode for N User Equipments with Energy Harvesting. Electronics 2019, 8, 167. https://doi.org/10.3390/electronics8020167
Tran T-N, Voznak M. Multi-Points Cooperative Relay in NOMA System with N-1 DF Relaying Nodes in HD/FD Mode for N User Equipments with Energy Harvesting. Electronics. 2019; 8(2):167. https://doi.org/10.3390/electronics8020167
Chicago/Turabian StyleTran, Thanh-Nam, and Miroslav Voznak. 2019. "Multi-Points Cooperative Relay in NOMA System with N-1 DF Relaying Nodes in HD/FD Mode for N User Equipments with Energy Harvesting" Electronics 8, no. 2: 167. https://doi.org/10.3390/electronics8020167
APA StyleTran, T.-N., & Voznak, M. (2019). Multi-Points Cooperative Relay in NOMA System with N-1 DF Relaying Nodes in HD/FD Mode for N User Equipments with Energy Harvesting. Electronics, 8(2), 167. https://doi.org/10.3390/electronics8020167






