1. Introduction
In recent years, the continuous development in engineering-related fields, such as automatic systems, flight control and the aerospace industry as a whole, has contributed to the rapid growth of the area of Unmanned Aerial Vehicles (UAV), making it an appealing research topic in both military and civil applications. In terms of civil applications, it is important to mention those related with agricultural services, marine operations, natural disaster support, etc. Within the military field, UAVs are mostly used in missions in which there are high risks.
In order to increase the number and complexity, and hence, the performance efficiency of these applications, UAVs characterized by a dual flight envelop are currently needed. These unmanned vehicles, inheriting the advantages of both traditional fixed-wing aircraft and rotorcraft, have the ability to execute a VTOL maneuver and to aggressively inspect a certain area, as well as to perform a high-speed aerial surveillance over a wide region. For the aforementioned reasons, these vehicles are known as Hybrid UAVs.
According to [
1], hybrid UAVs can be categorized into two main types: Convertiplanes and Tail-Sitters. Firt of all, Convertiplanes category regroup those aerial vehicles that take off, cruise, hover and land with the aircraft reference line remaining horizontal. Respect to this class, there exist several vehicles implementing the idea such as FireFLY6 [
2] and TURAC [
3]; and also projects researching in this direction [
4,
5]. Second, a Tail-Sitter is an aircraft that takes off and lands vertically on its tail and the whole aircraft tilts forward using differential thrust or control surfaces to achieve horizontal flight. This category, as it is considered as a complex challenge from the point of view of control systems engineering, has become an interesting research concept as shown by vehicles like Quadshot [
6] or prototype [
7].
This paper presents recent work concerning the first stage in the development of a hybrid UAV that can be categorized as Tail-Sitter with the exceptions that in this case the aircraft takes off and lands vertically on its nose (using an external ground-station) and that this platform changes the sense of the rotors in order to perform the transition phase between hovering and cruising.
Figure 1 shows the manoeuvrability scheme of the proposed unmanned aerial vehicle. In addition, the prototype built based on this philosophy has been
nicknamed V-Skye.
In this article, the design of the control system is not only based on simulations, but also on an experimental procedure in which the controllers have to adequately stabilize the UAV allowing it to hover filtering external disturbances. In order to control the attitude, the vehicle is provided with two tilting rotors that allow alterations of its pitch angle and yaw rate and also, modifications in the motor throttles in order to handle roll and vertical speed variables. This is the first step of the development of the entire autonomous system, that will provide this UAV with the hybrid characteristics required by autonomous aviation market, as presented in [
8].
Different types of controllers can be designed for UAVs. The simplest ones are linear PID based on linearized models of UAVs. In the literature it is possible to find several approaches which solve the problem of controlling non-linear UAVs: non-linear PID based solutions [
9,
10,
11], non-linear robust approaches [
12,
13,
14], back-stepping algorithms [
15,
16,
17], sliding mode control [
12,
17],
control [
16] or non-linear observer based [
18,
19].
As commented, the objective of this article is to adequately stabilize the designed hybrid UAV in an experimental procedure. This is performed by using 4 linear PIDs tuned by a genetic algorithm. The genetic algorithm searches for the PID parameters that minimize a performance index such as the integral squared error or the settling time.
Using 4 linear PIDs can be considered as a first approach to the design of the control system, and also the easiest way to implement a control system from an experimental point of view. In further researches authors will try to apply more complex techniques such as non-linear PID [
9,
10] and non-linear robust approaches [
12,
13,
14].
The rest of this article is structured as follows.
Section 2 covers the description of the airframe that has been used during this project, while
Section 3 is focused on the explanation of the mathematical model that describes this aerial vehicle. In
Section 4, the design of the attitude control system is presented.
Section 5 gathers information related to the HIL simulation platform and finally,
Section 6 presents the simulation and real-test results that ensure the controller’s performance.
2. Airframe Description
A rigid body moving inside a three-dimensional (3D) space has a total of six-degrees-of-freedom (6DoF). In this way, a mechanical system formed by a single rigid body needs at least six independently manipulated interactions with the system (inputs) to drive it to an arbitrary orientation and position.
In a hovering maneuver, a flying vehicle is maintained motionless over a reference point at a constant altitude (constant reference position) and on a constant heading angle . Hence, only four of the six degrees of freedom are forced to a reference value (controlled) when hovering. The other two, i.e., pitch and roll angles are dependent variables that evolve along time according to the system equations of motion.
The V-Skye is designed with two tilting-rotors moved by servo-mechanisms. The result is a vehicle with two motors for which thrust and can be independently modified, not only in magnitude, but also in one direction. The system is thus provided with the amount of independent inputs needed for the hovering manoeuvre.
Figure 2 shows an outline drawing of the V-Skye. In order to simplify the dynamics, all actuation parts (motors, motor frames, servomotors and their transmission parts) are allocated as symmetrically as possible about the fixed coordinate axis
of the aircraft reference frame. In particular, all elements are placed on the
plane and symmetrical to the
plane.
For simplicity on the explanations, authors have divided the aircraft into three well-differentiated frames.
2.1. Main Body Frame
As depicted in
Figure 2, the main body has the constructive shape of a Flying-Wing aircraft, such as the ones used in [
20,
21]. It is a rigid body housing all the electronics as well as the two servomotors that allow rotation of the motor frames (see
Section 2.2 and
Section 2.3).
The reference system has its origin at the aircraft centre of mass and it is fixed to the main body frame. For its vertical flight phase, the direction points front, towards what would naturally be the upper part of the fuselage. The direction points down, towards the nose of the flying-wing. Finally, axis is perpendicular to the other two and points towards the right-side wing.
The earth coordinate axis
is a North-East-Down (NED) inertial frame of reference, also positioned at the aircraft centre of mass but fixed to the earth surface. Euler angles roll
, pitch
and yaw
define the main body orientation respect to the earth axis.
Figure 3 shows those three independent rotations.
2.2. Right Motor Frame
It is formed by the right motor, its right-handed propeller and a structure specially designed to hold it and stand any reaction force derived from the flight. It can be seen as a second rigid body attached to the aircraft by a rotatory joint, as
Figure 4 describes in detail.
Two coordinate systems are defined to describe the motion of this frame with respect to the main body. is fixed to the the main body frame and parallel to ; its centre is placed where the rotatory joint intersects the motor shaft axis. On the other hand, have its origin at ; the axis coincides with () and axis coincides with the motor shaft axis.
Because the right motor frame is attached to the main body by a rotatory joint, it has one single DOF: the angle rotated about the axis . When , both and have the exact same position and orientation. The direction of the right motor’s thrust is changed by actuating on the value, since the thrust has always the direction. For this reason, a servomotor is used to manipulate .
2.3. Left Motor Frame
The left motor frame includes namely the left motor with a left-handed propeller and the structure to hold it. The right and left propellers are designed to be right and left handed respectively. This makes the motors to rotate in opposite senses, helping to compensate motors torques.
Figure 5 illustrates the configuration and coordinate reference systems.
Similarly to the right motor frame, two coordinate systems are defined for the left motor frame: and with being the angle rotated by with respect to about the axis.
3. Mathematical Model
The equations that conform the 6-DOF non-linear dynamical model are derived in this paper assuming the following hypothesis:
The whole aircraft is assumed to be rigid body; it means that the distance between any two points in the airframe remains constant. This is a fundamental condition because it allows to understand the movement of the vehicle as a translation and a rotation around the center of mass independently.
Derived from the previous item, the changes in and angles do not affect the mass distribution along the aircraft body.
The rotational movement of the Earth is negligible with respect to the accelerations on the vehicle. i.e., the Earth frame is an inertial frame of reference.
The atmosphere is assumed to be calm (no wind or turbulence)
The plane { is a plane of symmetry. Hence, the inertia products about the axis
3.1. Translational Equations
Let
be the resultant force vector of all the external forces acting on the system,
m the total mass of the aircraft and
the aircraft linear velocity with respect to the earth frame. Newton’s second law can be written as:
where
,
,
,
u,
v and
w are the three components of the resultant force and the system velocity respectively, both magnitudes expressed in body axis. Velocity’s time derivative with respect to the earth frame might be now rewritten as the summation of its time derivative with respect to the body frame and the cross product of angular and linear velocities as follows
where
is the angular velocity of the body frame with respect to the earth frame, and
p,
q and
r its components expressed in body axis. Therefore, vector Equation (
1) is separated into three independent equations as shown next
The external forces considered in this work are the rotors’ thrust and the aircraft weight. Since the work is focused on the design of a control scheme for a hovering manoeuvre, the dynamics model does not consider aerodynamic effects on the aircraft body. In a VTOL procedure, the lift is totally generated through the thrust produced by the rotors. On the other hand, drag produced by the flying-wing airframe is taken as an external disturbance for the attitude tracking controller.
Denoting by
and
the thrust magnitudes of right and left rotors, respectively; the definition of the thrust forces in body axis is characterised by the angles
and
of the right and left motor frames with respect to the body frame.
In [
22], a complete study of the performance of several types of propellers at different airflow conditions is presented. Along the paper, John B. Brandt and Michael S. Selig., explain how to model thrust and torque at low Reynolds numbers, gathering data of these values to calculate aerodynamic coefficients for a large number of commercial propellers. Now, taking the equations presented in [
22] as a reference, and letting
T and
denote thrust and torque magnitudes of a propeller and
and
its force and torque coefficients, then
Hence, the relation between torque and thrust on the propeller can be written as
If we denote by
and
the motors throttle, and given that the aircraft will be mounting two brushless DC motors managed by electronic speed controllers (ESC), the two motor torques are related to their throttle by the expressions (
14) and (15).
and hence
is the torque’s throttle coefficient and is assumed to be constant for a given motor and ESC combination whereas
is the thrust’s throttle coefficient that depends on the airspeed and is constant for the static case. This leads to the following definition of thrust force:
The aforementioned force variables
are now substituted by their corresponding terms of thrust and weight forces in the body axis.
3.2. Rotational Equations
By definition of angular momentum about the mass centre
and considering a rigid-body configuration
where
are the moments of inertia of the aircraft body about its mass centre in body axis and
are the products of inertia.
Now, the total moment of forces about the aircraft’s mass centre is equal to its angular momentum’s time derivative with respect to the earth frame. Additionally, we can again split the time derivative of the angular momentum with respect to the earth frame into its time derivative with respect to the body frame and the cross product of the angular velocity and the angular momentum.
Equation (26) gives the following three independent equations
being
L,
M and
N the three body axis components of the total external moments applied on the aircraft centre of mass.
The right rotor thrust applied at right motor frame generates an external moment about the aircraft centre of mass. Denoting
as the position vector of the right motor frame, the total moment of the right rotor thrust about the centre of mass is given by Equations (
30) and (31). Note that
by design.
Additionally, the right motor torque applied to the propeller is translated to the right motor frame as a reaction torque (same direction but opposite sense). That torque is then translated to the body frame according to
angle. From Equation (
14)
In accordance, thrust moment and motor torque for the left rotor are given by expressions (
34) and (35)
Now, substituting the total external moments and torques into Equations (
27)–(29)
3.3. Collection of Non-Linear Equations
In addition to the six dynamics equations derived above, six kinematic equations can be stated to express the transformation from the body to the earth system of reference. The aircraft behaviour is therefore, described by a total of twelve equations of motion.
As a summary, the aircraft model is divided into the following sets.
3.3.1. Translational Dynamics Equations
3.3.2. Rotational Dynamics Equations
3.3.3. Kinematic Translational Equations
3.3.4. Kinematic Rotational Equations (Euler Angles)
4. Control System
The control problem associated with the presented UAV stabilization is challenging for several reasons. The complexity of flight dynamics resides in the system non-linearity, unstable nature and high degree of coupling. Furthermore, in this case, the system is under-actuated because only four control inputs can be used during take off, landing and hover manoeuvres, while the whole system is six-degree-of-freedom (6DoF). Therefore, robust and reliable feedback control strategies are needed to regulate the attitude of the UAV within an operational range.
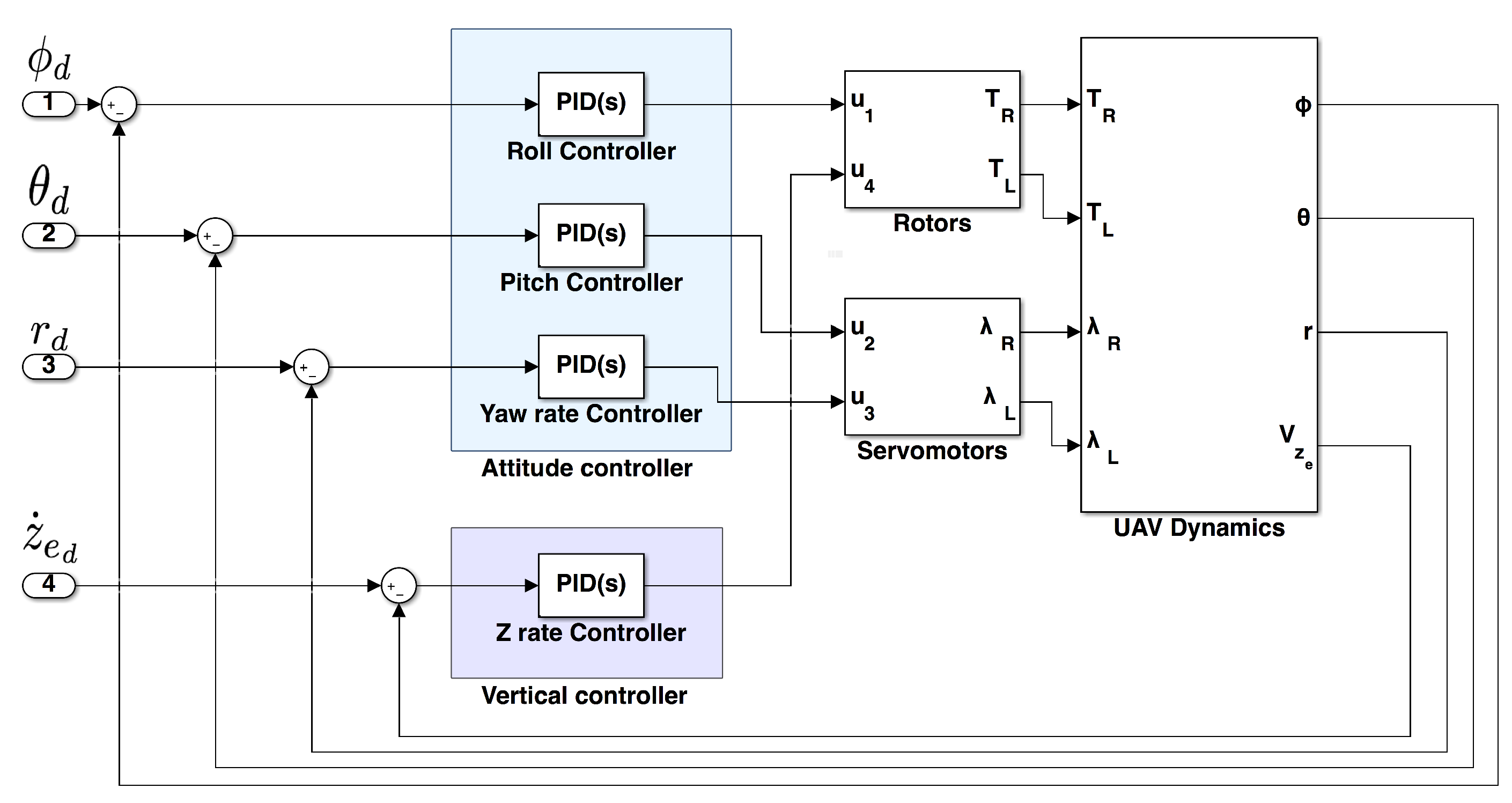
Due to their simplicity, ease of implementation and robust performance, a decentralised and linear control scheme based on four proportional-integral-derivative controllers (PID) has been chosen to design the attitude tracking controller.
Figure 6 shows the block diagram of the proposed feedback control scheme. It is composed by a controller for each angle of orientation and one for the vertical velocity.
Attending to the nonlinear equations of motion presented in
Section 3, a modification on one of the four system inputs
,
,
or
, excites more than one state variable at the same time. This means that the system dynamics are highly coupled. In an attempt to reduce the effect of coupled actuators, a set of four inputs
,
,
and
are defined as a combination of the real input variables. Equations (
51) to (54) show the new system input variables and their relationship with motors throttle and thrust angles
With this new definition of the system inputs, a change in has high effect on the variable, on , on and on . Now the different PID control schemes are defined accordingly.
4.1. Roll and Pitch Controllers
Controllers for roll and pitch angles are implemented similarly: both use standard PID controllers with feedback of estimated angles (roll or pitch) from a complementary filter, resulting in the following control law:
where
,
and
are the proportional, integral and derivative gains, respectively.
and
is associated with the reference angles or desired roll and pitch, while
is the controller action; on one hand,
corresponds to the differential thrust between two rotors, while
is associated with the tilt angle of both rotors.
4.2. Angular Velocity r Controller
Despite of the fact that the heading of the UAV is generally a less critical degree of freedom, external disturbances can generate undesired rotational movements around the Z axis during flying. In order to overcome this drift, a yaw rate PI controller has been implemented using the next expression:
In this case, the reference () is compared with the feedback yaw angular velocity (r) measured by a yaw rate gyroscope. The resulting difference is sent to the controller in order to generate opposite tilt angles by using a differential servo deflection ().
4.3. Vertical Velocity Controller
Due to the high coupling, changes on angles
and
, from the roll and
r controllers, induce variations on the vertical thrust, which leads to variations on vertical velocity. Therefore, a vertical velocity PID controller is implemented as shown in expression (
58).
where,
is the reference vertical velocity,
is the measured vertical velocity estimated from measures of the inertial magnetic unit (IMU) sensors.
corresponds to the increase in the same amount of thrust in both rotors.
4.4. Local Stability
The global close loop stability has been considered from two aspects. Firstly, the control structures presented in this Section have been adjusted to ensure that the poles of the closed loop system have all of them negative real terms [
23]. For this purpose, the particular transfer functions presented in
Section 5 (Equation (
59)) have been used. Obviously, this only guarantees stability close to the equilibrium point defined for the linearization and, therefore, it is a local stability constraint.
Secondly, in order to study the margin of the local stability, HIL simulations have been performed using the designed controllers against the full non-linear model of the UAV. In this way, the validity range of the controllers designed from the linear transfer function is tested by realistic simulations [
24,
25]. Obviously, this is not an overall guarantee of stability, but it is possible to define a range of operation with a high degree of confidence for the control design.
5. Test Prototype
The initial test platform presented in the work is a Flying-wing from Multiplex, model XENO UNI [
26]. This RC plane has been modified to add two tilt rotors, following the main concept of VTOL UAV described previously.
Figure 7 and
Figure 8 show the prototype assembled for real flight tests.
The set of aircraft parameters used for control design and simulation have been derived form the test platform described in the previous paragraph, and their particular values are as follows:
Wingspan: m
Fuselage length: m
Empty weight: kg
Operating weight: kg
= 15.7 and = 0.34
Brushless motors: T-MOTOR Antimass MT2814 770 KV
Propellers: T-MOTOR 12”x4” CF
Electric Speed Controllers: HW-09-V2-OEM
Tilt Rotor Servos: HITEC HS-5475HB
Flight Controller: CC3D OpenPilot Revolution
Battery: 2200 mAh 4 S 80/160 C
Apart from these geometrical characteristics, the engines provide a maximum thrust of N and the tilt-mechanism admit a deflection up to rad. The combination of engines, propellers, Electronic Speed Controllers (ESC) and servos employed in this airframe provide enough power and maneuverability to successfully accomplish the hovering mission even with a larger payload, such as an action camera.
In order to complete the tilt-rotor model parameters, the corresponding moments of inertia are: , y , and also a product of inertia of .
5.1. Prototype Model Linearization
In order to design the linear control approach described in
Section 4, first of all, the attitude dynamic model described by expressions of
Section 3 is decoupled into four linearized single-input single-output (SISO) models around the operational range of a hovering maneuver, which implies that
and
.
The four linear models are obtained by replacing the nonlinear equations of motion with their Taylor series approximation truncated to the first order with respect to the controlled variables and inputs. This linearization approach is well know and, frequently, it is defined as
Small Perturbation Theory [
27,
28,
29,
30]. Once the set of equations have a linear structure and after replacing the model parameters by their prototype value, the following transfer functions are obtained:
5.2. Tuning PID Loops for Prototype Control
After calculating the transfer functions, the controllers parameters can be obtained either using classical techniques, such as the Root-Locus method, or more modern techniques based on optimisation with genetic algorithms.
The use of Root-Locus method for PID tuning proves to be quite easy and useful compared to others techniques, since it indicates the manner in which the open-loop poles and zeros should be modified so that the response meets system performance specifications [
23]. However, a disadvantage of using this technique is that it is necessary to employ a linear model, which is only an approximation of the complex dynamics of the UAV.
On the other hand, PID tuning and optimisation using genetic algorithms is a modern technique that provides an adaptive searching mechanism inspired on Darwin’s principle of reproduction and survival of the fittest. The individuals (solutions) in a population are represented by chromosomes that are associated to a fitness value (problem evaluation). The chromosomes are subjected to an evolutionary process which takes several cycles. Basic operations are selection, reproduction, crossover and mutation [
31]. One of the main advantage of using genetic algorithms is that it is a global search technique of optimal and sub-optimal solutions of a problem and hence it can directly interact with the non-linear dynamics model.
Parameters of PID controllers obtained using both techniques are presented in
Table 1 and
Table 2.
In order to compare the performance of the attitude and vertical speed control system tuned using both classical and modern strategies, a numerical simulation with the nonlinear model of the UAV is made using both set of parameters and the accuracy requirements for the system are formulated in terms of the settling time (
) and the integral squared error index (
), which is related to the time response of the system.
The presented simulations consisted in transition with predefined dynamics from one steady state flight to another. Numerical results evaluating the proposed indexes are shown in
Table 3 and
Table 4.
Taking into consideration the proposed control effort indexes, PID tuning obtained by a genetic algorithm is the most comprehensive choice. For this reason, this set of parameters will be adopted during the simulations and flight tests (
Section 6).
5.3. HIL Simulation Platform
The HIL simulation platform is shown in
Figure 9. The main computation unit is a PXI laboratory computer from National Instruments. This equipment includes several boards to interface a great amount of external devices. As an example digital and analogue input/output boards, Ethernet and Serial ports or four USB ports. This hardware comes with a real-time operative system that can be configured to run Real-Time simulations [
25,
32,
33].
The set of 12 equations of motion derived in
Section 3 have been particularised for the prototype model and implemented in Matlab/Simulink. Simulink allows to compile the model to be run on the PXI real-time target [
34,
35].
A CC3D OpenPilot Revolution Board [
36] has been elected as the flight control unit (FCS). It is a digital board with a micro-controller that comes with the necessary onboard sensors and autopilot software already installed. The control algorithms have been modified and implemented on the FCS. Then the onboard sensors have been bypassed so that the values coming from the model are used to close the loop. Finally, the board has been connected to the PXI to send actuators values and receive state variables values. A joystick has also been connected to the board to send the reference value to the controllers.
6. Results
This section covers the analysis of the results obtained in simulation (using HIL simulation platform) and in real flight tests. The main goal is to understand the dynamical behaviour of the system while it is hovering at certain attitude configurations.
6.1. Simulation Results
The first simulation consists in coupled changes of roll and pitch that allow the reader to understand how the control actions (throttle and tilt-angle) have to be modified in order to follow the reference in attitude and vertical velocity.
Two conclusions can be drawn based on the previous
Figure 10. First of all, as it was already mentioned, the system deflects the rotors in the same direction in order to achieve certain pitch angles. As it can be observed, until
seconds there have only been modifications in the pitch angle, and therefore,
.
However, the interesting aspect of this result is what happens with the tilt-angle when a roll manoeuvre is being carried out. As mentioned, this rotation needs a different thrust generated by each of the rotors until the air-frame reaches the desired configuration. Therefore, during this procedure the total torque is no longer null, meaning that there exists a tendency to modify the yaw of the system by increasing its angular velocity r. The result of the coupling of these dynamical movements is that the attitude tracking controller produces opposite tilt-angles in order to maintain .
This effect is better explained in
Figure 11.
It is also important to remark that the system tends to modify its heading when the hovering takes place at configurations characterised by non-null pitch and roll angles. The reason of this azimuth variation is that the controller is based on the manipulation of the angular velocity r instead of the yaw angle , and therefore, the system acts in order not to change the heading that it has at a specific time t but if this modification occurs, the new heading would be the new reference and the system would not try to recover the initial orientation.
Once the time-response of the tilt-angles has been analysed at different attitude configurations, the same study with the thrust generated by each of the rotors has been performed, as shown in
Figure 12.
In this second study, it is important to remark two conclusions about the behaviour of the thrust when the system follows the attitude configurations shown in
Figure 10 and
Figure 11. First of all, as it was established in
Section 2, a change in roll implies the controller to modify the same absolute value of the rotational velocity in each of the rotor but with different sign. As a result, the thrust is not longer equal until the reference is reached.
The other conclusion refers to the thrust modification associated with changes in pitch from the equilibrium configuration. Although, this effect can not be graphically observed due to the resolution of the thrust signal, when a certain pitch angle is established as a reference, the engines have to create more thrust in order to compensate the fact that the entire system is tilted, and therefore, to maintain the equilibrium of external forces. This means that the higher the pitch angle is, the higher the increase in thrust has to be.
The last study linked to this changes in attitude is focused on the analysis of the time-response of the vertical velocity
shown in
Figure 13. Due to the control scheme design, when the aircraft takes non-equilibrium attitude configurations, it has a tendency to descend,
i.e., to increase the positive value of its velocity in the
axis of the earth reference frame. The vertical velocity controller tries to maintain a given reference value allowing to reduce variations in this velocity, but, because the altitude is not directly controlled, the system keeps changing its vertical position.
Figure 13 illustrates that each pitch or roll angle apart from the equilibrium (
or
) implies an increase in
, which is compensated by an increase in the thrust generated by the rotors. Again, since the controlled variable is the vertical velocity, each time a perturbation occurs there is a loss of altitude that is never recovered, but the vertical speed controller manages to stop falling and reaches again the
set-point.
6.2. Real Flight Results
In order to verify the performance of attitude control system designed for this UAV, the proposed PID control laws have been implemented in the on-board hardware using the OpenPilot Revolution Board [
36], which contains a full 10 DOF IMU with gyroscopes, accelerometers, magnetometers and barometric pressure sensors.
In the experimental test flight, the goal was the stabilisation of the UAV, compensating any external disturbance during vertical flight. Due to the lack of GPS, velocity and position can only be calculated by integration of accelerometers combined with the gyroscopes measures and with the barometric pressure sensor (sensor fusion [
37,
38]). As result, the measures of velocity and position are not reliable enough to close the loop. For this reason, in the experimental test presented, the vertical velocity controller has been annulled and the pilot directly acts on the
system input. That means, direct modification of motors nominal thrust which implies a manual (piloted) control of the speed and vertical position.
The experimental results for the platform control are presented in
Figure 14 as a time plot of all angles of the UAV and the controller actions.
As can be seen, the closed loop response of the UAV is stable because of the fact that Euler angles vary within a limited range, confirming the effectiveness of the proposed approach and theoretical results. Since vertical speed and altitude are manually piloted and the absence of GPS, it is impossible to define a 3D trajectory through waypoints. To cover this drawback, the real test flight demonstration video can be visualized on Youtube [
39] (V-Skye Prototype: Test Flight—
https://youtu.be/zS9oWur-Pss). Thanks to this video, readers can have an approximate idea of the 3D trajectory of the UAV during the test flight.
7. Conclusions and Future Work
The design and implementation of the attitude tracking controller for a Bi-Rotor VTOL UAV have been presented in this article. The simulations performed in a HIL environment showed the main aspects of the dynamical behaviour of this system, while the real test flight results presented verify the stability and viability for this UAV platform. Therefore, the UAV designed has the ability to hover despite its complex dynamics and allows future designs based on cascade control schemes focused on controlling global position and velocities. In addition, future works will explore the robust control design that allows the automatic transition between the two different flying modes: VTOL and cruise flight.