A Novel Three-Switch Z-Source SEPIC Inverter
Abstract
:1. Introduction
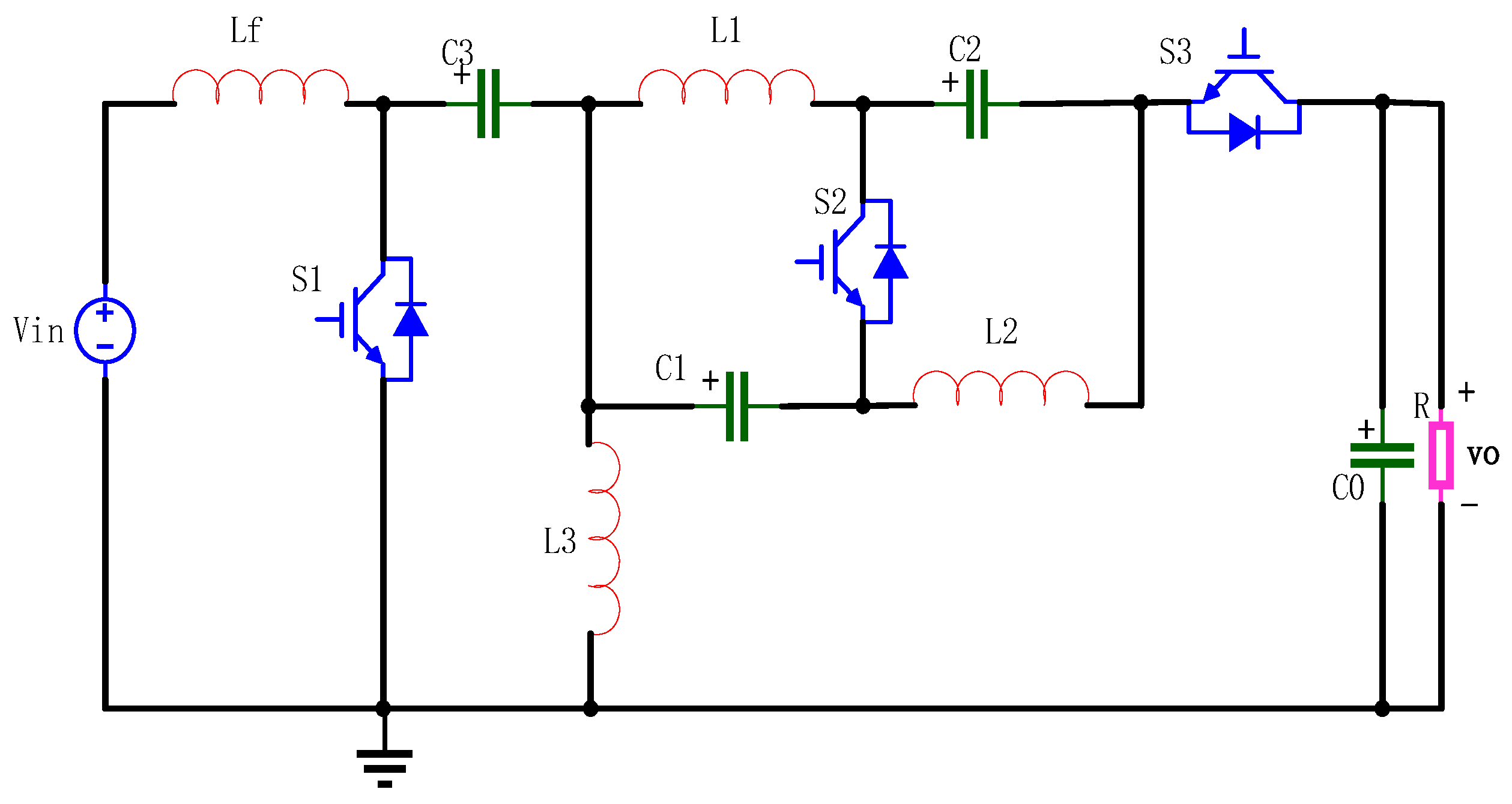
2. Operation Mode and Analysis of the Novel Inverter
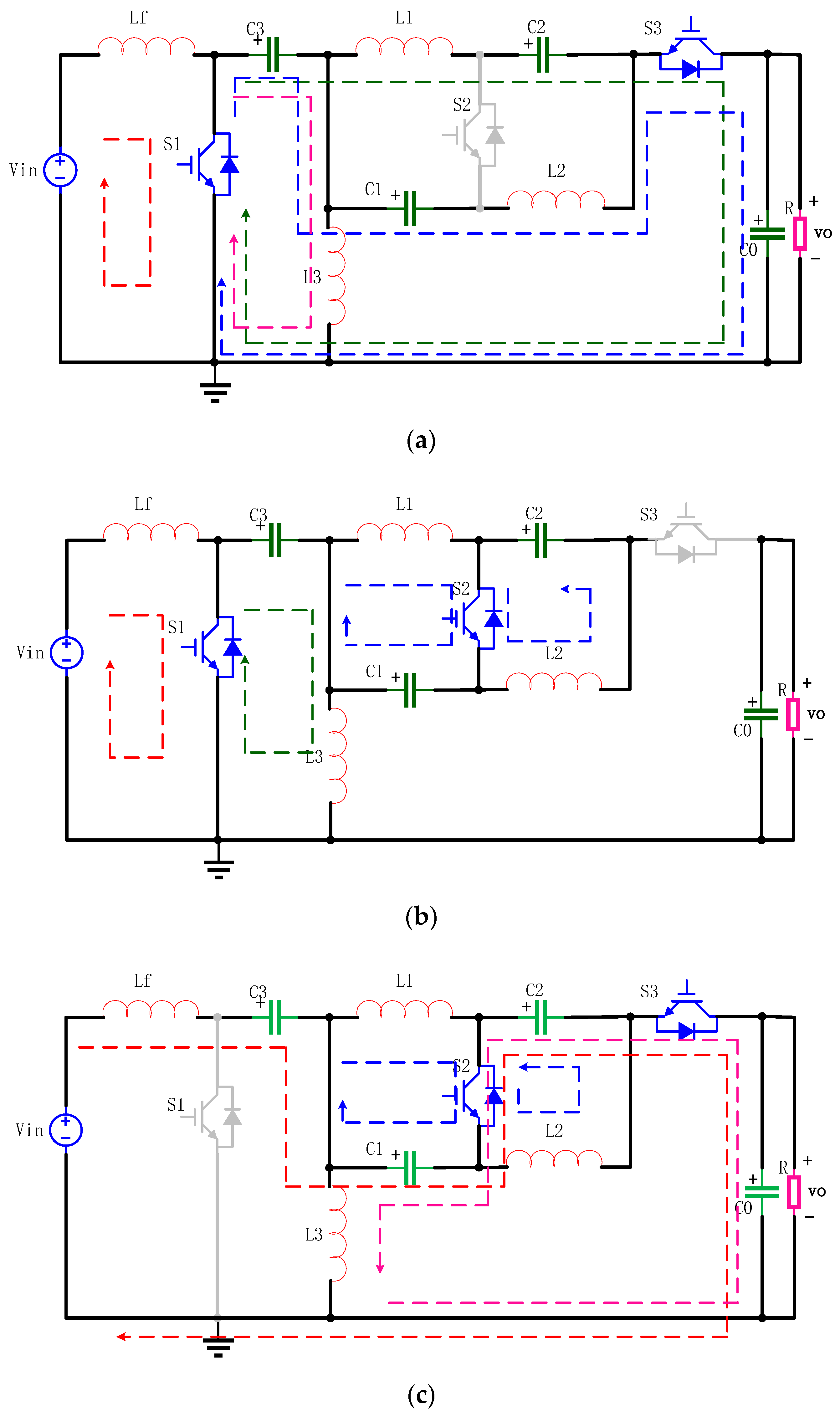
2.1. Structure and Operation Mode
2.2. Voltage in Capacitors and Current in Inductors
2.3. Design of Inductors
2.4. Design of Capacitors
2.5. Peak Voltage and Current in Switches and Analysis
3. Control Method
3.1. Expression of Duty Cycle
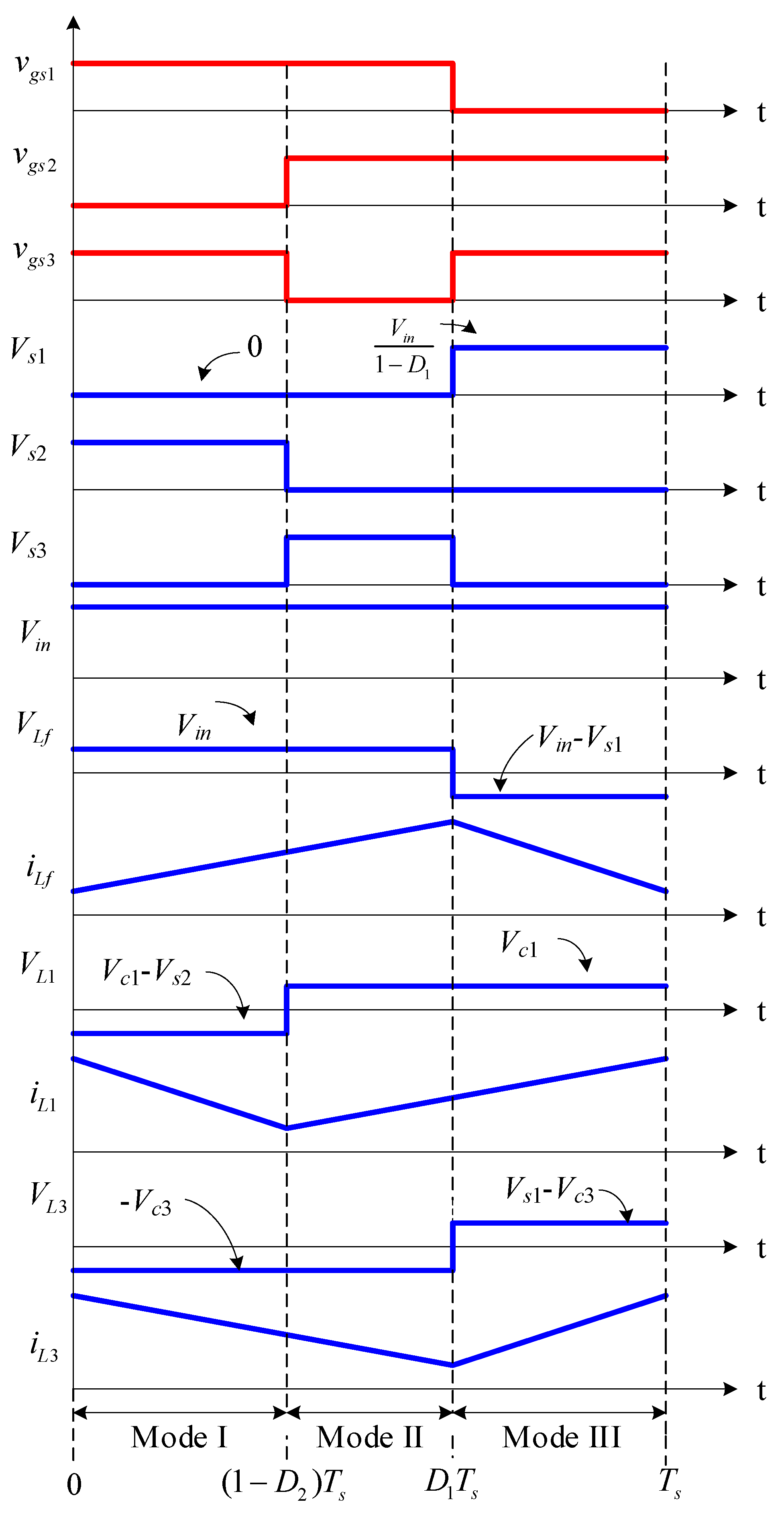
3.2. Key Waveforms in the Switching Cycle and Analysis
3.3. Control Diagram
4. Simulation and Experimental Results
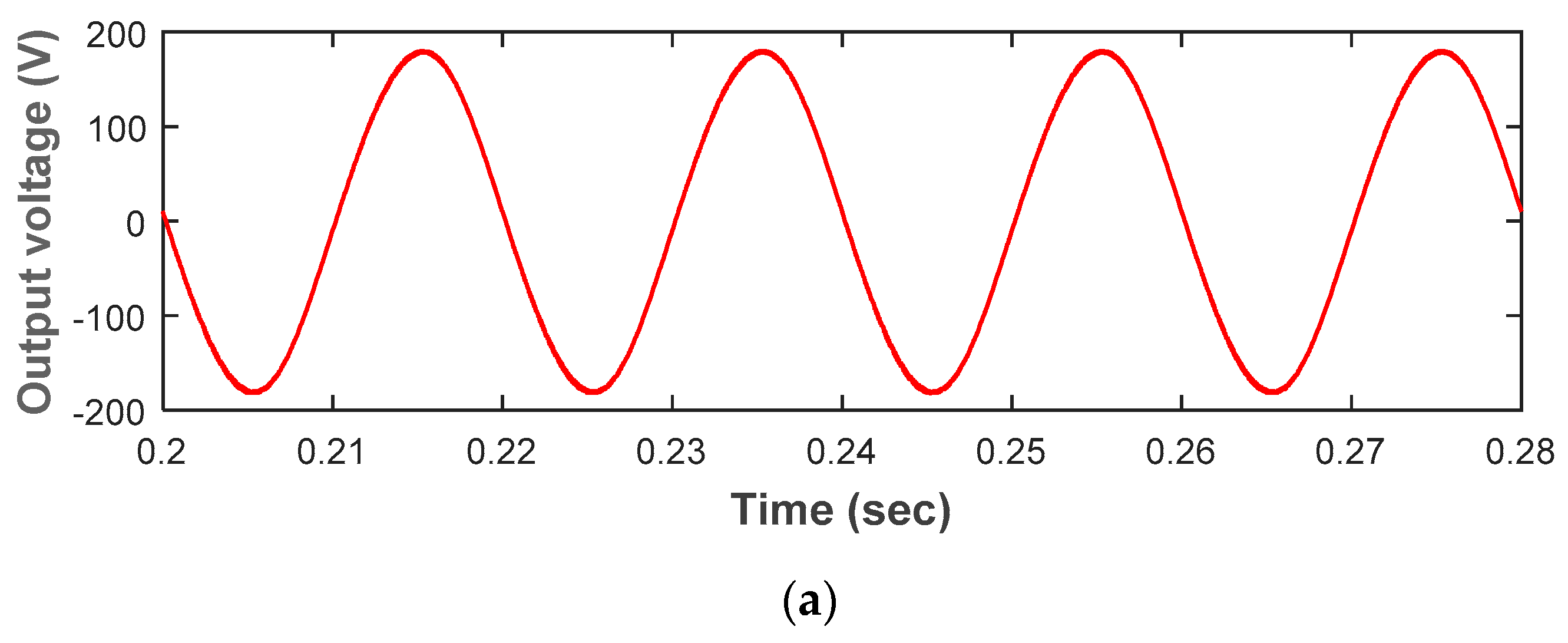
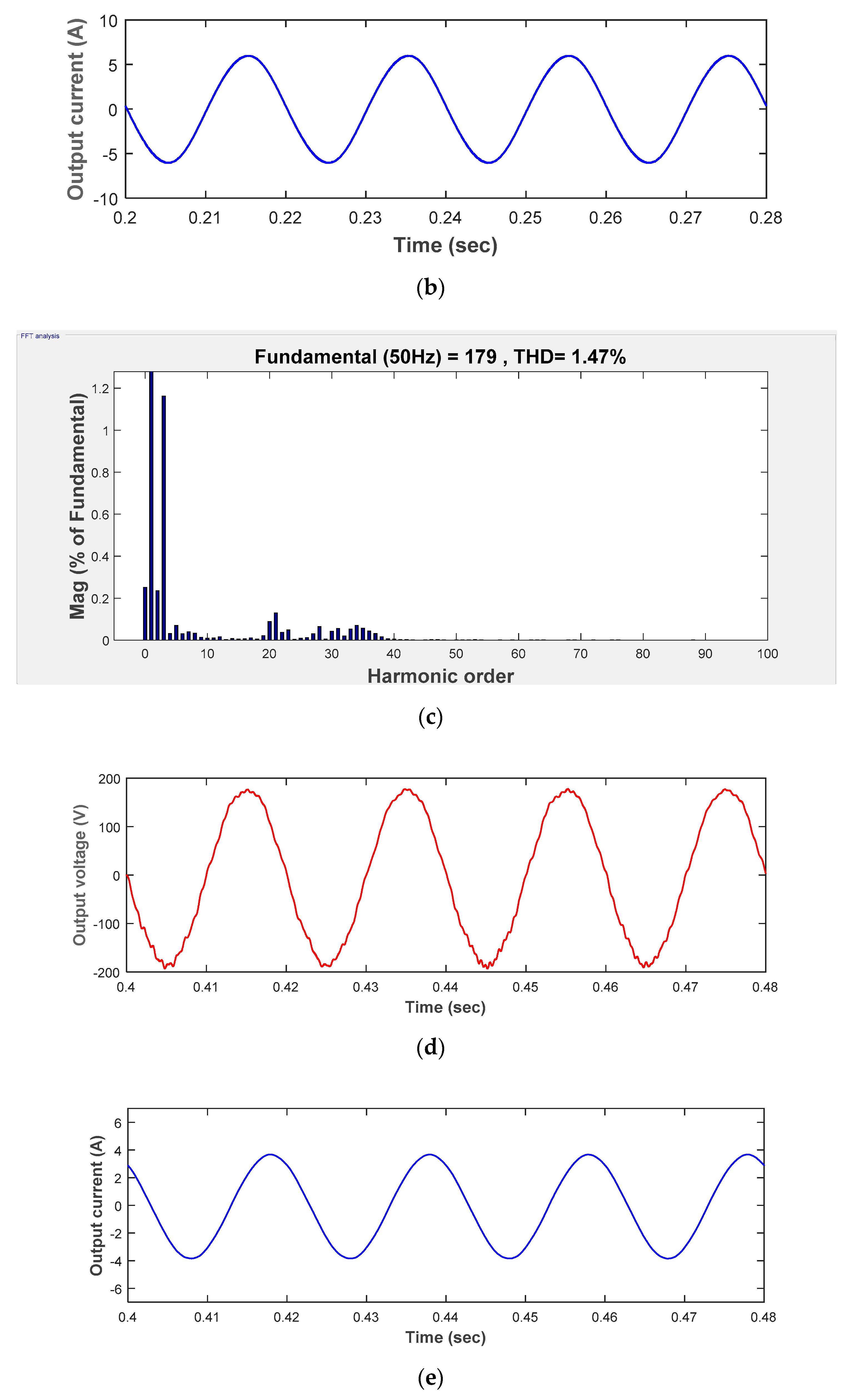
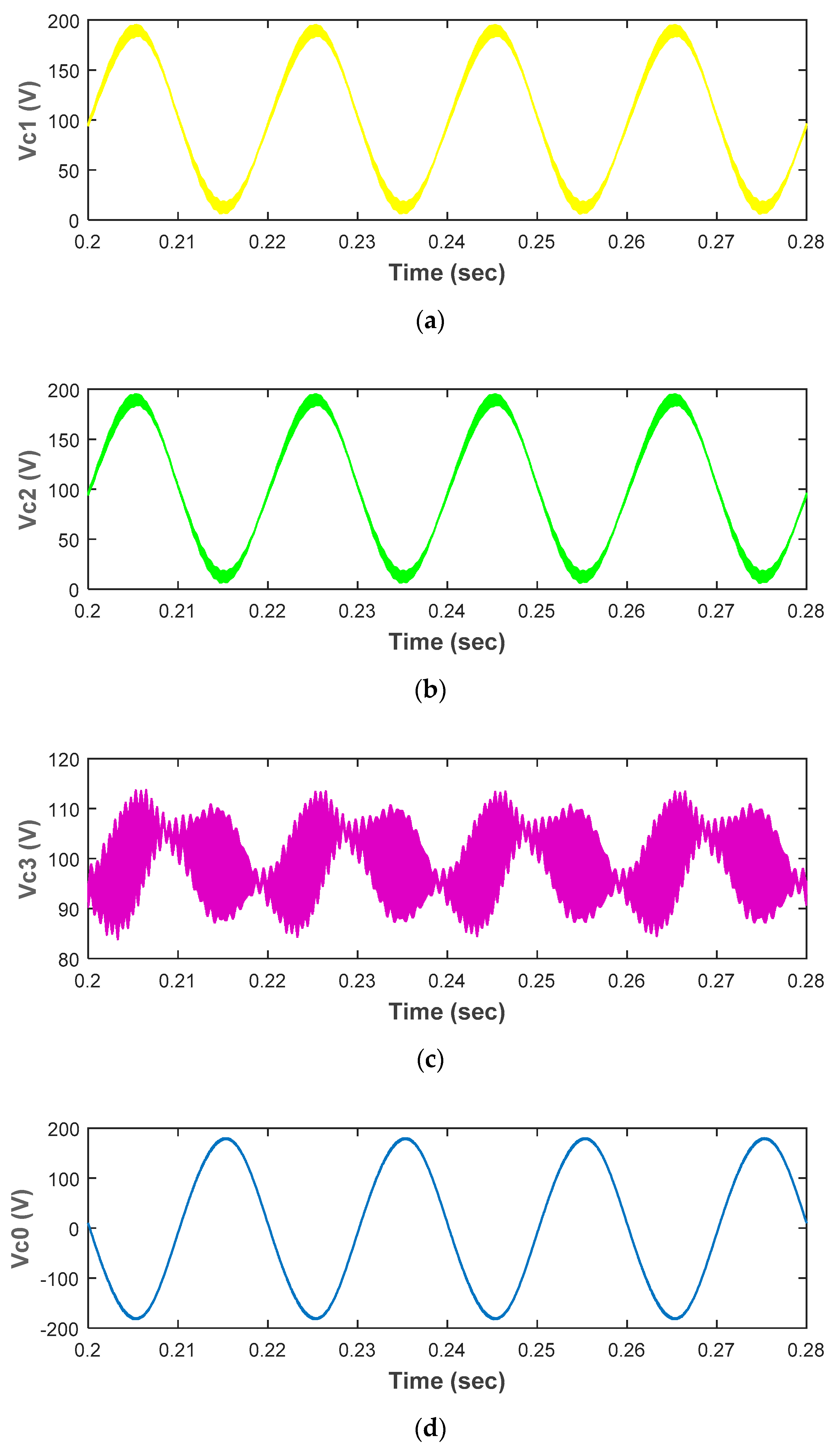
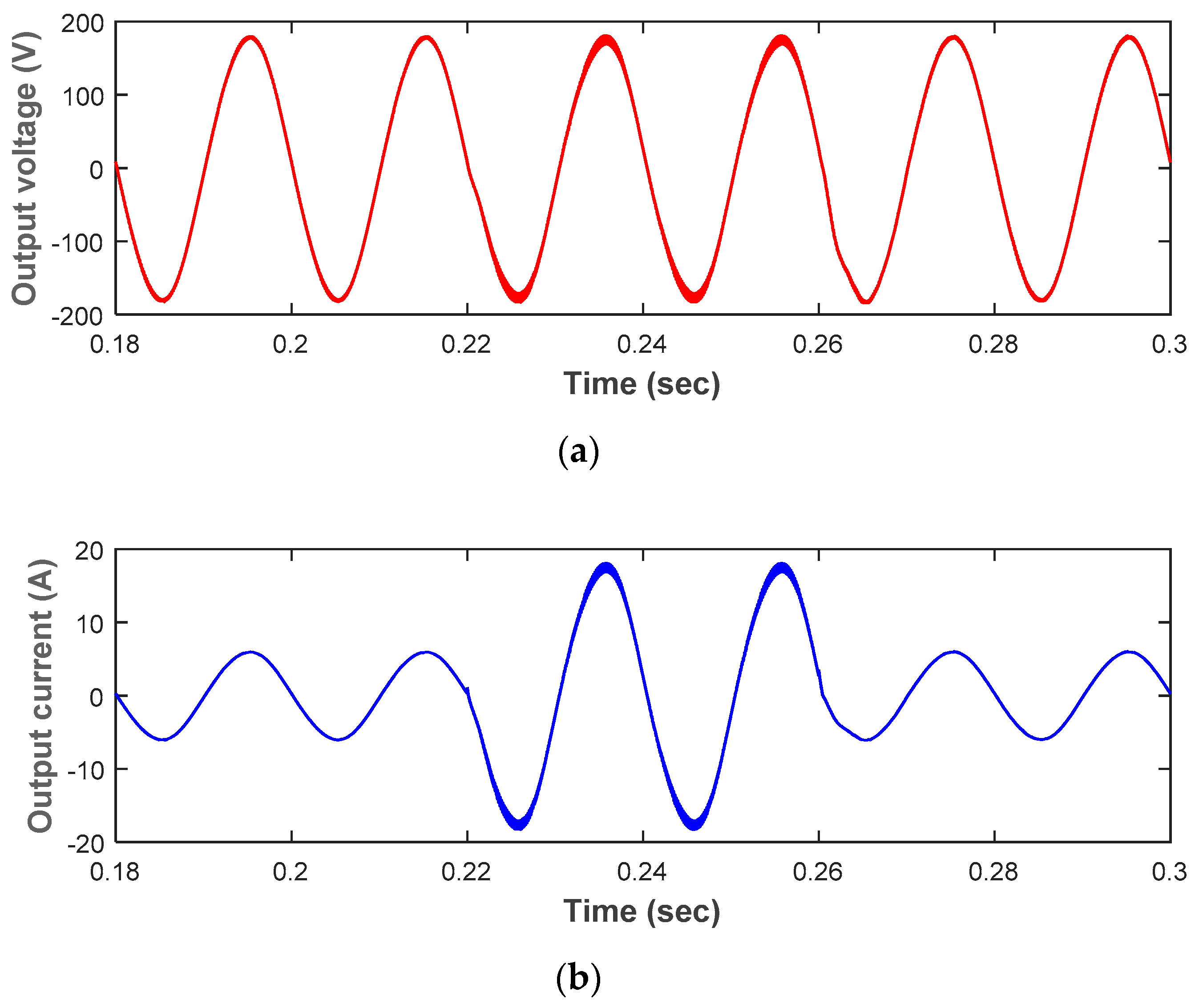
4.1. Simulation Results
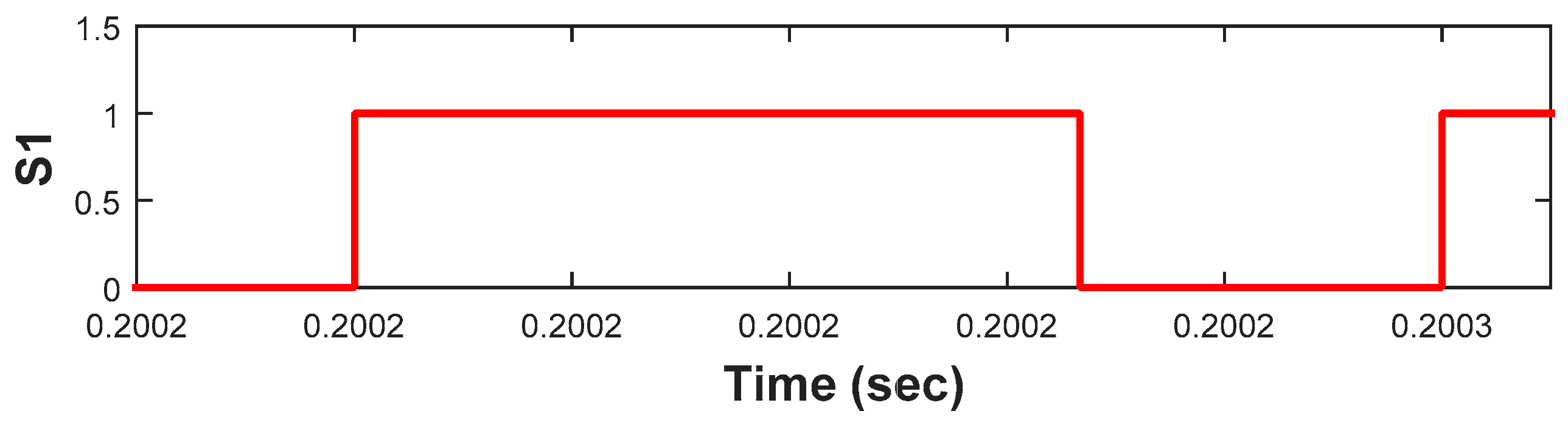
4.2. Experimental Results
4.3. Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Acronyms | |
| ZSI | Z-source inverter |
| VSI | Voltage source inverter |
| TSTS | Three-switch three-state |
| FFT | Fast Fourier transform |
| THD | Total harmonic distortion |
| SBI | Switched Boost Inverters |
| QSBI | Quasi-Switched Boost Inverters |
| UPWM | Unipolar Pulse Width Modulation |
| BPWM | Bipolar Pulse Width Modulation |
| HERIC | Highly Efficient Reliable Inverter Concept |
| IGBT | Insulated Gate Bipolar Transistor |
| SEPIC | Single Ended Primary Inductor Converter |
| Nomenclature | |
| A | Peak voltage gain |
| k | Maximum boost radio |
| , , | Duty cycle functions |
| Output voltage angular frequency | |
| S1, S2, S3 | Semiconductor switches |
| DC input voltage | |
| Voltage of inductors | |
| Voltage of capacitors | |
| Voltage of switches | |
| Current of inductors | |
| Current of capacitors | |
| Output peak current | |
| Current ripple of inductors | |
| Voltage ripple of capacitors | |
| Switching period | |
| fs | Switching frequency |
| EMI | Electromagnetic Interference |
References
- Sulake, N.R.; Devarasetty Venkata, A.K.; Choppavarapu, S.B. FPGA Implementation of a Three-Level Boost Converter-fed Seven-Level DC-Link Cascade H-Bridge inverter for Photovoltaic Applications. Electronics 2018, 7, 282. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, Y.; Zhou, J.; Ding, H.; Guo, X.; Padmanaban, S. Control Strategies of Mitigating Dead-time Effect on Power Converters: An Overview. Electronics 2019, 8, 196. [Google Scholar] [CrossRef]
- Nengroo, S.H.; Kamran, M.A.; Ali, M.U.; Kim, D.-H.; Kim, M.-S.; Hussain, A.; Kim, H.J. Dual Battery Storage System: An Optimized Strategy for the Utilization of Renewable Photovoltaic Energy in the United Kingdom. Electronics 2018, 7, 177. [Google Scholar] [CrossRef]
- Yu, B. An Improved Frequency Measurement Method from the Digital PLL Structure for Single-Phase Grid-Connected PV Applications. Electronics 2018, 7, 150. [Google Scholar] [CrossRef]
- Filippini, M.; Molinas, M.; Oregi, E.O. A Flexible Power Electronics Configuration for Coupling Renewable Energy Sources. Electronics 2015, 4, 283–302. [Google Scholar] [CrossRef]
- Renaudineau, H.; Donatantonio, F.; Fontchastagner, J.; Petrone, G.; Spagnuolo, G.; Martin, J.P.; Pierfederici, S. A PSO-Based Global MPPT Technique for Distributed PV Power Generation. IEEE Trans. Ind. Electron. 2015, 62, 1047–1058. [Google Scholar] [CrossRef]
- Xiao, G. A novel CH5 inverter for single-phase transformerless photovoltaic system applications. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 1197–1201. [Google Scholar]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. High-Performance Constant Power Generation in Grid-Connected PV Systems. IEEE Trans. Power Electron. 2016, 31, 1822–1825. [Google Scholar] [CrossRef]
- Kim, K.; Cha, H.; Kim, H.G. A New Single-Phase Switched-Coupled-Inductor DC–AC Inverter for Photovoltaic Systems. IEEE Trans. Power Electron. 2017, 32, 5016–5022. [Google Scholar] [CrossRef]
- Meraj, M.; Iqbal, A.; Brahim, L.; Alammari, R.; Abu-Rub, H. A high efficiency and high reliability single-phase modified quasi Z-Source inverter for non-isolated grid-connected applications. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015. [Google Scholar]
- Siwakoti, Y.P.; Blaabjerg, F. A novel flying capacitor transformerless inverter for single-phase grid connected solar photovoltaic system. In Proceedings of the 2016 IEEE 7th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Vancouver, BC, Canada, 27–30 June 2016. [Google Scholar]
- Sree, K.R.; Rathore, A.K.; Breaz, E.; Gao, F. Soft-Switching Non-Isolated Current-Fed Inverter for PV/Fuel Cell Applications. IEEE Trans. Ind. Appl. 2016, 52, 351–359. [Google Scholar] [CrossRef]
- Guo, X.; Jia, X. Hardware-based cascaded topology and modulation strategy with leakage current reduction for transformerless PV systems. IEEE Trans. Ind. Electron. 2016, 63, 7823–7832. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, K.; Xing, Y.; Xing, M. H6 transformerless full-bridge PV grid-tied inverters. IEEE Trans. Power Electron. 2014, 29, 1229–1238. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, X.; Guan, H.; Kerekes, T.; Blaabjerg, F. Three phase ZVR topology and modulation strategy for transformerless PV system. IEEE Trans. Power Electron. 2019, 34, 1017–1021. [Google Scholar] [CrossRef]
- Peng, F.Z. Z-source inverter. In Proceedings of the 2002 IEEE Industry Applications Conference, 37th IAS Annual Meeting, Pittsburgh, PA, USA, 13–18 October 2002; pp. 775–781. [Google Scholar]
- Chen, M.T.; Lin, S.H.; Cai, J.B.; Chou, D.Y. Implementing a single-phase quasi-Z-source inverter with the indirect current control algorithm for a reconfigurable PV system. In Proceedings of the IEEE International Conference on Industrial Technology, Taipei, Taiwan, 14–17 March 2016; pp. 323–328. [Google Scholar]
- Li, H.B.; Kayiranga, T.; Lin, X.; Shi, Y.; Li, H. A resonance suppression method for GaN-based single-phase quasi-Z-source PV inverter with high switching frequency. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015; pp. 2522–2526. [Google Scholar]
- Ahmed, T.; Mekhilef, S.; Nakaoka, M. Single phase transformerless semi-Z-source inverter with reduced total harmonic distortion (THD) and DC current injection. In Proceedings of the IEEE ECCE Asia Downunder, Melbourne, Australia, 3–6 June 2013; pp. 1322–1327. [Google Scholar]
- Huang, L.; Zhang, M.; Hang, L.; Yao, W.; Lu, Z. A Family of Three-Switch Three-State Single-Phase Z-Source Inverters. IEEE Trans. Power Electron. 2013, 28, 2317–2329. [Google Scholar] [CrossRef]
- Li, W.; Gu, Y.; Luo, H.; Cui, W.; He, X.; Xia, C. Topology Review and Derivation Methodology of Single-Phase Transformerless Photovoltaic Inverters for Leakage Current Suppression. IEEE Trans. Ind. Electron. 2015, 62, 4537–4551. [Google Scholar] [CrossRef]
- Wang, B.; Tang, W. A New CUK-Based Z-Source Inverter. Electronics 2018, 7, 313. [Google Scholar] [CrossRef]
- Wang, B.; Tang, W. A Novel SEPIC-Based Z-Source Inverter. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 4347–4352. [Google Scholar]
- Kafle, Y.R.; Town, G.E.; Guochun, X.; Gautam, S. Performance comparison of single-phase transformerless PV inverter systems. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017. [Google Scholar]
- Cao, D.; Jiang, S.; Yu, X.; Peng, F.Z. Low-Cost Semi-Z-source Inverter for Single-Phase Photovoltaic Systems. IEEE Trans. Power Electron. 2011, 26, 3514–3523. [Google Scholar] [CrossRef]
- Nguyen, M.K.; Tran, T.T. A single-phase single-stage switched-boost inverter with four switches. IEEE Trans. Power Electron. 2017, 33, 6769–6781. [Google Scholar] [CrossRef]
- Ribeiro, H.; Borges, B.; Pinto, A. Single-stage DC–AC converter for photovoltaic systems. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 604–610. [Google Scholar]
- Nguyen, M.K.; Le, T.V.; Park, S.J.; Lim, Y.C.; Yoo, J.Y. Class of high boost inverters based on switched-inductor structure. IET Power Electron. 2015, 8, 750–759. [Google Scholar] [CrossRef]
- Oleksandr, H.; Carlos, R.C.; Enrique, R.C.; Dmitri, V.; Serhii, S. Single phase three-level neutral-point-clamped quasi-Z-source inverter. IET Power Electron. 2015, 8, 1–10. [Google Scholar]
- Caceres, R.O.; Barbi, I. A boost dc–ac converter: Analysis, design, and experimentation. IEEE Trans. Power Electron. 1999, 14, 134–141. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, L.; Li, H. A high performance photovoltaic module-integrated converter (MIC) based on cascaded quasi-Z-source inverters (qZSI) using eGaN FETs. IEEE Trans. Power Electron. 2013, 28, 2727–2738. [Google Scholar] [CrossRef]
- Sun, D.; Ge, B.; Yan, X.; Bi, D.; Zhang, H.; Liu, Y.; Abu-Rub, H.; Ben-Brahim, L.; Peng, F.Z. Modeling, impedance design, and efficiency analysis of quasi-Z source module in cascade multilevel photovoltaic power system. IEEE Trans. Ind. Electron. 2014, 61, 6108–6117. [Google Scholar] [CrossRef]
- Tang, Y.; Xie, S.; Ding, J. Pulsewidth modulation of Z-source inverters with minimum inductor current ripple. IEEE Trans. Ind. Electron. 2014, 61, 98–106. [Google Scholar] [CrossRef]
- Vazquez, N.; Rosas, M.; Hernandez, C.; Vazquez, E.; Perez-Pinal, F.J. A New Common-Mode Transformerless Photovoltaic Inverter. IEEE Trans. Ind. Electron. 2015, 62, 6381–6391. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Le, T.-V.; Park, S.-J.; Lim, Y.-C. A Class of Quasi-Switched Boost Inverters. IEEE Trans. Ind. Electron. 2015, 62, 1526–1536. [Google Scholar] [CrossRef]
- Nguyen, M.K.; Lim, Y.C.; Park, S.J. Improved trans-Z-source inverter with continuous input current and boost inversion capability. IEEE Trans. Power Electron. 2013, 28, 4500–4510. [Google Scholar] [CrossRef]
- Nguyen, M.K.; Lim, Y.C.; Park, S.J.; Shin, D.S. Family of high-boost Z-source inverters with combined switched-inductor and transformer cells. IET Power Electron. 2013, 6, 1175–1187. [Google Scholar] [CrossRef]
- Veerachary, M. Power tracking for nonlinear PV sources with coupled inductor SEPIC converter. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1019–1029. [Google Scholar] [CrossRef]
- Hasanpour, S.; Baghramian, A.; Mojallali, H. A Modified SEPIC-Based High Step-Up DC-DC Converter with Quasi-Resonant Operation for Renewable Energy Applications. IEEE Trans. Ind. Electron. 2019, 66, 3539–3549. [Google Scholar] [CrossRef]





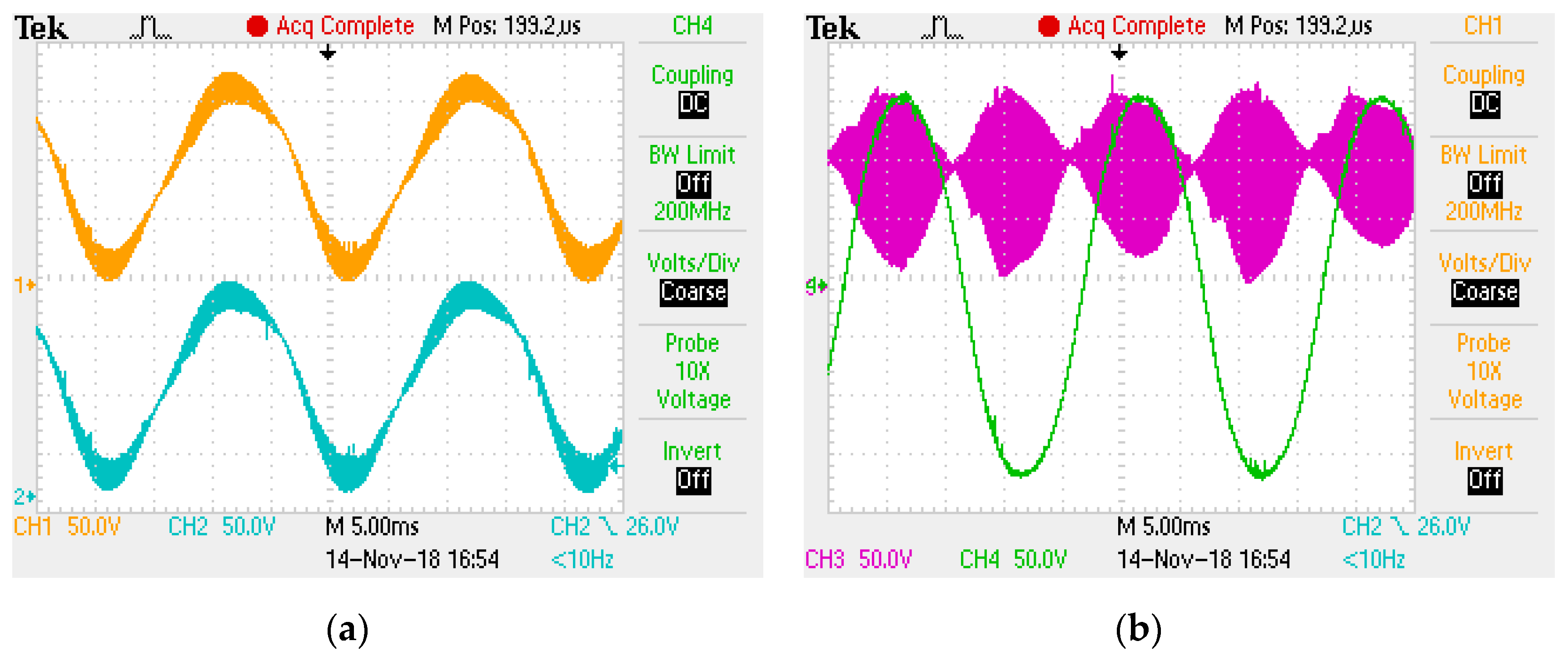

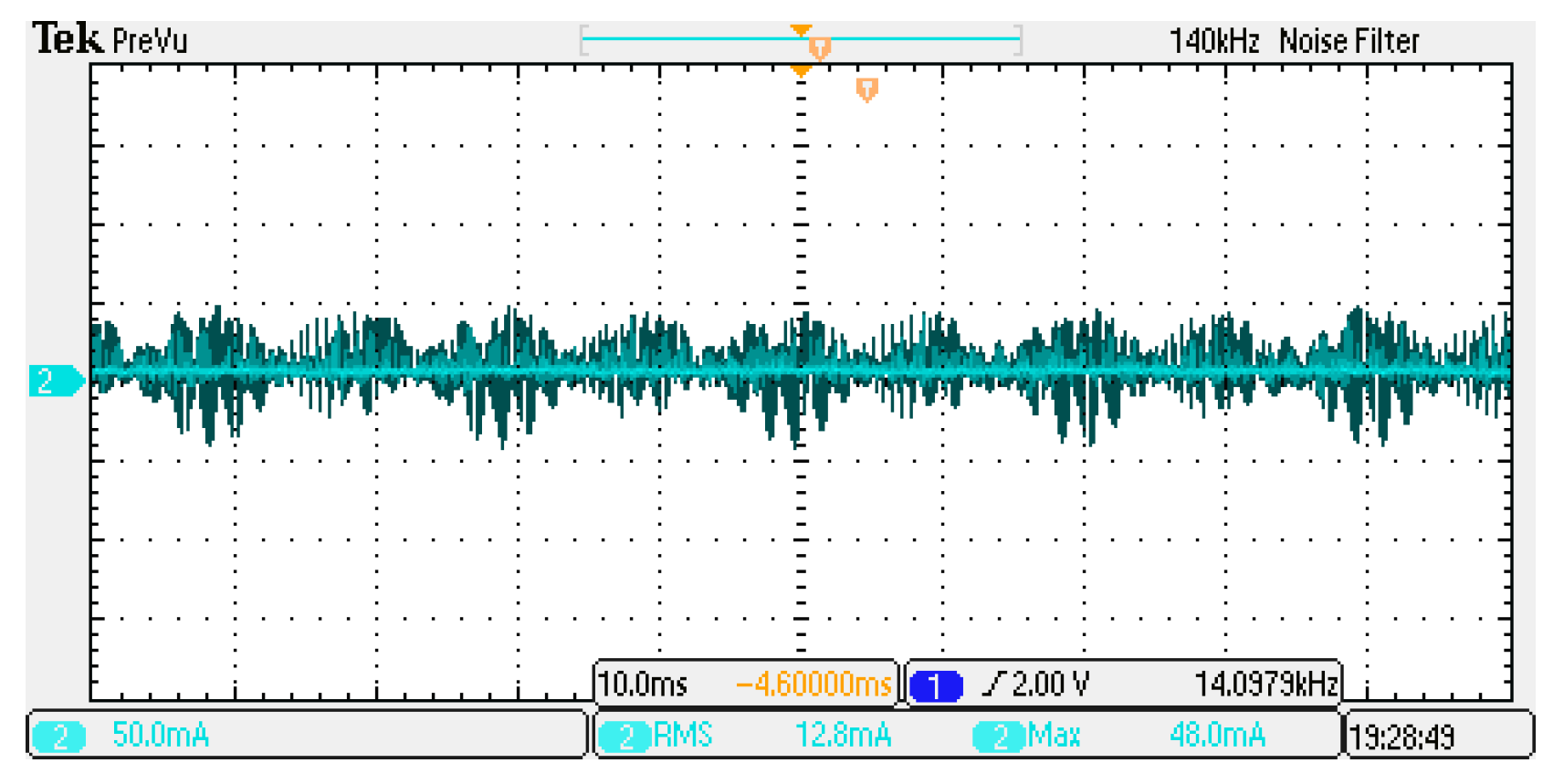
| Parameters | Vin (V) | Vo (rms, V) | fs (kHz) | A (Voltage Gain) | k | L3 (mH) | Lf (mH) | L1, L2 (mH) | C0 (µF) | C1, C2 (µF) | C3 (µF) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| value | 100 | 124 | 20 | 1.75 | 2 | 1.5 | 0.5 | 1.65 | 37.6 | 15 | 9 |
| Output power (W) | 120 | 204.5 | 311 | 358 | 431 |
| Efficiency (%) | 89.9 | 90.08 | 91.17 | 91.70 | 89.58 |
| L | C | D | S | Control Method | Voltage Gain | Common Ground | EMI | Soft Switch | |
|---|---|---|---|---|---|---|---|---|---|
| Semi-ZSI [25] | 2 | 2 | 0 | 2 | nonlinear | <1 | Yes | high | complex |
| Semi-ZS-based [34] | 3 | 3 | 0 | 2 | linear | <1 | Yes | high | complex |
| Basic SBI [35] | 1 | 1 | 2 | 2 | linear | >1 | No | high | complex |
| Embedded-type qSBI [35] | 1 | 1 | 2 | 2 | linear | >1 | No | high | complex |
| DC-linked-type qSBI [35] | 1 | 1 | 2 | 2 | linear | >1 | No | high | complex |
| CUK-based ZSI [22] | 4 | 4 | 0 | 3 | linear | >1 | Yes | low | complex |
| Boost-based ZSI [20] | 3 | 3 | 0 | 3 | linear | >1 | Yes | high | complex |
| Buck–boost-based [20] | 3 | 3 | 0 | 3 | linear | >1 | Yes | high | complex |
| Proposed in [23] | 4 | 4 | 0 | 3 | linear | >1 | Yes | low | simple |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Tang, W. A Novel Three-Switch Z-Source SEPIC Inverter. Electronics 2019, 8, 247. https://doi.org/10.3390/electronics8020247
Wang B, Tang W. A Novel Three-Switch Z-Source SEPIC Inverter. Electronics. 2019; 8(2):247. https://doi.org/10.3390/electronics8020247
Chicago/Turabian StyleWang, Baocheng, and Wei Tang. 2019. "A Novel Three-Switch Z-Source SEPIC Inverter" Electronics 8, no. 2: 247. https://doi.org/10.3390/electronics8020247
APA StyleWang, B., & Tang, W. (2019). A Novel Three-Switch Z-Source SEPIC Inverter. Electronics, 8(2), 247. https://doi.org/10.3390/electronics8020247




