An Inner- and Outer-Fed Dual-Arm Archimedean Spiral Antenna for Generating Multiple Orbital Angular Momentum Modes
Abstract
:1. Introduction
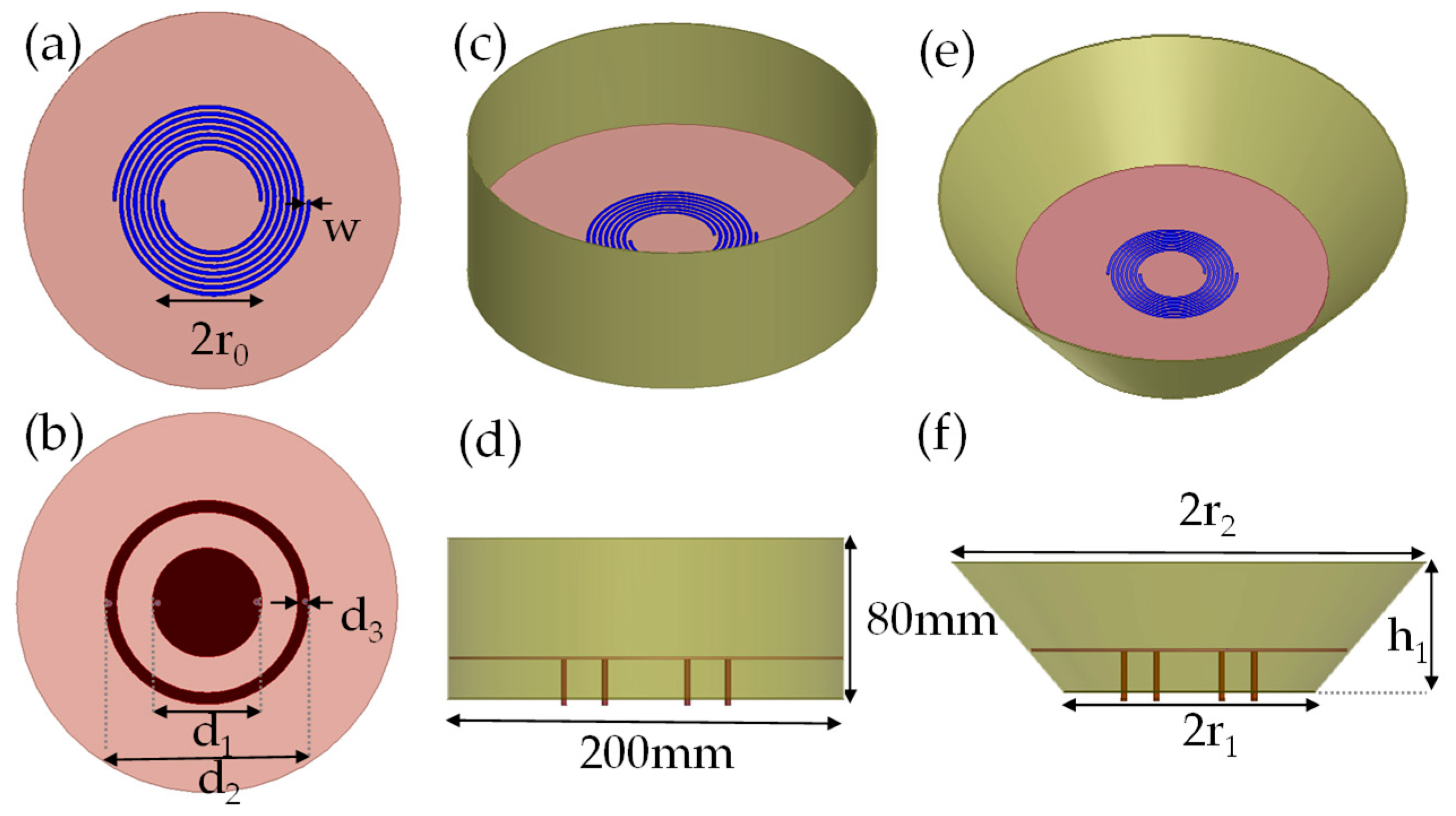
2. Antenna Design and Discussion
2.1. DASA Design
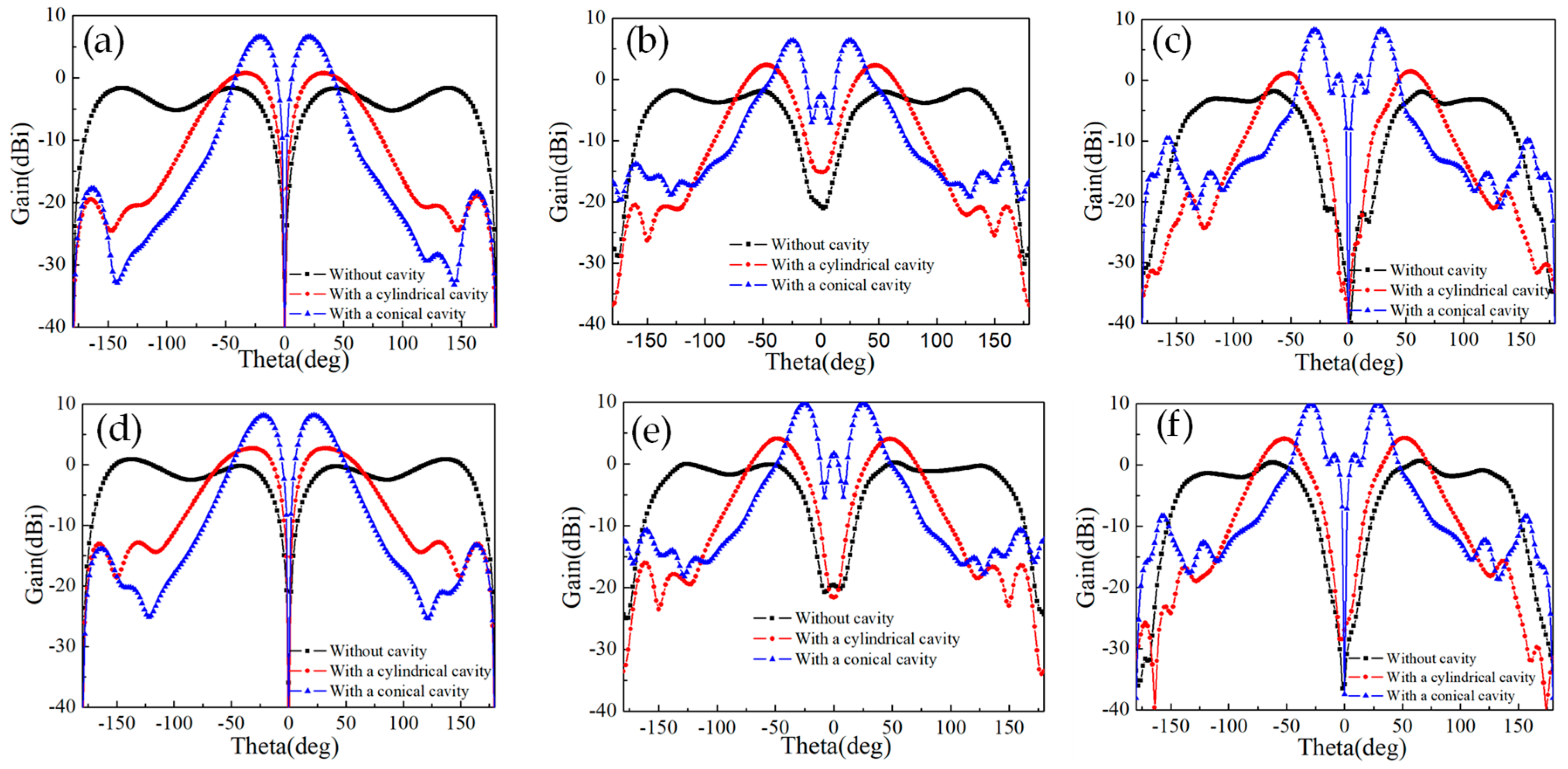
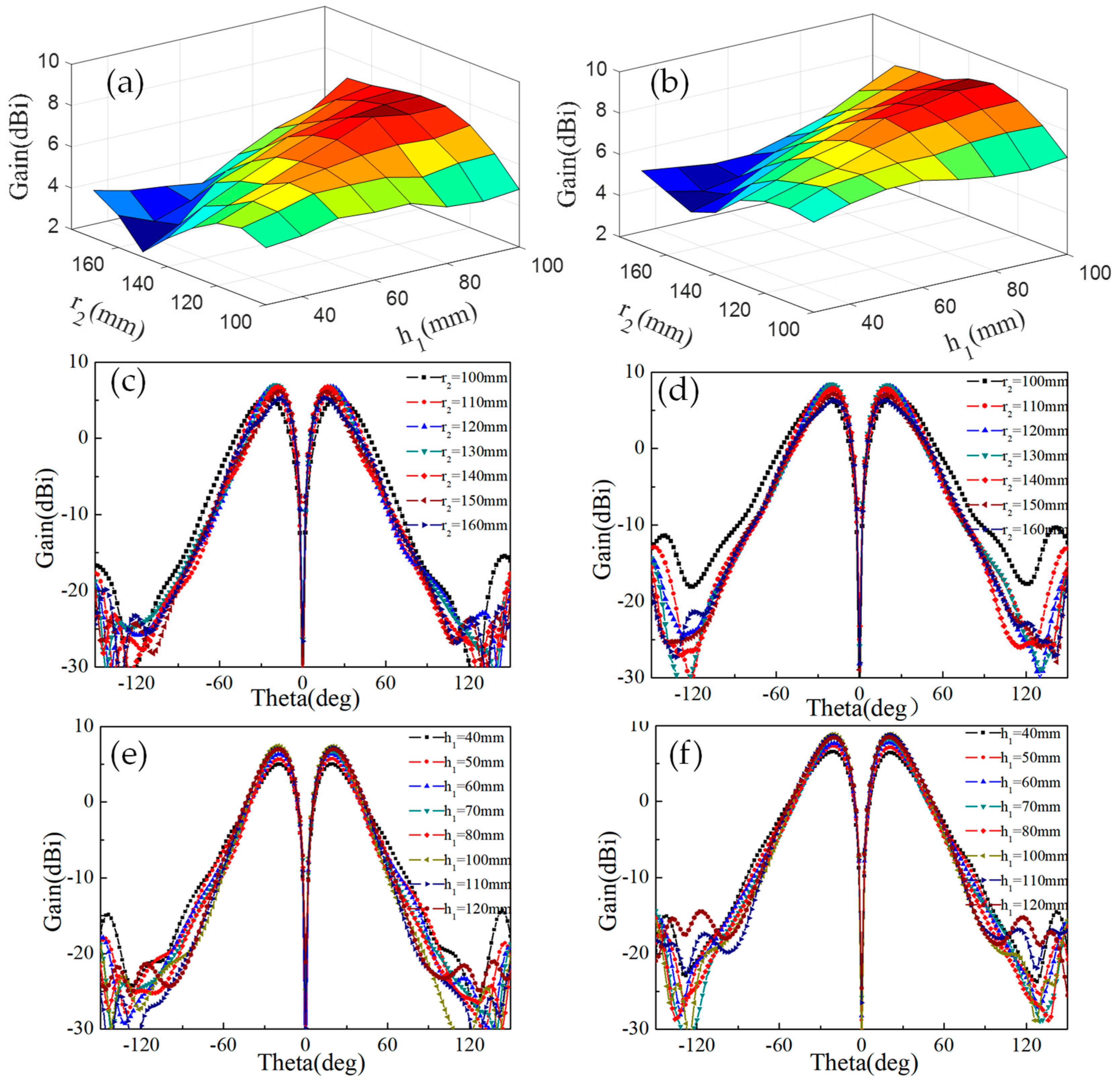
2.2. Optimization of DASA
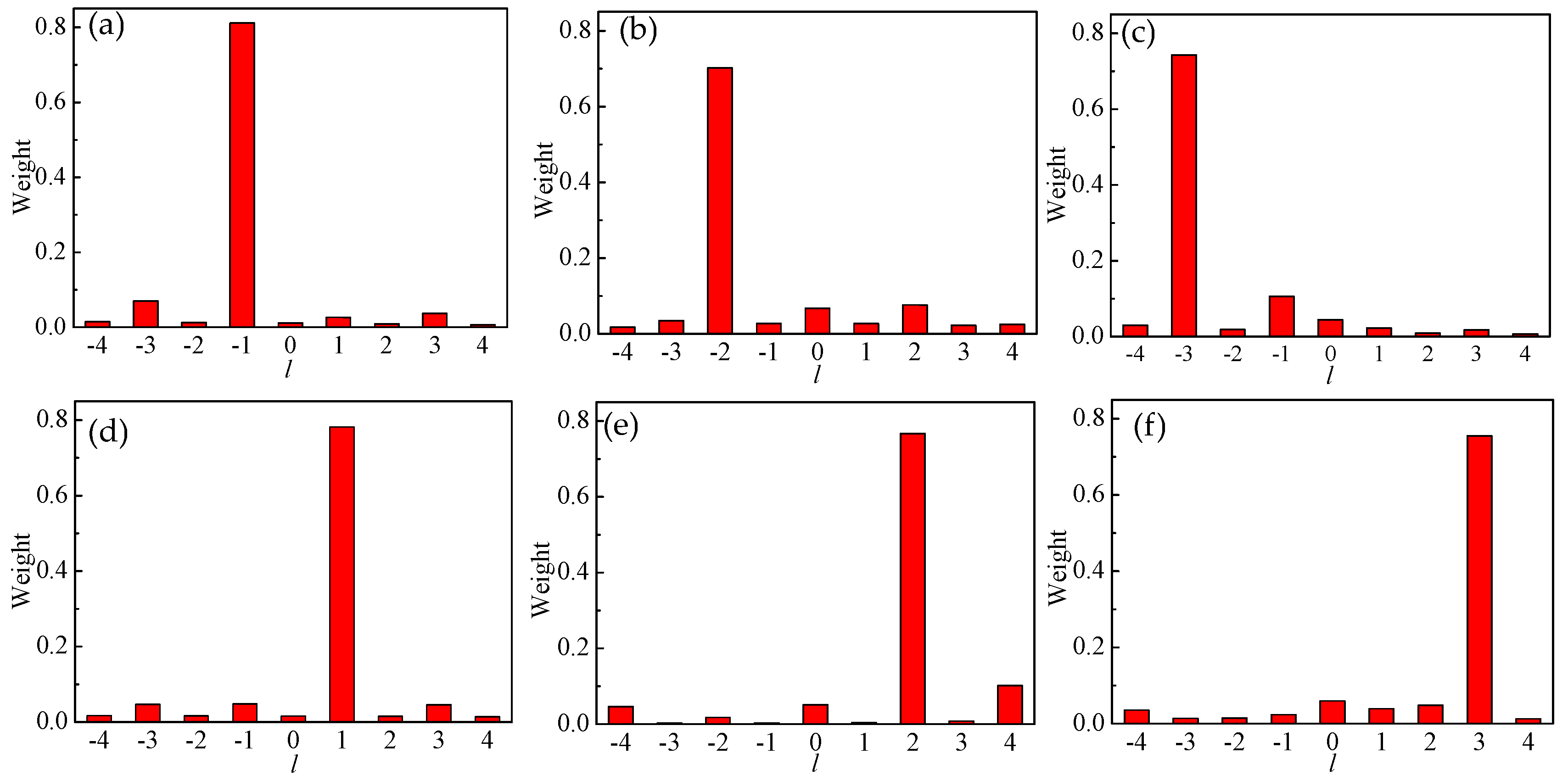
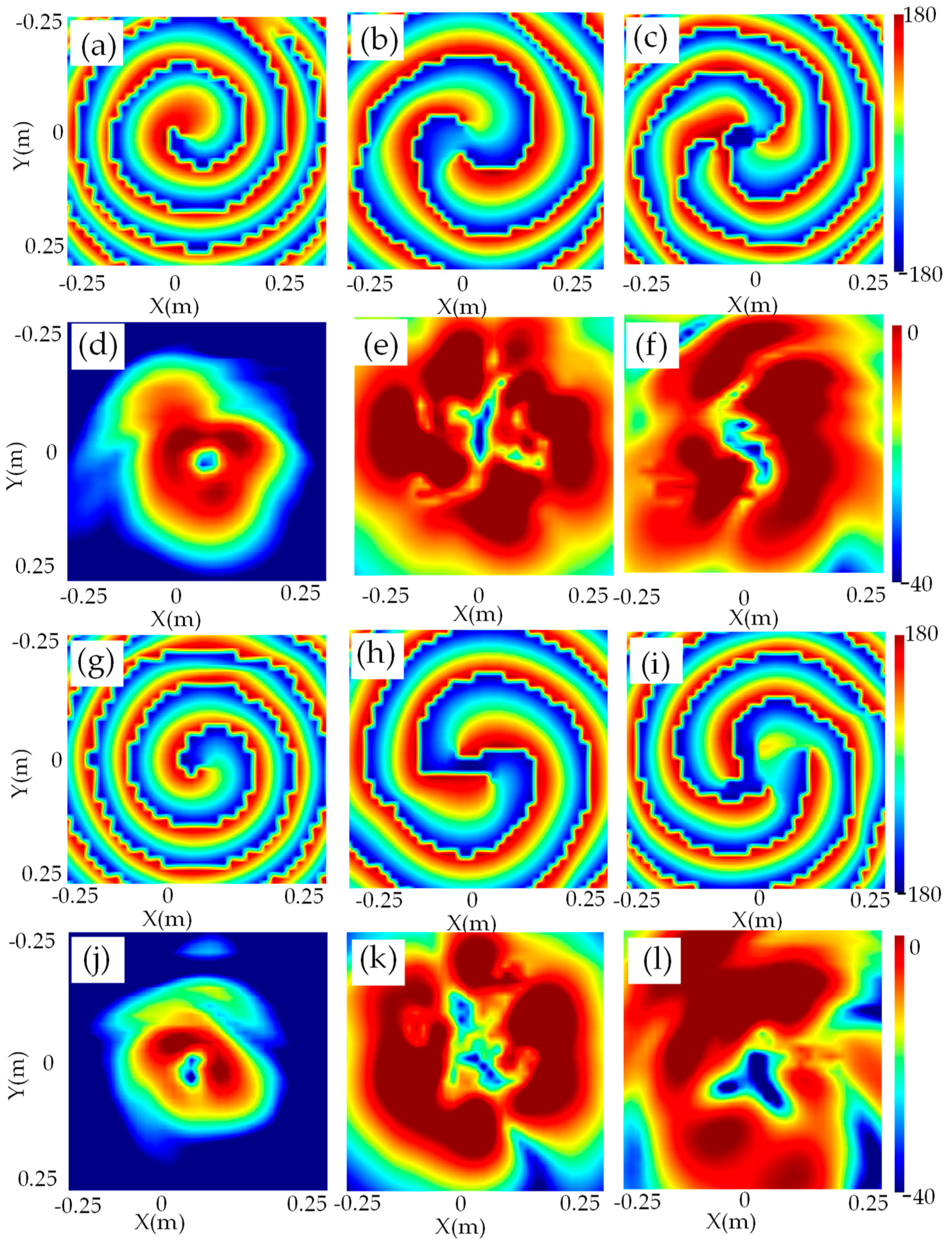
2.3. Purity Analysis
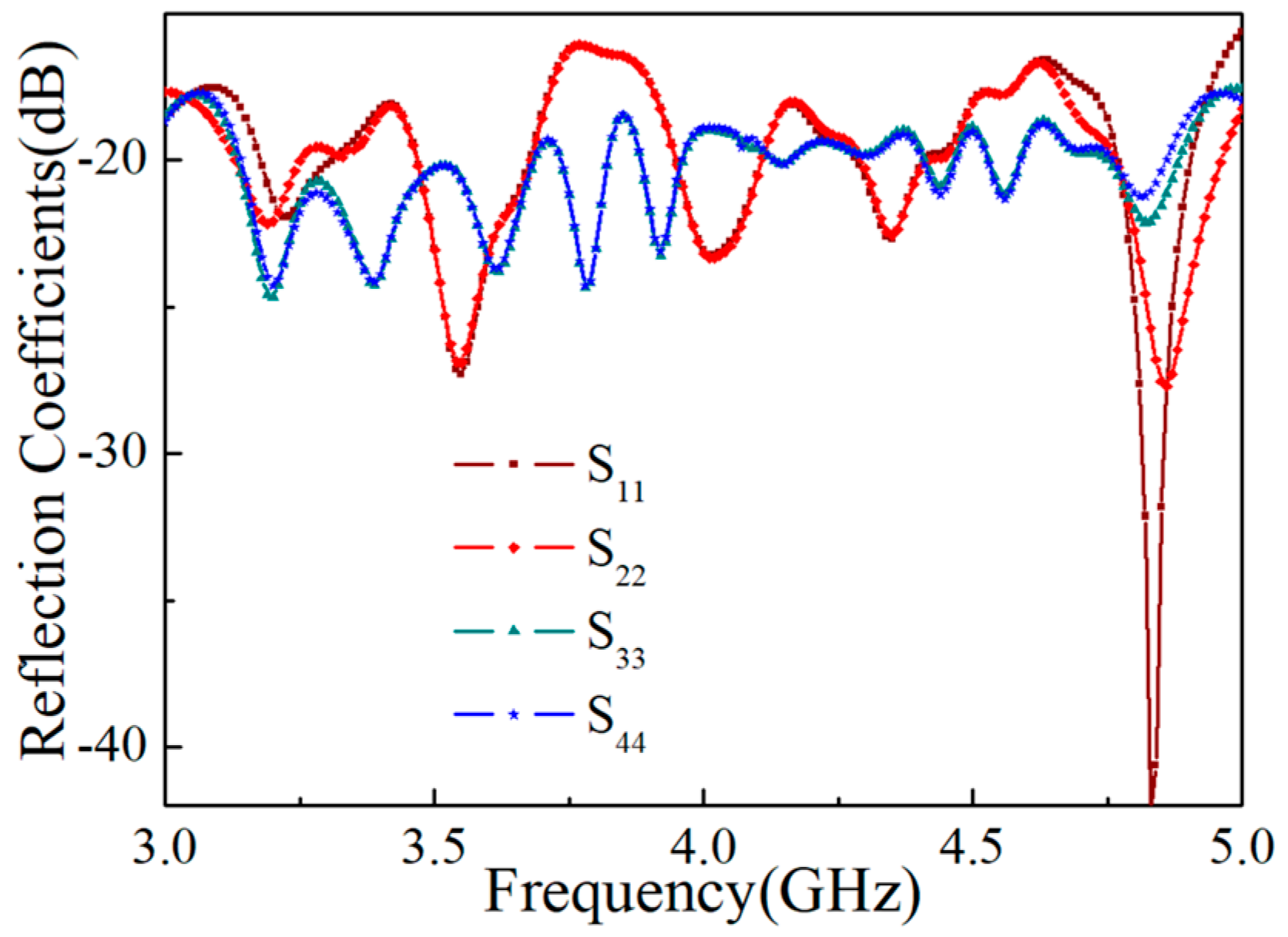
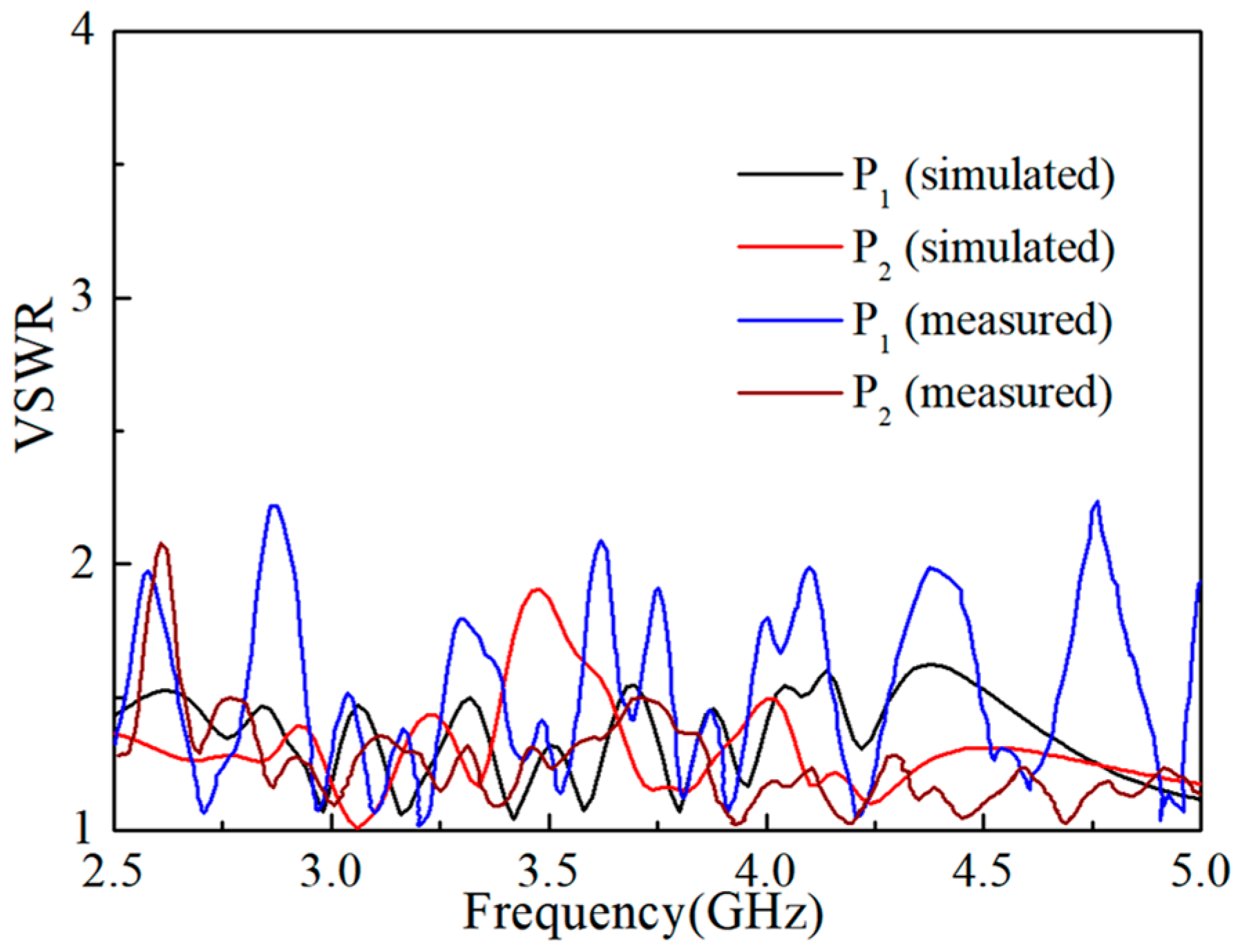
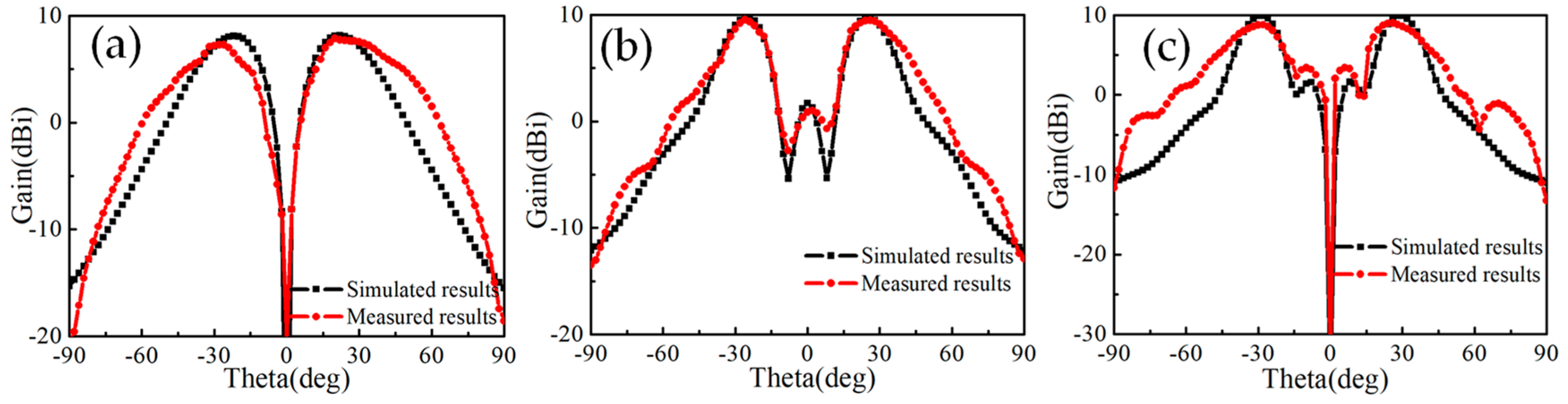
3. Fabrication and Measurement of the DASA
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Guo, Z.; Xu, Q.; Zhang, J.; Zhang, A.; Wang, W.; Liu, Y.; Li, Y.; Wang, X.; Qu, S. Calculating the torque of the optical vortex tweezer to the ellipsoidal micro-particles. Opt. Commun. 2015, 354, 34–39. [Google Scholar] [CrossRef]
- Kai, C.; Feng, Z.; Dedo, M.I.; Huang, P.; Guo, K.; Shen, F.; Gao, J.; Guo, Z. The performances of different OAM encoding systems. Opt. Commun. 2019, 430, 151–157. [Google Scholar] [CrossRef]
- Guo, Z.; Zhu, L.; Guo, K.; Shen, F.; Yin, Z. High-Order Dielectric Metasurfaces for High-Efficiency Polarization Beam Splitters and Optical Vortex Generators. Nanoscale Res. Lett. 2017, 12, 512. [Google Scholar] [CrossRef] [PubMed]
- Thidé, B.; Then, H.; Sjöholm, J.; Palmer, K.; Bergman, J.; Carozzi, T.D.; Istomin, Y.N.; Ibragimov, N.H.; Khamitova, R. Utilization of photon orbital angular momentum in the low-frequency radio domain. Phys. Rev. Lett. 2007, 99, 087701. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Cao, X.; Yang, H.; Gao, J. Radiation performance synthesis for OAM vortex wave generated by reflective metasurface. IEEE Access 2018, 6, 28691–28701. [Google Scholar] [CrossRef]
- Kai, C.; Huang, P.; Shen, F.; Zhou, H.; Guo, Z. Orbital Angular Momentum Shift Keying Based Optical Communication System. IEEE Photonics J. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Gaffoglio, R.; Cagliero, A.; Vecchi, G.; Andriulli, F.P. Vortex Waves and Channel Capacity: Hopes and Reality. IEEE Access 2018, 6, 19814–19822. [Google Scholar] [CrossRef] [Green Version]
- Yuan, T.; Wang, H.; Cheng, Y.; Qin, Y. Electromagnetic Vortex-Based Radar Imaging Using a Single Receiving Antenna: Theory and Experimental Results. Sensors 2017, 17, 630. [Google Scholar] [CrossRef]
- Turnbull, G.A.; Robertson, D.A.; Smith, G.M.; Allen, L.; Padgett, M.J. The generation of free-space Laguerre-Gaussian modes at millimetre-wave frequencies by use of a spiral phase plate. Opt. Commun. 1996, 127, 183–188. [Google Scholar] [CrossRef]
- Hui, X.; Zheng, S.; Hu, Y.; Xu, C.; Jin, X.; Chi, H.; Zhang, X. Ultralow reflectivity spiral phase plate for generation of millimeter-wave OAM beam. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 966–969. [Google Scholar] [CrossRef]
- Tamburini, F.; Mari, E.; Sponselli, A.; Romanato, F.; Bo, T.; Bianchini, A.; Palmieri, L.; Someda, C.G. Encoding many channels in the same frequency through radio vorticity: first experimental test. New J. Phys. 2012, 14, 78001–78004. [Google Scholar]
- Barbuto, M.; Trotta, F.; Bilotti, F.; Toscano, A. Circular Polarized Patch Antenna Generating Orbital Angular Momentum. Prog. Electromagn. Res. 2014, 148, 23–30. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, S.; Li, Y.; Wang, B.Z. A Circularly Polarized Multimode Patch Antenna for the Generation of Multiple Orbital Angular Momentum Modes. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 521–524. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, S.; Jin, X.; Chi, H.; Zhang, X. Generation of plane spiral OAM waves using traveling-wave circular slot antenna. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 8–11. [Google Scholar] [CrossRef]
- Bai, X.D.; Liang, X.L.; Sun, Y.T.; Hu, P.C.; Yao, Y.; Wang, K.; Geng, J.P.; Jin, R.H. Experimental Array for Generating Dual Circularly-Polarized Dual-Mode OAM Radio Beams. Sci. Rep. 2017, 7, 40099. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, H.; Kang, L.; Wei, F.; Cai, Y.M.; Yin, Y.Z. A low-profile dual-polarized microstrip antenna array for dual-mode OAM applications. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3022–3025. [Google Scholar] [CrossRef]
- Liu, B.Y.; Cui, Y.H.; Li, R. A Broadband Dual-Polarized Dual-OAM-Mode Antenna Array for OAM Communication. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 744–747. [Google Scholar] [CrossRef]
- Li, L.; Zhou, X. Mechanically Reconfigurable Single-Arm Spiral Antenna Array for Generation of Broadband Circularly Polarized Orbital Angular Momentum Vortex Waves. Sci. Rep. 2018, 8, 5128. [Google Scholar] [CrossRef]
- Wei, D.J.; Li, J.Y.; Yang, J.J. The vortical radio waves realized by helical antennas. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation and Usnc/ursi National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 175–176. [Google Scholar]
- Zhang, J.; Guo, Z.; Li, R.; Wang, W.; Zhang, A.; Liu, J.; Qu, S.; Gao, J. Circular polarization analyzer based on the combined coaxial Archimedes’ spiral structure. Plasmonics 2015, 10, 1255–1261. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Z.; Zhou, K.; Ran, L.; Zhu, L.; Wang, W.; Sun, Y.; Shen, F.; Gao, J.; Liu, S. Circular polarization analyzer based on an Archimedean nano-pinholes array. Opt. Express. 2015, 23, 30523–30531. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Li, Z.; Zhang, J.; Guo, K.; Shen, F.; Zhou, Q.; Zhou, H. Review of the functions of Archimedes’ spiral metallic nanostructures. Nanomaterials 2017, 7, 405. [Google Scholar]
- Rahman, M.; NaghshvarianJahromi, M.; Mirjavadi, S.; Hamouda, A. Bandwidth Enhancement and Frequency Scanning Array Antenna Using Novel UWB Filter Integration Technique for OFDM UWB Radar Applications in Wireless Vital Signs Monitoring. Sensors 2018, 18, 3155. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.; NaghshvarianJahromi, M.; Mirjavadi, S.; Hamouda, A. Resonator Based Switching Technique between Ultra Wide Band (UWB) and Single/Dual Continuously Tunable-Notch Behaviors in UWB Radar for Wireless Vital Signs Monitoring. Sensors 2018, 18, 3330. [Google Scholar] [CrossRef] [PubMed]
- Mao, F.; Huang, M.; Li, T.; Zhang, J.; Yang, C. Broadband generation of orbital angular momentum carrying beams in RF regimes. Prog. Electromagn. Res. 2017, 160, 19–27. [Google Scholar] [CrossRef]
- Nakano, H.; Satake, R.; Yamauchi, J. Extremely Low-Profile, Single-Arm, Wideband Spiral Antenna Radiating a Circularly Polarized Wave. IEEE Trans. Antennas Propag. 2010, 58, 1511–1520. [Google Scholar] [CrossRef]
- Kaiser, J. The Archimedean two-wire spiral antenna. IEEE Trans. Antennas Propag. 1960, 8, 312–323. [Google Scholar] [CrossRef]
- Johnson, R.C.; Jasik, H. Frequency-Independent Antennas. In Antenna Engineering Handbook, 3rd ed.; McGraw-Hill Book Company: New York, NY, USA, 1993; pp. 1–10. [Google Scholar]





| OAM Mode | Gain (dBi) | Direction Angle (deg) |
|---|---|---|
| −1 | 7.19 | 20 |
| −2 | 6.74 | 24 |
| −3 | 8.06 | 26 |
| 1 | 8.63 | 20 |
| 2 | 10 | 24 |
| 3 | 9.81 | 27 |
| References | Antenna Structure | f0 (GHz) | Bandwidth | OAM Modes | Gain (dBi) |
|---|---|---|---|---|---|
| [14] | Concentric patches | 5.65 | Narrow | 1,−2 | N.A |
| [15] | Cavity+ slot+ Horn | 10 | Narrow | 2,3,4 | 3.71 |
| [16] | Stacked MP 4 array | 4.8 | 30% | 1,−1 | 9 |
| [17] | * MP 4 array | 5.5 | Narrow | 1,−1 | 9.5,10.2 |
| [18] | * MP 4 array | 2.4 | 25% | 1,−1 | N.A |
| [19] | * MP 8 array | 4.05 | 25% | 1,2,3 | N.A |
| Proposed antenna | * MP + cavity | 3.75 | 66.6% | 1,2,3,−1,−2,−3 | 6.7–10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Chen, H.; Guo, K.; Shen, F.; Guo, Z. An Inner- and Outer-Fed Dual-Arm Archimedean Spiral Antenna for Generating Multiple Orbital Angular Momentum Modes. Electronics 2019, 8, 251. https://doi.org/10.3390/electronics8020251
Wang L, Chen H, Guo K, Shen F, Guo Z. An Inner- and Outer-Fed Dual-Arm Archimedean Spiral Antenna for Generating Multiple Orbital Angular Momentum Modes. Electronics. 2019; 8(2):251. https://doi.org/10.3390/electronics8020251
Chicago/Turabian StyleWang, Lulu, Huiyong Chen, Kai Guo, Fei Shen, and Zhongyi Guo. 2019. "An Inner- and Outer-Fed Dual-Arm Archimedean Spiral Antenna for Generating Multiple Orbital Angular Momentum Modes" Electronics 8, no. 2: 251. https://doi.org/10.3390/electronics8020251
APA StyleWang, L., Chen, H., Guo, K., Shen, F., & Guo, Z. (2019). An Inner- and Outer-Fed Dual-Arm Archimedean Spiral Antenna for Generating Multiple Orbital Angular Momentum Modes. Electronics, 8(2), 251. https://doi.org/10.3390/electronics8020251






