An Effective FPGA Solver on Probability Distribution and Preprocessing

Abstract

The Boolean satisfiability (SAT) problem is the key problem in computer theory and application. A novel algorithm is introduced to implement a SLS hardware solver called probSAT+. The algorithm has no complex heuristic, and it only depends on the concepts of preprocessing technology, probability distribution and centralized search. Through constraining the initial assignments of the variables, the number of flipped variables was reduced while the solver finding a solution. Moreover, the algorithm no longer adopts some non-continuous if-then-else decisions, but depends on a single continuous function f(x,v). The flipping probability is not obtained by complex calculations, instead being selected by looking up tables, which effectively improves the performance of the solver. As far as we know, the probability distribution selection strategy descripted by hardware description language is firstly adopted by hardware SAT solver, which can be easily transplanted to any programmable logic device. The experimental results show that the probSAT+ solver is generally lower than the advanced software solver in the number of flips (up to 9.8 $\times {10}^6$), and the speedup is approximately 2.6 times with single thread, which shows that the probSAT+ has better results with fewer variables flipping times when a solution can be found. In addition, the success ratio of the solver in finding a solution of the problem in a suitable time is 100%.

1. Introduction

As the first non-deterministic polynomial complete problem, the Boolean satisfiability (SAT) problem is the key problem in computer theory and application. Many real-world problems, arising in hardware design, computer vision, artificial intelligence, electronic design automation can be formulated as constraint satisfaction problems, which can be translated into Boolean formulas in conjunctive normal form (CNF). The classical solution for SAT is to implicitly enumerate the variables of the given formula. In the worst case, this method requires $O\left(2^n\right)$ time, where n is the number of variables in the given formula. Therefore how to accelerate the solution process of SAT solvers has important realistic significance.

The importance of the problem coupled with the large amount of computation involved motivated many attempts at hardware acceleration of SAT. The performance improvement of the SAT solver based on hardware is still limited by two factors [1]. Firstly, the simple algorithm cannot solve the large SAT problem instances in real-world. However, the complex algorithm is difficult to implement the control logic and memory access sequence by hardware; secondly, the industrial large-scale SAT problem instances generally have millions of variables, and ten millions of clauses. Therefore the storage of these variables and clauses has become a resource-intensive bottleneck in the hardware SAT solvers.

The problem of solving the satisfiability by FPGA has been addressed rather frequently in the last few years [2,3,4,5,6,7,8,9], due to FPGA’s increasing design capacity, high performance, massive flexibility and parallelism. Implementations based on reconfigurable hardware enable the primary operations of the respective algorithms to be executed in parallel. Consequently, the effect of exponential growth in the computation time can be delayed, thus allowing larger size instances of SAT to be solved. Besides, finding an efficient way to solve the SAT problem with the aid of reconfigurable hardware may help to accelerate the solution of other combinatorial optimization problems. Safar et al. [2] introduced a five-stage pipelined SAT complete solver by moving decision making and conflict analysis into hardware to eliminate the communication latency between a software host and the hardware accelerator. Kanazawa et al. [3,4] described an FPGA solver for large 3-SAT problems. By using off-chip memory banks, the solver can solve larger problems. References [5,6] proposed a new heuristic for SAT-encoded formal verification problems in which the functional dependencies among the clauses which are analyzed and utilized by flipping the literals that correspond to the output signals of the gates preferentially. They introduced a variable-way associative cache memory by using on-chip block RAMs to hide the DRAM access delay in their following research, and the solver has achieved higher performance than previous works. A DRAM-based Boolean constraint propagation (BCP) engine [8] was built in to address the limited capacity of faster memory and the solver is based on the conflict driven clause learning (CDCL) framework, but cannot adapt an existing SAT solver. Thong et al. [9] proposed a hardware architecture to accelerate BCP. In the solver, the incoming variable being assigned is a hardware address that points directly to what the algorithm need to access within the clause that contains this variable, so the access is more direct and faster, and they do not store any clause translation table in hardware, the memory layout is more compact, thus enabling larger SAT problem sizes theoretically. In reference [10], a hardware implementation method of probSAT algorithm based on a new high-level language logic synthesis technology named High-Level Synthesis is proposed, which can be transplanted quickly from the C language source code of the software solver. This method has high performance in solving the difficult small-scale problems.

In reference [11], an FPGA SAT solver based on enhanced constraint is proposed, this paper is an extension of our previous research, and still focus on the application of random local search algorithm in solving SAT problem. A novel SAT solver called probSAT+ is implemented. But unlike the former, the algorithm no longer adopts some non-continuous if-then-else decisions in terms of the selection strategy for flipping variables, but depends on a single continuous probability distribution function. As far as we know, this is the first solver based on probability distribution strategy using hardware description language, which can be easily transplanted to any programmable logic device. Besides, the algorithm has some constraint on the initial assignment of variables, which includes two aspects. On one hand, the algorithm use pure literal rules to determine the initial assignments of some particular variables; the other hand, the number of satisfied clauses is increased as far as possible, and the occurrence of local optimum is reduced by calculating the initial probability of the remaining variables as positive. In addition, a preprocessor using C language is designed in order to reduce the time cost and the computational burden of hardware. For a random 3-SAT instance, the probability distribution of each variable will be downloaded to the RAM of FPGA in the form of data table, which greatly reduces the complexity of the algorithm and is more convenient for hardware implementation. The testing, preprocessing program and software solver were run on Intel(R) Core(TM) i5 64-bit 2.3 GHz CPU with 4.0 GB main memory, the system is Linux Ubuntu-14.04. The experimental results show that the probSAT+ solver has better performance than the advanced software solver on solving efficiency and success ratio.

2. Preliminaries

The construction rule of the CNF formula is that the literal represents either a Boolean variable or its negation, and a clause is the disjunction of a number of literals, and the conjunction of a number of clauses constitutes a Boolean formula in CNF format.

Definition 1.

Given a CNF formula F, and a set of variables V, if there is an assignment of binary values to the variables V which makes the formula true, F is satisfied; Otherwise, F is not satisfied.

Definition 2.

Given a SAT instance represented by the CNF formula F, it is called a k-SAT formula if each clause in F contains at most k literals.

It has been proved that the k-SAT problem can be transformed into 3-SAT problem in polynomial time by the introduction of new variables [1]. Therefore the research of 3-SAT problem has great significance to solve the general SAT problem.

Definition 3.

For a variable p in a clause of the CNF formula, a break-value is defined as the total number of clauses that are true in the current assignment, but become false if the value of p is flipped.

There have been many different contributions to research on solving SAT problems. These algorithms are basically divided into two categories: complete algorithm and incomplete algorithm. A complete algorithm can either find a solution that satisfies the formula or infer that the instance is not satisfied. The advantage of this method is that it can definitely judge the satisfiability of the SAT problem by either giving a satisfiable assignment or a complete proof in the case of no solution. However, with the increasing of scale of the problem, the complexity of the solution space increases exponentially.

Incomplete algorithms to solve the SAT problem are mainly based on local search algorithm [12] and genetic algorithm [13]. In general the incomplete algorithms cannot guarantee to find a solution within a specified step. When a solution is found means the SAT problem is satisfied, but it cannot declare the problem is not satisfied when there is no solution.

In recent years, the complete methods have made great progress in solving many real-world problems including Boolean satisfiability, but they usually cannot scale well owing to the extreme size of the search space. One way to solve the combinatorial explosion problem is to sacrifice completeness, thus some of the best known methods using this incomplete strategy are local search algorithms. In general, the local search strategy starts from an initial solution, which may be randomly or heuristically generated. Then the search moves to a better neighbor according to the objective function, and terminates if the goal is achieved or no better solution can be found. Local search methods are underlying some of the best performing algorithms for certain types of problem instances, both from an empirical as well as from a theoretical point of view. As compared with the complete algorithm, the incomplete algorithm is generally faster and has more iteration per unit time. For some types of SAT problems, such as 3-SAT, especially the larger 3-SAT, it is more efficient.

3. Outline of probSAT+

Figure 1 illustrates the flow of our SAT solving system. A preprocessor transforms the SAT problem to make it more suitable for the solver without changing the satisfiability using the pure literal rule [14].

The algorithm has involved a lot of improvements based on classical incomplete algorithm in the following three aspects: Firstly, the initial value of the conditional variable is determined by the pure literal rules in the preprocessing stage; Secondly, the number of satisfied clauses is increased as far as possible by constraining the initial assignment of variables, so as to reduce the occurrence of falling into local optimal conditions and speed up the convergence of the algorithm. Finally, a probability mapping data structure suitable for hardware platform is proposed. The pseudo code of the algorithm is shown in Algorithm 1.

Algorithm 1. probSAT+.

Require: a CNF Formula F; Maxtries; Maxflips;

Ensure: Satisfying assignments (if found)

probSAT+(F, Maxtries, Maxflips)

{

$/\ast Preprocessing\ast /$

for (tries = 1 to Maxtries) {

determine the values of variables that conform to pure literal rules;

calculate the initial probability of the remaining variables as positive $P_x$;

V ← generate a set of random assignments according to $P_x$;

C ← search for unsatisfied clauses at the current initial assignments;

$/\ast MainProgram\ast /$

for (flips = 1 to Maxflips) {

if (C = $\varphi$) then

return V;

$C_u$ ← an unsatisfied clause selected at random;

for (x in $C_u$) {

calculate the break-value;

sort the break-value;

search for the flipping probability $Q_x$ of variables;

}

if ($break-valu{e}_{max}$ < $\theta$)

p ← flip a variable according to $Q_x$;

else

p ← select the variable with $break-valu{e}_{min}$;

V ← V with p flipped;

C ← update the set of unsatisfied clauses at the current value;

}

}

return “no satisfying assignment found”;

}

The flipping probability is calculated by polynomial distribution function [15] and $Q_x$ is calculated by Equation (1). The constant $\theta$ is introduced in the algorithm. The value of $\theta$ will directly affect the selection of the variables and the complexity of the algorithm. If the value is too small, the algorithm will preferentially select the variable with the minimum $break-value$. In other words, the search process will become more greedy, and the algorithm will easily fall into the local optimum and cannot find the solution of the instance. On the other hand, if the value is too large, most of the flipping variables will be calculated by probability distribution function, and then the complexity of the algorithm is increased substantially. For the hardware solver, the higher the complexity, the more time and area overhead it takes to implement the algorithm. The value of constant $\theta$ is described in detail in the next section. In the algorithm, the function $f(x,v)$ is a polynomial distribution function, in which $c_b$ is 2, and $\epsilon$ is 1 [15].

$$\left\{\begin{array}{c}{Q}_x={\displaystyle \frac{f(x,v)}{\begin{array}{c}{\sum }_{Z\in C_u}f(Z,v)\end{array}}}\hfill \\ f(x,v)={(\epsilon +break(x,v))}^{-c_b}\hfill \end{array}\right.$$

(1)

In the formula, Z is a variable contained in the unsatisfiable clause $C_u$. For 3-SAT problem instances, the final expression of $Q_x$ is shown in Equation (2).

$$\begin{array}{c}{Q}_x={\displaystyle \frac{{(1+break(x,v))}^{-2}}{{\displaystyle \sum _{j=1,Z_j\in C_u}^3}{(1+break(Z_j,v))}^{-2}}}\hfill \end{array}$$

(2)

The probSAT+ solver mainly consists of software preprocessing and hardware solving. The software preprocessor optimizes SAT problem, and then initializes assignment of variables and extracts address and clause information from the formula in DIMACS format. The hardware solving part of probSAT+ is implemented in the FPGA.

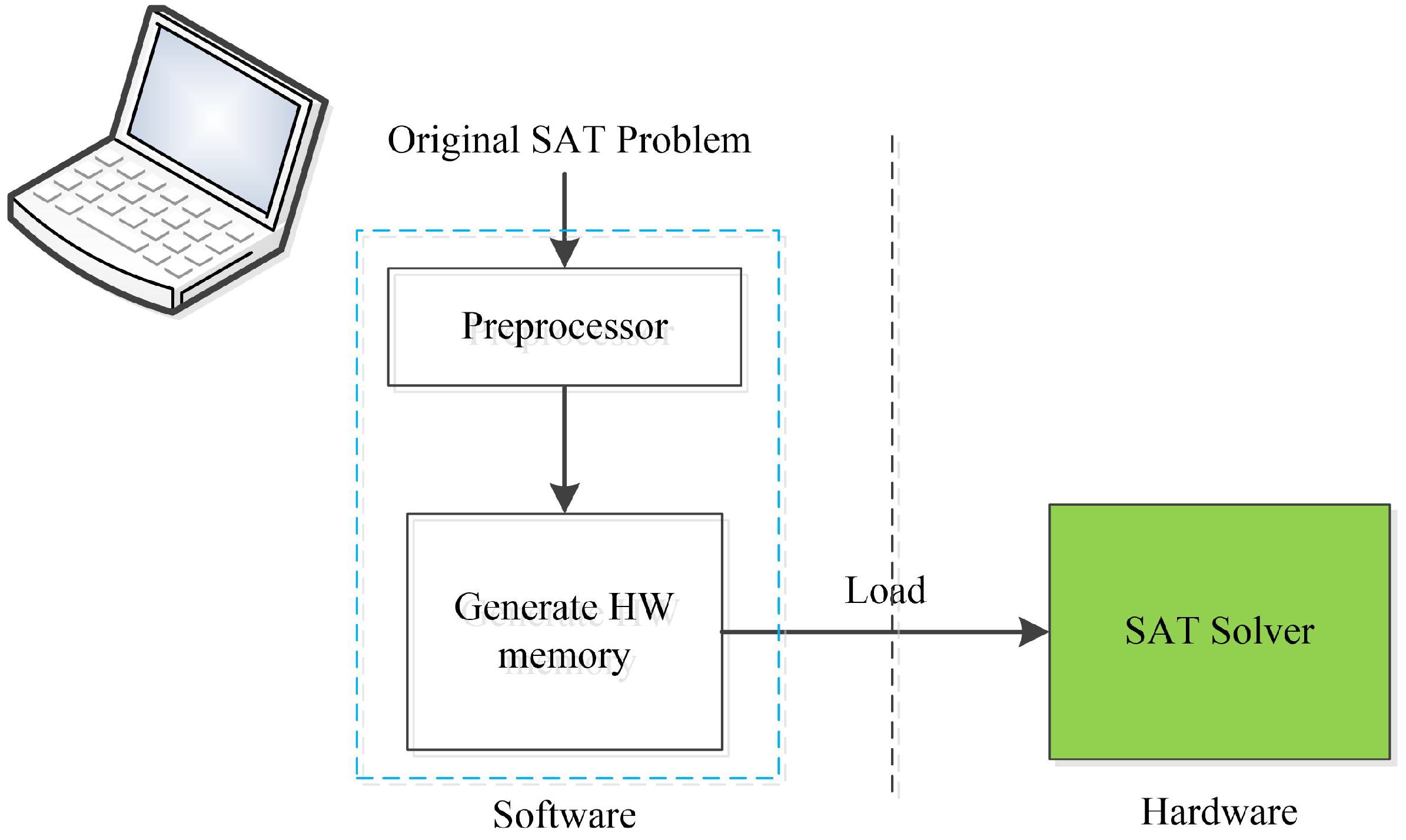
3.1. Software Preprocessing

As the complexity of SAT problem increases in practical applications, the scale of the problem increases rapidly at the same time. For example, the number of variables can reach as many as tens of millions. In random local search algorithms and other incomplete algorithms for solving SAT problem, most of them are by randomly generating a set of assignment as the starting point of search [16]. Reasonable variable assignment can greatly reduce the complexity of the problem and improve the efficiency of the solution. The SAT problem is similar to the mathematical constraint problem, so the relationship between the variables and the solution space of the SAT problem could be analyzed firstly, then some variables are assigned, and the process of solution is speeded up.

Definition 4.

Pure literal is defined as a literal is either a variable $x_i$ (i.e., a positive literal) or its complement $\neg x_i$ (i.e., a negative literal) in a CNF formula [14].

Therefore, the initial assignment of the variable $x_i$ in a formula F can be obtained by Equation (3).

$$x_i=\left\{\begin{array}{cc}1,\hfill & \left(x_i\mathrm{appears} \mathrm{only} \mathrm{in} \mathrm{positive} \mathrm{literal}\right)\hfill \\ 0,\hfill & \left(x_i\mathrm{appears} \mathrm{only} \mathrm{in} \mathrm{negative} \mathrm{literal}\right)\hfill \\ Uncertain,\hfill & (\mathrm{assign} 1 \mathrm{according} \mathrm{to}{P}_i,\mathrm{assign} 0 \mathrm{according} \mathrm{to}1-P_i)\hfill \end{array}\right.$$

(3)

In the expression, $P_i$ is the probability that the initial assignment of the variable is 1, which is calculated in Equation (4) [11].

$$p_i=\left\{\begin{array}{cc}{\displaystyle \frac{m_i\times \mathsf{\Delta }}{(m_i+n_i)}}+r_1,\hfill & (m_i>n_i,\frac{(1-\mathsf{\Delta })}{2}\le r_1<1-\mathsf{\Delta })\hfill \\ {\displaystyle \frac{m_i\times \mathsf{\Delta }}{(m_i+n_i)}}+r_2,\hfill & (m_i<n_i,0<r_2\le \frac{(1-\mathsf{\Delta })}{2})\hfill \\ 0.5,\hfill & (m_i=n_i)\hfill \end{array}\right.$$

(4)

In the formula, $m_i$ and $n_i$ are defined as the number of clauses with positive literal and negative literal for the variable i respectively. The constant $\mathsf{\Delta }$ is 0.5 to 1, in the algorithm, the value of $\mathsf{\Delta }$ is 0.9. $r_1$ and $r_2$ are random numbers between the ranges shown in the formula. When the number of clauses in which the variable i is positive is more than the number of negative clauses, the probability whose initial assignment of positive is greater than 0.5; Otherwise, the probability is less than 0.5.

The parameter $\mathsf{\Delta }$ has a great influence on the choice of variables and the complexity of the algorithm, so it is very important to determine the value of $\mathsf{\Delta }$. First, the break-value of the variable will be analyzed. For random k-SAT problems, the range of $break-value$ would be determined by calculating the number of literal occurrences in the problem.

Given a k-SAT formula with m variables and n clauses, $r={\displaystyle \frac{n}{m}}$ is defined as the ratio r of the number of clauses and variables for that instance. At this point, the number of literals is $k·n$, and $2·m$ literals can be generated for m variables, so the average occurrence of each literal in k-SAT is shown in Equation (5).

$$\begin{array}{c}{\displaystyle \frac{k·n}{2·m}}={\displaystyle \frac{k·r·m}{2·m}}={\displaystyle \frac{k·r}{2}}\hfill \end{array}$$

(5)

Numerous studies have shown that the satisfiability of the k-SAT formula is related to clauses-to-variables ratio [17,18,19,20]. It is pointed out in reference [19] that the difficulty and satisfiability of random k-SAT problem is closely related to the ratio. For a random 3-SAT problem, when the ratio r is less than a constant $r_k$, the satisfying probability of the formula approximates 1; When the ratio r is more than $r_k$, the unsatisfying probability of the formula is close to 1. The constant $r_k$ is called threshold. This phenomenon is described in detail and the value is accurately calculated in reference [20]. The results are shown in

Table 1. Threshold values for random k-SAT.

k	3	4	5	6	7
$r_k$	4.267	9.931	21.117	43.37	87.79

.

Therefore, for the 3-SAT problem, the maximum average value of $break-value$ for variables is $brea{k}_{max}={\displaystyle \frac{3\times 4.267}{2}}=6.04\approx 6$. Considering the worst case, the average maximum value of $break-value$ for random 3-SAT problem is six. In other words, the flipping variable can result in an average of six satisfied clauses becoming unsatisfied. According to Equation (2), when three variables have the same $break-value$, each variable has the same flipping probability. Similarly, for different permutations of the same set of $break-value$, the flipping probability of variable with the same $break-value$ is fixed. Based on the two principles, 78 combinations can be produced for random 3-SAT problems with average maximum $break-value$ of six. The probability distribution corresponding to each combination is calculated in advance.

From the result of probability distribution, it is not difficult to find that the higher the $break-value$ is, the lower the probability is. It is more obvious that when the distribution of three $break-value$ is imbalance, the variable with smaller $break-value$ is more easily flipped in order to make the algorithm in a more greedy way to search. We designed a test program with C language, and randomly selected 100 groups of 3-SAT instances with different scale from the standard SATLIB Benchmark Problems library for testing.

Figure 2 shows 16 groups of test results with the highest frequency. The total frequency of occurrence is as high as 85%. The x axis represents three break-values when three variables are flipped (the order is not taken into account), and the y axis denotes the frequency. It is clear that the $break-value$ is less than 4 (more than 80%) in most cases, while the probability of $break-value$ greater than 5 is relatively small (only less than 1%). Therefore, the parameter $\theta$ in the algorithm is set to 7. When the maximum value of the three break-values is less than 7, the algorithm selects the variable according to the probability distribution function. Otherwise, it selects the variable with the minimum $break-value$.

3.2. Hardware Architecture

The hardware architecture of probSAT+ is shown in Figure 3. The address and clause translation module mainly stores the address and clause information after the software preprocessing. During the execution of the algorithm, the module looks up the corresponding clause information according to the variable then outputs it. Clause evaluator module consists of on-chip memory and some simple logic. The initial values of $Maxtries$ group variables are downloaded to the memory of FPGA in order to realize $Maxtries$ search.

The address translation and clause output module store the address and clause information after software preprocessing. This module needs to search the corresponding clause information according to the variable, and output it. In the following discussion, $N_{c_i}$ is the number of clauses which include a specified literal i, $N_v$ is the number of variables. Therefore, the average of $N_{c_i}$ can be expressed as $N_{c_i}={\displaystyle \frac{3\times N_c}{2\times N_v}}$. The maximum value of $N_{c_i}$ is not determined by the size of formula, instead by the ratio of $N_c$ and $N_v$ [5].

The maximum value is less than 20 in many benchmark problems. In general for electronic design automation field SAT solvers, the fan-out of most signals is also less than 20 [5]. The parameter $N_{c_i}$ is 30 in this paper to improve the ability to solve large scale problems. Each clause in the table contains two literals, and the third literal is the address. The clauses are obtained by adding the third literal to them. A literal is represented as a 16-bits word, in which 1 bit for negation or not, and 15 bits for the variable number, the maximum value of $N_v$ is 32 k (2${}^{15}$ = 32 k). The maximum value of $N_c$ depends on how the clause data can be packed into clause table using address translation table, and is up to 128 k in theory because of preprocessing on the host computer. The address translation table includes address part and mask part, and each bit in the address part corresponding to $N_{c_i}$ clauses. The mask part is used to select the abscissa of the clauses table. The address translation table is accessed through the variable number and its negation bit, and the size is selected from 1 to $2\times Nv$. In this way, the clauses containing literal i can be found quickly.

For example, based on the DIMACS data format, the following data shown in Figure 4a corresponds to the CNF formula according to DIMACS data format. The contents of the address translation and clause table are shown in Figure 4b.

Figure 5 shows the internal structure of a clause evaluator II, which consists of three BRAM and some combinational logic. $Maxtries$ sets of variable initial values are downloaded to the BRAM successively. When the enable signal is high, the variable in the BRAM is searched according to the clauses information obtained by the output module of the clauses, and then the algorithm evaluates the clause. The values of the corresponding variable in all clause evaluators are updated according to the address of the actually flipped variable. Clause evaluator in Figure 3 are almost the same as the clause evaluator II, but they have two variable tables.

The $break-values$ of each variable derived from the clause evaluator module are counted and sorted by the $break-value$ counter. If the clauses are not satisfied, the results are temporarily stored in the buffer. The clause information in the corresponding buffer is output to the FIFO tree and the contents of the buffer are cleared according to the final flipped variable. The FIFO tree is composed of multilevel FIFO, and the time cost of data transmission can be effectively shortened. The architecture is shown in Figure 6. Random number generator module generates an address r$(r\le m)$ according to the number of unsatisfied clauses (m). It is discarded and a new clause is output from the last level of FIFO instead if the clause is satisfiable. When the unsatisfiable clause buffer and the FIFO tree are empty, the formula satisfies and the search stops.

The whole solving steps of probSAT+ is shown as follows.

(1) For a given CNF formula in the DIMACS format, the host optimizes the problem and extracts the data information.

(1.1) The algorithm simplifies the formula by means of true literal rule.

(1.2) Calculating the probability $P_i$ of each variable whose initial assignment is positive and generating a set of initial assignments that are downloaded to the RAM before the solution is started. $Maxtries$ sets of initial assignments of the variables are sequentially stored in the on-chip memory.

(1.3) Extracting address and clause information. The address and clause information are downloaded to the RAM of the address translation and the clauses table respectively.

(1.4) Searching unsatisfied clauses according to different initial values. The unsatisfied clauses are transfered into the RAM of the unsatisfied clause buffer.

(2) At the beginning of the solution, the address generation module generates an address randomly to output an unsatisfiable clause from the buffer. This clause may become satisfied due to the flipped of the variable, so it is evaluated by the clause evaluator module2, when it is satisfied, another clause is reselected.

(3) Reading the value of the corresponding variable from the RAM and flipping it temporarily for the three literals in the unsatisfied clause. All clauses including literal $L_1$ will become true, but the clauses that include $\neg L_1$ may change from true to false. The solver searches the clauses including $\neg L_1$. Clause evaluator module chooses the unsatisfied clauses. The break-value counter evaluates the $break-value$ of each variable and sorts it. If the values are in the probabilistic mapping table, the algorithm selects a variable to flip according to the probability. Otherwise, the variable with the minimum $break-value$ is selected.

(4) The unsatisfied clauses caused by variable flipped will be aggregated through multi-level FIFO. The new unsatisfied clauses generated will be stored in the last level FIFO for subsequent processing. The order of data writing to FIFO is at random. At the same time, the solver completes a search, repeat the steps (2)–(4).

(5) In this paper, the parameter $Maxtries$ indicates the number of new search sequence and $Maxflips$ indicates the maximum number of flips of variable values per try. If a set of clauses is finished but no solution was found, the address is incremented by a specified offset to continue the next iteration until it finds a satiable solution or is still no solution after $Maxtries$ times, and the algorithm will stop.

4. Results and Discussion

So far, there is a general lack of theoretical analysis of SAT stochastic local search algorithms, most of the research works are based on experimental statistics and empirical analysis [21]. The performance and improvement of the solver in this paper are also statistically evaluated and empirically analyzed by benchmark calculation.

4.1. Preprocessing Performance

The medium and large scale 3-SAT problems from the 2011 SAT Competition random instances [22] were selected to test the preprocessing performance. The two groups are represented by SC11_M and SC11_L respectively. There are 200 instances in SC11_M, and the clauses-to-variables ratio of these problems is 4.26, which are relatively difficult to solve. We randomly select 100 instances, and denote as MQ1, MQ2,…, MQ10 according to the number of variables in the instance. SC11_L has 100 instances and the clauses-to-variables ratio r is 4.2, from which we randomly select 50 instances, denote as LQ1, LQ2,…, LQ10. The random 3-SAT instances and parameters used in the experiments are shown in the

Table 2. Random-3-SAT instances (SC11).

Problems	${\mathit{N}}_{\mathit{v}}$	${\mathit{N}}_{\mathit{c}}$	Name
MQ1	350	1491	uf350-004, uf350-011, uf350-022, uf350-054, uf350-050, uf350-075, uf350-064, uf350-077, uf350-063, uf350-098
MQ2	400	1704	uf400-084, uf400-002, uf400-037, uf400-064, uf400-053, uf400-021, uf400-001, uf400-025, uf400042-, uf400-089
MQ3	450	1917	uf450-014, uf450-001, uf450-027, uf450-011, uf450-033, uf450-059, uf450-085, uf450-034, uf450-078, uf450-097
MQ4	500	2130	uf500-003, uf500-027, uf500-036, uf500-047, uf500-054, uf500-075, uf500-083, uf500-055, uf500-067, uf500-097
MQ5	550	2343	uf550-005, uf550-011, uf550-30, uf550-045, uf550-069, uf550-052, uf550-088, uf550-090, uf550-080, uf550-094
MQ6	600	2556	uf600-002, uf600-033, uf600-054, uf600-052, uf600-039, uf600-075, uf600-086, uf600-077, uf600-030, uf600-099
MQ7	650	2769	uf650-002, uf650-009, uf650-015, uf650-034, uf650-050, uf650-068, uf650-079, uf650-083, uf650-085, uf650-064
MQ8	700	2982	uf700-003, uf700-026, uf700-021, uf700-036, uf700-043, uf700-074, uf700-051, uf700-015, uf700-009, uf700-096
MQ9	750	3195	uf750-027, uf750-014, uf750-023, uf750-049, uf750-061, uf750-070, uf750-080, uf750-083, uf750-078, uf750-088
MQ10	800	3408	uf800-019, uf800-017, uf800-021, uf800-024, uf800-035, uf800-029, uf800-054, uf800-069, uf800-090, uf800-088
LQ1	2500	10,500	uf2500-004, uf2500-024, uf2500-038, uf2500-066, uf2500-088
LQ2	5000	21,000	uf5000-009, uf5000-025, uf5000-051, uf5000-077, uf5000-090
LQ3	10,000	42,000	uf10000-011, uf10000-031, uf10000-047, uf10000-068, uf10000-085
LQ4	15,000	63,000	uf15000-003, uf15000-026, uf15000-051, uf15000-059, uf15000-091
LQ5	20,000	84,000	uf20000-017, uf20000-029, uf20000-048, uf20000-076, uf20000-097
LQ6	25,000	105,000	uf25000-006, uf25000-018, uf25000-030, uf25000-066, uf25000-092
LQ7	30,000	126,000	uf30000-001, uf30000-028, uf30000-064, uf30000-076, uf30000-100
LQ8	35,000	147,000	uf35000-016, uf35000-022, uf35000-060, uf35000-078, uf35000-093
LQ9	40,000	168,000	uf40000-069, uf40000-003, uf40000-078, uf40000-085, uf40000-098
LQ10	50,000	210,000	uf50000-065, uf50000-015, uf50000-041,uf50000-003, uf50000-094

.

We take into account the randomness of the results, that is, there may be some deviation in the results obtained in different time. Therefore, in order to compare the preprocessing performance more persuasively, each problem is run five times independently, and the results are the average of the five times, and are shown in the Figure 7.

From the Figure 7a,b, it is not difficult to find that by further constraining the variables, the number of unsatisfied clauses assigned to initial value by probability calculation is less than random assignment. From the distribution of the results of each experiment, as shown in Figure 7c, the percentage of optimization of different instance is very uneven when the problem scale is small, the minimum percentage is 5.6%, and the maximum is 33.3%. It is easy to understand. Firstly, to some extent, this assignment algorithm stated above is a random assignment of strong constraints, and this constraint is not so effective when there are few unsatisfied clauses. Secondly, when the instance scale is small, the solution time is very short, and is generally in nanosecond. The runtime could not increase greatly with the small range of unsatisfied clauses. With the increasing of the instance size, the preprocessing technology shows good performance. The optimized percentage can be stabilized at 20% to 30%, in other words, the optimization trend of probability calculation is more obvious. On the other hand, however, with the scale of the SAT problem increasing, the degree of optimization did not continue to grow, and seemed to reach a bottleneck. This shows that the strategy of strengthening constrained assignment can reduce the number of unsatisfied clauses to a certain extent, but the optimization ability is limited. The internal relationship between instance variables and clauses need to be further explored so as to achieve greater optimization. This will be the subject of future research.

4.2. Solver Performance

The performance evaluation results of the solver are based on Xilinx Virtex-6 FPGA (XC6VHX565T). Virtex-6 FPGA is based on the third generation advanced silicon modular block (ASMBL) architecture of Xilinx. The chip has rich logic resources, containing up to 88 K slices and 32 K on-chip RAM, each slice consists of four LUTs and eight flip-flops, which can fully meet the design requirements. The circuit runs at 71.2 MHz, and it occupied 5% of slices and 86% of block RAM/FIFOs. The code of FPGA is designed with verilog hardware description language and developed under ISE design suite version 14.7.

To verify the feasibility and scalability of the solver, different instances were randomly selected from the 2011 SAT Competition Benchmark Problems [22]. According to the scope of this research, we focus on 10 medium scale random instances. We chose to use this benchmark rather than the latest one because it contains more test instances. The probSAT+ is a solver based on incomplete algorithm, all test instances selected are satisfiable. The problem size is randomly ranged from 350 variables, 1491 clauses to 800 variables, and 3408 clauses. In terms of the difficulty of solving these problems, the clauses-to-variables ratios are all around the threshold, and the probability of unsatisfiability and satisfiability is almost equal. Thus it can reflect the superiority and correctness of the algorithm by testing these problems.

In order to compare the performance of the solver more intuitively, two software solvers WalkSAT Version 51 [23] and Sparrow [24] were chosen to compare. The reason for choosing these two software solvers is that the former is the classical SLS solver, WalkSAT has a variety of variable selection heuristics, and the search strategy used in its algorithm is still used in many solvers today. The Sparrow solver won the gold medal of the random group that year. Therefore, these two solvers can well reflect the performance of the SLS solver.

The SAT solution based on probSAT+ is designed to achieve high performance and extensibility, so it will be tested and analyzed from the following two aspects. One aspect is the test and analysis of solving time. The solving time is to establish a basic concept that we expect to obtain the performance of this solver when using existing computing resources to deal with specific scale SAT problems. We consider that these algorithms are incomplete algorithms, in other words, the difficulty of finding a solution for the same SAT instance is unpredictable at different run. In addition, the random number generator is adopted to produce the initial assignments of the variables, the address of unsatisfied clause and the selection of the variable. These parameters play very important role in the efficiency of the solver. It is shown that the speed of solving the same problem varies greatly with different initial assignment and the number of unsatisfied clauses. In order to reduce the interference of these parameters to the solving time, three different sets of unsatisfied clauses are used, and each instance is tested ten times. The final solving time is the average of these ten results. Similarly, the experimental data of Sparrow solver is the average of the results obtained from five random seeds. The results in the table record the average solving time and the number of variable flips in all successful experiments. The experimental data are shown in

Table 3. Performance Comparison (Sparrow vs probSAT+).

Problems	${\mathit{N}}_{\mathit{v}}$	${\mathit{N}}_{\mathit{c}}$	Flips Number		Flips/Sec		Solving Time(s)		Speed Up
			Sparrow	probSAT+	Sparrow	probSAT+	Sparrow	probSAT+
uf350-042	350	1491	64,921	36,441	3,895,275	1,994,933	0.017	0.018	0.91
uf400-084	400	1704	123,446	270,823	3,429,065	6,728,517	0.036	0.040	0.89
uf450-014	450	1917	273,291	110,341	3,693,125	2,691,237	0.074	0.041	1.80
uf500-047	500	2130	42,860	27,513	3,061,425	2,751,300	0.014	0.010	1.40
uf550-038	550	2343	159,125	57,381	3,978,128	1,593,905	0.040	0.036	1.11
uf600-002	600	2556	358,903	169,469	3,450,992	2,689,989	0.104	0.063	1.65
uf650-079	650	2769	949,363	441,472	3,859,197	2,348,253	0.246	0.188	1.31
uf700-009	700	2982	7,673,077	2,393,852	4,379,610	2,358,475	1.752	1.015	1.73
uf750-027	750	3195	19,304,434	9,442,474	3,978,655	2,720,390	4.852	3.471	1.40
uf800-029	800	3408	246,110	54,290	3,238,287	1,872,070	0.076	0.029	2.62

. $N_v$ and $N_c$ show the number of variables and clauses.

From the table, it is not difficult to find that the probSAT+ solver reduces the solving time in varying degrees compared with the Sparrow software solver for the 10 medium scale problems in most cases. The number of flips per second (flips/s) is a key measure of the SLS solver when comparing the implementation of the algorithm or the performance of two similar algorithms [25]. From the results, the probSAT+ solver is generally lower than the Sparrow solver in the number of flips per second, which shows that the former has better results with fewer variables flipping times when the solution can be found (up to 2.6×). The reason is at the beginning of the search, the number of unsatisfied clauses is reduced in varying degrees by further constraining the value of the variables and probability calculation strategy guides the variable to assign initial values. To a certain extent, this reduces the number of variables that the solver needs to flip when finding a solution. In addition, unlike other solvers, which need to evaluate all variables of unsatisfiable clauses, probSAT+ solvers only need to evaluate the variables of a single unsatisfiable clause to determine whether or not they need to be flipped. In most solving processes, the probSAT+ algorithm no longer uses some non-continuous if-then-else decisions, but depended on a single continuous function f(x,v). In each step every variable has a probability greater zero to be picked for flipping, and this probability is not obtained by complex calculations, but selected by looking up tables. Therefore, the probSAT+ hardware solver shows good performance.

The other aspect is the test and analysis of the success ratio. An efficient solver can not only find the solution of the problem in a reasonable time, but also have a high success ratio. In this test, we used five typical heuristics (best, novelty, novelty+, rnovelty, rnovelty+) to the WalkSAT solver, and the Maxflips is set to 300,000,000. Ten different seeds are randomly entered to Sparrow solver. Each problem is run 10 times and the result is shown in Figure 8.

In the graph, the x axis represents different solvers, the y axis represents the success ratio, and the different color curves are 10 randomly selected SAT problems. It is not difficult to find that, the hardware solver probSAT+ can maintain a 100% success ratio as the WalkSAT-best, and Sparrow software solver, while the success ratio of other four heuristics (noverlty, noverlty+, rnoverlty, rnoverlty+) decreases in varying degrees, especially when the variables are greater than 600, the first three heuristics can hardly find the solution of the problem. The probSAT+ solver has achieved the performance of advanced software solver in solving success ratio.

5. Conclusions and Future Work

In this work, a simple design principle is introduced to implement a SLS hardware solver probSAT+. The algorithm has no complex heuristic and only depends on the concepts of probability distribution and centralized search. As far as we know, this is the first solver based on probability distribution selection strategy using hardware description language, which can be easily transplanted to any programmable logic device.

Different from the traditional random assignment method, the algorithm makes some constraints on the initial assignments of variables, which includes two aspects. On the one hand, the algorithm fully excavates the information of the variables and makes use of pure literal rules to determine the initial assignments of some particular variables, which reduces the effect of the remaining variables flipping on clause satisfiability to some extent; the other hand, the number of satisfied clauses is increased as far as possible, and the occurrence of local optimum is reduced by calculating the initial probability of the remaining variables as positive. Considering that complex exponential or polynomial operations in FPGA are not easy to implement, for a random 3-SAT instance, in order to reduce the time cost brought by the algorithm in calculating the flipping probability, and to reduce the computational burden of hardware in the algorithm search process, the probability distribution of each variable will be downloaded to the RAM of FPGA in the form of data table, which greatly reduces the complexity of the algorithm and is more convenient for hardware implementation.

Through experimental evaluation, probSAT+ achieves advanced performance on randomly 3-SAT problems. The simple structure of probSAT+ solver allows different functions and variable properties to be inserted into the algorithm. And it is easy to integrate with other solvers for parallel solving. In our view, this is a fruitful research direction and needs further analysis. Besides, more advanced technologies such as hybrid memory cubes (HMCs) will be used to increase the scale of problems.